1 Introduction

Graphs are widely used as data representations in various fields, denoted as G(V, E, L) for labeled graphs. Here, 'V' represents the set of vertices, typically interpreted as entities; 'E' denotes the edges, signifying relationships between entities; and 'L' comprises the labels, indicating attributes of entities. Graph data are notably applied in areas like information networks, exemplified by the semantic web [1], where they depict sets of entities and their interconnections. In bioinformatics, for instance, the protein–protein interaction (PPI) network [2] is effectively represented as a graph. Due to its capability to encapsulate complex structures and relationships, graph theory has found increasing application across numerous disciplines. A primary challenge in this realm is identifying a small query graph within a larger target graph or graph database. This task is inherently challenging, given the NP-completeness of subgraph isomorphism, which precludes any algorithm from ensuring a solution in polynomial time. As graph data grow in complexity and size, the development of efficient subgraph matching algorithms becomes increasingly crucial.

Most exact subgraph matching algorithms [3,4,5,6,7,8,9] employ a filtering-verification framework. In the filtering phase, a large portion of impractical matches are eliminated, yielding a more manageable set of candidates. The verification phase then conducts a subgraph isomorphism search on this set to identify exact matches for the query, typically using the Depth-First-Search (DFS) based Ullmann algorithm [10]. The exact subgraph matching problem can be categorized into two types: one involves finding all graphs in a database containing a specific query, and the other aims to locate all subgraphs within a large target graph isomorphic to a given query.

For the first type, graph indexing methods [3,4,5] are commonly used, quickly filtering out unsuitable target graphs, thereby allowing early matching techniques to focus on refining indexing strategies. However, for the second type, traditional index-based approaches become ineffective as they rely on substructures like paths or trees for indexing, leading to exponentially growing index sizes with larger target graphs, rendering them impractical [11]. In scenarios with small target graphs, these methods might directly apply the Ullmann algorithm without optimization in the verification stage. Yet, for larger target graphs, this verification process requires significant enhancements.

Responding to the growing scale of real-world graphs, several algorithms addressing the second type of problem have emerged [6,7,8]. Despite some successes, they still face challenges in terms of efficiency and robustness, as highlighted in [12]. Two main issues are evident:

  1. 1)

    While some filtering methods [6, 7] designed for single large graphs have been introduced, comprehensive performance analyses are lacking. Reports [12] indicate that these methods were less effective than QuickSI [8], which does not include any specific filter for large single graphs. This contrasts with the efficiency of index methods for the first type of problem, suggesting a disparity in filtering strategies for large target graph searches.

  2. 2)

    Improving the Ullmann algorithm necessitates an apt vertex-searching order for the query graph. Existing studies [6,7,8,9] often rely on intuitive justifications for their chosen orders, lacking a theoretical framework or solid rationale. While some algorithms show promising experimental results, the soundness of their reasoning is not always clear. Conflicting results from various algorithms, due to different experimental datasets, make drawing definitive conclusions challenging.

In this paper, our contributions are twofold: 1) We introduce the Multistage Graph Search Model (MGSM), a theoretical model to guide the selection of vertex-searching orders, a previously unaddressed issue, and define the optimal order for the Ullmann search. We reformulate the order selection problem into an optimization challenge. 2) Employing MGSM, we propose a pseudo-tree method to estimate the time cost of a given search order. Building on this, we develop a novel exact matching algorithm named “Tps”. In our experimental evaluation with large target graph and over 600 query graphs, Tps demonstrates enhanced efficiency by outperforming TurboISO in benchmarks. Furthermore, Tps is grounded in a robust theoretical framework.

2 Related work

In the field of subgraph matching, initial studies predominantly addressed problems where the target set consisted of numerous small graphs, emphasizing swift filtering methods based on indexing. Shasha et al.'s GraphGrep [4] employed paths as indexing features but faced limitations as the number of paths increased with larger target graphs. Yan et al.'s gindex [3] improved upon this by using subgraphs as features, focusing on their frequency and discriminative power [21] for more effective indexing.

Subsequently, innovations like TreePi [4] and Tree + delta [5] emerged, striking a balance between path-based and subgraph-based methods by utilizing subtrees as features. These approaches, based on the premise that the pruning power of the subtree is more effective than that of paths yet less costly than full subgraphs, represented a significant advancement in the field [22]. Other noteworthy works include FG-index [5] and gcode [15], introducing innovative verification approaches and no-feature index techniques, respectively [23].

As researchers turned their attention to larger single target graphs, a second problem type emerged [24]. Ullmann's algorithm [10] was pioneering in this area, using a DFS strategy to search large target graphs for a sequence of induced subgraphs. This approach was further refined by GraphQL [6] and SPath [7], which introduced neighbor signatures as effective filters and proposed estimation functions to optimize the vertex-searching order [13].

More recent developments have seen algorithms like QuickSI [8] and TurboISO [9] demonstrate exceptional performance for this second problem type. QuickSI transformed the order selection problem into a minimal spanning tree problem, thus bypassing the need for explicit estimations of search space size [25]. TurboISO introduced an efficient path filter, further avoiding the need for explicit order selection estimations [26].

In contrast, our Multistage Graph Search Model (MGSM) and Tps algorithm present a novel approach to optimizing the vertex-searching order in subgraph matching. Unlike the previous methods which primarily focus on indexing techniques or employ path and subtree features for efficiency, our MGSM approach analyzes the selection of vertex-searching order through a multistage graph representation. This allows for a more nuanced and dynamic optimization of the search order compared to the static approaches of earlier methods [16, 17].

Furthermore, the Tps algorithm, developed based on the theoretical foundations of MGSM, prioritizes finding an optimal vertex-searching order for both filtering and verification steps in subgraph matching. This contrasts with algorithms like QuickSI and TurboISO, which either simplify the order selection problem or avoid explicit estimations altogether. Our approach not only addresses the efficiency of the matching process but also bridges the theoretical gap in order selection strategies, marking a significant advancement in the field [18].

Inexact subgraph matching, another significant area of research [13, 15, 19, 20], employs different similarity measures for matching. Algorithms such as Ness [15], SAGA [19], and SIGMA [20] in this domain have greatly inspired our work, particularly in the development of versatile and adaptable matching strategies.

3 Preliminaries

3.1 Subgraph matching problem

In graph representation, we denote a graph G as G(V, E, L), where V represents the vertex set, E is the edge set, and L is the label set associated with the vertices.

Definition 1. (Graph Isomorphism)

For two graphs G1(V1, E1, L1) and G2(V2, E2, L2), if they are isomorphic, then a bijective function f: V1 → V2 exists such that: 1) for every edge(v1, v2) ∈ E1, a corresponding edge(f (v1), f (v2)) ∈ E2; and 2) for all vertices v, L(v) = L(f (v)). If G1 is subgraph isomorphic to G2, it implies that G2 contains a subgraph G3 isomorphic to G1.

Definition 2. (Exact Subgraph Matching)

Given a query graph Q and a target graph G, the objective of exact subgraph matching is to identify all subgraphs within G that are isomorphic to Q.

The exact subgraph matching problem, known for its NP-completeness, primarily employs a filtering-verification framework. The filtering phase eliminates infeasible matches, leading to a refined candidate set. The subsequent verification phase involves a subgraph isomorphism search on this candidate set to locate all embeddings of Q. Effective filtering techniques for large single target graphs include the neighbor signature filter, pseudo subgraph isomorphism search, and the path filter, as exemplified in TurboISO. The verification phase typically utilizes the Ullmann framework, characterized by a depth-first-search (DFS) process. A key challenge in optimizing this process is determining an effective vertex-search order.

3.2 Ullmann algorithm and vertex-searching order

To contextualize the Ullmann algorithm and vertex-searching order, we introduce:

Definition 3. (Induced Subgraph)

Given a graph Q = (V, E, L). Let V’ be a subset of V, E’ = {(v, u) |all v, u ∈ V’}, L’ is the label set associated with V’. The subgraph qs = (V’, E’, L’) is an induced subgraph of Q.

The Ullmann algorithm serves as a fundamental verification framework for the exact subgraph matching problem. It employs DFS to identify induced subgraphs q1, q2…qi of Q within G. During the DFS, vertices of Q are included in the search according to the vertex-searching order.

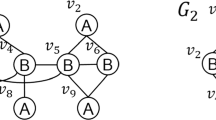
Figure 1 demonstrates the search process following the vertex-searching order of v1-v2-v3-v4. The Ullmann algorithm, using this order, examines a series of induced subgraphs. Considering the varying frequencies of subgraph qi in G, an optimal vertex-searching order can reduce the number of subgraphs requiring inspection during DFS. This, in turn, decreases the number of recursive calls, making the identification of an effective vertex-searching order a crucial factor in enhancing the efficiency of Ullmann-based search algorithms.

To establish an efficient vertex-searching order, algorithms like GraphQL and SPath have developed estimation functions to evaluate proposed orders. QuickSI utilizes the frequency of query edges as weight, determining the vertex-searching order through the Prim algorithm. Conversely, TurboISO sorts the paths of the spanning tree based on the frequency of leaves. The next section will delve into identifying the most effective vertex search order.

4 Multistage-graph search model

In this section, we introduce the Multistage-Graph Search Model (MGSM) to analysis the problem of selecting vertex-searching order.

Fig. 1
figure 1

Example of Ullmann search process

Full size image

Definition 4. (Multistage graph)

A multistage graph M can be represented by a directed graph M (s, t, V, D, W). V is the set of vertices. D is the set of directed edges. W is the set of weights associated with vertices. s is the source vertex, and t is the terminal vertex. Vertices are divided into several stages. Given a directed edge like (u, v), stage(v) = stage(u) + 1.

Definition 5. (MGSM)

Given a query Q = (V1, E1, L1) and a target graph G = (V2, E2, L2). Using a new vertex u to denote an induced subgaph qs of Q, and let U be the set of u for all induced subgraph of Q. Let D = {directed edge (u1, u2)| u1, u2 ∈ U, q(u1) is an induced subgraph of q(u2) that has one more vertex than q(u1)}. Let w(u) =|q(u)|. |q(u)| denotes the frequency, i.e., the number of matches of q(u) on G. W = {w(u) | u ∈ U}. The source vertex u0 denotes the empty set, terminal ut denotes Q itself. Now we have a multistage graph M (u0, ut, U, D, W). To reflect the relationship between M, Q and G, we rewrite it as M (u0, ut, U, D, W | Q, G), and we call M the MGSM of Q and G.

Figure 2 shows an example of induced subgraphs and MGSM. We can see that a vertex-searching order corresponds to a path on the multistage graph. Given an order v1-v2-v3-v4, the sequence of induced subgraphs been tested is q1.1, q2.1, q3.1, q4. So, the corresponding path is u0-1.1–2.1–3.1-ut.

Fig. 2
figure 2

MGSM example

Full size image

Theorem 1

Given query Q, target G and M (u0, ut, U, D, W | Q, G). The best vertex-searching order is the minimum weight path on M, from u0 to ut.

Proof

The weight of vertex on M denotes the frequency of induced subgraph of Q. So, the minimum weight path on M means if the Ullmann algorithm follows this search order, it tests the least induced subgraphs. So, the number of recursions calls of Ullmann algorithm is minimized.

4.1 ES-feature

Based on Theorem 1, the optimization of the vertex-searching order can be reformulated as follows:

Problem 1

Given query graph Q (V1, E1, L1), target graph G (V2, E2, L2) and M (u0, ut, U, D, W | Q, G), find a path p from u0 to ut on M, which minimizes.

$$\sum\limits_{{u}_{i}\in P}W\left({u}_{i}\right)$$

w(u) denotes the weight of u, which is equal to the frequency of induced subgraph represented by u. Obviously, it is extremely hard to solve this problem directly using methods such as dynamic programming, because according to the binominal theory, |U| is exponential based on |V1|, besides, w(u) is usually unknown.

However, if the precise frequencies of certain substructures such as edges or paths are pre-calculated, these could assist in estimating w(u). These pre-counted substructures are referred to as es-features.

For instance, GraphQL and SPath can determine the frequency of each query vertex using neighbor signature filtering, hence their es-feature is the vertex. QuickSI obtains the frequency of each query edge through indexing, hence its es-feature is the edge. TurboISO, through path filtering, can acquire both the frequency of vertices and paths.

It's straightforward to deduce that the greater the number of edges an es-feature encompasses, the more accurate the estimation. Being significantly larger than a vertex or edge, the path as an es-feature is one reason why TurboISO outperforms others. On the contrary, the pseudo subgraph isomorphism test, acting as a global filter, cannot offer large es-features comparable to the path filter. The filtering step, therefore, not only reduces the candidate set but also provides prior information for the optimization of the verification step.

4.2 Estimation problem of induced subgraph

Given a vertex u on M (u0, ut, U, D, W | Q, G), the induced subgraph q(u) usually contains more than two es-features. So, we must consider how to estimate w(u) by frequencies of es-features. According to the estimating approach, recent algorithms can be divided into two groups:

  1. 1)

    The first group includes GraphQL and SPath. They have designed estimation function E(u) to estimate w(u). Since they choose vertex as es-feature, E(u) is proportional to ∏|C(vq)|. C(vq) is the candidate set of query vertex vq. So, the order optimization problem (1) are converted into an approximate form.

Problem 2

Given a query graph Q, a target graph G and M (u0, ut, U, D, W |Q, G), find a u0- ut path p on M, which minimizes.

$$\sum\limits_{u\in P}E\left(u\right)$$

This kind of estimation function has three shortages: (1) It uses vertex as es-feature, whose structural complexity is far less than subgraph. (2) If an induced subgraph qs has more than one es-feature, E(qs) is obviously unrealistic. Forexample, suppose qs can be divided into two segments q1, q2. Even if E(q1) and E(q2) are exactly equal to |q1| and |q2|, E(qs) will be proportional to E(q1) *E(q2), which can hardly reflect the true value of |qs|. (3) The optimization problem deduced from this estimating function cannot be solved in polynomial time.

  1. 2)

    QuickSI and TurboISO belong to the second group, which claims no need to estimate the w(u). But, the second group uses greedy strategy to get vertex-search-order. However, we have found that both have similar approach to estimate w(u) implicitly. They just take the frequency of a most frequent es-feature, such as most frequent edge or path, as the approximate value of w(u). So, the order optimization problem (1) is converted into an approximate form.

Problem 3

Given a query graph Q, a target graph G and M (u0, ut, U, D, W |Q, G), find a u0- ut path p on M, which minimize.

$$\sum\limits_{u\in P}maxF\left(u\right)$$

maxF(u) denotes the largest frequency of es-feature contained in u. The following examples show how the two algorithms, QuickSI and TurboISO, can be derived from similar ways.

Example 1

Consider how to select a spanning tree T on Q and take the edge set of T as es-feature set. It means that given an induced subgraph q(u) and the most frequent edge ef ∈ Edge(q(u)) ∩ Edge(T), we use the frequency |ef| upon target graph to be the value of w(u). Then problem (1) naturally converts into minimal spanning tree problem. So, we get the basic order-selection strategy of QuickSI.

Example 2

Given a spanning tree T on Q, we take the r-l path (Given a spanning tree of a query graph, an r-l path is a path from root to a leaf.) on T as es-feature. It means that we use the most frequent r-l path pf within q(u) to estimate w(u). Then problem (3) can be solved by sorting all r-l paths based on their frequency. Now we get the basic order-selection strategy of TurboISO.

QuickSI and TurboISO use most frequent es-feature to estimate |qs|, and it is true that their estimations may be very accurate. The |E(qs)-|qs|| can be much smaller. However, |E(qs)-|qs|| does not determine whether an estimation is reasonable or not. Imagine that if we multiply E(qs) with a large number such as 210, |E(qs)-|qs|| will increased dramatically. However, it has no influence on the selection of vertex-searching order. When qs contains more than one es-feature, this estimation will overlook the complexity of graph.

For example, as shown in Fig. 3, G1 is a path with frequency of 100. G2 is a tree having two r-l paths each with a frequency of 50 and |u1|= 1. The most frequent path estimation of G1 is 100 and the estimation of G2 is 50. But the real frequency of G2 is 2500 which is much more than G1. To solve this problem, this estimation must choose more complex structure to be es-feature, for example, a tree. However, mining tree will increase the cost of filtering.

Fig. 3
figure 3

Irrationality of most frequent path estimation

Full size image

5 Tps algorithm

In this section, we introduce Tps, a novel subgraph matching algorithm that emphasizes the importance of identifying an optimal vertex-searching order. Drawing from our previous analysis, Tps seeks to address two key questions:

  1. 1)

    Feature Selection for es-features: What attributes should be selected as es-features, and how can we ascertain their frequency? We suggest that TurboISO's approach, which advocates for paths as a suitable choice, provides a solid answer. This concept will be further elaborated in Section 4.1.

  2. 2)

    Frequency Estimation of Induced Subgraphs: How can we estimate the frequency of each induced subgraph of a query based on the selected es-feature? Our approach tackles this in two stages: During the filtering phase, we calculate the approximate frequency of each subtree using the exact frequency of each path, as detailed in Section 4.2. Post-filtering, we estimate the frequencies of certain induced subgraphs based on the exact frequencies of paths and the approximate frequencies of subtrees, discussed in Section 4.3.

5.1 Path-feature filtering

Traditional index-based filtering methods, such as the G-index, become ineffective with large target graphs due to the exponential increase in index size. Recently, non-index filtering approaches, like the pseudo subgraph isomorphism test, have been proposed to reduce the candidate set size. However, these methods often overlook that the filtering step also provides critical information for determining an effective search order in the verification phase.

Additionally, these approaches can be time-consuming, sometimes yielding only a modestly reduced candidate set. For instance, while GraphQL can attain the smallest candidate set in certain scenarios using a pseudo subgraph isomorphism test, its verification phase often takes longer than other algorithms like QuickSI. Furthermore, since the pseudo subgraph isomorphism test primarily yields the exact frequency of query vertices, it falls short in estimating the frequency of induced subgraphs. Its filtering runtime often exceeds that of other methods, as the pseudo subgraph isomorphism test can be more complex than the actual subgraph isomorphism verification process.

Therefore, an effective filtering method must meet three criteria: Firstly, it should significantly reduce the candidate set, thereby narrowing the verification step's search space. Secondly, it should aid in determining frequencies for larger subgraphs, facilitating the development of an efficient vertex-searching order for verification. Lastly, it should be executable within a reasonable timeframe. To achieve these objectives, we have devised the following filtering strategy.

Filtering ruler 1

Given a spanning tree T of query graph Q, we execute depth-first search (DFS) to find all mapping functions f: VQ → VG that satisfies: for each leaf vertex vleaf on T, the path vroot-v1-v2-…vleaf is isomorphic to f(vroot)-f(v1)-f(v2)-…f(vleaf). Then f(v) will be add into v’s candidate set C(v).

During the DFS, we adopt an additional filtering ruler to speed up this searching process and reduce the size of C(v).

Filtering ruler 2

Let NL(v) denotes the label set of v’s neighbors. If u ∈ C(v), v then u must satisfy: label(v) = label(u), degree(v) ≤ degree(u) and NL(v) ⊂ NL(u).

We combine these two rulers as a filtering method to get refined candidate set C(v) for each query vertex, and then store C(v) in a tree structure. Given a query vertex v and its parent vp on T, and a target vertex u ∈ C(vp), we use a node structure cNode(v, u) to store a candidate match set {uv ∈ C(v) ∩ neighbor(u)}. For the target graph G and a spanning tree T shown in Fig. 4, all cNode (v, u) can make up a tree structure cTree shown in Fig. 5. cTree is built along with DFS filtering.

Fig. 4
figure 4

Example about spanning tree and target graph

Full size image
Fig. 5
figure 5

The example of cTree (candidate set)

Full size image

From the common view of filtering method, ruler 2 is a local filter, i.e., it only considers the local information (such as vertex label, degree, neighbor label). And ruler 1 is a global filter, since it takes all the vertices and paths on T into consideration. This combination can effectively reduce the size of candidate set.

Form the view of MGSM, ruler 1 implies that we choose the root-leaf paths on T as es-features. This is because searching for mapping functions which satisfy ruler 1 needs to execute subgraph isomorphism searching for these paths. So, the outputs of this filtering method include not only a refined candidate set cTree, but also the exact frequency of each root-leaf path of T. One of the reasons we consider path as es-feature is because the filtering procedure can be time-efficient.

Theorem 2

Searching for mapping functions satisfy ruler 1 can be done in polynomial time.

Proof

Given a path p, we use Fiso(p) to denote its isomorphism embedding set. For a mapping function fi satisfies ruler 1, ∪ fi(p) is only a subset of Fiso(p). It is already known that subgraph isomorphism search for path query can be done in polynomial time and each embedding path fi(p) is scanned once because fi is not injective. Thus, our filtering step can also be done in polynomial time.

If we take more complex substructures such as subtree or subgraph as es-feature, Theorem 2 does not apply and the filtering will take a long time. It is interesting to know that if fi is changed to be injective, the ruler 1 is equal to searching the exact matches of whole T. Maybe we can use the exact frequencies of paths to estimate the frequency of subtree.

5.2 Pseudo-tree estimation

We now try to guess the approximate frequency of some subtrees of Spanning tree T. The kind of subtree we are interested in is defined as:

Definition 6

(full subtree): Given a tree T and a vertex v on T, the full subtree st(v) is the subtree composed by v and all v’s descendants.

Given a query vertex v and a target graph vertex u, the term ea(v|u) denotes the estimated local frequency of st(v), when v is matched to u. If v is a leaf, ea(v|u) is set to be 1. Otherwise, ea(v|u) is calculated as Eq. (1) and Eq. (2). The term et(v|u) denotes the estimated local frequency of st(v), when v’ parent is matched to u.

$${e}_{a}\left(v\left|u\right.\right)\prod_{i}{e}_{t}\left({v}_{i}\left|u\right.\right),{v}_{i}\epsilon\;child\left(v\right)$$
(1)
$$\begin{array}{cc}{{\text{e}}}_{t}\left({v}_{i}\left|u\right.\right)=\sum_{j}{e}_{a}\left({v}_{i}{\left|u\right.}_{j}\right),& {u}_{j}\in c\;Node\left({v}_{i},u\right)\end{array}$$
(2)

Given a target graph G, a query graph Q and its spanning tree T, we estimate the global frequency, on G, of every T’s full subtree st(v) by.

$$\begin{array}{cc}{E}_{p}\left(st\left(v\right)\right)=\sum\limits_{k}{e}_{a}\left(v\left|{u}_{k}\right.\right),& {u}_{k}\in C\left(v\right)\end{array}$$
(3)

This estimating approach is called pseudo-tree estimation, because of the following Theorem:

Theorem 3

Given a tree t and a graph G, if any two vertices v1 and v2 on t without ancestor–descendant relationship have different labels, Ep(t) is equal to the exact number of t ‘s embedding of G, which have been refined by both of the two Filtering rulers in Section 4.1.

Proof

According to Filtering ruler 1, for any two query vertices v1 and its descendant v2, the path v1-v2 is isomorphic to f(v1)-f(v2). Then for a query vertex v3 that doesn’t have ancestor–descendant relationship and same label with v1, we have f(v1) ≠ f(v3). So, if any two vertices on tree t without ancestor–descendant relationship have different labels, the tree f(t) is isomorphic to t. As a further deduction from Eq. 1, eat(up) equals to the exact number of embedding of st(v) on target graph when f(v) = u. Obviously, if ea(v|u) is exact, Ep(st(v)) must be exact too.

Although pseudo-tree estimation is based on the output of path filtering, it can be performed during path filtering instead of waiting for the filtering step to be finished. The algorithm 1 shows that the DFS procedure combines path filtering with pseudo-tree estimation. Suppose that there are two query vertices, v and v’s child vi, and two target vertices, u = f(v) and u ‘s neighbor uj. When uj is added into cNode (vi, u), et(vi|u) will be updated by Eq. (2) (line 11). When cNode (vi, u) is appended to cTree, Ep(st(vi)) and ea(v|u) will be updated (line 17 and 18). If all neighborhoods of u cannot match vi, then the candidate matches stored in the subtree of cNode (vi, u) are all false matches (line 12). In this case, a function clean will be called to cut the subtree, i.e., delete all the false matches and undo the update of Ep(st(vk)) for each vk (line 13), where vk is a descendant of vi.

Since the pseudo-tree estimation does not add any recursion calls to DFS, the filtering step can still be done in polynomial time.

figure a

Algorithm 1 filtering (query vertex v, target vertex u, cNode(v, u’)).

5.3 Order selection

To find a good vertex-searching order for verification step, we first constrain the order selection within the scope of depth-first-walk order of spanning tree T. Setting this limited scope can help us make reasonable choice, since in this way we can make use of the frequencies of paths and subtrees outputted by filtering step.

By adjusting the visiting order of full subtrees of T, we can have different depth-first-walk orders. As suggested by MGSM, a given searching order corresponds to a certain sequence of induced subgraphs. To estimate the frequencies of these subgraphs, they will be categorized into two groups.

1) The induced subgraph g contains only root-leaf paths but no full subtree. Suppose that the most frequent path is pm (denote its frequency as freq(p)), We estimate the approximate frequency of g as.

$$E\left(g\right)=freq\left({p}_{m}\right)$$
(4)

2) The induced subgraph contains full subtrees. Suppose the most frequent path is pm, and the most frequent (approximately) full subtree is tm. We estimate the approximate frequency of g as.

$$E\left(g\right)=max\left(freq\left({p}_{m}\right),{E}_{p}\left({t}_{m}\right)\right)$$
(5)

Based on pseudo-tree estimation, the optimization problem 1 is converted into the following.

Problem 4

Given a query graph Q, a target graph G, Q’s spanning tree T, find a depth-first-walk order Ov, which minimizes.

$$\begin{array}{cc}cost\left(T, {O}_{v}\right)=\sum_{i}E\left({g}_{i}\right),& i\in \left\{\mathrm{1,2},\dots ,\left|{O}_{v}\right|\right\}\end{array}$$
(6)

where gi is the induced graph composed by first i vertices of Ov.

This problem can be exactly solved by algorithm 2 and 3. First, for T’s root and each of its child vc, adjust the visiting order within st(vc) to get a depth-first-walk order Oc that minimizes E(st(vc), Oc) (algorithm 2 line 2, algorithm 3 line 1). Then numerate all visiting sequence of these full subtrees to find the sequence that minimizes E(T, Ov) (algorithm 3 line 3), so the whole spanning tree is adjusted. At last, the vertex-searching order Ov is achieved by DFW on T (algorithm 2 line 3). But in experiment, we implement an approximate version based on greedy strategy with lower cost: perform DFW on T directly. At each recursion step, choose the unvisited child with largest E(g) to perform the next recursion step. The visiting order Ov is the vertex-searching order we want. This approximate way can usually get the same result as the exact one.

figure b

Algorithm 2 order_selection(T).

figure c

Algorithm 3 Adjust(vertex v).

5.4 Subgraph matching

The verification step is based on Ullmann framework. As shown in algorithm 4, DFS verification on candidate set is executed, and the searching order is the output of our order selection method. The difference between the verification procedure and naive Ullmann algorithm is that during each recursion step, we do not need to test the whole C(v), but the cNode(v, f (parent of v)), a subset of C(v) at the local region around the current matches of v’s parent (algorithm 5, line 12).

Based on these, we proposed a subgraph matching algorithm called Tps. As shown in algorithm 5, Tps includes three step: Step 1, convert query graph Q into spanning tree T (algorithm 5 line 1). Step 2, perform path filtering to achieve refined candidate set cTree and perform pseudo-tree estimation to achieve vertex-searching order Ov (algorithm 5 line 2–5). Step 3, perform Ullmann algorithm based on Ov and find all embedding of Q (algorithm 5 line 6).

figure d

Algorithm 4 verification( query vertex v, candidate set C, vertex-searching order Ov, current match f, match set M).

figure e

Algorithm 5 Tps(query Q, target graph G).

6 Optimization of filtering step

Comparing Ullmann algorithm and algorithm 1, it is easy to see Ullmann algorithm and path filtering have one thing in common: both are based on DFS. So, it is reasonable to assume that a good vertex-searching order can also reduce the number of times for recursive calls of filtering. We have already given the method for optimizing the searching order of Ullmann algorithm, now let’s address the same question for path filtering.

To find a good vertex-searching order for filtering is equal to generate a good spanning tree and determine the visiting order of subtrees. Unlike pseudo-tree estimation, we have little prior information such as frequency of path. So, the main approach is first to index the target vertices with some pruning conditions. Then, by searching on index, we can get the initial candidate set Cinitial(v) for each query vertex v. |Cinitial(v)| will be chosen as es-feature, and we use most frequent es-feature to estimate the frequency of induced subgraph. Then, convert the optimization problem 2 into corresponding form. The spanning tree T will be achieved by solving the optimization problem. At last, perform depth-first walk on T to get the vertex-searching order for filtering step.

6.1 Index

If u is a feasible match of v, it is easy to draw a simple necessary condition: label(v) = label(u), degree(v)≦degree(u). If v and u satisfy this condition, we add u to the initial candidate set Cinitial(v). It is easy to index all target vertices according to their labels and degrees. The space complexity of this index is O(n), which is much more compact than the feature-based indexes.

Figure 6 shows the structure of our three-level index. The third level of index has three fields: vertex label, degree threshold, and amount. The amount stores the total number of vertices who share the same label and whose degrees are less than degree threshold. Given a query vertex v, |Cinitial(v)| is equal to the value of amount in the index entry whose vertex label is label(v) and degree threshold is equal to degree(v).

Fig. 6
figure 6

Three-level index

Full size image

6.2 Spanning tree generation

Choosing |Cinitial(v)| to be es-feature and adopting most frequent feature estimation, we get a new form of problem 2.

Problem 5

Given a query Q, find a spanning tree T and determine its subtree visiting order, minimize:

$$sumV\left(T\right)=\sum_{i}maxV\left(i\right)$$
(7)

maxV(i) is the largest |Cinitial(v)| of the first i vertices during the depth-first walk. In fact, to find such T exactly is very costly. We propose an approximate solution: if we have already get T, it is easy to adjust the visiting order of the subtrees of T in order to minimize sumV(T).

As shown in algorithm 6, we firstly find a minimal spanning tree by using Prim algorithm (algorithm 6 line 1). Then for each root’s children vc, adjust the visiting order within full subtrees st(vc) recursively to minimize sumV(st(vc)) (algorithm 7 line 1). After that, enumerate all the permutation of the subtrees to get the best subtree-visiting order which minimizes sumV(T) (algorithm 7 line 3). At last, perform DFW on T to get the vertex-searching order Of for filtering. Algorithm 7 is very similar with algorithm 4 (adjust function of pseudo-tree estimation), the only difference is that the optimization target is replaced by sumV(T) since we adopt a different estimation function.

figure f

Algorithm 6 Spanning_tree_generation(query Q).

figure g

Algorithm 7 Adjust(vertex v).

7 Experiments

In this section, we present experimental results obtained from a large synthetic graph to demonstrate the effectiveness of the Tps algorithm. For comparative analysis, we also include results from TurboISO in our tests. Note that the "combine and permute" strategy typically employed in TurboISO is removed for three primary reasons: 1) This strategy shows significant benefits mainly for specific types of query graphs, such as clique queries, which do not represent our general graph queries. 2) In scenarios where this strategy is effective, Tps can be adapted to function similarly to TurboISO, thus not markedly affecting the comparative outcomes. 3) Our research primarily focuses on optimizing vertex-searching order, a factor more influential to query algorithm performance than other optimization methods. Discussions on alternative optimization approaches are reserved for future studies.

7.1 Comparison for filtering step

Our target graph encompasses 3,000 vertices and 40,000 edges, generated using the method adopted by GraphQL [14]. This involves creating 'n' vertices and 'm' edges with randomly selected end vertices, with each vertex assigned a label. To ensure fairness in comparison, every query was designed to have as many embeddings as possible, with the label set comprising 40 distinct labels. The query set was generated following the procedure proposed by [6]. We began with a small 5-edge graph as the seed and randomly added edges, resulting in a 6-edge query set with each query having over 50 matches. We continued this process up to 11-edge queries, resulting in a set of 643 queries.

7.2 Comparison for filtering step

Figure 7 and 8 illustrate the number of recursions calls and the running time for the filtering step, respectively. Although both Tps and TurboISO implement path filtering, Tps optimizes the vertex-searching order within this process as outlined in Section 5. In contrast, TurboISO randomly selects the spanning tree and its corresponding order. Figure 7 shows that Tps consistently requires fewer recursion calls than TurboISO, indicating the influence of optimized vertex-searching order in filtering, albeit less pronounced than in the verification phase. This is partly due to limitations in estimating the most frequent es-feature, especially when the es-feature is overly simplistic (e.g., a vertex). Figure 8 reveals that the filtering running times of both algorithms are similar, attributable to the marginal improvement in vertex-searching order and the additional time incurred by Tps for pseudo-tree estimation during path filtering.

Fig. 7
figure 7

Recursion calls for filtering step

Full size image
Fig. 8
figure 8

Running time for filtering step

Full size image

7.3 Comparison for verification step

Our comparative analysis of the subgraph isomorphism verification step for Tps and TurboISO focused on two aspects: query graph size and frequency. Figure 9 and 10 show the average number of recursions calls and running times for verification, respectively. The performance disparity between the two algorithms is minimal for queries with less than 7 edges. However, as the query size increases, the difference becomes more significant. For queries exceeding 10 edges, Tps's recursion calls are only about one-third of those in TurboISO, demonstrating the effectiveness of pseudo-tree estimation over the most frequent es-feature. Similarly, Tps's average running time outperforms TurboISO by up to four times.

Fig. 9
figure 9

Running time for verification step (view of query size)

Full size image
Fig. 10
figure 10

Recursion calls for verification step (view of query size)

Full size image

Figures 11, 12, 13 and 14 present the results segmented by query frequency. Queries with over 1,000 matches were classified into the high-hit group, comprising 335 queries, and further divided into four subsets with step sizes of 2,000. The remaining queries fell into the low-hit group, divided into five subsets with 200 step sizes. For queries with frequencies below 800, Tps's average running time closely matches that of TurboISO, yet with significantly fewer recursion calls. The performance gap widens with increasing query frequency. Notably, for frequencies above 7,000, Tps outperforms TurboISO by nearly a factor of 5.

Fig. 11
figure 11

Running time for verification step (low hit)

Full size image
Fig. 12
figure 12

Recursion calls for verification step (low hit)

Full size image
Fig. 13
figure 13

Running time for verification step (high hit)

Full size image
Fig. 14
figure 14

Recursion calls for verification step (high hit)

Full size image

8 Conclusions

In this study, we present the Multistage Graph Search Model (MGSM), a novel theoretical framework for analyzing vertex-search order selection in graph matching. Our findings reveal that the optimal search order aligns with the minimum weight path in a multistage graph. Leveraging this insight, we developed Tps, an innovative matching algorithm that effectively optimizes search orders for both filtering and verification phases. A key aspect of our approach is the introduction of the pseudo-tree estimation method which improves the order selection process. The primary contributions of this work include the development of the Tps algorithm and the establishment of a theoretical foundation for order selection in graph matching.

Looking forward, our research aims to further refine these findings. We plan to construct a more comprehensive query set for balanced comparative analysis. Additionally, we intend to conduct extensive comparisons with existing algorithms, not only to assess overall performance but also to evaluate their order selection methodologies and estimation techniques. We hope future work will advance our understanding of graph matching algorithms and their practical applications.