1 Introduction

The shape registration process is a fundamental computer vision task with broad applications in many fields, including robot navigation [82], medical image matching [31], face recognition [22, 81], Remote Sensing [85], large-scale 3D reconstruction and object tracking [41, 95]. Image registration is the alignment process of two or more images of the same object captured at different times, from different perspectives, or by different imaging machines. As input for the alignment, a reference image (fixed image) and another one named the target used for the transformation estimation. Mathematically, the shape registration is to determine the optimal spatial geometric transformations that yield the best alignment between these two inputs.

Several registration algorithms were operated to determine the Euclidean transformation, also known as E(2), presented by a rotation followed by a translation. However, to reconstruct a three-dimensional object from two of its projections, the transformation assembling them is frequently modeled by a planar homography [20]. Unfortunately, planar Equi-projective re-parametrization curves are required for the matching of curves up to a planar homography, which necessitates at least five numerical derivations [80]. This causes approximation errors equal to the value order of the quantities to estimate. For which, replacing the homography with the associated affine transformation is frequently proposed.

Consequently, if the object is planar and sufficiently distant from the camera, the pose can be approximated by a 2D special affine transformation SA(2,R) [11]. In this context, the ACMA (Affine Curve Matching Algorithm) is developed to estimate the special affine transformation to align 2D shapes [19]. To improve the robustness of this method’s numerical approximations, we involve adding the multi-scale notion to the ACM Algorithm. However, we notice that most of the works have chosen the scale number empirically, which can cause information loss at a certain level of smoothing. Furthermore, in [64], we suggest applying the Binary Expectation Maximisation (Binary-EM) [14], which is a statistical method to adjust this choice. However, despite the improvement obtained through this adjustment process, the choice of the number of scales is still vast, and the execution time can still be improved.

This work aims to present a new Affine Multi-Scale Curve Registration (AMSCR) based on an unsupervised Bayesian classification. This method has two input curves (source image, target image) normalized sequentially with affine arc-length parametrization and smoothed. Then, we use the K-means and Elbow method to automate choosing the optimal class number. After that, we apply Multiclass-EM as a robust probability density estimator to find the best scales. Finally, the alignment process is still done by the ACM Algorithm. The AMSCR based on an unsupervised Bayesian classification enhances the registration process’s complexity and performance.

The rest of the paper is structured as follows: Section 2 introduces the related work to our approach. Then, we recall the affine curve matching algorithm representing the affine arc length reparametrization and the pseudo-inverse matrix calculation in Section 3. Section 4 presents the Optimized Affine Multi-Scale Curve Registration (AMSCR) based on unsupervised Bayesian classification. In Section 6, we evaluate the accuracy of the proposed approaches in the task of shape retrieval using MPEG-7, MCD, Kimia-99, Kimia216, ETH-80, and the Swedish leaf database. Finally, the conclusion is presented in the end section.

2 Related work

Before delving into the specific details of our approach to shape registration, we will take a quick look at what’s already out there. Shape matching is a topic that has received considerable attention in the scientific community. Indeed, there are numerous approaches related to Euclidean transformations. For example, in [27], the researchers suggest a new technique for rigid motion estimation based on Nyquist–Shannon theorem and B-spline approximation. In [35], they use the alignment criterion, Mutual Information (MI), to obtain the optimal transformation parameters, which defines a theoretical measure of the statistical dependencies between inputs. Another method for shape registration is named shape context invented by Belongie et al. [4]. The authors in [45] introduce an inner-distance shape context (IDSC) which is the shortest path between two feature points. In addition, Kang et al. [37] present a global registration technique based on a graph for constructing a 2D mosaic from a collection of images. The graph represents temporal and spatial connectivity and demonstrates that the constructed graph can obtain the global registration by searching for an optimal path. [59] propose an approach based on Dynamic Programming (DP) for motion estimation where this method handles occluded, noisy, and distorted shapes. Additionally, in [66], the Analytical Fourier-Mellin Transform (AFMT) is adopted to define a complete family of invariant descriptors under any planar similarity. The researchers in [33] combine multiscale description and distance metrics in order to develop global descriptors MDM (multiscale distance matrix). This technique helps to obtain high efficiency and effectiveness in plant leaf retrieval. Shu et al. [69] suggested the multi-scale contour flexibility shape signature, which is a shape descriptor. It represents, however, the deformation characteristics of the 2D shape profile. Moreover, [60] introduce a non-rigid registration method in which motion estimation is cast into a feature matching problem using Graph Wavelets within the Log-Demons framework. In [91] present a new descriptor for non-rigid 2D shape matching based on Triangular Centroid Distances (TCDs). This method treats the occluded shape matching issue. Yang et al. [89] invent an approach named the invariant multi-scale descriptor for shape alignment. The DIR (distance interior ratio) is presented in [38] as a shape signature which is the intersection of line segments with the curve and a histogram alignment method. Yang and Yu [86] develop for shape identification a new method named multiscale Fourier descriptor based on triangular features. Benkhlifa et al. [5] introduce a new method called Generalized Curvature Scale Space (GCSS) to improve the almost complete property. In [1] Adamek et al. present a multi-scale convexity and concavity method for shape matching. A two-dimensional matrix represents the contour convexities and concavities at different scale levels. Wang and Gao [78] develop a method named Hierarchical String Cuts (HSCs) to satisfy the curve matching process. In [96] they build a descriptor named a weighted Fourier and wavelet-like descriptor based on inner distance shape context (IDSC-wFW) for shape matching. They followed these steps to implement the previously mentioned descriptor; the first step was rewriting the shape histograms of IDSC descriptors, changing the histogram of a point to the histogram of a field, and setting the field’s histogram as a one-dimensional signal. Then transform this one-dimensional signal using a Fourier transform and a Haar wavelet. Finally, the results of the two transforms are linearly combined to form a new descriptor. Furthermore, in [97] the researchers present a new MultiScale Fourier Descriptor using Group Features (MSFDGF). Then, they use this descriptor and Shape Histograms to construct a global descriptor MSFDGF-SH. These prior approaches are only applicable to shapes up to a Euclidean or similarity transform. In practice, however, a camera captures the contour in an arbitrary orientation that certain geometric transformations may have distorted. As mentioned in [44], the affine transformation can simplify and approximate this distortion. Consequently, several methods for constructing representations of invariant objects under affine transformation have been developed. In [83] introduce a hybrid shape descriptor combining three invariants: area invariant, arc length invariant, and central distance invariant. Due to these three invariants, the description becomes representative and discriminative. Moreover, Cyganski et al. [12] propose a method for the affine transformation, where each contour is transformed to its affine invariant parametrization. Then, the over-determined system minimizes the Euclidean distance between two objects. Cyganski et al. [11] use the linear signal space decomposition technique for shape correspondence. In [3] they propose to use the oriented elliptical Gaussian neighborhoods to find the best correspondence between two curves from images. Pauwels et al. [58], Moons et al. [53] use the semi- differential invariant to develop affine invariant descriptions to estimate the affine transformations. Gope et al. [29] introduce a method for affine shape matching using the area of mismatch, where this area is gated by aligning the curves optimally based on the minimum affine distance involving their specific points. The authors in [57] use The Hu invariant moment to describe a technique for affine global curves matching. Moreover, in [32] they use the Hungarian method and dynamic programming for points matching between two curves. Elghoul and Ghorbel [20] develop a fast approach for 2D special affine transformation based on a complete and stable descriptor. In [54] the researchers suggest an extended Scale-Invariant Feature Transform SIFT algorithm named Affine SIFT (ASIFT) for affine invariant matching. Kovalsky et al. [40] propose a technique for estimating the geometric and radiometric transformations for two objects. Bryner et al. [7] develop a novel framework for affine invariance based on Riemannian geometry. Afterward, they propose in [8] a Bayesian active contour with affine invariance. For the affine n-space curve, Liu [46] defines centro-affine invariant arc length and curvature functions. In [62] authors present the affine invariant pseudo-metric for surfaces.

There is also a large body of research work for iterative approaches proposed to improve the performance of point set registration. One of the most widely used point set matching algorithms is Iterative Closest Point (ICP) [6, 63]. In [61] the authors develop a multiview registration method for aligning a large data set. Also, in [48] the researchers propose an iterative method to estimate the transformation between two-point sets. First, they use a feature descriptor such as shape context to establish correspondence. Then the geometric transformation is done using a robust estimator L_2E. The Expectation-Maximization (EM) algorithm is an iterative, statistical, and probabilistic technique used to estimate the transformation between two-point sets. For this, Jian et al. [36] propose a framework for the rigid and non-rigid point sets registration problems. First, they describe the two input point sets using Gaussian mixture models. Then they align these two obtained Gaussian mixtures. In [56], Myronenko and Song suggest a probabilistic algorithm for rigid and non-rigid point sets registration named Coherent Point Drift (CPD). Moreover, [30] propose Multi-scale EM-ICP for an iterative point set mapping. Similarly, in [9] They use mixture models to represent the registration problem as maximum likelihood or Bayesian maximum a posteriori estimation problems. For this reason, they develop an EM-like technique to estimate transformations between the two mixture models. Chui et al. [10] model a feature-based registration algorithm called TPS–RPM (Thin-plate splines (TPS), Robust point matching (RPM)) to determine the correspondence between non-rigid point sets. Wang and Chen [77] propose fuzzy correspondences guided Gaussian mixture model for matching. In [47] the authors propose a novel technique that combines the shape context and Expectation-Maximization (EM) method to determine the geometric transformation parameters. Yang et al. [92] use a popular probability model, which is the Gaussian mixture model, to preserve the global structure of the point set. And they use the expectation-maximization algorithm to update model parameters. Lastly, Matuk et al. [51] build a Bayesian framework for shape alignment and transformation estimation.

3 Recall of affine curve matching algorithm

The affine curve matching algorithm (ACMA) [20] is a partial 2D affine curve alignment method based on a pseudo-inverse calculation. In the following part, we will recall the main steps of this technique. Starting with the shape normalization, which is done by the affine arc length re-parametrization [72] where enough points represent the input curves. The number of result equations is higher than the unknown variables. Then, the computation of the pseudo-inversive matrix that allows the minimization of L2 distance and obtains an affine part-to-part registration curve.

3.1 Affine arc length re-parametrization

Generally, curves extracted from the different images of the same object are parameterized differently. Thus, to compare these two curves, they must have the same parametrization (same speed). It is obvious that a curve can be represented with several different parametrizations: For example, the ellipse can be represented by the two following parametrizations;

$$ \begin{array}{@{}rcl@{}} f_{1}(t)=(x_{1} = a \cos t; y_{1} = b \sin t)_{t \in [0,2\pi]} \\ f_{2} (t) =(x_{2}(u) = a \cos \log U; y_{2}(u) = b \sin \log U)_{U \in [1, e^{2 \pi}]} \end{array} $$
(1)

with a , b positive real number, these two parametrizations describe the same ellipse curve (a and b are the minor axis and the major axis respectively). Therefore, we re-sample the contours with the normalized affine arc length function l(t) defined by [12]:

$$ l(t)=\frac{1}{L} {{\int}_{0}^{t}}\|\operatorname{det}(\dot{f}(u), \ddot{f}(u))\|^{\frac{1}{3}} \mathrm{d} u $$
(2)

Let denote f(t) as the original parametrization of one of the two curves. L the affine totale length of the curve. det represents the determinant operator. \(\dot {f}\) and \(\ddot {f}\) are respectively the first and second derivatives of f. Then, the relationship obtained between the two curves f and h after the normalization step is defined by:

$$ h(l)=A f(l+l_{0})+B $$
(3)

It is well known that simple planar curves can be classified into open and closed ones. In the first case, the starting point can be chosen from one of the two curve extremities. By fixing a given orientation in the plane, l0 defined in the formula (2) can be reduced to 0. For the second case, the curvature functions of each closed curve are estimated after maximization of the correlation between curvatures; it also becomes possible to make for l0 the zero value. Therefore, we will use the following relation:

$$ h(l)=A f(l)+B $$
(4)

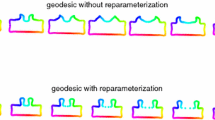
In Fig. 1, there are some examples of affine arc length re-parametrization with N = 100. The condition to find the best number of normalization points is studied in [21]. So we based the sampling choice on that work.

Fig. 1
figure 1

Examples of affine arc length re-parametrization with N = 100

Full size image

3.2 Recall of pseudo-inverse Affine matrix calculation

To estimate the apparent movement bettween curves we calculate the pair A and B wehere A the special linear transformation and B the translation vector. The re-sampling of two curves by the normalized affine arc length provides 2N equations and 6 unknown variables to the following rectangular system:

$$ \left\{\begin{array}{l} h^{x}(l_{1})=f^{x}(l_{1})a_{11}+f^{y}(l_{1})a_{12}+B^{x}\\ h^{y}(l_{1})=f^{x}(l_{1})a_{21}+f^{y}(l_{1})a_{22}+B^{y}\\ ....\\ h^{x}(l_{N})=f^{x}(l_{N})a_{11}+f^{y}(l_{N})a_{12}+B^{x}\\ h^{y}(l_{N})=f^{x}(l_{N})a_{21}+f^{y}(l_{N})a_{22}+B^{y} \end{array}\right. $$
(5)

with fx(la),fy(la) and hx(la),hy(la) (a= 1..N) are the two re-sampling cures related to the input shapes f(t) and \(h(t^{\prime })\), A = (aij)i,j= 1,2 and B = (Bx,By). We attempt to minimize the error between these two shapes, by calculating the pair A and B using:

$$ \min_{(A, B)}=\left\|A f\left( l_{a}\right)+B-h\left( l_{a}\right)\right\|^{2} \approx e $$
(6)

The system (3) can be written in matrix notation as follows:

$$ H=DU $$
(7)

Where: \(H=\begin {bmatrix} h_{{l_{1}^{x}}} h_{l_{1}}^{y} h_{l_{2}}^{x} h_{l_{2}}^{y}... h_{l_{N}}^{x}h_{l_{N}}^{y} \end {bmatrix}\); U = [a11a12a21a22BxBy]t and

$$ D=\begin{pmatrix} f^{x}(l_{1}) &f^{y}(l_{1}) & 0 & 0 & 1 &0 \\ 0& 0 &f^{x}(l_{1}) &f^{y}(l_{1}) & 0 & 1\\ f^{x}(l_{2})& f^{y}(l_{2}) & 0 & 0 & 1 & 0 \\ 0 & 0& f^{x}(l_{2}) & f^{y}(l_{2}) & 0 &1 \\ . & . & .& .& . &. \\ f^{x}(l_{{N} }) & f^{y}(l_{N}) & 0 & 0 & 1 & 0\\ 0 & 0 &f^{x}(l_{{N}}) & f^{y}(l_{N}) & 0 & 1 \end{pmatrix} $$
(8)

This rectangular system can be solved by the pseudo-inverse calculation of the matrix D. The following formula determines the unknown vector U.

$$ U=(D^{t}D)^{-1} D^{t} H $$
(9)

4 Optimized AMSCR based on unsupervised Bayesian classification

We noticed in [64] that we solved the problem of levels’ choice by developing the adjusted AMSCR method using Binary-EM. In contrast, this method has a high computational cost, incredibly time-consuming. For this reason, we create an efficient unsupervised Bayesian approach to select the optimized smoothing levels by applying Multiclass-EM. For the choice of the Multiclass-EM class, we use the K-means and Elbow method to automate this choice (class number). This unsupervised 2D shape registration technique is developed according to the shape complexity. As a result, we obtain a shorter equation system that minimizes the errors. Figure 2 summarizes its workflow. Furthermore, this pipeline introduces how we choose the optimal scales using the Affine Multi-scale Curve Registration (AMSCR) based on unsupervised Bayesian classification. This method is divided into two parts; the first one presents the AMSCR process where it has as input pairs of source and target 2D shapes, and the output is a vector \(S = \{\min \limits { L_{\sigma _{i}}^{2}}_{(1 \leq i \leq p)}\}\). However, the second part presents the unsupervised Bayesian classification process.

Fig. 2
figure 2

AMSCR based on unsupervised Bayesian classification

Full size image

4.1 Part A: AMSCR process

The affine Multi-Scale Curve Registration (AMSCR) procedure is summarized in the following steps.

  • A-1: re-sampling each input shape f and h with affine arc-length parameterization.

  • A-2: filter each component of the two re-sampling curves \(f_{\sigma _{k}}^{x}\), \(f_{\sigma _{k}}^{y}\) and \(h_{\sigma _{k}}^{x}\), \(h_{\sigma _{k}}^{y}\) with a Gaussian function \(g_{\sigma _{k}}\) at different levels of the scale (σk)(1≤k≤p). Where p represents the number of smoothing levels. Hence, the resulting components related to the curve \(f_{\sigma _{k}}\) is represented by:

    $$ f_{\sigma}^{x}(l, \sigma)=f^{x} * g(l, \sigma) \quad \quad \quad \quad f_{\sigma}^{y}(l, \sigma)=f^{y} * g(l, \sigma) $$
    (10)
    $$ g(l, \sigma_{k})=\frac{1}{2 \pi {\sigma_{k}^{2}}} e^{-\left( l^{2}\right) / 2 {\sigma_{k}^{2}}} $$
    (11)

    With ∗ denoting the convolution operation. The same process is adopted for the second curve \(h_{\sigma _{k}}\).

  • A-3: the retrieved p systems at each level (σk)(1≤k≤p) formed by the following 2N linear equations.

    $$ \begin{array}{@{}rcl@{}} \left\{\begin{array}{l} h_{\sigma_{1}}(l_{{1}})= \hat{A}_{\sigma_{1}} f_{\sigma_{1}}(l_{{1}})+\hat{B}_{\sigma_{1}}\\ h_{\sigma_{1}}(l_{{2}})= \hat{A}_{\sigma_{1}} f_{\sigma_{1}}(l_{{2}})+\hat{B}_{\sigma_{1}}\\ ...\\ h_{\sigma_{1}}(l_{{N-1}})= \hat{A}_{\sigma_{1}} f_{\sigma_{1}}(l_{{N-1}})+\hat{B}_{\sigma_{1}}\\ h_{\sigma_{1}}(l_{{N}})= \hat{A}_{\sigma_{1}} f_{\sigma_{1}}(l_{{N}})+\hat{B}_{\sigma_{1}} \end{array}\right. \left\{\begin{array}{l} h_{\sigma_{2}}(l_{{1}})= \hat{A}_{\sigma_{2}} f_{\sigma_{2}}(l_{{1}})+\hat{B}_{\sigma_{2}}\\ h_{\sigma_{2}}(l_{{2}})= \hat{A}_{\sigma_{2}} f_{\sigma_{2}}(l_{{2}})+\hat{B}_{\sigma_{2}}\\ ...\\ h_{\sigma_{2}}(l_{{N-1}})= \hat{A}_{\sigma_{2}} f_{\sigma_{2}}(l_{{N-1}})+\hat{B}_{\sigma_{2}}\\ h_{\sigma_{2}}(l_{{N}})= \hat{A}_{\sigma_{2}} f_{\sigma_{2}}(l_{{N}})+\hat{B}_{\sigma_{2}} \end{array}\right. \textbf{...} \\ \left\{\begin{array}{l} h_{\sigma_{p}}(l_{{1}})= \hat{A}_{\sigma_{p}} f_{\sigma_{p}}(l_{{1}})+\hat{B}_{\sigma_{p}}\\ h_{\sigma_{p}}(l_{{2}})= \hat{A}_{\sigma_{p}} f_{\sigma_{p}}(l_{{2}})+\hat{B}_{\sigma_{p}}\\ ...\\ h_{\sigma_{p}}(l_{{N-1}})= \hat{A}_{\sigma_{p}} f_{\sigma_{p}}(l_{{N-1}})+\hat{B}_{\sigma_{p}}\\ h_{\sigma_{p}}(l_{{N}})= \hat{A}_{\sigma_{p}} f_{\sigma_{p}}(l_{{N}})+\hat{B}_{\sigma_{p}} \end{array}\right. \end{array} $$
    (12)

  • A-4: by applying the ACM Algorithm [21] to each system indexed by k, we obtain the pair \(\hat {A}_{\sigma _{k}}\) and \(\hat {B}_{\sigma _{k}}\), which are the elements of Special Affine group SA(2,R).

  • A-5: we use the pair \(\hat {A}_{\sigma _{k}}\) and \(\hat {B}_{\sigma _{k}}\) to compute the L2 distance (Euclidean distance) between the normalized input shape (source and target curves in step 1), then we obtain a vector where it storge all σk and the corresponding \(L_{\sigma _{k}}^{2}\), which is denoted by:

    $$ L_{\sigma_{k}}^{2}=\min_{(\hat{A}_{\sigma_{k}}, \hat{B}_{\sigma_{k}})}=\left\|\hat{A}_{\sigma_{k}} f\left( l_{a}\right)+\hat{B}_{\sigma_{k}}-h\left( l_{a}\right)\right\|^{2} \approx e $$
    (13)

    The workflow of Steps 4,5 is depicted in comprehensive detail in Fig. 3.

Fig. 3
figure 3

Pipeline of Step 4,5

Full size image

Figure 4 illustrates the acquired set S of distances with a minimum value of \({\min \limits } L_{\sigma _{k}}^{2}\). For each different shape, each subfigure represents the minimum \({\min \limits } L_{\sigma _{k}}^{2}\) that can be achieved depending on the value of σk. However, when we smooth the normalized input contours using a Gaussian kernel with an increasing standard deviation, the shape starts to lose information at a certain level (becomes an ellipse). This leads us to select the sigma that has a smaller \({\min \limits } L_{\sigma _{k}}^{2}\) distances.

Fig. 4
figure 4

\({\min \limits } L_{\sigma _{k}}^{2}\) distance variation depending on σk

Full size image

4.2 Part B: unsupervised Bayesian classification

Part B describes the process of unsupervised Bayesian classification to choose the optimal scale levels for the registration. In the following, we detail each step separately.

  • B-1: Applying K-means: It is commonly known that the K-means algorithm [49] requires a large initial set to start clustering. As a result, the K-means approach is preferred for many clustering tasks, especially those involving small datasets. On the other hand, the unsupervised clustering process of K-Means needs fewer iterations and is therefore quicker. In addition, the k-means algorithm has undergone several changes to increase its performance. Algorithm 1 implements K-means unsupervised clustering.

    Calculating the SSE distance:

    The Sum of Squared Errors (SSE) is the sum of the average Euclidean Distance of each point from the centroid.

    $$ SSE= \sum\limits_{i=1}^{n} d^{2} $$
    (14)

    d: is the distance between the data and the cluster center

  • B-2: Visualization of the Elbow graph: The elbow method [74] is presented to explain and evaluate the consistency of clustering analysis to assist in choosing the correct number of clusters that should be present in the data set. This technique is referred to as an optimal clustering technique. In order to initiate the Binary-EM, we have decided to use this illustrated method in order to find the ideal amount of classes to use. Figure 5 demonstrates the use of the Elbow method in the Brid class of shapes.

  • B-3: Choosing the best classes ‘K’: The graph is used to determine the class number. A class is actually represented by each Elbow. The optimal K class number is then the graph-derived number.

  • B-4: Applying the Multiclass-EM: The algorithm employs an iterative process to determine the probability distribution parameters with the highest likelihood of its attributes. We use EM based on Gaussian mixture models (GMM) for this approach.

    • The input parameters of Multiclass-EM are the set S of all values of \(\{\min \limits { L_{\sigma _{i}}^{2}}_{(1 \leq i \leq p)}\}\).

    • K is the number of clusters estimated by the Elbow method. (optimally chosen from Elbow plot)

    • The output is presented in Fig. 6.

  • B-5: Bayes Classification: The new threshold s0 is deduced after the application of the Bayesian rule, as shown in Fig. 6. Thus we obtain \(S^{*}=\{\sigma _{k}={\arg \min \limits {L^{2}_{{\sigma _{k}}_(1 \leq k \leq p)}} / L_{\sigma _{k}}^{2} \leq s_{0}}\}\), let denoted q = Card(S∗).

  • B-6: we select only the scale levels belonging to S∗, which we are denoted by \(\sigma _{j_{(1 \leq j \leq q)}}\).

  • B-7: The registration is done with our new approach Affine Multi-scale Curve Registration (AMSCR) based on unsupervised Bayesian classification.

Algorithm 1
figure a

K-means.

Full size image
Fig. 5
figure 5

Example of Elbow method visualization for Brid class of shapes

Full size image
Fig. 6
figure 6

Calculate the new threshold \(s^{\prime }_{0}\) using Bayesian Rule

Full size image

The procedure of our Affine Multi-scale Curve Registration (AMSCR) based on unsupervised Bayesian classification is described in Algorithm 2.

Algorithm 2
figure b

AMSCR based on unsupervised Bayesian classification.

Full size image

Figure 7 presents a comparison of the resulting registration using different approaches. Hence, in the first column, the registration is done by the Affine Multi-scale Curve Registration (AMSCR) [64], in the second column, the alignment is achieved using the adjusted Affine Multi-scale Curve Registration (AMSCR) with Binary-EM [64]. Finally, we use the optimized AMSCR based on Multiclass-EM to do the registration in the third one. As we constat, the optimized AMSCR algorithm Multiclass-EM gives us the best alignment compared to the two other registered shapes.

Fig. 7
figure 7

a,d,g,j: registration using AMSCR method [64]; b,e,h,k: registration using AMSCR with Binary-EM [64]; c,f,i,l: registration using AMSCR optimized with Multiclass-EM

Full size image

5 Experiments

The proposed method is tested on well-known datasets such as MPEG-7, Multiview Curve Dataset (MCD), Kimia-99, Kimia-216, ETH-80, and the Swedish leaf dataset. So, we test the performance of the optimized AMSCR based on unsupervised Bayesian Classification. The comparison is made to the existing shape alignment methods in the stat-of-art. The outcomes of the various methods for these datasets are derived from their respective articles. Furthermore, the evaluation is conducted under the same conditions as the other methods. MATLAB was used to implement the entire algorithm. And for the resampling conditioning, we use the parameterization according to the study done in [19].

5.1 MPEG-7 Image database retrieval

The MPEG-7 shape database [42] is divided into two categories based on shape variations: Set-A and Set-B. The MPEG-7 set-A contains rigid objects with some transformations such as rotations or scale invariance, defined by 840 shapes from 140 classes. The MPEG-7 set-B, represented by 1400 shapes classified into 70 classes, is used for similarity-based retrieval and shape descriptor robustness under various arbitrary shape distortions. Set-B is divided into two parts, Set-B1 and Set-B2, for articulations and missing or altered contour portions, respectively. Figure 8 depicts some examples from each category. To put the proposed approaches to the test in the shape retrieval task, we compute the bull’s eye rates defined in [4, 78, 91]. The first step is to compare each curve to the whole dataset curves and recover the number of the same class contour in the middle of the 2Nc most similar, with Nc being the sample number per class. Then, we calculate the ratio of the number of correct results and the highest possible number of right results [24].

Fig. 8
figure 8

MPEG7 Dataset

Full size image
Fig. 9
figure 9

Different shape images from the MCD dataset, two images from each class

Full size image

Table 1 covers the Bull’s Eye scores of the proposed algorithms with the existing methods. We note that the ACM algorithm [21] 91.55% outperformed the other registration methods proposed in the literature in terms of bull’s eye score, such as Fast and non-rigid global registration [20] 82.42%, Multiscale Fourier descriptor [86] 83.94%, AICD [24] 84.26%, MSFDGF-SH [97] 87.76%, IDSC + AspectNorm + SR [73] 88.39%, Invariant multi-scale [84] 91.25% and IMTF [87] 91.26%. Whereas, IDSC + LCDP [88] 93.32%, IDSC + Affine Normlization [28] 93.67%, and Invariant multi-scale + LP [84] 94.51% achieve a high retrival performance scores compared to the ACM algorithm. For this, we implemented several steps to enhance these results in this paper, starting with Affine Multi-Scale Curve Registration (AMSCR), which improves the ACMA bull’s eye score by 2.06%. Then, the result becomes even better when we adjusted the Affine Multi-Scale Curve Registration (AMSCR) with Binary-EM, which improves the AMSCR algorithm score by 0.75%. Moreover, when we optimize the proposed AMSCR with Multiclass-EM, the results become more competitive, where this one outperformed AMSCR with Binary-EM by 0.12%. On the other hand, the method Invariant multi-scale + LP [84] remains more efficient then our suggested AMSCR with Multiclass-EM by 0.03%.

Table 1 Retrieval results on the entire MPEG-7 set B dataset
Full size table

5.2 MCD image database retrieval

Shape registration is one of the most significant applications of the algorithm proposed. Thus, we are going to test the Affine Multi-Scale Curve Registration (AMSCR) [64] and the optimized AMSCR based on Multiclass-EM on the Multiview Curve Dataset (MCD) [98] which is composed of 40 shape classes taken from the MPEG-7 database. Each category contains 14 sample curves that match the distortion of the original curve from a different perspective Fig. 9. Table 2 compares our proposed methods and some existing work in state-of-the-art. First, we noticed that the Affine Multi-Scale Curve Registration (AMSCR) 96.36% exceeds the other registration techniques such as the methods Partial Contour Matching Based on ACSS [52] 95.98%, ACMA [19] 94%, Fast and non-rigid global registration [20] 92.8%, Mai [50] 89% and Rube [16] 79%. Then the result becomes better when we adjust the AMSCR with Binary-EM [64], and we obtain 96.58% as a rate. Moreover, the optimized AMSCR based on Multiclass-EM performs substantially more than the other techniques with a 96.61% rate.

Table 2 Retrieval results on the entire MCD dataset
Full size table

5.3 Euclidian distance (L 2) Computation

Figure 10 shows some graphics obtained from the Euclidian Distance (L2) computation. From the MCD database, we take shape as a query and register it with another shape that belongs to the same class of shapes. Then we calculate the L2 distance between them using the two approaches, the AMSCR adjusted with Binary-EM and the optimized AMSCR based on Multiclass-EM. The first subfigure (a) compares the Butterfly’s L2 distance, done with the AMSCR with Binary-EM and the AMSC based on Multiclass-EM. However, we note that the AMSCR based on Multiclass-EM improves the Euclidian Distance in most cases. In the second subfigure (b), we can see that using the optimized AMSCR based on Multiclass-EM improves the computation of L2 distance for a Brid form significantly. Finally, the new optimized AMSCR based on Multiclass-EM performs well with the Spider shape in the majority of cases.

Fig. 10
figure 10

Computation of the Euclidian Distance between two shapes: the blue curve represents the L2 distance using the adjusted AMSCR with Binary-EM. The red one describes the same L2 using the optimized AMSCR based on Multiclass-EM

Full size image

5.4 KIMIA-99 image database retrieval

In shape registration and retrieval, the Kimia-99 dataset [65] is commonly used for evaluation. There are 99 shapes in 9 classes, with 11 in each category (Fig. 11). This dataset contains certain occlusions and articulations. Table 3 displays various well-known methods as a retrieval rate of the top-1 to top-10 alignment shapes. For each of them, the best possible result is 99. The results show that the Affine Multi-Scale Curve Registration (AMSCR) [64] outperforms other approaches. However, the adjusted AMSCR with Binary-EM [64] and the optimized AMSCR based on Multiclass-EM perform very similarly and give competitive results comper to the most existing methods such as Generative model[75], HF [79], IDSC+LBP [67], ACMA [19], and SMR by data-driven EM [76].

Fig. 11
figure 11

Kimia-99 database, where each row shows a different class

Full size image
Table 3 Top 10 closest matching shapes for Kimia-99 dataset
Full size table

5.5 KIMIA-216 image database retrieval

The Kimia-216 dataset [65] is made up of 216 curves divided into 18 classes, each one with 12 shapes. Figure 12 illustrates all 216 forms in this database, each in a column belonging to a class. Columns depict birds, bones, bricks, camels, cars, children, classic cars, elephants, faces, forks, fountains, glass, hammers, hearts, keys, misks, rays, and turtles from left to right. The Affine Multi-Scale Curve Registration (AMSCR) [64] is tested first, followed by the AMSCR adjusted with Binary-EM [64] and the optimized AMSCR based on Multiclass-EM. The outcomes demonstrate that the proposed algorithm exceed other techniques such as CPDH+EMD(eucl) [68], CPDH+EMD(shift) [68], PS+LBP [26], IDSC+LBP [79], even the ACMA [19] method (Table 4).

Fig. 12
figure 12

Example of curves in Kimia-216 database. One object for each one of the 18 categories is shown

Full size image
Table 4 Top 11 closest matching shapes for Kimia-216 dataset
Full size table

5.6 ETH-80 image database retrieval

ETH-80 benchmark contains 3280 images. It is divided into eight classes. Each class includes ten objects containing 41 images obtained from various poses. Figure 13 depicts some examples from the ETH-80 dataset [43]. To classify the different categories in the experiment, we use the 1-nearest neighbor algorithm. Each image is compared to the other 79 images in the same category to determine the recognition rate. Table 3 shows the accuracy of the proposed approaches with other existing methods. We notice that the Affine Multi-Scale Curve Registration (AMSCR) [64] has a rate equal to 88.98%. However, when we adjusted AMSCR with Binary-EM [64], the accuracy increased by 0.25%. The result improved by 89.45% when the AMSCR has optimized with Multiclass-EM. Our approach gives better accuracy compared to other existing techniques such as Multiscale Fourier descriptor [86] (86.91%), EGCSS [5](87.5%), Fast and non-rigid global registration [20] (87.95%) and Height function [79] (88.72%). However, our method’s accuracy is inferior to that of the deep learning method for hierarchical features based on CNN [39] (95.80%) (Table 5).

Fig. 13
figure 13

ETH-80 database

Full size image
Table 5 Retrieval rates on the entire ETH-80 dataset
Full size table

5.7 Swedish leaf dataset

This section evaluates our proposed method in the Swedish leaf dataset. This benchmark contains 1125 objects from 15 different leaf categories. As illustrated in Fig. 14, each class includes 75 forms. This dataset contains forms of the same category with significant variability and shapes belonging to a diverse category that can be very similar. We evaluate the performances in the same state indicated in [70] to compare the proposed method with state-of-the-art. We choose 25 learning objects randomly from each category, and the remaining objects serve as a test. The sample object is then aligned with the training objects. The shape will be classified using the 1-nearest neighbor and the distance L2 following registration. Table 6 summarizes the accuracy rates. The method Affine Multi-Scale Curve Registration (AMSCR) [64] gives us a score equal to 96.3% which is better than several other techniques such as Multiscale Fourier descriptor [86] (86.91%), Fast and non-rigid global registration [20] (95.61%). Moreover, the adjusted AMSCR with Binary-EM [64] enhance the result by 96.51%, and the score is better when the AMSCR optimized by Multiclass-EM (96.73%). Contrariwise, there are some other methods in the state of the art that give better rates such as HSC [78] (96.91%) and IMTF [87] (97.87%).

Fig. 14
figure 14

Swedish leaf dataset

Full size image
Table 6 Retrieval rates on the entire Swedish leaf dataset
Full size table

6 Analysis of time consumption

The effectiveness of our proposed approach is compared with those of other methods. Shape smoothing and normalization time are not considered while estimating time consumption. According to [86], the suggested method’s time consumption is identical to that of the other approaches. Table 7 shows that for MPEG-7 datasets, the proposed process takes 31 s, encouraging the use of our method in real-time applications.

Table 7 Efficiency of different methods on the MPEG-7 dataset
Full size table

7 Conclusion

In this paper, we have proposed an optimized Affine Multi-Scale Curve Registration (AMSCR) based on the multiclass-EM algorithm. This method’s main idea is to automatically select the best set of smoothing parameters in the sense of the minimum of the Euclidean distance between the target and the source curves.

Thus, we have obtained a global rectangular linear system corresponding to this selected set of their smoothed parameters. The number of the class is founded by the application of the k-means and Elbow method. The registration process is achieved by the application of the pseudo-inverse algorithm.

Based on several experiments on MPEG-7, MCD, Kimia-99, Kimia216, ETH-80, and the Swedish leaf benchmarks, we have proven that the proposed method gives one of the best scores in the mean of precision. We aim, in future works, to study the stability and the complexity of our registration system. And we intend to improve the gigantic stitching mosaic done for the virtual Tunisian Bardo Museum.