Probabilistic intuitionistic fuzzy c-means algorithm with spatial constraint for human brain MRI segmentation

Abstract

Segmentation of brain MRI images becomes a challenging task due to spatially distributed noise and uncertainty present between boundaries of soft tissues. In this work, we have presented intuitionistic fuzzy set theory based probabilistic intuitionistic fuzzy c-means with spatial neighborhood information method for MRI image segmentation. We have investigated two well known negation functions namely, Sugeno’s negation function and Yager’s negation function for representing the image in terms of intuitionistic fuzzy sets. The proposed approach takes leverage of intuitionistic fuzzy set theory to address vagueness and uncertainty present in the data. The spatial neighborhood information term in the segmentation process is included to dampen the effect of noise. The segmentation performance of the proposed method is evaluated in terms of average segmentation accuracy and Dice score. Further, the comparison of the proposed method with other similar state-of-art methods is carried out on two publicly available brain MRI dataset which shows the significant improvements in segmentation performance in terms of average segmentation accuracy and Dice score. The proposed approach achieves on average 91% average segmentation accuracy in the presence of noise and intensity inhomogeneity on BrainWeb simulated dataset, which outperformed the state-of-art methods.

1 Introduction

In the recent past, diagnostics have been revolutionized with the advancement of many medical imaging modalities such as positron emission tomography (PET), magnetic resonance imaging (MRI), computed tomography (CT), Mammogram, X-rays, Ultrasound etc. These modalities help in delineating the human anatomy for disease diagnosis. Among all, MRI [26] is the frequently used modality for capturing the soft tissues present in the human brain such as gray matter(GM), white matter(WM) and cerebrospinal fluids (CSF). The image sequences [14] are captured in MR images by applying an appropriate setting of pulse parameters such as repetition time (TR), echo time (TE), spin-echo, gradient-echo, inversion-recovery etc. TE and TR are the two key parameters for obtaining different image contrast. Due to this, the MRI machines can delineate the multi-spectral image with high contrast. Nowadays, these diagnostic machines are easily accessible which produce huge amount of medical data for disease diagnosis. Manual analysis of these images for disease diagnosis requires the expert radiologist. This being a time consuming process and may involve human error. There is a requirement of analyzing these MRI images in less time for faster diagnosis. The computer aided diagnosis [8] may help the expert radiologist in faster analysis of medical images. In some situations, the quantification and localization of different normal and abnormal tissues are required for brain related diseases using MRI modality. For this, these MRI images need to be segmented in different similar regions. The manual segmentation of MRI images is a challenging task as images are likely to have artifacts during the delineation process. The main factors affecting the quality of MRI segmented images includes (a) a non-uniform intensity variation is introduced in the MRI images. This variation is due to radio frequency utilized in the MRI, termed as bias field effect or intensity in-homogeneity (IIH) or intensity non-uniformity (INU) [1]; (b) noise; (c) partial volume effect. The presence of such artifacts adversely affect segmentation as well as visual evaluation based on absolute pixel intensities [13].

Machine learning (ML) based techniques are the most extensively used for segmenting brain MR images. These techniques are further classified into supervised and unsupervised techniques. The supervised segmentation techniques are fully automatic and effective segmentation approaches [2, 10, 16, 29, 42, 47, 48]. Although the segmentation accuracy is improved by the supervised ML techniques by incorporating prior knowledge, the major drawbacks of supervised techniques are as follows [2]: (a) training classifier with the same training set for a large number of MR images may often lead to biased results due to physiological variability between different subjects; (b) several parameters are required by the classifiers to be trained, thus necessitating the requirement of fast processing devices with large amount of main memory.

Unsupervised segmentation techniques [46] can be described as partitioning the image into different groups or regions, each having alike features such as texture, color, etc. Clustering is one of the popular unsupervised techniques to explore and analyze the structural information associated with the unlabeled data. The conventional way of obtaining clusters is the Hard c-means (HCM) clustering method, which results in c-crisp partitions of the data set [39]. Assigning a data point to exactly one cluster ignores the uncertainty about the data point belonging to more than one cluster especially at the boundary and therefore tending to lose it’s interpretability for many real world applications.

Fuzzy c-means (FCM) [5] overcomes this problem by assigning membership values to each data point to c number of clusters where each cluster is represented by fuzzy sets. FCM [6] is the most widely used clustering algorithm for segmenting brain MR images [8, 9, 23]. The reason for wide acceptance of FCM for MRI image segmentation is its ability to handle (a) uncertainty present in image boundaries/regions; (b) imprecise gray levels in images; (c) vagueness in defining class. The performance of FCM degrades in presence of imaging artifacts because it does not consider any spatial information [52]. In the past, many research work has been done by incorporating the local spatial information to the FCM clustering algorithm [1, 11, 13, 33, 36, 37, 41, 45, 48, 50, 56, 62, 63]. Several other research work related to brain MRI segmentation also reported in [4, 31, 32, 49] etc.

The methods discussed so far are dependent on selection of optimal parameter values and lose their fine image details. Krindis et al. [33] addressed this issue by proposing a fuzzy local information clustering method (FLICM) to tackle the problem of noise in image segmentation. This method is similar to FCM_S [1] as it uses the neighboring pixels deviation from centroid’s intensity, weighted by a fuzzy factor and spatial distance of neighbours. The FLICM doesn’t take into account any parameter but calculates the local information term for each iteration and hence makes it a time consuming segmentation method. The literature reports that the objective value is not minimized further by FLICM rather converging the fuzzy partition matrix only. Guo et al. proposed an Adaptive fuzzy c-means (NDFCM) [22] method, which is based on local noise detection. In this method, the spatial parameters for each pixel were dependent on the noise level in a given immediate neighbourhood. In spite of being the noise adaptive algorithm, NDFCM has a high computational complexity because it depends on the three input parameters which are required to be fine tuned for good performance. Recently a fast and robust fuzzy c-means algorithm (FRFCM) was proposed by Lei et al., which gave magnificent results with significantly low time complexity [35]. The pre-processing step in FRFCM employed morphological reconstruction operation, which made it robust to a variety of noises. The post processing step uses membership filtering for avoiding the heavy computation in measuring the distance between the neighbour pixels and centroids to handle noisy pixels. The FRFCM performs well for several noise varieties, but shows its poor performance on high noise samples because the sharp edges and shapes are not preserved. In another research work Deviation-sparse fuzzy c-means with neighbor information constraint (DSFCMN) algorithm [60] is proposed, which modeled the deviation between the original pixel values and measured noisy pixels value as residual and incorporated this value in the optimization function. The residual term in DSDCMN is sparse matrix and uses the L1 norm distance measure in objective function as a constraint over residuals. However DSFCMN did not show good results when tested on a dataset with high noise. Further, Wang et. al. proposed Weighted Residual fuzzy c-means (WRFCM) [55], which uses weighted L2-norm measure for residual estimation and showed satisfactory performance compared to the previous research methods.

In order to deal with non-linear structure present in any image, many research methods have been reported in literature that utilize the kernel distance measure. The research work [61] proposed a kernel generalized fuzzy c-means (KGFCM) clustering with spatial information for image segmentation. Most kernel based methods are dependent on optimal selection of input parameters values for satisfactory segmentation performance. The grid search method is mostly used to find the optimal values of these parameters which is a time consuming process. Gong et al. [21] proposed a variant of FLICM method by replacing the Euclidean distance with kernel metric and further introduced a trade off weighted fuzzy factor to better use the neighbor information in an adaptive manner termed as KWFLICM. The performance of KWFLICM method is better in comparison to the FLICM method but still it inherits the problem of FLICM method.

The membership values in variants of FCM depend on the distance between cluster centroids and image pixels. In some situations, the image acquisition process leads to uncertainty due to imprecise pixel intensity value. Hence, calculation of membership values of a given pixel to different clusters is imprecise [44]. Therefore to handle such problems, an intuitionistic fuzzy set (IFS) introduced by Atanassov [3] that deals with imprecise and vagueness in defining the membership value [12, 28]. For this, IFS set includes non-membership and hesitancy components along with membership value. The introduction of IFS theory into the clustering process increases the segmentation accuracy. Further, it makes the segmentation method robust and faster in comparison to FCM algorithm [27]. The research work [57], suggested a fuzzy clustering of data represented in terms of IFS which utilizes the Euclidean distance measure [51] defined for IFS. Chaira [12] introduced the concept of IFS theory to incorporate hesitation in defining the membership value in FCM algorithm. The research work [12] increases the significant data points in a given cluster. The problem of variations in pixel intensities is studied in the research work [18] which utilizes the IFS theory to represent the MRI images in terms of IFSs and further these data are clustered for image segmentation. PIFCM [40] is a recently proposed clustering algorithm which uses probabilistic Euclidean distance measure (PEDM) in the objective function. The presence of PEDM in the PIFCM have shown following advantages over conventional IFCM algorithms: (1) It is an adaptive algorithm, as it uses probabilistic weights; (2) reduced number of iterations for convergence; (3) lower sensitivity towards the fuzzy factor m, therefore, leads to higher stability. Further, the research work [53] suggested an improved Probabilistic Intuitionistic Fuzzy c-Means Clustering Algorithm. The improved PIFCM uses the min-max normalization as a membership function which minimizes the matrix computation of the original PIFCM. The PIFCM and Improved PIFCM handle the uncertainty in the dataset very well but are susceptible to the noisy dataset as in the case of MRI images. The performance of IFS theory based clustering method for image segmentation process deteriorates in presence of noise. To handle noise, the incorporation of local spatial information is advocated in literature.

The research work [25] proposed neighborhood information based IFCM algorithm with genetic algorithm (NIFCMGA) for automatic optimal parameter selection. It reduces the effect of noise and outliers in medical images segmentation but consumes more time as it utilizes genetic algorithm. The research work [54] suggested improved IFCM (IIFCM) to handle noise which combines both local spatial and grey level information together for MRI segmentation. Their algorithm is free from parameter tuning but have considerably higher running time. The research work [34] proposed IFCM with spatial neighborhood information (IFCM-SNI). The spatial neighborhood information (SNI) term is incorporated in the objective function of IFCM algorithm and is capable of dealing with noise without losing the fine image details. Their model gives better results on highly noisy MRI images.

From the above discussion, it is evident that noisy pixels can be correctly classified by incorporating spatial neighborhood information in the image segmentation process. The performance of the PIFCM [40] method is not giving promising results for image segmentation in presence of noise. To address this issue, we have proposed a intuitionistic fuzzy clustering that uses probabilistic Euclidean distance measure with spatial constraints (PIFCM_S). The proposed PIFCM_S method utilizes a spatial regularization term in the optimization problem for obtaining the clusters. This spatial regularization term utilizes the mean filtered image to dampen the effect of noise with a regularization parameter. The spatial regularization parameter sets a trade off between the level of noise and the segmentation performance. Higher the noise in the image, the value of this regularization parameter should be high. Further, we have investigated two well known intuitionistic fuzzy generators, namely, Sugeno’s negation function and Yager’s negation function for representing the image in terms of IFS. To validate the performance of the proposed method, we have utilized two publicly available brain MRI image dataset. Further, the performance of the proposed method is compared with several state-of-the-art methods in terms of average segmentation accuracy and Dice score.

The rest of the paper is organized as follows: preliminaries and related works are included in Section 2. The PIFCM_S algorithm and its formulation is discussed in Section 3. Section 4 discusses experimental setup and results. Finally, conclusion is included in Section 5.

2 Preliminaries and related works

The description of notations and related work used throughout the paper are discussed in the section.

The fuzzy set (FS) F, is defined by using membership function μ_F(x), x ∈ X and μ_F(x) ∈ [0,1]

Intuitionistic Fuzzy Set (IFS) [3], A is defined using membership function μ_A(x) and non-membership function ν_A(x) and is represented as:

$$ \begin{array}{@{}rcl@{}} A &=& \{\langle x,\mu_{A}(x),\nu_{A}(x)\rangle|x \in X\} \end{array} $$

(1)

Here μ_A: X→ [0,1] and ν_A: X→ [0,1] simultaneously assigns membership value and non-membership value respectively to each element x ∈ X with respect to A, if

$$ \begin{array}{@{}rcl@{}} 0 \leq\mu_{A}(x)+\nu_{A}(x)\leq 1. \end{array} $$

(2)

For every x ∈ X in A, If ν_A(x) = 1 − μ_A(x), then set A reduces to fuzzy set.

In an IFS, the hesitancy value, π_A(x) defines the uncertainty in definition of membership function and is calculated as:

$$ \pi_{A}(x)=1-\mu_{A}(x)-\nu_{A}(x), \text{~where~}0 \leq\pi_{A}(x)\leq 1. $$

(3)

Hence, due to presence of hesitancy value in IFS, the membership value lies in the interval [μ_A(x),μ_A(x) + π_A(x)].

2.1 Construction and representation of intuitionistic fuzzy sets for gray images

The image acquisition process involves conversion of energy response received on sensing devices to gray levels. This introduces the imprecise estimation of gray levels for many of the pixels in the image which in turn includes uncertainty in representing the gray levels in the image. This issue is resolved by converting the medical image into an intuitionistic fuzzy domain. In this way, a given gray level corresponding to a pixel is represented using membership value, non-membership value and hesitancy value. The membership value for a given pixel in the gray image is obtained by normalizing in the range [0 1]. The non-membership value and hesitancy value for the pixel is calculated using the membership value through intuitionistic fuzzy generators (discussed below). We have used two intuitionistic fuzzy generator functions namely, Yager negation function [58] and Sugeno negation function [43] for our study.

An intuitionistic fuzzy generator [12] is a function $g :[0,1]\rightarrow [0,1]$ satisfying the following properties :

• 1. g(μ) ≤ 1 − μ for all μ ∈ [0,1],

• 2. g(0) = 1 and g(1) = 0

If g is continuous, decreasing (increasing) then the intuitionistic fuzzy generator is called continuous, decreasing (increasing). The non-membership function NM(μ) for a given generating function g(.) is defined as:

$$ \begin{array}{@{}rcl@{}} NM(\mu)&=& g^{-1}(g(1)-g(\mu)) \end{array} $$

(4)

where, g^− 1(.) is inverse of generating function g(.).

• Yager’s negation function (YNF) [58, 59]: The Yager’s generating function g_Y(μ) with negation parameter β is given as follows:

  $$ g_{Y}(\mu) = \mu^{\beta} $$

  (5)

  Its inverse $g^{-1}_{Y}(\mu )$ is given by:

  $$ g_{Y}^{-1}(\mu) = \mu^{\frac{1}{\beta}} $$

  (6)

  Yager’s negation function calculates the non-membership value using (4), (5) and (6) which is given by:

  $$ \nu_{A}(x) =NM(\mu_{A}(x))=(1-{\mu_{A}(x)}^{\beta})^{\frac{1}{\beta}}, ~ \beta > 0 \ $$

  (7)

  where μ_A(x) represents membership value of IFS A.

• Sugeno’s negation function (SNF) [43]: The Sugeno’s generating function g_S(μ) with negation parameter β is given as:

  $$ g_{S}(\mu)= \frac{1}{\beta} \log(1+ \beta \mu), ~~\beta >0 $$

  (8)

  Its inverse $g^{-1}_{S}(\mu )$ is given by:

  $$ g_{S}^{-1}(\mu) = \frac{1}{\beta}(\exp(\beta \mu)-1), ~~\beta >0 $$

  (9)

  Sugeno’s negation function calculates the non-membership value using (4), (8) and (9) which is given by:

  $$ \nu_{A}(x) =NM(\mu_{A}(x))=\frac{1-\mu_{A}(x)}{1+ \beta \mu_{A}(x)}, ~ \beta > 0 \ $$

  (10)

  where μ_A(x) represents membership value of IFS A.

The intuitionistic fuzzy generator defined above is used to construct the intuitionistic fuzzy data for gray image. Let X be the set of p number of pixel and x_i represent the pixel intensity value corresponding to i^th pixel in X, where $i \in \{1,2,{\dots } p\}$. Therefore, each pixel in an image can be represented by an IFS as $X^{IFS} = \left \{\left <\mu _{X}(x_{i}), \nu _{X}(x_{i}), \pi _{X}(x_{i})\right >|~i=1,2,\dots ,p \right \}$, where μ_X(x_i) is membership value obtained by normalization of image in range [0 1] and ν_X(x_i) is non-membership value calculated using negation function described in (7) and (10) corresponding to Yager’s negation function and Sugeno’s negation function respectively.

The probabilistic intuitionistic fuzzy distance measure between i^th element $X_{i}^{IFS}$= $\left <\mu _{X}(x_{i}), \nu _{X}(x_{i}), \pi _{X}(x_{i})\right >$ and j^th element $X_{j}^{IFS}$= $\left <\mu _{X}(x_{j}), \nu _{X}(x_{j}), \pi _{X}(x_{j})\right >$ of IFS X^IFS can be defined as [40]

$$ \begin{array}{@{}rcl@{}} {\tilde{d}_{2}(X_{i}^{IFS},X_{j}^{IFS})} &=& \left[{\frac{1}{2}}\left( {p_{ij}} {(\mu_{X}(x_{i}) - \mu_{X}(x_{j}))^{2}} + {q_{ij}} {(\nu_{X}(x_{i}) - \nu_{X}(x_{j}))^{2}} \right.\right.\\ &&\left.\left.+ {\rho_{ij}} (\pi_{X}(x_{i}) - \pi_{X}(x_{j}))^{2}\right) \right]^{1/2} \end{array} $$

(11)

Here the probabilistic weights p_ij, q_ij and ρ_ij corresponding to the membership value, non-membership value and hesitancy value respectively are data driven. The weight ρ_ij corresponding to the hesitancy value is computed using the following formula of correlation coefficient.

$$ \begin{array}{@{}rcl@{}} && \rho_{ij} = 1 - \frac{\omega}{3(1+\omega)}\\ \text{where } \omega &=& |\mu_{X}(x_{i}) - \mu_{X}(x_{j})| + |\nu_{X}(x_{i}) - \nu_{X}(x_{j})| + |\pi_{X}(x_{i}) - \pi_{X}(x_{j})|. \end{array} $$

(12)

2.2 Fuzzy clustering with spatial constraints

An approach was proposed in the research work [1] to increase the robustness of FCM to noise by an addition of a penalty term in the FCM objective function. The penalty term makes the smoothing of a pixel within its specified neighborhood. The modified objective function of FCM_S algorithm [1] is given as:

$$ \begin{array}{@{}rcl@{}} J_{m}(U,V:X) &=&{\sum\limits_{i=1}^{p}}{\sum\limits_{j=1}^{c}} {u^{m}_{ij}} \left\lVert{x_{i}-v_{j}}\right\rVert^{2} + \frac{\alpha}{N_{R}} {\sum\limits_{i=1}^{p}}{\sum\limits_{j=1}^{c}} {u^{m}_{ij}} {\sum\limits_{r \in N_{i}}} \left\lVert{x_{r}-v_{j}}\right\rVert^{2} \end{array} $$

(13)

Here $X=\{x_{1},x_{2}, \dots , x_{p}\}$ are p pixels, $m~(1 < m < \infty )$ is the fuzzification factor, c (1 < c < p) represents the number of clusters which are fixed, u_ij (0 ≤ u_ij ≤ 1) represents the membership degree for i^th pixel in j^th cluster, N_i denotes the number of neighboring pixels around the center pixel x_i and N_R is cardinality of N_i. The parameter α controls the trade-off effects of the neighboring pixel. The optimization problem (13) can be solved by the Lagrange method of undetermined multipliers. Membership value and cluster centroid are given as [1]:

$$ \begin{array}{@{}rcl@{}} u_{ij} &=& \frac{\left( \left\lVert{x_{i}-v_{j}}\right\rVert^{2} + \frac{\alpha}{N_{R}} {\sum\limits_{r \in N_{i}}}\left\lVert{x_{r}-v_{j}}\right\rVert^{2}\right)^{-\frac{1}{m-1}}}{{\sum\limits_{k=1}^{c}}\left( \left\lVert{x_{i}-v_{k}}\right\rVert^{2} + \frac{\alpha}{N_{R}} {\sum\limits_{r \in N_{i}}}\left\lVert{x_{r}-v_{k}}\right\rVert^{2}\right)^{-\frac{1}{m-1}}} \end{array} $$

(14)

$$ \begin{array}{@{}rcl@{}} v_{j} &=& \frac{{\sum\limits_{i=1}^{p}}u_{ij}^{m} \left( x_{i} + \frac{\alpha}{N_{R}}{\sum\limits_{r \in N_{i}}}x_{r}\right)}{(1+\alpha){\sum\limits_{i=1}^{p}}u_{ij}^{m}} \end{array} $$

(15)

The value $\frac {1}{N_{R}}{\sum \limits _{r \in N_{i}}}x_{r}$ in (15) represents the mean value of gray-level around the pixel x_i within a specified window. However, FCM_S algorithm have high computation time. In order to decrease computation time of FCM_S algorithm, a variant of FCM_S algorithm, named the FCM_S1 is proposed in [13]. The mean filtered image in FCM_S1 consists of its neighbor average gray values around each pixel within a window. The objective function of FCM_S1 algorithm is given as:

$$ \begin{array}{@{}rcl@{}} J_{m}(U,V:X) &=&{\sum\limits_{i=1}^{p}}{\sum\limits_{j=1}^{c}} {u^{m}_{ij}} \left\lVert{x_{i}-v_{j}}\right\rVert^{2} + \alpha {\sum\limits_{i=1}^{p}}{\sum\limits_{j=1}^{c}} {u^{m}_{ij}} \left\lVert{\Bar{x_{r}}-v_{j}}\right\rVert^{2} \end{array} $$

(16)

where $\tilde {x}_{r}$ represents the mean value of neighboring pixels around the pixel x_r and is computed in advance. The optimization problem (16) can be solved by the Lagrange method of undetermined multipliers. Membership value and cluster centroid are given as [13]:

$$ \begin{array}{@{}rcl@{}} u_{ij} &=& \frac{\left( \left\lVert{x_{i}-v_{j}}\right\rVert^{2} + \alpha \left\lVert{\Bar{x_{r}}-v_{j}}\right\rVert^{2}\right)^{-\frac{1}{m-1}}}{{\sum\limits_{k=1}^{c}}\left( \left\lVert{x_{i}-v_{k}}\right\rVert^{2} + \alpha \left\lVert{\Bar{x_{r}}-v_{k}}\right\rVert^{2}\right)^{-\frac{1}{m-1}}} \end{array} $$

(17)

$$ \begin{array}{@{}rcl@{}} v_{j} &=& \frac{{\sum\limits_{i=1}^{p}}u_{ij}^{m} \left( x_{i} + \alpha \Bar{x_{r}}\right)}{(1+\alpha){\sum\limits_{i=1}^{p}}u_{ij}^{m}} \end{array} $$

(18)

The neighborhood term of the FCM_S algorithm is simplified in FCM_S1 algorithm. FCM_S is suitable for images which are contaminated by Gaussian noise. The parameter α controls the trade-off effect between the mean filtered image and original image. If the parameter α is set to zero, then both FCM_S and FCM_S1 reduce to the FCM algorithm. The outline of FCM_S1 algorithms [13] is given in Algorithm 1.

Algorithm 1

FCM_S1 algorithm.

2.3 Probabilistic intuitionistic fuzzy C-Means algorithm

Probabilistic Intuitionistic Fuzzy C-Means (PIFCM) [40] is an adaptive IFS based clustering algorithm. It incorporates the advantage of IFS for handling uncertainty which arises due to imprecise and incomplete information. The peculiarity of PIFCM is that it assigns weights p_ij, q_ij and ρ_ij corresponding to membership, non-membership and hesitancy value respectively in the objective function (19) directly from the dataset. Therefore, this algorithm gives weightage to each data point in every cluster. PIFCM algorithm divides p data points into c clusters by optimizing the objective function through continuous updation of the centroid ($v_{j}^{IFS}$) and membership degree (u_ij) until the termination condition is achieved. The objective function of PIFCM was formulated as follows:

$$ \begin{array}{@{}rcl@{}} J_{m}(U,V^{IFS}: X^{IFS})&=&{\sum\limits_{i=1}^{p}}{\sum\limits_{j=1}^{c}} {u^{m}_{ij}} {\tilde{d}_{2}(X_{i}^{IFS},v_{j}^{IFS})} \\ \text{subject to, ~~~} {\sum\limits_{j=1}^{c}}{u_{ij}} &=& 1,~~ 1 \leq i \leq c \end{array} $$

(19)

Here m is a fuzzy parameter, $X =\{x_{i}^{IFS}\}_{p \times 1}$ represents the image in terms of IFS, and the i^th element $X_{i}^{IFS}$= $\left <\mu _{X}(x_{i}), \nu _{X}(x_{i}), \pi _{X}(x_{i})\right >$, U = [u_ij]_p×c is the fuzzy partition matrix in which each entry u_ij represents the membership value of i^th data point into the j^th cluster, $V=\{v_{j}^{IFS}\}_{c \times 1}$ denotes cluster centroid and PEDM ${\tilde {d}_{2}(X_{i}^{IFS},v_{j}^{IFS})}$ computes the distance between image pixel $X_{i}^{IFS}$ and centroid pixel $v_{j}^{IFS}$. The weights p_ij, q_ij and ρ_ij is obtained using Algorithms 2, 3 and 4 respectively. The solution of the optimization problem given in (19) can be obtained using Lagrange method of undetermined multiplier which is given as:

$$ \begin{array}{@{}rcl@{}} u_{ij}&=& \left\{{\sum\limits_{k=1}^{c}} \left( \frac{{ \tilde{d}_{2}(X_{i}^{IFS},v_{j}^{IFS}) } }{{\tilde{d}_{2}(X_{i}^{IFS},v_{k}^{IFS}) }} \right)^{\frac{2}{m-1}}\right\}^{-1} \end{array} $$

(20)

$$ \begin{array}{@{}rcl@{}} \mu_{V}(v_{j}) &=&\frac{ \sum\limits_{i=1}^{p}p_{ij} u_{ij} {\mu_{X}(x_{i})}}{ \sum\limits_{i=1}^{p}p_{ij} u_{ij} }, ~~ \forall~~ 1 \leq j \leq c \end{array} $$

(21a)

$$ \begin{array}{@{}rcl@{}} \nu_{V}(v_{j}) &=&\frac{ \sum\limits_{i=1}^{p}q_{ij} u_{ij} \nu_{X}(x_{i})}{ \sum\limits_{i=1}^{p}q_{ij} u_{ij} } , ~~ \forall~~ 1 \leq j \leq \end{array} $$

(21b)

$$ \begin{array}{@{}rcl@{}} \pi_{V}(v_{j}) &=&\frac{ \sum\limits_{i=1}^{p}\rho_{ij} u_{ij} {\pi_{X}(x_{i})}}{ \sum\limits_{i=1}^{p}\rho_{ij} u_{ij} } , ~~ \forall~~ 1 \leq j \leq c \end{array} $$

(21c)

Algorithm 2

Weight matrix P for membership values.

Algorithm 3

Weight matrix Q for non-membership values.

Algorithm 4

Weight matrix R for hesitancy values.

The outline of PIFCM method is depicted in Algorithm 5 [40].

Algorithm 5

PIFCM algorithm.

3 Probabilistic intuitionistic fuzzy c-means with spatial constraint (PIFCM_S)

The acquisition process in an image gives rise to noise, which may bring variation in the pixel intensity value. Hence, the noisy pixels show an anomalous behaviour in its adjacency which leads to incorrect segmentation of image. The PIFCM algorithm does not incorporate any spatial information in its objective function (19) to handle such noises and results in poor segmentation performance. Secondly, the presence of noise in an image makes boundaries around the pixels sensitive and hence affecting the membership degree (20) of a given pixel to cluster. Therefore in this section, we formulate an optimization problem robust to noise, named probabilistic intuitionistic fuzzy c-means with spatial information (PIFCM_S). The inclusion of spatial regularization term in the optimization problem of PIFCM_S makes it robust to handle the problem of noise and uncertainty present between the boundaries in images in the segmentation process. The optimization problem of the PIFCM_S algorithm is defined as:

$$ \begin{array}{@{}rcl@{}} \min J_{m}(U, V^{IFS}: X^{IFS})&=& {\sum\limits_{i=1}^{p}}{\sum\limits_{j=1}^{c}} {u^{m}_{ij}} {\tilde{d}^{2}_{2}(X_{i}^{IFS},v_{j}^{IFS})} \\ &&+ \alpha {\sum\limits_{i=1}^{p}}{\sum\limits_{j=1}^{c}} u^{m}_{ij} {\tilde{d}^{2}_{2}(\Bar{X_{r}}^{IFS},v_{j}^{IFS})} \end{array} $$

(22)

where, U = [u_ij]_p×c(0 ≤ u_ij ≤ 1) represents the fuzzy partition matrix, $X =\{x_{i}^{IFS}\}_{p \times 1}$ represents the image in terms of IFS, and the i^th element $X_{i}^{IFS}$= $\left <\mu _{X}(x_{i}), \nu _{X}(x_{i}), \pi _{X}(x_{i})\right >$, m is a fuzzy parameter, $V=\{v_{j}^{IFS}\}_{c \times 1}$ denotes cluster centroid, α is spatial regularization parameter value and should be tuned proportionally to the noise level present in the image, $\Bar {X_{r}}^{IFS}$ = $\left <\Bar {\mu }_{X}(x_{r}), \Bar {\nu }_{X}(x_{r}), \Bar {\pi }_{X}(x_{r})\right >$ represents mean value of neighboring pixels around the pixel and ${\tilde {d}_{2}(X_{i}^{IFS},v_{j}^{IFS})}$ computes PEDM between image pixel $X_{i}^{IFS}$ and centroid pixel $v_{j}^{IFS}$. The Lagrange method of undetermined multiplier method is used to solve the optimization problem (22). The Lagrangian of optimization problem of PIFCM_S with ζ_i as Lagrange multiplier is defined as:

$$ \begin{array}{@{}rcl@{}} L(U, V^{IFS},~ X^{IFS}:\zeta_{i}) = {\sum\limits_{i=1}^{p}}{\sum\limits_{j=1}^{c}} {u^{m}_{ij}}{\tilde{d}^{2}_{2}(X_{i}^{IFS},v_{j}^{IFS})} \\ + \alpha {\sum\limits_{i=1}^{p}}{\sum\limits_{j=1}^{c}} u^{m}_{ij} {\tilde{d}^{2}_{2}(\Bar{X_{r}}^{IFS},v_{j}^{IFS})} - {\sum\limits_{i=1}^{p}} \zeta_{i}\left( {\sum\limits_{j=1}^{c}}u_{ij} -1\right) \end{array} $$

(23)

Calculating partial derivative of L with respect to μ_V(v_j), ν_V(v_j) and π_V(v_j) and equate them to zero, we have

$$ \underset{\underset{1 \leq j \leq c}{1 \leq i \leq p}} {\forall}~~ \frac{\partial L}{\partial \mu_{V}(v_{j})} ~=~ \frac{\partial L}{\partial \nu_{V}(v_{j})} ~=~ \frac{\partial L}{\partial \pi_{V}(v_{j})} ~=~0 $$

(24)

Simplifying (24), 1 ≤ j ≤ c we obtain

$$ \begin{array}{@{}rcl@{}} \mu_{V}(v_{j}) &=&\frac{ \sum\limits_{i=1}^{p}p_{ij} u^{m}_{ij} {\left( \mu_{X}(x_{i}) + \alpha \Bar{\mu}_{X}(x_{r}) \right)}}{(1+ \alpha) \sum\limits_{i=1}^{p}p_{ij} u^{m}_{ij} } \end{array} $$

(25a)

$$ \begin{array}{@{}rcl@{}} \nu_{V}(v_{j}) &=&\frac{ \sum\limits_{i=1}^{p}q_{ij} u^{m}_{ij} {\left( \nu_{X}(x_{i}) + \alpha \Bar{\nu}_{X}(x_{r}) \right)}}{(1+ \alpha) \sum\limits_{i=1}^{p}q_{ij} u^{m}_{ij} } \end{array} $$

(25b)

$$ \begin{array}{@{}rcl@{}} \pi_{V}(v_{j}) &=&\frac{ \sum\limits_{i=1}^{p}\rho_{ij} u^{m}_{ij} {\left( \pi_{X}(x_{i}) + \alpha \Bar{\pi}_{X}(x_{r}) \right)}}{(1+ \alpha) \sum\limits_{i=1}^{p}\rho_{ij} u^{m}_{ij} } \end{array} $$

(25c)

Similarly, calculate the partial derivative of L with respect to u_ij and ζ_i and equating them to zero, we have

$$ \underset{\underset{1 \leq j \leq c}{1 \leq i \leq p}} {\forall}~~ \frac{\partial L}{\partial u_{ij}}~=~0 \text{~and~} \underset{1 \leq i \leq p} {\forall}~~ \frac{\partial L}{\partial \zeta_{i}}~=~0 $$

(26)

After simplifying (26), we get

$$ u_{ij} = \left\{{\sum\limits_{k=1}^{c}} \left( \frac{{\tilde{d}^{2}_{2}(X_{i}^{IFS},v_{j}^{IFS})} + \alpha {\tilde{d}^{2}_{2}(\Bar{X}_{r}^{IFS},v_{j}^{IFS})}}{{\tilde{d}^{2}_{2}(X_{i}^{IFS},v_{k}^{IFS})} + \alpha {\tilde{d}^{2}_{2}(\Bar{X}_{r}^{IFS},v_{k}^{IFS})}} \right)^{\frac{1}{m-1}}\right\}^{-1} $$

(27)

The final solution is obtained using (3) and (27) with the help of an alternating optimization algorithm which is given in Algorithm 6. The value of spatial regularization parameter α = 0 in (22) reduces to solution of the optimization problem (19)

Algorithm 6

PIFCM_S algorithm.

4 Experimentation setup and results

To check the efficacy of the proposed PIFCM_S algorithm in comparison to other existing counterparts such as FCM [7], IFCM [57], FCM_S [1], FLICM [33], KFCM_S [13], ARKFCM [19], IIFCM [54], KIFCM [38], PIFCM [40], KWFLICM [21], NDFCM [22], WRFCM [55], FRFCM [35] and DSFCMN [60], experiments have been conducted on two publicly available brain MRI dataset. The PIFCM_S method performs clustering of the pixels of the image represented in terms of IFS for image segmentation. For this purpose, we have investigated two well-known intuitionistic fuzzy generation functions, namely Sugeno’s and Yager’s negation functions to convert the MRI images in IFS. Both the variants of proposed method are denoted as PIFCM_S(S) and PIFCM_S(Y) corresponding to Sugeno’s negation function and Yager’s negation function respectively for representing the image. The segmentation performance of both the variants of proposed PIFCM_S method is compared with the state-of-art methods in terms of average segmentation accuracy (ASA) and Dice score (DS). The mathematical definition of the performance measures indexes are summarized in Table 1. In this table, c is the number of clusters; X_i represents the pixels belonging to the manually segmented MRI image (ground truth) and Y_i represent the pixels belonging to the experimental segmented MRI image corresponding to i^th region; mod X_i represents the cardinality of X_i. The datasets used for experimentation are described in Section 4.1.

Table 1 List of performance measures

4.1 Datasets:

4.1.1 Brain MRI datasets :

Two publicly available real world dataset are also used for experimentation. The description about the brain MRI datasets is given as :

• Simulated MRI brain volumes: It is a publicly available dataset from the McConnell Brain Imaging Center of the Montreal Neurological Institute, McGill University [15]. The dataset contains simulated T1-weighted MRI images with different levels of noise (1%, 3%, 5%, 7% and 9%) and intensity inhomogeneity or intensity non-uniformity (INU) (0%, 20% and 40%) of resolution 1 × 1 × 1mm³ with 181 × 217 × 181 dimension with ground truth.

• Internet Brain Segmentation Repository (IBSR): It is a real MRI brain images that has been acquired from the Internet Brain Segmentation Repository (IBSR)¹ which has the ground truth data along with it. For all the MRI images, the brain extraction tool² is utilized for skull striping.

4.1.2 Tool used for experimental results

All the Experimental results are obtained using MATLAB version 9.6 running on a PC having 3.40 GHz frequency and 16 GB of RAM.

4.1.3 Parameter selection:

In this work, we have applied grid search for obtaining the optimal parameter values for all the methods along with the proposed PIFCM_S method based on the optimal value of objective function and the performance measures corresponding to the optimal parameter value is quoted. The proposed PIFCM_S algorithm involves mainly three parameters; fuzzifier factor m, spatial regularization factor α and intuitionistic fuzzy generator parameter β, which have significant impact on the solution of its optimization problem, i.e., cluster centroids and fuzzy partition matrix according to (3) and (27) thereby affecting the cluster performance measures. The optimal values of the parameters in the proposed PIFCM_S and other related methods have been obtained using the grid search method [24]. The parameter value is set based on the maximum average segmentation accuracy obtained. The range of Yager’s negation parameter and Sugeno’s negation parameter is searched in the interval [0,2] and [0,5], respectively, with 0.05 step-size. The optimal value of spatial regularization factor α is chosen in the interval [0,5] with 0.1 step-size depending on the noise level present in the MRI image. The fuzzifier factor m and tolerance criterion 𝜖 are set to 2 and 10^− 5, respectively.

4.2 Results and discussion on BrainWeb datasets

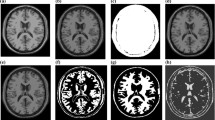
In this section, a detailed discussion and comparison of the performance of the proposed methods, namely, PIFCM_S(S) and PIFCM_S(Y) is presented with other state of art methods in terms of aforementioned performance measure indexes (see Table 1) on BrainWeb simulated MRI datasets. Figure 1 represents the Original image (INU = 40% and noise level = 9% ) and ground truth corresponding to WM, GM and CSF. Figure 2 represents the qualitative segmentation results obtained for WM, GM and CSF using the proposed method and the state-of-the-art methods on this image. From Fig. 2, It can be noted that the qualitative segmentation results obtained using the proposed methods, namely, PIFCM_S(S) and PIFCM_S(Y) better in comparison to the state of art methods. Figure 3(a)-(f) depicts the bar chart of variation of average segmentation accuracy with different levels of INU for a given level of noise. Figure 4(a)-(c) shows the line graph of the variation of average segmentation accuracy with different levels of noise for a given level of INU. Table 2 shows the performance in terms of average segmentation accuracy on brainweb simulated MRI datasets for high levels of noise (7 % and 9%) with different levels of INU (0 %, 20 % and 40 %). From Figs. 3(a)-(f), 4 (a)-(c) and Table 2, the observation drawn is discussed as follows:

• 1. The performance of the proposed method is better than other state of the art methods for a given noise level.

• 2. For a given level of noise, the performance of the proposed method is steady for different levels of INU over state of the art methods where the performance is debased substantially. Although FCM, FCM_S, IFCM and IIFCM methods perform well on INU (40 %) images with low noise (0 %, 1 %, 3 % and 5 %) compared to the proposed method but lag behind on high level of noises (5 % and 7 %).

• 3. As the level of the noise increases (see Fig. 3(a)-(f)), the performance of all the methods debased as expected, but it is less in case of our proposed method in comparison to other related methods.

• 4. Figure 3(f) clearly depicts that the proposed method gives better segmentation accuracy compared to other methods such as ARKFCM, KFCM_S and KIFCM to handle both noise and INU.

• 5. For a given level of INU, the average segmentation accuracy is always going to be debased as the level of the noise increases. But this debasement of the segmentation performance in the proposed method is less in comparison to other methods. This shows that the proposed method is robust towards noise due to successful exploitation of spatial constraint.

• 6. For a given level of INU, the performance of all the methods debased as the level of noise increases from 0 % to 9 % (See Fig. 4(b)-(c)). However, the debasement in the performance of the proposed methods is less in comparison to other methods that shows its robustness towards the INU.

Further, to show the effectiveness of the proposed method over the state-of-art methods for tissue segmentation evaluation, the Dice score for GM and WM is summarized in Tables 3 and 4, respectively. The high values of the DS for both GM and WM tissue evidence the correct identification of the regions in an image using the proposed PIFCM_S method in presence of both noise and INU. From Tables 3 and 4, it is clear that the state-of-art methods are unable to provide comparable results in terms of DS for GM and WM corresponding to the proposed PIFCM_S method except for the FLICM and KFCM_S methods. It is also observed from Figs. 3 and 4 that for low levels of noises (0 %, 1 % and 3 %), the proposed PIFCM_S method gives better performance in terms of ASA when the image is represented in IFS using Yager’s negation function. Whereas, for higher levels of noises (5 %, 7 % and 9 %), the performance of the proposed method is better when the image is represented in IFS using Sugeno’s negation function. This shows the effectiveness of both Yager’s negation function and Sugeno’s negation function over different levels of noise on Brainweb MRI dataset.

Fig. 1

Original image (INU = 40% and noise level = 9% ) and ground truth corresponding to WM, GM and CSF

Fig. 2

Qualitative results for WM, GM and CSF for different methods (Cont..)

Fig. 3

Variation in performance in terms of average segmentation accuracy with INU level of for given level of noise on Brain Web dataset a) 0 % b)1 % c) 3 % d) 5% e) 7% and f) 9%

Fig. 4

Variation in performance in terms of average segmentation accuracy with noise level of for given level of INU on Brain Web dataset a) 0 % b) 20 % c) 40 %

Table 2 Comparison of PIFCM_S with other methods in terms of ASA for Brain Web dataset

Table 3 Comparison of PIFCM_S with other methods in terms of DS for GM for Brain Web dataset

Table 4 Comparison of PIFCM_S with other methods in terms of DS for WM for Brain Web dataset

4.3 Results discussion on real brain MRI dataset

The effectiveness of the proposed PIFCM_S method with other state-of-art methods is further checked on real normal brain MR images from IBSR database for which ground truth is available. For this, the 134th axial slice of T1-weighted image is extracted from IBSR dataset for 8 cases 110_3, 111_2, 11_3, 12_3, 15_3, 16_3, 1_24 and 205_3 and corrupted with 10 % Rician noise to test the performance of the segmentation methods in noisy environment. Table 5 shows the performance of the proposed PIFCM_S method along with state-of-art methods in terms of ASA. From Table 5, it can be clearly seen that the proposed method on real brain MRI images corrupted with 10 % Rician noise outperforms the other related methods. Whereas, the performance of the existing methods for high noise images could not provide satisfactory performance. The utilization of the spatial constraints in the proposed PIFCM_S method provides resistance to noise for real brain MRI images in the IFS framework. Table 6 shows the tissue segmentation performance measure in terms of Dice Score (DS) corresponding to GM on these images. It can be noted from these tables that the proposed PIFCM_S method performs well except on the images 11_3 and 15_3 in comparison to other methods in terms of DS. However, the average value of the proposed PIFCM_S method is higher than other state-of-arts methods (see Fig. 5). Figure 5 shows the average value of ASA and DS for GM over 8 cases of real brain MRI images with 10 % Rician noise. It is evident from Fig. 5 that the proposed PIFCM_S method with Sugeno’s negation function performs well on average over all 8 cases of real brain MRI image in terms of ASA and DS (GM). It reveals the performance of the proposed PIFCM_S method on these images has significant improvement in terms of the performance measures used while comparing with other state-of-art methods.

Table 5 Comparison of PIFCM_S with other methods in terms of ASA for IBSR dataset with Rician noise (σ = 10)

Table 6 Comparison of PIFCM_S with other methods in terms of DS for GM for IBSR dataset with Rician noise (σ = 10)

Fig. 5

Average value of ASA and DS (GM) over 8 cases of the IBSR dataset with 10% Rician noise

4.4 Statistical test

Friedman test, a two way non-parametric statistical test is conducted to find out the significant difference among the proposed and other segmentation methods for both the publicly available datasets. The null hypothesis (H₀) of this test is that there is no significant difference in the performance of the proposed and other segmentation methods whereas the alternative hypothesis (H₁) defines as the performance of the proposed and other methods are different. For a given performance measure M, the H₀ and H₁ can be defined as:

$$ \begin{array}{@{}rcl@{}} H_{0} &:& \mu_{FCM} = \mu_{IFCM(S)} = \mu_{IFCM(Y)} = \mu_{FCM\_S} \\ &=& \mu_{FLICM} =\mu_{KFCM\_S} = \mu_{ARKFCM} = \mu_{IIFCM} \\ &=& \mu_{KIFCM} = \mu_{PIFCM(S)}= \mu_{PIFCM(Y)} \\ &=& \mu_{KWFLICM} = \mu_{NDFCM}= \mu_{WRFCM} \\ &=& \mu_{FRFCM} = \mu_{DSFCMN} = \mu_{PIFCM\_S(S)}= \mu_{PIFCM\_S(Y)} \end{array} $$

(28)

$$ \begin{array}{@{}rcl@{}} H_{1} &:& \mu_{FCM} \neq \mu_{IFCM(S)} \neq \mu_{IFCM(Y)} \neq \mu_{FCM\_S} \\ &\neq& \mu_{FLICM} \neq \mu_{KFCM\_S} \neq \mu_{ARKFCM} \neq \mu_{IIFCM} \\ &\neq& \mu_{KIFCM} \neq \mu_{PIFCM(S)} \neq \mu_{PIFCM(Y)} \\ &\neq& \mu_{KWFLICM} \neq \mu_{NDFCM} \neq \mu_{WRFCM} \\ &\neq& \mu_{FRFCM} \neq \mu_{DSFCMN} \neq \mu_{PIFCM\_S(S)}\neq \mu_{PIFCM\_S(Y)} \end{array} $$

(29)

The rank of different segmentation methods, according to the different performance measures is obtained for comparing the methods separately. In Friedman test, the average rank R_j of j^th methods for a given N number of images is obtained with respect to a given performance measure as:

$$ R_{j} = \frac{1}{N}\sum\limits_{i=1}^{N}{r_{i}^{j}} $$

(30)

where ${r_{i}^{j}}\in \{1, 2, \dots , k\}(1\le i\le N,1\le j\le k )$ is rank value for i^th image and j^th method. Table 7 shows the average Friedman ranking of different segmentation methods corresponding to ASA for 9 BrainWeb brain images and 8 synthetic images used for experiment [17, 20]. Lowest numerical value of rank for a segmentation method shows its better performance compared to other methods for a given performance measure. On the basis of Friedman ranking, the proposed method PIFCM_S(S) performs better in terms of ASA. The statistical hypothesis test proposed by Iman and Davenportis is used. The statistic F_ID is defined by Iman and Davenport [30] is given as:

$$ F_{ID} = \frac{(N-1){\chi_{F}^{2}}}{N(k-1)-{\chi_{F}^{2}}} $$

(31)

which is distributed according to F-distribution with k − 1 and (k − 1)(N − 1) degrees of freedom, where ${\chi _{F}^{2}}$ is the Friedman’s statistic defined as $\frac {12N}{k(k+1)}\left [{\sum }_{j} {R_{j}^{2}} - \frac {k(k+1)^{2}}{4}\right ]$. In our experiments k = 18 and N = 17. The p-value obtained by Iman and Davenport statistic is 0.0 corresponding to the performance measures ASA, which advocate the rejection of null hypothesis H₀ as there is significant difference among different segmentation methods at the significance level of 0.05.

Table 7 Average Friedman Rankings of the algorithms

However, these p-values obtained are not suitable for comparison with the control method, i.e. the one that emerges with the lowest rank. So adjusted p-values [17] are computed which take into account the error accumulated and provide the correct correlation. This is done with respect to a control method which is the proposed method PIFCM_S(S) (lowest rank for ASA). For this, a set of post-hoc procedures are defined and adjusted p-values are computed. The most widely used post-hoc method [17] to obtain adjusted p-values is Holm procedure. Table 8 shows the various values of adjusted p-values obtained. Table 8 indicate that the performance of proposed PIFCM_S method with Sugeno’s negation function and Yager’s negation function in terms of ASA performance measures have no significant difference.

Table 8 Adjusted p-values (Friedman) corresponding to performance measure ASA

5 Conclusion

In this research work, we have presented a intuitionistic fuzzy set theoretic clustering for image segmentation problem that uses probabilistic Euclidean distance measure with a spatial regularization term (PIFCM_S). For this, we have utilized the mean filter image in the spatial regularization term in the segmentation process to dampen the effect of noise. The optimization problem of the proposed approach has the advantage of probabilistic Euclidean distance measure and regularization term to handle the noise in IFS framework. The image representation in terms of IFS increases the representational capability and hence improves segmentation performance. For this, two well-known intuitionistic fuzzy negation functions, namely Yager’s negation function and Sugeno’s negation function have been utilized to convert the gray image in terms of IFS. The experiments are carried out on two publicly available brain MRI dataset for checking the efficacy of the proposed method. Moreover, the comparison of the performance of the proposed PIFCM_S method with other state-of-art methods is carried out on the datasets. The results obtained on these two publicly available datasets show significant improvement in the segmentation performance of the proposed PIFCM_S method in comparison to other related methods in terms of average segmentation accuracy and Dice score. It is clearly depicted from the results that Sugeno’s negation function gives better performance for higher level of noise whereas Yager’s negation function gives better performance for lower level of noise. Further, a statistical test has been performed to check the significant difference in the performance of the proposed PIFCM_S method with the state-of-art methods. The statistical test shows that the performance of the proposed PIFCM _S method is superior over other related methods. The limitation of the proposed PIFCM_S method is the manual tuning of the intuitionistic negation parameter and spatial regularization parameter, which is important to obtain the accurate segmentation. In the future direction, we may investigate an adaptive way to choose the optimal value of these parameters based on the image itself.