Diffusion tensor image denoising via geometric invariant nonlocal means on the tensor manifold

Abstract

Diffusion tensor imaging (DTI) is an advanced magnetic resonance technology that describes subtle brain structures using a diffusion tensor at each point. The obtained DTI image is always degraded since diffusion-weighted imaging sequences, which are used to estimate DTI images, are corrupted by noise. In this paper, we propose an approach called geometric invariant nonlocal means on the tensor manifold (GINLM-TM) to reduce undesired components in the degraded DTI image. We transform the diffusion tensor into a positive definite matrix (called a tensor) to measure the intrinsic property of the diffusion tensor. Then, we directly regularise DTI images in the tensor manifold endowed with an affine invariant metric. Finally, geometrically invariant measures of patches of tensors are used to define the similarity function of patches to ensure the similarity between patches is more accurate and robust. It is experimentally demonstrated that the proposed method performs adequately in reducing undesired components without blurring the boundaries of DTI images. The results of fractional anisotropy (FA) images and fibre tracking of our restored data indicate that our method performs well in denoising the DTI image.

1 Introduction

Diffusion tensor imaging (DTI) [10] is a special form of magnetic resonance imaging (MRI) and describes subtle brain structure using a 3 × 3 symmetric matrix (called diffusion tensor) at each point. Compared with other medical imaging methods, such as computed tomography (CT [7, 9]), MRI, DTI can provide unique information such as white matter fibre travel which has great practical meaning. However, the obtained DTI image is usually degraded as the diffusion-weighted imaging (DWI) sequences, which are used to estimate DTI images, are polluted by Rician noise [26]. The degraded DTI images limit clinical applications, such as the tracked fibre structure not being smooth enough and the fractional anisotropy (FA) measurement [25] of a DTI image is degraded due to the diffusion tensor being disordered and irregular in direction. Therefore, the denoising of DTI images is crucial for theoretical and applied research. In this paper, we provide a novel method to remove the undesired components from the DTI images to improve their qualities.

The nonlocal mean (NLM) filter [8, 18] performs well in denoising digital images, which uses redundant image information to restore the clear image and maximizes the images’ detail features while denoising. The classical NLM filter is generated in [31] to the tensor manifold and is used to regularise DTI images directly. Moreover, a novel nonlocal mean method is proposed in [27] to denoise the DTI data in diffusion tensor space, and they compare the denoise performances of Euclidean distance, Riemann distance, and log-Euclidean distance are used as the nonlocal weighted mean. It shows that using the Riemannian distance can achieve a better denoising effect and that the Riemannian metrics for a similar patch search on the Riemannian geometric space can better preserve the diffusion tensor geometry.

However, the NLM filter measures the patch similarity using the weighted average differences between diffusion tensors in the fixed order. Thus, the geometric information of the patch of diffusion tensors is ignored. In this paper, we introduce two statistics to measure the geometric information of the patch and improve the NLM filter reasonably. Moreover, we use the tensor manifold (each element of which is a symmetric positive definite (SPD) matrix) to measure the diffusion tensor similarity since the Riemannian manifold does measure the intrinsic property of diffusion tensors. However, although most diffusion tensors in DTI images are SPD matrices, there still exist some diffusion tensors that have negative or zero eigenvalues. The existing methods in the Riemannian manifold have ignored these diffusion tensors but processed the diffusion tensors whose eigenvalues are positive. In our work, we provide a method of transforming diffusion tensors into SPD matrices to make sure our filter can use the tensor manifold to measure the intrinsic properties of diffusion tensors.

In general, we propose the geometric invariant nonlocal means on the tensor manifold (GINLM-TM) method to directly regularise DTI images using the tensor manifold. Our main contributions are summarized as follows.

• By transforming diffusion tensors as the SPD matrix, we propose an approach to directly regularise DTI images on the tensor manifold endowed with an affine invariant Riemannian metric. Using the tensor manifold can accurately measure the intrinsic property of diffusion tensors.

• We use geometric invariant measures of tensors’ patches to define the similarity function that is used in our regularisation method, ensuring the accuracy of tensors’ similarity measurement. Here, we derive the intrinsic measures of the tensor patch, which do not change under rigid transformations (e.g., rotation, translation), to define the novel weights to ensure that our method is more robust.

2 Related works

There are mainly three types of methods for denoising DTI images, i.e., denoising DTI images by filtering DWI images, denoising DTI images directly and denoising DTI images using the tensor manifold.

Denoising DTI images by filtering DWI images

At present, some works focus on regularising DTI images by removing noises in DWI sequences using a filter, such as the block-matching fourth-dimensional (BM4D) filter [17], the multichannel Wiener filter [19], or the linear minimum mean square error estimator [1]. In addition, [6] applied Weickert anisotropic filter to DWI smoothing, which can better protect the boundary information of the structure whilst removing noise. The nonlocal means (NLM) algorithm is used in [31] to remove noise in DWI data. The regularised Perona & Malik filter was provided in [33], where the DWI images are denoised by convolving the gradient with a non-Gaussian smoothing kernel. According to the characteristics of DWI images, the weighted nuclear norm denoising algorithm was proposed in [32] for diffusion-weighted image denoising. Translational invariant BayesShrink wavelet thresholding and total variation regularisation are used to remove noise and pseudo-Gibbs phenomena in DWI images in [13].

Denoising DTI images directly

Moreover, some works denoise DTI images by directly normalising diffusion tensors. The coefficients of diffusion tensor matrices are smoothed in [28] using an anisotropy scheme based on the partial differential equations (PDE) to ensure the positive or semipositive properties of the diffusion tensor. The shortcoming of this regularisation is that the information of diffusion tensors is falsified. Diffusion tensors are regularised in [30] during the processing of estimation using Cholesky decomposition of the diffusion tensor. However, such Cholesky decomposition requires that all eigenvalues of diffusion tensors be greater than zero, but the eigenvalues of some diffusion tensors will also have zero or negative values. The feature information of the diffusion tensor is used in [5, 14, 24] to regularise DTI images directly. Lui et al. [14] proposed diffusion tensor imaging denoising based on a Riemannian geometric framework and sparse Bayesian learning. The work of [24] used the energy function of the Markov model to regularise the main eigenvector of the diffusion tensor, while [5] used the iterative recovery method to regularise the eigenvector of the diffusion tensor. However, they only considered the main eigenvectors, which will lead to the loss of some important information during the filtering process.

Denoising DTI images using the tensor manifold

The 3 × 3 diffusion tensor of each voxel in the obtained DTI image is a 3 × 3 diffusion tensor that shares some property of a 3 × 3 SPD matrix (called tensor). Therefore, domestic and foreign scholars apply the Riemannian manifold of tensors to DTI denoising. Several Riemannian or Euclidean metrics for the space of tensors were proposed in [23]. Subsequent studies found that the Euclidean metric was no longer suitable for regularised diffusion tensor images, and the Riemann metric proposed by [2, 4, 21] was effective. The Gaussian filter, anisotropic regularisation method, and harmonic regularisation method under the Riemannian framework were proposed in [22, 29] to restore DTI images. Combined with anisotropic filtering of the structure tensor and Riemannian geometric frame, [16] denoised DTI images based on the complex shearlet in multiscale geometric transformation. Liu et al. [15] learned the prior distribution of patch groups that searched using the Riemannian similarity measures. Lebrun et al. [3] denoised DTI images using the total variation regulariser defined by the extended discrete Riemannian gradient. By reinterpreting the Bayesian approach of [12], a two-step nonlocal patch-based method is proposed in [11] to restore the manifold-valued images, wherein the estimated result of the first step is used to accurately define the distance of patches that is used in the second step.

The remaining parts of this work are organised as follows. Our method is described in Section 3, where the problem of DTI denoising and the motivations of our method are defined in Section 3.1; the transformation of the diffusion tensors are described in Section 3.2; the tensor manifold and geodesic distance between two tensors are described in Section 3.3, and the geometric invariant weights of our method are defined in Section 3.4. Then, several experiments are shown in Section 4. The details are described in the following.

3 Methodology

3.1 Problem formulation

The obtained DTI image can be modeled as F(x) = G(x) + η(x),x ∈Ω, where Ω is a M × N × K 3D grid, F : Ω↦Sym₃ is an obtained DTI image that is degraded by undesired random components η : Ω↦Sym₃, $G: {\Omega } \mapsto Sym_{3}^{+}$ is the clear DTI image, with $Sym_{3}^{+}$ and Sym₃ referring to the tensor space and 3 × 3 symmetric matrix space, respectively.

The purpose of DTI denoising is to design an operator T to ensure $\hat {G}(x) = T(F(x))\approx G(x), x\in {\Omega }$, which means that the undesired components η in the degraded DTI image F are removed, and $\hat {G}$ is the restored DTI image. A suitable denoising approach (corresponding to T) is to convolute the neighbourhood of F(x) by a kernel, i.e.,

$$ \begin{array}{@{}rcl@{}} \hat{G}(x)={\int}_{y\in \nu(x)}w(x,y)F(y)dy, \ \ \ {\sum}_{y\in \nu(x)}w(x,y)=1, \end{array} $$

(1)

where ν(x) is the neighbourhood of x, and w(x,y) is the normalised coefficients defined by x and y (or F(x) and F(y)). Using the maximum similarity expression, the regularisation described in (1) can be reformulated as

$$ \begin{array}{@{}rcl@{}} \hat{G}(x)^{*}=\underset{\hat{G}} {arg \min} {\int}_{y\in \nu(x)}w(x,y)\|F(y)-\hat{G}(x)\|^{2} dy. \end{array} $$

(2)

The definitions of w(x,y) and ∥⋅∥ will significantly affect the performance of DTI denoising. It is reasonable to find a suitable strategy to define the norm ∥⋅∥, which measures the similarity of two diffusion tensors. To describe the intrinsic property of diffusion tensors, we transformed the diffusion tensor into an SPD matrix and defined ∥⋅∥ on the tensor manifold rather than a linear space.

Furthermore, the weight w(x,y) is normally defined by two methods: the space distance of x and y, such as the Gaussian method [22], and the similarity of diffusion tensors G(x) and G(y). Using the second method, the classical NLM method provides a more reasonable definition of w(x,y). Since we can obtain the degraded DTI image F, it is inaccurate to define the weight using F(x) and F(y). The NLM method uses the similarity between patches centered at x and y to estimate the similarity between G(x) and G(y) and finally to define w(x,y).

However, the geometric information of patches has been ignored since the similarity function in the NLM filter is defined by the distance of diffusion tensors arranged in a fixed order. We regard patches from the geometric view, and the similarity between them is measured accurately by their geometric properties that do not change under rigid transformations. Using the tensor manifold and the geometric information of patches, we propose the GINLM-TM approach to correct DTI, and the flowchart of our method is shown in Fig. 1, where the pipeline includes the following steps:

• (a). Target area detection. We first detect the target area that contains tissue information, where the DTI image is estimated by DWI sequences, and the target area is detected using the Ostu method and a DWI image.

• (b). Tensor transform. Diffusion tensors in the obtained DTI F are transformed into tensors using (3), and F_p is the transformed DTI image.

• (c). Assigning the search window and similar patches in F_p. To restore the diffusion tensor at x, we need to assign its neighbourhood (search window) and a series of tensor patches in F_p.

• (d). Calculating invariant measures and weights. Invariant measures of tensor patches are calculated first, and the similarity between patches is measured by both the fixed patch similarity w_ps and the geometric similarity w_gi.

• (e). Restoring the tensor G(x). The tensor is corrected by combining the convolution of the obtained area F(S) and corresponding weights w = w_ps ⋅ w_gi.

• (f). Results. The DTI image is restored by changing the position of the diffusion tensor and repeating steps (d-e) until all diffusion tensors are covered.

Fig. 1

Flow chart of the proposed method, where $M\doteq \mathcal {G}$ is the metric of the tensor manifold. $(M^{s^{3}},M_{p})$ is the space of s × s × s patches of tensors and M_p means that geometric information is used to measure the similarity of patches

The details of our method are described in the following.

3.2 Data preprocessing

DTI images are obtained using water molecule motion of tissue cells. Therefore, it is reasonable to remove the area that does not contain tissue cells and only process the DTI data with tissue information. Moreover, due to the existence of undesired components, some diffusion tensors in DTI images are 3 × 3 symmetric matrices, whose eigenvalues are negative or zero, although most diffusion tensors are SPD matrices. There exists a complete framework [23] for SPD matrix analysis, and the intrinsic properties of SPD matrices are measured under this framework. The symmetric matrix shares some properties of the SPD matrix, and the difference is that the eigenvalues of an SPD matrix are positive, while the eigenvalues of a symmetric matrix may be negative or 0. Therefore, we convert the diffusion tensors in the DTI image into SPD matrices to describe the essential property of diffusion tensors in the tensor manifold.

We preprocess the degraded DTI images in two stages before the denoising process, the details of which are provided as

• Target area detection. We detected the target area in an obtained DTI image by segmenting tissue voxels in the DWI image using the Otsu threshold algorithm. After this process, the DTI image to be regularised contains important tissues and organs of the brain and the areas that do not have anatomical meaning are ignored. Figure 2 shows the results of this procession, where Fig. 2(b) is the whole DTI image estimated from the DWI images Fig. 2(a), (c) and (d) show the detected target area and the DTI image with anatomical meaning, respectively.

• Diffusion tensor transformation. Due to the influence of undesired components, the eigenvalues of some diffusion tensors in the obtained DTI image might not be positive. To sufficiently measure the intrinsic property of the symmetry matrix, we transform the diffusion tensor to ensure its positivity by

  $$ \begin{array}{@{}rcl@{}} F_{p}(x)=U(S+k\cdot Id_{3})V^{T}, \ \ \text{with} \ \ x\in {\Omega}, \ \ \ F(x)=USV^{T}, \end{array} $$

  (3)

  where F_p(x) is the transformed tensor; F is the DTI image after target area detection; Id₃ is a 3 × 3 identity matrix; F(x) = USV^T is obtained using singular value decomposition, and k ≥ 0 is a parameter used to ensure that all eigenvalues are positive. In our experiments, we set k = 10^− 4. This process is reasonable since all eigenvalues have the same operation and k is so small that they do not severely influence the final results.

Fig. 2

Target DTI detection. (a) DWI image, (b) the whole degraded DTI image, (c) the target area to be regularised framed by blue color, (d) the target DTI image

3.3 The tensor manifold

A n × n SPD matrix ${\Sigma } \in Sym_{n}^{+}$ can be decomposed as Σ = UDU^T, where D is a diagonal matrix composed of the eigenvalues of Σ, U is the matrix of eigenvectors, and the decomposition is equal to ${\Sigma }={\Sigma }^{\frac {1}{2}}{\Sigma }^{\frac {1}{2}}$, with ${\Sigma }^{\frac {1}{2}}=U \sqrt {D}U^{T}$. This shows that the natural properties of the tensors are represented by eigenvalues and eigenvectors.

Therefore, $O_{n}{\Sigma } {O_{n}^{T}}$ and Σ have the same eigenvalues and eigenvectors, where O_n ∈ SO(n) is a rotation matrix and $SO(n)= \{ O_{n}\mid {O_{n}^{T}}O_{n}=Id, det(O_{n})=1\}$, Id is a n × n identity matrix. More generally, extending O_n to a matrix A ∈ GL(n) (the linear group of n × n matrices), an affine invariant metric is defined for the tensor manifold $(Sym_{n}^{+}, \mathcal {G})$ (a Riemannian manifold) [23]. The Riemannian metric $\mathcal {G}$ is chosen according to the invariant properties of tensors.

Affine invariant metric

The Riemannian metric of a tensor manifold smoothly assigns an inner product on $T_{\Sigma } Sym_{n}^{+}$ (the tangent space at Σ) to ${\Sigma } \in Sym_{n}^{+}$. The simplest inner product at the identity matrix Id is defined as

$$\left \langle W_{1}\mid W_{2} \right \rangle_{Id}=\text{Tr}({W_{1}^{T}}W_{2}),$$

where W₁ and W₂ are tangent vectors (i.e. symmetric matrices, not necessarily definite or positive) of $T_{Id}Sym^{+}_{n}$. This scalar product is invariant to rotation O_n, i.e.,

$$\left \langle O_{n}W_{1}{O_{n}^{T}} \mid {O_{n}^{T}}W_{2}{O_{n}^{T}} \right \rangle_{Id}=\left \langle W_{1} \mid W_{2} \right \rangle_{Id}.$$

More generally, when W₁ and W₂ are two tangent vectors of $T_{\Sigma }Sym^{+}_{n},{\Sigma } \neq Id$, the scalar product is required to be invariant by the action of any transformation A ∈ GL_n, i.e.,

$$ \begin{array}{@{}rcl@{}} \left \langle W_{1} \mid W_{2} \right \rangle_{\Sigma}=\left \langle A\star W_{1} \mid A\star W_{2} \right \rangle_{A\star {\Sigma}}. \end{array} $$

(4)

The action “⋆” is defined as A ⋆ Σ = AΣA^T. Choosing $A={\Sigma }_{1}^{- \frac {1}{2}}$, the affine invariant metric of the tensor manifold satisfies

$$ \begin{array}{@{}rcl@{}} \left \langle W_{1} \mid W_{2} \right \rangle_{\Sigma}=\left \langle {\Sigma}_{1}^{- \frac{1}{2}} W_{1}{\Sigma}_{1}^{- \frac{1}{2}} \mid {\Sigma}_{1}^{- \frac{1}{2}} W_{2} {\Sigma}_{1}^{- \frac{1}{2}}\right \rangle_{Id}, \end{array} $$

(5)

which means that the scalar product at any Σ can be transformed into the scalar product at identity Id using the affine invariant transformation. Figure 3 shows a tensor manifold endowed with an affine invariant Riemannian metric.

Fig. 3

(a) Tensor manifold $(Sym^{+}_{n},\mathcal {G})$ endowed with an affine invariant metric $M\doteq \mathcal {G}$. The geodesic Γ_Σ, tangent space $T_{\Sigma } Sym^{+}_{n}$ and tangent vector W_Σ at Σ can be transformed to the corresponding elements at Id using affine transformation A

Geodesic distance

Geodesic distance measures the natural distance of tensors and is the fundamental theorem for tensor manifold statistical analysis. Let γ(t),t ∈ [0,1] be the geodesic (the red curve line on the tensor manifold in Fig. 3) connecting Σ and Λ, and Γ(0) = Σ,Γ(1) = Λ. Thus, the length of the geodesic (called geodesic distance) between Σ and Λ is

$$ \begin{array}{@{}rcl@{}} {d_{g}^{2}}({\Sigma},{\Lambda})={{\int}_{0}^{1}}\left \| \frac{d\gamma(t)}{dt} \right \|^{2}_{\gamma(t)}=\left \| W \right \|^{2}_{\Sigma}, \end{array} $$

(6)

Based on the above analysis, the norm (corresponding to length) of a tangent vector W of $T_{\Sigma }Sym_{n}^{+}$ is defined as

$$\left \| W \right \|^{2}_{\Sigma}=\left \langle W \mid W \right \rangle_{\Sigma}= \left \| ({\Sigma}^{-\frac{1}{2}})W({\Sigma}^{-\frac{1}{2}})^{T}\right \|^{2}_{Id}.$$

Here, $W\in T_{\Sigma }Sym_{n}^{+}$ is a tangent vector at Σ and points to Λ, i.e., $W=\overrightarrow {\Sigma {\Lambda } }$. In a Riemannian manifold, a tangent vector is obtained using the manifold’s logarithmic map $\log _{\Sigma }:Sym^{+}_{n} \mapsto T_{\Sigma }Sym^{+}_{n}$, i.e., $W=\overrightarrow {\Sigma {\Lambda }}=\log _{\Sigma }{\Lambda }$.

The logarithmic map at Id is defined as

$$\overrightarrow{Id{\Sigma}}=\log ({\Sigma})=\log_{Id} (UDU^{T})=U\text{DIAG}(\log (d_{i}))U^{T},$$

with D = DIAG(d_i). Then, using the invariant metric, the logarithmic map at Σ is defined as

$$ \begin{array}{@{}rcl@{}} \log_{\Sigma}{\Lambda}={\Sigma}^{\frac{1}{2}}\log ({\Sigma}^{-\frac{1}{2}}{\Lambda} {\Sigma}^{- \frac{1}{2}}){\Sigma}^{\frac{1}{2}} \end{array} $$

(7)

Since the norm of a tangent vector is equal to the corresponding geodesic, a candidate geodesic distance d_g(Σ,Λ) between Σ,Λ is defined as

$$ \begin{array}{@{}rcl@{}} {d_{g}^{2}}({\Sigma}, {\Lambda})=\left \| \log({\Sigma}^{-\frac{1}{2}}{\Lambda} {\Sigma}^{- \frac{1}{2}}) \right \|^{2}_{Id}=\sum\limits_{i=1}^{n}(\log\sigma_{i})^{2}, \end{array} $$

(8)

where σ_i is the ith eigenvalue of ${\Sigma }^{-\frac {1}{2}}{\Lambda } {\Sigma }^{- \frac {1}{2}}$.

3.4 Geometric invariant nonlocal means method on tensor manifold

Since similar small patches may be found several times in an image, the classical NLM approach restores the diffusion tensor at x by

$$ \begin{array}{@{}rcl@{}} \hat{G}(x)=\frac{{\sum}_{y\in \nu(x)}w(x, y)F(y)}{{\sum}_{y\in \nu(x)}w(x, y)}, \ \ \ F(x)\in Sym_{3}^{+} \end{array} $$

(9)

with

$$ w(x,y)=\left\{\begin{array}{lllll} e^{-\frac{\left \| P_{x,s}-P_{y,s} \right \|_{2}}{2\tau^{2}}},& x\neq y\\ \max_{y\in \nu (x)}\{w(x,y)\}, & x= y \end{array}\right.$$

$$\left \| P_{x,s}-P_{y,s} \right \|_{2}=\frac{1}{Num}{\sum}_{i=1}^{Num} d_{g}^{\prime}(V(x_{i}),V(y_{i})), $$

and

$$ d_{g}^{\prime}(V(x_{i}),V(y_{i}))=\left\{\begin{array}{lllll}d_{g}(V(x_{i}),V(y_{i})), \ \ & V(x_{i}),V(y_{i}) \in Sym_{3}^{+}\\ + \infty , & others \end{array}\right.$$

where τ is a parameter, $\nu (x) \subseteq {\Omega }$ is a d × d × d window center at x, V (x_i) and V (y_i) are the i th diffusion tensors of the vector representation of the s × s × s patches P_x,s,P_y,s centred at x and y, respectively, and P_x,s = {F(y)∣y ∈ D_x,s} where $D_{x,s}\subseteq {\Omega }$ is a 3D window centre at x with radius s. Num is the number of cases that satisfy V (x_i) and V (y_i) are both tensors.

Using the similarity between patches P_x,s and P_y,s, rather than F(x) and F(y), to determine w(x,y) can reduce the influence of undesired random components on the similarity measurement to a certain extent. However, some diffusion tensors are not regulated as their eigenvalues are not positive, and they are not used to measure patch similarity $\left \| \cdot \right \|_{2}$. Moreover, the geometric information of patches has been ignored as the similarity between patches is defined by the sum of differences between the tensors arranged in a fixed order. Standing at the geometric viewpoint, we derived intrinsic mean tensor and tensor variance as two geometric invariant measures of the patches to define the similarity between patches. These geometric invariant measures are not influenced by the orientation and rigid transformations and can more accurately define the similarity function.

Therefore, our DTI regularisation approach is defined using the transformed DTI image F_p to make full use of the DTI image, and the geometric information of patches is used to define the similarity of patches. More precisely, our method is defined as

$$ \hat{G}(x)=\frac{{\sum}_{y\in \nu(x)}w_{ps}(x, y)w_{gi}(x,y)F(y)}{ {\sum}_{y\in \nu(x)} w_{ps}(x, y)w_{gi}(x,y)}, $$

(10)

where w_ps(x,y)w_gi(x,y) measures the similarity between patches; w_ps(x,y) is fixed patch similarity defined by the distance between patches $P^{\prime }_{x,s}$, and $P^{\prime }_{y,s}$ in the transformed DTI image F_p, w_gi(x,y) is geometric invariant similarity defined by the invariant measures of the patches. The details of these two types of weights are defined as follows.

The definition of w _ps(x,y)

The fixed patch similarity is defined as

$$ \begin{array}{@{}rcl@{}} w_{ps}(x,y)=\left\{\begin{array}{lllll} e^{-\left ({\sum}_{i=1}^{s^{3}}\frac{\left \| x_{i}-y_{i} \right \|_{e}^{2} d_{g}(V^{\prime}(x_{i}),V^{\prime}(y_{i}))}{s^{3}}\right)/2{\tau_{1}^{2}}},& x\neq y\\ \max_{y\in \nu (x)}\{w_{ps}(x,y)\}, & x= y \end{array}\right. \end{array} $$

(11)

where $\left \| x_{i}-x \right \|_{e}^{2}=\exp ^{-\left \| x_{i}-x \right \|_{2}}$ is defined by the spatial distances between x_i and y_i, which means that tensors that farther away from the center tensor have less impact on the similarity of patches. In our method, $P^{\prime }_{x,s}, P^{\prime }_{y,s}$ are the patches defined in the transformed DTI image F_p, which means all tensors are used to measure patches’ similarity, and $V^{\prime }(x_{i} )$ and $V^{\prime }(y_{i})$ are the i th tensors of the vector representation of $P^{\prime }_{x,s}, P^{\prime }_{y,s}$.

The definition of w _gi(x,y)

The geometric invariant similarity w_gi(x,y) is defined by the geometric invariant information of patches to find more similar tensors to restore G(x), and

$$ \begin{array}{@{}rcl@{}} w_{gi}(x,y)=\left\{\begin{array}{lllll} e^{-\left (d_{g}(\bar{P^{\prime}}_{x,s},\bar{P^{\prime}}_{y,s})+\mid \sigma_{x}-\sigma_{y}\mid \right)/2{\tau_{2}^{2}}},& x\neq y\\ \max_{y\in \nu (x)}\{w_{gi}(x,y)\}, & x= y \end{array}\right. \end{array} $$

(12)

where $\bar {P^{\prime }}_{x,s}$ is the intrinsic mean tensor of patch $P^{\prime }_{x,s}$ and can be calculated by minimising the sum of squared distances, i.e.,

$$\bar{P^{\prime}}_{x,s}= \underset{\bar{P}^{*}_{x,s}}{\arg} {\sum}_{i=1}^{s^{3}} d_{g}(\bar{P}^{*}_{x,s},V(x_{i}))^{2}, \ \ \ \bar{P}^{*}_{x,s} \in Sym_{3}^{+}.$$

The intrinsic mean tensor $\bar {P^{\prime }}_{x,s}$ is practically calculated by the intrinsic Newton gradient descent algorithm [20], i.e.,

$$\bar{P^{\prime}}_{x,s}^{t+1}=\exp_{\bar{P^{\prime}}_{x,s}^{t}}\left (\frac{1}{s^{3}}{\sum}_{i=1}^{s^{3}}\overrightarrow{\bar{P^{\prime}}_{x,s}^{t}V(x_{i})}\right)$$

σ_x is the standard deviation of patch $P^{\prime }_{x,s}$ and is calculated by ${\sigma _{x}^{2}}=\sum \nolimits _{i=1}^{s^{3}}d_{g}$ $(\bar {P^{\prime }}_{x,s}, V(x_{i}))^{2}$. This measure describes the dispersion of patches, and can be used to describe the reasonable similarity between patches.

Properties

Compared with the classic NLM method (9) defined using the difference between tensors in a fixed order, our method is more effective as all the diffusion tensors are regularised and as our similarity function of patches can much more accurately measure the similarity between patches, and the advantages of our similarity function are described in both flat areas and boundary areas:

• Boundary areas. When patches $P^{\prime }_{x,s}$ and $P^{\prime }_{y,s}$ are the boundary areas and $P^{\prime }_{x,s}$ can be obtained by the rotation transformation of $P^{\prime }_{y,s}$, our method prefers to use F(y) to restore F(x) since $P^{\prime }_{x,s}$ and $P^{\prime }_{y,s}$ are more similar from the geometric invariant view. It is reasonable, as F(y) is potentially more similar to F(x) than most other diffusion tensors in the neighbourhood ν(x).

• Flat areas. The similarity function designed using the geometric invariant information of patches can enlarge the differences of the patches, which means it is easier to distinguish more similar patches from all the candidate patches. For example, when $P^{\prime }_{x,s}$ and $P^{\prime }_{y,s}$ are flat areas but $P^{\prime }_{z,s}$ is a boundary area, and w_ps(x,y) = w_ps(x,z), our function tends to use F(y) rather than F(z) to restore G(x) since w₍gi)(⋅) extends the difference between $P^{\prime }_{y,s}$ and $P^{\prime }_{z,s}$.

Therefore, our method is more reasonable as the accumulation of dissimilar patches is avoided by accurately describing the similarity between patches.

4 Experiments and discussion

This section reports DTI regularisation within a platform constructed in MATLAB 2019b (MathWorks, USA). Our experiments were performed on clinical DTI images estimated from 19 DWI sequences of different directions. DWI sequences were obtained from Beijing Shunyi District Hospital with FS= 3, TR= 8000, and TE= 89, and each DWI series included 62 slices. In addition, considering the mechanisms of DTI contamination, we provide two types of comparison strategies.

• The compared methods in the first type are shortened as E-BM4D and E-NLM, respectively, which means that we remove noise in DWI sequences using the BM4D and NLM approaches to regularise DTI images. Then, the regularised DTI images are estimated using these denoised DWI sequences.

• The second type of compared method is the T-G and T-NLM methods, which means that the Gaussian filter [22] and NLM method [31] on the tensor manifold are used to restore DTI images.

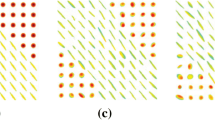
Besides, we show visual results using colour-coded DTI images and the associated FA images obtained with different methods. Each diffusion tensor in the DTI image is represented by an ellipsoid, and the colour is coded by the principal eigenvector (red: left/right, green anterior/posterior, blue: top/bottom), see Fig. 4.

Fig. 4

DTI correction results obtained by different methods, where (b)–(f) refer to the results of E-BM4D, E-NLM, T-G, T-NLM and our method, and (a) is the degraded DTI image

4.1 Comparison experiment

Figures 4 and 5 show the regularised DTI results obtained by different methods, and Fig. 5 is the FA image of Fig. 4. It shows that our method obtains better visual results than other methods in both DTI and FA images.

Fig. 5

FA images of corrected DTI obtained with different methods, where (b)–(f) refer to the results of E-BM4D, E-NLM, T-G,T-NLM and our method, and (a) is the degraded FA image

More precisely, most diffusion tensors in the DTI image (Fig. 4b) that are regularised by E-BM4D method have small eigenvalues although the noisy components are removed. The E-BM4D method severely smooths diffusion tensors and it is difficult to distinguish important boundaries which are provided in the obtained data Fig. 4a. Compared with the results of E-BM4D method with our method Fig. 4f, it can be found that our method performs better in preserving important boundaries and structures. It is because our method attempt to measuring the diffusion tensor instrinsic properties in the tensor manifold. This conclusion can also obtained from the FA measure Fig. 5 of the DTI images in Fig. 4. Figure 5b shows that the white matter in the FA image obtained by the E-BM4D method has been excessively smoothed and expanded. Although the contrast between white matter and gray matter was enhanced, the boundary was blurred, and boundary displacement even occurred.

The Figs. 4c and 5c show the results of the E-NLM method. It shows that most undesired components are still retained in both DTI and FA images after the regularisation using the E-NLM method (see the orange frame). Comparing the result of the E-NLM method and our result shows that using the tensor manifold to remove the noise in the DTI image is considerable.

Although denoising the DTI image base on the tensor manifold, the T-G method can’t obtain acceptable since it has severely blurred DTI and FA images, see Figs. 4–5d. It shows that using the redundant image information to restore DTI images is important. Moreover, Fig. 5e shows that the T-NLM method has obtained an acceptable FA image compared to the above methods, but they still retain some undesired components in the corrected DTI image; see the framed areas in Fig. 4e. However, our result in Fig. 4f shows that our method has the best performance when regularising DTI images, and the geometric features of the diffusion tensor were preserved when reducing most undesired components (see orange and black frames). It is mainly because we consider the instrinsic patch similarity from the shape pointview and use it to improove the NLM method. In addition, our method obtains an improved FA image (Fig. 5f) result without blurring boundaries (see orange and green frames).

Figures 6 and 7 show other comparison results of correcting DTI images. It can be observed from Fig. 7b that the E-BM4D method has shifted the boundaries of white matter, and the edges of the hippocampus (the crescent-shaped object) are difficult to distinguish. Figures 6–7c show that most artifacts are not removed by the E-NLM method. The restored DTI image and its FA image (Fig. 7d) are seriously blurred after the T-G method. The T-NLM method has obtained a considerable result, but some structures are ignored (see the green frame in Fig. 7e), and our method obtains the best results of DTI (Fig. 6f) and FA image Fig. 7f. Our method performs well in preserving details when regularising DTI images, especially the areas highlighted by colored frames. All these results show that using the tensor manifold to measure the intrinsic properties of diffusion tensors is reasonable for denoising DTI images. Moreover, the introduced invariant statistics of patches in our method perform well in preserving essential image boundaries.

Fig. 6

DTI correction results obtained by different methods, where (b)–(f) refer to the results of E-BM4D, E-NLM, T-G, T-NLM and our method, and (a) is the degraded DTI image

Fig. 7

FA images of corrected DTI obtained with different methods, where (b)–(f) refer to the results of E-BM4D, E-NLM, T-G,T-NLM and our method, and (a) is the degraded FA image

4.2 The analysis of the time consumption

The time complexity of our method is various according to d (the size the search area ν(x)) and s (the size of patches). By considering the trade-off between the computational costs and accuracy, we set d = 5 and s = 3, which means there are 125 diffusion tensors in the search area and 27 diffusion tensors in each patch. Then, as for a N × N × N image, the time complexity of our method is O(27 × 125 × N³). Moreover, the parameters τ₁ and τ₁ are respectively recommended to satisfy 1 ≤ τ₁,τ₂ ≤ 5 based on our experiments. In our experiment section, we set τ₁ = 3.0,τ₂ = 4.0 for obtaining acceptable results by using the proper proportion of the patch similarity.

Table 1 shows the time consumption comparison of various methods, where 0.57 × 19 means that the method need 0.57s when processing a DWI image. Therefore, there are total 0.57 × 19s to process these 19 DWI sequences. Table 1 indicates that the consumption time of our method is highest. However, the comparison between the consumption times of the E-NLM method in various platforms shows that the time consumption of a method is indeed dependent on the platform. It also shows that our method is potentially accelerated by another platform. Moreover, since each diffusion tensor processing is independent and does not interfere with each other, our method can be potentially accelerated by GPU parallel computing model, which can be investigated in future work.

Table 1 Time consumption (/s) of different methods with various platforms

4.3 Fibre tracking

Fibre tracking constructs nerve fibre bundles throughout the brain using both FA images and the main diffusion direction of DTI images. To evaluate our method, we tracked fibre structures of the brain using FA results obtained with different methods. Figures 8 and 9 respectively show the tracked fibres with different ROIs, wherein the ROI is the region of interest and the fibres passing through the ROI are tracked. Figures 8 and 9 are the results tracked using a slice of the DTI image and the hippocampus as ROIs.

Fig. 8

The fibres tracked using different methods, with a slice of the DTI image as the ROI

Fig. 9

The fibres tracked using different methods, with the hippocampus as the ROI

It can be seen from these two figures that the fibres of the original DTI image restored by the E-NLM method are messy sue to the existence of undesired components. The fibres obtained with the BM4D method are seriously outspread and do not well represent the fibre structure of the brain. The fibres of the T-G restored DTI image are sparsely distributed as the DTI image is oversmoothed. The fibres tracked using T-NLM and our methods can well represent the outline of the brain, but our method is better as the length of fibres is longer, see the orange framed areas in Fig. 8 and colored framed areas in Fig. 9.

We calculate several statistics to quantitatively evaluate the results of fibre tracking, such as the total number of fibres N_f; the length of the longest fibre L_max; the percentage of long fibres 100% ∗ N_l/N_f, where N_l is the number of fibres that longer than 2 ∗ L_max/3; the percentage of short fibres 100% ∗ N_s/N_f, where N_s is the number of fibres that are shorter than L_max/5; and the mean and variance of fibre length. All these metrics are useful for measuring the performance of fiber tracking. They measure the tracking results from various perspective. To evaluate the general performance of our algorithm on various statistics, we scored the performance of five methods, with “1” meaning the best method and “5” meaning the worst method. The detailed results are marked in black font in Table 2 and the final evaluation score for each algorithm is the sum of all sorts of statistics (marked as “Final”).

Table 2 Several statistics of different fibres that tracked using vary DTI regularisation methods, and the ROIs are respectively hippocampus (noted as 'Part') and all the brain (noted as 'All'), 'Noisy' means the DTI image without regularisation. The performance of each method is scored from 1(low) to 5 (high), which is boldly highlighted

Table 2 shows that when the ROI is the entire brain, our algorithm has the best performance, with a final score of 11, followed by the E-BM4D method with a score of 14. However, the total number of fibres tracked using the restored DTI image with the E-BM4D method is 15,947, which is 2605 larger than the value of the noisy DTI image. This is unreasonable and shows that the E-BM4D algorithm has severely expanded the boundary of the fibre structure. In addition, when the ROI is the hippocampus, the result of our method is slightly worse than that of the E-NLM algorithm but is still acceptable. This is because the FA values in the selected ROI area are almost constant, and the shortcomings of the E-NLM algorithm are ignored. It can also be seen from the numerical statistics of the two parts that our algorithm is better than the T-NLM algorithm and is an effective improvement to the NLM algorithm.

4.4 Discussion

It is observed from the experimental results that the correction of DTI using the geometric information of patches in the tensor manifold is effective. Regularising DTI by denoising multiple DWI sequences is not suitable for clinical application, where the E-BM4D method has seriously distorted the fibre structure of the brain, and the results of E-NLM have remained more undesired components. Moreover, such methods introduce other undesired elements to the restored DTI, such as boundary offset. Compared with other DTI regularisation approaches on the tensor manifold, our proposed method has obtained the best DTI and FA images and tracked fibres. The utilize of statistically invariant factors guarantees that the boundaries in DTI and FA images are accurate, and the natural properties of tensors are preserved well when reducing most undesired components. The tracked fibres can well represent the fibre structure of the brain when reducing noise.

5 Conclusion

We propose an approach for regularising DTI images on the tensor manifold using the geometric information of tensors. All diffusion tensors in the DTI image are transformed into SPD matrices to make full use of the property of symmetric matrices. The intrinsic property of diffusion tensors is measured on the tensor manifold, which is constructed as a Riemannian manifold endowed with an affine invariant metric and can more accurately measure the similarity between diffusion tensors. Then, the transformed DTI image and geometric information of patches of tensors are used to regularise the degraded DTI image. The invariant statistics (the intrinsic mean tensors and variance) are derived to measure the invariant geometric information of patches, and the similarity function of our method defined using these statistics can effectively restore the flat areas and preserve the boundary of the DTI image. The experiments show that the proposed method can regularise DTI more accurately than the compared methods, and retains well the geometric characteristics of the tensors. The NLM filter is indeed time-consuming, which is a drawback of our method. But the restoration of each diffusion tensor is independent and does not interfere with each other. Therefore, the process can be potentially accelerated by GPU parallel computing model.