1 Introduction

There are many tasks in the field of image processing. A literature often focuses on a specific task. For example, the literature [7] designed the multiple images steganography algorithm by studying adaptive payload distribution. The literature [8] proposed a convolutional neural network based forensic framework for detecting the image operations. Denoising is then one of the most fundamental problems in the field of image processing. Currently, a variety of denoising methods have been proposed in the different forms. Among these methods, window-based methods have achieved success. The classical window-based methods have the local Wiener filter method [11] and the nonlocal means (NLM) filter method [1]. They are the representative methods of the window-based local ones and the window-based nonlocal ones, respectively. The common point of two methods is that the denoised result of the processed pixel is obtained by employing the information of the pixels in a neighborhood window centered at the processed pixel. The different point of two methods is that the weights of pixels in the window are the same commonly in the window-based local methods while the weights of pixels in the window are different customarily in the window-based nonlocal methods. Currently, two methods have attracted significant attention. The window-based local methods are very efficient. There have been many variants [2, 4, 13, 18,19,20,21]. The methods in [4, 18,19,20,21] are the development of local Wiener filter. The methods in [4, 18] operate in the wavelet domain. The methods in [19,20,21] can also be seen as variants of nonlinear diffusion in [13]. In fact, nonlinear diffusion method (PMAD) is popular and has been attracting attention since it was proposed by Perona and Malik in [13]. For example, Gaussian filter acts on the image domain to overcome the theoretical and practical limitations of the PMAD model [2]. To solve PMAD model, a new algorithm based on mixed finite element method was proposed in [5]. Recently, a hybrid diffusion framework was established so that the desirable mathematical properties are obtained for PMAD model [9]. On the other hand, the window-based nonlocal methods [3, 6, 10, 12, 14, 15, 17] obtain better performance. But it has been found that the window-based nonlocal methods have usually high computational load. Therefore, some improvements [6, 15] are done to accelerate the window-based nonlocal methods. In addition, the parameters on window-based nonlocal methods are also researched. For example, the weight of the center pixel is modified so that the better results are obtained [12, 14, 17]. In [14], the center weight based on the Stein’s unbiased risk estimate principle was proposed. It is a global center weight which uses the constant weight for all pixels. In [17], a new local James-Stein type center pixel weight (LJSCPW) was developed. LJSCPW is locally tuned for each image pixel. In [12], the novel local center pixel weight estimation methods using Baranchik’s minimax estimator were proposed based on the LJSCPW method. In [3], NLM is improved by the shape-adaptive patches.

In view of good performance of the window-based nonlocal methods and efficiency of the window-based local methods, this paper presents a new image denoising method based on the neighborhood window centered at the processed pixel. The proposed method is different from the previous gradient domain methods. It is called multidirectional gradient domain image denoising (MGDID). This is because that it operates in the multidirectional gradient domain so that the image features can be better captured. And the time step size is adaptive for image contents. The proposed method is different from the NLM filter. This is because that the filter result is obtained in term of the iterative implementation of nonlinear diffusion. Experiment results show that the proposed MGDID obtains good results but is very efficient because of possessing the advantages of the window-based nonlocal and local methods.

The paper is organized as follows. Section 2 first reviews window-based gradient domain layered denoising method and window-based nonlocal method. And then, the derivation of the proposed method is presented. At last, the adjustment strategy of the parameters for the proposed method is described in detail. The experimental results are presented in Section 3. The simulation results show the proposed method achieves the desired effects. The paper is concluded in Section 4.

2 The proposed method

Assume an original image is degraded by additive noise and the noise is signal independent. The typical image degradation model at (i, j) in a two-dimensional coordinate can be written as

$$ {I}_0\left(i,j\right)=I\left(i,j\right)+n\left(i,j\right) $$
(1)

where I, I0, and n represent the original image, the observed image, and the additive Gaussian random noise with zero mean and variance σ2, respectively. The aim here is to restore the original pixel by using neighbor pixels centered at the processed pixel. In the following, the several respects on the proposed method are detailed.

2.1 Gradient domain layered denoising

Gradient domain image denoising based on nonlinear diffusion was proposed in [2, 13, 19,20,21]. Among these methods, the gradient domain local adaptive layered Wiener filter (LALWF) in [20] achieves the very good performance. This method is formed by researching the statistical property of gradient coefficients. In this method, the local Wiener filter [11] was successfully embedded into gradient domain. In term of [20], the scheme of gradient domain LALWF can be written as:

$$ {I}_k\left(i,j\right)={I}_{k-1}\left(i,j\right)+\beta \sum \limits_{u=-l}^l\sum \limits_{v=-l}^l\nabla {\hat{n}}_{k-1}^{u,v}\left(i,j\right) $$
(2)
$$ \nabla {\hat{n}}_{k-1}^{u,v}\left(i,j\right)= threshold\cdotp \nabla {I}_{k-1}^{u,v}\left(i,j\right) $$
(3)

where \( \nabla {I}_{k-1}^{u,v}\left(i,j\right)={I}_{k-1}\left(i+u,j+v\right)-{I}_{k-1}\left(i,j\right) \)(u = − l, − l + 1, ⋯, − 1, 1, ⋯, l and v = − l, − l + 1, ⋯, − 1, 1, ⋯, l) represent the differences of different distances in the different directions centered at (i, j) in the “square” search window, respectively. l ≥ 0 is an integer. β is a constant. Ik represents the kth denoised image. The \( \nabla {I}_k^{u,v}\left(i,j\right) \) is also called the gradient coefficient for image Ik. The computations of gradient coefficient of other images are the same as that of Ik. The (2) and (3) can also be used to describe the traditional gradient domain scheme in form. The difference lies in that threshold is taken as the local Wiener filter in gradient domain LALWF scheme. Obviously, the scheme (2) adopts the iterative scheme to remove noise layer by layer. The preceding step denoising result is the input of the current step denoising. The initial noisy image is input of the first step denoising. In the traditional gradient domain denoising including gradient domain LALWF, the pixels at (i, j), (i + 1, j), (i − 1, j), (i, j + 1) and (i, j − 1) are included in the (search) window. That is to say, the “+” shape (search) window is used in traditional gradient domain denoising. The advantage of the layered denoising lies in that the denoising amount can be flexibly grasped so that the features of image are preserved at the controllable degree.

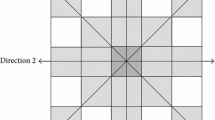
The proposed method will adopt the layered denoising scheme. But, unlike the previous gradient domain, the multidirectional (search) window is used. For the “square” multidirectional (search) window, please see Fig. 1 (l = 2). Multidirectional (search) window can be used to extract the more directional image features. In Fig. 2, clean House image is used for demonstrating the ability of the proposed method to extract multidirectional information. Image feature maps extracted by using multidirectional (search) window with l = 1 are shown. That is to say, the “square” 8 direction (search) window is used in Fig. 2. Obviously, compared to the “+” shape search window with 4 directions, multidirectional (search) window with the “square” 8 direction (search) window extracts more image information (Figs. 2b, d, f and h are the feature maps with “+” shape search window in four different directions).

Fig. 1
figure 1

The “square” search window

Full size image
Fig. 2
figure 2

Feature maps for House (256 × 256) image. Zoom into file for a better view. (a) noise-free House image. (b) (1,0)direction. (c) (1,−1)direction. (d) (0,−1) direction. (e) (−1,−1)direction. (f) (−1,0)direction. (g) (−1,1)direction. (h) (0,1)direction. (i) (1,1)direction

Full size image

In Fig. 2, for the sake of comparison, the feature map \( {f}_{\nabla {I}^{1,0}} \) in the (1, 0) direction is given by

$$ {f}_{\nabla {I}^{1,0}}\left(i,j\right)=\frac{{\left(\nabla {I}^{1,0}\left(i,j\right)\right)}^2-\operatorname{Min}{\left(\nabla {I}^{1,0}\right)}^2}{\operatorname{Max}{\left(\nabla {I}^{1,0}\right)}^2-\operatorname{Min}{\left(\nabla {I}^{1,0}\right)}^2}\cdotp 255 $$
(4)

where Min(∇I1, 0)2 and Max(∇I1, 0)2 are the minimum and maximum “signal” gradient (difference) maps of the clean image House in the (1, 0) direction. The computations of feature maps of different directions of other image are the same as above.

In the design of denoising algorithm, the pre-filter has been successfully used in wavelet transform domain and nonlinear diffusion such as gradient domain for image denoising. So, to better implement the denoising process, the pre-filter way is also adopted in the proposed method. The Gaussian filter is used in the stage of the pre-filter of the proposed method. It operates in the square gradient coefficient. Gaussian filter is used because it assigns the processed pixel the higher weight so that the edges can be retained in the process of denoising.

Gradient domain LALWF employs local Wiener filter to obtain good performance. Local Wiener filter shrinkage function is as follows:

$$ threshold=\frac{\sigma_{k-1}^2}{\sigma_{k-1}^2+\max \left({q}_{k-1}\left(i,j\right)-{\sigma}_{k-1}^2,0\right)} $$
(5)

where the \( \max \left({q}_{k-1}\left(i,j\right)-{\sigma}_{k-1}^2,0\right) \)is “signal” variance at iteration k, the qk − 1(i, j) in size (2l1 + 1) × (2l1 + 1) local (similar) window is computed as

$$ {q}_{k-1}\left(i,j\right)=\frac{1}{{\left(2{l}_1+1\right)}^2}\sum \limits_{i1=-{l}_1}^{l_1}\sum \limits_{j1=-{l}_1}^{l_1}{\left(\nabla {I}_{k-1}^{u,v}\left(i+i1,j+j1\right)\right)}^2 $$
(6)

From above, the conclusion can be drawn that the computation of local “signal” variance is based on the square gradient coefficient. This is the vital step so that Wiener filter can get the good performance. And then, the local Wiener filter shrinkage function is formed. Therefore, the proposed pre-filter way takes the advantage. That is that the proposed method approximately uses the advantages of local Wiener filter because the square gradient coefficient will be integrated into the following shrinkage function. This is different from the previous gradient domain filter. In the previous nonlinear diffusion gradient domain implementation, for example, the method in [2], the image domain Gaussian filter is used, and which is equivalent to the gradient domain Gaussian filter on the gradient coefficient.

2.2 Nonlocal means (NLM)

In the NLM algorithm [1], the restored intensity \( \hat{I}\left(i,j\right) \) is the weighted average of all the pixel intensity values of the processed pixel neighborhood in the noisy image. This method is expressed as:

$$ \hat{I}\left(i,j\right)=\sum \limits_{\left({i}^{\prime },{j}^{\prime}\right)\in N\left(i,j\right)}\omega \left(\left({i}^{\prime },{j}^{\prime}\right),\left(i,j\right)\right){I}_0\left(i,j\right) $$
(7)

where N(i, j) represents the neighborhood at (i, j) and is called the search window. The weight ω((i′, j′), (i, j)) depending on the similarity between I0(i, j) and I0(i′, j′) satisfies 0 ≤ ω((i′, j′), (i, j)) ≤ 1 and \( \sum \limits_{\left({i}^{\prime },{j}^{\prime}\right)\in N\left(i,j\right)}\omega \left(\left({i}^{\prime },{j}^{\prime}\right),\left(i,j\right)\right)=1 \). The similarity between I0(i, j) and I0(i′, j′) depends on the similarity of the intensity gray level vectors I0(Ns(i, j)) and I0(Ns(i′, j′)). Here, Ns(i, j) and Ns(i′, j′) represents the neighborhoods at (i, j) and (i′, j′), respectively. This similarity is measured as a decreasing function of the weighted Euclidean distance \( {\left\Vert {I}_0\left({N}_s\left(i,j\right)\right)-{I}_0\left({N}_s\right({i}^{\prime },{j}^{\prime}\left)\right)\right\Vert}_{G_{\rho}}^2={G}_{\rho}\ast {\left\Vert {I}_0\left({N}_s\left(i,j\right)\right)-{I}_0\left({N}_s\right({i}^{\prime },{j}^{\prime}\left)\right)\right\Vert}^2 \) where Gρ is the Gaussian kernel with standard deviation ρ. The weights are computed as:

$$ \omega \left(\left({i}^{\prime },{j}^{\prime}\right),\left(i,j\right)\right)=\frac{1}{C\left(i,j\right)}{e}^{-\frac{{\left\Vert {I}_0\left({N}_s\left(i,j\right)\right)-{I}_0\left({N}_s\right({i}^{\prime },{j}^{\prime}\left)\right)\right\Vert}_{G_{\rho}}^2}{h^2}} $$
(8)

where C(i, j) is the normalizing constant

$$ C\left(i,j\right)=\sum \limits_{\left({i}^{\prime },{j}^{\prime}\right)\in N\left(i,j\right)}{e}^{-\frac{{\left\Vert {I}_0\left({N}_s\left(i,j\right)\right)-{I}_0\left({N}_s\right({i}^{\prime },{j}^{\prime}\left)\right)\right\Vert}_{G_{\rho}}^2}{h^2}} $$
(9)

and the parameter h acts as a degree of filtering. It controls the decay of the exponential function.

Here, let\( {O}_h={e}^{-\frac{s{h}^2}{h^2}} \)(\( sh=\sqrt{{\left\Vert {I}_0\left({N}_s\left(i,j\right)\right)-{I}_0\left({N}_s\right({i}^{\prime },{j}^{\prime}\left)\right)\right\Vert}_{G_{\rho}}^2} \)), and Oh is called the shrinkage coefficient. sh describes the difference degree between two pixels I0(i, j) and I0(i′, j′). And then let Ratio = O18/O14. Figure 3 presents the picture of Ratio changing with sh. A conclusion can be drawn. The change of h will lead to greater change of the shrinkage coefficient Oh with larger sh. Larger sh often describes more important features of image. Larger h can remove more noise, but may also destroy image features. So, the proper h is very important for denoising performance. In the classical NLM [1], h is σ so that the good result is obtained.

Fig. 3
figure 3

Ratio = O18/O14 varies with the difference degree sh between two pixels (\( {O}_h={e}^{-\frac{s{h}^2}{h^2}} \),\( sh=\sqrt{{\left\Vert {I}_0\left({N}_s\left(i,j\right)\right)-{I}_0\left({N}_s\right({i}^{\prime },{j}^{\prime}\left)\right)\right\Vert}_{G_{\rho}}^2} \))

Full size image

2.3 Derivation for the proposed multidirectional gradient domain image denoising (MGDID)

In fact, after a series of manipulations, the nonlocal scheme (7) can be written as

$$ \hat{I}\left(i,j\right)={I}_0\left(i,j\right)+\frac{1}{C\left(i,j\right)}\sum \limits_{\left({i}^{\prime },{j}^{\prime}\right)\in {N}_0\left(i,j\right)}{e}^{-\frac{{\left\Vert {I}_0\left({N}_s\left(i,j\right)\right)-{I}_0\left({N}_s\right({i}^{\prime },{j}^{\prime}\left)\right)\right\Vert}_{G_{\rho}}^2}{h^2}}\left({I}_0\left({i}^{\prime },{j}^{\prime}\right)-{I}_0\left(i,j\right)\right) $$
(10)

where N0(i, j) represents the hollow neighborhood at (i, j). That is, (i, j) is not included in N0(i, j). From (10), it can be seen that (7) can be considered as one step gradient domain filter scheme. Only unlike the previous scheme, the information of multiple directions is used. This is one advantage of (7) and (10). But (10) has no the merits of the layered denoising. Inspired by (2) and (3), (10) is improved as

$$ {I}_k\left(i,j\right)={I}_{k-1}\left(i,j\right)+\frac{1}{C\left(i,j\right)}\sum \limits_{\left({i}^{\prime },{j}^{\prime}\right)\in {N}_0\left(i,j\right)}{e}^{-\frac{{\left\Vert {I}_{k-1}\left({N}_s\left({i}^{\prime },{j}^{\prime}\right)\right)-{I}_{k-1}\left({N}_s\right(i,j\left)\right)\right\Vert}_{G_{\rho}}^2}{h^2}}\left({I}_{k-1}\left({i}^{\prime },{j}^{\prime}\right)-{I}_{k-1}\left(i,j\right)\right) $$
(11)

Now, the scheme (11) is established. Gaussian filter is used. This is because that Gaussian filter achieves success in NLM. To remedy (11), two factors are introduced. One is h′, and it is a linear factor. Another is θ, and it is a nonlinear remedied factor.

The two factors are used to control the denoising amount at each step. So, the proposed scheme is formulated as:

$$ {I}_k\left(i,j\right)={I}_{k-1}\left(i,j\right)+\frac{h^{\prime }}{C^{\prime}\left(i,j\right)+\theta}\sum \limits_{\left({i}^{\prime },{j}^{\prime}\right)\in {N}_0\left(i,j\right)}{e}^{-\frac{{\left\Vert {I}_{k-1}\left({N}_s\left({i}^{\prime },{j}^{\prime}\right)\right)-{I}_{k-1}\left({N}_s\right(i,j\left)\right)\right\Vert}_{G_{\rho}}^2}{h^2}}\left({I}_{k-1}\left({i}^{\prime },{j}^{\prime}\right)-{I}_{k-1}\left(i,j\right)\right)\left(1\le k\le K\right) $$
(12)

where C′(i, j) = C(i, j) − 1. The step size is \( \frac{h^{\prime }}{C^{\prime}\left(i,j\right)+\theta } \). Obviously, the step sizes at the different locations are changed in a linear proportional fashion with h′. For so, h′ is called a linear factor. On the other hand, \( \frac{h^{\prime }}{C^{\prime}\left(i,j\right)+\theta }/\frac{h^{\prime }}{C^{\prime}\left(i,j\right)}=\frac{C^{\prime}\left(i,j\right)}{C^{\prime}\left(i,j\right)+\theta }=1-\frac{\theta }{C^{\prime}\left(i,j\right)+\theta } \). Here, the parameter θ is a constant. Compared to NLM with “zero” center weight, the bigger C′(i, j) is, the less the step sizes change in the proportion of the reduction. The smaller C′(i, j) is, the greater the step sizes change in the proportion of the reduction. The noisy pixel with more similar pixels will be smoothed more deeply (at this time, C′(i, j) is big). The noisy pixel with less similar pixels will be smoothed more slightly (at this time, C′(i, j) is small). For so, θ is called a nonlinear remedied factor. It plays an important role in tuning the denoising amount at different locations.

In the classical NLM filter, θ is the weight of center pixel. It is taken to be 1 or 0 or the maximal value of weight of pixels in the neighborhood. In the different literature, the value of θ is presented in term of the different ways [12, 14, 17]. This means the role of θ is very important for the denoising performance. But to my knowledge, the optimal θ for the different images at the different cases is still in the study until now. The different literature presents the different computations of θ in NLM implementation. In the proposed diffusion iterative based denoising scheme, the value of θ will be set by empirically in the proposed iterative scheme. Good results are obtained. In the following Section 2.4, the determination of h′,θ and other parameters will be detailed.

In (12), let

$$ {e}^{-\frac{{\left\Vert {I}_{k-1}\left({N}_s\left({i}^{\prime },{j}^{\prime}\right)\right)-{I}_{k-1}\left({N}_s\right(i,j\left)\right)\right\Vert}_{G_{\rho}}^2}{h^2}}\left({I}_{k-1}\left({i}^{\prime },{j}^{\prime}\right)-{I}_{k-1}\left(i,j\right)\right)= threshold\cdotp \left({I}_{k-1}\left({i}^{\prime },{j}^{\prime}\right)-{I}_{k-1}\left(i,j\right)\right) $$
(13)

This shows that threshold is the function of the Gaussian filter result of square difference domain \( {\left({I}_{k-1}\left({i}^{{\prime\prime} }+\left({i}^{\prime }-i\right),{j}^{{\prime\prime} }+\left({j}^{\prime }-j\right)\right)-{I}_{k-1}\left({i}^{{\prime\prime} },{j}^{{\prime\prime}}\right)\right)}^2={\left(\nabla {I}_{k-1}^{i^{\prime },{j}^{\prime }}\left(i,j\right)\right)}^2 \)((i″, j″)covers the image domain) at (i, j). And then, threshold · (Ik − 1(i′, j′) − Ik − 1(i, j)) is rewritten as \( {e}^{-\frac{{\left(\nabla {I}_{k-1}^{i^{\prime },{j}^{\prime }}\right)}_{G_{\rho}}^2\left(i,j\right)}{h^2}}\cdotp \nabla {I}_{k-1}^{i^{\prime },{j}^{\prime }}\left(i,j\right) \) in a simpler form where \( {\left(\nabla {I}_{k-1}^{i^{\prime },{j}^{\prime }}\right)}_{G_{\rho}}^2\left(i,j\right) \) represents the Gaussian filter result of squared difference gradient domain at (i, j).

Finally, the proposed MGDID is expressed as follows:

$$ {I}_k\left(i,j\right)={I}_{k-1}\left(i,j\right)+\frac{h^{\prime }}{C^{\prime}\left(i,j\right)+\theta}\sum \limits_{\left({i}^{\prime },{j}^{\prime}\right)\in {N}_0\left(i,j\right)}{e}^{-\frac{{\left(\nabla {I}_{k-1}^{i^{\prime },{j}^{\prime }}\right)}_{G_{\rho}}^2\left(i,j\right)}{h^2}}\nabla {I}_{k-1}^{i^{\prime },{j}^{\prime }}\left(1\le k\le K\right) $$
(14)

In fact, by contrasting (14) and (7), an important advantage of MGDID can easily be found. That is, the simplicity of the computation compared to the classical NLM (7). The denoising process of MGDID can be more easily implemented by matrix calculation. Since the optimization way of matrix calculation has been very mature, the computation time of the proposed scheme (14) can be reduced dramatically. Section 3 will verify this by running the related methods in the Matlab software.

2.4 Parameters for the proposed MGDID

In MGDID, the size of the filter windows including Gaussian kernel (similar window) and search window, standard deviation ρ of Gaussian kernel, h, h′, θ and iteration number K need to be determined. An intuition is that algorithms should be equipped with almost same parameters for images with the similar structure. The idea has been successfully used in [20]. So, in practice, to determine the parameters under different cases for different images, one image can be taken as test image. This is because that each of natural images consists of many features such as homogeneous domains, edges and details and etc. The optimal parameters of other images can be roughly considered as the vicinity of optimal parameters of the taken image. Based on which, one can determine the parameters of other images by hand in the tests. In the test, the Lena image is taken to determine the parameters.

For each iteration step of the proposed method involves the contributions of more pixels compared to the traditional four-direction gradient domain, the less iteration number is needed. In the test, because of simplicity, K = 2 is selected. For this, the proposed algorithm is a two-stage algorithm in essence. The flowchart of algorithm is shown in Fig. 4. In the first stage (step), noise is removed roughly. In the second stage (step), noise is removed deeply and carefully.

Fig. 4
figure 4

The flowchart of the proposed MGDID

Full size image

In term of the above guidance of determining the parameters. to better preserve the edges, the sizes of the search and similar windows and the standard deviation of Gaussian kernel are smaller in the second step. Let the search window size and the similar window size vary in [3, 5, 7, 9, 11,13,15]. The standard deviation ρ of Gaussian kernel is in [1, 3, 5, 7, 9,11,13,15]. The h′ ranges in [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0,1.1,1.2,1.3,1.4,1.5]. In term of [20], the noise variance is aσ2 (a = 2) in the gradient domain. In practice, a can be set be bigger so that noise can be removed better (in this test, a is taken as 2.2). Assume h is set to be h1 in the first step, and then h is set to be \( {h}_2=\sqrt{a-{h}_1^2}\sigma \) in the second step. In this way, it is expected that the noise can be completely eliminated. As for θ, it varies with 0.005λ(λ ∈ Z). It is noted that the other parameters of the first step are presented first by experience for some θ. And then, the other parameters of the second step is determined carefully when the high PSNR are get. And then, it is found that search window size, h′ and h in two steps have been optimized relatively. Therefore, one adjusts θ by reducing similar window size and the standard deviations ρ of Gaussian kernel. The adjustment is repeated so that the good PSNR result is get.

After a series of tests, the parameters achieving the high peak signal-to-noise ratio (PSNR) is as follows. h1 is 0.70σ and \( {h}_2=\sqrt{2.2-{h}_1^2}\sigma \) in turn. And then h′ is 0.90 and 0.60 by hand in turn. Here, in the second step, the larger h will remove the noise located in image features such as edges deeply. In fact, the role of h has been displayed in Fig. 3. At the same time, smaller h′ is used so that the noise can not be removed excessively. This is because that excessive removal of noise at feature points will destroy image information more seriously such as boundary, texture and so on if h is inappropriate but large. The search window sizes are 11 and 3 in turn. The similar window sizes (Gaussian kernel size) are 13 and 5 in turn. The standard deviations ρ of Gaussian kernel are 5 and 1 in turn from the first step to the second step.

And then, after other parameters is determined, for θ, it is found that the good results are obtained by taking α = 0.015with λ = 3. The influence of the parameter θ is shown in Fig. 5. In Fig. 5, the noisy Lena image (σ = 20) is processed. With the change of θ from 0 to 1, PSNR first increases and then decreases. The optimal θ is taken when the highest PSNR is obtained. The computational error changes the denoising contribution of different pixels so that the proper θ brings the good performance. The computation error behavior is very complex so that it is not possible to provide a more rigorous explanation for the successful use of θ and other parameters. Although other parameter sets are tried, the results with more gains are not obtained.

Fig. 5
figure 5

The role of the nonlinear remedied factor θ for the denoising performance

Full size image

3 The experimental results

The proposed method is applied to several test images corrupted with simulated noises at five different power levels σ ∈ [5, 10, 15, 20, 25]. The test set comprises images from the well-known images such as Lena, House, Boat, Barbara, Peppers and Cameraman of size 256 × 256. Comparisons of restoration performance in terms of quantitative and visual comparisons have been made among the proposed MGDID, GRAD [2], NLM [1] (the center weight is taken as zero), NLM-SAP [3], NLM-LJSCPW [17] and LALWF [20]. For NLM-SAP, NLM-LJSCPW and LALWF, the parameters are set according to the value given by their authors in the corresponding paper. Only for LALWF, the iterative number (IN) is taken so that the highest PSNR is achieved. For GRAD, Gaussian kernel size and standard deviation are 3 and 1, respectively. The diffusion function is the exponential function proposed by Perona and Malik in [2]. The gradient threshold is 0.30σ. The iteration number is taken so that the best results are obtained. For NLM, the center weight is taken as zero. And other parameters are taken according to its Matlab code [10]. For the proposed method, the parameters are taken according to Section 2.4. Restoration performance is quantitatively evaluated by peak signal-to-noise ratio (PSNR) and mean structural similarity (MSSIM) [16] which are defined as

$$ \mathrm{PSNR}\left(\mathrm{in}\ \mathrm{dB}\right)=10{\log}_{10}\frac{255^2}{\frac{1}{PQ}\sum \limits_{i=-1}^P\sum \limits_{j=-1}^Q{\left({E}_{i,j}-{F}_{i,j}\right)}^2} $$
(15)
$$ \mathrm{MSSIM}\left(E,F\right)=\frac{\sum \limits_{ij=1}^R\mathrm{SSIM}\left(x,y\right)}{R} $$
(16)
$$ \mathrm{SSIM}\left(x,y\right)=\frac{\left(2{\mu}_x{\mu}_y+{C}_1\right)\left(2{\sigma}_{xy}+{C}_2\right)}{\left({\mu}_x^2+{\mu}_x^2+{C}_1\right)\left({\mu}_x^2+{\mu}_x^2+{C}_2\right)} $$
(17)

respectively. In (15)–(17), PQ represents the image size;E and F denotes the original image and the denoised image, respectively. x and y are the image contents at the ij-th local window in the original and the denoised image, respectively. R is the total number of local windows in the image; μx and μy are the mean intensity of x and y; σx and σy are the standard deviation; σxy is covariance between of x and y; C1 = (k1L)2 and C2 = (k2L)2 are two variables. L is the range of the pixel values. The default k1 and k2 values are 0.01 and 0.03, respectively.

3.1 Comparison of PSNR and MSSIM values

Table 1 lists the PSNR and MSSIM values of three iterative methods including GRAD, LALWF and the proposed MGDID. The iteration number (IN) of three methods is also presented. The proposed method always outperforms the GRAD in PSNR and MSSIM. In most cases, the proposed MGDID also obtains the higher PSNR and MSSIM compared to LALWF. For example, under thirty cases in PSNR, the result with the proposed method is inferior to LALWF only in two cases. Under thirty cases in MSSIM, the result with the proposed method is inferior to LALWF only in five cases. Furthermore, the iteration number of the proposed method is fixed. The iteration number of LALWF has also some changes for different cases. That of GRAD has great changes for different cases. In practice, the iterative number is hard to manipulate. The proposed method avoids this problem. It is robust in PSNR and MSSIM, and can be implemented easily.

Table 1 The iterative number (IN) used and the PSNR (in dB) and MSSIM results presented by GRAD, [2] LALWF [20] and the proposed method
Full size table

Table 2 lists the PSNR and MSSIM values of NLM, NLM-SAP, NLM-LJSCPW and the proposed method. Obviously, the MGDID method is more stable in terms of PSNR and MSSIM compared to other evaluated methods. It can be seen that the MGDID method is always better than NLM both in PSNR and MSSIM. For Lena, House and Peppers, the MGDID always obtains the highest PSNR and MSSIM. For House, Barbara and Cameraman, the proposed method does not always achieve the best results compared with NLM-SAP and NLM-LJSCPW. But the proposed MGDID is very close to the best results on average. NLM-LJSCPW has usually the bigger difference from the best results. For House, Barbara and Cameraman, the proposed method and NLM-SAP is very close in PSNR and MSSIM. But the proposed method always wins NLM-SAP for Lena, House and Peppers by bigger gains. For example, MGDID wins NLM-SAP 0.72 dB for Lena at σ = 25.

Table 2 The PSNR (in dB) and MSSIM results presented by three NLM methods and the proposed method
Full size table

In a word, in terms of PSNR and MSSIM from Tables 1 and 2, the proposed method is stable and good in performance. Table 3 presents the comparison of LALWF, NLM and the proposed method. For Barbara image with the rich repetitive texture feature, the proposed MGDID outperforms NLM from 0.33 dB to 1.66 dB in PSNR. For Barbara image, NLM usually wins the local adaptive layered Wiener filer (LALWF) based on nonlinear diffusion Scheme 0.44 dB at least in PSNR. Only for Barbara at σ = 5, the proposed method is slightly inferior to LALWF in PSNR. In MSSIM, the proposed method almost always also outperforms LALWF and NLM under all kinds of cases. This shows that the proposed method is the successful development of NLM and nonlinear diffusion methods.

Table 3 The PSNR (in dB) and MSSIM results presented by NLM, [1] LALWF [20] and the proposed method
Full size table

3.2 Comparison of visual performance

Figure 6 shows the denoised results of all the evaluated methods applied to the noisy Barbara image with σ = 20. The observation from Fig. 6 shows that the NLM and NLM-LJSCPW methods cannot suppress noise effectively. The NLM-SAP method leads to the over-smoothing effect near the edges and in the textural areas. In the result with the GRAD, there is a lot of speckles and noise. In the result with LALWF, there are the blurred textures and many spurious blocks. By comparison, the proposed MGDID method provides the best restoration results because it can suppress noise effectively while preserving image details no matter in smooth regions or detail regions. Figure 7 shows the denoised results of all the evaluated methods applied to the noisy Lena image with σ = 10. Compared to NLM and NLM-SAP methods, the proposed method better processes the details. For example, see the hair in the square domain in Fig. 7h. Compared to Fig. 7a, the details of hair are preserved well. But the details of hair in Fig. 7d with NLM and Fig. 7f with NLM-SAP are almost not invisible. The processed results with other methods produce some artifacts or have more residual noises. In a word, the proposed method better processes the noisy image from Figs. 6 and 7.

Fig. 6
figure 6

Comparison of the restoration results from the different methods. Zoom into file for a better view. (a) original Barbara (256 × 256) image. (b) noisy image (σ =20). (c-h) shows restored Barbara images using GRAD, NLM, NLM-LJSCPW, NLM-SAP, LALWF and Proposed, respectively

Full size image
Fig. 7
figure 7

Comparison of the restoration results from the different methods. Zoom into file for a better view. (a) original Lena (256 × 256) image. (b) noisy image (σ = 10). (c-h) shows restored Lena images using GRAD, NLM, NLM-LJSCPW, NLM-SAP, LALWF and Proposed, respectively

Full size image

3.3 Comparison of computational time

The computational burden of the filters is measured as CPU time provided those are filtering the same image in Matlab on the same computer. Table 4 presents the computational time by different methods. The proposed method takes more times compared to GRAD and LALWF. However, the proposed method achieves the overall improvements in performance. Furthermore, the iteration number of the proposed method is fixed. The iteration number of GRAD and LALWF varies with images. More importantly, the proposed method saves more time compared to NLM, NLM-SAP, and NLM-LJSCPW when achieving good results. Therefore, the proposed MGDID is very efficient.

Table 4 The computation load by different methods
Full size table

4 Conclusion

A new approach has been presented for performing high quality image denoising. It is the new development of LALWF. The proposed MGDID operates in multidirectional gradient domain. Inspired by NLM and LALWF, the parameters of the proposed MGDID are designed effectively. Experimental results demonstrate the proposed approach outperforms the state-of-the-art gradient domain and NLM methods in both objective and subjective quality. Especially compared to NLM methods, the proposed method is very efficient. Future research in this field includes optimization of the related parameter and selection of more effective pre-filter.