3D non-rigid shape similarity measure based on Fréchet distance between spectral distance distribution curve

Abstract

3D non-rigid shape similarity is a meaningful and challenging task in deformable shape analysis. In this paper, we present a 3D non-rigid shape similarity measure framework based on Laplace-Beltrami operator which achieves the state-of-the-art performance in shape analysis tasks. The presented framework is used to measure 3D non-rigid shape similarity by calculating the Fréchet distance between the shape spectral distances distribution curves extracting geometry and topology information of shapes. Here, the wave diffusion distance within shape spectral distances is selected because it can describe the shape with high accuracy and does not depend on the time parameter. In addition, our framework is more flexible and computationally efficient: it can be generalized to any distance distribution curves and different distances between the shape distances distribution curves. Experiment results show that the proposed framework can measure 3D non-rigid shape similarity accurately and robustly on benchmarks and have good performance in 3D non-rigid shape retrieval.

1 Introduction

The 3D non-rigid shape similarity measure is a fundamental issue in many fields [10], including shape recognition [12], shape retrieval [9], shape classification [19, 26] and shape registration [2, 15]. At the same time, 3D non-rigid shape similarity measure also provides the theoretical datum and practical base for three-dimensional visualization [47], face recognition [31, 46], and bioinformatics [49]. Especially in recent years, the application of shape similarity in 3D protein model analysis [6, 17] has achieved effective results. Similarity analysis between protein models has become an important topic in protein analysis, through which the structure and function of proteins can be revealed. The basic idea of 3D non-rigid shape similarity is as follows: first, the 3D non-rigid shapes are mapped into the feature space, and the local or global features of the 3D non-rigid shapes or combination of them are selected to replace the non-rigid 3D shape to be desired; second, a cost function or distance function is selected to measure the distance between features as a pair of 3D non-rigid shape similarity. The process can be summarized as two key steps: (1) extracting effective shape features; (2) selecting an appropriate similarity measure. Shape descriptors can capture the effectively features to describe the semantics and geometry information of shapes [21, 25, 38]. The efficient shape descriptors should invariant to structure-preserving non-rigid deformations, particularly isometric, topological and sampling deformation. At the same time, the similarity measure between the captured shape descriptors should be easy to define and calculate. In our paper, we propose a novel global 3D non-rigid shape descriptor with isometric invariance, topological robustness and sampling robustness, can be used to define a 3D non-rigid shape similarity measure. The local features of 3D shapes are integrated into our proposed global descriptor vector using the cumulative distribution curve based on the spectral method.

1.1 Related work

In the rapidly growing field of computer graphics, computer vision and pattern recognition, a number of methods have been proposed so far for defining shape descriptors. Shape descriptors generally include four types: based on shape surface features [7, 14, 29], on shape statistical features [22, 30, 32], on shape topology [40, 43, 45], and those based on spectral analysis methods [33, 39, 42]. Among the above four descriptors mentioned, only descriptors based on spectral analysis can maintain isometric invariance, topological and sampling robustness at the same time. Isometric transformation refers to the transformation in which the shape keeps the length of any curve on the surface unchanged, such as bending the arm. The invariance of the shape after isometric transformation is isometric invariance [41]. Descriptors based on spectral analysis are called spectral shape descriptors and the spectral distance between any two spectral descriptors is defined as the spectral distance [34]. Spectral shape descriptors are derived from the eigenvalues λ_i and eigenfunctions ϕ_i of the Laplace-Beltrami operator (LBO) on the surface of a Riemannian manifold [23].

The global point signature (GPS) is a global spectral shape descriptor that maps the 3D non-rigid shape into an infinite-dimensional space called global point signature embedding dominant [33, 39]. In infinite-dimensional space, GPS(x) at point x on M is defined as follows: $GPS(x) = (\frac {{{\phi _{1}}(x)}}{{\sqrt {{\lambda _{1}}} }},\frac {{{\phi _{2}}(x)}}{{\sqrt {{\lambda _{2}}} }},...,\frac {{{\phi _{n}}(x)}}{{\sqrt {{\lambda _{n}}} }})$. The heat kernel signature (HKS), which incorporates a spectral method for constructing a shape descriptor, was proposed by Sun et al. [42]. Assume a heat source μ_0(x) on the manifold; HKS_t(x,y) defines the heat transferred from point x to point y at time t: ${HKS_{t}}(x,y) = \sum \limits _{i = 0}^{\infty } {{e^{- {\lambda _{i}}t}}} {\phi _{i}}(x){\phi _{i}}(y)$. HKS_t(x,x) is the amount of heat retained at point x after time t: ${HKS_{t}}(x,x) = \sum \limits _{i = 0}^{\infty } {{e^{- {\lambda _{i}}t}}} {\phi _{i}}{(x)^{2}}$. To take into account both the local and global features of shapes, the biharmonic signature (BS) was researched by [28]; the BS balances the local and global features of shapes by regularizing the eigenvalues of the LBO, $BS(x) = (\frac {{{\phi _{1}}(x)}}{{{\lambda _{1}}}},\frac {{{\phi _{2}}(x)}}{{{\lambda _{2}}}},...,\frac {{{\phi _{n}}(x)}}{{{\lambda _{n}}}})$, BS does not depend on the time parameter and overcomes the shortcomings of HKS relying on the time parameter. However, most of the above spectral shape descriptors use low-pass filters, which filter out high-frequency information when describing shape features, the wave kernel signature (WKS) uses a bandpass filter to clearly separate different sets of frequencies on the shape and allows for access to high-frequency information and does not rely on the time parameter [5]. Thus, in our paper, we choose WKS to define a novel descriptor not only inheriting the advantages of WKS but also meeting the requirements mentioned below.

After shape feature extraction, researchers wish to calculate the distance between shape descriptors of a pair of shapes as shape similarity; and they need to ensure that the number of sampling vertices are the same and to find all corresponding points of a pair of shapes. This task is challenging for researchers to perform. A shape distance distribution is a kind of descriptor that extracts shape geometry information and topology by defining metrics on the shape surface. Osada et al. [32] applied statistical methods to select a suitable shape metric function such as the Euclidean distance and calculated the distribution histogram of the shape metric function without finding all corresponding points of the pair of shapes. Other works [18, 27] improved on this developed method, using the geodesic distance distribution [8, 22] as a shape descriptor to compare shape similarity. However, the geodesic distance is not robust to topological changes. In particular, we calculate the wave diffusion distance cumulative distribution function (can be abbreviated as wdd(M)) of WKS on M as a novel shape descriptor, which has isometric variance, is robust to topology and sampling and does not require the corresponding points to be found before calculating the similarity. We compare our method to the method with Bronstein [11], who proposed the diffusion distance distribution and commute-time distance distribution using 3D non-rigid shape recognition.

1.2 Contributions

By defining the wdd(M), we map shapes into a new space, which is called the shape feature space. In this space, each shape is mapped to its cumulative distribution function value of the wave diffusion distance. In addition, we define the shape as a continuous curve in shape feature space. The similarity assessment is calculated by adjusting the similarity threshold such that similar shapes are placed in the same category, and dissimilar shapes are placed in different categories. Common similarity measures include the Manhattan distance (L¹), the Euclidean distance (L²), the Chebyshev distance (L^inf), correlation coefficient, and cosine distance. In our study, we map shapes to a 1D feature space. The Fréchet distance achieves effective results in terms of curve similarity calculations relative to other approaches; therefore, we calculate the Fréchet distance between the wdd(M) and wdd(N) and define this result as the similarity measure of a pair of 3D non-rigid shapes M and N.

The contributions of our research are:

• We present a theoretical and computational framework for 3D non-rigid shape similarity using the shape spectral distances distribution curves based on Laplace-Beltrami operator. The framework is applicable to various shape distance distributions of different shape descriptors. At the same time, the distance between those curves can be selected flexibly, in this paper, we choose the Fréchet distance and researchers can choose other distances flexibly according to their application requirements;

• We propose a new concise shape descriptor called the wave diffusion distance cumulative distribution function curve (wdd(M)) and give the discrete calculation of wdd(M) in detail, the local features of shapes are integrated into global wdd(M) curve using the cumulative distribution curve (CDF) based on the spectral method. It not only has the stability of global statistical method but also inherits the invariance properties of local wave diffusion distance;

• We map the 3D non-rigid shapes into a 1D feature space, and transform the problem of measuring 3D non-rigid shape similarity into a computation of distance between the curves wdd(M) and wdd(N). Compared with other shape similarity measures, the effectiveness and robustness of our method are shown through a large number of detailed comparative experiments on four different types of public databases (SHREC 2011, TOSCA, Bosphorus and SCAPE) and our method performs well in 3D non-rigid shape retrieval based on SHREC2015 database.

The remainder of this paper is organized as follows. In Section 2, we introduce the fundamentals and pipeline of our framework. In Section 3, we construct the feature space and present the definition and discrete calculation of the wdd(M), discuss the invariance of the wdd(M) in detail. In Section 4, we introduce the Fréchet distance and give the calculation method of curve similarity to measure the 3D non-rigid shape similarity, and we also give the calculation for some common distances. In Section 5, we show our experimental results. Finally, we draw conclusions regarding our study in Section 6.

2 Fundamentals and pipeline

In this section, we introduce the pipeline of shape distance distributions for 3D non-rigid shape similarity. Our method is based on spectral analysis theory; in mathematics, the spectral analysis method is derived from the Laplace-Beltrami operator (LBO) on the surface of a Riemannian manifold. The LBO is a well-known intrinsic operator that is decomposed by spectral decomposition, the eigenfunction and eigenvalue of the LBO can be used in different spectral shape descriptors and spectral distances. By calculating the spectral distance distributions of a pair of shapes, the global matching of a pair of shapes can be compared, and a similarity result between a pair of 3D non-rigid shapes is obtained. This section first gives the definition, the discrete calculation and spectral decomposition form of the LBO and then gives the general framework of the shape spectral distance distribution for 3D non-rigid shape similarity. Finally, the pseudo code of our method is given.

2.1 LBO

To effectively represent the intrinsic information and geometric features of the shape, we consider the 3D non-rigid shape as a manifold M. Let M be a two-dimensional smooth compact manifold with boundary equipped with a Riemannian metric d, and let (M,d) be a metric space. For a compact Riemannian manifold M, we apply the spectral distance method to define shape features, which is closely connected with the notion of LBO. The Laplace operator is a differential operator defined by the gradient and divergence of a C² real-valued function f(x,y,z) in Euclidean space:

$$ {\Delta} f = \nabla \cdot \nabla f = {\nabla^{2}}f = \frac{{{\partial^{2}}f}}{{\partial {x^{2}}}} + \frac{{{\partial^{2}}f}}{{\partial {y^{2}}}} + \frac{{{\partial^{2}}f}}{{\partial {z^{2}}}}\ $$

(1)

By equipping the Laplace operator with a Riemannian manifold metric, we obtain the LBO. According to the definition of Riemannian manifold gradient and divergence, if g is the metric tensor on M, G is the determinant of the matrix g_ij, then the LBO can be expressed as [48]:

$$ {\Delta} f = \nabla \cdot \nabla f = \frac{1}{{\sqrt G }}\sum\limits_{i,j = 1}^{n} {{g^{ij}}} \frac{\partial }{{\partial {x^{i}}}}(\sqrt G {g^{ij}}\frac{{\partial f}}{{\partial {x^{j}}}}) $$

(2)

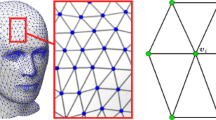
Since the LBO is self-adjoint and semipositive definite, the LBO on M is decomposed into the matrix product of eigenvalue and eigenfunction: Δ_Mϕ_i = λ_iϕ_i, where λ_i is the i − th eigenvalue, and ϕ_i is the corresponding eigenfunction . If the Neumann boundary condition is used in a closed region then the first eigenvalue is 0, and the smallest nonzero eigenvalue is λ₂ (λ₁ < λ₂ < ...λ_i). The LBO can be analytically calculated for some geometrical shape (e.g. rectangular or cylindrical). The LBO eigenfunctions are intrinsic to the manifold, and the ones related to smaller eigenvalues correspond to smooth and slowly varying functions. For numerical computation, the shape M can be represented by a finite set of points. In discrete mathematics, the finite-dimensional discrete LBO is typically called the discrete Laplace-Beltrami matrix. On a triangular mesh with a vertex number of n, the discrete LBO at the v_i of the vertex on mesh can be calculated:

$$ LBO(f({v_{i}})) = \sum\limits_{j = 1}^{n} {{\omega_{ij}}(f({v_{i}}) - f({v_{j}}))} $$

(3)

Equation 3 represents a triangular surface sketch of a vertex v_i, where f(v_i) and f(v_j) denote the scalar function values defined on M, w_ij are weights; for vertex v_i, the discrete LBO can be calculated by [48].

2.2 The Wave Kernel Signature

For each point on a shape, a shape descriptor called the wave kernel signature (WKS) operator is defined by measuring the average probability distribution of quantum particles with different energy levels. The evolution of the quantum particles is governed by the wave function, which is obtained by solving the Schrȯdinger equation [5]:

$$ \frac{{\partial \phi }}{{\partial t}}(x,t) = i{\Delta} \phi (x,t) $$

(4)

The wave function expresses the oscillation of energy, where x is a point in a shape, Δ is the LBO, and i is the imaginary number; the product of the LBO and i ensures that the energy will not decay after oscillating at different frequencies. ϕ(x,t) is the wave function, when t is 0, the expectation of the function ϕ(x,t) is E, and the probability distribution is f_E(λ_k). ϕ(x,t) can be calculated as $\phi (x,t) = \sum \limits _{k = 0}^{\infty } {{e^{i{\lambda _{k}}t}}{\phi _{k}}(x)} {f_{E}}({\lambda _{k}})$, where ${\left | {\phi (x,t)} \right |^{2}}$ is the probability distribution of the particles at point x. The time parameter t has no direct effect on the probability distribution. If we consider only the energy parameters, we define the WKS as a particle whose energy at point x is E and can be measured as the average probability $WKS(x,E) = \mathop {\lim }\limits _{T \to \infty } \frac {1}{T}{\int \limits _{0}^{T}} {{{\left | {\phi (x,t)} \right |}^{2}}}$. Since the functions of $e^{i \lambda _{k}t}$ are orthogonal for the L² norm:

$$ WKS(x,E) = \sum\limits_{k = 0}^{\infty} {{\phi_{k}}{{(x)}^{2}}} {f_{E}}({\lambda_{k}}) $$

(5)

To facilitate calculation, the upper formula is concretely expressed, and the detailed derivation process can be observed [5]. When e_N is the energy scale parameter, e_N = log(E), λ_k is the k − th eigenvalue of LBO, σ is the variance, and ${C_{e}} = {(\sum \limits _{k} {{e^{\frac {{{\text { - }}{{({e_{N}} - \log {\lambda _{k}})}^{2}}}}{{2{\sigma ^{2}}}}}}} )^{- 1}}$ is the regularized WKS function, the wave function WKS(x,e_N) of the particle is given by

$$ WKS(x,{e_{N}}) = {C_{e}}\sum\limits_{k} {{\phi_{k}^{2}}(x){e^{\frac{{{\text{ - }}{{({e_{N}} - \log {\lambda_{k}})}^{2}}}}{{2{\sigma^{2}}}}}}} $$

(6)

In this function, the time parameter has been replaced by energy, which is a very useful aspect; because the energy is directly related to the eigenvalues of the LBO.

2.3 Pipeline

In this paper, we calculate the Fréchet distance between the cumulative distribution function curves of the shape spectral distances as a shape similarity measure. Figure 1 schematically describes the generic framework for measuring the similarity of a pair of 3D non-rigid shapes described by the shape spectral distances distribution curves. This paper selects the wave diffusion distance as an example to illustrate this framework in detail. What’s more, this framework is also adapt to other shape distances. Given a pair of shapes, we can capture some features to describe the shape properties, and researchers can choose other shape features according to their own need, such as GPS, HKS, etc. We can calculate the shape distances between shape features of any two points on a shape and obtain the cumulative distribution function curve of the shape distances. The shape distances distribution curve as a 3D non-rigid shape similarity measure is shown in Algorithm 1. The specific procedure is shown in the following steps:

• A. Input 3D shapes: The first step is to select a pair of 3D shapes. There are a variety of 3D shape storage methods, and this paper deals with triangle mesh models; for example, we wish to compare the similarities between a dog model and a man model named David.

• B. Calculate Shape LBO: For 3D non-rigid shape, its discretion format is triangular mesh. The real-valued function f is defined on its surface. The LBO can be obtained by calculating the divergence value of the gradient value of the real value function. For the calculation method of LBO operator, please refer to (2) and (3).

• C. Calculate Shape Descriptor: According to the spectral decomposition of the LBO, we can obtain the eigenvalue and corresponding eigenfunction of the LBO. And a shape spectral descriptor can be defined at each point of the shape based on the eigenvalue and corresponding eigenfunction of the LBO; for example, in our paper, we select wave kernel signature. For the calculation method of shape descriptor, please refer to (5) and (6).

• D. Calculate Shape Distance: The shape distance is a geometric quantity that characterizes the differences of any two points in a shape and indirectly reflects the characteristics of a shape. We calculate the shape distance of shape spectral descriptor values at any two points in a shape; in our paper, we select the wave diffusion distance. D. For the calculation method of shape distance, please refer to (10) to (12).

• E. Calculate Shape distances distribution curve: According to the statistical method, the cumulative distribution function curve of the shape spectral distances is calculated, and the curve is taken as the feature of the 3D non-rigid shape, and we map the 3D non-rigid shapes into the feature space. For the calculation method of shape distances distribution curve, please refer to (18) and (19).

• F. Calculate Shape Similarity: In the feature space, we measure the similarity of those two curves wdd(M) and wdd(N), which describe the similarity of the corresponding pair of 3D non-rigid shapes. There are many ways to measure the similarity of curves, such as the variance and standard deviation of discrete curves. In this paper, we calculate the Fréchet distance between two curves as a similarity measure of them. For the calculation method of shape similarity, please refer to (20) to (23).

Fig. 1

3D non-rigid shape similarity calculation framework based on the shape spectral distance distribution

3 Feature space construction

To simplify the 3D non-rigid shape into a 1D vector distance, we construct a feature space equipment the wave kernel distance distribution curves. Building the feature space is challenging, as there is intertwined various 3D shapes and topology variability yielding the complex feature parameters of multiple correlated intrinsic properties. The basic method of constructing the feature space is capturing the features from original shapes,then combination the features of original shapes into a new low-dimensional space. The feature in the feature space is the abstraction of original shapes. In this paper, we extract the wave kernel distance distribution function curves as the shape feature based on the method of shape distribution.

3.1 Spectral distance

The spectral distance is induced by the spectral shape descriptor defined on the surface of the shape.

$$ {d^{2}}(x,y) = \sum\limits_{i = 0}^{N} {{f^{2}}} ({\lambda_{i}}){\left| {\phi (x) - \phi (y)} \right|^{2}} $$

(7)

Where f(λ_i) is the filter used for different spectral shape descriptors, the discretization of the spectral distance on the triangular patches is:

$$ {d^{2}}(p,q) = \sum\limits_{i = 0}^{N} {{f^{2}}} ({\lambda_{i}}){({{v_{pi}} - {v_{qi}}} )^{2}} $$

(8)

So we define the distance between WKS values of two points in a shape is the wave diffusion distance. Defining a metric space on the manifold M, the wave diffusion distance is given by

$$ {d_{wks}}^{2}(x,y) = {{\text{C}}_{e}}\sum\limits_{i = 1}^{N \to \infty } {{e^{^{\frac{{{\text{ - }}{{(e_{N} - \log {\lambda_{i}})}^{2}}}}{{2\sigma 2}}}}}{{(\phi (y) - \phi (x))}^{2}}} $$

(9)

For numerical calculation, v_pi and v_qi represent the i − th eigenfunction of the LBO applied to the vertices p and q, respectively. Therefore, wave diffusion distance can be calculated as the following discrete value:

$$ {d_{wks}}^{2}(p,q) = {{\text{C}}_{e}}\sum\limits_{i = 1}^{N} {{e^{\frac{{{\text{ - }}{{(e_{N} - \log {\lambda_{i}})}^{2}}}}{{2\sigma 2}}}}{{({v_{pi}} - {v_{qi}})}^{2}}} $$

(10)

Assuming that there are Num_M vertices on the manifold M (vertex number starting from 1), if we seek the wave diffusion distance for any two vertices on M, the wave diffusion distance matrix of the shape is an Num_M ∗ Num_M symmetric matrix and the main diagonal element is 0 (d_wks(x,x) = 0). The wave diffusion distance matrix D_M is:

$$ D_{M}=\begin{array}{cccc} 0 & {d_{wks}}(1,2) & \hdots & {d_{wks}}(1,Num_{M}) \\ {d_{wks}}(2,1) & 0 & \hdots & {d_{wks}}(2,Num_{M})\\ \hdots \\ {d_{wks}}(Num_{M},1) & {d_{wks}}(Num_{M},2) & \hdots & 0 \end{array} $$

(11)

If we use the distance matrix D_M to calculate the shape similarity, the computational complexity is very high, for example, when Num_M is 10000, D_M is a very large high-dimensional matrix. Therefore, in the next section, we define the cumulative distribution function curve of the distance matrix as a new shape descriptor based on the method put forward by Osada et al. [32].

3.2 Shape distance distribution curve

Due to the different sizes and styles of shapes, the cumulative distribution function curves of the wave diffusion distance of different shapes are also different. So we first normalize the distance before calculating the shape distance distribution curve.

3.2.1 Normalizing the distance matrix

To compare the similarities of different types of shapes and cluster the same type of shapes, we normalize the distance. Normalizing the data can not only improve the calculation accuracy, but also ensure the reliability of the similarity calculation. In our study, we use Z-score normalization, where $\mu _{D_{M}}$ is the mean wave diffusion distance of M and $\sigma _{D_{M}}$ is the standard deviation of the wave diffusion distance of M, dwks∗(x,y) denotes the wave diffusion distance between x and y on M after normalization

$$ {d^ *_{wks}}(x,y) = \frac{{d_{wks}}(x,y) - {\mu_{D_{M}}}}{{{\sigma_{D_{M}}}}} $$

(12)

We normalize the distance matrix and remove the diagonal elements in the matrix as set D^∗ follows:

$$ {D^ * } = {\text{\{ }}{d^ *_{wks}} (1,1),{d^ *_{wks}} (1,2),{d^ *_{wks}} (x,y),...,{d^ *_{wks}} ((Num_{M},Num_{M}){\text{\}}}. $$

(13)

3.2.2 The wave diffusion distance distribution

For any shapes, δ is the distance threshold (the threshold is divided by the difference of the distance and the number of frequency histograms, as given in (15)), μ is a norm metric defined in M, and χ is the indicator function. Let the minimum value of D^∗ is $D^{*}_{min}$, the maximum value is $D^{*}_{max}$, and the interval $[D^{*}_{min},D^{*}_{max}]$ is divided into I segments. To keep the frequency positive, we shift the coordinate axis to $D^{*}_{min}$ to eliminate negative values caused by normalization. Therefore, the frequency histogram can be defined as

$$ {p_{M}}(i) = \int\limits_{1}^{I+1} {{\chi_{((i - 1)\delta + {D^{*} }_{min}) < {d_{wks}^{*}(x,y)} \le (i\delta + {D^ * }_{min}}}}) d\mu (x)d\mu (y) $$

(14)

$$ \delta = \frac{{{D^{*}_{max}} - {D^{*}_{min}}}}{I} $$

(15)

p_M(i) defined this way is the measure of pairs of points with their distance no larger than D^∗_min + iδ and larger than D^∗_min + (i − 1)δ. In probability theory and statistics, the cumulative distribution function (CDF) is an integral of the probability density function (PDF), which is used to fully specify the probability distribution of random variables. For a manifold M, the CDF of a wave diffusion distance F_M(δ) is calculated by

$$ {f_{M}}(i) = \frac{{{p_{M}}(i )}}{{{Num_{M}*(Num_{M}-1)}}} $$

(16)

$$ {F_{M}}(i) = \int\limits_{1}^{I+1} {{f_{M}}} (\delta )d\delta $$

(17)

The total number of D^∗ is Num_M ∗ (Num_M − 1), where f_M(i) is the PDF of wave diffusion distance on M. By integrating f_M(i), we obtain F_M(i), and F_M(i) defined this way is the cumulative probability of pairs of points with distance not larger no larger than D^∗_min + iδ. In this paper, we take the CDF of wave diffusion distance on M as a new shape descriptor and call it wave diffusion distance cumulative distribution function curve wdd(M).

3.2.3 Discrete computing of w d d(M)

Given the wave diffusion distance set D^∗, for any wave diffusion distances after normalization $d_{wks}^{*}(x,y)$, δ is the distance threshold, and the discretization calculation of frequency histogram for D^∗ is:

$$ \begin{array}{c} p_{M}(i) = \frac{{num({D^{*}_{L}} \cap {D^{*}_{R}})}}{{Num_{M}*(Num_{M}-1)}},1 \le i \le Num_{M}\\ {D^{*}_{L}} = \{ d^{*}_{wks}(x,y) |d^{*}_{wks}(x,y) - ((i - 1)\delta + {D^{*}_{min}}) > 0,d^{*}_{wks}(x,y) \in D^{*}\} ;\\ {D^{*}_{R}} = \{ d^{*}_{wks}(x,y) |(i\delta + {D^{*}_{min}}) - d^{*}_{wks}(x,y) \ge 0,d^{*}_{wks}(x,y) \in D^{*}\} \end{array} $$

(18)

Because the distance has been normalized, in Equation.12, it is necessary to add the translation value Dmin∗, where ${{num({D^{*}_{L}} \cap {D^{*}_{R}})}}$ is the number of ${{{D^{*}_{L}} \cap {D^{*}_{R}}}}$, DL∗ represents the subset of D^∗ for which dwks∗(x,y) is larger than (i − 1)δ + Dmin∗, and DR∗ represents the subset of D^∗ for which dwks∗(x,y) is smaller than or equal to iδ + Dmin∗. Because δ is the distance threshold for any dwks∗(x,y), the cumulative distribution function of dwks∗(x,y) can be calculated as discrete:

$$ {F_{M}}(i) = \sum\limits_{i = 1}^{I+1} {f_{M}(i)}, $$

(19)

3.3 Invariance of w d d(M)

The framework we propose is very versatile, making it easy for researchers to choose different filter functions. At the same time, the spectral distance cumulative distribution function inherits the advantages of different spectral descriptors and has good invariances under different transformation. According to this principle, the wdd(M) as a linear shape descriptor, inherits the beneficial features of the wave kernel signature, which has the following characteristics:

Isometric invariance::

The wave diffusion distance has many advantages, among which is isometric invariance; this means that the wave diffusion distance is an intrinsic property of the manifold. Therefore, if we calculate the wdd(M) before and after the isometric change of the shape separately, the theoretical wdd(M) remains unchanged. In general, we use the first 100 eigenvalues and eigenfunctions in the discrete computation of the wave diffusion distance. At the same time, to improve the computational efficiency, we choose 100 discrete points (namely I = 99 in the Equation 15) in the wdd(M) to calculate the shape similarity. Therefore, in practical experiments, the discrete wdd(M) is similar to the theoretical wdd(M).

Topological robustness::

In many real scenarios, the shape not only undergoes isometric deformation but aso suffer from ”topological noise”. WKS uses a bandpass filter for higher stability. Due to the high robustness of the wave diffusion distance to topological changes, the wdd(M) is also robust to topological changes, which is one of the reasons we chose the distribution of the wave diffusion distance as the descriptor.

Sampling robustness::

For the shape M, if the vertices of the triangular mesh model of M are resampled (upsampling, downsampling), including upsampling and downsampling, the resampled wdd(M) is very close to the original wdd(M). Because the wdd(M) is a cumulative distribution curve based on statistical ideas, the number of samples does not affect the shape of the distribution curve.

4 Shape similarity

There are many methods to calculate the similarity of curves, and the most commonly used methods are the Fréchet distance [1] and Hausdorff distance [4]. The Fréchet distance is a similarity measurement between curves that was introduced by Fréchet; this measure is typically explained as the relationship between a person and a dog connected by a leash walking along the two curves and trying to keep the leash as short as possible. The Hausdorff distance is a measure between two sets. Unfortunately, the Hausdorff distance considers only each point in a group without considering how the same group of points interact.

$\boldsymbol {Fr\acute {e}dist~distance}$ [1]: Let the binary group (S,d) be a metric space, where d is the metric function on S. Let A and B are two continous curves on S, $A:[0,1] \rightarrow S$, $B:[0,1] \rightarrow \boldsymbol {S}$, α and β are two reparameterization functions of the unit interval [0,1], namely $\alpha :[0,1] \rightarrow \boldsymbol {S}$, $\upbeta :[0,1] \rightarrow \boldsymbol {S}$. Set t be the time parameter, at time t, the sampling point on curve A is A(α(t)), and the sampling point on curve B is B(β(t)). So the Fréchet distance FD(A, B) of curve A and B is defined as:

$$ FD(A,B)=\mathop {{\text{inf~ max}}}\limits_{\alpha,\upbeta,t \in [0,1]} \begin{Bmatrix}{{\boldsymbol{d}(A(\alpha(t)),B(\upbeta(t)))}} \end{Bmatrix} $$

(20)

In this paper, let the wdd(M): $[0,1] \rightarrow \boldsymbol {S}$ be a continuous, open curve representing a 3D shape, the time parameter t is a constant value, so it is omitted in the calculation later. We calculate the Fréchet distance between two curves wdd(M) and wdd(N) as the similarity measure of a pair of 3D shapes $D_{Fr\acute {e}dist}(M,N)$:

$$ \begin{aligned} D_{Fr\acute{e}dist}(M,N)&= FD(wdd(M) ,wdd(N))\\&=\mathop {{\text{inf~ max}}}\limits_{i\in [1,I+1]} \begin{Bmatrix}(d({F_{M}}(i), {F_{N}}(i))\end{Bmatrix} \end{aligned} $$

(21)

inf is the infimum. In order to calculate the discrete Fréchet distance [16], let wdd(M) and wdd(N) be polygonal curves, wdd (M) = (u₁,...,u_p) and wdd (N) = (v₁,...,v_q). A coupling L between wdd (M) and wdd (N) is a sequence:

$$ \left \| L \right \|=\underset{i\in[1,I+1]}{max}d(u_{i},v_{i}) $$

(22)

Given polygonal curves wdd(M) and wdd(N), their discrete Fr’echet distance is defined to be:

$$ FD(wdd(M) ,wdd(N)) = min\begin{Bmatrix}\left \| L \right \| | ~L~ is~a~coupling~between~wdd(M)~and~wdd(N) \end{Bmatrix} $$

(23)

The Fréchet distance satisfies the following properties:

• Nonnegativity: FD(M,N) >= 0

• Nullity: FD(M,N) = 0 if and only if M = N

• Symmetry: FD(M,N)= FD(N,M)

• Triangle inequality: FD(M,Q) + FD(Q,N) > FD(M,N)

Many classic distances have been studied, both in machine learning and shape analysis and there are many ways to calculate the shape similarity, as shown in Table 1. The list of distances between wdd(M) and wdd(N) are provided in Table 1 will be used in Section 5. Since the discrete computation of Fréchet distance and Hausdorff distance choosing the Euclidean distance, this article no longer compares Euclidean distances.

Table 1 Other distance calculation methods

5 Experiments

We perform several experiments on 64-bit 32G memory, Win10 system Matlab2015 based on the query sets of SHREC 2011 database, SCAPE database [3], Bosphorus database [50], the TOSCA high-resolution database [13] and SHREC 2015 database [35]. The query sets of SHREC 2011 include 13 shape classes. For each shape, transformations are split into 12 classes (isometric, topology, holes, scaling, noise, missing parts, sampling, and so on). In each class, the transformation appears in five different strength levels. This database provides the robustness benchmark for 3D non-rigid shape matching/retrieval algorithms. SCAPE is a 3D non-rigid human database with realistic muscle deformation; the database contains 71 registered meshes of a particular person in different poses. The Bosphorus Database is intended for research on 3D and 2D human face processing tasks including expression recognition, facial action unit detection, facial action unit intensity estimation, face recognition under adverse conditions, deformable face modeling, and 3D face reconstruction. There are 105 subjects and 4666 faces in the Bosphorus database. TOSCA high-resolution database contains a total of 80 objects with a variety of poses, including 11 cats, 9 dogs, 3 wolves, 8 horses, 6 horses, 4 gorillas, 12 females, and 2 different male images; the typical vertex count is approximately 50000. SHREC 2015 contains a training and testing sets (there are 10 different types of models in each set, 10 models in each class, totaling 100 models.) and is made by combining a selection of models from the SHREC’11 non-rigid dataset [24], and the SHREC’14 non-rigid humans dataset [36]; some of the models contain holes, such as eyes and mouth, and some contain self intersecting triangles. Selected shapes of the above databases are shown in Fig. 2.

Fig. 2

Shapes from SHREC 2011, TOSCA 2010 high-resolution, Bosphorus, SCAPE and SHREC 2015

5.1 Experimental set

We perform several experiments to compare the robustness, invariance and high efficiency of wdd(M) and other three spectral distance CDF curves, including commute-time distance (cd(M)) between GPS(x), diffusion distance (dd(M)) between HKS(x), biharmonic distance (bd(M)) between BS(x) and wave diffusion distance (wdd(M)).

First, we select the query sets of SHREC 2011 database including isometric, sampling, topology, holes, noise and scale which is suitable for comprehensive comparison of different distance distribution curves performance. Second, we select the SCAPE database which focus on human with realistic muscle deformation to compare in detail the topological robustness of wdd(M) and other distance distribution curves. Third, selected six expressions collected by all 105 subjects based on Bosphorus database to show the robustness of the proposed operator wdd(M) to approximately isometric deformations (general expressions) and non isometric deformations (laughter, etc.). Last, we select the TOSCA database which includes various isometric transformations of different shapes to show the isometric invariance and sampling robustness of different spectral distance distribution curves in detail; and compare the DVI with different shape similarities which are combined by different spectral distance distributions and different distances; the results are shown seen in Figs. 2 to 7, Tables 2 to 4. Fourth, we conduct non-rigid 3d shape retrieval on SHREC2015 database to show the high efficiency of wdd(M), the results are shown seen in Fig. 8 and Table 5.

Table 2 Robustness of shape similarity using the spectral shape distance CDF curves applied on SHREC 2011 shapes

5.2 Experimental results

5.2.1 SHREC 2011 results

Table 2 shows the different robustness of shape similarity by calculating the Euclidean distance between the original shape and deformable shapes (including isometric, sampling, topology, scale, and noise) by using the four spectral shape distance CDF curves based on SHREC 2011 (we randomly choose five examples: stallion, cat, horse, dog and lion). In the Table 2, the minimum values of the Euclidean distance between the original shape and the changed shapes by using the four spectral shape distance CDF curves are bold. Among the most deformations, wdd(M) has good robutness than other spectral shape distance. For noise, the wdd(M) can achieve a better robustness in most instances, cd(M) is second only to MD and those value is very close. As seen in the Table 2, the robutness of wdd(Stallion) is weaker than that of cd(Stallion) and because there are individual differences in SHREC2011. And we can see from the Fig. 3, the wdd(stallion) curve is not completely close to wdd(stallion with noise) curve, the model show that the noise deformation of the stallion is relatively large. We found that most of the results (including isometric, sampling, topology) by using the wdd(M) are smallest. This shows that the wdd(M) is more robust than other three spectral shape distances CDF curves, particularly in the isometric, resampling, topological and scale deformations.

Fig. 3

The CDF curves of wdd(stallion) and wdd(stallion with noise)

5.2.2 SCAPE results

To compare the topological robustness of the four spectral distance CDF curves in detail, we first calculate the Fréchet distances of the 71 shapes and the benchmark shape by using the four spectral distance CDF curves and clustered the 71 shapes. Then the Fréchet distance between any two shapes was calculated as the distance matrix and the DVI [20] of the cluster of the four spectral CDF curves were calculated. In our paper, we choose DVI to evaluate the classification accuracy of using different similarity methods:

$$ DVI = \frac{{\mathop {\min }\limits_{0 < m \ne n < K} \left\{ {\mathop {\min }\limits_{\forall {x_{i}} \in {{\Omega}_{m}},{x_{j}} \in {{\Omega}_{n}}} \{ \left\| {{x_{i}} - {x_{j}}} \right\|\} } \right\}}}{{\mathop {\max }\limits_{0 < m \le K} \mathop {\max }\limits_{\forall {x_{i}},{x_{j}} \in {{\Omega}_{m}}} \left\{ {\left\| {{x_{i}} - {x_{j}}} \right\|} \right\}}} $$

(24)

Ω_m and Ω_n are the m − th and n − th clusters, K is the number of clusters, DVI characterizes the minimum value of the smallest distance between any two clusters (between classes) divided by the maximum value of the largest distance of the two points in any cluster (within classes). The larger the DVI, the larger the distance between the classes of the shape and the smaller the distance within the class. Therefore, we hope that the DVI of the selected shape similarity is as large as possible.

Figure 4 shows the clustering results and DVI results. The clustering results of wdd(M) are more concentrated, indicating that the topological robustness of wdd(M) is higher than the other three spectral distance distribution curves. DVI of wdd(M) is the biggest one among the four shape spectral distance CDF curves, this shows that when using wdd(M) to describe the shape, the distance within the class is small, and wdd(M) has strong topological robustness.

Fig. 4

Clustering results of the Fréchet distances by using four different shape spectral distance curves on the SCAPE database

5.2.3 Bosphorus results

After verify the isometric, resampling, topological, scale and noise robustness of four CDF curves, we focus on show the robustness of wdd(M) to approximately isometric deformations (different expressions) based on Bosphorus database. There are 105 subjects with different expressions in the Bosphorus database, but not all of them have the same expressions. Some expressions are only collected by some subjects, such as fear, anger, disgust, etc. In order to compare the robustness of different expressions of 105 subjects(bs001-bs104), we selected six expressions collected by all 105 subjects for the experiment. We transform the model format(.bnt to .txt), encapsulate it into triangle mesh structure (.obj), remove the self intersection inside the model, denoise and manifold it. Finally, we get 630 mesh models as experimental models. We calculate the wdd(M) robustness of five expressions and the initial model (bs***NN0 models). Last, we give the violin plot for wdd(M) robustness of five expressions.

Table 3 shows the robustness of wdd(M) by calculating the euclidean distance between the original model (NN0 models) and five models with different expressions (including EHAPPY, PRSD0, UFAU, LFAU12, LFAU27) based on Bosphorus database. From the Table 3, we can see that the wdd(M) has strong robustness to approximate isometric transformation (different expression changes of 3D face).

Table 3 The robustness of five expression models of 105 subjects and their original models based on Bosphorus database

In order to clearly see the distribution of the robustness of five expressions of 105 subjects, we draw the violin plot according to the data in Table 3. Violin plot is used to display data distribution and its probability density, which combines the characteristics of box plot and density plot. The middle blue line is the median, and the blue line running through the violin plotting represents the range from the minimum value to the maximum value. Figure 5 shows the violin plotting for five expressions in Bosphorus database.

Fig. 5

The violin plot for five expressions in Bosphorus database

From the Table 3 and Fig. 5, The median and average values of EHAPPY models are the largest among the five expression models, which indicates that EHAPPY models have relatively large deformation. At the same time, the median value of EHAPPY models is greater than the average value, indicating that its overall distribution is in an up (left) skew; unlike EHAPPY models, the median value of other four groups of expression models is less than the average value, indicating that its overall distribution is in a down (right) skew. This shows that the robustness of 105 EHAPPY models is slightly lower than that of the other four expression models, and this conclusion is also consistent with the property of spectral distance. In a word, the overall data above show that wdd(M) is robust to approximately isometric changes.

5.2.4 TOSCA results

In order to compare the sampling robustness and isometric invariance of different shape similarities and quick calculation, we downsample the vertices of shapes of the TOSCA database to 50 percent of original shapes and performed several experiments with these based on TOSCA database. We first display CDF curves of wave diffusion distance of shapes from the TOSCA database (the result is shown in Fig. 6). Second, we use a thermodynamic diagram to demonstrate the results of shape similarity: the more similar two shapes are, the blacker the color; the more dissimilar, the redder the color. When similarity equals the mean value, the color is white. The aim is that the color of each class in the thermodynamic diagram is as distinct as possible and that the color differences between classes are as large as possible to show that the similarity measure method can measure different classes of shapes (the result is shown in Fig. 7). Last, we calculate the DVI for different shape similarities (the result is shown in Table 4).

Fig. 6

Wave diffusion distance distribution CDF and PDF of selected TOSCA database shapes

Table 4 Dunn validity index of resampling the TOSCA shape similarity using different shape descriptors

Figure 6 displays CDF curves of wave diffusion distance distributions of shapes from the TOSCA database. As shown in Fig. 6, the CDF curves of the isometric shapes can be easily clustered and curve separation is large for different types of shapes, but David and Michael are both models taken from humans; thus, their curves are very close. Researchers can use CDF curves efficiently to calculate the similarity.

Figure 7 displays different shape similarities of four spectral distance distribution CDF curves of shapes from the TOSCA database (the more similar two shapes are, the blacker the color; the more dissimilar, the redder the color. When similarity equals the mean value, the color is white.). We use six similarity measures to measure the similarity of six different equidistant shapes: david, dog, cat, horse, centaur, and michael. In this experiment, we do not need to consider how the same group of points interact, so Hausdorff distance can obtain the same discrete results as the Fréchet distance. Figure 7a shows that using the cd(M), it is difficult to separate the six types of shapes. The distance between different classes is small. Figure 7b shows using the dd(M), six kinds of similarities can well distinguish six kinds of shape. In addition, the Fréchet distance and Hausdorff distance perform better than the other four kinds of similarity measure. We find that using the Fréchet distance and Hausdorff distance, the DVI of each type is higher, and we obtain the best performance. Figure 7c shows using the bd(M), the six kinds of measures cannot distinguish the six kinds of shapes well. Here, the L^inf distance performance is the worst, the results of the other five shape measures are consistent. Figure 7d shows that using the wdd(M), all six kinds of measures can accurately distinguish six kinds of shapes. Fréchet distance, Hausdorff distance, correlation distance, and cosine distance perform better than the other two kinds of similarity measure. The above analysis indicates that in the four spectral distance distributions, the overall performance of the wave diffusion distance distribution is better than the other distances, and the Fréchet distance and Hausdorff distance are better than the other four types of similarity measure.

Fig. 7

Shape similarities of 6 shape classes using different similarity measure

Further we calculate the DVI of different shape similarities. As shown in Table 4, when wdd(M) is selected, the DVI of the six distances is relatively high, the DVI of the Fréchet distance and the Hausdorff distance is the largest. As can be seen from the Table 4, the DVI of the L^inf distance is larger than the ones evaluated by cosine and correlation, because the intra-class distance of the shape using the L^inf distance is very small. At the same time, DVI of bd(M) are relatively small, and this result is also consistent with section 5.2.1, the isometric invariance of bd(M) is relatively worse than other spectral distance CDF values.

5.2.5 SHREC 2015 retrieval results

After showing the robustness, invariance of wdd(M) we proposed by comparing to other five distances between four spectral distance CDF curves, we conduct 3D shape retrieval by our proposed shape similarity using wdd(M) and compare the effectiveness to some retrieval methods including eleven different canonical forms using the CM-BOF method given in paper [35, 37], which proposed SHREC 2015 database and gave the 3D non-rigd shape retrial benchmark results on SHREC 2015. For canonical forms’ retrieval performance analysis, we can refer to paper [35, 37].

Table 5 shows the retrieval accuracy of our method and eleven different canonical forms using the CM-BOF retrieval algorithm on three evaluation criteria: the nearest neighbour (NN), first tier (FT), second tier (ST) [44]. The measurement ranges of the three different evaluation criteria are 0 to 1. The higher the measurement, the better the performance of the retrieval method. The bold numeric values show the highest performance. Among all the evaluation criteria, our method depicts the highest value and the table thus demonstrates that search performance of our method is superior to the canonical forms.

Table 5 Retrieval accuracy on different methods using the NN, FT and ST

Figure 8 shows the PR curves for our method and the CM-BOF retrieval algorithm on the ten different sets of canonical forms. The precision-recall (PR) curves reflects the relationship between precision and recall. The higher the curve is, the more effective the feature is. Figure 8 shows that our method improved the precision for both low and high recall values, indicating that our method is better than these canonical forms.

Fig. 8

Precision-Recall curve performance comparison on SHREC 2015 database

Both Table 5 and Fig. 8 show that our method is effective for non-rigid shapes because it employs global statistics based on local feature(WKS) which describes the details of shapes. Through conducting non-rigid 3D shape retrieval which is an application of shape similarity, it is shown again that the method proposed in this paper has good performance.

5.3 Discussion

cd(M) curve can accurately reflect the context of all points of the shape information, but its ability to describe the local characteristics is weak. The dd(M) curve is sensitive to time parameters, so the local and global attributes of the shape cannot be represented at the same time. The bd(M) curve balances the large-scale distance (reflecting the global property) and the small-scale distance (reflecting the local property), but it lose some robustness. The greatest advantage of wdd(M) is not interaction with time parameters; the wdd(M) uses a band-pass filter that clearly separates the different sets of frequencies in the shape. At the same time, the wdd(M) has multiscale characteristics by selecting different energy levels. If the quantum particles with higher energy level are selected, the shorter the wavelength distribution, the closer the distribution is to the shape point and the local characteristic of the shape; in contrast, low-energy quantum particles reflect the global property of the shape.

6 Conclusions

We propose a framework for measuring the 3D non-rigid shapes similarity by combining the geometric properties and statistical characteristics of shapes. In our method, we measure the 3D non-rigid shape similarity using shape spectral distance distribution curves. Our method extends the invariance properties to non-rigid deformation and could not find the corresponding vertices of shapes in advance. Compared to the framework proposed by Bronstein [11], our framework is more ubiquitous for measuring the similarity of 3D non-rigid shapes, which allows users to flexibly apply this framework according to their needs. In this paper, we choose the wave diffusion distance within the spectral distances and experiment results show the wave diffusion distance could describe the shape properties well and improve the accuracy of shape similarity measure by calculating the Fréchet distance between wave diffusion distance cumulative distribution function curves of shapes. At the same time, as an application of shape similarity, our method performs well in 3D non-rigid shape retrieval. Through this paper, we profound the theoretical significance and engineering practicality of our method in 3D non-rigid shape similarity calculations.