Topology-preserving nonlinear shape registration on the shape manifold

Abstract

Shape registration is a vital task in computer vision and image processing, but the topology changes always occur in registration process of two shapes with large deformation. In this paper, we address the shape registration with large deformation by an atlas based method. Concretely, we first represent the shape by the square root velocity functions (SRVFs) which makes registration of two shapes with small deformation well. Then, we hierarchically cluster all shapes and form a clustering tree under this representation. Further, by searching the shortest path connecting two shapes we realize the registration with topology preserving. Finally, the numerical results on the Kimia shape dataset show that our proposed method achieves a better performance of registration than the conventional method. That is, the atlas-based strategy is valid for shape registration with large deformation.

1 Introduction

Shape registration is to find the best correspondence between two or more shapes, which is widely used in computer vision, medical image analysis, and object recognition, etc. It offers an efficient way to the huge size image registration because the shape is a sparse and well representation for the image. On the other hand, the shape also has the advantage of invariant representation for scaling, configuration, color, and texture, etc. Therefore, in recent years shape registration shows the irreplaceable advantage than the conventional image registration methods in the fields of 3D vision and object recognition [14, 22]. For example, facial matching [5, 30], human pose estimation [26, 31], etc. With the wide application of shape registration, more and more researches have been done on shape registration [18, 28].

Due to the difference between shape representation, there are mainly two ways to register them. The first way is the landmark-based approach, which is first established by Kendall [16]. Later, from the viewpoint of the point cloud, Besl and McKay establish the iterative closest point (ICP) framework for 3D shape registration [4]. Then, Ying et al. extend this framework to the scale registration [27] while Du et al. to the affine registration [9]. Later, Du et al. extend their framework to the nonrigid shape registration [10]. Recently, Wu et al. develop a nonrigid registration method based on a correntropy metric [24]. On the other hand, Cootes and his coauthors propose the active shape models (ASM) for shape analysis [6], and further active appearance model (AAM) [7]. By scaling the shapes to the unit length and suitably selecting the start point, they analyze the corresponding landmarks and then align them together. This kind of approach offers an efficient way to establish the shape space and describe the shapes on it, but it should be pointed out that they ignore how to systemically select the landmarks on the shape, while different landmark selection may lead to large error. To overcome this shortage, on the other way, the variation-based methods are developed [12]. For example, Klassen and Srivastava establish the shape analysis framework via functional data analysis and elastic registration [17, 19], where they regard the shapes as functions on the interval D = [0,1] and represent them by their discovered square root velocity functions (SRVFs). This kind of representation makes it easier to find the best correspondences between non-systemically selected landmarks and translate the elastic metric to a simple L² metric. At the same time, the SRVFs of isometric curves form a sphere under such a metric, which offers a well mathematical structure to shape analysis. Further, they apply the representation of SRVFs to the shape registration [20]. More recently, Demisse et al. establish a deformation based representation space for curved shapes [8]. All these approaches offer an efficient way to register two shapes without complex and large deformations. However, there are still some issues for that with complex and large deformations. For example, the topology of shape may change in the process of registration, which is unreasonable in many real applications, especially in the field of medical image analysis.

Fortunately, it is seen that the topology of shape is always well preserved in registering two similar shapes. According to this observation, recently, the groupwise registration methods have been developed to align two shapes or images with large deformations. The basic idea of them is warping all shapes or images simultaneously onto a common space and then registering two shapes by this intermediate shape or image. That is, they improve the performance of registration by utilizing the distribution information of all shapes or images. For example, Joshi et al. propose a computational method for the mean image based on the notion of Karcher mean [15]. Later, Ashburner and Friston apply this mean to compute a shaped tissue probability template [2], while Fletcher and Joshi applied it to the statistical analysis of diffusion tensor data [11]. At the same time, Xie and his coauthors construct the image atlas by using the intrinsic mean on the image manifold [25]. On the other hand, similar techniques have been applied to construct the shape atlas [21]. It should be pointed out that one critical limitation of these algorithms is the use of simple averaging in estimating the group-mean image. Although no bias is introduced in the registration and avoiding the dependence of the large size of samples, it causes the unrecoverable information loss in terms of details of anatomical structures, especially when the samples are faraway from the center [23]. To overcome the shortage of one center, Ying et al. propose the HUGS by shrinking all images without utilizing the center image [29].

Inspired by this hierarchical strategy, it is not necessary to calculate only one common mean shape for atlas-based shape registration. That is, the distribution information of shapes can be well described by their relative relations. By this assumption, we only need to construct these relationships on the shape manifold, and then register two shapes by the shortest path between them. Therefore, the keys of this idea are finding the shortest path connecting two shapes and how to compute this path. In this paper, we firstly construct a hierarchical structure to represent the relative relationships between shapes. It is realized by an intrinsic clustering on the shape manifold, where the geodesic distance is utilized to describe the similarity of shapes. Then, the shortest path is calculated by searching the tree structure got from the graph. It should be pointed out that we will adopt the SRVFs to calculate the geodesic between two shapes with small deformations because of its advantage [20]. Therefore, the main contribution of this paper is designing a topology-preserving shape registration approach by a piecewise path on the tree based atlas. That is, we offer an efficient way to the shape registration with a large deformation by well utilizing the information of all shapes.

The rest of this paper is organized below. In Section 2, we recall the SRVFs for shape representation and then calculate the geodesic distances between shapes. Then, we propose a framework for SRVFs-based shape clustering and further apply it to the hierarchical structure construction and the the shape registration in Section 3. Section 4 displays numerical experiments to validate the efficiency of the proposed methods by comparing the conventional SRVFs-based registration method. Finally, whole paper is concluded in Section 5.

2 Shape representation and computation of geodesic distance

To establish a systematic framework for shape analysis, we first recall the SRVFs representation [19], which is a nice representation for shapes. Then, we utilize this representation to calculate the geodesic between two shapes.

2.1 Shape representation

In this paper, we adopt the square root velocity functions (SRVFs) to describe the shapes [19]. Let β be a parameterized curve, which is denoted by $\beta : [0,1]\rightarrow \mathbb {R}^{n}$, and C be the space of all curves. Denote a mapping $F: \mathbb {R}^{n} \rightarrow \mathbb {R}^{n}$ with $F(v)\equiv \frac {v}{\sqrt {\|v\|}}$. Then, the velocity and the square root velocity function are defined by $\dot {\beta (t)}$ and $q(t) \equiv F(\dot {\beta (t)}) = \frac {\dot {\beta (t)}}{\sqrt {\|\dot {\beta (t)}\|}}$, respectively. According to the definition, the SRVFs of the shape curve has following properties.

• (1) The SRVF representation is one-to-one in the shape space, which means different curve has different SRVF and each SRVF represents one curve.

• (2) The SRVF of curve is invertible and $\beta (t) = {{\int \limits }_{0}^{t}}q(s)\|q(s)\|ds$.

Before processing the shape, we re-parameterize the curve to be unit length to avoid the difference of shapes sizes caused by stretching, translation and sampling methods. This restriction of unit length ensure ${\int \limits }_{S^{1}}{\|q(t)\|^{2} dt=1}$ equivalently. Thus, the shape space of all curves with unit length can be described as

$$ \begin{array}{@{}rcl@{}} C = \left\{q\in \mathbb{L}^{2} (S^{1}, \mathbb{R}^{n}) | {\int}_{S^{1}} {\|q(t)\|}^{2} dt = 1\right\}. \end{array} $$

(1)

where $\mathbb {L}^{2} (S^{1}, \mathbb {R}^{n})$ is the space of all square integrable functions from S¹ to $\mathbb {R}^{n}$.

Then we divide the shape into open curves and closed curves. Because open curves have a relatively simple representation and geometric properties, we can directly find the evolution process between any two open curves and then calculate the distance for statistical analysis. For closed curves, based on its special geometric properties, the SRVF of each closed curve can be regarded as a point on the shape manifold. Therefore, in this paper, we mainly concern the registration of closed curves. That is, the shape representation satisfies the condition ${\int \limits }_{S^{1}} q(t) \|q(t)\| dt = 0$. The space of all closed curves is defined by

$$ \begin{array}{@{}rcl@{}} C^{c} = \left\{ q \in \mathbb{L}^{2} (S^{1},\mathbb{R}^{n}) | {\int}_{S^{1}} {\|q(t)\|}^{2} dt = 1, {\int}_{S^{1}} q(t) \|q(t)\| dt = 0 \right\}. \end{array} $$

(2)

It is necessary to point out that C^c is not a shape space, and is called as preshape space because we should consider the influence of translation, rotation, and reparameterization on shape curves. In the preshape space, if one shape can coincide to another shape after translation, rotation or reparameterization, they are located in the same orbit in preshape space. Every orbit in preshape space can be considered as an equivalent class and then as a point in shape space. Therefore, two shapes are considered as the same shape in the shape space, if they coincide after translation, rotation, and reparameterization.

To remove the influence of rotation and reparameterization, we first consider the special orthogonal group

$$ \begin{array}{@{}rcl@{}} SO(n) = \left\{ O\in\mathbb{R}^{n\times n} | O^{T}O=I_{n}, \det(O)=1 \right\}, \end{array} $$

(3)

and the repatameterization group

$$ \begin{array}{@{}rcl@{}} {\varGamma} = \{ \gamma : C^{c} \rightarrow C^{c} |\gamma\ \text{is an orientation-preserving diffeomorphism} \}. \end{array} $$

(4)

Then, the group action of SO(n) and Γ on SRVF of curve β are defined by

$$ \begin{array}{@{}rcl@{}} && SO(n) \times C^{c} \rightarrow C^{c}:(O,q)\mapsto Oq \end{array} $$

(5)

$$ \begin{array}{@{}rcl@{}} && {\varGamma}\times C^{c} \rightarrow C^{c}:(\gamma, q)\mapsto (q\circ\gamma) \sqrt{\dot{\gamma}}. \end{array} $$

(6)

It is proved that these two group actions are isomorphic under the $\mathbb {R}^{2}$ metric. Therefore, the closed shape space is just a quotient group of C^c, which inherits the metric in C^c, under the action of SO(n) and Γ. Then, the orbit of q in the preshape space is defined by

$$ \begin{array}{@{}rcl@{}} [q] = \left\{ O(q\circ\gamma)\sqrt{\dot{\gamma}} | (\gamma, O) \in {\varGamma}\times SO(n),\ q\in C^{c} \right\}. \end{array} $$

(7)

This orbit in C^c is just a point in shape space. In this way, every point in shape space is translation, rotation and reparameterization invariant. Therefore, the shape space is defined by

$$ \begin{array}{@{}rcl@{}} S = C^{c}/{\varGamma} \times SO(n) = \{ \overline{[q]} | q\in C^{c} \} \end{array} $$

(8)

where $\overline {[q]}$ means the closed orbit of q.

2.2 Computation of the geodesic distance

In this part, we will compute the geodesic between two shapes [3] of curves and then their distance under the SRVFs representation of curves. First, we define the distance between two shapes by the shortest distance between their orbits. Then, we have

$$ d(q_{0},q_{1}):=d_{S}(\overline{[q_{0}]}, \overline{[q_{1}]}) = \inf\limits_{(\gamma,O)\in{\varGamma}\times SO(n)} d_{C^{c}}(q_{0}, O(q_{1}\circ\gamma)\sqrt{\dot{\gamma}}) $$

(9)

To calculate the geodesic distance between two shapes by minimizing problem (9), we decompose it into two subproblems. The first is obtaining the optimal rotation by the minimization problem

$$ \hat{O} = \underset{O\in SO(n)}{\arg\min} \| \tilde{q}_{0}-O\tilde{q}_{1} \|^{2}, $$

(10)

where $\tilde {q}_{0}, \tilde {q}_{1}$ are two centered shapes of q₀,q₁. Then, the optimal rotation has a closed form as $\hat {O}=UV^{T}$, where UΣV^T = SVD(A) and $A={{\int \limits }_{0}^{1}} \tilde {q}_{0}(t) \tilde {q}_{1}(t)^{T} dt$. On the other hand, with the optimal rotation we adpot the dynamical programming to calculate the optimal $\hat {\gamma }$. The details of computation of the optimal rotation and reparameterization in (9) are displayed below.

Then, the geodesic distance between q₀ and q₁ is converted to the geodesic distance between q₀ and q₃, which can be obtained by using a path straightening method in [20]. It works well when two shapes are similar, but it still should be pointed out that this method is maybe invalid for two shapes with large variance. The large deformation may lead to the following two issues.

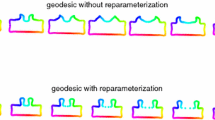
The first is in the reparameterizing procedure. As Fig. 1 shown, two red shapes on the top line are the original shapes and two black shapes on the bottom line are the corresponding reparameterized shapes. Due to the large difference between two original shapes, many details of the shapes are missing by reparameterization. It is because the red shape of a hand tries to cater to the red shape of a fish.

Fig. 1

Reparametrization result of two shapes

Secondly, when two shapes have a large difference, the topology of the source shape may be changed in iterations. In the shape registration problem of large deformation, the reason why the topological structure changes is in the process of sealing the unclosed curve. If the error of the tangent vector and shape curve are large, when closing the shape curve, curve crossing will occur. It will result in the change of topology structure. Figure 2 illuminates a geodesic path between the shapes of the hand and the fish under the SRVFs representation. It is seen that the topology of the warped shapes are changed many times even if the topologies at the beginning are the same. It is not reasonable in many real applications, especially in the field of medical image analysis.

Fig. 2

The geodesic path between the shapes of the hand and the fish

To solve both mentioned issues, we can add some topology-preserving regularization in the registration model. But it is difficult to describe such prior knowledge. Fortunately, although the SRVFs representation does not always work for shape registration with large deformation, it is well done for the most cases, especially for the shape registration with small deformation. By this observation, we can decompose the large deformation registration into several small deformation registration processes, which are always topological preserved. That is, we register the shapes by a piecewise smooth path on the shape manifold, which is constructed from the shape dataset directly. Below, we will display the process in detail.

3 Atlas-based shape registration

In this section, we will establish an atlas-based shape registration framework by using the SRVFs representation and the distribution information on the shape manifold. To obtain an atlas to well describe the distribution of shapes, first, we hierarchically cluster all shapes to form a discrete graphic manifold under the SRVFs representation and corresponding geodesic distance. Then, by searching the tree structure from the graph, we obtain the shortest path connecting two shapes, and each of them makes the topology of warped shapes preserved.

3.1 Hierarchical shape clustering based on SRVFs representation

To well describe the distribution of shapes, we first should establish a shape manifold. An efficient way is through the clustering method. Here, we adopt the hierarchical clustering approach to build the clustering tree [13], where the geodesic distance between two shapes are calculated under the SRVFs representation. In detail, let $\{q_{i}\}_{i=1}^{n}$ be the set of all shapes, and we first calculate the geodesic distances d_ij = d(q_i,q_j) between shapes q_i and q_j for all i = 1,2,⋯ ,n by (9). As mentioned above, it is possible that the topology structure of warped shapes will be changed when the deformation between two shapes is large. While, this situation does not definitely affect the result of clustering, the change of topology is always corresponding to the large distance. Then, we obtain the symmetrical distance matrix W_n×n whose elements w_ij is defined by $w_{ij}=\frac {d_{ij}+d_{ji}}{2}$. After getting the distance matrix, we start to cluster the shapes hierarchically as follow.

In the initial step, we divide n shapes into n classes where each class includes one and only one shape, and then calculate the distances between classes which are just the distances between corresponding shapes. Then, we merge the nearest two classes into one class and recalculate the distances between different classes, where the distance of two classes is defined by the largest geodesic distance of shapes in them. By this operation, the number of class is reduced by one. Further, we repeat above operation until all classes are merged into one class. Then, we get a hierarchical structure of classes.

It should be pointed out that the result of clustering establishes a clustering tree, where the shape stored in each node of the tree is represented by the average of the shapes belonging to this node. Due to the nonlinearity of the variation of shapes, and hence we apply the Karcher mean to calculate this average which is the generalization of arithmetic mean on manifold. Concretely, let $\{[q_{i}]\}_{i=1}^{N} \subset S$ be the representative elements in one class, the Karcher mean of them is defined by

$$ \begin{array}{@{}rcl@{}} \overline{[q]} = \underset{{[q]}\in S}{\arg\min} \frac{1}{N} \sum\limits_{i=1}^{N} {d_{S}^{2}} ({[q]},[q_{i}]), \end{array} $$

(11)

where d_S([q],[q_i]) means the geodesic distance between [q] and [q_i]. It is seen that the Karcher mean of $\{[q_{i}]\}_{i=1}^{N}$ is the shape which is the most similar with all given shapes.

Then, we adopt the Riemannian steepest descent method to calculate the Karcher mean of all shapes because all shapes form a shape manifold. The key is how to calculate the gradient of the objective function in (11). It can be achieved by computing all velocities of the geodesics connecting [q] and [q_i] at the shape [q]. From the definition in (9), the distance d_S is calculated by

$$ d_{C}(q, \hat{O_{i}}(q_{i}\circ\hat\gamma_{i})\sqrt{\dot{\hat\gamma}_{i}}), $$

(12)

where $\hat {O_{i}}$ and $\hat \gamma _{i}$ are the optimal rotation and the optimal orientation-preserving diffeomorphism of C between q and q_i. Let $\hat {q_{i}} = \hat {O_{i}}(q_{i}\circ \hat \gamma _{i})\sqrt {\dot {\hat \gamma }_{i}}$, then the (11) is transferred to

$$ \bar{q} = \underset{{q}\in C^{c}}{\arg\min} \frac{1}{N} \sum\limits_{i=1}^{N} {d_{C}^{2}} ({q},\hat{q}_{i}), $$

(13)

Let v_i be the velocity of the geodesic from q to $\hat {q}_{i}$ at q, then from the KKT condition we have all velocities are balanced at $\bar {q}$. That is, ${\sum }_{i=1}^{N} \bar {v}_{i} = 0$, where $\bar {v}_{i}$ is the velocity of the geodesic connecting $\bar {q}$ and q_i at $\bar {q}$. Then, the rest is how to calculate v_i. Fortunately, Arsigny and his coauthors propose an efficient way to approximately estimate the velocity [1]. Concretely, we assume that the curve q ∈ C^c is moving in the direction of v_i ∈ T_qC^c and then get $q^{\prime } = \exp (q,v_{i})$, where $\exp (q,\cdot )$ is the exponential map at q. In fact, when the velocity vector v_i is small enough, its exponential map can be efficiently approximated by the linearization method. That is, we have $q^{\prime } = \exp (q,v_{i})\approx (Id + v_{i})\cdot q$, where ⋅ means an action. For the case of large velocity v_i, we can choose a positive integer N such that $\frac {v_{i}}{2^{N}}$ is significantly small. Then, $\exp (q,\frac {v_{i}}{2^{N}})\approx (Id + \frac {v_{i}}{2^{N}})\cdot q$ and $\exp (q, v_{i})\approx \underbrace {(Id + \frac {v_{i}}{2^{N}})\circ \cdots \circ (Id + \frac {v_{i}}{2^{N}})}_{2^{N}} \cdot q$, where ∘ is the composition operator. There is an advantage that the exponential map can be hierarchically combined N times.

Therefore, given two shapes $q, \hat {q}_{i} \in C^{c}$, the velocity of the geodesic connecting them is computed by the following minimizing problem,

$$ v_{i} = \underset{v}{\arg\min} \|\hat{q}_{i} - \exp(q, v)\|^{2} \approx \|\hat{q}_{i} - q - v\cdot q\|^{2}, $$

It is notable that this is a least square problem and there is a closed form for it. That is,

$$ v_{i} = \langle q, \hat{q}_{i} - q \rangle/\|q\|^{2}, $$

Then, we combined velocity v in T_qC^c as follows.

$$ v = \frac{1}{N} \sum\limits_{i=1}^{N} \langle q, \hat{q}_{i} - q \rangle/\|q\|^{2}. $$

(14)

Further, we define an iteration for solving $\bar {q}$ as follows.

$$ q \leftarrow q \exp(q, v). $$

(15)

Therefore, in general, the process of building the clustering tree of all shapes is summarized by the following algorithm.

3.2 Shape registration based on clustering

After constructing the clustering tree of all shapes, we can register two shapes with large deformation by a connected path in the tree. First, we calculate the distances between father nodes (shapes) and their child nodes (shapes) in the clustering tree. In fact, they are calculated by measuring deformations between them. Then, the rest is searching the shortest path connected them in the tree. It is well done by the conventional searching strategy on the tree. Here, we adopt the Dijkstra’s algorithm. It can be completed in a linear time. After obtaining the shortest path, we orderly combine all deformations between connected nodes along this path and obtain a deformation between two given shapes.

4 Numerical experiments

To validate the effectiveness of the proposed shape registration approach, we do experiments on Kimia database,¹ which contains different objects’ shapes of different types. The Srivastave’s method [20] is utilized as a benchmark method to compare with the proposed method on the shapes. All algorithms are implemented in matlab environment.

4.1 Data description and parameter setting

In this experiment, we adopt the Kimia database. It contains three subset Kimia25, Kimia99 and Kimia216, which include six, nine and eleven groups, respectively. Here, we use the Kimia216, which includes 216 shapes. First, we use the Sobel operator to extract the edges of all shapes and translate them into point sets. Then, we set the number of iterations be five in calculating the Karcher mean of shapes.

4.2 Experiment results

The shape at each node of the tree is represented by the Karcher mean of all shapes belonging to this node. According to the properties of tree structure, for any two tree root nodes, we find a connecting path from the tree between shapes. Using hierarchical clustering method, we cluster all shape data. When the number of classes is reduced to 16, we regard these 16 classes as root nodes of the tree. The hierarchical clustering tree is obtained by clustering these 16 classes.

To be better illuminated, Fig. 3 shows the partial results after hierarchical clustering. Figure 3a only shows 16 classes of clustering results of all shapes. Each row represents a class and the numbers are the labels of classes. It is seen that the close shapes are well clustered in a same group. Figure 3b shows the clustering tree which is starting from the 16 classes. From this figure, we see that the geodesic distance under SRVFs representation is well describe the similarity of shapes.

Fig. 3

Result of clustering and building the tree

First, to valid the efficiency of our proposed method, we register shapes with small deformations. Figure 4 shows two groups of registration results by our method. The left shapes are source shapes while the right ones are the target shapes. From the clustering tree in Fig. 3b, they are both close. It is seen that the registration process is topology preserving as well as offer a well change path.

Fig. 4

The registration process between two shapes with small deformations

To further validate the efficiency of our proposed method. We compare it with Srivastave’s benchmark method. To show more intuitively, two typical examples are given. We randomly select two groups of shapes with large deformations. For example, we hope to find the deformation from a fish to a palm, which are shown in Fig. 5. The left column of Fig. 5a and b show the source shapes while the right column the target shapes. From the clustering tree in Fig. 3b, they are actually large different. The top rows of (a) and (b) are registered by the benchmark method and the bottom ones are registered by our method. First, we see that the shapes of are large different but they have the same topology. On the other hand, it is seen that our proposed method does well preserve the topology of the shape in the registration process while the benchmark method is failure. The reason is that there is no constraints to limit the cross deformation of the curve in the registration process of benchmark method, while the registration process in our method is constrained in a path determined by several close shapes. Therefore, from the results, we conclude that our method can avoid the situation of topology changes.

Fig. 5

The registration process between two shapes with large deformations

Other shapes registration are also done and show the same results as above. Therefore, it is shown that the atlas-based shape registration method is efficient to topology preserving. It at least has following advantages.

1. The registration process obtained by the atlas-based method does not only satisfy the precondition of the shortest distance. When we deal with the template data manually, we can fully consider the limitations of physical conditions on the image evolution process. The constraints considered in the processing of template data will have an impact on the final results obtained on the new image data.

2. It can greatly reduce the computation time and improve the robustness. Atlas based method takes a long time in establishing the template transformation process. But such cost is one-time. After getting such representative template data, it is only need to establish a relation between the new data and the template when we need to process any new data.

3. In all kind of image processing problems, large deformation is always a difficult problem because of the complexity of geometric properties. The atlas-based method can always solve this problem well. Because in this method, we will ensure that the deformation process in the template is reasonable. For the new data, we only need to find the template image closest to it, so that we can avoid calculating the geodesic between two shapes whose distance is large.

5 Conclusions

In this paper, we proposed an atlas-based shape registration method. Concretely, according to the strong representation for shape registration, the square root velocity functions (SRVFs) is used to represent the shape. Then, under this representation, we hierarchically cluster all shapes and form a clustering tree. Further, by searching the shortest path connecting two shapes we realize the registration with topology preserving. Finally, by comparing with the conventional method, the numerical results on the Kimia shape dataset show that our proposed method achieves a better performance of registration. Especially, for the large deformation cases. As a conclusion, the atlas-based strategy is valid for shape registration with large deformation and well address the topology preserving issue.