1 Introduction

Visual tracking is one of the most challenging tasks in computer vision with various applications such as intelligent video surveillance, video analysis, scene understanding, and so on [4, 23, 42]. In the past decades, much attention has been attracted on model-free tracking that initializes a bounding-box of an unknown target at the first frame. Generally, based on the different appearance models, these trackers can be categorized into generative and discriminative methods[5, 18, 53,54,55,56,57, 64]. Among them, the generative methods only exploit target information while the discriminative ones also consider rich information from backgrounds, thereby usually yielding much better performance than the generative ones [50]. Therefore, most state-of-the-art trackers are discriminative with much effort being expended to improve their core components such as target representation, sampling, or online update strategy [49].

Recent years have witnessed an explosive popularity of discriminative correlation filters (DCF) for visual tracking [1, 15, 16, 25, 37, 39, 44, 52, 59,60,61, 63] because of their high efficiency and accuracy. The standard DCF [16] facilitates using a variety of high-dimensional features such as HOGs [16] and convolutional network (CNN) features [32] to design an efficient and effective target representation. Furthermore, it employs efficient dense sampling in learning and detection through circulantly shifting a base sample, which can use FFT for acceleration. However, due to the circularity, the learned filters suffer from boundary effects. Besides, it simply utilizes linear interpolation for online model update, which causes severe errors when suffering from significant appearance variations. To address these issues, the SRDCF [10] has been proposed that employs a spatial Gaussian window to penalize CF coefficients depending on their spatial locations. Besides, SRDCF formulates its model on multiple training images from historical frames, and couples DCF learning and model updating, which does benefit the tracking accuracy. Galoogahi et al. [20] present background-aware CFs for visual tracking that enables to learn CFs with real negative examples from the background. Mueller et al. [34] alleviate the boundary effects by explicitly modelling global context in CF learning. Li et al. [25] introduce spatial-temporal regularization into CF learning to handle the boundary effects. Lin et al. [29] utilize localization-aware meta learning to guide the object tracking, aiming to handle the occluded or changed features. However, these DCF-based approaches lead to some issues: first, it makes DCF unable to exploit the circularity in learning, resulting in high computational cost; second, it makes DCF difficult to efficiently exploit nonlinear kernels, and so DCF concatenates a set of features into a high-dimensional feature vector and then learn rigid regression as a linear predictor, which may confuse the invariance-discriminative power of the features [47], further affecting the performance boosting. Consequently, a natural choice is to exploit a multi-kernel feature that combines several kernels to yield one strong feature.

In this paper, we study how to benefit from both spatial regularization and large training set as SRDCF and how to make full use of the invariance-discriminative power of the features via multiple kernel learning (MKL), yet without losing efficiency. Specifically, we introduce temporal regularization to reformulate the SRDCF with only one training image, and find that our formulation can reasonably approximate the SRDCF with multiple training images, but the former can be efficiently solved via ADMM. Furthermore, we introduce two types of kernels with circulant data matrices into our formulation, fully taking advantages of the complementary traits of color and Histogram of Oriented Gridients (HOG) features to construct a robust representation. By exploiting the circularity, the proposed tracking is formulated as learning CFs and the weight for each kernel via FFTs. We conduct extensive experiments on OTB100 and VOT2016, demonstrating that the proposed tracker achieves favorable performance against a variety of state-of-the-art trackers with a speed of 40 fps on a single CPU (8 × speed up against SRDCF). Meanwhile, compared to SRDCF, our tracker achieves a gain of 5.5% AUC score on OTB100 and 8.4% EAO score on VOT2016.

In the related work section, we briefly review the correlation filter tracking methods and the spatial-temporal CF approaches. In the third section, we present our STRCKCF model, which contains multiple kernels in the correlation filter learning. Furthermore, in the experiment part, we make the state-of-the-art comparisons on the VOT and OTB benchmarks, respectively. Finally, we obtain our conclusion in the last section. The The main contributions of this paper are summarized as three-fold:

  1. 1.

    An effective color-kernel and hog-kernel complementary tracking model is proposed to yield the robustness to the target color variations.

  2. 2.

    A novel spatial-temporal regularized correlation filter is formulated to constrain the kernelized CF coefficients, which solves the temporal variation problem of object tracking task very well.

  3. 3.

    The proposed STRCKCF with hand-crafted features achieves competitive results on the OTB100 and VOT2016 datasets in terms of both accuracy and speed.

2 Related work

In the following, we briefly introduce some most related works to our method, and please refer to [23, 26, 51] for detailed surveys about visual tracking.

Since Bolme et al. [3] introduce MOSSE into adaptive visual tracking that learns CFs with a few samples in the frequency domain, numerous effort has been made to greatly advance state-of-the-art tracking performance. Galoogahi et al. [19] present a multi-channel MOSSE with promising performance. Henriques et al. [16] learn a kernelized CF (KCF) via kernel trick with circulant kernel matrix and multi-channel features. Danelljan et al. [9] further improve the multi-channel KCF with adaptive color attributes. In [24], Li and Zhu learn the multi-channel KCF with a combination of the HOG and color naming (CN) features and present an effective scale estimation scheme for visual tracking. Hong et al. [17] and Ma et al. [33] integrate both short-term and long-term memories for robust tracking with KCF as the short-term tracker. Ma et al. [32] ensemble the response maps of CFs with a set of CNN features in a coarse-to-fine manner to accurately estimate the target location. Bertinetto et al. [1] present a simple and efficient tracker that linearly combines color histograms and HOGs in a ridge regression framework. Choi et al. [7] propose an ensemble tracking approach with various CFs, each of which is weighted by a spatially attentional weight map. Qi et al. [36] present a robust tracking that employs an adaptive hedge scheme to effectively ensemble the response maps of CFs from deep CNN features. Liu et al. [30] present a structural CF tracking approach that makes use of circulant shifts of part-based CF tracking to model motions. Zhang et al. [58, 59] model the interdependencies among different features to jointly learn some CFs for visual tracking. In [61], Zhang et al. further present correlation particle filter based tracking that integrates the strength of each particle. Tang et al. [46] improve the MKL version of KCF [45] by optimizing the upper bound of its objective function, thereby alleviating the negative mutual interference of different kernels effectively. Danelljan et al. [12] introduce a factorized convolution operator into the discriminative correlation filter tracking framework, drastically reduces the size of model. Bertinetto et al. [2] equip the tracking algorithm with a fully-convolutional Siamese Net, achieving a significant breakthrough based on the correlation filter trackers. Furthermore, based on subspace learning Chen et al. [6] propose a novel robust object tracking technique to solve the drift problems caused by occlusions and illuminative variations.

The CF trackers mentioned-above undergo the boundary effects due to periodic repetitions when learning a CF for tracking, thereby significantly degrading the tracking performance. To address this issue, Danelljan et al. [10] present the SRDCF that regularizes the coefficients of the learned CFs by a spatial Gaussian function depending on their spatial locations. Cui et al. [8] learn a spatial matrix predicted with a multi-directional RNN as the spatial regularization term, and Zhang et al. [62] learns a spatial regularization mask via video segmentation technique. As SRDCF, Lukezic et al. [31] tackle the boundary effects using a spatial reliability map to restrict the coefficients of the learned CFs. Different from SRDCF that employs fixed spatial regularization weights, Sun et al. [44] learn a dynamic spatial regularization weight matrix that focuses on the reliability information of the target. Qi et al. [40] leverage contextual attribute information to facilitate training an effective classifier for visual tracking. Ding et al. [13] propose a scalable tracker to estimate the scale based on the four corners. Fan et al. [14] utilize recurrent neural network (RNN) to model object structure, improving the robustness to similar distractors. Very recently, Li et al. [28] employ the discriminative power in the gradients to dynamically update the template in the siamese net tracker. Li et al. [27] exploit the dependence among the input features to learn a target-oriented feature representations for visual tracking.

3 Spatial-temporal regularized complementary KCFs

In this section, we first introduce the KCF with complementary kernel learning (CKL), and then introduce the SRDCF and its approximated version. Next, we present our STRCKCF model that is solved via ADMM. The fast detection process is presented at last.

3.1 Complementary KCFs

We first set the size of the basis sample to 1.5 × the target size, including some useful context. Afterwards, we represent it by color histograms and HOGs denoted by \( {x}_{1}\in \mathbb {R}^{MND}\), where M, N and D are the width, height and channel number, respectively. Then, we construct a circulant matrix \( {X}=[ {x}_{1}^{\top };\ldots ; {x}_{MN}^{\top }]\) whose element xi is designed by circularly shifting the vector x1 along M and N dimensions. The circulant matrix X can be diagonalized by discrete Fourier transform (DFT) [16] as

$$ {X} = {F}diag({\hat{x}}_{1}){F}^{H}, $$
(1)

where \( {\hat {x}}_{1}=\sqrt {MN} {Fx}_{1}\) is the DFT of the vector x1, FH is the Hermitian transpose of the Fourier matrix F, and diag(⋅) denotes the diagonal matrix from a vector. Given the training samples in the circulant matrix X with their corresponding regression scores y = [y(1),…, y(MN)]⊤, the objective of KCF [16] is to find a function f(x) that minimizes the ridge regression loss as follows

$$ \min_{f} \sum\limits_{i}(f({x}_{i})-{y}(i))^{2}+\lambda\|f\|_{k}^{2}, $$
(2)

where f(⋅) lies in a bounded convex subset of a Reproducing Kernel Hilbert Space defined by a positive definite kernel function k(⋅), λ > 0 is the regularization parameter.

By means of the Representer Theorem [41], the solution of (2) can be represented as

$$ f({x}) = \sum\limits_{i=1}^{MN}\alpha_{i}k({x}_{i},{x}), $$
(3)

and then \(\|f\|_{k}^{2}\triangleq \alpha ^{\top } {K} \alpha \), where α = [α1,…, αMN]⊤ and K is a positive semi-definite kernel matrix with its elements κij = k(xi, xj). Replacing f by (3), (2) can be reformulated as

$$ \min_{\alpha} \|{y}-{K}\alpha\|_{2}^{2}+\lambda\alpha^{\top} {K}\alpha. $$
(4)

Recently, some works [43, 45, 46] have demonstrated that using MKL in KCF enables to improve the tracking performance, and hence we employ two types of kernels to ensemble the complementary advantages of color and HOG features. Given that \( {x}_{i}=\{ {x}_{i}^{color}, {x}_{i}^{HOG}\}\), where \( {x}_{i}^{color}\) and \( {x}_{i}^{HOG}\) denotes the RGB color and HOG features, respectively, we employ the kernel \(k( {x}_{i}, {x}_{j})=\gamma k_{1}( {x}_{i}^{color}, {x}_{j}^{color})+(1-\gamma )k_{2}( {x}_{i}^{HOG}, {x}_{j}^{HOG})\) that convexly combines two base kernels with weight 0 ≤ γ ≤ 1. Here, we choose interaction and Gaussian kernels as the base kernels

$$ \begin{array}{@{}rcl@{}} &&k_{1}({x}_{i}^{color},{x}_{j}^{color})={\sum}_{m}\min({x}_{i}^{color}(m),{x}_{j}^{color}(m)),\\ &&k_{2}({x}_{i}^{HOG},{x}_{j}^{HOG})=\exp\left( -\frac{\|{x}_{i}^{HOG}-{x}_{j}^{HOG}\|_{2}^{2}}{\sigma}\right),\sigma>0. \end{array} $$
(5)

These base kernels construct the base kernel matrices K1 and K2, respectively, and we have

$$ {K} = \gamma{K}_{1}+(1-\gamma){K}_{2}, $$
(6)

Replacing K in (4) by (6), we have the objective function F(α, γ) of the complementary KCF as follows

$$ \begin{array}{@{}rcl@{}} \min_{\alpha,0\leq \gamma\leq 1}F(\alpha,\gamma)&=&\|(\gamma{K}_{1}+(1-\gamma){K}_{2})\alpha-{y}\|_{2}^{2}\\ &+&\lambda\alpha^{\top}(\gamma{K}_{1}+(1-\gamma){K}_{2})\alpha. \end{array} $$
(7)

3.2 Spatially regularized DCF

The SRDCF [10] aims to learn a D-channel CF w with a set of T training images whose feature representations are denoted by \(\{( {X}_{t}^{d}, {y}_{t})\}_{t=1,\ldots ,T}^{d=1,\ldots ,D}\), where \( {X}_{t}^{d}\) is the d-th channel circulant matrix of the base sample xt, and yt denotes its class label vector. The SRDCF is formulated by minimizing the objective as

$$ \arg\min_{{w}}F_{T}({w})=\sum\limits_{t=1}^{T}{\upbeta}_{t}\|\sum\limits_{d=1}^{D}{X}_{t}^{d} {w}^{d}-{y}_{t}\|_{2}^{2}+\sum\limits_{d=1}^{D}\|{m}\odot {w}^{d}\|_{2}^{2}, $$
(8)

where ⊙ denotes the Hadamard product, m is the spatial regularization matrix, and βt is the weight that emphasizes more to the recent samples.

Although in (8) the SRDCF enables to well handle the negative boundary effects and make online model update stable via introducing the spatial regularization matrix m and jointly training CFs with multiple samples, it fails in exploiting the circulant matrix structure for efficient computation. In [10], Danelljan et al. employ the Gauss-Seidel method to iteratively update the CFs, resulting in solving a DMN × DMN large sparse linear equation system. While the Gauss-Seidel method can solve (8) using the property of sparse matrix, it still takes high computational cost. Moreover, the SRDCF also needs a long start-up time to learn the CFs in the first frame because the Gauss-Seidel method converges very slow. In addition, since the SRDCF cannot exploit the circularity, it is difficult to efficiently extend the SRDCF to the kernel space, further limiting to boost its performance.

To solve the above issues, we first show some interesting findings by further analyzing the objective of SRDCF, serving as the guide to design our STRCKCF tracker. The objective of SRDCF (8) can be reformulated by

$$ F_{T}({w}) = F_{T-1}({w}) + {\upbeta}_{T}\|{\sum}_{d=1}^{D}{X}_{T}^{d}{w}^{d}-{y}_{T}\|_{2}^{2}. $$
(9)

Given the optimal CFs at frame T − 1 as \( {w}_{T-1} = \arg \min \limits _{ {w}} F_{T-1}( {w})\), we have the 2rd order Taylor expansion of FT− 1(w) as \(F_{T-1}( {w}) \approx F_{T-1}( {w}_{T-1})+\frac {1}{2}( {w}- {w}_{T-1})^{\top } {H}( {w}- {w}_{T-1})\), where H is the Hessian matrix, and for simplicity, we assume that the Hessian matrix is an identity matrix as H = I. Replacing FT− 1(w) in (9) and reducing the constant term FT− 1(wT− 1), we have

$$ F_{T}({w}) \approx \frac{1}{2}\|{w}-{w}_{T-1}\|_{2}^{2} + {\upbeta}_{T}\|{\sum}_{d=1}^{D}{X}_{T}^{d}{w}^{d}-{y}_{T}\|_{2}^{2}. $$
(10)

Here, \(\| {w}- {w}_{T-1}\|_{2}^{2}\) can be seen as a temporal regularization term, and FT(w) only contains one training image, thereby facilitating using the circularity for efficient computation.

3.3 Proposed STRCKCF

Our work is inspired by the STRCF [25] that introduces spatial-temporal regularization to regularize CF learning for visual tracking, but our work extends spatial-temporal regularized CF learning to multi-kernel condition. Motivated by the findings from further analyzing the objective of SRDCF (10), we introduce a temporal regularization term \(\| \alpha - \alpha _{t-1}\|_{2}^{2}\) and the spatial regularization matrix m into the complementary KCF (7), yielding the objective of our STRCKCF as

$$ \begin{array}{@{}rcl@{}} \min_{\alpha,0\leq \gamma\leq 1}F(\alpha,\gamma)&=&\|(\gamma{K}_{1}+(1-\gamma){K}_{2})\alpha-{y}\|_{2}^{2}\\ &+&\lambda ({m}\odot\alpha)^{\top}(\gamma{K}_{1}+(1-\gamma){K}_{2})({m}\odot\alpha)\\ &+&\rho\|\alpha-\alpha_{t-1}\|_{2}^{2}, \end{array} $$
(11)

where ρ > 0 is a regularization parameter.

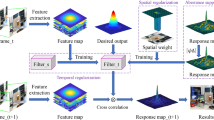
In Fig. 1, we show the relationships of the STRCKCF, SRDCF and approximated SRDCF on learning CFs. From it we can observe that similar to the approximated SRDCF, STRCKCF also implements simultaneous learning CFs and updating models by introducing the temporal regularizer, and thus it can rationally approximate the SRDCF with multiple training images.

Fig. 1
figure 1

Comparison of the SRDCF (see (8)), the approximated SRDCF (see (10)) and our STRCKCF (see (11)) on learning CFs. The SRDCF learns the CFs with multiple historical samples and pays more attention on the recent samples, while the approximated SRDCF learns its CFs with the current sample and the former learned CFs. Different from the SRDCF and the approximated SRDCF that learn the CFs on the primal space, our STRCKCF learns its CFs on the dual space with the complementary kernel that ensembles the merits of both color and HOGs features

Full size image

The above model in (11) is convex that can be minimized to yield the globally optimal solution via ADMM. To this end, we introduce an auxiliary variable g that requires g = α, and then the Augmented Lagrangian form of (11) can be formulated as

$$ \begin{array}{@{}rcl@{}} L(\alpha,{g},\gamma, {s})&=&\|(\gamma{K}_{1}+(1-\gamma){K}_{2})\alpha-{y}\|_{2}^{2}\\ &+&\lambda ({m}\odot{g})^{\top}(\gamma{K}_{1}+(1-\gamma){K}_{2})({m}\odot{g})\\ &+&(\alpha-{g})^{\top} {s}+\frac{\mu}{2}\|\alpha-{g}\|_{2}^{2}+\rho\|\alpha-\alpha_{t-1}\|_{2}^{2}, \end{array} $$
(12)

where s and μ are the Lagrange multiplier and penalty factor. By setting \( {h}=\frac { {s}}{\mu }\), (12) can be reformulated as

$$ \begin{array}{@{}rcl@{}} L(\alpha,{g},\gamma, {h})&=&\|(\gamma{K}_{1}+(1-\gamma){K}_{2})\alpha-{y}\|_{2}^{2}\\ &+&\lambda ({m}\odot{g})^{\top}(\gamma{K}_{1}+(1-\gamma){K}_{2})({m}\odot{g})\\ &+&\frac{\mu}{2}\|\alpha-{g}+{h}\|_{2}^{2}+\rho\|\alpha-\alpha_{t-1}\|_{2}^{2}. \end{array} $$
(13)

The subproblem to minimize L(α, g, γ, h) in (13) on each variable has a closed-form solution when other two variables are known, and the above optimization problem can be efficiently solved via ADMM by alternatingly solving the following subproblems:

$$ \begin{array}{@{}rcl@{}} \alpha^{i+1}=\arg\min_{\alpha}\|{K}\alpha-{y}\|_{2}^{2}+\frac{\mu}{2}\|\alpha-{g}+{h}\|_{2}^{2}\\ +\rho\|\alpha-\alpha_{t-1}\|_{2}^{2}, \end{array} $$
(14)
$$ \begin{array}{@{}rcl@{}} {g}^{i+1}=\arg\min_{{g}}\lambda({m}\odot{g})^{\top}{K}({m}\odot{g})\\ +\frac{\mu}{2}\|\alpha-{g}+{h}\|_{2}^{2}, \end{array} $$
(15)
$$ \begin{array}{@{}rcl@{}} {h}^{i+1} = {h}^{i} + \alpha^{i+1}-{g}^{i+1}, \end{array} $$
(16)
$$ \begin{array}{@{}rcl@{}} \gamma^{i+1} = \arg\min_{0 \leq\gamma\leq 0}\|(\gamma{K}_{1}+(1-\gamma){K}_{2})\alpha-{y}\|_{2}^{2}\\ +\lambda ({m}\odot{g})^{\top}(\gamma{K}_{1}+(1-\gamma){K}_{2})({m}\odot{g}), \end{array} $$
(17)

where K is denoted by (6).

The solution to each subproblem is detailed below:

  1. Step 1:

    update α. Fixing γ, g and h, by setting the gradient of the right formulation in (14) to zero, we have

    $$ (2{K}^{\top} {K}+(\mu+2\rho){I})\alpha = 2{K}^{\top} {y}+\mu({g}-{h})+2\rho\alpha_{t-1}, $$
    (18)

    where I is an identity matrix.

    Since the base kernels K1 and K2 are circulant, and the sum of circulant matrices are still circulant [16], K is circulant. With the property of circulant matrix (1), (18) can be transformed into the Fourier domain as

    $$ (2\hat{{k}}^{*}\odot\hat{{k}}+\mu+2\rho)\odot\hat{\alpha}=2\hat{{k}}^{*}\odot\hat{{y}}+\mu(\hat{{g}}-\hat{{h}})+2\rho\hat{\alpha}_{t-1}, $$
    (19)

    where \(\hat { {k}} = \gamma \hat { {k}}_{1}+(1-\gamma )\hat { {k}}_{2}\) with \(\hat { {k}}_{1}\) and \(\hat { {k}}_{2}\) denoting the kernel correlation of \( {x}_{1}^{color}\) and \( {x}_{1}^{HOG}\) with themselves in the Fourier domain,∗ denotes the conjugate operator, and the solution of (19) is:

    $$ \alpha = \mathcal{F}^{-1}\left( \frac{2\hat{{k}}^{*}\odot\hat{{y}}+\mu(\hat{{g}}-\hat{{h}})+2\rho\hat{\alpha}_{t-1}}{2\hat{{k}}^{*}\odot\hat{{k}}+\mu+2\rho}\right), $$
    (20)

    where \(\mathcal {F}^{-1}\) is the inverse FFT.

  2. Step 2:

    update g. Fixing γ, α and h, and let M = diag(m) that is a diagonal matrix. The subproblem on g can be reformulated as:

    $$ \min_{{g}}\|{g}-\alpha-{h}\|_{2}^{2}+\frac{2\lambda}{\mu} ({Mg})^{\top} {KMg}. $$
    (21)

    Solving (21), we has the closed-form solution as

    $$ {g} = ({M}^{\top} {KM} + \frac{\mu}{2\lambda}{I})^{-1}(\alpha+{h}). $$
    (22)
  3. Step 3:

    update h. Fixing α and g, update h via (16).

  4. Step 4:

    update γ. Fixing α and g, (17) can be reformulated as

    $$ \begin{array}{@{}rcl@{}} \min_{0\leq \gamma\leq1}F(\gamma)&=&\|\gamma({K}_{1}-{K}_{2})\alpha+{K}_{2}\alpha-{y}\|_{2}^{2}\\ &+&\lambda\gamma(({m}\odot{g})^{\top}({K}_{1}-{K}_{2})({m}\odot{g})). \end{array} $$
    (23)

    The partial derivative of F(γ) with respect to γ is

    $$ \begin{array}{@{}rcl@{}} \frac{\partial F(\gamma)}{\partial \gamma}&=&2(\alpha^{\top}({K}_{1}-{K}_{2})^{\top}({K}_{1}-{K}_{2})\alpha)\gamma\\ &+&\lambda({m}\odot{g})^{\top}({K}_{1}-{K}_{2})({m}\odot{g})\\ &+&2\alpha^{\top}({K}_{1}-{K}_{2})^{\top}({K}_{2}\alpha-{y}). \end{array} $$
    (24)

    Setting \(\frac {\partial F(\gamma )}{\partial \gamma }=0\), we have

    $$ \begin{array}{@{}rcl@{}} \gamma &= & -\frac{\lambda({m}\odot{g})^{\top}({K}_{1}-{K}_{2})({m}\odot{g})+2\alpha^{\top}({K}_{1}-{K}_{2})^{\top}({K}_{2}\alpha-{y})}{2(\alpha^{\top}({K}_{1}-{K}_{2})^{\top}({K}_{1}-{K}_{2})\alpha)}\\ &=&\frac{\alpha^{\top} \mathcal{F}^{-1}(\hat{{q}})+2C\mathcal{F}^{-1}(\hat{{p}})^{\top}(\mathcal{F}^{-1}(\hat{{k}}_{2}\circ\hat{\alpha})-{y})}{2\mathcal{F}^{-1}(\hat{{p}})^{\top} \mathcal{F}^{-1}(\hat{{p}})}, \end{array} $$
    (25)

    where \(\hat { {p}}=(\hat { {k}}_{1}-\hat { {k}}_{2})^{*}\circ \hat { \alpha }\) and \(\hat { {q}}=(\hat { {k}}_{1}-\hat { {k}}_{2})^{*}\circ \widehat {( {m}\odot {g})}\).

    Considering the constraint 0 ≤ γ ≤ 1, the solution γ⋆ of (23) is

    $$ \gamma^{\star}=\left\{ \begin{array}{ll} &\gamma, if~0\leq \gamma\leq 1, \\ &0, if~\gamma< 0, \\ &1, if~\gamma>1. \end{array} \right. $$
    (26)
  5. Step 5:

    update μ: μ is updated by

    $$ \mu^{i+1} = min(\mu^{max},\epsilon\mu^{i}), $$
    (27)

    where μmax is the maximum value of μ and 𝜖 denotes the scale factor.

3.4 Fast detecting

As KCF [16], we model the densely sampled object patches by circularly shifting the base sample \( {z}_{1}=\{ {z}_{1}^{color}, {z}_{1}^{HOG}\}\), which enlarges the tracked object rectangle to 1.5 × the target size to include more useful context information.

Then, we design the kernel matrix \( {K}^{ {z}_{1}}\) as

$$ {K}^{{z}_{1}} = \gamma{K}_{1}^{{z}_{1}^{color}{x}^{color}}+(1-\gamma){K}_{2}^{{z}_{1}^{HOG}{x}^{HOG}}, $$
(28)

where the first row of the circulant matrix \( {K}_{1}^{ {z}_{1}^{color} {x}^{color}}\) is the intersection kernel correlation of \( {z}_{1}^{color}\) and xcolor, and so does the circulant matrix \( {K}_{2}^{ {z}_{1}^{HOG} {x}^{HOG}}\) whose first row is the Gaussian kernel correlation of \( {z}_{1}^{HOG}\) and xHOG.

The classifier scores in (3) for all the candidate samples z = {z1,…, zMN} can be calculated by

$$ {f}({z})={{K}^{{z}_{1}}}^{\top}\alpha, $$
(29)

where f(z) = [f(z1),…, f(zMN)]⊤, which can be efficiently calculated by FFT as

$$ {f}({z})=\mathcal{F}^{-1}({\hat{{k}}^{{z}_{1}}}\circ\hat{\alpha}), $$
(30)

where \({ {k}}^{ {z}_{1}}\) denotes the first row of \( {K}^{ {z}_{1}}\). Finally, maximizing f(z) yields the tracked object location. To extend the CKSCF with multiple scale estimation, as [24], we compute responses on several scales in parallel and take the maximum response as the tracking results.

3.5 Complexity analysis of the proposed method

Since most of the matrices in the algorithm 1 has circulant structures, we only need to compute the first row of these matrix (e.g.kz). Thus, we can employ fast fourier transform to operate the calculations and the our complexity burden mainly lies in the optimization iterations in solving α. The complexity of solving α is \(\mathcal {O}\left ({N_{Iter}}{HWD}\log HW \right )\), where NIter denotes the numbers of iterations, meanwhile H, W and D indicates feature’s height, weight and channel dimension, respectively.

figure a

Furthermore, the computational cost for g(\(\mathcal {O}\left ({HWD}\log HW \right )\)) and h(\(\mathcal {O}\left ({HWD}\right )\)) is lower than α, for simplicity, we do not pay much attention on it. More details can refer to algorithm 1.

4 Results

4.1 Experimental setup

We first resize the resolutions of the videos to 240 × 320 pixels, which are helpful to adapt varying target sizes during tracking [49]. Then, each image patch is resized to a canonical size of 64 × 64 pixels to extract RGB color and HOG features. Specifically, the original image patches are employed to extract the raw intensity and HOG features for the gray videos, and for the color videos, the image patches are used to extract RGB color features, and the original RGB image patches are taken to extract the HOG features. Also, we conduct the experiments on the popular convolution network based feature, which further enhances the discriminative power of our model.

The hyper-parameters are based on the experiments and experience. Here we show the optimal parameters in brief. The search radius for training and detection is set automatically based on the square root of the target area, and to make a trade-off between accuracy and speed, the size of image patch is normalized to 400 pixels. As suggested by [24], we employ the parameter set {1,0.995,0.990,0.885,1.005} to estimate scale. We employ a spatial Gaussian function with respect to the object position to model the regression scores y. The parameters λ and ρ in (11) is set to λ = 20 and ρ = 10. We set the initial parameter μ0, the maximum value μmax and scale factor 𝜖 to 10, 90 and 1.1, respectively. We set the kernel parameter for the Gaussian kernel to σ = 0.8, and fix all the parameters during experiments.We empirically find that the proposed ADMM can converge within 5 iterations on most of the sequences, and thus we set the iteration number to 5 for efficiency.

We implement our tracker in MATLAB that runs at 40 fps on a desktop computer with Intel i7 CPU (3.60 GHz) and 12 GB memory.

4.2 Evaluation datasets

We employ two popular visual tracking benchmarks including VOT-2016 [21] and OTB-2015 [51] for the performance comparisons. Furthermore, the sequences in OTB-2015 are annotated into 11 attributes for more detailed analysis [51].we analyze the compared trackers using success rate and precision plots quantitatively [50]. The area under curve (AUC) of each success plot is leveraged to rank the evaluated trackers. We report the results of both success and precision plots in one-pass evaluation (OPE). We demonstrate the success plots of OPE of the evaluated trackers and use the AUC score to rank them

In VOT-2016, we mainly apply the expected average overlap (EAO) for the comparison as suggested by [21]. Follow the common practice in the VOT community, we also report the accuracy and robustness score in the form of table.

4.3 Results on the OTB100 dataset

OTB100 is provided by [51], including the results of 29 popular trackers evaluated on 100 videos. To measure the tracking performance, it uses one-pass evaluation (OPE) of success plot and precision plot. Among them, the success plot shows the percentage of frames with overlap between the tracked bounding box and the ground truth larger than all thresholds in [0,1], and it employs the Area Under the Curve (AUC) metric as the measurement index. The precision plot shows the percentage of frames whose tracked locations fall within the threshold = 20 pixels to the ground truth. Specifically, we compare the results of our STRCKCF with 8 state-of-the-art tracking approaches, such as BACF [20], SRDCF [10], Staple [1], ECO [12], ECO-HC [12], STRCF [25], STRCF [25], SiamFC [2].

4.3.1 Analysis of overall performance

Figure 2 shows the overall OPE success and precision plots on OTB100. Among all the other demonstrated CF based trackers as BACF, Staple, SRDCF, ECO, and STRCF that only employ single kernel to measure feature similarities, the proposed STRCKCF yields the best performance with an AUC score of 68.4%, significantly outperforming the second best deep CNN feature based method (ECO) that achieves an AUC score of 67.0% by 1.4%, validating the effectiveness of introducing the temporal regularizer and the CKL. Although the ECO performs better than our hand-crafted version (STRCKCF-HC), the complex feature extraction phase of ECO is computationally expensive. However, it sacrifice its real-time ability and our STRCKCF-HC has a high speed. In contrast to our method, the Staple and SRDCF use color and HOG features for visual tracking, yet both only employ a linear kernel to measure the feature similarities, thereby achieving similar performance in terms of both success and precision plots. Among them, Staple yields an AUC score of 57.9% while SRDCF achieves an AUC score of 59.8%, and both are much worse than our STRCKCF-HC, showing the effectiveness of our CKL strategy. Furthermore, although STRCF employs deep CNN features that are much more discriminative than the color and HOG features in our method, the proposed STRCKCF-HC performs a little worse than STRCF by a tiny margin (0.7%), further demonstrating the powerful discrimination of the adopted CKL strategy.

Fig. 2
figure 2

Overall one pass mode success-precision plots of the 9 trackers in the OTB, where the ranking scores for each tracker are shown in the legend

Full size image

Table 1 lists the results of comparing speed between our STRCKCF-HC and other 5 trackers shown in Fig. 2, among which we can observe that STRCKCF achieves the 3rd place with 40 fps, following KCF and Staple with a speed of 106 and 65 fps, respectively. Furthermore, the proposed STRCKCF-HC achieves a 8 × speedup than SRDCF that achieves a speed of 5 fps, demonstrating the efficiency of the employed ADMM optimization strategy.

Table 1 Comparing speeds (in fps) on OTB100
Full size table

4.3.2 Analysis of attribute-based performance

In [51], the attributes of the videos in OTB100 are categorized into illumination variation (IV), out-of-plane rotation (OPR), scale variation (SV), occlusion (OCC), deformation (DEF), motion blur (MB), fast motion (FM), in-plane rotation (IPR), out-of-view (OV), background clutter (BC) and low resolution (LR). To further demonstrate the strength and weakness of the proposed STRCKCF and STRCKCF-HC, we conduct a comprehensive evaluation with the 10 trackers on the videos with these attributes.

Figure 3 illustrates the success-rate plots with various attributes, and Fig. 4 shows the qualitative examples in several video sequences. The STRCKCF achieves the best performance on the most attributes in terms of both success and precision plots. However, in the case of FM, OCC, and MB, our method ranks in the 2nd place. Among them, ECO outperforms STRCKCF by a gain of \(0.5\sim 1.3\%\). Especially for FM (refer to MotorRolling shown in Fig. 4) and OCC, the gains of ECO to STRCKCF are 0.3% and 1.0%, respectively, demonstrating the effectiveness of the temporal regularizer and CKL for these attributes. On the other hand, the STRCKCF ranks the 3rd in the case of motion blur (MB) with an AUC score of 69.6%, and the STRCF achieves the second best performance in the case of MB, which is shown in Fig. 4) (refer to Skating1 and Soccer. The proposed STRCKCF-HC achieves a gain of 5.8% and 7.2% compared to SRDCF and 2.5% and 2.2% compared to ECO-HC, respectively. The promising results again show that the temporal regularizer and CKL scheme equipped by the proposed STRCKCF (STRCKCF-HC) is effective to handle a variety of challenging factors in visual tracking.

Fig. 3
figure 3

Success plots with different attributes

Full size image
Fig. 4
figure 4

Sample results of the proposed STRCKCF for targets suffering from rotations. From top to bottom, the targets in Biker, MotorRolling, Skating1, Girl2 and Soccer suffer from IPR, ORP, IPR, OCC and FM respectively

Full size image

4.4 Results on the VOT2016 dataset

To further evaluate the proposed STRCKCF, we compare it with a variety of state-of-the-art trackers on VOT2016 [21], which contains the results of 70 trackers on 60 videos submitted to the VOT2016 challenge.

Table 2 lists the results of the top-ranked trackers in terms of expected average overlap (EAO), accuracy (A) and robustness (R). Among them, EAO estimates the average overlap that a tracker is expected to obtain on a large number of short-term sequences with the same visual properties as the given dataset, A is the average overlap between the predicted and ground truth bounding boxes during successful tracking periods, and R measures how many times the tracker loses the target during tracking. Among them, the proposed STRCKCF ranks 2rd with an EAO score of 0.328 almost on a par with the first-ranked CCOT with an EAO score of 0.331, closely following the third-ranked TCNN with an EAO scor of 0.325. Moreover, the STRCKCF significantly outperforms the SRDCF with an EAO score of 0.247 with a gain of 8.4%. Note that the strict state-of-the-art bound indicated by the VOT2016 report [21] is with an EAO score of 0.251, and for the trackers higher than this bound can be regarded as state-of-the-art. Our STRCKCF significantly outperforms the state-of-the-art bound by 7.7%, demonstrating its state-of-the-art performance. Furthermore, STRCKCF achieves the second-best accuracy with a score of 0.572 and a fourth-ranked competitive R score of 0.253 on par with the third counterpart EBT with an R score of 0.252. The AR analysis indicates that the STRCKCF has a high accuracy and rare failures, again demonstrating the powerful expressiveness of the proposed CKL mechanism and the effectiveness of the adopted spatial-temporal regularization.

Table 2 Results of EAO, A and R raw values on VOT2016
Full size table

4.5 Failure cases

In Fig. 5, we show some failure examples of the proposed approach. In the first row, the target soccer suffers from the drastic motion, also the object regions contain few colors, limiting the discriminative power of the color-based complementary model. The failure of fast motion case is due to the lack of enough temporal cues (e.g. the optical flow), which will be taken into account in our future works. Furthermore, in the second sequence (the bottom row), our method fails to track the leaf due to it suffering from low resolution. It is because that the color-based and hog-based representations are not enough to capture the whole foreground object and background scenario. Although the spatio-temporally regularized complementary CF is learned, in the low-resolution frames, the deep convolutional network based features are needed to enhance the discriminative ability, which is one of our future directions.

Fig. 5
figure 5

Failure examples of the proposed tracking algorithm, where the red and green bounding boxes indicate our results and ground-truths, respectively

Full size image

5 Conclusions

In this paper, we have proposed a novel STRCKCF based tracking approach. First, by introducing spatial-temporal regularization to the filter learning, we formulate its model with only one training image, which can not only facilitate exploiting the circulant structure in learning, but also reasonably approximate the SRDCF with multiple training images. Furthermore, by incorporating two types of kernels whose matrices are circulant, the proposed STRCKCF is able to fully take advantage of the complementary traits of the color and HOG features to learn a robust target representation efficiently. Besides, our STRCKCF can be efficiently optimized via the ADMM. Extensive evaluations on OTB100 and VOT2016 visual tracking benchmarks have demonstrated that the proposed method achieves favorable performance against state-of-the-art trackers with a speed of 40 fps on a single CPU. Compared with SRDCF, the proposed STRCKCF achieves a 8 × speedup and has a gain of 5.5% AUC score on OTB100 and 8.4% EAO score on VOT2016.