1 Introduction

During the acquisition and transmission process, images are often contaminated by various noises, such as Gaussian white noise in optical images [1, 6, 12]. The presence of noise reduces the resolution of the original image and seriously affects the subsequent classification and recognition of the target. Therefore, image denoising has become an important method for image preprocessing. Image denoising is to improve image quality and highlight the features of the image itself [17]. As Donoho et al. proposed the concept of nonlinear wavelet threshold denoising [21], the denoising method based on wavelet transform has been widely used. In recent years, the research focus for wavelet denoising is the study of statistical model of image wavelet coefficients, which is to accurately model the non-Gaussian image wavelet coefficients with certain correlations [15]. The basic idea of this type of algorithm is to use the statistical model as a priori probability model of the wavelet coefficients, and then use this prior information to estimate the wavelet coefficients of the original image in the Bayes framework. For example, an image denoising method combined with wavelet domain and SUREShrink threshold estimation (WT + SUREShrink) was proposed in [14]. This method is based on SURE (Stein’s Unbiased Risk Estimation) criterion, which is an unbiased estimate of the mean square error criterion, and the SURE threshold approaches the ideal threshold. an image denoising method combined with the wavelet domain and BayesShrink threshold estimation (WT + BayesShrink) was proposed in [7], which is based on the assumption that no-noise image wavelet coefficients obey the generalized Gaussian distribution.

However, with the increasing manifestation of the limitations of wavelet transforms, such as the non-sparseness of high-dimensional time coefficients, lack of multi-directional selectivity, multi-scale geometric analysis methods have emerged. Contoulet transform [4] is a powerful and versatile two-dimensional signal transformation tool. Compared with wavelet transform, it has better multi-resolution, multi-directional performance, and can accurately capture the intrinsic geometry of the image. For example, an image denoising method combined with Contourlet domain and BayesShrink threshold estimation (CT + BayesShrink) was proposed in [10]. However, because Contourlet lacks translation invariance, on this basis, Cunha et al. proposed the nonsubsampled contourlet transform (NSCT) [2], which uses non-subsampled laplacian pyramid (LP) and directional filter bank (DFB) to construct the decomposition structure. This process can avoid the downsampling process, so as to make the transformation has translation invariance, and further improve the performance of the Contourlet transform in the field of image denoising [3, 22].

In addition, there is a problem in the NSCT coefficient variance estimation algorithm based on the traditional Bayes principle, that is, how to select an appropriate prior probability coefficient model of the original image and the noise coefficient. To solve this problem, the Variational Bayes (V-Bayes) method can be used. The basic idea of V-Bayes is to approximate the true posterior probability distribution with a more easily approximated distribution. It realizes the estimation by minimizing the Kullback-Leibler (KL) divergence between the approximate distribution and the real posterior probability distribution [5, 9].

For this reason, this paper combines NSCT bivariate model and V-Bayes estimation, and proposes an image denoising algorithm. The simulation analysis was performed on the standard test images Lena, Barbara, and Peppers and compared with the existing classical methods. The results show that the proposed algorithm can effectively remove the noise in the image and obtain the highest PSNR value and noise suppression capability.

2 Nonsubsampled Contourlet transforms and bivariate model

2.1 Contourlet transform

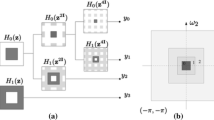
Contourlet transform is implemented by Laplacian Pyramid (LP) decomposition and Directional Filter Bank (DFB). The LP decomposition decomposes the original image into low-frequency sub-band and high-frequency sub-band, where the low-frequency sub-band is generated from the original image by two-dimensional low-pass analysis filtering and down-sampling. The low-frequency sub-band is subjected to up-sampling and two-dimensional low-pass synthesis filtering to form the same low-frequency components as the original image size. The original image is subtracted from the low-frequency components to form another high-frequency sub-band. The high-frequency sub-band is further decomposed into \( {2}^{l_j} \) sub-bands by a directional filter bank (for different scales j and lj can take different values). Repeating the above process for low-frequency sub-band can achieve multi-scale multi-direction decomposition [13, 18]. Figure 1 is a schematic diagram of the decomposition of the high-frequency sub-band by DFB, and Fig.2 shows the sub-band of the Lena image after 2-layer Contourlet transform.

Fig. 1
figure 1

Decomposition of high-frequency sub-band by DFB

Full size image
Fig. 2
figure 2

The sub-band of the Lena image after 2-layer Contourlet transform

Full size image

The Contourlet transform process is expressed as [20]: (1) Using LP to perform the first-order multiscale decomposition of the original image to obtain the first-order low-pass sub-band and the first-order band-pass sub-band; (2) Using DFB to combine singular points that have the same direction and are not continuous into a new coefficient, and the first-order band-pass sub-band is decomposed in multiple directions to obtain a directional sub-band; (3) Repeat steps 1 and 2 for the directional sub-bands to obtain the low-pass sub-bands at different scales; (4) Contourlet reconstruction transformation is performed on LP and DFB to obtain a transformed image matrix.

2.2 Nonsubsampled Contourlet transform (NSCT)

The contourlet transform can sparsely represent the image in an optimal way, and can efficiently capture curved and oriented geometrical structures in images. Because down-sampling is performed in both LP and DFB, the redundancy of the Contourlet coefficients of the image is greatly reduced (redundancy is only 4/3) [23]. As a result, this transformation lacks translation invariance. Therefore, if the Contourlet transform is used directly for image denoising, there will be a noticeable ringing effect.

In order to solve the above problems, this paper uses the NSCT. The NSCT is a non-orthogonal transform that discards the down-sampling operations in the Contourlet transform, but combines the nonsubsampled pyramid (NSP) and nonsubsampled directional filterbanks filter banks (NSDFB).After the transformation, the size of the sub-bands in each direction on each scale is the same as that of the original image, and its redundancy reaches \( 1+{\sum}_{j=1}^J{2}^{l_j} \) (J denotes the decomposition layer number of NSP). Therefore, the improvement of the redundancy of the coefficients makes the transform have a translation invariance, which is beneficial to the effect of image denoising [16]. Fig.3 is a schematic diagram of a 2-layer nonsubsampled Contourlet transform.

Fig. 3
figure 3

NSCT decomposition schematic

Full size image

2.3 Bivariate model

A large number of studies have shown that the image wavelet transform coefficients are not independent, but there is a certain degree of correlation, including intra-scale correlation and inter-scale correlation. In addition, the distribution of the wavelet coefficients of each sub-band is not Gaussian, but forms a curve with high peaks and long tails. Based on the above two properties of image wavelet coefficients, various statistical models have been proposed. Among them, the bivariate model fully exploited the inter-scale correlation of image wavelet coefficients [11], used the non-Gaussian density function to model the distribution of “parent” and “child” coefficients, and used Bayes statistical theory to obtain the analytical expression of the maximum posterior estimate. Therefore, it has achieved good results in the application of image denoising.

Because the coefficients in the NSCT transform domain have similar distribution characteristics with the wavelet coefficients, that is, the decomposition coefficients between the adjacent scales have strong correlation. For this reason, the processing idea of the bivariate model in the wavelet domain can be used to extend it into the NSCT transform domain [8].

Considering the relationship between the current coefficient and its parent coefficient, the image observation signal can be expressed as

$$ y=\omega +n $$
(1)

where ω = [ω1, ω2], ω1 is the NSCT coefficient of the original image scale, and ω2 is the NSCT coefficient with the same spatial position in the previous scale as the parent coefficient of ω1. y = [y1, y2] and n = [n1, n2] represent the vectors composed of the NSCT decomposition coefficient of observation image and the noise, respectively.

In the NSCT domain, the objective of image denoising is to obtain ω‘s estimate \( \overset{\frown }{\omega } \) from y. The maximum posterior probability (MAP) can be used to estimate \( \overset{\frown }{\omega }(y)=\arg \underset{\omega }{\max }{p}_{\omega \mid y}\left(\omega |y\right) \), and then use Bayes’ rule to obtain

$$ \overset{\frown }{\omega }(y)=\arg \underset{\omega }{\max}\left[\log \left({p}_n\left(y-\omega \right)\right)+\log \left({p}_n\left(\omega \right)\right)\right] $$
(2)

From the above equation, we must first know the probability distribution of the NSCT decomposition coefficient of noise. Here assume that the noise density function pn obeys a Gaussian distribution with a mean of 0 and a variance of \( {\sigma}_n^2 \):

$$ {p}_n(n)=\frac{1}{2\pi {\sigma}_n^2}\exp \left(-\frac{n_1^2+{n}_2^2}{2{\sigma}_n^2}\right) $$
(3)

According to the distribution of NSCT decomposition coefficients, the model proposed in [19] was modified to fit the distribution of ω by the probability distribution represented by the following formula:

$$ {p}_{\omega}\left(\omega \right)=\frac{3}{2\pi {\sigma}^2}\exp \left(-\frac{\sqrt{3}}{\sigma}\sqrt{\omega_1^2+{\omega}_2^2}\right) $$
(4)

where σ represents the model edge variance of each NSCT coefficient. Since pω(ω) follows the properties of the convex function and can be derived, so that f(ω) = lg(pω(ω)), then (2) is equivalent to solving the system of equations:

$$ \Big\{{\displaystyle \begin{array}{l}\frac{y_1-{\overset{\frown }{\omega}}_1}{\sigma_n^2}+{f}_1\left(\overset{\frown }{\omega}\right)=0\\ {}\frac{y_2-{\overset{\frown }{\omega}}_2}{\sigma_n^2}+{f}_2\left(\overset{\frown }{\omega}\right)=0\end{array}} $$
(5)

where fi is the partial derivative of f(ω) to ωi. Then, the applicable bivariate threshold function in the NSCT transform domain can be solved:

$$ {\overset{\frown }{\omega}}_1=\frac{{\left(\sqrt{y_1^2+{y}_2^2}-\frac{\sqrt{3}{\sigma}_n^2}{\sigma}\right)}_{+}}{\sqrt{y_1^2+{y}_2^2}}{y}_1 $$
(6)

where the symbol ( f )+ represents ( f )+ = 0 when f < 0, otherwise ( f )+ = f. Equation (6) is the MAP estimate of the current coefficient ω1 in the bivariate model and is called the bivariate atrophy function. It can be seen that if we want to obtain \( {\overset{\frown }{\omega}}_1 \), we must estimate the NSCT coefficient variance \( {\sigma}_n^2 \) of the noise first. In this paper, the variation Bayes estimation method is used to estimate the variance.

3 Variational Bayes threshold estimation

3.1 Bayes estimation

For the estimation of the variance \( {\sigma}_n^2 \) of the NSCT coefficients, a Bayes estimation method can be used. Also consider the relationship between the original image and noise NSCT decomposition coefficients

$$ y=\omega +n $$
(7)

In the process of image blurring, the edge area is affected more than flat areas and often contains more information. Therefore, we will perform denoising in the image gradient domain. Let ∇ω and ∇y denote the gradient of the NSCT coefficients of the original image and the noisy image, respectively, so the eq. (7) can be converted as

$$ \nabla y=\nabla \omega +n $$
(8)

Given the gradient ∇y of the noisy image, according to the Bayes principle, the posterior probability of ∇ω can be expressed as

$$ p\left(\nabla \omega |\nabla y\right)=\frac{p\left(\nabla y|\nabla \omega \right)p\left(\nabla \omega \right)}{p\left(\nabla y\right)} $$
(9)

According to the (9), one of the key problems of the NSCT coefficient variance estimation algorithm based on the Bayes principle lies in how to select an appropriate noise function and prior probability coefficient model of the original image coefficient and noise coefficient.

3.2 Variational Bayes estimation (V-Bayes)

In order to solve the above problem of traditional Bayes estimation, the variational Bayes method provides an effective solution to the problem. The basic idea is to approximate the true posterior probability distribution p(∇ω| ∇y) with an easy-to-handle approximation distribution q(∇ω). The KL divergence can measure the distance between two distributions, so estimation can be achieved by minimizing the KL divergence between the approximate distribution and the real posterior probability distribution.

$$ {\displaystyle \begin{array}{l} KL\left\{q\left(\nabla \omega, {\sigma}^2\right)\Big\Vert p\left(\nabla \omega |\nabla y\right)\right\}\\ {}=\int q\left(\nabla \omega, {\sigma}^2\right)\ln \frac{q\left(\nabla \omega, {\sigma}^2\right)}{p\left(\nabla \omega |\nabla y\right)}d\nabla \omega +\ln p\left(\nabla y\right)\ge 0\end{array}} $$
(10)

The above equation holds if and only if q(∇ω, σ2) = p(∇ω| ∇y).

Note that p(∇y) is always a constant throughout the estimation process, so a cost function CKL can be defined to get the optimal value of the approximate distribution:

$$ {\displaystyle \begin{array}{l}{C}_{KL}= KL\left\{q\left(\nabla \omega, {\sigma}^2\right)\Big\Vert p\left(\nabla \omega |\nabla y\right)\right\}-\ln p\left(\nabla y\right)\\ {}\kern2em =\int q\left(\nabla \omega \right)\ln \frac{q\left(\nabla \omega \right)}{p\left(\nabla \omega \right)}d\nabla \omega \\ {}\kern3.199999em +\int q\left(-{\sigma}^2\right)\ln \frac{q\left(-{\sigma}^2\right)}{p\left(-{\sigma}^2\right)}d\left(-{\sigma}^2\right)\end{array}} $$
(11)

The variational Bayes estimation minimizes the cost function through an iterative approach (that is, variation Bayes expectation maximization theorem), thereby estimating the noise function.

4 Image denoising steps

From the previous discussion, it can be seen that the NSCT has the advantages of anisotropy, multi-directional selectivity and translation invariance, while the bivariate model can fully exploit the inter-scale correlation of image wavelet coefficients. At the same time, we have reason to believe that the transform coefficients and the wavelet coefficients of the image Contourlet and the NSCT have very similar properties in terms of correlation and distribution characteristics. Therefore, this paper combines the two and proposes an image denoising algorithm based on NSCT and bivariate model. The detailed steps of the algorithm are as follows:

  1. Step 1:

    NSCT is performed on the noisy image, in which the NSP decomposition layer number and the number of NSDFB decomposed direction sub-bands on each scale can be set.

  2. Step 2:

    Estimate the NSCT coefficient variance \( {\sigma}_n^2(k) \) of the noise.

    (2.1) Perform NSCT on noisy images and estimate noise standard deviation σn using V-Bayes estimation method.

    (2.2) Generate a Gaussian white noise image with the same size as the original image with an average value of 0 and a variance of \( {\sigma}_n^2 \).

    (2.3) Perform NSCT on this noise image, and square the transformed coefficients to obtain the NSCT coefficient variance \( {\sigma}_n^2(k) \) of noise.

    (2.4) Go to step (2.2), repeat the above method several times (the number of repetitions in this experiment is 10), take the average, and get the final\( {\sigma}_n^2(k) \).

  3. Step 3:

    For each high frequency direction sub-band, use local adaptive method to estimate the model edge variance σ2(k) for each coefficient, ie, \( {\sigma}^2(k)=\max \left({\sigma}_{v1}^2(k)-{\sigma}_n^2(k),0\right) \), where \( {\sigma}_{v1}^2(k)=\frac{1}{M}\cdot \sum \limits_{v1(k)\in N(k)}{y}_1^2(k) \). Here, N(k) represents a square window centered on the current NSCT coefficient y1(k), and M is the number of coefficients in the window.

  4. Step 4:

    Substitute \( {\sigma}_n^2(k) \) and σ2(k) into (6) to obtain the bivariate threshold \( {\overset{\frown }{\omega}}_1 \).

  5. Step 5:

    Reconstruct the denoised Contourlet coefficient matrix and perform an inverse NSCT to obtain a denoised image.

5 Simulation and analysis

5.1 Simulation settings

On the PC with Intel i5–7500 CPU and 8G memory, various denoising algorithms are executed through Matlab R2014 software. Three 512 × 512 standard test images Lena, Barbara, and Peppers were selected for the simulation experiment. Gaussian white noise with zero mean and different levels of standard deviation was added. The noise standard deviations σn were 10, 20, 30, 40, 50. For system parameters, appropriate parameters were set according to the analysis of the result of previous experiments. In this experiment, we set the number of NSCT layers to 5, and the number of directional sub-bands was 4, 8, 8, 16, and 16 in order from coarse to fine scale. The window coefficient M is 13 × 13.

In order to evaluate the effectiveness of the NSCT domain+V-BayesShrink threshold estimation denoising algorithm (NSCT+V-BayesShrink) proposed in this paper, we compared three typical algorithms in the current denoising field, these are wavelet domain + SUREShrink threshold estimation method (WT + SUREShrink) [14], the wavelet domain + BayesShrink threshold estimation method (WT + BayesShrink) [7], the Contourlet domain + BayesShrink threshold estimation method (CT + BayesShrink) [10].

5.2 Performance parameters

For the real images I, a denoised image S is obtained after denoising. In this paper, we select the following indicators for judging the denoising effect of an image:

1) Peak signal-to-noise ratio (PSNR), which represents the difference between a denoised image and a real image.

$$ PSNR=20\log \left(\frac{255}{\sqrt{MSE}}\right) $$
(12)

where, MSE is the mean square error value of the real image I and the denoised image S, expressed as

$$ MSE=\frac{1}{M\times N}\sum \limits_{i=1}^M\sum \limits_{j=1}^N\left(I\left(i,j\right)-S\left(i,j\right)\right) $$
(13)

2) The noise suppression parameter (ρ), the greater the value, the stronger the suppression of noise.

$$ \rho =\frac{\varGamma \left(I-\overline{I},S-\overline{S}\right)}{\sqrt{\varGamma \left(I-\overline{I},I-\overline{I}\right)}\sqrt{\varGamma \left(S-\overline{S},S-\overline{S}\right)}} $$
(14)

where, the symbol “一” means taking an average of the image. The definition of operator Γ isΓ(A, B) =  ∑ A(i, j)B(i, j).

In addition, visually judging the degree of noise pollution of the image, the important edge and detail information retention in the image is also an important criterion for the performance of denoising algorithm.

5.3 Performance comparison

Figure 4 shows the standard Lena image and Gaussian noise image with standard deviation of σn = 30. Figure 5 shows the denoised Lena image processed by various denoising methods. Figure 6 shows the standard Barbara image and Gaussian noise image with standard deviation of σn = 40. Figure 7 shows the denoised Barbara image processed by various denoising methods. From a visual point of view, the NSCT+V-BayesShrink algorithm well preserved the edge details of the image, effectively removed the noise, and the denoised image content became clearer. The parts such as brims, hair, eyes, and eyebrows that are rich in edge details are clearer than the corresponding parts in other denoised images.

Fig. 4
figure 4

Lena image, (a) original image, (b) noise image (σn = 30)

Full size image
Fig. 5
figure 5

Denoised Lena image, (a) WT + SUREShrink, (b) WT + BayesShrink, (c)CT + BayesShrink, (d)NSCT+V-BayesShrink

Full size image
Fig. 6
figure 6

Barbara image, (a) original image, (b) noise image (σn = 40)

Full size image
Fig. 7
figure 7

Denoised Barbara image, (a) WT + SUREShrink, (b) WT + BayesShrink, (c)CT + BayesShrink, (d)NSCT+V-BayesShrink

Full size image

Table 1 shows the PSNR of the noise images obtained by adding the noise with the standard deviations σn of 10, 20, 30, 40, and 50 to the Lena, Barbara, and Peppers images, respectively. It can be seen that after adding noise, the PSNR of the image is significantly reduced, and the larger the noise standard deviation, the lower the PSNR.

Table 1 PSNR (dB) of the noise-added image on three images
Full size table

For each image, 10 tests were repeated at each noise level, and calculate the average PSNR. The experimental results are shown in Figs. 8, 9 and 10. Table 2 shows the average PSNR of the various algorithms over the three images. In addition, the average ρ values of various algorithms on three images under different noise levels are also calculated, as shown in Table 3.

Fig. 8
figure 8

Comparison of denoising performance on Lena images

Full size image
Fig. 9
figure 9

Comparison of denoising performance on Barbara images

Full size image
Fig. 10
figure 10

Comparison of denoising performance on Peppers images

Full size image
Table 2 Average PSNR (dB) of denoised images obtained by various algorithms
Full size table
Table 3 Average ρ of denoised images obtained by various algorithms
Full size table

From Fig. 8 to Fig. 10, it can be seen that as the noise level increases, the PSNR of the denoised image of various methods will also decrease. In addition, for the three images, the denoising performance on the Barbara image is slightly worse than that of the Lena and Peppers images. This is because the Barbara image has more directional texture information, which makes it more difficult to denoise.

The above experimental results show that the NSCT+V-BayesShrink algorithm has good performance both in terms of objective indicators and subjective effects. From Tables 2 and 3, it can be seen that in all simulation experiments, the PSNR and the value of NSCT+V-BayesShrink algorithm are the highest. With different noise levels, the PSNR is about 0.7 dB higher than CT + BayesShrink algorithm, and the average value is about 0.01 higher than CT + BayesShrink algorithm. The reasons for this are as follows:

  1. 1)

    Use of NSCT. NSCT has many advantages such as anisotropy, translation invariance, multi-direction selectivity and so on, which make the image denoising very advantageous. As a result, the NSCT+V-BayesShrink algorithm achieves better results than the WT-based algorithm, effectively maintains the directional information in the original image, and largely avoids the appearance of the ringing effect. Although the WT-BayesShrink algorithm is also based on the bivariate model, the WT transform only has approximate translation invariance and directional selectivity of 6 directions on each scale, so this algorithm is not as good as NSCT-based algorithm.

  2. 2)

    Selection of bivariate models. Bivariate model fully exploits the inter-scale correlation of image coefficients, and has the atrophic function expression associated with the “father” coefficient. In addition, NSCT+V-BayesShrink algorithm uses a local adaptive method when estimating the model edge variance of the current coefficient, that is, taking into account the influence of the surrounding coefficients on the current coefficient, which is equivalent to the use of intra-scale correlation of the coefficients. In other words, the algorithm considers both the intra-scale and inter-scale correlations of the coefficients. Compared with the CT-BayesShrink based on the generalized Gaussian model which only considers intra-scale correlations, the results of NSCT+V-BayesShrink are more reasonable than CT-BayesShrink.

  3. 3)

    Use of V-Bayes. V-Bayes estimation is used to estimate the variance of the noise coefficient in NSCT+V-BayesShrink. Compared with the median estimation method proposed by Donoho in the wavelet domain, V-Bayes estimation method is more suitable for the Contourlet domain, and the estimated noise coefficient variance is also more accurate.

6 Conclusion

This paper combines NSCT bivariate model with V-Bayes estimation and proposes an image denoising algorithm. Using the advantages of translation invariance and multi-direction selectivity of the NSCT bivariate model, the V-Bayes valuation theory is used to derive the threshold function. Finally, the denoised coefficients are inverse-transformed by NSCT to obtain denoised images. The simulation analysis on the standard test image shows that the denoised image obtained by the algorithm has a significant improvement in the subjective visual effects, PSNR and noise suppression performance ρ.