1 Introduction

The use of image moments constitutes one of the hotly debated issues in pattern recognition and image classification. The basic idea of the theory of moments is the projection of the data space on a complete orthogonal basis to often extract useful information. These latter are extracted as the projection coefficients called moments. Each family of moment is directly related to the basis of used projection. We can distinguish between three types of moments: the non-orthogonal moments as the geometric moments [16] and the complex moments [1], the continuous orthogonal moments as Legendre [47], Zernike [21], Pseudo-Zernike [48], Gegenbauer [15] and Fourier-Mellin [59] and the discrete orthogonal moments as Tchebichef [35], Krawtchouk [52], Racah [62], Charlier [12] and Hahn [43]. The computation of non-orthogonal moments and the continuous orthogonal moments requires appropriate transformations of the coordinates of the image in the interval of definition of the polynomials and also of the integrals by finite summations as well, because the function of the image intensity is always defined on a discrete domain. These approximations cause the discretization errors [25]. To definitely eliminate these errors, the researchers proposed using a discrete orthogonal moment based on the discrete orthogonal polynomials as the polynomials of Tchebitchef, Krawtchouk, Racah, Dual-Hahn, Hahn, Charlier and Meixner for image analysis. The use of this type of polynomials as basis functions for the computation of moments of the image eliminates the need for numerical approximation and satisfies exactly the orthogonality property in discrete space coordinates of the image. This property makes the discrete orthogonal moment higher than the conventional continuous orthogonal moment in terms of the capacity of the image representation. Recently, a novel set of discrete orthogonal moments based on the bivariate discrete orthogonal polynomials have been introduced into the field of the image analysis and pattern recognition [13, 49, 61]. These series of bivariate polynomials are solutions of the second-order partial differential Eqs [6, 8, 23].. The use of discrete orthogonal moments is limited by the high computational cost and the propagation of a numerical error in the computation of polynomials values [64]. To limit this error, the scientists apply the recurrence relation with respect to the variable x instead of the order n in the computation of the discrete orthogonal polynomials [64]. Thus, To reduce the computational time cost of moments, several algorithms are introduced in literature [9, 14, 37, 38, 40, 41, 45, 46].

Although most work has focused on the discrete moments based on the bivariate discrete orthogonal polynomials of Tchebichef-Krawtchouk [61], Tchebichef-Hahn [61], Hahn-Krawtchouk [61], Charlier-Tchebichef [12], Charlier-Krawtchouk [12] and Charlier-Hahn [12], no attention has been paid to the study of discrete orthogonal moments based on the bivariate discrete orthogonal polynomials of Charlier-Meixner.

In this paper, we will apply the discrete orthognal moments for the classification problem of images in heterogeneous bases. The classification of image passes by the selection of the primitives, the latter is an important step in any pattern recognition system. This selection of primitives is considered a combinatorial optimization problem and has been researched in many disciplines. Its main purpose is to reduce their number by eliminating redundant and irrelevant primitives from the recognition system. The second objective of this selection of primitives is also to maintain and / or improve the performance of the classifier used by the recognition system. Invariant moments are used to solve this type of primitive selection problem in pattern recognition.

In this paper, we will present a new application of discrete orthogonal moments in the field of classification. This new method is applied to solve the problem of selecting a subset of primitives in a pattern recognition problem. The latter is based on the use of slice and block image representation to extract the primitives of each image from the blocks of each slice, it allows us to improve the classification result and speed up the process of pattern recognition without affecting the property of invariance. In our case, we use the discrete orthogonal moments based on the product of Charlier and Meixner discrete orthogonal polynomials which are denoted Charlier-Meixner moments (CMM). We also present an approach to accelerate the time computation of CMM based on two notions:

  • The methodology of the image block representation (IBR) and the image slices representation (ISR): In this method the image is decomposed into series of non-overlapped binary slices and each slice is described by a number of homogenous rectangular blocks. Once the image is partitioned into slices and blocks, the computation of CMM can be accelerated as the moments can be computed from the blocks of each slice.

  • The computation of the bivariate discrete orthogonal polynomials of Charlier-Meixner by using the recurrence relation with respect to the variable x instead of the order n.

We devote the rest of this paper to image classification systems by the content in heterogeneous databases. The images in this type basis belong to different concepts and are heterogeneous content. For this reason, we will test the ability of discrete orthogonal moments of Charlier-Meixner (CMM) for image classification in heterogeneous databases. For the purpose of objects classification, it is vital that the proposed moments of CMM is independent of rotation, scale and the translation of the image. For this, we have proposed a new set of discrete invariant moments of Charlier-Meixner (CMMI) under translation, scaling and rotation of the image. The invariant moments of Charlier-Meixner (CMMI) are derived algebraically from the geometric invariant moments.

The obtained results during the selection of the primitives made it possible to reduce the complexity of the classification. The number of primitives has been significantly reduced compared to all the primitives extracted from the pattern recognition system while maintaining the system recognition rate performance. A fast computational algorithm of CMMI is also presented using the image slice representation method. In fact, we tested the ability of classification of our descriptor CMMI compared to other descriptors of Hu invariant moments, Charlier invariant moments (CCMI) and Meixner invariant moments (MMMI) for the three databases COIL-100, CALTECH-256 and COREL using as classifier the support vector machines (SVM) for number of the classes between 3 to 35. We will also compare our classification method with classification methods based on Convolution Neural Network (CNN), on Histograms of Oriented Gradient (HOG) and on scalable invariant characteristic transformation (SIFT). So, the classification results show the efficiency of the CMMI in terms of classification accuracy of images compared to those of Hu, CCMI and MMMI.

Hence, The rest of the paper is organized as follows: In Section 2, we present the work related to our contribution. In Section 3, we present the bivariate discrete orthogonal polynomials of Charlier-Meixner. Section 4 presents the fast computation of Charlier-Meixner’s discrete orthogonal moments. Section 5 focuses on the deriving of CMMI from the geometric moments by two methods. Section 6 provides some experimental results concerning the invariability, the objects classification by CMMI and the support vector machine. Section 7 concludes the work.

2 Related work

Several works have dealt with the theory of moments and their applications in the image domain, especially for image classification. In this context, one quotes the works of Hu [16] which extracted seven invariant primitives of the geometric moments. Chong et al. [3, 4] have introduced an effective method to construct the translation and scale invariants of Legendre and Zernike moment. Zhu et al. [63] have proposed a method directly based on Tchebichef polynomials to make the translation and scale invariants of Tchebichef moments. Karakasis et al. [20] have proposed a generalized expression of the weighted dual Hahn moment invariants up to any order and for any value of their parameters based on a linear combination of geometric moments. Beyond what orthogonal moments can bring to the different fields of imagery, these can be exploited in combination with machine learning methods in other areas of research, such as recognition actions based on collected data [27,28,29,30], or the prediction of your career from your data on social networks [31, 39, 54], and many other possibilities of use, the discrete orthogonal moments are well suited for decision support.

The application of moment theory in the image domain is limited by the computational time cost of moments. To solve this problem, Spiliotis and Mertzios [46] have presented a fast algorithm to calculate the geometric moments for binary images using the image block representation (IBR). Hosny [14] has given a fast algorithm to calculate the geometric moments for gray-scale images using the image slice representation. Lim et al. [26] have presented a fast computation technique to calculate exactly Zernike moments by using cascaded digital filter outputs, without the need to compute geometric moments.

Shu et al. [45] introduced an approach to accelerate the time computation of Tchebichef moments by deriving some properties of Tchebichef polynomials. Sayyouri et al. have proposed in [41] and [42] a fast method to accelerate time computation of Charlier and Hahn moments using the image bloc representation.

For the learning problem, several works have dealt with this subject. In this context, Zechao et al. in [58] propose a novel data representation learning algorithm by jointly exploiting image understanding, feature learning and feature correlation. They also proposed a deep metric learning method by exploiting the heterogeneous data structure of community-contributed images [56, 57].

Inspired by the statistical theory of learning, the SVM support vector classifier is a binary classification method for supervised learning. Originally, SVM relies on the existence of a linear classifier that separates two classes into an appropriate space. Its extension to multi-class problems is quickly highlighted. [2, 19] In addition, to allow optimal separation in non-linearly separable cases, SVMs have proven that the use of multiple kernels generates more flexibility and improves the interoperability of these methods [24]. Given its performance, this classification method has become in a short period a standard tool in the state of the art for several recognition problems, in particular heterogeneous images by the content. Within this framework, Hu et al. in [17, 18, 53, 55, 60] propose the use of the support vector machine to classify defects in steel strip surface images, to effectively recognize aerial photographs and for categorization of fine-grained images by hierarchically locating discriminating object parts in each image. Other works [32, 33] are focused on the recognition of semantic involvement and the relationship between medical and medical conditions.

Recently a new series of discrete orthogonal moments is introduced by several researchers to improve the quality of image processing either for reconstruction or for classification. Dunkl and Xu in [6] have proposed an excellent paper of bivariate discrete orthogonal polynomials as a product of two families of classical discrete orthogonal polynomials with one variable. Zhu has studied in [61] seven types of the continuous and discrete orthogonal moments based on the tensor product of two different orthogonal polynomials with one variable. Hmimid et al. have proposed in [12] a new set of bivariate discrete orthogonal polynomials, which are the product of Charlier’s discrete orthogonal polynomials with one variable by Tchebichef, Krawtchouk, and Hahn discrete orthogonal polynomials with one variable.

3 The bivariate discrete orthogonal polynomials

In this section, we present the definition and the basic properties of classical discrete orthogonal polynomials of two variables of Charlier-Meixner [7, 51]. The discrete orthogonal polynomials with two variables satisfy the following second partial order difference equation.

$$ {\displaystyle \begin{array}{l}{A}_{1,1}\left(x,y\right){\Delta}_1{\nabla}_1{P}_n\left(x,y\right)+{A}_{1,2}\left(x,y\right){\Delta}_1{\nabla}_2{P}_n\left(x,y\right)+{A}_{2,1}\left(x,y\right){\Delta}_2{\nabla}_1{P}_n\left(x,y\right)\\ {}+{A}_{2,2}\left(x,y\right){\Delta}_2{\nabla}_2{P}_n\left(x,y\right)+{B}_1\left(x,y\right){\Delta}_1{P}_n\left(x,y\right)+{B}_2\left(x,y\right){\Delta}_2{P}_n\left(x,y\right)=\lambda {P}_n\left(x,y\right)\end{array}} $$
(1)

where Ai, j and Bifor i, j = 1, 2 are polynomials and λ is a real number.

The forward and the backward partial difference operators Δi and ∇i for i = 1, 2 are defined by

$$ {\displaystyle \begin{array}{lll}{\Delta}_1u\left(x,y\right)=u\left(x+1,y\right)-u\left(x,y\right)&; & {\Delta}_2u\left(x,y\right)=u\left(x,y+1\right)-u\left(x,y\right)\\ {}{\nabla}_1u\left(x,y\right)=u\left(x,y\right)-u\left(x-1,y\right)&; & {\nabla}_2u\left(x,y\right)=u\left(x,y\right)-u\left(x,y-1\right)\end{array}} $$
(2)

The bivariate discrete orthogonal polynomials are constructed from the product of the classical discrete orthogonal polynomials with one variable [7]. Using this method, we can produce the bivariate discrete orthogonal polynomials of Charlier-Meixner.

3.1 Bivariate discrete orthogonal polynomials of Charlier-Meixner

The bivariate discrete orthogonal of Charlier-Meixner are defined as the product of the Charlier and Meixner discrete orthogonal polynomials with one variable as follows [51]:

$$ {CM}_{n,m}\left(x,y,{a}_1,\beta, \mu \right)={C}_n^{a_1}(x)\times {M}_n^{\left(\beta, \mu \right)}(y)\kern0.5em ;n\ge 0\kern0.5em ;m\ge 0 $$
(3)

where \( {C}_n^{a_1}(x) \) is the nth discrete orthogonal polynomials of Charlier and \( {M}_n^{\left(\beta, \mu \right)}(x) \) is the nth discrete orthogonal polynomials of Meixner.

The bivariate discrete orthogonal of Charlier-Meixner are orthogonal on the set \( V=\left\{\left(i,j\right):\mathrm{i}\in IN,j\in IN\right\} \) with respect to the weight function of the Charlier-Meixner discrete orthogonal polynomials wC, M(x, y):

$$ {w}_{C,M}\left(x,y\right)={w}_C(x)\times {w}_M(y) $$
(4)

where wC(x) is weight function of Charlier and wM(x) is weight function of Meixner.

The bivariate discrete orthogonal polynomials of Charlier-Meixner CMn, m(x, y, a1, β, μ) satisfy the following linear partial difference equation:

$$ x{\Delta}_1{\nabla}_1u\left(x,y\right)-\frac{1}{\mu -1}y{\Delta}_2{\nabla}_2u\left(x,y\right)+\left[{a}_1-x\right]{\Delta}_1u\left(x,y\right)-\frac{1}{\mu -1}\left[\mu \left(y+\beta \right)-y\right]{\Delta}_2u\left(x,y\right)- nu\left(x,y\right)=0 $$
(5)

where u(x, y) = CMn, m(x, y, a1, β, μ).

In the next section, we will present a brief introduction to the theoretical background of discrete orthogonal polynomials with one variable of Charlier and Meixner [22, 36].

3.2 Discrete orthogonal polynomials with one variable of Charlier and Meixner

The discrete orthogonal polynomials with one variable of Charlier \( {C}_n^{a_1}(x) \) and Meixner \( {M}_n^{\left(\beta, \mu \right)}(x) \) satisfy the following first-order partial difference Eq. [31].

$$ \sigma (x)\varDelta \nabla {P}_n(x)+\tau (x){P}_n(x)+{\lambda}_n{P}_n(x)=0 $$
(6)

Where σ(x) and τ(x) are the functions of second and first degree (Table 1), respectively, λn is an appropriate constant.

Table 1 Data for Charlier \( {C}_n^{a_1}(x) \) and Meixner \( {M}_n^{\left(\beta, \mu \right)}(x) \)
Full size table

The nth discrete orthogonal polynomials with one variable of Charlier \( {C}_n^{a_1}(x) \) and Meixner \( {M}_n^{\left(\beta, \mu \right)}(x) \) are defined by using a hypergeometric function as follows [63]:

$$ {C}_n^{a_1}(x)={{}_2F}_0\left(-n,-x;1/{a}_1\right)=\sum \limits_{k=0}^n{\varepsilon}_{k,n}^{a_1}{x}^k $$
(7)

where x, n = 0, 1, 2…. N − 1 ;  a1 > 0

$$ {M}_n^{\left(\beta, \mu \right)}(x)={\left(\beta \right)}_n{}_2F{}_1\left(-n,-x;\beta; 1-1/\mu \right)=\sum \limits_{k=0}^n{\alpha}_{k,n}^{\left(\beta, \mu \right)}{x}^k\kern0.5em $$
(8)

where x, n = 0, 1, 2. . …N − 1; β > 0 and 0 < μ < 1.

The set of Charlier’s \( \left\{{C}_n^{a_1}(x)\right\} \), Meixner’s \( \left\{{M}_n^{\left(\beta, \mu \right)}(x)\right\} \) discrete orthogonal polynomials forms and a complete set of discrete basis functions with weight function satisfy the orthogonal condition:

$$ \sum \limits_{x=0}^Nw(x){P}_n(x){P}_m(x)=\rho (n){\delta}_{nm}\kern0.5em $$
(9)

with \( {P}_n(x)={C}_n^{a_1}(x)\; or\;{M}_n^{\left(\beta, \mu \right)}(x) \).

where ρ(n) denotes the square of the norm of the corresponding orthogonal polynomials, w(x) denotes the weight function and δnm denotes the Dirac function.

To avoid fluctuations in the numerical computation of Charlier and Meixner discrete orthogonal polynomials, we use their normalized form defined as:

$$ {\tilde{P}}_n(x)={P}_n(x)\sqrt{\frac{w(x)}{\rho (n)}} $$
(10)

The computation of the values of polynomials of Charlier and Meixner, and from their definitions hypergeometric, requires a high cost of computing time which drives us to use a different strategy of computation which is the recursive strategy.

3.2.1 Recurrence relation with respect to order n

As the computation of the normalized form of Charlier and Meixner polynomials by the hypergeometric function has a great computational time cost, we use the following three-term recurrence relations with respect to the order n [22]:

$$ {\tilde{P}}_n(x)=\frac{B\times D}{A}{\tilde{P}}_{n-1}(x)-\frac{C\times E}{A}{\tilde{P}}_{n-2}(x) $$
(11)

where A,B,C,D and E are the coefficient defined in Table 1.

The two initial values of Charlier’s and Meixner’s polynomials are defined as follows:

$$ {\tilde{C}}_0^{a_1}(x)=\sqrt{\frac{w_C(x)}{\rho_C(0)}}\kern1em ;\kern1em {\tilde{C}}_1^{a_1}(x)=\frac{a_1-x}{a_1}\sqrt{\frac{w_C(x)}{\rho_C(1)}} $$
(12)

and

$$ {\tilde{M}}_0^{\left(\beta, \mu \right)}(x)=\sqrt{\frac{w_M(x)}{\rho_M(0)}}\kern1em ;\kern1.75em {\tilde{M}}_1^{\left(\beta, \mu \right)}(x)=\left(\beta +x-\frac{x}{\mu}\right)\sqrt{\frac{w_M(x)}{\rho_M(1)}} $$
(13)

3.2.2 Recurrence relation with respect to variable x

In order to extract the recurrence formula with respect to the variable x we will use the partial difference equations and the forward and backward finite difference operators. The recurrence relations of Charlier’s and Meixner’s discrete orthogonal polynomials with respect to the variable x can be obtained through Eqs. (2) and (6) as follows:

$$ {\tilde{p}}_n(x)=\frac{\sqrt{w(x)}}{\sigma \left(x-1\right)+\tau \left(x-1\right)}\times \left[\frac{2\sigma \left(x-1\right)+\tau \left(x-1\right)-{\lambda}_n}{\sqrt{w\left(x-1\right)}}{\tilde{p}}_n\left(x-1\right)-\frac{\sigma \left(x-1\right)+\tau \left(x-1\right)}{\sqrt{w\left(x-2\right)}}{\tilde{p}}_n\left(x-2\right)\right] $$
(14)

The initial values of recurrence relation with respect to the variable x are defined as:

$$ {\tilde{C}}_n^{a_1}(0)=\sqrt{\frac{w_c(0)}{\rho_c(n)}}\kern0.5em ;\kern0.5em {\tilde{C}}_n^{a_1}(1)=\frac{a_1-n}{a_1}\sqrt{\frac{w_c(1)}{w_c(0)}}{\tilde{C}}_n^{a_1}(0) $$
(15)

and

$$ {\tilde{M}}_n^{\left(\beta, \mu \right)}(0)={\left(\beta \right)}_n\sqrt{\frac{w_M(0)}{\rho_M(n)}}\kern0.5em ;\kern0.5em {\tilde{M}}_n^{\left(\beta, \mu \right)}(1)=\frac{\mu \left(n+\beta \right)-n}{\mu \beta}\sqrt{\frac{w_M(1)}{w_M(0)}}{M}_n^{\left(\beta, \mu \right)}(0) $$
(16)

4 Discrete orthogonal moments of Charlier-Meixner

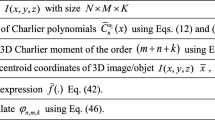
The two-dimensional (2-D) discrete orthogonal moments of Charlier-Meixner (CMM) of order (n + m) for an image intensity function f(x, y) with size M × N are defined as

$$ { CM M}_{nm}=\sum \limits_{x=0}^{M-1}\sum \limits_{y=0}^{N-1}{CM}_{nm}\left(x,y,{a}_1,\beta, \mu \right)f\left(x,y\right) $$
(17)

where CMnm(x, y, β, μ, a1) are the bivariate discrete orthogonal polynomials used as the moment basis set.

Using the orthogonal property of discrete orthogonal polynomials, Eq.(17) also leads to the following inverse moment transform:

$$ f\left(x,y\right)=\sum \limits_{n=0}^{M-1}\sum \limits_{m=0}^{N-1}{CM M}_{nm}{CM}_{nm}\left(x,y,{a}_1,\beta, \mu \right) $$
(18)

The computation of Charlier-Meixner discrete orthogonal moments using Eq.(17) seems to be a time consuming task mainly due to two factors. First, the need of computing a set of complicated quantities for each moment order. Second, the need to evaluate the polynomial values for each pixel of the image. So, to accelerate the time computation of discrete orthogonal moments, we propose a new computation method of moments by describing an image with a set of blocks instead of individual pixels. Two algorithms of the image block representation: IBR for binary images [12, 43] and ISR for gray-scale images are applied. [13]

In the following two subsections, we will present a new formula for fast computing the discrete orthogonal moments of Charlier-Meixner by using the image block representation for binary and the image slice representation for gray-scale images.

4.1 For gray-scale images

The approach of the image slice representation (ISR) decomposes a gray-scale image f(x, y) in series of slices of two levels fi(x, y)

$$ f\left(x,y\right)=\sum \limits_{i=1}^L{f}_i\left(x,y\right) $$
(19)

where L is the number of slices and fi(x, y) the intensity function of the ith slice. After the decomposition of the gray scale image into several slices of two levels, we can apply the algorithm IBR [46]. The gray-scale image fi(x, y) can be redefined in terms of blocks of different intensities as follows:

$$ f\left(x,y\right)=\left\{{f}_i\left(x,y\right),i=1,2,\dots, L\right\}=\left\{{b}_{ij},j=1,2,\dots, {K}_i-1\right\} $$
(20)

where bij is the block of the edge i and Ki is the number of image blocks with intensity.

The fast discrete orthogonal moments of Charlier-Meixner for a gray-scale image f(x, y) is given by:

$$ {\displaystyle \begin{array}{c}{CM M}_{nm}=\sum \limits_{x=0}^{N-1}\sum \limits_{y=O}^{N-1}{CM}_{nm}\left(x,y,{a}_1,\beta, \mu \right)f\left(x,y\right)\\ {}=\sum \limits_{x=0}^{N-1}\sum \limits_{y=O}^{N-1}{\tilde{C}}_n^{a_1}(x){\tilde{M}}_m^{\left(\beta, \mu \right)}(y)\sum \limits_{i=1}^L{f}_i\left(x,y\right)\\ {}=\sum \limits_{i=1}^L\sum \limits_{x=0}^{N-1}\sum \limits_{y=O}^{N-1}{\tilde{C}}_n^{a_1}(x){\tilde{M}}_m^{\left(\beta, \mu \right)}(y){f}_i\left(x,y\right)\\ {}=\sum \limits_{i=1}^L{f}_i\sum \limits_{x=0}^{N-1}{\tilde{C}}_n^{a_1}(x)\sum \limits_{y=O}^{N-1}{\tilde{M}}_m^{\left(\beta, \mu \right)}(y)\\ {}=\sum \limits_{i=1}^L{f}_i\sum \limits_{j=0}^{K_i-1}\left[\sum \limits_{x={x}_{1,{b}_j}}^{x={x}_{1,{b}_j}}{\tilde{C}}_n^{a_1}(x)\right]\left[\sum \limits_{y={y}_{1,{b}_j}}^{y={y}_{1,{b}_j}}{\tilde{M}}_m^{\left(\beta, \mu \right)}(y)\right]\end{array}} $$
(21)

Note that, the binary images are particular cases of gray-scale images for L = 1.

5 Invariant moments of Charlier-Meixner

To use the Charlier-Meixner’s moments for the objects classification, it is indispensable that these moments must be invariant under rotation, scaling, and translation of the image. Therefore to obtain the translation, scale and rotation invariants moments of Charlier-Meixner (CMMI), we adopt the same strategy used by Sayyouri et al., for Hahn’s moments in [43]. Thus, we derive the CMMI through the geometric moments using the direct and the fast method based on the image slice representation methods.

5.1 Geometric invariant moments

For a digital image f(x, y) with size M × N, the geometric moments GMnm are defined using discrete sum approximation as:

$$ {GM}_{nm}=\sum \limits_{x=0}^{N-1}\sum \limits_{y=0}^{N-1}{x}^n{y}^mf\left(x,y\right) $$
(22)

The set of geometric invariant moments (GMI) by rotation, scaling and translation can be written as [16]:

$$ { GM I}_{nm}={GM}_{00}^{-\gamma}\sum \limits_{x=0}^{N-1}\sum \limits_{y=0}^{N-1}{\left[\left(x-\overline{x}\right)\cos \theta +\left(y-\overline{y}\right)\sin \theta \right]}^n{\left[\left(y-\overline{y}\right)\cos \theta -\left(x-\overline{x}\right)\sin \theta \right]}^m $$
(23)

with

$$ \overline{x}=\frac{MG_{10}}{MG_{00}};\overline{y}=\frac{MG_{01}}{MG_{00}};\gamma =\frac{n+m}{2}+1;\theta =\frac{1}{2}{\tan}^{-1}\frac{2{\mu}_{11}}{\mu_{20}-{\mu}_{02}} $$
(24)

The (n + m) th central geometric moments is defined in [16] by:

$$ {\mu}_{nm}=\sum \limits_{x=0}^{N-1}\sum \limits_{y=0}^{N-1}{\left(x-\overline{x}\right)}^n{\left(y-\overline{y}\right)}^mf\left(x,y\right) $$
(25)

5.2 Computation of Charlier-Meixner’s invariant moments

The Charlier-Meixner’s moments of f(x, y) can be written in terms of geometric moments as:

$$ {\displaystyle \begin{array}{c}{CMM}_{nm}={\left[{\rho}_c(n){\rho}_M(m)\right]}^{-1/2}\sum \limits_{x=0}^{M-1}\sum \limits_{y=0}^{N-1}{c}_n^{a_1}(x){M}_m^{\left(\beta, \mu \right)}(y)f\left(x,y\right)\\ {}={\left[{\rho}_c(n){\rho}_M(m)\right]}^{-1/2}\sum \limits_{i=0}^n\sum \limits_{j=0}^m{\varepsilon}_{i,n}^{a_1}{\alpha}_{j,m}^{\left(\beta, \mu \right)}{GM}_{ij}\end{array}} $$
(26)

where the nth order of Charlier and Meixner discrete orthogonal polynomials are given by:

$$ {C}_n^{a_1}(x)=\sum \limits_{k=0}^n{\varepsilon}_{k,n}^{a_1}{x}^k\kern0.5em \mathrm{and}\kern0.5em {M}_n^{\left(\beta, \mu \right)}(x)=\sum \limits_{k=0}^n{\alpha}_{k,n}^{\left(\beta, \mu \right)}{x}^k $$
(27)

The Charlier-Meixner’s invariant moments (CMMI) can be expanded in terms of GMI Eq. (23) as follows:

$$ {CMMI}_{nm}=\sum \limits_{i=0}^n\sum \limits_{j=0}^m{\varepsilon}_{i,n}^{a_1}{\alpha}_{j,m}^{\left(\beta, \mu \right)}{V}_{i,j} $$
(28)

where \( {\varepsilon}_{i,n}^{a_1} \) and \( {\alpha}_{j,m}^{\left(\beta, \mu \right)} \) are the coefficients relative to Eq.(27) and Vi, j are the parameters defined as:

$$ {V}_{nm}=\sum \limits_{q=0}^n\sum \limits_{p=0}^m\left(\begin{array}{l}n\\ {}p\end{array}\right)\left(\begin{array}{l}m\\ {}q\end{array}\right){\left(\frac{N\times M}{2}\right)}^{\left(\left(p+q\right)/2\right)+1}\times {\left(\frac{N}{2}\right)}^{n-p}\times {\left(\frac{M}{2}\right)}^{m-p}\times {GMI}_{pq} $$
(29)

5.3 Fast computation of Charlier-Meixner’s invariant moments

In order to accelerate the time computation of CMMI, we will apply the algorithms of the image slice representation described previously.

By using the binomial theorem, the GMI defined in Eq. (23) can be calculated as follows:

$$ {\displaystyle \begin{array}{c}{ GM I}_{nm}={GM}_{00}^{-\gamma}\sum \limits_{i=0}^n\sum \limits_{j=0}^m\left(\begin{array}{c}n\\ {}i\end{array}\right)\left(\begin{array}{c}m\\ {}j\end{array}\right){\left(\cos \theta \right)}^{i+j}{\left(\sin \theta \right)}^{n+m-i-j}\times {\left(-1\right)}^{m-j}{\mu}_{m+i-j,n+j-i}\\ {}=\sum \limits_{i=0}^n\sum \limits_{j=0}^m\left(\begin{array}{c}n\\ {}i\end{array}\right)\left(\begin{array}{c}m\\ {}j\end{array}\right){\left(\cos \theta \right)}^{i+j}{\left(\sin \theta \right)}^{n+m-i-j}\times {\left(-1\right)}^{m-j}{\eta}_{m+i-j,n+j-i}\end{array}} $$
(30)

with ηnm are normalized central geometric moments defined as:

$$ {\eta}_{nm}=\frac{\mu_{nm}}{GM_{00}^{\gamma }} $$
(31)

By applying the IBR algorithm, the normalized central moments defined in Eq. (31) can be calculated as follows:

$$ {\displaystyle \begin{array}{l}{\eta}_{nm}=\frac{\mu_{nm}}{GM_{00}^{\gamma }}=\frac{1}{GM_{00}^{\gamma }}\sum \limits_{x=0}^{N-1}\sum \limits_{y=0}^{M-1}{\left(x-\overline{x}\right)}^n{\left(y-\overline{y}\right)}^mf\left(x,y\right)\\ {}\kern1.25em =\frac{1}{GM_{00}^{\gamma }}\sum \limits_{x=0}^{N-1}\sum \limits_{y=0}^{M-1}{\left(x-\overline{x}\right)}^n{\left(y-\overline{y}\right)}^m\left(\sum \limits_{k=1}^s{f}_k\left(x,y\right)\right)\\ {}\kern1.5em =\frac{1}{GM_{00}^{\gamma }}\sum \limits_{k=1}^S{f}_k\times \sum \limits_{x_k=0}^{N-1}\sum \limits_{y_k=0}^{M-1}{\left(x-\overline{x}\right)}^n{\left(y-\overline{y}\right)}^m\\ {}\kern1.25em =\frac{1}{GM_{00}^{\gamma }}\sum \limits_{k=1}^S{f}_k\times \sum \limits_{j=0}^k\left[\left(\sum \limits_{x_k={x}_{1,{b}_j}}^{x_{2,{b}_j}}{\left(x-\overline{x}\right)}^n\right)\left(\sum \limits_{y_k={y}_{1,{b}_j}}^{y_{2,{b}_j}}{\left(y-\overline{y}\right)}^m\right)\right]\\ {}\kern1.25em =\frac{1}{GM_{00}^{\gamma }}\sum \limits_{k=1}^S{f}_k\times {\eta}_{nm}^k\end{array}} $$
(32)

where

$$ {\eta}_{nm}^k=\sum \limits_{j=0}^k\left[\left(\sum \limits_{x_k={x}_{1,{b}_j}}^{x_{2,{b}_j}}{\left(x-\overline{x}\right)}^n\right)\left(\sum \limits_{y_k={y}_{1,{b}_j}}^{y_{2,{b}_j}}{\left(y-\overline{y}\right)}^m\right)\right] $$
(33)

and fk ; k = 1, 2, . . …S is the slices intensity functions, S is the number of slices in image f. bj ; j = 1, 2,.…k is the block in each slice. The vectors \( \left({x}_{1,{b}_i},{y}_{1,{b}_i}\right) \) and \( \left({x}_{2,{b}_i},{y}_{2,{b}_i}\right) \) are respectively the coordinates in the upper left and lower right block bj.

Using the previous equations Eq.(31) and Eq.(33), the GMI of Eq.(30) can be rewritten as:

$$ {\displaystyle \begin{array}{c}{ GM I}_{nm}=\sum \limits_{i=0}^n\sum \limits_{j=0}^m\left(\begin{array}{c}n\\ {}i\end{array}\right)\left(\begin{array}{c}m\\ {}j\end{array}\right){\left(\cos \theta \right)}^{i+j}{\left(\sin \theta \right)}^{n+m-i-j}\times {\left(-1\right)}^{m-j}{\eta}_{m+i-j,n+j-i}\\ {}=\frac{1}{GM_{00}^{\gamma }}\sum \limits_{i=0}^n\sum \limits_{j=0}^m\left(\begin{array}{c}n\\ {}i\end{array}\right)\left(\begin{array}{c}m\\ {}j\end{array}\right){\left(\cos \theta \right)}^{i+j}{\left(\sin \theta \right)}^{n+m-i-j}\times {\left(-1\right)}^{m-j}\sum \limits_{k=1}^S{f}_k\times {\eta}_{m+i-j,n+j-i}^k\\ {}=\frac{1}{GM_{00}^{\gamma }}\sum \limits_{k=1}^S{f}_k\sum \limits_{i=0}^n\sum \limits_{j=0}^m\left(\begin{array}{c}n\\ {}i\end{array}\right)\left(\begin{array}{c}m\\ {}j\end{array}\right){\left(\cos \theta \right)}^{i+j}{\left(\sin \theta \right)}^{n+m-i-j}\times {\left(-1\right)}^{m-j}\times {\eta}_{m+i-j,n+j-i}^k\end{array}} $$
(34)

Therefore the Charlier-Meixner invariant moments CMMI under translation, scaling and rotation of the image can be obtained from the equations Eqs. (28), (29) and (34).

6 Results and simulations

In this section, we give experimental results to validate the theoretical results developed in the previous sections. This section is divided into four subsections. In the first subsection, the invariability of the proposed discrete orthogonal moments of Charlier-Meixner under three transformations: translation, scale and rotation is shown. In the second, we test the precision of the classification of the CMMI invariant moments for four image databases. The results of our classification methods are compared to other moment descriptors for the classification of objects. In the third subsection, we will compare the proposed classification method with classification methods based on non-moment descriptors such as HOG, SIFT and CNN features. In the fourth subsection, we will compare the calculation time of the Charlier-Meixner invariant moments by two methods: the direct method and the proposed fast method.

6.1 Invariability

In this section, we test the invariability of Charlier-Meixner invariant moments CMMI under the translation, the scale and the rotation of the image. For this, we will use a gray-scale image “Car” (Fig. 1) whose size is 128 × 128 pixels chosen from the well-known Columbia database (http://www.cs.columbia.edu/CAVE/databases). This image is scaled by a factor varying from 0.5 to 1.5 with interval 0.05, rotated from 00 to 3600 with interval 100 and translated by a vectors varying from (−5,-5) to (5,5). Each translation vector consists of two elements which represent a vertical and a horizontal image shift respectively. All invariant moments of CMMI is calculated up to order two for each transformation. Finally, in order to measure the ability of the CMMI to remain unchanged under different image transformations, we define the relative error between the two sets of invariant moments corresponding to the original image f(x, y) and the transformed image g(x, y) as:

$$ {E}_{CMM}\left(f,g\right)=\frac{\left\Vert CMMI(f)- CMMI(g)\right\Vert }{\left\Vert CMMI(f)\right\Vert } $$
(35)

where ‖.‖ denotes the Euclidean norm and CMMI(f);  CMMI(g) are invariant moments of Charlier-Meixner for the original image f and the transformed imageg.

Fig. 1
figure 1

Car gray-scale image

Full size image

Figure 2 compares the relative errors between the proposed invariant moments of CMMI, the invariant moments of Meixner MMMI [44] and the invariant moments of Charlier CCMI [12] relative to rotation of the image. It can be seen from this figure that the CMMI is more stable under rotation (very low relative error) and has a better performance than the CCMI and MMMI whatever the rotational angle.

Fig. 2
figure 2

Comparative study of relative errors between the rotated image and the original image by MMMI, CCMI and CMMI

Full size image

Figure 3 shows the relative errors between the CMMI, CCMI, and MMMI relative to scale. The figure shows that, in most cases, the relative error of CMMI is more stable and lower than the CCMI and MMMI.

Fig. 3
figure 3

Comparative study of relative errors between the scaled image and the original image by MMMI, CCMI and CMMI

Full size image

Figure 4 shows the relative errors between the MMMI, CCMI, and CMMI relative to translation. The figure shows again that, in most cases, the relative error of CMMI is more stable and has a better performance than the CCMI and MMMI, whatever the translation vectors. Note that, the results are plotted in Figs. (2, 3 and 4) for the case a1 = 80 for the Charlier’s polynomials and β = 60,  μ = 0.5 for Meixner’s polynomials.

Fig. 4
figure 4

Comparative study of relative errors between the translated image and the original image by MMMI, CCMI and CMMI

Full size image

The results show that the CMMI is more stable under the translation, the scale and the rotation of the image than the CCMI, and MMMI.

To test the robustness to noise, we have respectively added a white Gaussian noise (with mean μ = 0 and different variances) and salt and pepper noise (with different noise densities). Results are respectively depicted in Figs. 5 and 6. It can be seen that, if the relative error increases with the noise level, the proposed descriptors of CMMI are more robust to noise than CCMI and MMMI.

Fig. 5
figure 5

Comparative study of relative errors between the corrupted image (salt & pepper) and the original image by MMMI, CCMI and CMMI

Full size image
Fig. 6
figure 6

Comparative study of relative errors between the corrupted image (white Gaussian) and the original image by MMMI, CCMI and CMMI

Full size image

6.2 Classification

In this section, we will provide experiments to validate the precision of the classification of objects using the CMMI. For this, we will put in place the characteristic vectors defined by:

$$ V=\left[{CMMI}_{ij}\right];i,j=0,1,2 $$
(36)

To perform the classification of objects to their appropriate classes, we use classifiers based on support vector machines SVM.

6.2.1 Classifier support vectors machines (SVM)

The classifier (SVM) was introduced by Vladimir Vapanik as a binary classification method for supervised learning [50]. This classification method has become in a short time a standard tool in the state of the art for several recognition problems. Initially, SVM relies on the existence of a linear classifier that separates two classes into an appropriate space. In addition, to allow optimal separation in non-linearly separable cases, SVMs have proven that the use of multiple nuclei generates more flexibility and improves the interoperability of these methods [11]. For two given classes of images, the goal of SVMs is to find a linear classifier that separates images while maximizing the distance between these two classes. This is a hyper-separation plan. The images closest to this hyper-plane, that is to say the most difficult to classify, are called support vectors. It is obvious that there is a multitude of valid hyper-plans but the remarkable property of the SVMs is that this hyper-plan must be optimal. Formally, this amounts to looking for a hyper-plane whose minimal distance to the different support vectors is maximal. There are two cases of SVM models: the linearly separable case and the non-linearly separable cases. The most used techniques for extending SVM to multi-class problems are based on “One- Against -One” or “One- Against -All” algorithms.

In our case, we will use the One-Against-All algorithm to implement the classification. And as descriptors, we use the invariant moments of Charlier-Meixner instead of using the images, we define the classification accuracy as:

$$ \eta =\frac{\mathrm{Number}\ \mathrm{of}\ \mathrm{correctly}\ \mathrm{classified}\ \mathrm{images}}{\mathrm{The}\ \mathrm{total}\ \mathrm{of}\ \mathrm{images}\ \mathrm{used}\ \mathrm{in}\ \mathrm{the}\ \mathrm{test}}\times 100\% $$
(37)

To validate the precision of the classification of objects using the CMMI, we well use three image databases. These databases are standard ones used by the scientific community during the testing and the validation of their approach and are freely available on the Internet. Each image database has defined the classes where each image belongs to one class. The first database is the Columbia Object Image Library (COIL-100) database (http://www.cs.columbia.edu/CAVE/databases) (Fig. 7). The total number of images is 7200 distributed as 72 images for each object. All images of this database have the size 128 × 128. The second image database is CALTECH-256 database (http://www.vision.caltech.edu/Image_Datasets) (Fig. 8). This latter is composed of images from 256 different categories; it contains 80 to 827 images by a category. The total number of images contained in this database is 30,608 images of size 300 × 300 pixels. This database is known by a large variability between and within classes. The third image database is the COREL database (http://wang.ist.psu.edu/docs/home.shtml). The total number of images is 6000 of size 256 × 384 distributed as 29 categories (Fig. 9). These databases are considered as references for specialists working on image classification in heterogeneous databases. Samples of different classes of images contained in the three databases are shown in Figs. 7, 8 and 9. We tested the ability of the classification of our descriptor CMMI compared to other descriptors of Hu’s invariant moments [16], Charlier’s invariant moments (CCMI) [12] and Meixner’s invariant moments (MMMI) [44] for the three databases.

Fig. 7
figure 7

Collection of Columbia objects

Full size image
Fig. 8
figure 8

Collection of CALTECH-256 objects

Full size image
Fig. 9
figure 9

Collection of Corel objects

Full size image

The three figures (Figs. 10, 11 and 12) show the results of the classification of three image databases COIL-100, CALTECH-256 and COREL using as descriptors the moment invariants of Charlier-Meixner and as a classifier the support vector machines SVM for the number of the classes between 3 to 35. The classification results are compared with the results obtained by Hu [16], Charlier (CCMI) [12] and Meixner (MMMI) [44] invariant moments.

Fig. 10
figure 10

Classification results of Columbia (COIL-100) database

Full size image
Fig. 11
figure 11

Classification results of Caltech database

Full size image
Fig. 12
figure 12

Classification results of Corel database

Full size image

The classification results (Figs. 10, 11 and 12) show the efficiency of the CMMI in terms of classification accuracy of images, compared to those of Hu [16], CCMI [12] and MMMI [44]. Our experiments show that the proposed CMMI descriptors improve the accuracy of image classification in heterogeneous databases compared to other descriptors. However, the accuracy of the conventional method is generally proportional to the number of classes. In fact, for the database COIL-100, accuracy is more than 90%. Similarly, for the databases of CALTECH-256 and COREL, the accuracy is over 60%. This comparison results show the effectiveness and the robustness of the proposed moments relative to other moments for three image database and for different classes.

6.3 Comparison of classification methods

In this section, we will compare our method of classification based on the shape descriptors which are invariant moments of CMMI with the classification method based on the descriptors based on Convolution Neural Network (CNN) [10], on Histograms of Oriented Gradient (HOG) [5] and on the Scale-Invariant Feature Transform (SIFT) [34].

The discriptors CNN is a hierarchical deep learning architecture. It is based on repeated convolutional operations which repeatedly filter the image at each stage. The filters are trainable, that is, they learn to adapt to the task at hand during learning.

The discriptors HOG is based on first order image gradients. The image gradients are pooled into overlapping oriention bins in a dense manner.

The discriptors SIFT is Based on first order gradients, it is evaluated around scale invariant feature points obtained using the difference of gaussian key point detector.

To assess the individual discriminant power of each of these characteristics, we have performed the tests of classification on two heterogeneous image databases COREL (http://www.vision.caltech.edu/Image_Datasets) and CALTECH-256 (http://wang.ist.psu.edu/docs/home.shtml).

In this test, four sub-image databases, consisting respectively of 3, 7, 10 and 20 classes are used from the COREL database and the CALTECH-256 database. The performance of classification corresponding to each model, for the different sub databases used, are measured using simple classifiers based on Euclidean distances. Values of the accuracy of the recognition of assessed models for the four sub-bases of the COREL database and the CALTECH-256 are presented in Tables 2 and 3. The best and worst performances in these tables are shown in bold for the different sub- databases of the used images. The both Tables 2 and 3 show that the illustrated performances of classification well vary obviously depending on the different used characteristics. The performances of classification of a model of a given characteristic vary in terms of different sub databases of the used images. This proves that the discriminating power of each feature is not absolute, but it varies considerably depending on the contents of the considered image.

Table 2 The classification rate of the sub-bases of COREL database by using the different features CNN, HOG, SIFT and CMMI
Full size table
Table 3 The classification rate of the sub-bases of CALTECH-256 database by using the different features CNN, HOG, SIFT and CMMI
Full size table

According to Tables 2 and 3, the descriptors of the shape of CMMI is the most efficient among the various used CNN, HOG and SIFT for the classification of sub-bases of COREL and CALTECH-256 with 3, 7, 10 and 20 classes.

Finally we can see that among all the extracted features: CNN, HOG, SIFT and CMMI the descriptors of the shape of CMMI are often the most relevant that the descriptors of CNN, HOG and SIFT.

6.4 Computational time

In this sub-section, we will compare the computational time of Charlier-Meixner’s invariant moments by two methods: the direct method described in sub-section 6.2 and the proposed fast method based on the image slice representation defined previously in section 6.3. For this, we will measure the computational time of the characteristic vector defined in equation Eq. (36) by two methods. To compare the two computational methods we will use the execution time improvement ratio (ETIR) as a criterion. This ratio is defined as ETIR = (1 − Time1/Time2) × 100, where Time1 and Time2 are the execution time of the first and the second methods. ETIR = 0 if both execution times are identical.

In the this experiment, a set of five gray-scale images with a size of 128 × 128 pixels, shown in Fig. 13, selected from the Columbia Object Image Library (COIL-100) database [52] were used as test images. The computational processes are performed for each of the five images where the average times and execution-time improvement ratio (ETIR) are included in Table 4 for CMMI invariant moments using the proposed method descriped by the Eq. (28) and the direct method descriped by the Eq. (34). The result indicates again that our proposed method has a better performance than the direct method. Note that the algorithm was implemented on a PC Intel Core i5 2.40 GHz, 4GB of RAM.

Fig. 13
figure 13

Set of test binary images a Car, b Duckc Box, d Cat and e Objet

Full size image
Table 4 Average times and reduction percentage for CMMI invariant moments of the five images
Full size table

The table shows that the proposed method is faster than the direct method and the saving of time reaches 60% because the computation of discrete orthogonal invariant moments CMMI proposed by the proposed method depends solely on the number of blocks and slices on the other hand the computation of the moments by the direct method depends on all the image.

7 Conclusion

In this paper, we have proposed a new method for the classification of the objects. This method is performed using a new set of discrete orthogonal moments of Charlier-Meixner and the image slice representation. Furthermore, we have derived a new set of Charlier-Meixner’s invariant moments from the geometric invariant moments of each block in each slice of the image. Moreover, the accuracy of classification of the proposed CMMI in the classification of the object is carried out for three image databases. Hence, the classification results by our descriptor CMMI are better than that of Hu, CCMI and MMMI. In addition, our classification method is also better than other methods non-moments like the CNN, HOG and SIFT features. So, these moments have a desirable image representation capability and can be useful in the the recognition domain. In order to reduce the calculation cost of the Charlier-Meixner moments when classifying image databases which contains a large number of classes, we propose to study the reduction of the characteristic vector in the next work.