1 Introduction

As one of the most significant local features of images, corners are frequently utilized in many computer vision applications, such as scene analysis, 3D reconstruction, image retrieval [10], camera calibration and saliency detection [11], to name just a few. Corner detection algorithms of gray images can be divided into three kinds mainly: contour-based [1, 3, 4, 7, 9, 12, 14, 15, 17,18,19, 22, 24,25,26,27,28,29,30,31,32], gradient-based [8, 16, 21] and template-based [20, 23]. Compared with gradient-based and template-based corner detectors, contour-based corner detectors have some specific applications for their low rate of detection error.

In the field of contour-based corner detection, corner is usually defined as the point with local maximal curvature on the contour or the intersection point of two line contours in images. Each point on the contour has a calculated corner response value which reflects the sharpness of the curve changes at that location. For both single-scale and multi-scale contour-based corner detectors, what really counts is how to measure the corner response function effectively, since it usually decides the performance and computational complexity of corner detectors.

Plenty of contour-based corner detectors have been proposed over the last few decades and the most classical one is the CSS [15] corner detector. Mokhtarian proposed curvature scale-space (CSS) corner detector based on curvature scale-space technique and it became the landmark algorithm in this field. After that, various CSS based corner detectors were proposed, making certain improvements based on the original CSS detector, such as ECSS [14], ACSS [9], ARCSS [3], DCSS [32] and MSCP [27]. For instance, Zhong et al. proposed direct curvature scale-space (DCSS) algorithm [32] as a derivative technique of CSS to decrease the computational complexity.

All of these CSS based corner detectors utilized the curvature as the corner response value, but as described in [1], the curvature is very sensitive to the local variation and noise on the curve. Hence, researchers also proposed various contour-based corner detectors which apply other mechanisms such as geometric relations between the points on the contour to extract corners [1, 4, 24, 28]. Among those methods, a corner detector named CPDA [1] using chord-to-point distance accumulation to measure the corner response value is reported to have robust performance compared with other contour-based corner detectors [1, 2, 4,5,6]. But there still are some drawbacks. The first one is the maximum normalization utilized in CPDA corner detector, since the normalized corner response function cannot reflect the curvature of contour when the corner response values on the contour are almost equal, such as the contour of straight-line or circle. Besides, in CPDA corner detector, three different values of chord parameter are utilized to calculate the corner response value, which is computationally expensive. Last but not least, the chord-to-point distance used in CPDA detector cannot well reflect the curvature of the contour because the distance is closely related to the selection of chord length.

In this paper, we overcome these drawbacks in CPDA corner detector and propose a new corner detector named altitude-to-chord ratio accumulation (ACRA) corner detector on the basis of CPDA detector. Firstly, we utilize the altitude-to-chord ratio which is insensitive to the selection of chord length to measure the corner response degree of contour points. Then a linear normalization is adopted to replace the maximum normalization used in CPDA detector, which projects the corner response value into the range [0,1]. Finally, instead of using three different values of chord parameter in CPDA corner detector, we just utilize a single chord length parameter to calculate the corner response value because the measurement proposed by us is insensitive to the selection of the chord length. Numerical experiments demonstrate that our proposed ACRA corner detector outperforms CPDA and other seven state-of-the-art methods.

The rest of this paper is organized as follows. Introduction of the CPDA corner detection algorithm is described in Section 2. The proposed ACRA approach based on CPDA algorithm is presented in Section 3. Section 4 presents the performance analysis and result discussion in terms of two evaluation datasets and two evaluation metrics. Finally, conclusions are presented in Section 5.

2 CPDA corner detection algorithm

CPDA algorithm was proposed by Awrangjeb et al. [1], in which the authors theoretically analyzed the shortcomings of existing contour based corner detection algorithms, especially for CSS based corner detection algorithms, and introduced the corner response function based on the chord-to-point distance accumulation technique.

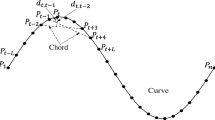
For various contour based corner detection algorithms, as shown in Fig. 1, the key point lies in the calculation of the corner response function, which directly determines the performance of the algorithm. For a contour Γ shown in Fig. 2 , it is made up of various points P1, P2, P3, ⋯, Pn, where P1 is the starting point and Pn is the terminal point. Take the point Pk as an example. As for a certain chord length parameter L, we take Pk as the beginning and count backward L numbers of points along the curve so we can get the point Pk−L. Likewise, we count forward one point along the curve so we can get the point Pk+ 1. Then we calculate the distance between point Pk to the chord Pk−L+ 1Pk+ 1, and the distance is marked as dk,k−L+ 1. Next we move the two end-points for one point along the curve then we can also get the distance dk,k−L+ 2. We calculate all the distances until one of the two end-points is Pk. The summation of all the distances is the distance accumulation hL(k). The process can be represented as

$$ h_{L}(k) = \sum\limits_{i = k-L + 1}^{k-1} d_{k,i} $$
(1)
Fig. 1
figure 1

The overall flowchart of CPDA and ACRA corner detection algorithms

Full size image
Fig. 2
figure 2

Chord-to-point distance accumulation technique for a chord length L = 10

Full size image

The main steps of CPDA algorithm can be summarized as:

  1. (1)

    Utilize Canny algorithm to detect the edges of images and do some basic preprocessing so as to get the image contours and T-corners [1].

  2. (2)

    Calculate the chord-to-point distance accumulationhL(k) based on (1) under three different chord length parameters L as 10, 20, 30, and perform maximum normalization

    $$ h^{\prime}_{L}(k) = \frac{h_{L}(k)}{\max{(\boldsymbol{h}_{L})}} $$
    (2)

    Then multiply three distance accumulation values as the final corner response value

    $$ H(k) = h^{\prime}_{10}(k)\times h^{\prime}_{20}(k) \times h^{\prime}_{30}(k) $$
    (3)
  3. (3)

    Choose those points with local maximal value of H(k) as the candidates and eliminate pseudo corners using a global threshold Q.

  4. (4)

    Calculate the global angle of every candidate and eliminate the pseudo candidates based on an angle threshold. Compare T-corners with the detected corners and add those T-corners which are far away from the detected corners. [1]

Figure 1 displays the overall flowchart of the CPDA algorithm. CPDA algorithm is able to conquer some shortcomings that exist in the CSS based methods. For example, the calculation of curvature used in CSS based approaches involves the first and second order derivatives, resulting that the algorithms are sensitive to noise and local variations, while the CPDA algorithm uses the chord-to-point distance accumulation technique instead, which can successfully get rid of the above-mentioned problems.

3 ACRA corner detection algorithm

In this section, we identify the weakness of CPDA corner detection algorithm and introduce the proposed ACRA approach on the basis of CPDA algorithm. As is mentioned in Sections 1 and 2, the disadvantages of CPDA algorithm lie in three aspects and we make corresponding improvement for every drawback.

3.1 Corner response function

The most serious drawback of CPDA corner detection algorithm is the definition of corner response function. As is shown in (1) and Fig. 3 , the distance hL(k) is closely related to the selection of chord length. For point Pk on a contour, selecting different values of chord length parameters, the chord to point distance may be tremendously changed. Although three different chords with L = 10,20,30 are utilized to tackle this problem, it also restricts the performance of corner detection to some extent. Besides, it increases the computational complexity correspondingly.

Fig. 3
figure 3

Chord-to-point distance vs. altitude-to-chord ratio in terms of a hypothetical contour

Full size image

Inspired by [24] and our previous work [13] on 3D mesh corner detection, we introduce the triangular principle into our ACRA detector to make improvement in the definition of corner response function, in which we utilize the altitude-to-chord ratio to calculate the corner response function. For a contour shown in Fig. 3, the distances d1 and d2 are closely related to the selection of chord, but the ratios d1/C1 and d2/C2 are almost equal, which is insensitive to the selection of the chord.

Here as for the considered point Pk in Figs. 2 and 3, it is able to form a triangle with the near two points Pk−L + i and Pk + i, where k − L + 1 ≤ i ≤ k − 1, as is described in Section 2. Then we calculate the ratio between two distances. The first distance dk,i is between the point Pk to chord Pk−L + iPk + i, and the second distance is the chord length. Then all of the possible ratios are accumulated to form the final corner response function:

$$ h_{L}(k) = \sum\limits_{i = k-L + 1}^{k-1} \frac{d_{k,i}}{C_{k,i}} $$
(4)

where Ck,i represents the chord length for the point Pk. Because the ratio in (4) means fully considering the local geometric relations of the analyzed point, it can well reflect the sharpness of the curve change at that location.

3.2 Normalization operation

It is unreasonable to use maximum normalization method to normalize the accumulation of distance value into range [0,1], which is described in step 2 of CPDA detection process. It may cause uneven data projection in some situations. For instance, if the image contour is a straight line or a circle, each value of the points on the contour would be almost equal. When we perform normalization operation using (2), each value would be close to 1. Since the CPDA method is defined to regard those points with local maximal value as candidate corners, it would be misleading using maximum normalization. Although the authors designed an angle threshold step to eliminate the pseudo corners which may be caused by the normalization process, it decreased the performance and computational efficiency of the whole CPDA algorithm.

In order to solve this problem, we use the linear normalization method in the proposed ACRA approach, which can be described as:

$$ h^{\prime}_{L}(k) = \frac{h_{L}(k) - \min{(\boldsymbol{h}_{L})}}{\max{(\boldsymbol{h}_{L})} - \min{(\boldsymbol{h}_{L})}} $$
(5)

where min(hL) and max(hL) represent the minimal and maximal corner response value of the points on the contour. Using linear normalization can project these values into range [0,1] appropriately and evenly, hence it works well by choosing those points with local maximal value as candidate corners.

3.3 Chord length parameter selection

In CPDA algorithm, three different chord length parameters are considered, which is described in step 2 of CPDA detection process. The reason why in CPDA algorithm three different chord length parameters are required is that the chord-to-point distance is closely related to the selection of chords, and cannot fully reflect the sharpness of the curve. However, in the proposed ACRA approach, the corner response function is able to fully deal with almost all of the situations, which means it is unnecessary to perform the distance accumulation step for three times in different parameter values. So in the proposed ACRA approach, we just utilize a single chord to calculate the corner response function.

4 Numerical experiments

In this section, we evaluate the performance of the proposed ACRA corner detection algorithm and compare it against eight state-of-the-art corner detection methods in terms of two datasets and two evaluation metrics. The eight popular contour-based corner detection algorithms are MSCP[27], ARCSS [3], He & Yung [9], GCM [29], DoG [28], CPDA [1], FAST-CPDA [4] and ANDD [22]. Because the ACRA approach is based on the CPDA algorithm, we emphasize the comparison with CPDA algorithm, in terms of both detection accuracy and computational complexity.

4.1 Evaluation datasets and metrics

Following the standard process in literatures [1, 4, 6], we use the publicly available CPDA dataset,Footnote 1 including some synthetic images like ”Block” and real world images like ”Lena”, to evaluate the performance of the contour-based corner detectors. Figure 4 shows that several synthetic images and natural images for testing in CPDA dataset. There are totally 23 original images in CPDA dataset. As is shown in Table 1 and Fig. 5, seven types of image transformations are done for the images of CPDA dataset to generate the testing images, including rotation, uniform scale, non-uniform scale, combined transformations, lossy JPEG compression, Gaussian noise and shearing. Awrangjeb and Lu [1] gives the associated information about the seven types of image transformation. For any one of the original images in dataset, there are total 378 transformed images as testing ones. Except for the CPDA dataset, similar with [12], we also randomly select 32 natural scene images from Mikolajczyk’s datasetFootnote 2 to construct a dataset. And the seven types of image transformations [1] are also done to generate the testing dataset.

Table 1 Seven types of image transformations (gn: Gaussian noise; jpg: Lossy JPEG compression; rot: Rotation; us: Uniform scale; nus: Non-uniform scale; rotscl: Rotation and scale; sh: shearing)
Full size table
Fig. 4
figure 4

Several synthetic images (the first row) and natural images (the second rows) in the CPDA dataset

Full size image
Fig. 5
figure 5

Seven types of image transformations of ”Lena” image. a Original image; b Gaussian noise; c Lossy JPEG compression; d Non-uniform scale; e Uniform scale; f Shearing; g Rotation; h Combined transformations (rotation and scale)

Full size image

The repeatability and localization error are the two basic evaluation metrics for corner detection [1, 3, 4, 24, 29]. Repeatability R measures the proportion of repeated corners between original and testing images. Localization error Le is defined as the amount of pixel deviation of a repeated corner. It is measured as the root-mean-square-error (RMSE) of the repeated corner locations in the original and test images. All of them can be computed as follows:

$$ R = \frac{N_{r}}{2}\left( \frac{1}{N_{o}}+\frac{1}{N_{t}}\right), $$
(6)
$$ L_{e} = \sqrt{\frac{1}{N_{r}}{\sum}_{i = 1}^{N_{r}}(x_{oi}-x_{ti})^{2}+(y_{oi}-y_{ti})^{2}}, $$
(7)

where No represents the number of reference corners in the original image; Nt represents the number of detected corners in the test image; Nr represents the number of repeated corners between the original and test image; (xoi,yoi) and (xti,yti) are the positions of the i-th repeated corners in the original image and test image respectively. An RMSE value of maximum three pixels is allowed to find a repetition.

4.2 Experimental results and analysis

4.2.1 Parameters setting

Parameter L in Section 3 has a direct influence on how many neighborhood contour points are utilized in our approach. Because corner is a local feature, a small parameter L will lead to the lack of available information to detect corners. But a large parameter L will damage the local structure information of current contour point. Parameter Q controls the number and quality of corner candidates. The larger the parameter Q is, the sharper the corner is, and the less the number of corner candidates is. Those contour points with corner response value smaller than a threshold Q are directly detected as non-corners. Fig. 6 shows the average repeatability scores of the proposed ACRA approach for CPDA dataset under various values of parameters L and Q. In the proposed ACRA approach, we set the parameter L = 16 and parameter Q = 0.15.

Fig. 6
figure 6

Average repeatability scores of the proposed ACRA approach in terms of CPDA dataset under various parameters L (chord length) and Q (global threshold)

Full size image

4.2.2 Computational efficiency

For both CPDA and the proposed ACRA corner detection algorithms, the main operation related to computational efficiency is the square root operation. So, we compare the complexity of CPDA algorithm and the proposed ACRA approach by counting the CPU times of calculating square root operation. Besides, we calculate the CPU times of CPDA and the proposed ACRA algorithms to further demonstrate the superiority of the proposed ACRA approach in computational efficiency.

For CPDA algorithm, as is shown in (1), a contour with n points is estimated using three chord length parameters. So, the total number of square root operations calculated by the CPDA algorithm is n(L10 − 2) + n(L20 − 2) + n(L30 − 2), while the total number of square root operations needed by the proposed ACRA approach is n(L16 − 1). Table 2 displays the average times for each image with CPDA and Mikolajczyk’s dataset, the experiments are done with the MATLAB 2016 (a) environment is obtained on a Windows 7 computer with 3.09 GHZ AMD A8-7600 and 8.00 GB RAM. From the Table 2, we can see that the average CPU time clearly demonstrates the superiority of the proposed ACRA approach compared against CPDA algorithm.

Table 2 Computational efficiency comparison between CPDA and ACRA algorithms with two datasets
Full size table

4.2.3 Module performance study

In order to further verify that the three improvements are valid. In this section, three variants of ACRA algorithms are developed to do comparison experiments. We use the scheme of control variables to study the impact of each module on the performance of the algorithm. As shown in Tables 3 and 4, we denote the three algorithms as ACRA1, ACRA2, ACRA3 respectively, where

  • ACRA1: replace the altitude-to-chord ratio accumulation in ACRA with the chord-to-point distance accumulation used in CPDA, which corresponds with the improvement described in Section 3.1.

  • ACRA2: replace the linear normalization in ACRA with maximum normalization used in CPDA, which corresponds with the improvement described in Section 3.2.

  • ACRA3: replace the one chord length parameter in ACRA with three chord length parameters used in CPDA, which corresponds with the improvement described in Section 3.3.

From Tables 3 and 4, it is obvious that for each improvement, there are different gain in performance. When compared ACRA against ACRA1, we can see that the altitude-to-chord ratio accumulation is more robust than chord-to-point distance accumulation, not only in terms of repeatability, but also in terms of localization error. From the results of ACRA and ACRA2, it seems that there is no large gain in performance. But it does not mean that this improvement does not make sense. The normalization operations have direct influence on the corner candidates. But for the ACRA and CPDA algorithms, as is shown in Fig. 1, there exists a step to refine the corner candidates, which reduces the effect of this improvement to some extent. But from the analysis shown in Section 3.2, linear normalization does make more sense compared with maximum normalization. When compared ACRA against ACRA3, it is obvious that using one chord length is much better than using three chord lengths in ACRA algorithm. The main reason lies in that the corner response function defined in this paper is not sensitive to the chord length. Using three chord lengths will decrease the performance of the algorithm in return.

Table 3 Repeatability of the three variants of ACRA, ACRA and CPDA algorithms in terms of CPDA benchmark
Full size table
Table 4 Localization Error of the three variants of ACRA, ACRA and CPDA algorithms in terms of CPDA benchmark
Full size table

4.2.4 Compared performance study

To fully verify the performance, we compare the proposed ACRA approach with other eight algorithms. Visualizations of comparative results can be found in Fig. 7 , where the corners of ”Block” image detected by the proposed ACRA and other eight corner detection algorithms are presented. In Fig. 7 , we can see that on the one hand, the proposed ACRA approach can detect corners more accurately compared with CPDA, FAST-CPDA, ARCSS and MSCP methods. On the other hand, the corners detected by the proposed ACRA approach include less pseudo corners, such as noise, local variations and these points located on the edges, compared with DoG, GCM, He & Yung and ANDD methods.

Fig. 7
figure 7

Corners of ”Block” image detected by nine contour based corner detection algorithms.

Full size image

In order to quantitatively analyze the performance of nine algorithms, we calculate the repeatability and localization error of various testing images under different image transformations. Figures 8, 9, 10 and 11 shows the repeatability and localization error of nine algorithms in terms of four kinds of image transformations respectively. At the top of each figure, the corresponding descriptions are given. For example, Repeatability - Gaussian - CPDA means the repeatability metric in terms of Gaussian transformation for the CPDA dataset. In this section, we analyze these situations one by one.

Fig. 8
figure 8

Repeatability and localization error in terms of two datasets under Gaussian noise image transformations

Full size image
Fig. 9
figure 9

Repeatability and localization error in terms of two datasets under lossy JPEG compression image transformations

Full size image
Fig. 10
figure 10

Repeatability and localization error in terms of two datasets under rotation image transformations

Full size image
Fig. 11
figure 11

Repeatability and localization error in terms of two datasets under uniform scale image transformations

Full size image

For Gaussian noise image transformation, as is shown in Fig. 8, with the increase of Gaussian standard deviation, the repeatability scores of all the methods are decreased gradually, and the localization error of all the methods are increased gradually. The more the testing image polluted by noise, the poor the performance of algorithm is. From the Fig. 8, we can see that our proposed ACRA approach performs best in general compared with other methods, followed by the CPDA algorithm. For both datasets, ACRA algorithms outperforms other methods largely in terms of localization error metric, shown in right part of Fig. 8. Although the CPDA algorithm has good performance in terms of repeatability, the proposed ACRA approach also has remarkable performance compared with CPDA algorithm, shown in left part of Fig. 8.

For lossy JPEG compression image transformation, as is shown in Fig. 9, with the increase of the quality factors, the repeatability scores of all the methods are increased gradually, and the localization error of all the methods are decreased gradually. The low the quality of testing image is, the poor the performance of algorithm is. From Fig. 9, we can see that ACRA slightly outperforms other methods in terms of repeatability metric, but largely outperforms other methods in terms of localization error metric.

For rotation image transformation, as is shown in Fig. 10, when the rotation angle close to π/4 and − π/4, all the algorithms perform terrible. The main reason lies in that in these situations, the quality of the corresponding contour is poor, which directly impact the performance of the corner detection algorithm. Although the proposed ACRA approach doesn’t outperform other methods like DoG, GCM, etc, for Mikolajczyk’s dataset in terms of repeatability metric, in other situations shown in Fig. 10 proposed ACRA approach enjoys the excellent performance compared with other eight methods, in other situations shown in Fig. 10.

For uniform scale image transformation, as is shown in Fig. 11, with the increase or decrease of scale factor, the repeatability scores of all the methods are decreased gradually, and the localization error of all the methods are increased gradually. Most of contour based corner detection algorithms do not have excellent performance in terms of scale image transformation, especially for Mikolajczyk dataset, and the same with the proposed ACRA approach. The main reason for this phenomenon lies in that for most contour based corner detection algorithms, the corner response is defined only using the fixed neighborhood contour points, which is not scale-adaptive. The proposed ACRA approach performs mediocre under uniform scale transformation compared with other eight methods, shown in Fig. 11.

To reach an overall performance ranking, Fig. 12 shows the overall experimental results under seven types of transformations, where average repeatability and localization error in two datasets are calculated. In general, all the methods perform remarkable in terms of lossy JPEG compression and perform terrible in terms of shearing and uniform scale. For most situations, the proposed ACRA approach offer highest average repeatability and lowest localization error compared with other eight methods. Although for some individual cases, such as rotation, uniform scale, and combined transformations of Mikolajczyk’s dataset, the proposed ACRA approach does not offer highest average repeatability or lowest localization error as shown in Fig. 12, the proposed ACRA approach still performs best in most of the situations and shows its superiority over the original CPDA algorithm. Table 5 gives the quantitative experimental results. It is obvious that the proposed ACRA approach proves to perform best in two metrics for two datasets.

Fig. 12
figure 12

Average repeatability and localization error in two datasets with seven types of image transformations. (gn: Gaussian noise; jpg: JPEG compression; rot: rotation; us: uniform scale; nus: non-uniform scale; rotscl: combined transformations; sh: shearing)

Full size image
Table 5 Performance of various contour-based corner detection algorithms in CPDA and Mikolajczyk’s datasets
Full size table

5 Conclusion and future work

In this paper, we propose ACRA algorithm to overcame three drawbacks in CPDA corner detection algorithm. Altitude-to-chord ratio accumulation is utilized to calculate the corner response function for its insensitive to the selection of chord length compared with chord-to-point distance accumulation technique. Instead of maximum normalization used in CPDA algorithm, we utilize the linear normalization to avoid the uneven data projection. Finally, since the measurement is insensitive to the selection of chord, we utilize a single chord instead of three chords used in CPDA method. Numerical experiments demonstrate that the proposed ACRA approach outperforms eight testing methods.

As discussed in Section 4.2, all the contour based corner detection algorithms seriously depends on the extracted contours, which is a bottleneck for contour based corner detection algorithms. Besides, most of them only utilize the fixed number of neighborhood contour points to calculate the corner response function, which might be sensitive to some situations, for example, uniform scale image transformation.

In the future, we will address these two problems to further improve the performance of ACRA approach, and an adaptive scheme of selecting neighborhood contour points and a robust contour extraction scheme will be utilized.