1 Introduction

The rapid progress of digital-image-editing software has enabled the easy manipulation of digital images, leaving no perceptible trace. Digital image forensics is an emerging branch of image processing aimed at determining the authenticity and origin of digital images [32, 38]. A great number of digital images are continuously produced in our daily lives and the majority of consumer images are created without containing any digital watermark or signature [21, 45]. Therefore, a digital image forensics technique needs to be developed in a passive manner for its use in a wide range of applications [17, 36, 44].

Digital images can be tampered with or manipulated in many different ways. Copy-move forgery (CMF), which copies a part of the image and pastes it into another region, is one of the most common methods for digital image tampering [25, 31]. In the CMF scenario, a tampered region might not be exactly the same as another region since it usually undergoes a sequence of post-processing operations such as rotation, scaling, blurring, and noising for a better visual appearance. Therefore, it becomes increasing difficult to manually identify tampered regions even for practiced users (see Fig. 1). Accordingly, the detection of the CMF has become one of the most actively researched topics in passive image forensics [6, 30]. Many CMF detection (CMFD) algorithms have been introduced to efficiently find tampered regions in images. Basically, CMFD algorithms identify tampered regions under the assumption that, although digital forgeries may leave no visual clue, they alter the underlying statistics of the image [7].

Fig. 1
figure 1

Examples of image tempering. It is very difficult to manually identify tampered regions. a red_tower. b fisherman. c writing_history. d ship

Full size image

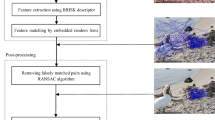
In this work, we focus on passive image forensics and introduce a new methodology for CMFD. In the proposed CMFD design, keypoints and their descriptors are extracted from the image based on the Scale Invariant Feature Transform (SIFT). Then, an improved matching operation is performed to handle both single and multiple copy-move forgeries. Further, we introduce a new verification algorithm exploiting the SIFT scale space representation. The proposed verification algorithm precisely selects a subset of matched pairs based on their scale spaces and the subset is used to estimate the geometric transformation. Finally, duplicated regions are localized using the estimated transformation. Experimental results verify that the proposed algorithm robustly detects the CMF and its complexity is much lower than those of existing CMFD algorithms.

The rest of this paper is organized as follows. In Section 2, detailed overviews of conventional CMFD algorithms are given. In Section 3, we introduce the keypoint matching scheme. Section 4 presents the proposed verification and localization techniques. Comparative experimental results of the proposed and conventional algorithms are presented in Section 5. Finally, our conclusions are drawn in Section 6.

2 Related works

In the literature, a large number of CMFD algorithms have been proposed, which can be classified into two main categories: block-based and keypoint-based methods. The first CMFD method was proposed by Fridrich in 2003 [13]. This method divides an image into 8 ×8 overlapping blocks and extracts discrete cosine transform (DCT) features from the blocks. Feature vectors are lexicographically sorted, and then similar feature vectors are identified to judge forgery. Thereafter, more efficient block-based algorithms have been introduced including blur-invariant moments [28], principal component analysis (PCA) [18, 37], Hu moments [41], discrete wavelet transform (DWT) features [19, 30, 42], improved DCT features [16], Fourier-Mellin transform (FMT) [4, 24], Zernike moments (ZERNIKE) [39], and upsampled log-polar Fourier (ULPF) descriptor [35]. It was reported in [9] that the ZERNIKE algorithm shows relatively good performance when duplicated regions are rotated. Note that all the algorithms mentioned above divide the input image into overlapping blocks and apply a feature extraction process to each block. The main drawback of the block-based algorithms is their high computational complexity [20]. For example, the algorithms proposed in [28] and [16] usually need a huge amount of processing time for CMFD.

The other type of CMFD algorithm does not utilize block-based feature representations. These algorithms identify high-entropy regions (keypoints) in the image and extract feature vectors only at the keypoints. Therefore, the number of feature vectors is reduced and the processing times of the keypoint-based algorithms are relatively lower than those of the block-based algorithms. On the other hand, duplicated regions are often sparsely covered by matched pairs in the keypoint-based algorithms. This may result in the degradation of detection performance and, in some cases, the duplicated regions being completely missed. Therefore, the detection performance of the keypoint-based algorithms needs to be improved further without increasing the computational complexity.

A number of keypoint-based descriptors such as SIFT [27], speed up robust feature (SURF) [3], and gradient localization oriented histogram (GLOH) [29] have been widely used for image retrieval and object recognition. In recent years, there have been attempts to apply SIFT and SURF features to CMFD applications [1, 2, 15, 23, 33, 40]. In this paper, we focus on the CMFD algorithms based on SIFT features.

A preliminary CMFD algorithm using SIFT features was proposed in [15]. There, the authors only try to find matched keypoints and numerical results to evaluate objective performance of the proposed algorithm are not provided. The CMFD algorithm in [33] finds geometric transformations between duplicated regions and constructs a correlation map using the extracted transformations. Further, the duplicated regions are localized using the correlation map. The algorithm adopts the keypoint matching scheme that finds reliable matched pairs by using distance ratio between the most similar match and the second similar match. This procedure is referred to as the 2NN test. The generalized 2NN (g2NN) test [2] was proposed to detect multiple copy-move forgeries. The g2NN test iterates the 2NN test until the distance ratio is greater than a predefined threshold. In the next section, we explain the 2NN and g2NN tests in detail and further investigate the matching operation using the distance ratio. Recently, clustering-based and segmentation-based algorithms were proposed in [1] and [23], respectively. Basically, these algorithms enhance the localization accuracy of CMF regions by adopting pre-processing schemes with additional computational overheads. It was reported in [23] that, when a simulation is performed on a computer with 3.3GHz CPU and 4G RAM, the segmentation process takes about 15 seconds for an image of 0.48 megapixels. It is worthwhile to note that the proposed CMFD approach does not utilize any pre-processing schemes such as clustering and segmentation.

3 Feature extraction and keypoint matching

In Sections 3 and 4, we introduce a new CMFD processing pipeline that can be successfully used for real world applications. The first step of the proposed algorithm is the keypoint detection and feature extraction based on SIFT features. We detect keypoints that are stable local extrema in the scale space and extract SIFT feature descriptors at the detected keypoints. Using the results, the proposed algorithm performs a matching operation to identify similar local regions.

The straightforward way to match keypoints is to fix a global threshold on the Euclidean distance between descriptors. However, this approach does not perform well due to the high-dimensionality of the SIFT descriptor [1]. Several matching techniques have been introduced for the efficient matching operation. The 2NN test [33] performs the matching operation using the distance ratio between the closet neighbor to the second-closest one. Supposed that, for a given image, N keypoints and the corresponding feature descriptors have been extracted using SIFT features. Let k ∗ be the currently inspected keypoint and f ∗ be its feature descriptor. The 2NN test defines a similarity vector D = {d 1, d 2,…,d N−1} containing sorted Euclidean distances between k ∗ and the other keypoints {k 1, k 2,…,k N−1}, which is computed as

$$\begin{array}{@{}rcl@{}} d_{i} = ||f^{*}-f_{i}||_{2} \end{array} $$
(1)

where f i , i = 1,2,…,N − 1, is the descriptor of k i . The inspected keypoint k ∗ is matched with k 1 if the following constraint is satisfied:

$$\begin{array}{@{}rcl@{}} d_{1}/d_{2} < T \end{array} $$
(2)

where T is set to 0.5 in [33]. In the 2NN test, the inspected keypoint can be matched with only a single keypoint even when the source region is copied-moved several times.

To address this issue, the g2NN test [2], the generalization of 2NN, iterates the 2NN test between d i /d i+1 until this ratio is greater than 0.5. Assume that the procedure terminated at i = m. Then, the keypoints {k 1, k 2,…,k m−1}, 1 ≤ m < N, in correspondence to {d 1, d 2,…,d m−1} are considered as matches for the inspected keypoint k ∗. The weakness of the g2NN test is that, if the source region is copied-moved several times and copied regions are very similar to each other, the keypoint in the copied regions can not be correctly matched. Figure 2 shows an example of multiple copy-move forgeries. In Fig. 2, the g2NN test can detect only a single matched pair among six matches.

Fig. 2
figure 2

Graphical explanation of the proposed matching operation. The above figure shows a part of the brisks image of the popular Christlein et al.’s database [9], where copied regions are rescaled by 120%. In the image, four keypoints, k a , k b , k c , and k d , are matched with each other. In the bottom figure, D a and C a represent the similarity vector and matched candidates of k a , respectively. At the end of matching operation, the proposed method obtains six matched pairs from the four keypoints. On the other hand, the 2NN and g2NN tests extract only a single matched pair (k a , k c )

Full size image

Based on these observations, we propose an adaptive 2NN (a2NN) test. Similar to the 2NN and g2NN tests, the proposed a2NN test utilizes the similarity vector D in the matching operation. However, instead of computing the distance ratio of successive elements in D, the a2NN test calculates the adaptive distance ratio between elements by considering their distribution. In detail, the a2NN test proceeds as follows.

  • The a2NN test constructs a set of matched candidates of each keypoint. The following procedures are applied to each keypoint:

    1. √

      Construct the similarity vector D for the current keypoint k ∗.

    2. √

      Calculate the distance ratio \(r^{i}_{i+1}=d_{i}/d_{i+1}\) between d i and d i+1. This procedure begins at i = S and repeats by decreasing i by 1 until it reaches 1 (i ≥ 1). If \(r^{i}_{i+1}<0.2\), this procedure is terminated immediately. The initial value S controls the maximum number of duplicated regions which can be detected using the proposed algorithm. In our simulation, S was set to 4.

    3. √

      Suppose that the procedure terminated at i = m. Then, the algorithm constructs a set C = {k 1, k 2,…,k m } of matched candidates. Note that, if m = 1, there is only a single matched candidate for k ∗. Otherwise, if m > 1, k ∗ has multiple matched candidates.

  • After obtaining matched candidates of all keypoints, the a2NN test constructs a set R of real-matched pairs. The following procedures are applied to each keypoint:

    1. √

      For the current keypoint k ∗, examine the reliability of each matched candidate in C = {k 1, k 2,…,k m }. To verify the reliability of the pair (k ∗, k j ), j = 1,2,…,m, the algorithm examines whether k ∗ belongs to the matched candidates C j of k j . If k ∗∈C j , the pair (k ∗, k j ) is considered a real-matched pair and will be an input of the following step. Otherwise, if k ∗∉C j , the pair is not involved in the following step.

    2. √

      Calculate adaptive distance ratios of the resultant real-matched pairs. For each pair, the adaptive distance ratio is computed as \(r^{j}_{m+1}=d_{j}/d_{m+1}\). Then, the matched pairs (k ∗, k j )’s are inserted into R in the ascending order of \(r^{j}_{m+1}\).

Figure 2 shows a graphical explanation of the proposed matching operation.

Through the above procedure, multiple matched pairs of a single keypoint can be included in R. We observed that, in some cases, the number of pairs in R is unnecessarily large, especially for the plain copy-and-move attack. This may significantly increase the computational complexity of the remaining detection processes. To address this problem, we only consider first M elements with relatively low adaptive distance ratios in the remaining processes. Through extensive simulation, we found that M = 300 shows a good trade-off between time complexity and detection performance.

4 Improved verification and localization

A way to detect possible geometric transformations between duplicated regions is to use the same affine transformation selection (SATS) [8], clustering algorithms [1], or segmentation based ones [12, 23, 26]. In this paper, we introduce a new verification technique exploiting the SIFT scale space representation. The proposed algorithm selects a random subset of the matches satisfying given constraints and estimates the geometric transformation using the subset. Finally, the transformations with reasonable inliers are chosen for possible attacks.

4.1 Precise sampling based on scale space representation

In order to detect stable keypoints in scale space, the SIFT algorithm utilizes a scale space representation that is implemented as an image pyramid. An initial image is repeatedly smoothed with a Gaussian blur and then sub-sampled in order to achieve a higher level of the pyramid. The difference-of-Gaussian (DoG) image is computed by subtracting adjacent image scales. Formally, the DoG is computed as

$$\begin{array}{@{}rcl@{}} D(x,y,\sigma)& = & (G(x,y,h\sigma)-G(x,y,\sigma))*I(x,y) \\ &=&L(x,y,h\sigma)-L(x,y,\sigma) \end{array} $$
(3)

where L(x,y,h σ) is the convolution of the image I(x,y) with the Gaussian blur G(x,y,h σ) at scale h σ. In order to detect the local extrema of D(x,y,σ), each sample point is compared to its eight neighbors in the current scale and nine neighbors in the scales above and below. Then, the point that is larger (or smaller) than all of these neighbors is selected as a keypoint. Each octave of scale space (i.e., doubling of σ) is divided into an integer number n of intervals such that h = 21/n. Note that n + 3 DoG images need to be computed for each octave for finding local extrema [27].

Let o and l be the octave and blur level from which a keypoint k is extracted. Then, given o and l, we can derive the scale level u of k as

$$\begin{array}{@{}rcl@{}} u &=& 2^{o-1} \cdot 2^{(l/n)} \\ &=& 2^{o+ (l/n)-1}. \end{array} $$
(4)

Let p = {k s, k c} be a matched pair in R obtained in the previous matching step, and v s and v c be the pixel coordinates of k s and k c, respectively. Then, for the pair p, we can compute the variation ratio \(\tilde {u}\) of scale levels as

$$\begin{array}{@{}rcl@{}} \tilde{u} = u^{c}/u^{s} \end{array} $$
(5)

where u s and u c are the scale levels of k s and k c, respectively.

In the CMF scenario, a local region undergoes a geometric transformation and is pasted into another region. We use the affine transformation in order to model the geometric distortion between the source and copied regions. Let us assume that two matched pairs, p 1 and p 2, are generated by a common CMF attack. In this case, the two pairs share a common geometric transformation and their scale variations should be the same as each other. Therefore, we can derive the following relationship between p 1 and p 2:

$$\begin{array}{@{}rcl@{}} \tilde{u}_{1} = \tilde{u}_{2} \end{array} $$
(6)

where \(\tilde {u}_{1}\) and \(\tilde {u}_{2}\) are the variation ratios of scale levels of p 1 and p 2, respectively. Further, since the affine transformation preserves the ratio of lengths of line segments, we may approximately estimate the length of the transformed segment using that of the original segment as follows (see Fig. 3) [10]

$$\begin{array}{@{}rcl@{}} ||\textbf{v}_{1}^{c}-\textbf{v}_{2}^{c}||_{2} \approx \tilde{u}_{1}||\textbf{v}_{1}^{s} - \textbf{v}_{2}^{s}||_{2}. \end{array} $$
(7)
Fig. 3
figure 3

Lengths of common line segments in the source and copied regions

Full size image

Based on these observations, we propose a precise sampling strategy exploiting the scale space representation. Note that, in order to compute the affine transformation, three non-collinear pairs need to be selected. At first, the proposed algorithm randomly selects an initial pair \(\textbf {p}_{1}=\{{k_{1}^{s}},{k_{1}^{c}}\}\) from R. Then, we select another pair \(\textbf {p}_{2}=\{{k_{2}^{s}},{k_{2}^{c}}\}\) satisfying the following constraints:

$$ \left\{ \begin{array}{ll} \tilde{u}_{1} = \tilde{u}_{2}, \\ \left| ||\textbf{v}_{1}^{c}-\textbf{v}_{2}^{c}||_{2} - \tilde{u}_{1} ||\textbf{v}_{1}^{s} - \textbf{v}_{2}^{s}||_{2}\right| < E \end{array} \right. $$
(8)

where E is a predefined threshold for the reprojection error. Similarly, p 3 can be selected. The resultant three pairs, p 1, p 2, and p 3, will be used for calculating the geometric transformation in the next subsection.

4.2 Affine transformation calculation

As mentioned, we model the geometric distortion of duplicated regions as the affine transformation to cope with various geometric transformations such as rotation, scaling, shearing, and reflection. Let us denote by A a 2 × 2 linear matrix, which is represented by

$$\begin{array}{@{}rcl@{}} \textbf{A}= \left[\begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22} \end{array}\right] \end{array} $$
(9)

where (a 11, a 12, a 21, a 22) are the parameters specifying rotation and scaling transformations. Then, the relationship between matched keypoints can be expressed as

$$\begin{array}{@{}rcl@{}} \textbf{v}^{c}_{\alpha} = \textbf{A} \textbf{v}^{s}_{\alpha} + \textbf{t} \end{array} $$
(10)

where α = 1,2,3 and t = [t x , t y ]T is the translation factor. We obtain a unique solution of (10) using the three pairs, p 1, p 2, and p 3. In particular, we solve (10) using Maximum Likelihood estimation of the homography [14]. After computing the affine transformation A and t, we count the number Q of inliers among R, which satisfy the following constraint:

$$\begin{array}{@{}rcl@{}} ||\textbf{v}^{c}-(\textbf{A}\textbf{v}^{s}+\textbf{t})||_{2} < E. \end{array} $$
(11)

Only the transformations that produce more than or equal to M/10 inliers (Q ≥ M/10) are taken as true ones. To detect multiple duplicated regions in the image, we perform the sampling and affine transformation estimation 100 times.

4.3 Localization of duplicated regions

After obtaining the transformation matrices, we generate the warped image W for each transformation matrix. We localize the duplicated regions using zero mean normalized cross-correlation (ZNCC) between the original image I and the warped image W:

$$\begin{array}{@{}rcl@{}} {}Z(x,y) \,=\, \frac{{\sum}_{(x^{\prime},y^{\prime})\in \textbf{B}(x,y)}(I(x^{\prime},y^{\prime})\,-\,\mu_{I})(W(x^{\prime}, y^{\prime})\,-\, \mu_{W})}{\sqrt{{\sum}_{(x^{\prime},y^{\prime})\in \textbf{B}(x,y)}(I(x^{\prime},y^{\prime})\,-\, \mu_{I})^{2}{\sum}_{(x^{\prime},y^{\prime})\in \textbf{B}(x,y)}(W(x^{\prime},y^{\prime})\,-\,\mu_{W})^{2}}} \end{array} $$
(12)

where B(x,y) is a set of pixels located in the 5 × 5 window centered at (x,y); μ I and μ W are, respectively, the average pixel intensities of I and W computed on B(x,y). Next a binary image is created by thresholding the union of Z(x,y)′ s. In the binary image, small isolated regions (less than 100 pixels) are discarded and small holes (less than 100 pixels) are filled using mathematical morphological operations [22, 34].

5 Experimental results

We evaluated the performance of the proposed CMFD algorithm by comparing it with state-of-the-art algorithms. We first implemented two SIFT-based algorithms, SIFT-1 [33] and SIFT-2 [2], which performs the matching operation using 2NN and g2NN, respectively. We also implemented threshold-based algorithm SIFT-T that performs the matching by fixing a global threshold on the Euclidean distance between descriptors. In the simulations, the global threshold was set to 1000. Further, we implemented the ULPF descriptor that is the state-of-the-art block-based algorithm [35]. All algorithms were implemented using a highly efficient ANSI-C code and the performance was evaluated on an Intel i7 3.4GHz CPU with 16 GB RAM.

Basically, we measured the forgery detection performance of the algorithms using the common CMFD processing pipeline introduced in [9]. We used the kd-tree with the Best Bin First (BBF) search algorithm in identifying similar feature vectors in the matching step [5]. In the simulations, the reprojection threshold E in (8) and (11) was set to 3. We used 4 octaves and 3 blur levels for extracting the SIFT features.

5.1 Datasets and evaluation criteria

There exist several benchmarking datasets for evaluating the performance of CMFD algorithms. In our simulations, we used the realistic and challenging dataset introduced in [9]. The tampered images in the dataset were manually created by skilled artists. In addition, common noise sources, such as JPEG artifacts, Gaussian noise, additional scaling or rotation, are automatically included using a software framework. The dataset also provides ground truth images that are very useful for the performance evaluation. The average size of the images is about 3000 × 2300 pixels.

To quantitatively evaluate the detection performance, we adopt two metrics, precision M p and recall M r , which are calculated as [16]

$$\begin{array}{@{}rcl@{}} M_{p}=\frac{\text{\#correctly detected pixles}}{\text{\#all detected pixels}} \end{array} $$
(13)

and

$$\begin{array}{@{}rcl@{}} M_{r} = \frac{\text{\#correctly detected pixles}}{\text{\#all forged pixels}}. \end{array} $$
(14)

Hence, precision is the fraction of pixels identified as tampered that are truly tampered and recall is the fraction of tampered pixels that are correctly classified as such. A trade-off exists between precision and recall. Larger precision might decrease recall and vice versa. To consider both precision and recall, we compute their harmonic mean M F , called F 1-score, as follows

$$\begin{array}{@{}rcl@{}} M_{F} = \frac{2M_{p} M_{r}}{M_{p}+M_{r}}. \end{array} $$
(15)

Using these metrics, we show how precisely the CMFD algorithms identify tampered regions.

5.2 Performance evaluation

We evaluate the performance of the CMFD algorithms for four CMF scenarios: rotation, scaling, JPEG compression, and additive white Gaussian noise (AWGN). Next, the measured CMFD processing times and memory requirements are presented.

5.2.1 Rotation invariance

In this scenario, the copied regions are rotated in the range of 0∘ and 10∘ in steps of 2∘. Further, we test three larger rotation angles of 20∘, 60∘, and 180∘. Figure 4 shows the measured results for the CMF with rotation. As shown in Fig. 4, the SIFT-1, SIFT-2, SIFT-P algorithms usually achieve better detection performance than the SIFT-T algorithm. The result indicates that the matching scheme based on distance ratio is more effective than that based on the fixed threshold.

Fig. 4
figure 4

Measured M p , M r , and M F for the CMF with rotation

Full size image

We see from Fig. 4 that SIFT-P shows a better detection performance than the other algorithms. The recall of SIFT-P is constantly higher than those of the other algorithms over the entire range of rotation angles. Especially, SIFT-P achieves a significant performance improvement for large amounts of rotation as compared to the existing algorithms. In our simulation, the average M r ’s of SIFT-T, SIFT-1, SIFT-2, and SIFT-P are 0.67, 0.74, 0.76, and 0.81, respectively. Further, the average M F ’s of SIFT-T, SIFT-1, SIFT-2, and SIFT-P are 0.71, 0.74, 0.75, and 0.79, respectively. To show the result more clearly, we present the CMFD results of the algorithms for the rotation of 60∘ in Fig. 5.

Fig. 5
figure 5

Examples of the CMFD results for the rotation of 60∘. The first column a shows the test images, fisherman, bricks, giraffe, and tree, and their ground truths from the dataset. The columns, b, c, d, and e, show the detection results of SIFT-T, SIFT-1, SIFT-2, and SIFT-P, respectively

Full size image

In addition, we compare the proposed SIFT-P to the state-of-the-art block-based ULPF in Fig. 4. We observed that the average M F of ULPF is slightly higher than that of SIFT-P by about 0.01. Especially, the ULPF scheme shows better performance for the plain CMF with the rotation angle of 0∘. And, SIFT-P shows relatively good performance for the rotation angle of 180∘.

5.2.2 Scale invariance

We investigate the case in which the copied regions are scaled between 101 and 109% of its original size in increments of 2% as well as 120% and 200%. Figure 6 presents the results for the CMF with scaling. Similar to the CMFD of rotation, SIFT-1, SIFT-2, SIFT-P show a better detection performance than SIFT-T. Especially, for the scaling of 109%, M F of SIFT-T is lower than that of SIFT-P by about 0.2. Indeed, the distance-ratio-based scheme is more effective than the fixed-threshold-based one.

Fig. 6
figure 6

Measured M p , M r , and M F for the CMF with scaling

Full size image

Similar to the CMFD of rotation, SIFT-1, SIFT-2, and SIFT-P show a good scale invariance. Basically, this can be achieved scale invariant features of SIFT. The proposed SIFT-P exhibits the best scale invariance in the experiments. Especially, SIFT-P achieves a significant performance improvement in terms of recall. In our simulation, the average M r ’s of SIFT-T, SIFT-1, SIFT-2, and SIFT-P are 0.64, 0.74, 0.75, and 0.79, respectively. Accordingly, the F 1-score of SIFT-P is higher than those of SIFT-T, SIFT-1, and SIFT-2.

When the copied regions are scaled, ULPF show a relatively weak invariance. The detection performance of ULPF decreases sharply as the scale factor increases. This means that the block-based ULPF can be used to only handle a moderate amount of scaling. We see from Fig. 6 that the proposed SIFT-P shows constantly good detection performance over the entire range of scale factors.

5.2.3 Robustness to JPEG compression artifacts

Next, we test the robustness of the CMFD algorithms against JPEG compression artifacts. The quality factor of JPEG is varied between 100 and 20 in steps of 10. In general, SIFT-1, SIFT-2, and SIFT-P outperform SIFT-T and ULPF. As shown in Fig. 7, M F ’s of SIFT-T and ULPF decrease sharply as the quality factor decreases. On the contrary, M F ’s of SIFT-1, SIFT-2, and SIFT-P moderately decrease. Therefore, the three algorithms yield a good robustness to JPEG compression artifacts. For the high quality factors, M F ’s of SIFT-P and ULPF are slightly higher than those of the other algorithms. We can observe that M F of SIFT-P is constantly higher than those of the other algorithms for the quality factor between 80 and 20.

Fig. 7
figure 7

Robustness to JPEG compression artifacts

Full size image

5.2.4 Robustness to Gaussian noise

We also evaluate the robustness of the algorithms to AWGN. We normalize the image intensities between 0 and 1, and add zero-mean Gaussian noise with standard deviations of 0.02, 0.04, 0.06, 0.08, and 0.10 to the tampered regions. In Fig. 8, we clearly see that the detection performance of all the algorithms decreases as the standard deviation increases. As compared to the CMFD against JPEG compression artifacts, M F ’s of the algorithms decrease sharply for AWGM. When the standard deviation is 0.04, M F ’s of ULPF, SIFT-T, SIFT-1, SIFT-2, and SIFT-P decrease to 0.25, 0.51, 0.69, 0.69, and 0.74, respectively. The results indicate that the performance degradation of ULPF is much more severe than those of the other algorithms. We can see that M F of SIFT-P is consistently higher than those of the other algorithms.

Fig. 8
figure 8

Robustness to Gaussian noise

Full size image

5.2.5 Computational complexity and memory requirement

The processing time of the CMFD algorithm varies depending on the matching and verification schemes and the number of used matched pairs. The measured processing times are listed in Table 1. As shown in Table 1, our implementation is highly optimized in terms of the processing time. We see that ULPF, SIFT-1, and SIFT-2 yield relatively high processing times as compared to SIFT-T and SIFT-P. In our simulations, the processing time of ULPF is the highest among all the methods. As we expected, the processing time of SIFT-P is lower than those of the other algorithms. For example, SIFT-P takes only 1.92 seconds on average for a low resolution image of 1.01 megapixels.

Table 1 Average CMFD processing time
Full size table

We also measure the average memory requirements of the algorithms. In our simulations, the SIFT-based algorithms, SIFT-T, SIFT-1, SIFT-2, and SIFT-P, require 40.2 megabytes and 7.4 megabytes of memory on average for high and low resolution images, respectively. The block-based ULPF algorithm requires a much larger memory space as compared to the SIFT-based algorithms. The average memory requirement of ULPF is 1822.1 megabytes for a high resolution image and 240.4 megabytes for a low resolution image.

In our simulations, we observed that tampered regions in smooth regions are often sparsely covered by matched pairs, thereby resulting in the duplicated regions being completely missed. To handle this issue, we can adopt one of conventional algorithms [11, 43]. For example, after extracting keypoints from the entire image based on the SIFT, we may use Harris corner detector to extract additional keypoints which are located in the small and smooth regions.

6 Conclusions

A new SIFT-based CMFD algorithm was proposed for the efficient detection of CMF. The proposed CMFD algorithm has a solid theoretical background and its actual performance is superior than existing algorithms based on SIFT features. The simulation results demonstrate that the proposed algorithm achieves a very stable detection performance for four CMF scenarios: rotation, scaling, JPEG compression, and AWGN. In addition, the processing time of the proposed algorithm is the lowest among the SIFT-based CMFD algorithms. Therefore, we strongly recommend the use of the proposed algorithm for the applications that need to detect CMF. Especially, the proposed algorithm can be utilized to provide quantitative measures of image authenticity in criminal investigation, product inspection, journalism, intelligence services, and surveillance systems.