1 Introduction

Assessing the quality of an image is one of the most important and indispensable issue in image processing. The best reference for evaluating the quality of an image might be human being. However it might be person-dependent, expensive, time-consuming and tedious, especially when applied to a huge number of images.

Objective metrics, on the other hand, provide a quantitative measure in an acceptable time and with a reasonable precision. These metrics can be classified in three categories, namely, full-reference (FR), reduced-reference (RR) and no-reference (NR) metrics, based on their need to the reference image information. Full-reference objective metrics need the pristine reference image to compare with the image under evaluation. These metrics have a crucial role in tuning image processing systems that their process accompanied with some degradations. Image compression is an example of such systems. The reduced-reference methods need only some descriptive information about the reference image. These metrics are often used in transmission issues where the quality of received images are assessed with extra information. The no-reference methods evaluate the quality of an image without the need for the reference image. These methods are difficult to develop because they need intrinsic information about the quality of the image.

An image might be affected by various distortions, which can be categorized in nonstructural and structural ones [25]. Nonstructural distortions, like a change of luminance or brightness, a change of contrast, Gamma distortion, and spatial shifts, impose unpleasant visual effects on image without destroying its structure; while the structural distortions, like additive noise, blurring and lossy compression, ruin the major structure of image so that the observer cannot distinguish the image contents in severe conditions. Blurriness, among these distortions, is a common structural distortion, which has been assessed in various ways, that can be categorized in spatial and non-spatial methods. The spatial methods, often, model the total or local variations on statistics like variance [5, 21], autocorrelation and energy of the first and second derivatives [2], edge profile distributions [1, 4, 6], or dominant eigenvalues of image covariance matrix [28], and use them to define a metric to assess the blurriness. These methods have the benefits of low complexity cost. The non-spatial methods obtain their features through some suitable subband or statistical decompositions. These methods often describe images through varieties of basis functions and then attempt to assess the blurriness by estimating the amount of energy attenuation in the high frequency basis functions. In [3] blurriness is measured as the kurtosis of DCT coefficients of blocks. In [11] the uniformity of image spectrum is assessed by entropy and is used as a blurriness metric. Another blur metric called FISH [22], uses the logarithm of wavelet sub-band energies in three different scales. In [9, 10] the local phase coherence in wavelet domain is measured and is employed in computing the blurriness metric. The authors in [20] performed an SVD decomposition on image and employed the ratio between the k most significant singular value and all singular values as a blur metric. In [16] the properties of singular values curve is used to assess the blurriness.

In this paper we evaluate the blurriness of an image by considering both its structural and nonstructural residual defections. Proposed blur metric employs the structural and residual features arises from the SVD-based basis images, which formed from the product of the left and right singular vectors, accompanied with the corresponding singular value. In recent years, there has been an increasing attention to SVD as an efficient decomposition for image quality assessment. For instance, beside two aforementioned SVD-based blur metrics in [16, 20], there exist methods like those proposed in [19, 23, 24, 31], which their main concern are overall quality evaluation, but their results on blurriness are also noticeable.

The rest of this paper is organized as follows: Sections 2.1 and 2.2 give a brief review on the singular value decomposition concepts and the basis images analysis, respectively. A detailed description of our proposed measure is given in Section 2.3. Performance evaluations and results analysis are presented in Section 3. Finally the paper is concluded in Section 4.

2 Proposed SVD-based blur evaluation metric

2.1 A brief review of singular value decomposition

The singular value decomposition is one of the most efficient tools in linear algebra to decompose a matrix into a series of basis matrices which represent the underlying structure of the matrix. Every real matrix X with dimension m × n can be decomposed into a three matrices as below,

$$ X=U_{m\times r}\times S_{r \times r}\times V_{r\times n} $$
(1)

where U and V are orthogonal matrices (U T U = I, V T V = I) containing left and right singular vectors of X, respectively, and S is a diagonal matrix containing the singular values of X in descending order. The number of non-zero singular values, r, is the rank of matrix X. These matrices can be shown as below,

$$ \left\{ \begin{array}{l} U=(u_{1},u_{2},...,u_{r})\\ V=(v_{1},v_{2},...,v_{r})\\ S=diag(\delta_{1},\delta_{2},...,\delta_{r}) \end{array} \right. $$
(2)

Considering the above, (1) can be rewritten as below:

$$ X=\sum\limits_{i=1}^{r}X_{i}=\sum\limits_{i=1}^{r}u_{i}\delta_{i} {v_{i}^{T}} $$
(3)

The basis images (X i ) corresponding to higher singular values contain the major information of image which encoded in its low frequency components. On the other hand the ones corresponding to lower singular values expose the nonstructural details of the image, i.e. the high frequency contents. Figure 1b-h show the basis images corresponding to the seven higher singular values of the reference image shown in Fig.1a. The number of basis images which can be extracted for an image is equal to the rank of the image, r ≤ m i n(r o w s,c o l u m n s).

Fig. 1
figure 1

(a) Original Image, (b-h) Basis images corresponding to the seven higher singular values of image (a), respectively

Full size image

2.2 Structural and residual portions of an image

Recall (3), by setting a positive integer p, 0 ≤ p ≤ r and computing the summations in (4), we can obtain two complementary portions of image X, which we call them Structural Portion (SP) and nonstructural Residual Portion (RP).

$$ \left\{\begin{array}{l} S{P_{X}^{p}}={\sum}_{i=1}^{p}u_{i}\delta_{i} {v_{i}^{T}}\\ R{P_{X}^{p}}={\sum}_{i=p+1}^{r}u_{i}\delta_{i} {v_{i}^{T}}\\ \end{array} \right. $$
(4)

For small values of p, the SP portion contains the major structure of the image without its high frequency components, while these high frequency components will be in RP portion. By increasing the value of p toward r, the SP portion will become more similar to the original image and the RP portion will become sparser. Figure 2 shows the two portions SP and RP for different values of p.

Fig. 2
figure 2

Illustration of the structural (left) and residual (right) portions of the reference image shown in Fig.1(a), for the various values of p ∈ {1, 5, 20, 140}. Note the pixel intensities is scaled to [0,255] for better representation

Full size image

The concepts of structural and residual portions have been introduced in [23] (namely, content-dependent and content-independent parts), where they employed the gradient and contrast similarities between the content-dependent parts of the reference and the distorted images, besides the normalized PSNR of content-independent parts. Here we concentrate on the inherent properties of these portions and obtain more accurate results for assessing blur.

Back to (4), the energy of structural and residual portions (E S P X and E R P X , respectively), for a given value of p, can be calculated via Frobenious norm as belowFootnote 1,

$$ \left\{ \begin{array}{l} ES{P_{X}^{p}}=\left\|S{P_{X}^{p}}\right\|_{F}=\sqrt{{\sum}_{i=1}^{p}{\delta_{i}^{2}}} \\ ER{P_{X}^{p}}=\left\|R{P_{X}^{p}}\right\|_{F}=\sqrt{{\sum}_{i=p+1}^{q}{\delta_{i}^{2}}} \\ \end{array} \right. $$
(5)

The resulted vectors contain valuable information about the image blurriness. To further investigate, let we choose an arbitrary source image and produce various of its blurred version via applying Gaussian smoothing filters with different values of σ. The E S P X and E R P X of the image for various p have been computed and shown in Fig. 3. As it can be considered from the figure, the slope of changes in E S P X and E R P X highly depends to the image blurriness. These behaviors, from our experience on various reference images, can be described mathematically as below:

$$ \left\{ \begin{array}{l} ES{P_{X}^{p}}\approx log(p^{\alpha}) \\ ER{P_{X}^{p}}\approx\frac{1}{log(p^{\beta})} \\ \end{array} \right. $$
(6)

where the values of α and β determine the curves in Fig. 3a and b, respectively, and are proportional with the variance (σ) of the Gaussian function involved in blurriness.

Fig. 3
figure 3

Plots of vectors (a) E S P X and (b) E R P X , corresponding to the energy of structural and residual portions, respectively, for the blurred versions of image in Fig.1(a), with variances σ ∈ [0.5,...,9.5] with steps of 1. The circle symbols indicate the corresponding energies of the reference image

Full size image

2.3 Proposed method of blurriness assessment

The blurriness affects the image quality by decreasing the image’s high frequency details and introducing to the low frequency components in the form of some uniform redundancies in neighboring pixels. Hence, we face with two kinds of destructions, first losing the high frequency details, and second damaging the image structure by introducing the low frequency redundancies. Here, we try to estimate both of these effects by considering the properties of \( ES{P_{X}^{p}} \) and \( ER{P_{X}^{p}} \), respectively. To do this, the sequences \( ES{P_{X}^{p}} \) and \( ER{P_{X}^{p}} \) are computed for both the reference and the blurred images, and then the following ratios are built upon them:

$$ \frac{ES{P_{B}^{p}}}{ES{P_{R}^{p}}}\approx\frac{log(p^{\alpha_{B}})}{log(p^{\alpha_{R}})}=\frac{\alpha_{B} log(p)}{\alpha_{R} log(p)}=\frac{\alpha_{B}}{\alpha_{R}} \\ $$
(7)
$$ \frac{ER{P_{B}^{p}}}{ER{P_{R}^{p}}}\approx\frac{\frac{1}{log(p^{\beta_{B}})}}{\frac{1}{log(p^{\beta_{R}})}}=\frac{\beta_{R} log(p)}{\beta_{B} log(p)}=\frac{\beta_{R}}{\beta_{B}} \\ $$
(8)

where α R and β R determine the curves of structural and residual portion energies, respectively, belong to the reference image. Similarly, the values of α B and β B indicate the corresponding curves in blurred image. Since the values of α R and β R are constant for a given reference image, the ratios in (7) and (8) can determine the rate of blurriness. These ratios characterize the structural and residual distortions, respectively, and can be served in a blur indicator. We involve their contribution via a nonlinear pooling scheme and make our final proposed Blur Metric (B M), as below:

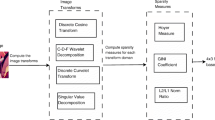
$$ proposed BM =\frac{1}{q}\left( \sum\limits_{p=1}^{q}\frac{ES{P_{B}^{p}}}{ES{P_{R}^{p}}+\epsilon}\right)^{\gamma}.\left( \sum\limits_{p=1}^{q}\frac{ER{P_{B}^{p}}}{ER{P_{R}^{p}}+\epsilon}\right)^{1-\gamma} $$
(9)

where the parameter γ, 0 ≤ γ ≤ 1, is a tuning parameter and can be determined empirically to achieve the best correlation with the subjective scores. In the next section we will provide more discussion around this parameter. In order to avoid division by zero, the extra small value of 𝜖 is added in the denominators. The dynamic range of our proposed blur metric is (0, 1], with the best value achieved when the blurred and the reference images are equal. Figure 4 exhibits a flowchart for the proposed full-reference blur evaluation algorithm.

Fig. 4
figure 4

Flowchart of the proposed SVD-based image blur assessment approach

Full size image

3 Performance evaluation

In the implementation stage, we must determine two parameters in our proposed method. First the parameter q in (5), which determines the size of sequences \( S{P_{R}^{p}} \) and \( R{P_{R}^{p}} \), and is a nonzero value smaller than the rank of the image. We found empirically that the best value of this parameter is around \(q=\left \lfloor \frac {min(m,n)}{3}\right \rfloor \). The second parameter to set, is the value of γ in (9) which controls the contribution of the two aforementioned portions. Through a series of experiments, which will be explained in the following subsection, this parameter sets as γ = 0.95.

A popular method for validating the ability of a blur metric is to investigate the algorithm’s performance in monotonically predicting the blurriness of images with uniformly increasing the standard deviation. In the first experiment, we have produced several blurred images with different standard deviation σ ∈ {0.5, 1.5, ..., 9.5}. Figure 5 shows the values of the proposed blur metric for these blurred images against the values of standard deviation. As the figure shows, by increasing the blurriness, the values of the proposed metric are decreased monotonically.

Fig. 5
figure 5

The plot of objective scores of blurriness, evaluated by proposed blur metric, versus different variance (σ) values in blurring the image

Full size image

In order to further evaluate the proposed blur metric, we verify its ability to predict the subjective scores of the blurred image subsets of LIVE(Laboratory for Image and Video Engineering) [18], TID2008 [15] and CSIQ [12] databases. The LIVE is a standard database for image quality metrics performance evaluation, which contains 29 high-resolution original and 145 Gaussian blurred images. The TID2008 is a comprehensive quality-related database with 25 reference images blurred each in four levels of blurriness. The CSIQ is also a popular quality related image database, contains 150 blurred images (30 references each blurred in five different severity).

We used four criteria to assess the performance of proposed algorithm following [8]: (1) The Pearson correlation coefficient (PCC), which measures the amount of predictions correlation with the subjective scores, (2) The Spearman rank order correlation (SROCC) and (3) the Kendall rank order correlation (KROCC), which measure both the relative monotonicity between the predictions and subjective scores, and (4) the root mean square error (RMSE) which validates the predictions accuracy, like PCC. Before evaluating these criteria, we applied the following five-parameter logistic transform suggested by [8], to the values obtained from our blur metric to bring them on the same scales as the TID2008’s MOS, LIVE’s DMOS and CSIQ’s DMOS values:

$$ MOS_{e} = \beta_{1}\left( \frac{1}{2}-\frac{1}{1+exp\left( \beta_{2} BM-\beta_{3}\right)}\right)+\beta_{4} BM+\beta_{5} $$
(10)

where M O S e is the estimated MOS by our proposed blurriness metric BM. The coefficients β i are determined so that the minimum MSE between the MOS and the M O S e achieved. Figures 6a, c and e show the scatter plots of the objective scores for the proposed blur metric versus the subjective ones of TID2008, LIVE and CSIQ databases, respectively. The solid curves are the results fitted with the above logistic function. In addition, the scatter plots of M O S e versus MOS is shown in Fig. 6b, d and f, for TID2008, LIVE and CSIQ databases, respectively. The correlation between the values of M O S e and MOS demonstrates that the proposed metric has well consistency with human opinions of quality. In addition Table 1 shows the values of the predefined evaluation criteria for the proposed blur metric on these databases. It can be observed that the PCC and SROCC between the scores of the proposed metric and the subjective scores of test databases are impressive.

Fig. 6
figure 6

Scatter plots of subjective scores versus the proposed blur metric on blurred subsets of IQA databases: (a) TID2008, (c) LIVE and (e) CSIQ databases. (b), (d) and (f) Scatter plots of the same data as (a), (c) and (e), respectively, after nonlinear regression. The corresponding evaluation criteria are shown in Table 1

Full size image
Table 1 The values of performance evaluation criteria for the proposed blurriness metric
Full size table

As another validation step, we compare the results of the proposed method with the results of some other well accepted quality metrics including PSNR, SSIM [27], MS-SIM [26], ADM [13], VIF [17], MAD [12], FSIM [29], SVDR [14], VGS [30] and the SVD-ELM based method proposed in [24]. In this comparison, we only employ the SROCC criterion and forget the others because of their similar results. As Table 2 shows, the SROCC of the proposed method on LIVE database dominates the SROCC of all other metrics, which is an impressive achievement. For TID2008 and CSIQ databases, our proposed metric doesn’t sit among the three dominant metrics, but its distances to them are not considerable.

Table 2 the values of SROCCs of some blurriness metrics applied on subset of blurred images of LIVE, TID2008 and CSIQ databases
Full size table

3.1 The role of Gamma

Recall from (9), our proposed blur metric is achieved through an exponentially weighted pooling scheme, in which the parameter γ controls the amount of contributions of structural and residual portions. A series of experiments performed on TID2008, LIVE and CSIQ databases with the aim of detecting the best value of this parameter. Figure 7 indicates the resulted SROCC between the MOS values of these image databases and the objective blur measures achieved by our blur metric with different values of γ ∈ [0,1]. Surprisingly eliminating the second term in (9) (i.e. the rate of residual portion energies) by setting the value of γ = 1, exposes more destructive effect on blur metric, compared to removing the first term (i.e. the rate of structural portion energies) by setting γ = 0. It can be realized that the existence of residual portion information, has impressive improvement on the proposed metric, even with an small exponential weight. The reason was investigated by observing the behavior of the first and the second terms in (9), separately, for different blur versions of the first image of TID2008 database, namely ”I01.bmp”, which are shown in Fig. 8. As can be seen in Fig. 9, the first term in (9) has a low sensitivity to the blur severity, while the second term behaves in opposite direction and expresses a high keenness to the blurriness extremity. These different dynamic ranges of changes for these two terms were foresighted. The first term always includes the first singular value of the image, which is the most dominant one. On the other hand the second term includes the details information, which changes drastically by introducing blur effects. These observations reinforce our assumption about the two kinds of destructions in a blurred image.

Fig. 7
figure 7

The plot of different SROCC values between the MOS provided by TID2008, LIVE and CSIQ image databases and proposed blur metric scores, versus different values of γ in (9)

Full size image
Fig. 8
figure 8

The first image of the TID2008 database (i.e. ’I01.bmp’). a the original image, (b-e) four blurred versions of (a) with increasing blur severity

Full size image
Fig. 9
figure 9

The different dynamic ranges of (a) the first term, and (b) the second term of (9), before exponentially weighting by γ, for different blurred versions of the first image of the TID2008’s image database, shown in the Fig. 8(b-e). Please note to the scale of vertical axis in the both two plots

Full size image

Back to Fig. 7, the value of γ = 0.82 is the best when we consider only the LIVE database. This setting yields an SROCC equal to 0.9812 for this database, which is a very good score. But to have a reasonable results on the whole three aforementioned databases, we set the final value of this parameter as γ = 0.95.

3.2 Computational complexity of proposed metric

In order to calculate the structural and residual portion energies, we only need the singular values of SVD decomposition. Hence, according to [7], we can obtain them with the order of O(m i n(m n 2,m 2 n)), where m and n are the number of image’s rows and columns, respectively. To calculate the proposed metric, we need to call the SVD function twice and a loop with O(q 2) iterations, and finally perform an averaging with O(q). Thus the overall computational complexity of our metric summarized as O(m i n(m n 2,m 2 n) + m i n(m,n)2). We compared our proposed metric with some other IQA indexes by running unoptimized MATLAB code (version R2013b) on a modern desktop with a 2.67GHz Intel Corei5 CPU and a 4G RAM. The average consuming times for assessing the blurriness of TID2008 images, with sizes of 512 × 384, are shown in Table 3, ascendantly. It can be seen that the efficiency of our proposed metric is better than the most modern IQA indexes.

Table 3 Consuming time for each IQA index (in seconds per image
Full size table

4 Conclusions

In this paper we addressed the image blurriness as two different distortions: destructed high frequency details, and redundancy-polluted low frequency structure. Motivated by this assumption, we proposed a novel full-reference blurriness measure, which extracts the two structural and nonstructural residual portions of the image. In the structural portion we assess the amount of low frequency redundancies, while in nonstructural residual portion we measure the amount of high-frequency degradation. These portions are constructed by summation of the SVD based basis image matrices corresponding to the low frequency and high frequency components of the image, respectively. We showed that the basis images corresponding to the higher singular values contain the structural information of the image, while the residual basis images provide the nonstructural details. The ratio of these portions energies for the reference and blurred images serves as the proposed blur metric.

The experimental results on images with various levels of blurriness convince the monotonic behavior of the proposed blurriness metric. In addition, the results achieved by applying the proposed metric on the blurred subsets of LIVE, TID2008 and CSIQ databases have also been quite satisfactory, showing a high correlation with the human perception of quality. The proposed metric has also been compared with other state-of-the-art blurriness metrics, standing among the best, specially have the first rank for the LIVE database.