1 Introduction

As demand for mobile data increases, Internet service providers (ISPs) are turning to new types of smart data pricing to bring in additional revenue and to expand the capacity of their current network [1]. One way to keep up funding such investment is content sponsorship. Content providers (CPs) split the cost of transferring mobile data traffic, and sponsor the user’s access to the content by making direct payment to the ISPs. For example, GS Shop, a Korea TV home shopping company, has partnered with SK Telecom to sponsor data incurred from its application, so consumers are incentivized to continue browsing and making purchases from their mobile devices without ringing up data charges [2]. Content sponsoring may benefit all players in the market: the ISPs can generate more revenue with CP’s subsidies, and users can enjoy free or low-cost access to certain services, which in turn increases the demand and attracts more traffic, resulting in higher revenue of the CP.

There are several studies on content sponsoring despite of a short history. Most of the works either focus on a simple model with a single ISP and a single CP interacting in a game theoretic setting, or considers Quality-of-Service (QoS) prioritization and its implications for net neutrality [3,4,5,6]. In a two-sided market with a single ISP providing connection between CPs and EUs, profit maximization of the players under sponsoring mobile data has been studied in [7, 8]. In [7], single monopolistic ISP determines optimal price to charge the CPs and the EUs, while the authors in [8] study the contractual relationship between the CPs and the ISP under a similar model. Nevertheless, none of them consider the interaction between multiple ISPs. Although the authors in [9] proposes a model with a transit ISP and a user-facing ISP, their understanding of the interaction between these non-cooperative ISPs are limited to the environments without content sponsoring. Other works, e.g. [10,11,12], have analyzed content sponsorship from the economic point of view. They examine the implications of sponsored data on the CPs and the EUs, and identify how sponsored data influence the CP inequality.

In many Internet markets, there are multiple ISPs that cooperate to provide end-to-end connectivity service between the CPs and the EUs, in which case the assumption of a single representative ISP no longer holds. Since each ISP aims to maximize its own profit, the establishment of interconnection among multiple ISPs is a thorough process that depends on specific profit sharing/inter-charging arrangements.

As the most commercial traffic originates from the CPs and terminates at the EUs, some ISPs positioned on the middle of the traffic delivery chain will have more power and request a transit-price. An ISP serving a large population of users might have a dominant influence in determining the transit price paid by other relatively weak ISPs for traffic delivery. For an example, a large entertainment company Netflix directly uses the service provided by ISPs such as Level 3, which is connected with residential broadband ISPs like Comcast to get access to the customers [13]. Level 3 charges Netflix and Comcast charges the users. Netflix may partially or fully sponsor its traffic, which is likely to increase the amount of traffic through both ISPs. Due to high traffic volume, the access ISP (Comcast) may require additional transit price for traffic delivery, which will impact on the pricing decision at Level 3 and subsequently on the sponsoring decision at Netflix. In this work, we are interested in the dynamics between the players with focus on content sponsoring and transit pricing. To this end, we study the interplay among two Internet Service Providers (ISPs), Content Provider (CP), and End User (EU), where each player selfishly maximizes its own profit. We model this non-cooperative interaction between ISP1, ISP2, CP, and EU as a four-stage Stackelberg game. We aim to understand the behaviors of the players in non-cooperative equilibrium and their decisions to maximize their own utility. Also we investigate the responses of the players when the ISPs cooperate with each other. We show that, under collaboration with appropriate revenue sharing, each ISP can achieve a higher revenue while improving the social welfare.

The rest of the paper is organized as follows. We present the basic system model in Section 2, and investigate the strategies of the CP, the EU, and the ISPs to maximize their utility in Section 3. We also study the effect of collaboration and build our revenue sharing model based on Shapley value mechanism in Sections 4 and 5, respectively. Numerical results are presented in Section 6, followed by the conclusion and future work in Section 7.

2 Two-ISP Pricing Model

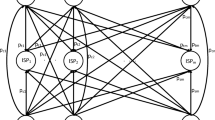
We consider an Internet market model with one CP and two ISPs as shown in Fig. 1. Two interconnected ISPs have their own cost structures and each provides connectivity to either the CP or the EU. The CP-facing ISP (ISP1) obtains its profits by directly charging the CP (CP) by pcp per unit traffic while the EU-facing ISP (ISP2) charges the EU (EU) by peu per unit traffic. Further ISP2 charges ISP1 with transit-price ptr for traffic delivery. CP can sponsor the cost of EU by s ⋅ peu per unit traffic with s ∈ [0,1]. We assume that the sponsored amount is paid to ISP1 and then indirectly delivered to ISP2 through the transit price, which allows both ISPs to benefit from the sponsoring. Let m1 and m2 denote the marginal costs of traffic delivery for ISP1 and ISP2, respectively. We denote x as the traffic amount of flow between CP and EU.

Fig. 1
figure 1

Two-sided Internet market

Full size image

We assume that the players in this non-cooperative game make decisions in four stages as follows:

  1. 1.

    ISP2 sets prices peu and ptr to charge EU and ISP1, respectively.

  2. 2.

    ISP1 determines the optimal value of pcp to charge CP.

  3. 3.

    CP decides how much content to sponsor, i.e., the value of s.

  4. 4.

    The traffic volume is decided by both EU and CP.

Each player selfishly maximizes its own profit subject to the others’ decisions. We model this non-cooperative interaction as a four-stage Stackelberg game. In game theory, a Stackelberg competition is a sequential game in which the leader moves first and then the follower makes its move [14, 15]. Specifically, in our model, we assume that the EU-facing ISP (residential ISP) has a dominant power and can be considered as the game leader, who decides the transit cost preceding the choice of the CP-facing ISP (transit ISP). The Stackelberg model can be solved to find the subgame perfect Nash equilibrium or equilibria (SPNE), i.e. the strategy profile that serves best each player, given the strategies of the other players, and that entails every player playing in a Nash equilibrium in every subgame. The objective of the game is to find the equilibrium point, from which neither the leaders nor the followers have incentives to deviate [14,15,16]. By modeling the problem as a four-stage Stackelberg game, we can find each subgame perfect equilibrium using the backward induction method with the optimal strategy of each player.

Let us define the utility of EU by the multiplication of a scaling factor σeu ≥ 0 and a utility-level function. The utility represents user’s desire to obtain traffic, and has been widely adopted in resource allocation problems to capture the property of decreasing marginal satisfaction [17,18,19,20]. In this work, we assume a concave and non-decreasing utility function \(u_{eu}(x) = \frac {x^{1-\alpha _{eu}}}{1-\alpha _{eu}}\) with parameter αeu ∈ (0,1). Given unit price peu that ISP2 charges user, EU will maximize its utility minus the payment by solving

$$\begin{array}{@{}rcl@{}} \pmb{(EU-P)} && \underset{x}{\max} \quad \sigma_{eu}\cdot u_{eu}(x) - (1-s)\cdot x\cdot p_{eu}, \\ & &s.t. \quad x\geq 0, \end{array} $$
(1)

where s ∈ [0,1] denotes the sponsored percentage, and (1 − s) ⋅ x ⋅ peu denotes the payment of EU to ISP2. The solution \( x_{eu}^{*}\) to Eq. 1 can be obtained as \( x_{eu}^{*}(s, p_{eu}) = (\frac {\sigma _{eu}}{(1-s)p_{eu}})^{\frac {1}{\alpha _{eu}}}\).

Similarly, we model the behavior of CP. The utility of CP is given by σcpucp(x), where σcp ≥ 0 is a scaling factor (e.g., the popularity of the content) and ucp(x) is a concave utility-level function \( u_{cp}(x) = \frac {x^{1-\alpha _{cp}}}{1-\alpha _{cp}}\) with parameter αcp ∈ (0,1). CP will maximize its payoff by solving

$$\begin{array}{@{}rcl@{}} \pmb{(CP-P)} \quad && \underset{x, s}{\max} \quad \sigma_{cp}\cdot u_{cp}(x) - s\cdot x\cdot p_{eu} - x\cdot p_{cp}, \\ & &s.t. \quad x\geq 0 \quad and \quad 0\leq s \leq 1. \end{array} $$
(2)

In the objective, the first term denotes its utility, the second term denotes the cost due to sponsorship, and the third term is from the network usage cost to ISP1. Given s, pcp, and peu, it can be easily shown that the optimal amount of traffic for CP is \( x_{cp}^{*}(s, p_{cp}, p_{eu}) = (\frac {\sigma _{cp}}{sp_{eu} + p_{cp}})^{\frac {1}{\alpha _{cp}}}\).

Since ISP1 obtains its revenue from charging CP, it decides the optimal value of pcp to maximize its total profit as

$$\begin{array}{@{}rcl@{}} \pmb{(ISP1 - P)} \quad && \underset{p_{cp}}{\max} \enspace (p_{cp} + s^{*}\cdot p_{eu} - p_{tr} - m_{1}) \cdot x^{*}(p_{cp}, p_{eu}), \\ && s.t. \quad \quad p_{cp} \geq 0, \end{array} $$
(3)

where m1 is the marginal costFootnote 1 for traffic delivery and thus pcp + s∗⋅ peu − ptr − m1 is the net-gain of ISP1 per unit traffic.

ISP2 obtains its revenue from charging ISP1 with transit-price ptr and charging EU with traffic-price peu. Therefore, in order to maximize its total profit, it will solve

$$\begin{array}{@{}rcl@{}} \pmb{(ISP2 - P)} \quad && \underset{p_{eu}, p_{tr}}{\max} \enspace ((1 - s^{*})\cdot p_{eu} + p_{tr} - m_{2}) \cdot x^{*}(p_{cp}, p_{eu}), \\ & &s.t. \quad p_{eu}\geq 0 \quad and \quad p_{tr} \geq 0, \end{array} $$
(4)

where m2 is the marginal cost for traffic delivery.

Through the sequential decision, we investigate the interactions of the players described in Eqs. 1, 2, 3, and 4, and find the optimal strategies for pricing and sponsoring.

3 Strategies for Utility Maximization

In this section, we sequentially find the optimal strategies of CP, ISP1, and ISP2 by exploiting the backward induction.

3.1 Sponsoring of Content Provider (CP)

Note that each solution to Eqs. 1 and 2 results in user-side traffic demand \(x^{*}_{eu}\) and CP-side traffic amount \(x^{*}_{cp}\), respectively, and the actual traffic amount x∗ between CP and EU will be determined by their minimum, i.e., \(x^{*} = min\{x^{*}_{cp},x^{*}_{eu}\}\). In general \(x^{*}_{eu} \neq x^{*}_{cp}\). For instance, a certain website may restrict the number of simultaneous on-line clients, which implies \(x^{*}_{cp} \leq x^{*}_{eu}\).

Suppose that peu and pcp are given. The actual traffic x∗(s) will be determined by the sponsoring rate s, and CP will decide its optimal sponsored percentage s∗ by solving the following problem:

$$\begin{array}{@{}rcl@{}} \pmb{(CP - P)} \quad && \underset{s}{\max} \quad \sigma_{cp}\cdot u_{cp}(x^{*}(s)) - s\cdot x^{*}(s)\cdot p_{eu} - x^{*}(s)\cdot p_{cp}, \\ & &s.t. \quad 0\leq s \leq 1. \end{array} $$
(5)

We assume αeu = αcp = α ∈ (0,1), i.e., EU and CP utility components have the same utility shape. This assumption is reasonable in the scenarios where CP makes its pricing decision according to the user response. On the other hand, the scaling factors σeu and σcp of EU and CP can be quite different. The sponsoring behavior will be affected by whether the traffic volume is constrained by EU or CP. If \(x_{eu}^{*} \leq x_{cp}^{*}\), we have \(s \leq \frac {\sigma _{cp}p_{eu} - \sigma _{eu}p_{cp}}{(\sigma _{eu} + \sigma _{cp})p_{eu}}\) and \(x^{*} = x_{eu}^{*}\). Similarly, if \(x_{eu}^{*} \geq x_{cp}^{*}\), we have \(s \geq max\left (\frac {\sigma _{cp}p_{eu} - \sigma _{eu}p_{cp}}{(\sigma _{eu} + \sigma _{cp})p_{eu}}, 0 \right )\) and \(x^{*} = x_{cp}^{*}\). We consider each case.

Case i):

When \(x^{*} = x_{cp}^{*}\). The profit of the CP can be written as

$$ V(s)=\sigma_{cp}\cdot u_{cp}(x_{cp}^{*}(s)) - s\cdot x_{cp}^{*}(s)\cdot p_{eu} - x_{cp}^{*}(s)\cdot p_{cp}. $$
(6)

By substituting \( x_{cp}^{*}(s, p_{cp}, p_{eu}) = \left (\frac {\sigma _{cp}}{sp_{eu} + p_{cp}}\right )^{\frac {1}{\alpha }}\) into Eq. 6, it can be easily shown that V (s) is a decreasing function of s, and we have the optimal value \(s^{*} = max(\frac {\sigma _{cp}p_{eu} - \sigma _{eu}p_{cp}}{(\sigma _{eu} + \sigma _{cp})p_{eu}}, 0 )\). Thus, the traffic amount and the sponsoring rate will be

$$ (x^{*}_{cp},s^{*}) = \left\{\begin{array}{lllllll} \left( \left( \frac{\sigma_{cp}}{p_{cp}}\right)^{\frac{1}{\alpha}},\quad 0\right), & if \enspace \frac{\sigma_{cp}}{\sigma_{eu}} \leq \frac{p_{cp}}{p_{eu}},\\ \left( \left( \frac{\sigma_{cp} + \sigma_{eu}}{p_{cp} + p_{eu}}\right)^{\frac{1}{\alpha}}, \quad \frac{\sigma_{cp}p_{eu} - \sigma_{eu}p_{cp}}{(\sigma_{eu} + \sigma_{cp})p_{eu}}\right), & if \enspace \frac{\sigma_{cp}}{\sigma_{eu}} > \frac{p_{cp}}{p_{eu}}. \end{array}\right. $$
(7)

The maximum profit of CP is given as

$$ V^{*}(x_{cp}^{*}, s^{*}) = \left\{\begin{array}{llllllll} \frac{\alpha(\sigma_{cp})^{\frac{1}{\alpha}}}{1-\alpha}(p_{cp})^{1 - \frac{1}{\alpha}}, & if \quad \frac{\sigma_{cp}}{\sigma_{eu}} \leq \frac{p_{cp}}{p_{eu}},\\ \frac{\alpha\sigma_{cp}}{1-\alpha}\left( \frac{p_{eu} + p_{cp}}{\sigma_{eu} + \sigma_{cp}}\right)^{1 - \frac{1}{\alpha}}, & if \quad \frac{\sigma_{cp}}{\sigma_{eu}} > \frac{p_{cp}}{p_{eu}}. \end{array}\right. $$
(8)
Case ii):

When \(x^{*} = x_{eu}^{*}\). In this case, we have \(s \leq \frac {\sigma _{cp}p_{eu} - \sigma _{eu}p_{cp}}{(\sigma _{eu} + \sigma _{cp})p_{eu}}\), \( x_{eu}^{*}(s, p_{eu}) = \left (\frac {\sigma _{eu}}{(1-s)p_{eu}}\right )^{\frac {1}{\alpha }}\) and \(\frac {\sigma _{cp}}{\sigma _{eu}} > \frac {p_{cp}}{p_{eu}}\). CP will optimize its sponsorship percentage by solving

$$\begin{array}{@{}rcl@{}} max \quad & \textstyle \frac{\sigma_{cp}\left( \frac{\sigma_{eu}}{p_{eu}}\right)^{\frac{1}{\alpha} -1}}{1-\alpha}(1-s)^{1 - \frac{1}{\alpha}} - \frac{(sp_{eu} + p_{cp})(\frac{\sigma_{eu}}{p_{eu}})^{\frac{1}{\alpha}}}{(1-s)^{\frac{1}{\alpha}}}, \\ & \textstyle s.t. \quad 0 \leq s \leq \frac{\sigma_{cp}p_{eu} - \sigma_{eu}p_{cp}}{(\sigma_{eu} + \sigma_{cp})p_{eu}} , \quad \frac{\sigma_{cp}}{\sigma_{eu}} > \frac{p_{cp}}{p_{eu}}. \end{array} $$
(9)

From the first order condition, the optimal data rate x∗ and the optimal sponsoring rate s∗ can be obtained as

$$ \small (x^{*}_{eu},s^{*}) = \left\{\begin{array}{lllllll} \displaystyle \left( \left( \frac{\sigma_{eu}}{p_{eu}}\right)^{\frac{1}{\alpha}}, 0\right), & \textit{if} \frac{p_{cp}}{p_{eu}} \!<\! \frac{\sigma_{cp}}{\sigma_{eu}} \leq \alpha + \frac{p_{cp}}{p_{eu}},\\ \left( \left( \frac{\sigma_{cp} + (1-\alpha)\sigma_{eu}}{p_{cp} + p_{eu}}\right)^{\frac{1}{\alpha}}, \frac{\frac{\sigma_{cp}}{\sigma_{eu}} - \alpha - \frac{p_{cp}}{p_{eu}}}{\frac{\sigma_{cp}}{\sigma_{eu}} + 1 - \alpha}\right), &\textit{if} \frac{\sigma_{cp}}{\sigma_{eu}} \!>\! \alpha + \frac{p_{cp}}{p_{eu}}, \end{array}\right. $$
(10)

and the maximum profit of CP is

$$ \small V^{*}(x^{*}_{eu},s^{*}) = \left\{\begin{array}{lllllll} \left( \frac{\sigma_{eu}}{p_{eu}}\right)^{\frac{1}{\alpha}}\left[ \frac{\sigma_{cp}p_{eu}}{(1-\alpha)\sigma_{eu}} - p_{cp}\right] & \textit{if} \scriptsize \enspace \frac{p_{cp}}{p_{eu}} \!\!<\!\! \frac{\sigma_{cp}}{\sigma_{eu}} \!\leq\! \alpha + \frac{p_{cp}}{p_{eu}},\\ \\ \frac{\alpha(p_{cp}+p_{eu})}{1-\alpha}\left( \frac{\sigma_{cp} + (1-\alpha)\sigma_{eu}}{p_{cp} + p_{eu}}\right)^{\frac{1}{\alpha}} & \textit{if} \scriptsize \enspace \frac{\sigma_{cp}}{\sigma_{eu}} \!>\! \alpha + \frac{p_{cp}}{p_{eu}}. \end{array}\right. $$
(11)

From the two-case response of CP, we can obtain the following Proposition.

Proposition 1

Given prices p c p and p e u , the optimal sponsorship rate s ∗ of the CP is

$$ \begin{array} {ll} \text{case 1) if}~~ \frac{\sigma_{cp}}{\sigma_{eu}} \leq \frac{p_{cp}}{p_{eu}}, &~~s^{*} = 0,\\ \text{case 2) if}~~ \frac{p_{cp}}{p_{eu}} < \frac{\sigma_{cp}}{\sigma_{eu}} \leq \alpha + \frac{p_{cp}}{p_{eu}}, &~~s^{*} = 0,\\ \text{case 3) if}~~ \frac{\sigma_{cp}}{\sigma_{eu}} > \alpha + \frac{p_{cp}}{p_{eu}}, &~~s^{*} = \frac{\frac{\sigma_{cp}}{\sigma_{eu}} - \alpha - \frac{p_{cp}}{p_{eu}}}{\frac{\sigma_{cp}}{\sigma_{eu}} + 1 - \alpha}. \end{array} $$
(12)

Proof

For case 1, the maximum available profit of CP can be easily obtained as \(V^{*}(x_{cp}^{*}, s^{*}) = \frac {\alpha (\sigma _{cp})^{\frac {1}{\alpha }}}{1-\alpha }(p_{cp})^{1 - \frac {1}{\alpha }}\) from Eq. 8.

For \(\frac {\sigma _{cp}}{\sigma _{eu}} > \frac {p_{cp}}{p_{eu}}\), the CP will choose the largest one among available profits of \(V^{*}(x_{cp}^{*}, s^{*})\) and \(V^{*}(x_{eu}^{*}, s^{*})\), given in Eqs. 8 and 11, respectively. Let \(\sigma = \frac {\sigma _{cp}}{\sigma _{eu}}\) and \(p =\frac {p_{cp}}{p_{eu}}\). We decompose it into two subcases as below.

  1. 1)

    When p < σ ≤ α + p, each profit function can be written as

    $$\begin{array}{llllll} V^{*}(x_{cp}^{*}, s^{*}) &\textstyle =\frac{(\sigma_{eu})^{\frac{1}{\alpha}}(p_{eu})^{1-\frac{1}{\alpha}}}{(1-\alpha)}(\frac{1 + p}{1 + \sigma})(\frac{1 + p}{1 + \sigma})^{-\frac{1}{\alpha}} \alpha \sigma, \\ V^{*}(x^{*}_{eu},s^{*}) &=\textstyle \frac{(\sigma_{eu})^{\frac{1}{\alpha}}(p_{eu})^{1-\frac{1}{\alpha}}}{(1-\alpha)}(\sigma - (1-\alpha)p). \end{array} $$

    Consider the ratio \(\frac {V^{*}(x_{eu}^{*}, s^{*})}{V^{*}(x^{*}_{cp},s^{*})}\). By using the generalized form of Bernoulli’s inequality (1 + x)r ≥ 1 + rx for r ≤ 0 or r ≥ 1 and x > − 1, we can obtain

    $$\begin{array}{llllllll} \textstyle \frac{V^{*}(x_{eu}^{*}, s^{*})}{V^{*}(x^{*}_{cp},s^{*})} &\textstyle \geq (\sigma - (1-\alpha)p)(\frac{1 + \sigma}{1 + p})(1 + \frac{p-\sigma}{(1+\sigma)\alpha}) \frac{1}{\alpha \sigma} \\ &\textstyle \geq 1 + \frac{(1-\alpha)(\sigma - p)(p +\alpha - \sigma)}{\sigma \alpha^{2}(1+p)}. \end{array} $$

    Hence, if p < σ ≤ α + p, we have \(\frac {V^{*}(x_{eu}^{*}, s^{*})}{V^{*}(x^{*}_{cp},s^{*})} \geq 1\), implying \(x^{*} = x^{*}_{eu}\) and s∗ = 0 from Eq. 10.

  2. 2)

    When σ > α + p, we have

    $$\begin{array}{llllll} V^{*}(x_{cp}^{*}, s^{*}) &\textstyle = (\frac{\alpha}{1-\alpha})(p_{eu} + p_{cp})^{1-\frac{1}{\alpha}} (\sigma_{eu})^{\frac{1}{\alpha}}(\sigma)(1 + \sigma)^{\frac{1}{\alpha} -1},\\ V^{*}(x^{*}_{eu},s^{*}) &\textstyle = (\frac{\alpha}{1-\alpha})(p_{eu} + p_{cp})^{1-\frac{1}{\alpha}} (\sigma_{eu})^{\frac{1}{\alpha}}(1 + \sigma - \alpha)^{\frac{1}{\alpha}}. \end{array} $$

    Again we consider the ratio \(\frac {V^{*}(x^{*}_{eu},s^{*})}{V^{*}(x_{cp}^{*}, s^{*})} = \frac {1 +\sigma }{\sigma }(1 - \frac {\alpha }{1 + \sigma })^{\frac {1}{\alpha }}\). Applying the generalized form of Bernoulli’s inequality, we have \(\frac {V^{*}(x^{*}_{eu},s^{*})}{V^{*}(x_{cp}^{*}, s^{*})}\geq \frac {1 + \sigma }{\sigma } \left (1 - \frac {1}{1 + \sigma }\right ) = 1\), and thus we have \(x^{*}=x^{*}_{eu}\) and \(s^{*} = \frac {\frac {\sigma _{cp}}{\sigma _{eu}} - \alpha - \frac {p_{cp}}{p_{eu}}}{\frac {\sigma _{cp}}{\sigma _{eu}} + 1 - \alpha }\) from Eq. 10.

□

According to Proposition 1, CP has no incentive to invest in sponsored data plan when \(\frac {\sigma _{cp}}{\sigma _{eu}} \leq \alpha + \frac {p_{cp}}{p_{eu}}\). On the other hand, when \(\frac {\sigma _{cp}}{\sigma _{eu}} > \alpha + \frac {p_{cp}}{p_{eu}}\), CP will invest in sponsoring as in Eq. 10. The data rate under sponsoring will be

$$ \begin{array} {l} \textit{case 1) if}~ \frac{\sigma_{cp}}{\sigma_{eu}} \leq \frac{p_{cp}}{p_{eu}}, ~~~~~~~~~~~x^{*}(p_{cp}, p_{eu}) = \left( \frac{\sigma_{cp}}{p_{cp}}\right)^{\frac{1}{\alpha}},\\ \textit{case 2) if}~ \frac{p_{cp}}{p_{eu}} \!<\! \frac{\sigma_{cp}}{\sigma_{eu}} \!\leq\! \alpha + \frac{p_{cp}}{p_{eu}}, ~~x^{*}(p_{cp}, p_{eu}) = \left( \frac{\sigma_{eu}}{p_{eu}}\right)^{\frac{1}{\alpha}},\\ \textit{case 3) if}~ \frac{\sigma_{cp}}{\sigma_{eu}} \!>\! \alpha + \frac{p_{cp}}{p_{eu}}, ~~~~x^{*}(p_{cp}, p_{eu}) = \left( \frac{\sigma_{cp} + (1-\alpha)\sigma_{eu}}{p_{cp} + p_{eu}}\right)^{\frac{1}{\alpha}}. \end{array} $$
(13)

3.2 Utility Maximization of I S P 1

ISP1 also tries to maximize its total profit in each region specified in Eq. 13. We obtain the optimal response of ISP1 in each case.

Case 1):

When \(x^{*} =\left (\frac {\sigma _{cp}}{p_{cp}}\right )^{\frac {1}{\alpha }}\) and s∗ = 0. From Eq. 3, ISP1 maximizes \((p_{cp} - p_{tr} - m_{1})\cdot \left (\frac {\sigma _{cp}}{p_{cp}}\right )^{\frac {1}{\alpha }}\) subject to \(\frac {\sigma _{cp}}{\sigma _{eu}}\cdot p_{eu} \leq p_{cp}\). The best response \(p_{cp}^{*}\) of ISP1 can be easily obtained as \( p^{*}_{cp} = \frac {p_{tr} + m_{1}}{1- \alpha }\). The maximum profit \(P^{*}_{1}\) is

$$\textstyle P^{*}_{1} = \left[\frac{\alpha(m_{1} + m_{2})}{(1-\alpha)}\cdot \frac{\sigma}{1+\sigma(1-\alpha)}\right] \cdot \left( \frac{\sigma_{cp}(1-\alpha)(1 + \sigma(1-\alpha))}{\sigma(m_{1} + m_{2})}\right)^{\frac{1}{\alpha}}, $$

where \(\sigma =\frac {\sigma _{cp}}{\sigma _{eu}}\).

Case 2):

When \(x^{*} =\left (\frac {\sigma _{eu}}{p_{eu}}\right )^{\frac {1}{\alpha }}\) and s∗ = 0. From Eq. 3, ISP1 has the objective of \(\underset {p_{cp} \geq 0}{\max } \quad (p_{cp} - p_{tr} - m_{1})\cdot \left (\frac {\sigma _{eu}}{p_{eu}}\right )^{\frac {1}{\alpha }}\) subject to \(\frac {p_{cp}}{p_{eu}} - \frac {\sigma _{cp}}{\sigma _{eu}} \leq 0\) and \(\frac {\sigma _{cp}}{\sigma _{eu}} - \alpha - \frac {p_{cp}}{p_{eu}} \leq 0\). From the constraints, we have \(p_{cp} \in \left [\left (\frac {\sigma _{cp}}{\sigma _{eu}} - \alpha \right )p_{eu}, \frac {\sigma _{cp}}{\sigma _{eu}}p_{eu}\right ]\). Note that since the objective is an increasing function of pcp, we set the largest \(p_{cp}=\frac {\sigma _{cp}}{\sigma _{eu}}\cdot p_{eu}\) for the optimal solution, which gives us maximum utility \(P^{*}_{1} = \left (\frac {\sigma _{cp}}{\sigma _{eu}}\cdot p_{eu} - p_{tr} - m_{1}\right )\cdot \left (\frac {\sigma _{eu}}{p_{eu}}\right )^{\frac {1}{\alpha }}\). By differentiating it with respect to peu, we can find \(p_{eu}^{*}=\frac {\sigma _{eu}}{\sigma _{cp}}\cdot \left (\frac {p_{tr} + m_{1}}{1- \alpha }\right )\) that maximizes \(P^{*}_{1}\), which results in the optimal \( p^{*}_{cp} = \frac {p_{tr} + m_{1}}{1- \alpha }\). The maximum profit is

$$\textstyle P^{*}_{1} = \left[\frac{\alpha(m_{1} + m_{2})}{(1-\alpha)} \cdot \frac{\sigma}{1+\sigma(1-\alpha)}\right] \cdot \left( \frac{\sigma_{eu}(1-\alpha)(1 + \sigma(1-\alpha))}{(m_{1} + m_{2})}\right)^{\frac{1}{\alpha}}. $$
Case 3):

When \(x^{*} = \left (\frac {\sigma _{cp} + (1-\alpha )\sigma _{eu}}{p_{cp} + p_{eu}}\right )^{\frac {1}{\alpha }}\) and \(s^{*} = \frac {\frac {\sigma _{cp}}{\sigma _{eu}} - \alpha - \frac {p_{cp}}{p_{eu}}}{\frac {\sigma _{cp}}{\sigma _{eu}} + 1 - \alpha }\). The problem can be rewritten as \(\underset {p_{cp}\geq 0}{\max } (p_{cp} + s^{*}p_{eu} - p_{tr} - m_{1})\cdot \left (\frac {\sigma _{cp} + (1-\alpha )\sigma _{eu}}{p_{cp} + p_{eu}}\right )^{\frac {1}{\alpha }}\), subject to \(p_{cp} \leq \left (\frac {\sigma _{cp}}{\sigma _{eu}} - \alpha \right )p_{eu}\). From the first order condition, we can obtain the optimal price \(p^{*}_{cp} = \frac {(k + 1)(p_{tr} + m_{1})}{k(1- \alpha )} - p_{eu}\), where \(k=\frac {\sigma _{cp}}{\sigma _{eu}} - \alpha \). The maximum profit is

$$\textstyle P^{*}_{1} = \alpha\left( \frac{m_{1} + m_{2}}{1-\alpha}\right)^{1-\frac{1}{\alpha}} \cdot (\sigma_{cp} + (1-\alpha)\sigma_{eu})^{\frac{1}{\alpha}} \cdot\left (\frac{1 + k(1-\alpha)}{1+k}\right)^{\frac{1}{\alpha}} \cdot \frac{k}{1 + k(1-\alpha)}. $$

3.3 Utility Maximization of I S P 2

For the behaviors of ISP2, we also consider the three cases of Eq. 13 and find the best strategy of ISP2 for each case.

Case 1) :

When \(x^{*}(p^{*}_{cp}, p_{eu})=\left (\frac {\sigma _{cp}}{p^{*}_{cp}}\right )^{\frac {1}{\alpha }}\) and s∗ = 0. We already have \(p^{*}_{cp} = \frac {p_{tr} + m_{1}}{1- \alpha }\). From Eqs. 4 and 13, the ISP2 determines its prices peu and ptr by solving \(\underset {p_{eu}\geq 0, p_{tr} \geq 0}{\max } ((1- s^{*})\cdot p_{eu} + p_{tr} - m_{2})\cdot \left (\frac {\sigma _{cp}}{p^{*}_{cp}}\right )^{\frac {1}{\alpha }}\), subject to \(\frac {\sigma _{cp}}{\sigma _{eu}} - \frac {p^{*}_{cp}}{p_{eu}} \leq 0\).

Let P denote the objective function. From the Karush-Kuhn-Tucker (KKT) conditions, we have \(\frac {\partial P}{\partial p_{eu}} = 0\), \(\frac {\partial P}{\partial p_{tr}} = 0\), and \(\lambda \cdot \left [\frac {\sigma _{cp}}{\sigma _{eu}} - \frac {p^{*}_{cp}}{p_{eu}}\right ]= 0\). By solving these equations, we have the optimal prices

$$\textstyle p^{*}_{eu}= \frac{(m_{1} + m_{2})}{(1-\alpha)(1 + (k + \alpha)(1 - \alpha))} \enspace and \enspace p_{tr}^{*}=\frac{(k + \alpha)(m_{1} + m_{2})}{(1 + (k + \alpha)(1 - \alpha))} - m_{1}, $$

at which the maximum profit \(P^{*}_{2}\) is

$$\textstyle P^{*}_{2} = \left[\frac{\alpha(m_{1} + m_{2})}{(1-\alpha)}\right]\left( \frac{\sigma_{cp}(1-\alpha)(1 + (k+\alpha)(1-\alpha))}{(k+\alpha)(m_{1} + m_{2})}\right)^{\frac{1}{\alpha}}, $$

where \(k = \frac {\sigma _{cp}}{\sigma _{eu}} - \alpha \).

Case 2) :

When \(x^{*}(p^{*}_{cp}, p_{eu}) =(\frac {\sigma _{eu}}{p_{eu}})^{\frac {1}{\alpha }}\) and s∗ = 0. In this case, we have \(p^{*}_{cp} = \frac {p_{tr} + m_{1}}{1- \alpha }\). From Eqs. 4 and 13, the ISP2 determines its prices by solving \(\underset {p_{eu}\geq 0, p_{tr} \geq 0}{\max } \quad ((1-s^{*})\cdot p_{eu} + p_{tr} - m_{2})\cdot (\frac {\sigma _{eu}}{p_{eu}})^{\frac {1}{\alpha }}\), subject to \(\frac {p^{*}_{cp}}{p_{eu}} - \frac {\sigma _{cp}}{\sigma _{eu}} \leq 0\) and \(\frac {\sigma _{cp}}{\sigma _{eu}} - \alpha - \frac {p^{*}_{cp}}{p_{eu}} \leq 0\).

From the KKT conditions, we have \(\frac {\partial P}{\partial p_{eu}} = 0\), \(\frac {\partial P}{\partial p_{tr} }= 0\), \(\lambda _{1}\cdot \left (\frac {p^{*}_{cp}}{p_{eu}} - \frac {\sigma _{cp}}{\sigma _{eu}}\right ) = 0\) and \( \lambda _{2}\cdot \left (\frac {\sigma _{cp}}{\sigma _{eu}} - \alpha - \frac {p^{*}_{cp}}{p_{eu}}\right )= 0\), where λi ≥ 0, pcp ≥ 0, and peu ≥ 0. There are three possible subcases: i) λ1 = 0, λ2≠ 0, ii) λ1≠ 0, λ2 = 0, iii) λ1 = 0 and λ2 = 0. The solution to each subcase can be obtained as follows.

  1. i)

    When λ1 = 0 and λ2≠ 0, the optimal prices will be

    $$\textstyle p_{eu}^{*}=\frac{m_{1} + m_{2}}{(1-\alpha)(1 + k(1-\alpha))} \enspace and \enspace p_{tr}^{*} = \frac{k(m_{1} + m_{2})}{1 + k(1-\alpha)} - m_{1}, $$

    where \(k = \frac {\sigma _{cp}}{\sigma _{eu}} - \alpha \), and we have the maximum profit

    $$\textstyle P^{*}_{\lambda_{1}} =\left[ \frac{\alpha(m_{1} + m_{2})}{(1- \alpha)}\right]\left( \frac{(\sigma_{cp} - \sigma_{eu}\alpha)(1 - \alpha)^{2} + \sigma_{eu}(1- \alpha)}{m_{1} + m_{2}}\right)^{\frac{1}{\alpha}}. $$
  2. ii)

    When λ1≠ 0 and λ2 = 0, the optimal prices will be

    $$\textstyle p^{*}_{eu}= \frac{(m_{1} + m_{2})}{(1-\alpha)(1 + (k + \alpha)(1 - \alpha))} \enspace and \enspace p_{tr}^{*}=\frac{(k + \alpha)(m_{1} + m_{2})}{(1 + (k + \alpha)(1 - \alpha))} - m_{1}, $$

    and the maximum profit

    $$\textstyle P^{*}_{\lambda_{2}} =\frac{\alpha(m_{1} + m_{2})}{(1- \alpha)}\left( \frac{\sigma_{cp}(1 - \alpha)^{2} + \sigma_{eu}(1- \alpha)}{m_{1} + m_{2}}\right)^{\frac{1}{\alpha}}. $$
  3. iii)

    When λ1 = 0 and λ2 = 0, the two inequality constraints should be an active constraint (i.e., the equalities hold). However, it is not possible to satisfy both equalities, and hence, this case is infeasible.

From \(P^{*}_{\lambda _{2}} > P^{*}_{\lambda _{1}}\), we should have λ2 = 0 and the best response of the ISP2 is that of ii), which also equals the result of Case 1.

Case 3) :

In this case, we have the optimal sponsoring rate \(s^{*} = \frac {\frac {\sigma _{cp}}{\sigma _{eu}} - \alpha - \frac {p_{cp}}{p_{eu}}}{\frac {\sigma _{cp}}{\sigma _{eu}} + 1 - \alpha }\) and the traffic demand is \(x^{*}(p^{*}_{cp}, p_{eu}) =\left (\frac {\sigma _{cp} + (1-\alpha )\sigma _{eu}}{p_{cp} + p_{eu}}\right )^{\frac {1}{\alpha }}\). As shown in Section 3.2, the best-response \(p^{*}_{cp}\) of ISP1 is \(\frac {(k + 1)(p_{tr} + m_{1})}{k(1- \alpha )} - p_{eu}\). From Eqs. 4 and 13, ISP2 determines its prices by solving \(\underset {p_{eu}\geq 0, p_{tr} \geq 0}{\max } ((1-s^{*})\cdot p_{eu} + p_{tr} - m_{2}) \cdot \left (\frac {\sigma _{cp} + (1-\alpha )\sigma _{eu}}{p^{*}_{cp} + p_{eu}}\right )^{\frac {1}{\alpha }}\), subject to \(\frac {p^{*}_{cp}}{p_{eu}} + \alpha - \frac {\sigma _{cp}}{\sigma _{eu}} \leq 0\).

From the KKT conditions, we have \(\frac {\partial P}{\partial p_{eu}}= 0\), \(\frac {\partial P}{\partial p_{tr}}= 0\), and \( \lambda \cdot [\frac {p^{*}_{cp}}{p_{eu}} + \alpha - \frac {\sigma _{cp}}{\sigma _{eu}}] = 0\). By solving the equations, we can obtain without difficulty that

$$\textstyle p_{eu}^{*}= \frac{(m_{1} + m_{2})}{(1-\alpha)(1 + k(1- \alpha))}\enspace and \enspace p_{tr}^{*} = \frac{k(m_{1} + m_{2})}{(1 + k(1- \alpha))} - m_{1}. $$

The maximum profit \(P^{*}_{2}\) will be

$$\textstyle P^{*}_{2} = \alpha\left( \frac{m_{1} + m_{2}}{1-\alpha}\right)^{1-\frac{1}{\alpha}}(\sigma_{cp} + (1-\alpha)\sigma_{eu})^{\frac{1}{\alpha}}\left( \frac{1 + k(1-\alpha)}{1+k}\right)^{\frac{1}{\alpha}}. $$

We have shown the optimal responses of the EU, the CP, and two ISPs in a non-cooperative equilibrium. The results show the sponsoring rate s∗ and the pricing of \(p^{*}_{cp}\), \(p^{*}_{eu}\), and \(p^{*}_{tr}\) when each player maximizes its own utility in a greedy manner. We further investigate the players’ behaviors when the two ISPs cooperate.

4 Cooperative Model

In this section, we study the effect of collaboration to the pricing structure and the traffic demand between CP and EU, and analyze their implications for the total payoff of ISPs. Instead of maximizing their own profit, the two ISPs can make an agreement to cooperate in order to achieve a higher total profit [15, 16]. The total profit can be obtained as the total revenue of the two ISPs minus their marginal cost for traffic delivery. Since the transit cost simply moves some profit from one ISP to the other, we can ignore it in calculation of the total profit. Full collaboration allows them to make decisions on pcp and peu to maximize the total profit, which makes them behave as if one single ISP. A good example of such cooperation is the agreement between Verizon, a residential broadband ISP with a large user population, and Cogent, a transit ISP, in 2015 [21, 22]. They have made a peering agreement to improve the quality of interconnection without any bilateral payments.

In our model, when ISP1 and ISP2 collaborate to deliver traffic from CP to EU, we can consider them as one ISP who obtains its revenue from charging CP by pcp and EU by peu. The two ISPs are in peering with no transit-cost: neither party pays the other in association with the exchange of traffic. Instead, they need to fairly redistribute the total revenue according to their marginal contributions. We will use Shapley value mechanism for this purpose.

We first obtain the total revenue of the ISPs. The utility maximization of the ISPs can be written as

$$\begin{array}{@{}rcl@{}} \pmb{(ISP-P)} \quad & \underset{p_{cp}, p_{eu}}{\max} \quad (p_{cp} + p_{eu} - m_{1} - m_{2}) \cdot x^{*}(p_{cp}, p_{eu}), \\ & s.t. \quad \quad p_{cp} \geq 0 \enspace and \enspace p_{eu} \geq 0. \end{array} $$
(14)

Given unit price peu that ISP charges user, EU will maximize its utility minus the payment by solving

$$\begin{array}{@{}rcl@{}} \pmb{(EU-P)} \quad & \underset{x}{\max} \quad \sigma_{eu}\cdot u_{eu}(x) - (1-s)\cdot x\cdot p_{eu}, \\ & s.t. \quad x\geq 0, \end{array} $$
(15)

where s ∈ [0,1] denotes the sponsored percentage, and (1 − s) ⋅ x ⋅ peu denotes the payment of EU to ISP. The solution \( x_{eu}^{*}\) to Eq. 2 can be obtained as \( x_{eu}^{*}(s, p_{eu}) = \left (\frac {\sigma _{eu}}{(1-s)p_{eu}}\right )^{\frac {1}{\alpha _{eu}}}\). Similarly, CP will maximize its payoff by solving

$$\begin{array}{@{}rcl@{}} \pmb{(CP-P)} \quad & \underset{x, s}{\max} \quad \sigma_{cp}\cdot u_{cp}(x) - s\cdot x\cdot p_{eu} - x\cdot p_{cp}, \\ & s.t. \quad x\geq 0 \quad and \quad 0\leq s \leq 1, \end{array} $$
(16)

where the first term denotes its utility, the second term denotes the cost due to sponsorship, and the third term is from the network usage cost to ISP. Given s, pcp, and peu, it can be easily shown that the optimal amount of traffic for CP is \( x_{cp}^{*}(s, p_{cp}, p_{eu}) = (\frac {\sigma _{cp}}{sp_{eu} + p_{cp}})^{\frac {1}{\alpha _{cp}}}\).

Since the actual traffic amount x∗ between CP and EU will be determined by their minimum, i.e., \(x^{*} = min\{x^{*}_{cp},x^{*}_{eu}\}\), we can obtain the optimal sponsorship rate s∗ and the data rate under sponsoring by considering three cases as before. We omit the detailed derivation and provide the result as

$$ \begin{array}{llllllll} &(x^{*}, s^{*}) = \\ &\left\{\begin{array} {l} \left( \left( \frac{\sigma_{cp}}{p_{cp}}\right)^{\frac{1}{\alpha}}, 0\right), ~~~~~~\textit{if}~~ \frac{\sigma_{cp}}{\sigma_{eu}} \leq \frac{p_{cp}}{p_{eu}},\\ \left( \left( \frac{\sigma_{eu}}{p_{eu}}\right)^{\frac{1}{\alpha}}, 0\right), ~~~~~~\textit{if}~~ \frac{p_{cp}}{p_{eu}} < \frac{\sigma_{cp}}{\sigma_{eu}} \leq \alpha + \frac{p_{cp}}{p_{eu}},\\ \left( \left( \frac{\sigma_{cp} + (1-\alpha)\sigma_{eu}}{p_{cp} + p_{eu}}\right)^{\frac{1}{\alpha}}, \frac{\frac{\sigma_{cp}}{\sigma_{eu}} - \alpha - \frac{p_{cp}}{p_{eu}}}{\frac{\sigma_{cp}}{\sigma_{eu}} + 1 - \alpha}\right), ~~\textit{if}~~ \frac{\sigma_{cp}}{\sigma_{eu}} > \alpha + \frac{p_{cp}}{p_{eu}}. \end{array}\right. \end{array} $$
(17)

ISPs cooperate and try to maximize their total profit in each region specified in Eq. 17. We obtain the optimal response of ISPs in each case.

Case 1) :

When \(x^{*}(p_{cp}, p_{eu})=\left (\frac {\sigma _{cp}}{p_{cp}}\right )^{\frac {1}{\alpha }}\) and s∗ = 0. From Eqs. 14 and 17, the coalition-ISP determines its prices peu and pcp by maximizing \((p_{cp} + p_{eu} - m_{1} - m_{2})\cdot \left (\frac {\sigma _{cp}}{p_{cp}}\right )^{\frac {1}{\alpha }}\), subject to \(\frac {\sigma _{cp}}{\sigma _{eu}} - \frac {p_{cp}}{p_{eu}} \leq 0\), peu ≥ 0, and pcp ≥ 0.

Let P denote the objective function. From the Karush-Kuhn-Tucker (KKT) conditions, we have \(\frac {\partial P}{\partial p_{eu}} = 0\), \(\frac {\partial P}{\partial p_{cp}} = 0\), and \(\lambda \cdot \left [\frac {\sigma _{cp}}{\sigma _{eu}} - \frac {p_{cp}}{p_{eu}}\right ]= 0\). By solving these equations, it is not difficulty to obtain the optimal prices of

$$ \textstyle p^{**}_{eu}= \frac{\sigma_{eu}(m_{1} + m_{2})}{(1-\alpha)(\sigma_{cp} + \sigma_{eu})} \quad and \quad p_{cp}^{**}=\frac{\sigma_{cp}(m_{1} + m_{2})}{(1-\alpha)(\sigma_{cp} + \sigma_{eu})} , $$
(18)

at which the maximum profit P∗∗ equals

$$\textstyle P^{**} = \alpha\left( \frac{m_{1} + m_{2}}{1-\alpha}\right)^{1-\frac{1}{\alpha}}(\sigma_{cp} + \sigma_{eu})^{\frac{1}{\alpha}}. $$
Case 2) :

When \(x^{*}(p_{cp}, p_{eu}) =(\frac {\sigma _{eu}}{p_{eu}})^{\frac {1}{\alpha }}\) and s∗ = 0. From Eqs. 14 and 17, the coalition-ISP determines its prices by solving \(\underset {p_{eu}\geq 0, p_{cp} \geq 0}{\max } (p_{cp} + p_{eu} - m_{1} - m_{2})\cdot \left (\frac {\sigma _{eu}}{p_{eu}}\right )^{\frac {1}{\alpha }}\), subject to \(\frac {p_{cp}}{p_{eu}} \leq \frac {\sigma _{cp}}{\sigma _{eu}} \leq \alpha + \frac {p_{cp}}{p_{eu}}\).

From the KKT conditions, we have \(\frac {\partial P}{\partial p_{eu}} = 0\), \(\frac {\partial P}{\partial p_{cp} }= 0\), \(\lambda _{1}\cdot \left (\frac {p_{cp}}{p_{eu}} - \frac {\sigma _{cp}}{\sigma _{eu}}\right ) = 0\) and \( \lambda _{2}\cdot \left (\frac {\sigma _{cp}}{\sigma _{eu}} - \alpha - \frac {p_{cp}}{p_{eu}}\right )= 0\), where λi ≥ 0, pcp ≥ 0, and peu ≥ 0. There are four possible subcases: i) λ1 = 0, λ2≠ 0, ii) λ1≠ 0, λ2 = 0, iii) λ1 = 0 and λ2 = 0, iv) λ1≠ 0 and λ2≠ 0.

  1. i)

    When λ1 = 0 and λ2≠ 0, the optimal prices will be

    $$\textstyle p_{eu}^{**}=\frac{m_{1} + m_{2}}{(1-\alpha)(1+k)} \quad and \quad p_{cp}^{**} = \frac{k(m_{1} + m_{2})}{(1-\alpha)(1+k)}, $$

    where \(k = \frac {\sigma _{cp}}{\sigma _{eu}} - \alpha \), and we have the maximum profit

    $$\textstyle P^{**}_{\lambda_{1}} =\alpha(\frac{m_{1} + m_{2}}{1-\alpha})^{1-\frac{1}{\alpha}}(\sigma_{cp} + (1-\alpha)\sigma_{eu})^{\frac{1}{\alpha}}. $$
  2. ii)

    When λ1≠ 0 and λ2 = 0, the optimal prices will be

    $$ \textstyle p^{**}_{eu}= \frac{\sigma_{eu}(m_{1} + m_{2})}{(1-\alpha)(\sigma_{cp} + \sigma_{eu})} \quad and \quad p_{cp}^{**}=\frac{\sigma_{cp}(m_{1} + m_{2})}{(1-\alpha)(\sigma_{cp} + \sigma_{eu})} , $$
    (19)

    and the maximum profit \(P^{**}_{\lambda _{2}}=\alpha (\frac {m_{1} + m_{2}}{1-\alpha })^{1-\frac {1}{\alpha }}(\sigma _{cp} + \sigma _{eu})^{\frac {1}{\alpha }}\).

  3. iii)

    When λ1 = 0 and λ2 = 0, the two inequality constraints of \(\frac {p_{cp}}{p_{eu}} \leq \frac {\sigma _{cp}}{\sigma _{eu}} \leq \alpha + \frac {p_{cp}}{p_{eu}}\) should be an active constraint (i.e., the equalities hold). However, it is not possible to satisfy both equalities, and hence, it is infeasible.

  4. iv)

    Similarly, when λ1≠ 0 and λ2≠ 0, we cannot find a feasible solution for any α > 0.

From \(P^{**}_{\lambda _{2}} > P^{**}_{\lambda _{1}}\), we should have λ2 = 0 and the best response of the ISPs is Eq. 19, which is exactly the same as in Eq. 18.

Case 3) :

In this case, we have the optimal sponsoring rate \(s^{*} = \frac {\frac {\sigma _{cp}}{\sigma _{eu}} - \alpha - \frac {p_{cp}}{p_{eu}}}{\frac {\sigma _{cp}}{\sigma _{eu}} + 1 - \alpha }\) and the traffic demand is \(x^{*}(p_{cp}, p_{eu}) =\left (\frac {\sigma _{cp} + (1-\alpha )\sigma _{eu}}{p_{cp} + p_{eu}}\right )^{\frac {1}{\alpha }}\). From Eqs. 14 and 17, ISPs determine their prices by solving \(\underset {p_{eu}\geq 0, p_{cp} \geq 0}{\max } (p_{cp} + p_{eu} - m_{1} - m_{2}) \cdot \left (\frac {\sigma _{cp} + (1-\alpha )\sigma _{eu}}{p_{cp} + p_{eu}}\right )^{\frac {1}{\alpha }}\), subject to \(\frac {p_{cp}}{p_{eu}} + \alpha - \frac {\sigma _{cp}}{\sigma _{eu}} \leq 0\). From the KKT conditions, we have \(\frac {\partial P}{\partial p_{eu}}= 0\), \(\frac {\partial P}{\partial p_{cp}}= 0\), and \( \lambda \cdot [\frac {p_{cp}}{p_{eu}} + \alpha - \frac {\sigma _{cp}}{\sigma _{eu}}] = 0\). By solving the equations, we can obtain without difficulty that

$$\textstyle p^{**}_{eu}= \frac{(m_{1} + m_{2})}{(1-\alpha)(k + 1)} \quad and \quad p_{cp}^{**}=\frac{k(m_{1} + m_{2})}{(1-\alpha)(k + 1)}, $$

where \(k=\frac {\sigma _{cp}}{\sigma _{eu}} - \alpha \), with the maximum profit as

$$\textstyle P^{**} = \alpha(\frac{m_{1} + m_{2}}{1-\alpha})^{1-\frac{1}{\alpha}}(\sigma_{cp} + (1-\alpha)\sigma_{eu})^{\frac{1}{\alpha}}. $$

Comparing the results with those in non-cooperative scenarios, we can obtain the following proposition.

Proposition 2

The ISPs obtain higher total payoff when they collaborate.

$$ P^{**} \geq P^{*}_{T}, $$
(20)

where \(P^{*}_{T}\) denotes the total profit in non-cooperative case, i.e., \(P^{*}_{T} = P^{*}_{1} + P^{*}_{2}\).

Proof

We consider each case as before.

For Case 1. From our previous results for non-cooperative game, we know that the maximum profits of ISP1 and ISP2 are \(\left [\frac {\alpha (m_{1} + m_{2})}{(1-\alpha )}\cdot \frac {\sigma }{1+\sigma (1-\alpha )}\right ] \left (\frac {\sigma _{cp}(1-\alpha )(1 + \sigma (1-\alpha ))}{\sigma (m_{1} + m_{2})}\right )^{\frac {1}{\alpha }}\) and \( \left [\frac {\alpha (m_{1} + m_{2})}{(1-\alpha )}\right ] \cdot \left (\frac {\sigma _{cp}(1-\alpha )(1 + \sigma (1-\alpha ))}{\sigma (m_{1} + m_{2})}\right )^{\frac {1}{\alpha }}\), respectively, where \(\sigma =\frac {\sigma _{cp}}{\sigma _{eu}}\). Hence, the total profit is

$$\textstyle P^{*}_{T} = \left[\frac{\alpha(m_{1} + m_{2})}{(1-\alpha)}\cdot \frac{1 + \sigma + \sigma(1-\alpha)}{1+\sigma(1-\alpha)}\right] \left( \frac{\sigma_{cp}(1-\alpha)(1 + \sigma(1-\alpha))}{\sigma(m_{1} + m_{2})}\right)^{\frac{1}{\alpha}}. $$

We can rewrite the total profits of ISPs for each non-cooperative and cooperative case as

$$\begin{array}{lllllll} P^{*}_{T} &\textstyle = \alpha(\frac{m_{1} + m_{2}}{1-\alpha})^{1-\frac{1}{\alpha}}(\sigma_{eu})^{\frac{1}{\alpha}}(1 + \sigma(1-\alpha))^{\frac{1}{\alpha}}\left( \frac{1 + \sigma + \sigma(1-\alpha)}{1 + \sigma(1-\alpha)}\right),\\ P^{**} &\textstyle =\alpha(\frac{m_{1} + m_{2}}{1-\alpha})^{1-\frac{1}{\alpha}}(\sigma_{eu})^{\frac{1}{\alpha}}(1 + \sigma)^{\frac{1}{\alpha}}. \end{array} $$

Considering the ratio \(\frac {P^{**}}{P^{*}_{T}}= \left (\frac {1+\sigma }{1+\sigma -\alpha \sigma }\right )^{\frac {1}{\alpha }}\left (\frac {1 + \sigma - \alpha \sigma }{1 + \sigma + \sigma -\alpha \sigma }\right )\) and applying the generalized form of Bernoulli’s inequality, we obtain

$$\textstyle \frac{P^{**}}{P^{*}_{T}} \geq \left( 1 + \frac{\sigma}{1 + \sigma -\alpha\sigma}\right)\left( \frac{1 + \sigma - \alpha\sigma}{1 + \sigma + \sigma -\alpha\sigma}\right) = 1, $$

which immediately implies \(P^{**} \geq P^{*}_{T}\).

For Case 2, we have the same total profits \(P^{*}_{T}\) and P∗∗ as in Case 1. Thus, we have \(P^{**} \geq P^{*}_{T}\).

For Case 3, from Sections 3.2 and 3.3, The total profits in non-cooperative and cooperative cases can be written as

$$\begin{array}{lllllllll} P^{*}_{T} &\textstyle = \alpha\left( \frac{m_{1} + m_{2}}{1-\alpha}\right)^{1-\frac{1}{\alpha}}(\sigma_{cp} + (1-\alpha)\sigma_{eu})^{\frac{1}{\alpha}}\left( \frac{1 + k(1-\alpha)}{1 + k}\right)^{\frac{1}{\alpha}}\frac{k + 1 + k(1-\alpha)}{1 + k(1-\alpha)},\\ P^{**} &\textstyle =\alpha\left( \frac{m_{1} + m_{2}}{1-\alpha}\right)^{1-\frac{1}{\alpha}}(\sigma_{cp} + (1-\alpha)\sigma_{eu})^{\frac{1}{\alpha}}, \end{array} $$

where \(k=\frac {\sigma _{cp}}{\sigma _{eu}} - \alpha \) and \(\sigma =\frac {\sigma _{cp}}{\sigma _{eu}}\). Again we apply Bernoulli’s inequality to \(\frac {P^{**}}{P^{*}_{T}}=\left (\frac {1 + k}{1 + k(1-\alpha )}\right )^{\frac {1}{\alpha }}\frac {1 + k(1-\alpha )}{k + 1 + k(1-\alpha )}\), and obtain

$$\begin{array}{llllllllll} \textstyle \frac{P^{**}}{P^{*}_{T}} &\textstyle \geq \left( 1 + \frac{k}{1 + k(1-\alpha)}\right) \cdot \frac{1 + k(1-\alpha)}{k + 1 + k(1-\alpha)} = 1. \end{array} $$

This completes the proof, and in all three cases, ISPs obtain a higher total payoff when they collaborate. □

5 Shapley Revenue Distribution

One remaining task under the collaboration is how to distribute the payoff P∗∗ to each ISP. To this end, we exploit the Shapley value mechanism. It is often adopted to solve the problem of n-person cooperative game, and it is an approach to allocate resources according to the contribution of each member in alliance, while improving the alliance initiative of the members [23]. It has the desirable properties of efficiency, symmetry, and linearity, and has been widely used in the literature to implement a profit-sharing mechanism and to analyze the cooperative interactions among the players [15, 24, 25].

We consider a network that consists of a set of ISPs denoted as \(\mathbb {N}\) with \(N = |\mathbb {N}|\). Any nonempty subset \(\mathbb {S}\subseteq \mathbb {N}\) is a coalition of ISPs. For any coalition \(\mathbb {S}, P(\mathbb {S})\) denotes the profit (i.e., revenue minus cost) generated by the sub-network formed by the set of ISPs \(\mathbb {S}\). We define the marginal contribution of ISPi to a coalition \(\mathbb {S}\subseteq \mathbb {N}\setminus \{i\}\) as \(\triangle _{i}(\mathbb {S}) = P(\mathbb {S} \cup \{i\}) - P(\mathbb {S})\). The Shapley value ϕ is defined by

$$ \phi_{i} = \frac{1}{N!} \sum\limits_{\pi \in {\Pi}} \triangle_{i}(\mathbb{S}(\pi, i)) \quad \forall i \in N, $$
(21)

where π is the set of all N! orderings of \(\mathbb {N}\) and \(\mathbb {S}(\pi ,i)\) is the set of players preceding i in the ordering π [25, 26]. The Shapley value depends only on the values \(\{P(\mathbb {S}):\mathbb {S} \subseteq \mathbb {N}\}\) and satisfies desirable efficiency and fairness properties [27]. Revenue sharing model based on the Shapley value belongs to a cooperation-based game theory, and the mechanism has a capacity to divide the revenue fairly between the involved parties [27, 28].

In our model, we have \(\mathbb {N} = \{1,2\}\), and ISP1 and ISP2 receive their Shapley value, which can be obtained as

$$ \begin{array}{llllllll} \textstyle \phi_{1} = \frac{1}{2}P(\{1\}) + \frac{1}{2}[ P(\{1, 2\}) - P(\{2\})],\\ \textstyle \phi_{2} = \frac{1}{2}P(\{2\}) + \frac{1}{2}[ P(\{1, 2\}) - P(\{1\})], \end{array} $$
(22)

where P({1,2}) = ϕ1 + ϕ2 is the total profit under collaboration, and \(P(\{1\}) = P^{*}_{1}\) and \(P(\{2\}) = P^{*}_{2}\) are the profit of ISP1 and ISP2 in non-cooperative case, respectively.

Recall that letting \(A=\alpha \left (\frac {m_{1} + m_{2}}{1-\alpha }\right )^{1-\frac {1}{\alpha }}(\sigma _{eu})^{\frac {1}{\alpha }}\), \(\sigma =\frac {\sigma _{cp}}{\sigma _{eu}}\) and \(k=\frac {\sigma _{cp}}{\sigma _{eu}} - \alpha \), we have

$$ \begin{array} {l l} \textit{if}~~ \frac{\sigma_{cp}}{\sigma_{eu}} \leq \alpha + \frac{p_{cp}}{p_{eu}}, &~P^{*}_{1}=A(1 + \sigma(1-\alpha))^{\frac{1}{\alpha}}\left( \frac{\sigma}{1 + \sigma(1-\alpha)}\right),\\ &~P^{*}_{2}=A(1 + \sigma(1-\alpha))^{\frac{1}{\alpha}},\\ \textit{if}~~ \frac{\sigma_{cp}}{\sigma_{eu}} > \alpha + \frac{p_{cp}}{p_{eu}}, &~P^{*}_{1}=A(1 + k(1-\alpha))^{\frac{1}{\alpha}}\left( \frac{k}{1 + k(1-\alpha)}\right),\\ &~P^{*}_{2}=A(1 + k(1-\alpha))^{\frac{1}{\alpha}}. \end{array} $$
(23)

From the results in Section 4, we can also obtain the total payoff P({1,2}) under cooperation as

$$ \begin{array} {ll} \textit{if}~ &\frac{\sigma_{cp}}{\sigma_{eu}} \leq \alpha + \frac{p_{cp}}{p_{eu}}, ~~~~\textit{(Cases 1 \& 2)}\\ &P(\{1, 2\})=\alpha\left( \frac{m_{1} + m_{2}}{1-\alpha}\right)^{1-\frac{1}{\alpha}}(\sigma_{eu})^{\frac{1}{\alpha}}(1 + \sigma)^{\frac{1}{\alpha}},\\ \textit{if}~ &\frac{\sigma_{cp}}{\sigma_{eu}} > \alpha + \frac{p_{cp}}{p_{eu}}, ~~~~\textit{(Case 3)} \\ &P(\{1, 2\})=\alpha\left( \frac{m_{1} + m_{2}}{1-\alpha}\right)^{1-\frac{1}{\alpha}}(\sigma_{cp} + (1-\alpha)\sigma_{eu})^{\frac{1}{\alpha}}. \end{array} $$
(24)

Plugging (23) and (24) into (22), we can compute the Shapley values ϕ1 and ϕ2.

The following proposition shows that the collaboration with revenue sharing of Shapley mechanism improves the profit of each ISP.

Proposition 3

The revenue sharing mechanism assures that an I S P i ’s revenue portion at least equals to the revenue gained without collaboration, i.e.

$$ \phi_{i} \geq P(\{i\}) $$
(25)

Proposition 3 states that for all regions specified in Eq. 17, we have ϕi ≥ P({i}), i.e., each ISP’s revenue in cooperative case exceeds the revenue gained without collaboration. We omit the proof and refer to our technical report [29].

6 Numerical Simulations

We verify our analytical results through numerical simulations. We consider one CP, one EU, and two ISPs as shown in Fig. 1, and assume that CP and the EU share the same utility-level function αeu = αcp = α ∈ (0,1). Figure 2a shows that, if \(\sigma (= \frac {\sigma _{cp}}{\sigma _{eu}}) > \alpha + p (=\frac {p_{cp}}{p_{eu}})\), CP has the maximum profit at σ = 0.4 and thus has incentive to invest in sponsored data plan. It implies that when CP has a higher utility level than EU (or similarly, when the price charged to CP is relatively lower than the price charged to EU), CP is willing to provide a higher sponsorship rate. In contrast, when σ ≤ α + p, the maximum payoff is achieved at s∗ = 0, i.e., the best strategy of CP is not sponsoring.

Next we observe the payoff of ISP2 as we change the price per unit traffic peu that charges to EU. Figure 2b illustrates the results and show that the payoff of ISP2 linearly rises till some point, and then declines exponentially, which is due to the fact that the demand of users is inversely proportional to peu. Although ISP2 obtains its revenue from charging ISP1 with transit-price ptr, the results show that increasing the ptr does not necessarily increase the payoff of ISP2. As the transit price becomes higher, CP is forced to increase pcp which in turn results in a decline of the traffic demand. Hence, the maximum point is achieved at ptr = 1 and peu = 2.

Fig. 2
figure 2

Payoff changes of CP and ISP2 when α = 0.5

Full size image

We examine the impact of ISP prices (pcp, peu, and ptr) and σ on the optimal sponsoring rate with different parameter sets. Figure 3a shows that as pcp increases, the sponsoring rate drops sharply. The decreasing rate can be mitigated with higher σ. Figure 3b shows that with the increase of peu, the marginal increase of the sponsoring rate is decreasing. Moreover, a larger σ value indicates a higher and rapidly growing sponsorship rate. Figure 3c demonstrates the change of the optimal sponsoring rate with respect to σ under different α values. The sponsorship rate logarithmically increases as σ increases. It can be explained from the fact that CP with higher revenue level can afford more investment on the sponsoring content. We can also observe that the variation in α has a little impact on the traffic demand. Figure 3d will help us to understand the effect of the transit cost ptr to the optimal sponsoring rate s∗. We can observe that the increase of the transit cost results in a sharp drop of s∗. The rise of transit cost will incur significant loss in ISP1’s revenue, which forces ISP1 to increase its charge to CP, resulting in a rapid drop of the sponsoring rate.

Fig. 3
figure 3

The optimal sponsoring rate with respect to pcp, peu, σ, and ptr

Full size image

We now observe the total payoff of ISPs in cooperative and non-cooperative cases. Figure 4a illustrates the results and show that the ISPs obtain higher total payoff when they collaborate. We also examine the impact of collaboration on the individual payoff of ISP1 and ISP2. Figure 4b and c shows that each ISP’s revenue portion in cooperative case increases sharply and highly exceeds the revenue gained without collaboration.

Fig. 4
figure 4

Payoff changes of ISP1 and ISP2 when α = 0.5

Full size image

7 Conclusion

In this work, we studied the inter-pricing among ISPs that jointly deliver the sponsored data from CP to EU. We derived the best response of the EU, the CP, and the ISPs, and analyzed their implications for the sponsoring strategy of the CP. We investigate the interactions between strategic EU, CP, and two interconnected ISPs through a sequential Stackelberg game, and verify our results through numerical simulations. Our results clarify the high impact of the transit price of intermediate ISP on the sponsoring strategies of the CP, and demonstrate in what scenarios sponsoring helps. We then study the effect of cooperation between the ISPs and show that the collaboration can improve the total payoff of the ISPs and leads to a higher social welfare. Based on the Shapley value mechanism, we further show that each ISP’s revenue portion in cooperative case exceeds the revenue gained without collaboration. In our future work, we will consider the network with multiple ISPs for the service to the EU or the CP which may result in competition between the ISPs and change the system dynamics.