Introduction

The phenomena associated with a long-term deformation of materials are called, in a broad sense, a creep, which manifests itself, in particular, in the growth of strains at constant stress (true “creep” in the narrow sense), in the decrease of stresses with time at a fixed strain (relaxation), as well as the attenuation of vibrations and phase shift during vibration tests. All these outwardly different phenomena are controlled by the same rheological properties of materials, so the adequacy of the constitutive equations proposed is checked by the possibility of describing these different phenomena by a single set of material parameters.

Among a wide class of traditional and modern models of viscoelasticity, a special place is occupied by hereditary creep theories based on the integral operators with difference kernels [1,2,3,4]. Precisely a “flexibility” of the hereditary creep theory equations enables to apply it to the most diverse classes of materials and phenomena.

The study of the creep of polymer composite materials is becoming an obligatory stage in the design of loadbearing composite structures.

Traditionally, the experimental determination of creep curves at a constant load is considered as the simplest and most correct approach, since the load is applied by a “dead weight”, and the strain is determined directly on the specimen. The relaxation test requires, it would seem, a simpler equipment, but fixing a specimen strain, we are forced to measure the stress (force) using a dynamometer included in the load circuit, and the change of its strain with decreasing force does not allow us to strictly maintain the condition of constant strain of the specimen. Meanwhile, the standard creep tests are the long-time ones and require periodic strain measurements over several days or months.

Therefore, the capability check of estimating the creep parameters based on the phase shift between cyclically changing stresses and strains is of considerable interest [5,6,7,8,9].

The objective of this work is to analyze the difficulties associated with the description of creep based on short-term vibration tests (dynamic mechanical analysis — DMA), and to substantiate the requirements for the required scope and accuracy of experimental data.

Relationship of the Dynamic Characteristics of a Material and Creep

The possibility to relate the frequency dependences of the complex modulus components to the creep parameters was considered as early as the middle of the last century [1,2,3, 5,6,7,8]. The implementation of some methods (Prony series, etc.) is considered in [10,11,12,13]. Similar results can be obtained using traditional models of viscoelastic bodies, however, in this work, a hereditary model of linear viscoelasticity is used.

It should be noted that we consider only one-dimensional, isothermal processes without taking into account anisotropy and temperature effects, and assume that the material is not subject to aging. Within the framework of these restrictions, the corresponding integral equations [1,2,3] are used to describe the processes of creep and relaxation:

$$ \varepsilon (t){\varepsilon}_0\left(1+{K}^{\ast}\right), $$
(1)
$$ \sigma (t)={\sigma}_0\left(1-{R}^{\ast}\right), $$
(2)

where \( {\varepsilon}_0=\frac{\sigma_0}{E} \) is the instantaneous elastic strain; σ0 is the instantaneous stress; E is the Young modulus.

The creep K* and relaxation R* integral operators are defined as follows:

$$ {K}^{\ast }u=\int_{-\infty}^tK\left(t-\tau \right)u\left(\tau \right) d\tau; {R}^{\ast }v=\int_{-\infty}^tR\left(t-\tau \right)v\left(\tau \right) d\tau, $$

where K(t − τ) and R(t − τ) are the creep and relaxation kernel, respectively; t − τ > 0.

Since the viscoelastic properties of polymer composites also appear during forced vibrations (with a frequency ω), the Eqs. (1) and (2) (taking into account the limitations above-described) can be applied to the harmonic law of strain change:

$$ \varepsilon ={\varepsilon}_0\exp i\omega t. $$
(3)

The originating stress will lag at the phase angle δ of mechanical losses:

$$ \sigma ={\sigma}_0\exp \left[i\left(\omega t+\delta \right)\right]. $$
(4)

The additive term in (4) can be neglected for a sufficiently long test time. Formally, the constant term vanishes when the lower limit of −∞ is used in the integral operators.

Substitution of the expressions (3) and (4) into the relation describing the relaxation process (2) allows us to obtain the relation between the frequency dependence of the complex modulus components and the relaxation kernel:

$$ E^{\prime}\left(\omega \right)=E\left(1-{R}_C\right), $$
(5)
$$ E^{{\prime\prime}}\left(\omega \right)={ER}_S, $$
(6)

where \( {R}_C=\int_0^{\infty }R(z)\cos \omega zdz\kern0.75em {R}_S=\int_0^{\infty }R(z)\sin \omega zdz. \)

Compliance components are determined similarly when using the creep equation (1).

Thus, the creep and relaxation kernels are, in principle, restored on the basis of the frequency dependences of the viscoelastic characteristics of the material. In this case, the relaxation kernel is determined using the inverse Fourier integrals:

$$ R(t)=\frac{2}{\pi}\int_0^{\infty}\left(\frac{E^{\prime}\left(\omega \right)}{E}-1\right)\cos\ \omega td\omega, $$
(7)
$$ R(t)=\frac{2}{\pi}\int_0^{\infty}\left(\frac{E^{{\prime\prime}}\left(\omega \right)}{E}\right)\sin\ \omega td\omega . $$
(8)

The method of restoring the creep kernel from the relaxation kernel is a separate problem and is not considered in this work. The procedures, briefly written by Eqs. (1)—(8), are described in the classical literature [1—3]. There are few examples of practical description of the relaxation processes of structural materials according to the dependences of the complex modulus components on frequency [12, 13].

We consider such technique as simple and promising one, if it could correctly describe a creep without long-term quasi-static tests. However, it is obvious that the initial dependences E ′ (ω)and E ″ (ω) for the implementation of this technique have to meet certain strict requirements, which imposes restrictions on its application area.

Requirements for the Asymptotics of the Frequency Dependence of the Complex Modulus of the Material

Let us consider the values taken by the complex modulus components a viscoelastic material under dynamic loading (DMA) by forced harmonic vibrations in a wide frequency range. The storage modulus E′ (the real part of the complex modulus) with a frequency decreasing tends to the static value of the long-term modulus \( {E}_0^{\prime }, \) which cannot be accurately determined either under monotonic loading or vibrations, since the strain rate has to be equal zero in this case. It is usually determined as a ratio of the stress to steady-state creep strain, if it is bounded by a horizontal asymptote. In the case of unlimited creep, the long-term modulus must be assumed to be zero. With an increase of the vibration frequency ω, the values E ′ (ω)increase, approaching the limit \( {E}_{\infty}^{\prime }, \) which is identical to the dynamic Young’s modulus E, since at high vibration frequencies, rheological effects practically do not appear. In principle, the dynamic Young’s modulus can be determined from the speed of propagation of the fastest dilatation wave, if one correctly assesses an influence of the Poisson effect during the wave evolution in the rod. The dynamic modulus is also determined in special high-speed tests at strain rates of the order of 102 s–1. It slightly (by 5-10%) exceeds the Young’s modulus, determined on the standard specimens at gripper speeds within those limits (2-10 mm/min), in which the effect of speed on the modulus is negligibly small. However, a direct estimation of the value \( {E}_{\infty}^{\prime } \) at ultrahigh vibration frequencies is associated with the problems of vibration heating, the effect of which is difficult to evaluate by calculation.

The dependence of the imaginary part of the complex modulus has the reverse view. At low frequencies, the loss modulus E″ is equal to the static value \( {E}_0^{{\prime\prime} }, \) and as the frequency increases, the rheological processes “do not have time” to manifest themselves, so its value decreases to the dynamic value \( {E}_{\infty}^{{\prime\prime} }, \) which is practically equal to zero. Formally, such dependences of the complex modulus components can be nonmonotonic, which does not contradict the thermodynamics and integrability of the corresponding functions, but for definiteness, based on the available experimental data, the monotonic tendency of the complex modulus components to asymptotic values at zero and at infinity is simply postulated.

Based on these conclusions, the following natural restrictions are introduced on the frequency dependence of the complex modulus components:

$$ \underset{\omega \to \infty }{\lim}\left(\frac{E^{\prime}\left(\omega \right)}{E_{\infty}^{\prime }}-1\right)=0, $$
(9)
$$ \underset{\omega \to \infty }{\lim}\left(\frac{E^{{\prime\prime}}\left(\omega \right)}{E_{\infty}^{{\prime\prime} }}\right)=0. $$
(10)

The experimental data corresponding to the constraints (9) and (10) not only agree with the “physics” of the process above-described, but also ensures integrability in the relations (7) and (8), since the inverse cosine and sine Fourier integrals possess the convergence criterion.

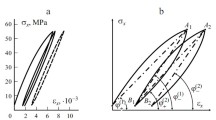
Unfortunately, in the available literature with regard to structural materials, very few experimental results meet the requirements above formulated. Published data [14] refer to soft polymers or rubber-like materials, the Young’s moduli of which are 2-3 orders of magnitude less those for glass- or carbon fiber-reinforced plastics (GFRPs and CFRPs). For structural polymer materials, the results of vibration tests have the form of a segment in a small frequency range without analyzing the asymptotics. An example of such a dependence is shown in Fig. 1.

Fig. 1
figure 1

Experimental dependence of the storage modulus E′ of CFRP vs. the frequency ω [16].

Full size image

Just such experimental data are presented in [10,11,12,13], and therefore, the techniques proposed there “bypass” the direct use of experiments in various ways. In this work, we place the emphasis on the required form of DMA results for the complex modulus components.

Approximation of Experimental Data

The real experimental data analysis leads to the conclusion that there are at least three fundamental reasons for the difficulties in using the dependences of the complex modulus components on the frequency of vibration loading.

Firstly, the static value of the long-term modulus cannot be directly experimentally determined (at zero strain rates), and its determining by extrapolating the results of vibration tests leads to a wide arbitrariness, providing a large scatter of the ultimate strain of limited creep.

Secondly, the asymptotic behavior at very high frequencies (at “infinite speeds”) is fundamentally important, but it is not possible to obtain such results on the existing vibration equipment, and the determination of the dynamic modulus from the wave speed or in high-speed tests is a separate experimental problem that requires fundamentally different equipment compared to DMA. Therefore, a reliable determination of the asymptotics of the complex modulus components at infinity is difficult.

Thirdly, it is extremely difficult to determine precisely the characteristic inflection point on the experimental dependence E ′ (ω), whereas the value of the corresponding frequency significantly affects the creep curve restored.

All these and similar difficulties are determined by the same problem. Approximation of the dependence E ′ (ω) within its entire limited frequency range turns out to be unstable: the experimental data can be described with the same accuracy by a completely different set of parameters of the mode l chosen.

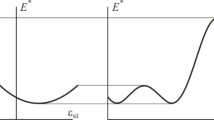
To approximate the frequency dependences, we propose to use sigmoid (S-shaped) curves, since they satisfy the requirements (9) and (10) and qualitatively reflect the features of dynamic processes.

The change of the storage modulus is proposed to approximate by the following relation:

$$ E^{\prime}\left(\omega \right)={E}_0^{\prime }+\left({E}_{\infty}^{\prime }-{E}_0^{\prime}\right)\frac{\omega^2}{\omega^2+{k}^2}. $$
(11)

The loss modulus dependence can be similarly approximated by the relation:

$$ E^{{\prime\prime}}\left(\omega \right)={E}_0^{{\prime\prime} }+\left({E}_{\infty}^{{\prime\prime} }-{E}_0^{{\prime\prime}}\right)\frac{\omega^2}{\omega^2+{k}^2}. $$
(12)

The parameters k and s of the Eqs. (11) and (12) are responsible for the character of the transition from static (long-term) values of the complex modulus components to dynamic ones. They are determined phenomenologically from the condition of the best fit with experiment, but, unfortunately, the distinct inflection points on the real frequency dependences are not observed.

The qualitative character of such dependences is shown in Fig. 2. In order to reliably estimate their parameters, it is necessary to obtain experimental data in a fairly wide frequency range. The test program for obtaining such dependences should be as follows: the vibration frequency varies in the range of several decimal orders, and the initial frequency values should be of the orders of 10–2-10–1, which is difficult to implement. The frequency has to be increased when its growth influences yet on the value of the modulus with the degree of ac curacy selected.

Fig. 2
figure 2

Characteristic forms of the frequency dependences of the storage modulus E′ (a solid line) and the loss modulus E″ (a dashed line) vs. the frequency ω .

Full size image

Restoring the Creep Function Based on the Approximation Proposed

To check the applicability of relations (11) and (12) for the description of the creep of polymer composites, based on the experimental dependence of the storage modulus of CFRP on frequency (see Fig. 1), we restored the kernel, function, and creep curves of the material at various values of parameters of the relation (11), describing the experiment.

The results obtained by the DMA method do not satisfy the above-mentioned requirements needed, and therefore, in order to test the technique, the experimental dependence obtained was finished constructing according to Eq. (11) based on the basic values of the parameters of the storage modulus dependence on the frequency: \( {E}_0^{\prime }=20\ \mathrm{GPa},{E}_{\infty}^{\prime }=180\ \mathrm{GPa},k=0.5\ \mathrm{rad}/\mathrm{s}. \)

The static value of the storage modulus (at zero frequency) cannot be determined experimentally, and it is estimated, in fact, by the ratio of the constant applied stress to the steady state strain of limited creep. The dynamic value of the storage modulus of unidirectional polymer composite material, which can be determined from the speed of the tension-compression wave or in high-speed tests, differs insignificantly (by 5-10%) from the value of Young's modulus determined in the standard tensile tests. The value of the parameter k, entering in expression (11), was chosen arbitrarily enough to obtain a qualitative agreement with the experiment. As a result, the problem of approximating and restoring the creep curves turned out to be unstable. The available limited set of experimental data can be described with the same accuracy by a completely different set of parameters of the approximating expression (11); the variants of its changing are presented in the Table 1.

Table 1 Variants of Variation of Parameters of Relation (11)
Full size table

Based on the finish constructing dependence that satisfies the asymptotic requirements, the creep kernel was restored, which for expression (11) has the form of an exponent:

$$ K\left(t-\tau \right)=C\ \exp \left[-a\left(t-\tau \right)\right], $$
(13)

where the constants of the exponential function C and a , as well as the modulus E are related to the parameters of expression (11) as follows:

$$ {E}_0^{\prime }=\frac{Ea}{a+C},{E}_{\infty}^{\prime }=E,k=a+C, $$

Then, based on kernel (13), expression (1) for the creep process at σ = const can be rewritten as

$$ \varepsilon (t)=\frac{1}{E}\left(\sigma -\sigma \left(\frac{C}{a}\left(\exp \left(- at\right)-1\right)\right)\right). $$
(14)

The creep curve of CFRP at a constant stress σ = 200 MPa, restored using expression (14) and the basic values of the parameters \( {E}_0^{\prime },{E}_{\infty}^{\prime }, \) and k, has a horizontal asymptote (Fig. 3) and describes a limited creep. However, the form of the initial stage of creep qualitatively agrees with the experimental curves. The creep curves calculated are presented only as an illustration of the technique applied, and the observed rapid achievement of ultimate strain is due to an arbitrary choice of parameters.

Fig. 3
figure 3

The restored creep curve ε (t) with difference kernel as an exponential function.

Full size image

To describe unlimited creep, one can use, for example, the Abel kernel [16]:

$$ K(t)=\frac{bt^{\alpha }}{\Gamma \left(1+\alpha \right)}, $$

where b and α are the parameters of Abel kernel; Γ(1 + α) is the Gamma function equaled to

$$ \Gamma (z)=\int_0^{\infty }{f}^{z-1}{e}^{-f} df. $$

For the Abel kernel, the form of the resolvent is known in the form of a fractional-exponential ∍α-function (R-function) of Rabotnov [1,2,3]:

$$ {\ni}_{\alpha}\left(\beta, t\right)={bt}^{\alpha}\sum \limits_{n=0}^{\infty}\frac{\beta^n{t}^{n\left(1+\alpha \right)}}{\Gamma \left[\left(n+1\right)\left(1+\alpha \right)\right]}. $$

Restoring of these type kernels using the inverse Fourier transform is a separate nontrivial problem that involves a different type of approximating relation like (11), and this procedure was not considered in this work. It should also be noted that the complication of the creep kernel will not allow one to bypass the main problem, namely, the complexity of the stable determination of parameters from a limited experiment.

Correctness of Restoring the Creep Curves

It is important to check how the restored creep curve is affected by changing the parameters (see Table 1) of the approximating expression (11). The long-term modulus \( {E}_0^{\prime } \) is responsible for the ultimate strain of the steady-state limited creep (Fig. 4). The dynamic modulus \( {E}_{\infty}^{\prime } \) determines the instantaneous elastic strain (Fig. 5). The possible values of the parameter k , which is responsible for the rate of transition from a static value to a dynamic one (Fig. 6), can only be guessed, since it is not possible to accurately determine this parameter from the available experimental data (see Fig. 1). All these three parameters, on the basis of which the creep curves are restored, are difficult to determine with any reliability from a limited set of experimentally obtained values \( {E}_i^{\prime}\left({\omega}_i\right). \)

Fig. 4
figure 4

The frequency dependence of the storage modulus E′ vs. log(ω) at various values of longterm modulus \( {E}_0^{\prime } \)(numbers at the curves in GPa). The dynamic modulus \( {E}_{\infty}^{\prime } \) and parameter k did not change.

Full size image
Fig. 5
figure 5

The frequency dependence of the storage modulus E′ vs. log(ω) at various values of dynamic modulus \( {E}_{\infty}^{\prime } \) (numbers at the curves in GPa). The long-term modulus \( {E}_0^{\prime } \) and parameter k did not change.

Full size image
Fig. 6
figure 6

The frequency dependence of the storage modulus E′ vs. log(ω) at various values of the parameter k (numbers at the curves in rad/s). The long-term \( {E}_0^{\prime } \) and dynamic \( {E}_{\infty}^{\prime } \) moduli did not change.

Full size image

Formally, one can choose three characteristic values of the storage modulus at different frequencies and, after substituting the values \( {E}_i^{\prime } \) and ωi in (11), from the three equations obtained, determine these three parameters. However, the resulting values of the parameters will significantly depend on the points selected. Another way is to use the methods of regression analysis (method of least squares) to determine the three parameters of the dependence (11) for any number of experimental points. However, the limited range of experimental frequencies does not allow one to provide reliably the required asymptotics at zero and at infinity.

Accounting for that the dynamic modulus \( {E}_{\infty}^{\prime } \) can be determined in an independent high-speed experiment, we can leave two unknown parameters \( {E}_0^{\prime } \) and k in relation (11), and reduce the relation (11) to a straight-line equation:

$$ {\displaystyle \begin{array}{c}\frac{E_{\infty}^{\prime }-{E}_0^{\prime }}{E^{\prime}\left(\omega \right)-{E}_0^{\prime }}=1+\frac{k^2}{\omega^2}\Rightarrow ay=1+{k}^2x,\\ {}a={E}_{\infty}^{\prime }/{E}_0^{\prime }-1,y={\left({E}^{\prime}\left(\omega \right)/{E}_0^{\prime }-1\right)}^{-1},x={\omega}^{-2}\end{array}}. $$
(15)

Then, the experimental data plotted in new coordinates ( x, y ) can be extrapolated by a straight line, and it will be clearly seen how much the character of approximation (11) agrees with the experiment.

To analyze the results sensitivity to the accuracy of estimating the approximation parameters (11), the creep curves (14) were restored for different variations of the initial data (see Table 1).

The calculation results (Fig. 7-9) show a significant effect of the approximation parameters (11) on the restored creep characteristics. An increase of the difference between the static and dynamic values of the storage modulus reflects the growth of rheological, hereditary effects, which manifests itself in an increase of creep strain (Fig. 7). At that, the change of the dynamic modulus affects the value of the instantaneous strain (Fig. 8). Materials, in which rheological effects cease to be significant at higher frequencies (with a larger value of the parameter k ), are more susceptible to creep. The earlier the recovery modulus begins to attenuate, which is associated with the inflection point of the frequency dependence, the sooner the horizontal asymptote is reached and the rheological effects are less noticeable (Fig. 9). Let us show how the parameter k is related to the inflection point of the function E ′ (ω). Since the parameter k is determined phenomenologically, from the condition of the best fit with the experimental data, it is convenient to establish a connection between the value of this parameter and the value of the conditional frequency ω∗ at the “inflection” point. It should be noted that the following asymptotics is valid for the proposed sigmoid dependence (11) (see Fig. 2)

Fig. 7
figure 7

The restored creep curves ε (t) at various values of the long-term modulus \( {E}_0^{\prime } \) (numbers at the curves in GPa). The dynamic modulus \( {E}_{\infty}^{\prime } \) and parameter k did not change.

Full size image
Fig. 8
figure 8

The restored creep curves ε (t) at various values of the dynamic modulus \( {E}_{\infty}^{\prime } \) (numbers at the curves in GPa). The long-term modulus \( {E}_0^{\prime } \) and parameter k did not change.

Full size image
Fig. 9
figure 9

The restored creep curves ε (t) at various values of the parameter k (numbers at the curves in rad/s). The long-term \( {E}_0^{\prime } \)and dynamic \( {E}_{\infty}^{\prime } \) moduli did not change.

Full size image
$$ \frac{d E^{\prime }}{d\omega}\underset{\omega \to 0;\omega \to \infty }{\to }0. $$

Equating the second derivative of expression (11) to zero, we can relate the conditional frequency \( {\omega}_k^{\ast } \) with the value of the parameter \( k:k={\omega}_k^{\ast}\sqrt{3}. \) Similarly for the dependence of the loss modulus, we have \( s={\omega}_s^{\ast}\sqrt{3}. \)

The main difficulty consists in the experimental determination of the frequency \( {\omega}_k^{\ast }, \) which corresponds to the inflection point (zero second derivative) on the experimental dependence E ′ (ω).If we take into account that the frequency scale within a large range is often taken logarithmic one, it becomes clear that even a small deviation from the frequency value \( {\omega}_k^{\ast } \) leads to a significant error in the restored parameters of creep function.

Thus, despite the correctness of all transformations, the use of limited experimental data on the frequency dependences of the complex modulus components leads to unstable results. Obtaining experimental dependences in a wide range of frequencies, with correct and clearly expressed asymptotics, is a required condition for a creep prediction. However, even obtaining exhaustive dependences of the complex modulus components with the required asymptotics does not guarantee an acceptable accuracy of the restored creep characteristics due to the strong sensitivity of the solution results of the inverse problem to the errors of primary experiments.

Analysis and Result Discussion

  1. 1.

    Creep prediction based on linear viscoelasticity requires experimental determination of the frequency dependences of the complex modulus components in a wide frequency range and with high accuracy.

  2. 2.

    At forced vibrations, an energy dissipation always takes place, which is partially converted into heat. A temperature increase leads to a change of the viscoelastic properties. Therefore, strictly speaking, the coupled thermoviscoelasticity problem should be solved. However, in standard experiments on vibrational loading, it is not possible to monitor strictly the temperature increase and the parameters of the constitutive relations, taking into account the temperature effect on the viscoelastic properties, are not known in advance. Therefore, in the first approximation, the process is considered to be isothermal, although the neglect of the temperature increase serves as an additional source of errors in the restoring the creep and relaxation kernels based on the results of vibration tests.

  3. 3.

    The results of the analysis lead to the conclusion that the static (long-term) modulus cannot be determined by conventional mechanical tests. The dynamic modulus can be determined independently: by the speed of propagation of the tensile-compression wave or in high-speed tests. High frequencies cannot be realized without an increase in temperature, which means that the experimental determination of the complex modulus dependences is correct only at intermediate frequencies and it can only serve for a comparative assessment of the parameters of the transition from statics to dynamics.

  4. 4.

    Convenient variants of the analytical description of the frequency dependences of the complex modulus components with the required asymptotics are proposed. It is formally possible to restore the creep kernel using this method, but a strong dependence of the results on the accuracy of obtaining the experimental data in a wide range of loading frequencies was revealed.

Conclusion

New results of the analysis of the well-known problem of predicting the creep of a material without long-term experiments are presented. The convenient variants of the analytical description of the frequency dependences of the complex modulus components on the frequency of forced vibrations were proposed. When substantiating the formal transformations, the requirements for the asymptotic behavior of the complex module components are indicated, which ensure the correctness of applying the Fourier transforms to restore the creep operator based on the results of vibration tests. The application of this approach should be based on experimental data obtained in a fairly wide frequency range. Such a technique would allow one to reduce the time compared to traditional creep tests. However, the procedure for restoring the creep curves from the frequency dependences of the complex modulus turns out to be extremely sensitive to the accuracy of the approximation of experimental data, and, therefore, its practical application remains extremely limited, encountering problems that are difficult to overcome.

Conflict of Interest. The authors confirm that there is no conflict of interest.