Introduction

Thus far, a great number of papers devoted to studying the mechanical properties of fibrous composites under cyclic loadings in the presence of creep have accumulated (see, for example, [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]). The greater part of them deal with investigating their residual rigidity and strength in multicyclic loadings by comparing the elastic modulus and strength after some number of loading cycles with their values found in the first cycle. On the basis of experimental data, as a rule, a relation between the current elastic modulus of the composite and the number of cycles is constructed. Results of such experiments for a cantilever beam of a fibrous composite can be found, e.g., in [12]. A review of various models describing the residual rigidity of composites is given, e.g., in work [13]. For fibrous composites on the basis carbon fibers and an epoxy binder, models describing their decreasing elastic modulus during repeated loadings are constructed in [14]. A differential relation for the decrease rate of the elastic modulus of a material as a function of the number of loading cycles is offered, which, integrated over the number of cycles, results in a final formula. On the basis of experiments on cyclic tension of samples of a fibrous composite with a ±35° stacking, a quite good agreement between the experiments and calculations according to the model constructed was found to exist. In work [15], the properties of a glass-fiber composite with a ±45° stacking were investigated in conditions of shear at a cyclic loading.

In work [16], results of a series of experimental studies on test samples of ±45° cross-ply fiber-reinforced composites, subjected to tension with various loading programs, allowing one to obtain reliable and correct results both at short- and long-term loadings are presented. In analyzing the stress-strain relations of the material, it is considered homogeneous, and the full axial strain is presented as the sum of four constituents — the instantaneous residual (irreversible), nonlinear reversible, irreversible creep, and reversible creep strains, because of the viscoelastic properties of matrix. To separate the last two strains, it is assumed that their rates at different instants of time are different. This assumption, together with the generalized Kachanov hypothesis, makes it possible first to obtain equations for increments of viscoelastic strains alone, and then to write equations in which unknown are only the viscoplastic strains. At the final stage of solution of the identification problem, values of the secant elastic modulus are found.

We should note that such investigations in conditions of compression of test samples face serious difficulties. They are connected, first of all, with the fact that it is impossible to ensure reliable results in conditions of long-term loadings of even short test samples — they suffer the transverse-longitudinal bending, although rather small. In this connection, important is the question is it possible to determine the parameters introduced in [16] from the results of experiments on tests samples in cyclic tension so that the methodology developed could further be used in theoretical-experimental investigations of test samples at cyclic compression?

Considering the aforesaid, in the given work, we will investigate the features of nonelastic behavior of a composite at cyclic tension. Contrary to [16], it is assumed that the total strain can be presented as the sum of instantaneous linearelastic, viscoelastic εv and irreversible creep εcr strains (as theoretical-experimental investigations have shown, the reversible nonlinear elastic strains introduced in [16] can be neglected, because they are small compared with the other ones). We will consider problems on constructing governing relations in the simplest, one-dimensional statement and will present results of experimental and theoretical studies on composite tests samples with a ±45° stacking. Experiments on such test samples are carried out for two reasons. First, the rheological properties of a composite showing up in it are caused mostly as shear strains, which are prevailing in the orthotropy axes of a fibrous material in such experiments. Second, in the general case, the governing relations written, for example, as relations between creep strains \( {\varepsilon}_{ij}^{cr} \) and stresses, even for plane stress state, will contain, as arguments, six invariants (three invariants found by convolution of the stress tensor with the direction vectors of orthotropy axes and three similar invariants found by convolution of strain tensor \( {\varepsilon}_{ij}^{cr} \) with these vectors). To construct them and to determine the parameters entering into them, a great number of various experiments and special methods of their processing are needed. There are works where, to reduce their number, various hypotheses are assumed or, for example, the governing relations are simplified by analyzing the features of material properties. For example, this is done in works [17,18,19], where reviews of studies in this direction are also given. Some other variants of such relations can be found, for example, in [20,21,22,23,24,25,26]. Moreover, when determining the parameters of deformation models, quite often there arise significant difficulties, because the problems formulated for their identification generally fall into the category of incorrect ones. Therefore, various special solution methods for them have to be elaborated (see for example, [22, 27, 28]).

The basic purpose of the given work is an analysis of the features of cyclic tension of test samples with a ±45° stacking and identification of the parameters contained in the constituents εcr (σ, t) and εv (σ, t) entered into the total strain.

1. Experiments on the Cyclic Tension of a Composite and Physical Relations

To clear up the structure of strains of test samples of fibrous composites with a ±45° stacking on the basis of an ELUR-P carbon tape and an ХТ-118 binder, they have been tested in short- and long-term static tension [16, 30, 31]. Four-layer test samples of average thickness h = 0.56 mm and width b = 24.60 mm and length of the working part l = 110 mm were used. The tests were carried at room temperature on a universal servoelectric Instron ElectroPuls E10000 test machine. The axial deformations were measured by an Instron extensometer, of B-1 accuracy class according the ASTM E83 standard, with a measurement base of 50 mm. Such tests are regulated by various standards (see, for example, GOST 32658-2014 and ASTM 3518). The tests samples were subjected to tension, and their axial stresses σx and strains εx were measured. The relations between stress and strains were significantly nonlinear and differed greatly in loading and subsequent unloading, with residual strains present always.

The tests were carried out in eight months after manufacturing the test samples according to the technology expounded in [29], when the polymerization of binder of the composite was completed. The maximum normal stress σx was the same in all loading-unloading cycles.

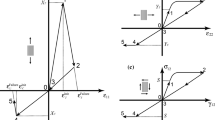
Preliminary, the limiting (breaking) stress \( {\sigma}_x^B \) was found. The repeated tension tests were performed at \( {\sigma}_x^{\mathrm{max}}=0.7{\sigma}_x^B \) = 65 МPа. The deformation diagrams of initial cycles, where the loading and unloading were performed at a rate of crosshead motion 0.5 mm / min, are shown on Fig. 1.

Fig. 1
figure 1

Deformation diagrams: a — at \( {\sigma}_x^{\mathrm{max}} \) = 55 MPa (continuous line — the 1st and 2nd cycles; dashed line — the 10th cycle); b — the same in a changed scale.

Full size image

The loadings and unloading branches did not coincide, forming a hysteresis loop, and the axial strain εx, in each subsequent cycle with the same cycle stress, increased by ∆εx, which decreased with the number of cycles.

The deformation diagram \( {\sigma}_x^{+}={\sigma}_x^{+}\left({\varepsilon}_x\right) \) for the first two loadings-unloading cycles presented, at a changed scale, on Fig. 1b. Here, the limiting points A1 and A2 corresponding to \( {\sigma}_x^{\mathrm{max}} \) = 55 MPa, the points B1 and B2 corresponding to \( {\sigma}_x^{\mathrm{min}} \) = 3 MPa, and the straight lines 0A1, A1B1, B1A2, and A2B2 and angles between them and the εx axis are entered into consideration. They allow one to determine the quantities \( {E}_{+}^{(i)}=\tan {\varphi}_{+}^{(i)} \) and \( {E}_{-}^{(i)}=\tan {\varphi}_{-}^{(i)} \) representing the secant elastic moduli in an ith loading (with a subscript “+”) and unloading (with a subscript “-”) cycle.

The tests were carried out at \( {\sigma}_x^{\mathrm{max}} \) = 45, 55, and 65 MPa with unloading down to \( {\sigma}_x^{\mathrm{min}} \) = 3 MPa, and the corresponding deformation diagrams σx = σx(εx) and the strain increments Δεx as functions of the number of cycles were found. On Fig. 2a, the relations the secant elastic moduli in loading and unloading are shown for the three stress levels considered.

Fig. 2
figure 2

Secant elastic moduli E+ and E− in loading (lines) and unloading (dots) vs. the number i of loading cycles: a — for \( {\sigma}_x^{\mathrm{max}} \) = 45, 55, and 65 MPa, the rate of crosshead motion 0.5 mm/min; b — different loading rates; for \( {\sigma}_x^{\mathrm{max}} \) = 45 MPa, the rates of crosshead motion are 2.0, 0.5, 0.125 mm/min.

Full size image

Besides, tests were performed to qualitative study the influence of loading rate on the magnitude of inelastic strains and secant elastic moduli at repeated loadings with \( {\sigma}_x^{\mathrm{max}} \) = 45 MPa (Fig. 2b).

It was established that there was a limiting stress \( {\sigma}_x^{\ast } \) on whose reaching during the cyclic loading destruction of the material begins. For the composite considered, this stress was \( {\sigma}_x^{\ast } \) = 65 MPa. As is seen from the data in Fig. 2, the secant modulus decreased with each loading cycle, i.e., after the stress reached its limiting value, the secant modulus was stabilized no longer — it decreased continuously.

The loading was slow enough, which allowed us not to take into account the inertial force. The stress was brought up to a preset value at a constant speed of the moving crosshead, and then was reduced at the same speed. From an analysis of the results obtained with the help of equipment of the test machine for recording loads and deformations, it followed that, after the first loading cycle, the law σ = σ(t) of pressure variation, with a high accuracy, could be considered linearly cyclic (Fig. 3). It is evident that, at the loading stage in different cycles, small deviations of σ(t) from a straight line took place only at the initial stage of the first cycle.

Fig. 3
figure 3

Stress σx (а) and strain εx (b) vs. time t.

Full size image

Proceeding from an analysis of experimental data and results of their processing in [29,30,31,32] and other literature sources, it can be concluded that the full axial strain at quasi-static loadings, with a sufficiently high degree of accuracy, can be presented as the sum (hereinafter the subscript “x” is not indicated)

$$ \varepsilon ={\varepsilon}^{el}+{\varepsilon}^{cr}\left(\sigma, t\right)+{\varepsilon}^{\mathrm{v}}\left(\sigma, t\right),\kern1em {\varepsilon}^{el}=\sigma /E. $$
(1.1)

Here, εel is the elastic strain, εcr is the irreversible creep strain, and εv is the viscoelastic strain. As before [16], representation (1.1) is based on the Kachanov hypothesis [33] that the strains εel, εv, and εcr develop independently of each other. We assume that strains are small.

The choice of a specific kind of physical relations for the strains εv and εcr has to be based on results of experiments. Further, we assume that, as a first approximation, the irreversible creep strains can be described by the relation of hardening theory.

$$ d{\varepsilon}^{cr}/ dt=F\left(\sigma, {\varepsilon}^{cr}\right). $$
(1.2)

The viscoelasticity was characterized by the Volterra integral relation

$$ {\varepsilon}^{\mathrm{v}}=\underset{0}{\overset{t}{\int }}H\left(t-\tau \right)\sigma \left(\tau \right) d\tau, $$
(1.3)

where H(t) is the creep kernel. We should note that, in the literature, instead of (1.3), the following relation is frequently used [2, 8]:

$$ {\varepsilon}^{\mathrm{v}}=\underset{0}{\overset{t}{\int }}\left[\Psi \left(t-\tau \right)\frac{d\sigma \left(\tau \right)}{d\tau}\right] d\tau, \kern1em \Psi (t)=\underset{0}{\overset{t}{\int }}H\left(\tau \right) d\tau, $$
(1.4)

where Ψ(t) is the creep potential. Relation (1.4) can be obtained from (1.3) by its integration by parts. And vice versa, integrating (1.4) by parts, relation (1.3) can be found. However, in some cases, representation (1.4) requires the introduction of generalized (Dirac and Heaviside) functions, for example, in the case of step loadings. Then, on segments with σ = const, stress rates turn out to be zero (i.e., according to (1.4), εv = 0, σ = const), and the derivatives \( \frac{d\sigma \left(\tau \right)}{d\tau} \) are unlimited on borders of these segments. This is not very convenient in numerical calculations, but relation (1.3) allows one to employ the methods of numerical integration in these cases too.

Further on, we will use Eq. (1.3) with the creep kernel, namely,

$$ {\varepsilon}^{\mathrm{v}}=B\underset{0}{\overset{t}{\int }}\frac{\sigma \left(\tau \right)}{{\left(t-\tau \right)}^{\alpha }}\sigma \left(\tau \right) d\tau, \kern1em 0<\alpha <1,\kern1em B>0. $$
(1.5)

Equation (1.5) is attractive in that it contains a small number of mechanical characteristics to be determined from test data. Besides, as is known, it is well confirmed by experiments (see, for example, [1, 9, 16]). However, a distinctive feature of relation (1.5) in comparison with other ones (for example, with the Koltunov–Rzhanitsyn relation [3, 4]) is that it does not lead to asymptotically restricted values of viscoelastic strains under infinitely long constant loadings. Here, only low-cycle loading will be considered; therefore, we assume that, to a sufficient accuracy, relation (1.5) can be used to describe the processes studied further. We should also note that such functions cannot be employed to describe relaxation kernels [4].

2. Features of the Rheological Models Considered at Cyclic Loadings and Their Use for Identification of the Parameters of Governing Relations

2.1. Specificity of the viscoelastic model with the Abel kernel at cyclic loadings

First, specific feature of relation (1.5) will be analyzed with the example of an elementary cyclic loading (not directly connected with the experiments carried out by the present authors, but allowing one to found results in the form of finite formulas). Let the loading occur linearly relative to strain, and unloading is instantaneous at the end of cycle. This process can be described as

$$ \sigma ={\sigma}_0\left(t-T\left(j-1\right)\right),\kern1em T\left(j-1\right)\le t\le Tj, $$

where T is the loading period and j is the cycle number. Then, on each cycle, relation (1.5) can be integrated analytically. For example, at the end t = T of the first cycle, we have

$$ {\varepsilon}_1^{\mathrm{v}}=\frac{B{\sigma}_0{T}^{2-\alpha }}{2-3\alpha +{\alpha}^2}, $$
(2.1)

but at the end t = 2T of the second cycle, relation (1.5) gives

$$ {\varepsilon}_2^{\mathrm{v}}=\frac{B{\sigma}_0{T}^{2-\alpha}\left({2}^{2-\alpha }+\alpha -2\right)}{2-3\alpha +{\alpha}^2}. $$
(2.2)

An analysis of relations (2.1) and (2.2) and calculation results for other cycle numbers and other types of loading shows that, by the end of each cycle, the ratio between the accumulated strain \( {\varepsilon}_j^{\mathrm{v}} \) and the strain \( {\varepsilon}_i^{\mathrm{v}} \) of an i th cycle depends neither on the period T of loading cycle, nor the stress amplitude, nor the parameter B, but only on the parameter α. For example, from (2.1) and (2.2) it follows that

$$ {\varepsilon}_2^{\mathrm{v}}/{\varepsilon}_1^{\mathrm{v}}=\left({2}^{2-\alpha }-2+\alpha \right). $$
(2.3)

Relations of type (2.3) allow one to facilitate, for example, the calculation of \( {\varepsilon}_j^{\mathrm{v}} \). For this purpose, it is necessary to perform the calculation only once at a given value of α and given law of cyclic loading and then to found the relation between the strains \( {\varepsilon}_j^{\mathrm{v}} \) and \( {\varepsilon}_1^{\mathrm{v}} \) in a tabular form or as regression functions f(j). For other values of the loading amplitude, parameter B and loading period T, the required values of \( {\varepsilon}_j^{\mathrm{v}} \) are determined by the formula

$$ {\varepsilon}_j^{\mathrm{v}}=f(j)\cdot {\varepsilon}_1^{\mathrm{v}}. $$

Similar results and relations can be found not only for the maximum stresses, but also for the viscoelastic strains εv at any other instants of time shifted by the period T. For example, if the strain εv on the first cycle at t1 = ξT, ξ < 1, is found, then, on the second cycle at t2 =T + ξT = T + t1, we obtain that

$$ {\varepsilon}_2^{\mathrm{v}}={\varepsilon}_1^{\mathrm{v}}\left[{\left({t}_2-{t}_1\right)}^{2-\alpha }+\left({t}_2^{2-\alpha }-{\left({t}_2-{t}_1\right)}^{1-\alpha}\left({t}_2+{t}_1-{t}_1\alpha \right)\right.\right]/{t}_1^{2-\alpha }. $$
(2.4)

Now, we will investigate the general case of cyclic loading. Let us consider instants of time differing by multiples of cycle period T. Then, in the general case, the viscous parts of strain found at these instants of time will not depend on the cycle period, loading amplitude, and the parameter B of creep kernel, but only on the parameter α at any type of cyclic loading. Really, as σ(τ) is a periodic function, it can be expanded in the trigonometric series

$$ \sigma \left(\tau \right)={S}_0+\sum \limits_{m=1}^{\infty}\left({S}_m\sin \frac{2\pi m\tau}{T}+{C}_m\cos \frac{2\pi m\tau}{T}\right). $$

Let us choose any its nonzero factor, designate it as σ0, and take it out of the parentheses.

Then, we will obtain that

$$ {\displaystyle \begin{array}{c}\sigma \left(\tau \right)={\sigma}_0\left[{s}_0+\sum \limits_{m=1}^{\infty}\left({s}_m\sin \frac{2\pi m\tau}{T}+{c}_m\cos \frac{2\pi m\tau}{T}\right)\right],\\ {}{s}_0=\frac{S_0}{\sigma_0},{s}_m=\frac{S_m}{\sigma_0},{c}_0=\frac{C_0}{\sigma_0}.\end{array}} $$
(2.5)

Let us change the variables,

$$ \tau \ast =\tau /T,\kern0.5em t\ast =t/T. $$
(2.6)

Then, it follows from (2.5) that

$$ \left(\tau \right)={\sigma}_0\left({s}_0+\sum \limits_{m=1}^{\infty}\left[{s}_m\sin \left(2\pi m{\tau}^{\ast}\right)+{c}_m\cos \left(2\pi m{\tau}^{\ast}\right)\right]\right)={\sigma}_0\cdot f\left(\tau \ast \right). $$
(2.7)

Hence, relation (1.5) can be written in the form

$$ {\varepsilon}^{\mathrm{v}}(t)={BT}^{1-\alpha }{\sigma}_0\underset{0}{\overset{t^{\ast }}{\int }}\frac{f\left({\tau}^{\ast}\right)}{{\left({t}^{\ast }-{\tau}^{\ast}\right)}^{\alpha }}d{\tau}^{\ast }. $$
(2.8)

Let us write now the expression for the strain εv at the instant of time differing by one loading period, i.e., for the time

$$ t=t\ast T+T=\left(t\ast +1\right)T. $$
(2.9)

From Eq. (2.8), it follows that

$$ {\varepsilon}^{\mathrm{v}}\left(t+T\right)={BT}^{1-\alpha }{\sigma}_0\underset{0}{\overset{t^{\ast }+1}{\int }}\frac{f\left({\tau}^{\ast}\right)}{{\left({t}^{\ast }+1-{\tau}^{\ast}\right)}^{\alpha }}d{\tau}^{\ast }. $$
(2.10)

Then, the ratio between the strains εv calculated at the times t+T and t is

$$ {\varepsilon}^{\mathrm{v}}\left(t+T\right)/{\varepsilon}^{\mathrm{v}}(t)=\underset{0}{\overset{t^{\ast }+1}{\int }}\frac{f\left({\tau}^{\ast}\right)}{{\left({t}^{\ast }+1-{\tau}^{\ast}\right)}^{\alpha }}d{\tau}^{\ast }/\underset{0}{\overset{t^{\ast }}{\int }}\frac{f\left({\tau}^{\ast}\right)}{{\left({t}^{\ast }-{\tau}^{\ast}\right)}^{\alpha }}d{\tau}^{\ast }. $$
(2.11)

As is seen from (2.11), this ratio depends neither on the amplitude of the stress σ0, nor on the period T of cyclic loading, nor on the parameter B of creep kernel, but only on the parameter α and the kind of loading f(τ*). For any instants of time differing by a multiple of the period T of loading cycle, we have

$$ {\varepsilon}^{\mathrm{v}}\left(t+ Tn\right)/{\varepsilon}^{\mathrm{v}}\left(t+ Tk\right)=\underset{0}{\overset{t^{\ast }+n}{\int }}\frac{f\left({\tau}^{\ast}\right)}{{\left({t}^{\ast }+n-{\tau}^{\ast}\right)}^{\alpha }}d{\tau}^{\ast }/\underset{0}{\overset{t^{\ast }+k}{\int }}\frac{f\left({\tau}^{\ast}\right)}{{\left({t}^{\ast }+k-{\tau}^{\ast}\right)}^{\alpha }}d{\tau}^{\ast }. $$
(2.12)

Thus, it can be concluded that the relations between the viscous parts of the strain calculated at instants of time differing by a multiple of T do not depend on T, σ0, and B.

We should note that other laws of viscoelastic deformation, for example, those using the Koltunov–Rzhanitsyn relation

$$ {\varepsilon}^{\mathrm{v}}=B\underset{0}{\overset{t}{\int }}\frac{\sigma \left(\tau \right)}{e^{\gamma \left(t-\tau \right)}{\left(t-\tau \right)}^{\alpha }} d\tau, $$

do not possess this property. In such cases, the relations of type (2.12) will contain not only the kernel parameters α and γ, but also the period T.

From (2.12), it also follows that the ratio between the absorbed energies calculated, for example, for one period of neighboring loading cycles does not depend on T, σ0, and B. Really, these energies are calculated as follows:

$$ {W}_n=\underset{T\cdot n}{\overset{T\cdot \left(n+2\right)}{\int }}\sigma (t){\varepsilon}^{\mathrm{v}}(t) dt={\left({\sigma}_0\right)}^2{BT}^{1-\alpha}\underset{t^{\ast }+n}{\overset{t^{\ast }+n+1}{\int }}\left[f\left({\theta}^{\ast}\right)\underset{n}{\overset{\theta^{\ast }+n}{\int }}\frac{f\left({\tau}^{\ast}\right)}{{\left({t}^{\ast }+n-{\tau}^{\ast}\right)}^{\alpha }}d{\tau}^{\ast}\right]d{\theta}^{\ast }, $$
(2.13)
$$ {W}_{n+1}=\underset{T\cdot \left(n+1\right)}{\overset{T\cdot \left(n+2\right)}{\int }}\sigma (t){\varepsilon}^{\mathrm{v}}(t) dt={\left({\sigma}_0\right)}^2{BT}^{1-\alpha}\underset{t^{\ast }+n+1}{\overset{t^{\ast }+n+2}{\int }}\left[f\left({\theta}^{\ast}\right)\underset{n+1}{\overset{\theta^{\ast }+n+1}{\int }}\frac{f\left({\tau}^{\ast}\right)}{{\left({t}^{\ast }+n+1-{\tau}^{\ast}\right)}^{\alpha }}d{\tau}^{\ast}\right]d{\theta}^{\ast }, $$
(2.14)

wherefrom

$$ \psi =\frac{W_n}{W_{n+1}}=\psi \left(n,\alpha \right). $$

It is easy to see that this is true not only for neighboring cycles.

We should also note that, in the theory of damped vibrations (see, for example, [34]), a similar experimentally established fact is known, according to which the quantity ψ does not depend on vibration period. However, in general, as noted in [34], ψ nevertheless depends on stress amplitude.

2.2. Identification of the parameters of viscoelasticity and viscoplasticity models

On the basis of Eq. (2.12), a method to solve the inverse problem of identification the parameter α of Abel creep kernel using data of cyclic loading experiments can be proposed. For this aim, we write Eqs. (2.12) for n = n1 and n = n2 and subtract the resulting equations, which gives

$$ {\displaystyle \begin{array}{c}\left[{\varepsilon}^{\mathrm{v}}\left(t+T{n}_1\right)-{\varepsilon}^{\mathrm{v}}\left(t+T{n}_2\right)\right]/\left[{\varepsilon}^{\mathrm{v}}\left(t+ Tk\right)\right]\\ {}=\left[\underset{0}{\overset{t^{\ast }+{n}_1}{\int }}\frac{f\left({\tau}^{\ast}\right)}{{\left({t}^{\ast }+{n}_1-{\tau}^{\ast}\right)}^{\alpha }}d{\tau}^{\ast }-\underset{0}{\overset{t^{\ast }+{n}_2}{\int }}\frac{f\left({\tau}^{\ast}\right)}{{\left({t}^{\ast }+{n}_2-{\tau}^{\ast}\right)}^{\alpha }}d{\tau}^{\ast}\right]/\underset{0}{\overset{t^{\ast }+k}{\int }}\frac{f\left({\tau}^{\ast}\right)}{{\left({t}^{\ast }+k-{\tau}^{\ast}\right)}^{\alpha }}d{\tau}^{\ast }.\end{array}} $$
(2.15)

A similar relation is found for n = n3 and n = n4:

$$ {\displaystyle \begin{array}{c}\left[{\varepsilon}^{\mathrm{v}}\left(t+T{n}_3\right)-{\varepsilon}^{\mathrm{v}}\left(t+T{n}_4\right)\right]/\left[{\varepsilon}^{\mathrm{v}}\left(t+ Tk\right)\right]\\ {}=\left[\underset{0}{\overset{t^{\ast }+{n}_3}{\int }}\frac{f\left({\tau}^{\ast}\right)}{{\left({t}^{\ast }+{n}_3-{\tau}^{\ast}\right)}^{\alpha }}d{\tau}^{\ast }-\underset{0}{\overset{t^{\ast }+{n}_4}{\int }}\frac{f\left({\tau}^{\ast}\right)}{{\left({t}^{\ast }+{n}_4-{\tau}^{\ast}\right)}^{\alpha }}d{\tau}^{\ast}\right]/\underset{0}{\overset{t^{\ast }+k}{\int }}\frac{f\left({\tau}^{\ast}\right)}{{\left({t}^{\ast }+k-{\tau}^{\ast}\right)}^{\alpha }}d{\tau}^{\ast }.\end{array}} $$
(2.16)

Dividing (2.15) by (2.16), we obtain that

$$ \left[{\varepsilon}^{\mathrm{v}}\left(t+{Tn}_1\right)-{\varepsilon}^{\mathrm{v}}\left(t+{Tn}_2\right)\right]/\left[{\varepsilon}^{\mathrm{v}}\left(t+{Tn}_3\right)-{\varepsilon}^{\mathrm{v}}\left(t+{Tn}_4\right)\right]={c}^{\mathrm{v}}, $$
(2.17)

where

$$ {\displaystyle \begin{array}{c}{c}^{\mathrm{v}}=\left[\underset{0}{\overset{t^{\ast }+{n}_1}{\int }}\frac{f\left({\tau}^{\ast}\right)}{{\left({t}^{\ast }+{n}_1-{\tau}^{\ast}\right)}^{\alpha }}d{\tau}^{\ast }-\underset{0}{\overset{t^{\ast }+{n}_2}{\int }}\frac{f\left({\tau}^{\ast}\right)}{{\left({t}^{\ast }+{n}_2-{\tau}^{\ast}\right)}^{\alpha }}d{\tau}^{\ast}\right]\\ {}/\left[\underset{0}{\overset{t^{\ast }+{n}_3}{\int }}\frac{f\left({\tau}^{\ast}\right)}{{\left({t}^{\ast }+{n}_3-{\tau}^{\ast}\right)}^{\alpha }}d{\tau}^{\ast }-\underset{0}{\overset{t^{\ast }+{n}_4}{\int }}\frac{f\left({\tau}^{\ast}\right)}{{\left({t}^{\ast }+{n}_4-{\tau}^{\ast}\right)}^{\alpha }}d{\tau}^{\ast}\right].\end{array}} $$
(2.18)

As is seen, there is only one mechanical characteristic in the right side of Eq. (2.17) — the parameter α. Thus, for its identification, it suffices to solve the direct problem of viscoelasticity with any elastic characteristics and the parameter B and to insert the experimentally found relation

$$ {c}_{\mathrm{exp}}^{\mathrm{v}}=\left[{\varepsilon}_{\mathrm{exp}}^{\mathrm{v}}\left(t+{Tn}_1\right)-{\varepsilon}_{\mathrm{exp}}^{\mathrm{v}}\left(t+{Tn}_2\right)\right]/\left[{\varepsilon}_{\mathrm{exp}}^{\mathrm{v}}\left(t+{Tn}_3\right)-{\varepsilon}_{\mathrm{exp}}^{\mathrm{v}}\left(t+{Tn}_4\right)\right] $$
(2.19)

into the right side of Eq. (2.17). The basic difficulty consists in isolating \( {\varepsilon}_{\mathrm{exp}}^{\mathrm{v}} \) from the general expression (2.1), because only the full strain εexp can be measured in experiments. To solve this problem for the material considered, we assume the hypothesis, confirmed by experiments, that the rates of the irreversible creep strain εcr and the hereditary elastic strains εv strongly differ at long times, namely, that the first rate is much smaller than the second one [16]. This second feature of the composite considered, concerning the viscoplastic strains, testifies that, after a sufficiently great number of cycles, increase only the viscoelastic strains εv. Then, instead of (2.18), it can be assumed that

$$ {c}_{\mathrm{exp}}^{\mathrm{v}}\approx {c}_{\mathrm{exp}}=\left[{\varepsilon}_{\mathrm{exp}}\left(t+{Tn}_1\right)-{\varepsilon}_{\mathrm{exp}}\left(t+{Tn}_2\right)\right]/\left[{\varepsilon}_{\mathrm{exp}}\left(t+{Tn}_3\right)-{\varepsilon}_{\mathrm{exp}}\left(t+{Tn}_4\right)\right]. $$
(2.20)

where all ni ≫ 1. The quantity cv can be calculated either by Eq. (2.18) or (1.5) at arbitrary values of B and T:

$$ {c}^{\mathrm{v}}=\left[{\varepsilon}^{\mathrm{v}}\left(t+{Tn}_1\right)-{\varepsilon}^{\mathrm{v}}\left(t+{Tn}_2\right)\right]/\left[{\varepsilon}^{\mathrm{v}}\left(t+{Tn}_3\right)-{\varepsilon}^{\mathrm{v}}\left(t+{Tn}_4\right)\right]. $$
(2.21)

For t, different values of time can be taken, for example, those corresponding to the maximum values of stress, as it is done further in processing experimental results.

Equating the right sides of Eqs. (2.20) and (2.21) at some values of ni, several equations in the parameter α are obtained. This overdetermined system can be solved, for example, by the method of minimization of its quadratic discrepancy.

Further, for some values of n1, n2 ≫ 1, we write an overdetermined system of equations to find the parameter B, namely,

$$ {\varepsilon}^{\mathrm{v}}\left(t+{Tn}_1\right)-{\varepsilon}^{\mathrm{v}}\left(t+{Tn}_2\right)={\varepsilon}_{\mathrm{exp}}\left(t+{Tn}_3\right)-{\varepsilon}_{\mathrm{exp}}\left(t+{Tn}_4\right). $$
(2.22)

The system is solved by the same minimization method.

Then, the relations for viscoplastic strains are approximated. In processing experimental results, the following relation of hardening theory was used:

$$ \frac{d{\varepsilon}^{cr}}{dt}=\frac{\chi_0\sigma (t)}{{\left(1+{\chi}_1{\varepsilon}^{cr}\right)}^m}. $$
(2.23)

A relation of this type was also employed in [16] and showed good results in an analysis of experiments on long-term loading for a similar material. To obtain a system of equations in the required parameters χ0, χ1, and m, the following relations for differences of strains at small times (i.e., at n1, n2 ≥ 1) are used:

$$ {\displaystyle \begin{array}{c}\Delta {\varepsilon}^{cr}+\Delta {\varepsilon}^{\mathrm{v}}=\Delta {\varepsilon}_{\mathrm{exp}},\\ {}\Delta {\varepsilon}^{cr}+{\varepsilon}^{cr}\left(t+{Tn}_1\right)-{\varepsilon}^{cr}\left(t+{Tn}_2\right),\kern1em \Delta {\varepsilon}^{\mathrm{v}}+{\varepsilon}^{\mathrm{v}}\left(t+{Tn}_1\right)-{\varepsilon}^{\mathrm{v}}\left(t+{Tn}_2\right),\end{array}} $$
(2.24)
$$ \Delta {\varepsilon}_{\mathrm{exp}}+{\varepsilon}_{\mathrm{exp}}\left(t+{Tn}_1\right)-{\varepsilon}_{\mathrm{exp}}\left(t+{Tn}_2\right). $$
(2.25)

To identify the parameters χ0, χ1, and m, system (2.24) was solved by minimizing its quadratic discrepancies.

At the last stage, the elastic modulus E is found. For this purpose, the deformation diagram of the loading cycle considered is used, but with account of the viscoelastic and viscoplastic deformation laws already found. Then, E is determined from the expression

$$ \Delta \left({\varepsilon}^{\mathrm{exp}}-{\varepsilon}^{cr}-{\varepsilon}^{\mathrm{v}}\right)=\Delta \sigma /E. $$
(2.26)

Proceeding from experimental data for the cyclic tension of a test sample of the fibrous composite with a ±45° stacking made from the ELUR-P carbon tape and the ХТ-118 binding of cold cure, the approach presented was used to determine the elastic and rheological characteristics of the composite. For the hereditary elastic strain εv, relation (1.5) was used, but the creep εcr was described by Eq. (2.23). By processing experimental found at σmax = 55 MPa and σmin = 3 MPa, the following values of required quantities were found:

$$ {\displaystyle \begin{array}{c}B=3.84\cdot {10}^{-6}\kern0.5em {\mathrm{s}}^{\alpha -1}/\mathrm{MPa},\kern0.5em \alpha =0.765,\kern0.5em E=12.9\kern0.5em \mathrm{GPa},\\ {}{\chi}_0=3.41\cdot {10}^{-6}/\left(\mathrm{MPa}\cdot \mathrm{s}\right),\kern0.5em {\chi}_1=9.25,\kern0.5em \mathrm{and}\kern0.5em m=506.8.\end{array}} $$
(2.27)

These characteristics were used to calculate strain–time relations at σmax = 45 MPa. On Fig. 4, the full strains (curves 1 and 2) and their inelastic parts (curves 3 and 4) at the maximum stress are illustrated. The maximum viscoelastic and viscoplastic strains were reached with a some delay in comparison with that of the maximum stress. However, as an analysis of experimental data and numerical calculations showed, the full strain reached its maximum simultaneously with that of stress, as is also evident on Fig. 3.

Fig. 4
figure 4

Full strains (1 and 2) and their inelastic parts (3 and 4) vs. the number i of loading cycles (lines — calculation, dots — experiment): 1 and 3 — at σmax = 55 MPa; 2 and 4 — at σmax = 45 MPa.

Full size image

As follows from the data of Fig. 4, at σmax = 55 and 45 MPa, the results of calculations found with the use of mechanical characteristics (2.27), agree with experimental data to a good accuracy.

We should note that, in the case of using the Koltunov–Rzhanitsyn-type creep kernel

$$ {\varepsilon}^{\mathrm{v}}=B\underset{0}{\overset{t}{\int }}\frac{\sigma \left(\tau \right)}{e^{\gamma \left(t-\tau \right)}{\left(t-\tau \right)}^{\alpha }} d\tau, $$
(2.28)

the identification technique is similar to that presented earlier, but it is no longer possible to reduce the problem to a successive determination of all parameters of the creep kernel. Nevertheless, it is possible to first write equations that contain only the quantities α and γ and then to derive equations for B. Then, instead of (2.18) we obtain the expression for cv

$$ {\displaystyle \begin{array}{c}{c}^{\mathrm{v}}=\left[\underset{0}{\overset{t^{\ast }+{n}_1}{\int }}\frac{f\left({\tau}^{\ast}\right){e}^{\gamma T{\tau}^{\ast }}}{{\left({t}^{\ast }+{n}_1-{\tau}^{\ast}\right)}^{\alpha }}d{\tau}^{\ast }-\underset{0}{\overset{t^{\ast }+{n}_2}{\int }}\frac{f\left({\tau}^{\ast}\right){e}^{\gamma T{\tau}^{\ast }}}{{\left({t}^{\ast }+{n}_2-{\tau}^{\ast}\right)}^{\alpha }}d{\tau}^{\ast}\right]\\ {}/\left[\underset{0}{\overset{t^{\ast }+{n}_3}{\int }}\frac{f\left({\tau}^{\ast}\right){e}^{\gamma T{\tau}^{\ast }}}{{\left({t}^{\ast }+{n}_3-{\tau}^{\ast}\right)}^{\alpha }}d{\tau}^{\ast }-\underset{0}{\overset{t^{\ast }+{n}_4}{\int }}\frac{f\left({\tau}^{\ast}\right){e}^{\gamma T{\tau}^{\ast }}}{{\left({t}^{\ast }+{n}_4-{\tau}^{\ast}\right)}^{\alpha }}d{\tau}^{\ast}\right].\end{array}} $$
(2.29)

Equating the right sides of (2.20) and (2.21), we arrive at equations for determining the parameters α and γ. Next, the parameter B is found from equation system (2.22) written at n1, n2 ≫ 1. Then, from relations (2.24) at n1, n2 ≥ 1, the parameters of hardening theory are determined.

Conclusion

In the present work, results of experimental studies on the cyclic tension of test samples with a ±45° stacking made from an ELUR-P carbon tape and an ХТ-118 binder of cold cure are presented. It is revealed that the secant elastic moduli are stabilized with growing number of loading cycles. On the basis of analysis of results for particular loading types, it is found that, when relations with the Abel creep kernel are used, ratios between the viscoelastic parts of strains at instants of time multiples of loading period depend neither on loading frequency, nor loading amplitude, nor the parameter determining a degree of viscosity of material, but only on the parameter determining the degree of attenuation of viscoelastic deformation. This is shown for the general case of cyclic loading too. The same effect is revealed for the amount of energy absorbed in one loading cycle. On the basis of this property, a method of successive determination of parameters of creep kernel is offered. To separate the hereditary elastic strains from experimental data, it is assumed that, at great times, the rate of irreversible creep strains is much lower than that of the hereditary elastic ones. This method is illustrated by an example of processing experimental results on cyclic tension of samples of a fibrous composite.

This work was performed with the support of the Russian Scientific Fund (projects No. 19-79-10018, sect. 1 and No. 19-19-00059, sect. 2).