Strain rate influence on hardening and damage characteristics of composite materials

Abstract

The paper presents models to characterize the dependence of hardening and strength characteristics of composite materials on damage and strain rate. The results of experimental studies of the behavior of composite materials in a wide range of strain rates are analyzed, and some regularities are determined. On the base of a failure criterion which includes the dependence of failure characteristics on damage and the rate of damage as well, taking into account the dependence of stiffness characteristics on the damage parameters, the stress–strain curves are determined for different strain rates, and they correlate quite well with the results of experimental studies. A method for the experimental determination of the material’s parameters is proposed. Some cases of complex, non-monotonic loading and unloading of composite materials are analyzed.

1 Introduction

Experimental investigations of fiber-reinforced composite materials under impact show a strong dependency of the stiffness and strength characteristics on the loading rate. Hsiao and Daniel [1, 2] used a split Hopkinson pressure bar (SHPB) for the off-axis tests of a unidirectional IM6G/3501-6 carbon/epoxy specimen. It was established that the strain rate increase from quasi-static mode to 1800 $\hbox {s}^{\mathrm {-1}}$ induces an initial transverse elastic modulus increase up to 37% and almost double failure stress for transverse compression. The initial shear modulus and failure stress increased up to 18% and 80%, correspondingly, with similar strain rate change, and highly nonlinear loading diagrams were observed. In Vogler and Kyriakides, study [3], shear and transverse compression strain rate dependency were observed in the strain rate range of $\sim 10^{{-5}}~{-}~10^{{0}}$ $\hbox {s}^{{-1}}$ for AS4/PEEK composite. This range of strain rates was accomplished by a custom electromechanical testing machine, allowing biaxial shear-compression loading. Both pure shear and transverse compression loading diagrams had a linear initial segment, which was identical for the all strain rate levels up to a certain strain value, above which the stress–strain curves became nonlinear. Koerber et al. [4] used the SHPB method for the off-axis tests of IM7/8552 composite in conjunction with the digital image correlation (DIC) system for the strain measurements. The authors also noticed a significant increase in elastic and strength characteristics with the strain rate. At the same time, the high strain rate compression in fiber direction of the same composite did not show any change in elastic modulus in comparison with the quasi-static case, but led only to an increase in the failure stress value to 40% [5]. Consideration of crack resistance curves for high strain rate and quasi-static cases also showed the fracture toughness growth for impact loading [6].

All the above effects of strain rate dependency of material characteristics are supposed to be considered in modeling procedures for composite materials. In particular, among the most important numerical simulation problems in this field are low velocity impact on a composite plate [7,8,9,10] and crashworthiness of composite profiles for absorbing structural applications [11,12,13,14,15]. The second problem seems to be more sensitive to impact hardening under higher strain rates, and for this reason it is the focus of the presented paper. A number of works and application results use commonly available static mechanical properties for FE analysis based on the shell element formulation, and they report satisfactory agreement of the specific absorption energy and the force–displacement curves with experimental results [16,17,18]. However, a direct use of shell elements may cause some ambiguity. First, the analysis of out-of-plane behavior becomes questionable [19] and requires additional modeling techniques for shell elements (cohesive elements [20] or special contact algorithms [21, 22]). Second, it is impossible to use shell elements to capture effect of chamfer on tube edge from impact side, which is used as a trigger to induce appropriate failure initiation [23]. Anyway, modern computational resources usually allow to verify convergence of the results based on shell and solid FEM formulation [24] and mesh sensitivity, and as a more significant question, if the high rate characteristics should be considered for the accurate analysis. For example, Chiu et al. [25] observed almost identical absorption characteristics of Hexcel HexPly T700/M21 carbon–epoxy tubes in the range from the quasi-static state and up to a strain $100\hbox { s}^{{-1}}$, while an increase in the absorption characteristics was demonstrated in [26, 27]. Thereby, many researchers noticed the contradiction in some experimental results and accept the importance of considering the effect of strain rate in every particular case [28, 29].

Numerous approaches exist for modeling the nonlinear behavior of composite materials with a polymer matrix, including strain rate dependency [30]. Gupta et al. [31] incorporated the continuum damage evolution model within the framework of irreversible thermodynamics. Thiruppukuzhi and Sun [32] from set of experiments concluded the independence of elastic deformation from the strain rate and developed a viscoplastic constitutive relation based on the Hill-type yield function [33], as applied to orthotropic material. Vogler et al. developed a plasticity model based on the non-associated flow rule to characterize nonlinear mechanical behavior under multi-axial loading conditions and under triaxial stress states prior to the onset of cracking. This model was enhanced by a smeared crack model [34] and further extended to the viscoplastic form [35]. Vasiukov et al. [36] introduced a coupled viscoelasticity–viscoplasticity model with anisotropic continuous damage mechanics in conjunction with the Hashin failure model [37]. Failure criteria usually can be simply modified from static ones by introduction of ultimate values depending on the strain rate, such as presented in [4] for the Puck criterion, or in [38] for a number of other criteria.

The present work proposes an extension the of damage model developed in [39,40,41,42,43] for a case of impact loading of laminated composite material with taking into account the strain rate sensitivity. The damage evolution mechanism is represented by two damage parameters, responsible for fiber and matrix failure modes. A novel concept of strain rate-dependence of the model lies in the expression of the strength criterion as a function of the damage rate without explicit involvement of the strain rate tensor. This strength function is decomposed into static and dynamic components, and the static component is also able to capture nonlinear effects, such as the nonlinear shear loading behavior. The material model can be calibrated using the minimum number of standard available static mechanical characteristics and a set of high rate loading tests, and it is possible to increase its accuracy in a simple manner using additional experiments. It suits the authors’ purpose to develop a model convenient for engineering applications.

2 Damage model

2.1 Constitutive relations for damaged material

The damage parameters are used to represent the damage, which can be interpreted as a degree of the material stiffness reduction. Formally, they can be introduced as multipliers to elastic moduli [39,40,41,42,43] similar to Kachanov’s discontinuity parameter [44]. Considering orthotropic composite material with possible fiber-dominant and matrix-dominant damage modes, a constitutive relation for damaged material can be written as follows:

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {\varepsilon _{11} } \\ {\varepsilon _{22} } \\ {\varepsilon _{33} } \\ {\gamma _{12} } \\ {\gamma _{13} } \\ {\gamma _{23} } \\ \end{array} }} \right\} =\left[ {{\begin{array}{*{20}c} {\frac{1}{\psi _{1} E_{11} }} &{}\quad {-\frac{\psi _{2} \nu _{21} }{E_{22} }} &{}\quad {-\frac{\psi _{2} \nu _{31} }{E_{33} }} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ {-\frac{\psi _{2} \nu _{12} }{E_{11} }} &{}\quad {\frac{1}{\psi _{2} E_{22}}} &{}\quad {-\frac{\psi _{2} \nu _{32} }{E_{33} }} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ {-\frac{\psi _{2} \nu _{13} }{E_{11} }} &{}\quad {-\frac{\psi _{2} \nu _{23} }{E_{22} }} &{}\quad {\frac{1}{\psi _{2} E_{33} }} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad {\frac{1}{\psi _{2} G_{12} }} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {\frac{1}{\psi _{2} G_{13} }} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {\frac{1}{\psi _{2} G_{23} }} \\ \end{array} }} \right] \left\{ {{\begin{array}{*{20}c} {\sigma _{11} } \\ {\sigma _{22} } \\ {\sigma _{33} } \\ {\sigma _{12} } \\ {\sigma _{13} } \\ {\sigma _{23} } \\ \end{array} }} \right\} , \end{aligned}$$

(1)

where $0\le \psi _{1} \le 1$ and $0\le \psi _{2} \le 1$ are damage parameters, associated with fiber and matrix failure correspondingly, where values of $\psi _{i} =1$ correspond to an undamaged initial state ($i = 1,2$). For real materials, the initial state is never perfect due to manufacturing defects, so an initial non-uniform distribution of them is probably needed for accurate predictions [45]. In case of determination of final failure, which can happen prior to the damage parameter reaching zero, to improve the simulation it is useful to put some critical deformations into the failure criterion. Because of the influence of damage parameters on the Poison’s ratio coefficients $\nu _{ij}$, the proposed constitutive relations have different members, which can increase and decrease values of stress components with progressive drop of the damage parameter $\psi _{2}$. The system of equations (1) is valid for orthotropic materials, but the equations can be written in invariant form. The approach can be used for materials with some waviness of fibers or in the cases of short fibers reinforcements with corresponding modifications, and then the contribution of the damage parameters to the stiffness reduction has to be reconsidered.

2.2 Damage initiation criterion

The damage initiation criterion for a unidirectional monolayer is simply chosen as maximum stress, so the undamaged conditions are expressed as follows:

$$\begin{aligned} \begin{array}{l} -X_{c} \le \sigma _{11} \le X_{T} ~ (\psi _{1} =1), \\ -Y_{c} \le \sigma _{22} \le Y_{T} ,{ }-Y_{c} \le \sigma _{33} \le Y_{T} (\psi _{2} =1), \\ \left| {\sigma _{12} } \right| \le S,{ }\left| {\sigma _{13} } \right| \le S { }\left| {\sigma _{23} } \right| \le S (\psi _{2} =1), \\ \end{array} \end{aligned}$$

(2)

where $X_{c}$ is the compression failure stress in fiber direction, $X_{T}$ the tension failure stress in fiber direction, $Y_{c}$ the compression failure stress in transverse direction, $Y_{T}$ the tension failure stress in transverse direction. All shear components have the same limit value S. The coordinate system is related to the fiber direction. In general, a certain simplification is made here for shear components, since shear load in fiber direction and perpendicular to the fibers may exhibit a noticeable difference [46], but for elastic deformation before damage initiation this difference is not significant.

2.3 Strength versus damage evolution

Following the assumptions of [39,40,41,42,43,44,45,46,47], we assume that the nonlinear material behavior is defined by the introduction of strength and damage parameters with special connection $\{X_{c}, X_{t}, Y_{c}, Y_{t}, S \} \sim \{\psi _{1} ,\psi _{2}\}$. The dependencies of the strength parameters on damage parameters can be more complex, and in the most general case they are coupled with each other. However, for the simplicity of the model we choose a combination where the matrix damage parameter has influence only on the matrix associated strength parameters $\{Y_{c}(\psi _{2}), Y_{T}(\psi _{2}), S(\psi _{2})\}$, and the fiber damage parameters are related only to fiber direction strength $\{X_{c}(\psi _{1}), X_{T}(\psi _{1})\}$.

Analyzing the works with progressive damage constitutive relations [47, 48] in combination with the analysis of experimental loading diagrams for unidirectional specimens of composite material [1, 2], it seems reasonable to assume as a typical relation between stress and strain components the one shown schematically in Fig. 1.

Fig. 1

Scheme of typical stress/strain curves

It is possible to see that for fiber direction uniaxial loading the curve has a linear drop after the ultimate strength is achieved (Fig. 1a, segment 1-2). If we stop the deformation increase and unload the material during damage accumulation (segment 2-3), the material is returned to the zero stress/strain state, without residual plastic strain. This is an assumption used for simplification of the model. The same situation occurs for transversal uniaxial and shear loadings: segment 2-3 returns the material to the beginning point.

Deformation with active damage accumulation of transversal uniaxial tension or compression (Fig. 1b) and shear (Fig. 1c) loadings have a nonlinear part, with some hardening of the material (segment 1-2). This nonlinear part of the material deformation, in contrast to the $\upsigma _{{11}}{\sim }\upvarepsilon _{{11}}$ loading curve, has no drop to zero stress at failure. This assumption imitates progressive brittle cracking of layers placed in layup with dissimilar layer orientations, and it is supposed to be used in modeling of layup failures. For the simple shear or tension loading of unidirectional specimens, the drop of maximum stress must be taken into account.

To represent the scheme of loading shown in Fig. 1, the following relations for strength parameters can be used for static failure analysis.

For fiber direction:

$$\begin{aligned} X_{T} (\psi _{1})= & {} \frac{A_{T}^{X} }{1+B_{T}^{X} /\psi _{1} },\nonumber \\ X_{C} (\psi _{1})= & {} \frac{A_{C}^{X} }{1+B_{C}^{X} /\psi _{1}}, \end{aligned}$$

(3)

where $A_{T}^{X}$, $B_{T}^{X}$, $A_{C}^{X}$ and $B_{C}^{X}$ are the material constants to be determined from quasi-static loading of a unidirectional specimen in fiber direction.

For transverse loading:

$$\begin{aligned} Y_{T} (\psi _{2} )= & {} A_{T}^{Y} +B_{T}^{Y} (1-\psi _{2})^{n_{T}^{Y} },\nonumber \\ Y_{C} (\psi _{2} )= & {} A_{C}^{Y} +B_{C}^{Y} (1-\psi _{2})^{n_{C}^{Y} }, \end{aligned}$$

(4)

where $A_{T}^{Y}$, $B_{T}^{Y}$, $A_{C}^{Y}$, $B_{C}^{Y}$ , $n_{T}^{Y}$ and $n_{C}^{Y}$ are material constants to be determined from quasi-static loading of unidirectional specimen in transverse direction.

For shear loading:

$$\begin{aligned} S(\psi _{2} )=A^{S}+B^{S}(1-\psi _{2} )^{n^{S}}, \end{aligned}$$

(5)

where $A^{S}$, $B^{S}$ and $n^{S}$ are material constants to be determined from quasi-static shear loading.

Some constants can be represented using standard engineering data:

$$\begin{aligned} A_{i}^{X}= & {} X_{i}^{0} \varepsilon _{i}^{Failure} /(\varepsilon _{i}^{Failure} -\varepsilon _{i}^{Init} ),\nonumber \\ B_{i}^{X}= & {} \varepsilon _{i}^{Init} (\varepsilon _{i}^{Failure} -\varepsilon _{i}^{Init} ),\nonumber \\&A_{i}^{Y} +B_{i}^{Y} =Y_{i}^{Ult},\nonumber \\ A_{i}^{Y}= & {} Y_{i}^{0} ,\nonumber \\ A^{S}= & {} S^{0}, \end{aligned}$$

(6)

where subscript i denotes tension or compression in accordance with Fig. 1, $X_{i}^{0}$, $Y_{i}^{0}$ denote limit stresses, and $Y_{i}^{Ult}$ denotes ultimate one.

3 Damage rate hardening

Most of the materials including layered composites inherit hardening under conditions of high strain rate. Probably, the most known approach to model this effect is associated with works of Johnson and Cook [49], where the rate of equivalent plastic strain is included into the plasticity criterion. The equivalent plastic strain is a quantity, which is responsible for hardening of the elastic-plastic material, and the consideration of the rate of it is the most natural way to model hardening, connected with a high deformation rate. In the case considered in this research, where all nonlinearity is caused by the damage parameters {$\psi _{1},~\psi _{2}$}, it is natural to suggest an idea of the dependence of strength characteristics on the rate of these parameters $\{d\psi _{1}{/dt,~d}\psi _{2}{/dt}\}$. Thus, we can consider strength characteristics as the functions of two scalar parameters and their rates $\{\psi _{1},~\psi _{2,}~d\psi _{1}{/dt, d}\psi _{2}{/dt}\}$:

$$\begin{aligned} X_{T}= & {} X_{T} (\psi _{1} ,\psi _{2} ,\dot{{\psi }}_{1} ,\dot{{\psi }}_{2} ),\nonumber \\ X_{C}= & {} X_{C} (\psi _{1} ,\psi _{2} ,\dot{{\psi }}_{1} ,\dot{{\psi }}_{2} ),\nonumber \\ Y_{T}= & {} Y_{T} (\psi _{1} ,\psi _{2} ,\dot{{\psi }}_{1} ,\dot{{\psi }}_{2} ),\nonumber \\ Y_{C}= & {} Y_{C} (\psi _{1} ,\psi _{2} ,\dot{{\psi }}_{1} ,\dot{{\psi }}_{2} ),\nonumber \\ S= & {} S(\psi _{1} ,\psi _{2} ,\dot{{\psi }}_{1} ,\dot{{\psi }}_{2}). \end{aligned}$$

(7)

Using the assumptions made in the previous section, we can eliminate some dependencies for strength parameters, keeping fiber damage parameters only in the fiber strength and the matrix damage parameters only in the matrix strength. This lets us rewrite strength parameters relations in the following form:

$$\begin{aligned} X_{T}= & {} X_{T} (\psi _{1} ,\dot{{\psi }}_{1} ), \nonumber \\ X_{C}= & {} X_{C} (\psi _{1} ,\dot{{\psi }}_{1} ), \nonumber \\ Y_{T}= & {} Y_{T} (\psi _{2} ,\dot{{\psi }}_{2} ), \nonumber \\ Y_{C}= & {} Y_{C} (\psi _{2} ,\dot{{\psi }}_{2} ), \nonumber \\ S= & {} S(\psi _{2} ,\dot{{\psi }}_{2} ). \end{aligned}$$

(8)

The analysis of experimental data of high strain rates reveals the non-sensitivity to the rate of loading in the case of uniaxial tension in fiber direction, and an insignificant influence on transverse tension characteristics [4, 5]. Taking this fact into account, the relations (8) can be reduced to:

$$\begin{aligned} X_{T}= & {} X_{T} (\psi _{1} ), \nonumber \\ X_{C}= & {} X_{C} (\psi _{1} ,\dot{{\psi }}_{1} ), \nonumber \\ Y_{T}= & {} Y_{T} (\psi _{2} ), \nonumber \\ Y_{C}= & {} Y_{C} (\psi _{2} ,\dot{{\psi }}_{2} ), \nonumber \\ S= & {} S(\psi _{2} ,\dot{{\psi }}_{2}). \end{aligned}$$

(9)

For the tensile parameters $X_{T }$ and $Y_{T }$, we can assume the same form as for static failure analysis, presented in Sect. 2.3. For the remaining parameters, we can continue the development of the relations to a more exact and practically suitable form. Following the ideas for modeling the plastic rate hardening [49], we can split the strength parameters into static and dynamic parts:

$$\begin{aligned} X_{C}= & {} X_{C}^{St} (\psi _{1})X_{C}^{Dyn} (\dot{{\psi }}_{1} ), \nonumber \\ Y_{C}= & {} Y_{C}^{St} (\psi _{2})Y_{C}^{Dyn} (\dot{{\psi }}_{2} ), \nonumber \\ S= & {} S^{St}(\psi _{2}) S^{Dyn}(\dot{{\psi }}_{2}). \end{aligned}$$

(10)

Now we can consider static and dynamic strength variation independently. For the static parts of the strength parameters we can use the relations given in Sect. 2.3. Thus, the dynamic multipliers have to be equal to 1 for a quasi-static analysis: $X^{Dyn}\rightarrow 1$ if $\dot{{\psi }}_{1} \rightarrow 0$, and $\{Y^{Dyn},S^{Dyn}\}\rightarrow \{1,1\},$ if $\dot{{\psi }}_{2} \rightarrow 0$.

Based on the analysis of experimental data [1, 2], in the research under consideration the following relations are proposed as specific forms of dynamic components for strength conditions:

$$\begin{aligned} X^{Dyn}\left( {\dot{\psi }_{1}}\right)= & {} 1+C_{X}\left( \_\dot{\psi }_{1} \big / \dot{\psi }_{1}^{0}\right) ^{N_{x}},\nonumber \\ Y^{Dyn}\left( {\dot{\psi }_{2}}\right)= & {} 1+C_{Y}\left( \mathrm{ln}\left( \_\dot{\psi }_{2}\big /\dot{\psi }_{2}^{0}\right) \right) ^{N_{Y}},\nonumber \\ S^{Dyn}\left( \dot{\psi }_{2}\right)= & {} 1+ \left( \hbox {sinh}\left[ C_{s} \mathrm{ln}(\_\dot{\psi }_{2}\big / \dot{\psi }_{2}^{0})\right] \right) ^{N_{s}}, \end{aligned}$$

(11)

where $C_{i}\, , N_{i}$ and $\dot{\psi }_{i}^{0}$ are material constants, and in the case when $\dot{\psi }_{i}<\dot{\psi }_{i}^{0}$ the dynamic components are equal to 1: $X^{Dyn}\equiv 1,Y^{Dyn}\equiv 1$ and $S^{Dyn}\equiv 1$.

Thus, the complete set of relations for strength characteristics formulated in terms of functions of damage parameters can be represented in the following form:

$$\begin{aligned} X_{T}= & {} \frac{A_{T}^{X} }{1+B_{T}^{X} /\psi _{1} }, \nonumber \\ X_{C}= & {} \left( \frac{A_{C}^{X}}{1+B_{C}^{X} /\psi _{1}} \right) \left( 1+C_{X} \left( \_\dot{\psi }_{1}\big /\dot{\psi }_{1}^{0}\right) ^{N_{X}}\right) ,\nonumber \\ Y_{T}= & {} A_{T}^{Y} +B_{T}^{Y} (1-\psi _{2} )^{n_{T}^{Y} }, \nonumber \\ Y_{C}= & {} \left( A_{C}^{Y} +B_{C}^{Y} (1-\psi _{2})^{n_{C}^{Y}}\right) \left( 1+C_{Y}\left( \text{ ln } \left( -\dot{\psi }_{2} \big /\dot{\psi }_{2}^{0}\right) \right) ^{N_{Y}}\right) , \nonumber \\ S= & {} \left( A^{S}+B^{S}(1-\psi _{2})^{n^{S}}\right) \left( 1+\left( \sinh \left[ C_{S} \text{ ln } \left( \_\dot{\psi }_{2}\big /\dot{\psi }_{2}^{0}\right) \right] \right) ^{N_{S}}\right) . \end{aligned}$$

(12)

4 Validation

Test correlation and an exact way for obtaining the constants required for the proposed relations can be carried out using conventional test equipment in the case of low rate loadings, and for high rates by means of a methodology based on the tests with the split Hopkinson pressure bar. For both cases, during the test deformation progress, we can assume that the loading strain rate is constant and the process of material damage accumulation is active. This means that the current stress component is equal to the corresponding strength limit; for example, $X_{c }$ can be determined by the following relation:

$$\begin{aligned} \sigma _{11} (t)= & {} X_{C} (t)=\left( \frac{A_{C}^{X}}{1+B_{C}^{X}/\psi _{1} (t)}\right) \left( 1+C_{X} \left( -\dot{\psi }_{1}(t)\big /\dot{\psi }_{1}^{0}\right) ^{N_{X}} \right) \end{aligned}$$

(13)

Using the system of constitutive equations (1), the stress components can be expressed in terms of strain and corresponding modulus:

$$\begin{aligned} \sigma _{11} (t)=\varepsilon _{11} (t)E_{11}^{Current} =vt\psi _{1} (t)E_{11}^{0}, \end{aligned}$$

(14)

where v is the strain rate, t is time, $E_{11}^{Current}$ the current modulus, $E_{11}^{0}$ the initial non-damaged modulus.

Substituting the relation for the stress component $\sigma _{11} (t)$ from Eq. (13) into (14) we obtain the following equation:

$$\begin{aligned} vt\psi _{1} (t)E_{11}^{0} =\left( \frac{A_{C}^{X} }{1+B_{C}^{X} /\psi _{1} (t)} \right) \left( 1+C_{X} \left( \_\dot{\psi }_{1}{t}\big /\dot{\psi _{1}^{0}}\right) ^{N_{X}}\right) . \end{aligned}$$

(15)

Equation (15) is an ordinary differential equation with initial condition $\psi _{1} (0)=1$, because initially the material is not damaged. Similar derivations are performed for other parameters:

• for transverse compression:

  $$\begin{aligned} vt\psi _{2} (t)E_{22}^{0} =\left( A_{C}^{Y} +B_{C}^{Y} (1-\psi _{2} (t))^{n_{C}^{Y}} \right) \left( 1+C_{Y} \left( \text{ ln }\left( -\dot{\psi }_{1}(t)\big /\dot{\psi }_{2}^{0}\right) \right) ^{N_{Y}} \right) ; \end{aligned}$$

  (16)

• for shear components:

  $$\begin{aligned} vt\psi _{2} (t)G_{12}^{0}= & {} \left( A^{S}+B^{S}(1-\psi _{2} )^{n^{S}} \right) \left( 1+\left( \sinh \left[ C_{S} \text{ ln } \left( \_\dot{\psi }_{2}(t)\big /\dot{\psi }\right) \right] \right) ^{N_{S}}\right) , \end{aligned}$$

  (17)

with initial conditions for both cases $\psi _{2} (0)=1.\,E_{22}^{0}$ is the initial non-damaged transverse modulus, and $G_{12}^{0}$ is the initial non-damaged shear modulus.

Now, using test loading curves for different deformation rates, we need to choose constants which fit best all of them. It should be noted that in spite of the simplicity of the obtained initial value problems of first order, with exact values for constants and practically used rates, these equations belong to a special class of stiff systems requiring special numerical solving techniques [50, 51].

The experimental correlation based on carbon/epoxy composite material IM6G/3501-6 is shown in Figs. 2, 3, and 4 [1, 2]. Corresponding constants are shown in Tables 1, 2, and 3.

Fig. 2

Experimental and predicted shear stress vs. strain diagrams

One can see that for both cases of shear and transverse loading at initial elastic stage of deformations and low strain rates, a discrepancy with experimental data is observed. It was intentionally chosen to avoid the use of a viscoelastic material model for better correspondence, but to cover a wide range of strain rates. In terms of energy spent on damage of the material, the error is quite minor, which makes the model suitable for engineering practice such as crush test or impact modelings, with keeping a minimum of required experimental data to validate material constants. Reduction of a range of loading rates or the implementation of a viscoelastic model can improve the precision of the proposed models at the noted stage of deformation, but with a correspondingly increasing complexity.

Fig. 3

Experimental and predicted transverse compression stress vs. strain diagrams

Fig. 4

Experimental and predicted fiber direction compression stress vs. strain diagrams

The compressive behavior of unidirectional material loaded in the reinforcement direction has its own features. The model has a curve drop to zero stress values. The reason for this is the most important contribution of this type of loading to strength of the composite layup material. The accurate modeling of this mode of failure directly influences the capability of the entire modeling approach for all practically used layups and constructions. All loading curves have a smooth gradient and a final drop due to the damage rate in strength conditions.

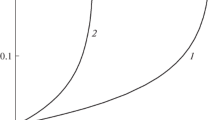
The next problem is concerned with the compressive strength estimation of cross ply layups [[0$_{\mathrm {8}}$/90$_{\mathrm {8}}$]$_{\mathrm {S}}$/0$_{\mathrm {4}}$]$_{\mathrm {S}}$ with different strain rates. For this numerical calculation, the software Abaqus has been used with specially developed user subroutines. Figure 5 shows the results of calculations in terms of strength versus strain rate for compression of unidirectional specimens and cross ply ones. It is possible to see that in spite of the perfect correlation between theoretical and experimental results for unidirectional specimens, the results of calculations for cross ply tests give understated ultimate loads for all loading rate. This probably can be explained by an imperfection of the method used to obtain $\upsigma _{\mathrm {11}}$~$\upvarepsilon _{\mathrm {11}}$ data. The material is stronger in transversally constrained compression tests, most likely due to the pure compression condition that causes buckling or barrel type deformation, and during the deformation process the stresses are redistributed, which means that only a part of the specimen section is loaded in pure compressive stress. However, in the final data presentation, the nominal cross-section area was used to obtain the stress components.

Table 1 Constants for shear strength limit $S(\psi ,\dot{\psi })$

Table 2 Constants for transverse compression strength limit $Y_{C}(\psi ,\dot{\psi })$

Table 3 Constants for fiber direction compression strength limit $X_{C}(\psi ,\dot{{\psi }})$

Fig. 5

Experimental and predicted fiber direction compressive strength for UD and cross ply

Nevertheless, the discrepancy of the theoretical values from experimental results for cross ply specimens is about 10%, which is quite satisfactory for any practical application. Thus, we can state that the presented approach has a good prediction capability.

Numerical analysis of the material response for non-monotonic and load reversal cycles with corresponding evolution of stress, strain and damage parameters in unidirectional material is carried out, too, and the results are presented in Figs. 6, 7, 8, and 9. The shear load cycle O-A-B-C-D-E-O is shown in Fig. 6 with the load increase segments OA, BC and DE and with final full unload EO. The corresponding matrix damage parameter evolution during shear loading versus strain is shown in Fig. 7. The shear strain grows non-monotonically in O-A, and the material gains initial damage, then a small load drop (segment A-B), then load increase (segment B-C) with additional damage, then a small load drop again (segment C-D) with the last increase in load D-E, and a final load drop to zero.

Figures 8 and 9 show similar results for a load cycle in longitudinal direction under a complex loading path of compression-tension-compression. The load grows up in compression in the step A-B-C with accumulation of some damage, and then the unloading with transformation to tension (C-D) occurs. It is possible to see that at point D, a sharp decrease of stress occurs before the nominal tension strength value is reached, because the material has initial damage caused by the prior compressive step. Then the material is unloaded with transition to second compression up to complete failure with zero stiffness (E-F-G). Figure 9 shows the corresponding evolution of the fiber damage parameter during this deformation process.

Fig. 6

Predicted stress–strain curve for shear load cycle O-A-B-C-D-E-O with final full unload

Fig. 7

Predicted strain vs. damage curve for shear load cycle O-A-B-C-D-E-O with final full unload

5 Conclusions

A composite material model, which takes into account the rate hardening effects, has been proposed with successful experimental correlation. The presented constitutive relations are capable of modeling different strength and hardening characteristics for different rates and types of loadings. The material model covers a wide range of strain rates from quasi-static loading to 1800 s$^{\mathrm {-1}}$. The predicted results for layup specimens slightly underestimate the experimental values of strength, which may be caused by an imperfection of the experimental technique for pure compression tests. One of the most innovative parts of this research is the use of damage rates in strength characteristics of the material. This approach allows us to formulate the failure model based only on damage parameters with minimum required experimental studies for their determination.

Fig. 8

Predicted stress–strain curve for longitudinal load cycle A-B-C-D-E-F-G with final compression to failure

Fig. 9

Predicted strain vs. damage curve for longitudinal load cycle A-B-C-D-E-F-G with final compression to failure