1. Identification of the Parameters of Internal Damping of Materials in a Linear Approximation

1.1. Logarithmic decrement of vibrations of materials in tension-compression. The test specimens (considered in [1] and recommended in [2]) of single-layer structure of thickness h 0, used as the base, and of a sandwich structure with layers made of a soft material (a rubber of thickness h r ), glued on both sides of the base, were cantilever plates of width b, length L, and thicknesses h = h 0 and h = h 0 + 2h r , respectively. The vibrations of such plates according to flexural modes with small amplitudes, to a high degree of accuracy due to h, h r < b, and b << L, can be described by an equation of motion based on the classical Kirchhoff–Love model. Such an equation, constructed assuming the cylindrical form of bending, laid at the basis of analysis of the aerodynamic component of damping [3] of a plate and written for the deflection w of its axial line, has the form (ρ 0 and ρ r are densities of the base material and rubber)

$$ \begin{array}{cc}\hfill {D}_{\Sigma}{w}^{IV}+{\rho}_{*}h\ddot{w}=H+P\hfill & \hfill {\rho}_{*}=\left({\rho}_0{h}_0+2{\rho}_r{h}_r\right)/h.\hfill \end{array} $$
(1.1)

Hereinafter, the rigidity factors are determined by the formulas (E 0, E r , μ 0, μ r are the elastic moduli and Poisson ratios of the base material and rubber, respectively)

$$ \begin{array}{c}\hfill {D}_{\Sigma}={D}_0+2{D}_1,\kern0.5em {D}_0={\tilde{E}}_0{h}_0^3/12,\hfill \\ {}\hfill {D}_1={\tilde{E}}_r\left[\frac{h_r^3}{12}+\frac{h_r{\left({h}_r+{h}_0\right)}^2}{4}\right],\kern0.5em {\tilde{E}}_0=\frac{E_0}{1-{\mu}_0^2},\kern0.5em {\tilde{E}}_r=\frac{E_r}{1-{\mu}_r^2};\hfill \end{array} $$
(1.2)

the primes denote differentiation with respect to x and dots — with respect to time t , while H and P stand for the forces of internal friction and the external aerodynamic resistance.

If the layer materials of test specimens are viscoelastic, the physical relations between the components of stress tensor σ ij , strain tensor ε ij , and strain rates \( {\dot{\varepsilon}}_{ij}=\partial {\varepsilon}_{ij}/\partial t \) can be presented in the form \( {\sigma}_{ij}={\sigma}_{ij}\left({\varepsilon}_{ij},{\dot{\varepsilon}}_{ij}\right) \). In the case of a uniaxial stress-strain state, the simplest of such dependences, most frequently used in practice, corresponds to the known Voigt model (see, for example, [4–7]):

$$ \sigma =E\varepsilon +\alpha \dot{\varepsilon}, $$
(1.3)

where E is the instantaneous elastic modulus; α is the viscosity factor, which, in harmonic vibrations at a frequency ω, when ε = ε 0 sin ωt (ε 0 is the peak value of strain), is connected with the logarithmic decrement of vibrations δ used in the literature by the relation

$$ \delta =\frac{\alpha \pi \omega }{E}. $$
(1.4)

Using the model (1.3), (1.4) described, Eq. (1.1) is presented in the form

$$ {D}_{\Sigma}{w}^{IV}+\frac{\delta_0}{\pi \omega }{D}_0{\dot{w}}^{IV}+\frac{2{\delta}_p}{\pi \omega }{D}_1{\dot{w}}^{IV}+{\rho}_{*}h\ddot{w}=P, $$
(1.5)

where δ 0 and δ p are the logarithmic decrements of vibrations of the base and rubber, respectively, which have to be determined.

The experimental logarithmic decrement of vibrations δ exp is calculated from the amplitude values of deflections A 1 and A 2 on two neighboring periods of vibrations:

$$ {\delta}_{\exp }= \ln \left({A}_1/{A}_2\right). $$
(1.6)

The similar parameter of internal damping of a sandwich test specimen with a flexural rigidity D Σ, corresponding to its damping vibrations in vacuum, is denoted by δ *. Upon vibration of the test specimen in a fluid (air), the parameters δ exp and δ * are related by the dependence

$$ {\delta}_{\exp }={\delta}_{*}+{\delta}_a, $$
(1.7)

where δ a is the aerodynamic component of damping, which, according to the results reported earlier [3], can be calculated from the formulas

$$ \begin{array}{c}\hfill {\delta}_a=\frac{b{\rho}_f}{h{\rho}_{*}}{F}_A,\kern0.5em {F}_A=\frac{6.14}{\sqrt{\beta }}+7\sqrt{k}\frac{\zeta^2}{\zeta^2+3.2},\kern0.5em \beta =\frac{b^2f}{v},\hfill \\ {}\hfill \zeta =k\left[2+1.78 \ln \Delta -\left(0.54+0.88 \ln \Delta \right) \ln \beta \right],k=A/b,\Delta =h/b,\hfill \end{array} $$
(1.8)

where A is the deflection amplitude of a test specimen in vibration according to the first mode; f is the frequency of flexural vibrations (Hz), and ν = 1.5·10−5 km/s2 is the kinematic viscosity of air of density ρ f = 1.29 kg/m3.

If the aerodynamic component δ a is subtracted from the parameter δ exp, found experimentally in [1], thereby determining the parameter δ * , the damped vibrations of a test specimen in vacuum can be described by the equation

$$ {D}_{\Sigma}{w}^{IV}+\frac{\delta_{*}}{\pi \omega }{D}_{\Sigma}{\dot{w}}^{IV}+{\rho}_{*}h\ddot{w}=0, $$
(1.9)

stemming from Eq. (1.5) at P = 0 if the condition

$$ {\delta}_{*}{D}_{\Sigma}=\delta {D}_0+2{\delta}_r{D}_1 $$
(1.10)

Let the parameters δ 0 and δ * be found by synthesis of the theory and experiment. Then, based on condition (1.10), the parameter δ r is calculated from the formula

$$ {\delta}_r={\delta}_{*}+\left({\delta}_{*}-{\delta}_0\right)\frac{E_0}{E_r\kappa }, $$
(1.11)

where \( \kappa =8{\tilde{h}}_0^3+12{\tilde{h}}_0^2+6{\tilde{h}}_0,\kern0.5em {\tilde{h}}_0={h}_r/{h}_0.. \)

The frequency of the first flexural mode of free vibrations of cantilever test specimens in vacuum can be found from the known relations

$$ {\omega}_0={\left(\frac{1.875}{L}\right)}^2\sqrt{\frac{D_0}{m_0}},\kern0.5em {m}_0={\rho}_0{H}_0, $$
(1.12)
$$ \omega ={\left(\frac{1.875}{L}\right)}^2\sqrt{\frac{D_{\Sigma}}{m}},\kern0.5em m={\rho}_0{h}_0+2{\rho}_r{h}_r, $$
(1.13)

written for the base and a sandwich bar with external layers made of a rubber, respectively. As is known (see, for example, [4–7]), vibration frequencies ω weakly depend on the parameters of internal and external (aerodynamic) damping, which was also completely confirmed by the experimental investigations performed in [1]. Therefore, assuming in formulas (1.12) and (1.13) that the frequencies ω are equal to those found experimentally (ω 0exp for the base and ω exp for the sandwich specimen), to determine the elastic moduli of base material E 0 and rubber E r , we come to the relations

$$ {E}_0=12{\left({\omega}_{0 \exp}\right)}^2{\rho}_0{L}^4/\left({1.875}^4{h}_0^2\right), $$
(1.14)
$$ {E}_r={E}_0\left[{\left({\omega}_{\exp }/{\omega}_{0 \exp}\right)}^2\left(1+2{\tilde{h}}_0\tilde{\rho}\right)-1\right]/\kappa, $$
(1.15)

where \( \tilde{\rho}={\rho}_r/{\rho}_0 \) is the relative density of materials of the layers of a sandwich test specimen.

We should note that formulas (1.11), (1.14), and (1.15) differ from those given in the Standard [2] only by the absence of the parameter δ 0 from formula (1.11), which is valid at δ 0 << δ *. Hence, the Standard [2] is also based on the model (1.3), (1.4), but, in determining the parameters δ 0 and δ r , the aerodynamic damping of specimens upon their vibration in air is not taken into account, thus identifying the experimentally found values of δexp with the parameter δ 0 in testing the base and with the parameter δ * in testing specimens of sandwich structure.

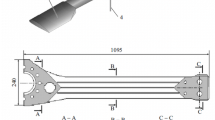
1.2. Results of experiments and identification of parameters. Figure 1 shows investigation results for test specimens of length L = 200mm, width b = 10mm, and thickness h = h 0 = 1mm for the base and h = h 0 + 2h r = 3.4 mm for the sandwich structure. In the latter case, the outer layers are made of a soft rubber used in the structure of torsion bar of the main rotor of a helicopter [1, 8] and having a density ρ r = 1600 kg/m3; the density of the steel base ρ 0 = 7800 kg/m3.

Fig. 1
figure 1

Experimental relations between the logarithmic decrements of vibrations δ exp and the amplitudes A of a test specimen of the base (1) and of a three-layer test specimen (h r = 1.2 mm) (2).

Full size image

The frequencies of the first tone of flexural damped vibrations of specimens, which were practically independent of vibration amplitude A, were ω 0exp = 116.8 rad/s for the base and ω exp = 96.1rad/s for the sandwich structure. Inserting them into Eqs. (1.14) and (1.15) for the dynamic elastic moduli of the base material (St 37 steel) and the rubber tested, we obtain that E 0 = 1.64·1011 Pa and E r = 0.56·108 Pa, respectively. The results of static tests in tension showed that, even at small tensile strains, the static elastic modulus of the rubber was by an order of magnitude lower than its dynamic elastic modulus, whereas that of the steel used for the base proved to be slightly lower than its static modulus.

Figure 2 illustrates relations between the aerodynamic component of vibration decrement δ a and amplitude A derived by using Eqs. (1.8), and Fig. 3 shows similar relations δ * = δ * ( A) describing only the internal damping of the base material and rubber in three-layer specimen.

Fig. 2
figure 2

Theoretical relations between the parameters of aerodynamic damping δ a and the amplitudes A of a test specimen of the base (1) and of a three-layer test specimen (h r = 1.2 mm) (2).

Full size image
Fig. 3
figure 3

Parameter of internal damping δ * as a function of amplitude A. Designations as in Fig. 2.

Full size image

Proceeding from the dependences presented in Fig. 3, according to Eq. (1.11) and the values of E 0 and E p found from Eqs. (1.14) and (1.15), relations between the logarithmic decrement of vibrations of rubber and the amplitude A, i.e., δ r = δ r ( A) , were constructed, which are shown in Fig. 4.

Fig. 4
figure 4

Parameter of internal damping δ r of rubber as a function of amplitude A.

Full size image

It is easily seen that, for the material (rubber) examined, the logarithmic decrement of vibrations depends on the amplitude, and hence on strains only, weakly. Therefore, in describing its damping properties with an accuracy acceptable in practical calculations, the parameter δ r in the model (1.3), (1.4) can be considered constant.

We should also note that the application of the suggested method to determining the internal damping properties of a material, as in [2], ensures reliable and trustworthy results only in the case where the rigidity B r = h r E r of material layers is sufficient, which can noticeably affect the dynamic behavior of a sandwich test specimen compared with that of the base specimen.

An analysis of the results obtained also shows that neglecting the aerodynamic damping can lead to errors of about 15% and higher toward underestimation of damping parameters of materials.

1.3. Logarithmic decrement of vibrations of a material in shear deformations. During damped flexural vibrations of sandwich specimens with rigid outer layers, each of thickness h 0, the soft midlayer made of a low-rigidity material of thickness h r is subjected to a practically pure transverse shear g constant across the thickness h r . Let us express the tangential stress τ, arising in it as a function of the strain γ, and its rate \( \dot{\gamma} \) by the relation

$$ \tau ={G}_r\gamma +{\alpha}_{\mathrm{sh}}\dot{\gamma}, $$

where G r is the dynamic (instantaneous) shear modulus; α sh is the viscosity factor of the material in shear, which is connected with the logarithmic decrement of vibrations in shear δ sh by the relationship

$$ {\delta}_{\mathrm{sh}}=\frac{\alpha_{\mathrm{sh}}\pi \omega }{G_r}. $$

To determine the shear modulus G r and vibration decrement δ sh of the soft layer from experimentally found parameters (from the frequency ω 0exp and vibration decrement δ 0 of the base, i.e., of a separate outer layer, and from the frequency ω exp and the vibration decrement δ * = δ exp + δ a of a specimen of sandwich structure), we can write formulas similar to (1.11) and (1.15). Such formulas can be found, in particular, in the Standard [2]; after some transformations and modifications, they take the form

$$ {G}_r={R}_{*}\frac{2\pi C{E}_0{h}_0{h}_r}{L^2\left[{\left(1-2R+2B\right)}^2+4{R}^2{\left({\delta}_{*}-{\delta}_0\right)}^2\right]}, $$
(1.16)
$$ {\delta}_{\mathrm{sh}}=\frac{R\left({\delta}_{*}-{\delta}_0\right)}{R_{*}}, $$
(1.17)

where

$$ \begin{array}{c}\hfill C=0.55959,\kern0.5em {R}_{*}=R-B-2{\left(R-B\right)}^2-2{R}^2{\left({\delta}_{*}-{\delta}_0\right)}^2,\hfill \\ {}\hfill R={\left({\omega}_{\exp }/{\omega}_{0 \exp}\right)}^2\left(2+\tilde{\rho}{\tilde{h}}_0\right)\left(B/2\right),\kern0.5em B=1/\left[6{\left(1+{\tilde{h}}_0\right)}^2\right].\hfill \end{array} $$

The method described was employed to determine the damping properties of a soft rubber whose layers were meant to ensure normalized damping properties of torsion bar of the main rotor of a helicopter [1, 8]. With this purpose, sandwich test specimens of width b = 10 mm, with load-carrying layers made of a St3 steel of thickness h 0 = 0.52 mm and a soft rubber filler of thickness h r = 0.6 mm, were prepared.

An analysis of the vibrorecords of damped vibrations of test specimens of the base and a sandwich bar of length L = 300 mm allowed us to obtain relations between the logarithmic decrements of vibrations and amplitude, as shown in Fig. 5.

Fig. 5
figure 5

Experimental relations between the logarithmic decrements of vibrations δ exp and the amplitudes A of a test specimen of the base (h 0 = 0.52 mm) (1) and of a three-layer test specimen (h r = 0.6 mm) (2).

Full size image

The frequencies of the first tone of flexural vibrations were found to be ω 0exp = 30.2 rad/s for the specimen of the base and ω exp = 71.6 rad/s for the sandwich test specimen, which made it possible to calculate the dynamic elastic modulus E 0 = 2.08·1011 Pa of material of the base from Eq. (1.14) and the dynamic shear modulus G r = 6.84·105 Pa of the tested rubber from Eq. (1.16).

For the test specimens examined, Fig. 6 illustrates the amplitude dependences of the aerodynamic component of logarithmic decrements of vibrations found from Eqs. (1.8). When they are taken into account, the amplitude dependence of logarithmic decrements of vibrations caused only by the internal damping of layer material takes the form shown in Fig. 7.

Fig. 6
figure 6

Theoretical relations between the parameters of aerodynamic damping δ a and the amplitudes A. Designations as in Fig. 5.

Full size image
Fig. 7
figure 7

Parameter δ * as a function of amplitude A of the test specimen of base (h 0 = 0.52 mm) (1) and of sandwich specimen (h r = 0.6 mm) (2).

Full size image

The dependences shown in Fig. 7 and formulas (1.17) were used to determine the relations δ sh = δsh ( A) between the logarithmic decrement of vibrations of rubber and vibration amplitude (Fig. 8). It is seen that, for the material (rubber) examined, the logarithmic decrement of vibrations strongly depends on the level of shear strain.

Fig. 8
figure 8

Parameter of the internal damping of rubber δ sh as a function of amplitude A.

Full size image

2. Determination of the Strain-Dependent Parameters of Internal Damping of Materials

2.1. Direct problem. Let us assume that a test specimen in the form of a cantilever sandwich plate has been preliminary curved (Fig. 9), and its right end x = L is simply supported and has a deflection amplitude w 00 at the initial instant of time. We assume that its vibration starts after the removal of the support mentioned. To determine the logarithmic decrement of vibrations of layer materials in tension–compression, as was already noted, the midlayer is assumed to be more rigid than the outer layers. In this connection, as in Sect. 1, within the framework of the classical Kirchhoff–Love model, the axial displacements and strains in an ith layer are determined by the expressions ( i is the number of a layer, Fig. 9)

$$ \begin{array}{ccc}\hfill {u}^i=-yw^{\prime}\left(x,t\right),\hfill & \hfill {w}^i=w\left(x,t\right),\hfill & \hfill {\varepsilon}^i=u^{\prime }=-yw^{\prime\prime },\hfill \end{array} $$
(2.1)

where h 1 = h 2 = h r and h 2 = h 0.

Fig. 9
figure 9

Diagram of testing of a specimen and the form of its transverse cross section.

Full size image

The physical relations for layer materials are taken according to the Voigt model (1.3):

$$ {\sigma}^i={\tilde{E}}^i{\varepsilon}^i+{\alpha}^i{\dot{\varepsilon}}^i,\kern0.5em {\alpha}^i={\tilde{E}}^i{\delta}^i/\left(\pi \omega \right). $$
(2.2)

We assume that the logarithmic decrement of vibrations δ i does not depend on vibration frequency (i.e., on strain rate), but, in the general case, depends on the strain level ε i . For simplicity, we will suppose that this level is the same both in tension and compression. To develop a method of fast solution to the direct problem on vibrations of the plate, the functions δ i (ε) are approximated by polynomials of the kind

$$ {\delta}^i\left(\varepsilon \right)={\delta}_0^i+{\delta}_1^i\left|\varepsilon \right|+{\delta}_2^i{\varepsilon}^2+{\delta}_3^i\left|{\varepsilon}^3\right|+\dots . $$
(2.3)

The system of equations of motion of the plate is written in the form

$$ \begin{array}{c}\hfill {M}_x^{\prime }={Q}_y{Q}_y^{\prime }=q\kern0.5em q=-m\ddot{w},\kern0.5em m={\rho}_1{A}_1+{\rho}_2{A}_2+{\rho}_3{A}_3,\hfill \\ {}\hfill {M}_x={\displaystyle \sum_{i=1}^3{\displaystyle \underset{A_i}{\int }{\sigma}^i yd{A}_i={\displaystyle \sum_{i=1}^3{E}_i{\displaystyle \underset{A_i}{\int}\left(w^{\prime \prime }+\frac{\delta^i}{\pi \omega}\dot{w}^{\prime\prime}\right){y}^2d{A}_i,}}}}\hfill \end{array} $$
(2.4)

where M x is the bending moment, Q y is the shearing force, A i is the cross-sectional area of an ith layer, and ρ i is density of this layer. System (2.4) yields the nonlinear equation in w

$$ \begin{array}{cc}\hfill {\displaystyle \sum_{i=1}^3{E}_i{\displaystyle \underset{A_i}{\int }{\left[w\prime \prime +\frac{\delta^i}{\pi \omega}\dot{w}\prime \prime \right]}^{\prime \prime }{y}^2dA+m\ddot{w}=0,}}\hfill & \hfill {\delta}^i={\delta}^i\left(\varepsilon \right)={\delta}^i\left(-yw^{\prime\prime}\right).\hfill \end{array} $$
(2.5)

To use the Ritz method instead of (2.5), let us construct a variational equation in the deflection w. With this purpose, we multiply Eqs. (2.5) by the variation of deflection δw and integrate by parts two times along the length of the plate with account of boundary conditions (in what follows, the symbol δ without indices means the variation sign):

$$ \delta w(0)=0,\delta w^{\prime }(0)=0,M(L)=0,Q(L)=0. $$
(2.6)

As a result, we come to the equation

$$ {\displaystyle \underset{0}{\overset{L}{\int }}\left({\displaystyle \sum_{i=1}^3{E}_i{\displaystyle \underset{A_i}{\int}\left(w^{\prime \prime }+\frac{\delta^i}{\pi \omega}\dot{w}^{\prime\prime}\right)\delta w^{\prime \prime }{y}^2d{A}_i}}\right)dx+m{\displaystyle \underset{0}{\overset{L}{\int }}\ddot{w}\delta wdx=0}.} $$
(2.7)

The solution for the deflection w(x) is sought in the form

$$ \begin{array}{ccc}\hfill w=\left[N(x)\right]\left\{V(t)\right\},\hfill & \hfill \left[N(x)\right]=\left[{N}_1(x),{N}_2(x),\dots \right],\hfill & \hfill \left\{V(t)\right\}={\left[{V}_1(t),{V}_2(t),\dots \right]}^{\mathrm{T}}.\hfill \end{array} $$
(2.8)

Hereinafter, the square brackets and braces designate matrices and vectors: [N] is the form function, {V} is the time-dependent vector composed of required scalar functions V 1(t),V 2 (t), … , and the superscript T denotes transposition.

Insertion of Eqs. (2.8) into Eq. (2.7) yields the equation

$$ \left[K\right]\left\{V\right\}+\left[{K}_D\right]\left\{\dot{V}\right\}=-m\left[M\right]\left\{\ddot{V}\right\}, $$
(2.9)

where

$$ \begin{array}{cc}\hfill \left[K\right]=\left({\displaystyle \sum_{i=1}^3{E}_i{\displaystyle \underset{A_i}{\int }{y}^2dA}}\right){\displaystyle \underset{0}{\overset{L}{\int }}{\left[B\right]}^{\mathrm{T}}\left[B\right]dx,}\hfill & \hfill \left[B\right]=\left[N^{\prime\prime}\right],\hfill \end{array} $$
(2.10)
$$ \left[{K}_D\right]={\displaystyle \underset{0}{\overset{L}{\int }}\left({\displaystyle \sum_{i=1}^3{E}_i{\displaystyle \underset{A_i}{\int}\frac{\delta^i\left(-yw^{\prime\prime}\right)}{\pi \omega }}{y}^2dA}\right){\left[B\right]}^{\mathrm{T}}\left[B\right]dx,\left[M\right]={\displaystyle \underset{0}{\overset{L}{\int }}{\left[N\right]}^{\mathrm{T}}\left[N\right]dx.}} $$
(2.11)

For Eq. (2.9), we will formulate the following initial conditions. At t = 0, ẇ = 0, while the initial deflection is described by the function

$$ {w}_0(z)=\left(\frac{Pl{x}^2}{2}-\frac{P{x}^3}{6}\right)/(EJ),\kern0.5em EJ={\displaystyle \sum_{i=1}^3{E}_i{\displaystyle \underset{A_i}{\int }{y}^2d{A}_i}.} $$
(2.12)

Here, P is the reaction of the right support, which is calculated from the initial deflection of the free end of the plate by the formula w 00 = PL 3 /(3EJ). From initial condition (2.12), it follows that

$$ \left[N(x)\right]\left\{V(0)\right\}={w}_0(x). $$
(2.13)

Using the method of minimization of the squared discrepancy in relation (2.13), we arrive at the equation for the initial vector{V (0)}

$$ \left[M\right]\left\{V(0)\right\}={\displaystyle \underset{0}{\overset{l}{\int }}{\left[N(x)\right]}^{\mathrm{T}}}{w}_0(x)dx. $$
(2.14)

The solution of Eq. (2.14) has the simplest form in the case of a polynomial function of the form [N(x)]. Let

$$ \left[N\right]=\left[{x}^2,{x}^3,{x}^4,\dots \right]. $$

Then, from Eq. (2.14), we have

$$ \left\{V(0)\right\}={\left\{\frac{3{w}_{00}}{2{L}^2},\frac{-{w}_{00}}{2{L}^3},0,0,\dots \right\}}^{\mathrm{T}}. $$
(2.15)

In addition, from the initial condition ẇ = 0, it follows that

$$ \left\{\dot{V}(0)\right\}={\left\{0,0,\dots \right\}}^{\mathrm{T}}. $$
(2.16)

Thus, the original problem is reduced to the initial problem (2.9), (2.15), (2.16) with respect to the vector {V (t)}. To find its numerical solution, time discretization was carried out by the finite-difference method with a uniform step Δt. At t = t n = Δtn, n = 0, 1, 2,…, the following approximations of time derivatives (further on, the braces for {V} are omitted for simplicity) were assumed:

$$ {\dot{V}}^{(n)}=\frac{V^{\left(n+1\right)}-{V}^{\left(n-1\right)}}{2\Delta t},{\ddot{V}}^{(n)}=\frac{V^{\left(n+1\right)}+{V}^{\left(n-1\right)}-2{V}^{(n)}}{{\left(\Delta t\right)}^2}. $$

The problem formulated was also solved by the Crank–Nicholson method. The calculations showed that the solutions derived on the basis of both time integration methods differ from each other only slightly (by no more than 1%).

For describing the behavior of plates, we also considered the cases where, in the function of form [N], various numbers of terms of polynomial were retained. It was found that, with only two terms retained in this polynomial, the results of solution of the problem (for frequencies, amplitudes, and vibration decrements) differed by no more than 5% from those obtained by using three and four terms of the polynomial.

For statement of the problem on vibrations of test specimens with a soft midlayer (Fig. 10), we assume the numbering of layers already adopted, starting from the lower one, still designating their thicknesses by h 1, h 2, and h 3, and the coordinates of layer boundaries by y i . But, in this case, we take that h 1 = h 3 = h 0 and h 2 = h p .

Fig. 10
figure 10

Arrangement of layers of a test specimen and the distribution of displacements across its thickness.

Full size image

Let us introduce, as unknowns, the displacements of points of the layer boundaries in the direction of x axis, designating them by U 1,U 2,… . Then, for the displacements u i and w i in an ith layer, we can assume the approximations

$$ \begin{array}{c}\hfill {u}^i\left(y,x,t\right)={U}_i\left(x,t\right)\frac{y_{i+1}-y}{h_i}+{U}_{i+1}\left(x,t\right)\frac{y-{y}_i}{h_i},{h}_i={y}_{i+1}-{y}_i,\hfill \\ {}\hfill {w}^i\left(y,x,t\right)=W\left(x,t\right),\hfill \end{array} $$
(2.17)

which, within each layer, correspond to the Timoshenko model without account of transverse compression. Their insertion into the Cauchy relations for determining the components of strain leads to the expressions

$$ \begin{array}{c}\hfill {\varepsilon}^i={\varepsilon}_{xx}^{(i)}=\frac{\partial {u}^i}{\partial x}={U}_i^{\prime}\left(x,t\right)\frac{\left(-y+{y}_{i+1}\right)}{h_i}+{U}_{i+1}^{\prime}\left(x,t\right)\frac{\left(y-{y}_i\right)}{h_i},\hfill \\ {}\hfill {\gamma}^i=2{\varepsilon}_{xy}^{(i)}=\frac{\partial {u}^i}{\partial y}+\frac{\partial {w}^i}{\partial x}=\frac{\left[{U}_{i+1}\left(x,t\right)-{U}_i\left(x,t\right)\right]}{h_i}+W^{\prime}\left(x,t\right).\hfill \end{array} $$
(2.18)

For the plate model assumed, the relations of type (1.3), (1.4) for an ith layer can be written in the form

$$ \begin{array}{c}\hfill {\sigma}^i={\sigma}_{xx}^{(i)}={E}^i{\varepsilon}^i+{\alpha}^i{\dot{\varepsilon}}^i\kern0.5em {\alpha}^i={E}^i{\delta}^i/\left(\pi \omega \right),\hfill \\ {}\hfill \begin{array}{cc}\hfill {\tau}^i={\tau}_{xy}^{(i)}={G}^i{\gamma}^i+{\beta}^i{\dot{\gamma}}^i,\hfill & \hfill {\beta}^i={G}^i{\delta}_c^i/\left(\pi \omega \right).\hfill \end{array}\hfill \end{array} $$
(2.19)

Since the plate is considered thin, it is possible to neglect the inertia of rotation and deformation shear. Then, to deduce the conclusion of the equations of motion, we can write the variational equation

$$ {\displaystyle \sum_{i=1}^3{\displaystyle \underset{V_i}{\int }{\sigma}^i\delta {\varepsilon}^id{V}_i+{\displaystyle \sum_{i=1}^3{\displaystyle \underset{V_i}{\int }{\tau}^i\delta {\gamma}^id{V}_i+{\displaystyle \sum_{i=1}^3{\displaystyle \underset{V_i}{\int}\rho \ddot{w}\delta wd{V}_i=0,}}}}}} $$
(2.20)

which, for plates with a rectangular cross section, is transformed to the form

$$ \begin{array}{c}\hfill {\displaystyle \sum_{i=1}^3{\displaystyle \underset{0}{\overset{L}{\int }}\left[{E}_i{I}_{1i}\left({U}_i^{\prime }+{\dot{U}}_i^{\prime }{\delta}^i/\pi \omega \right)\delta {U}_i^{\prime }+{E}_i{I}_{2i}\left({U}_{i+1}^{\prime }+{\dot{U}}_{i+1}^{\prime }{\delta}^i/\pi \omega \right)\delta {U}_{i+1}^{\prime}\right.}}\hfill \\ {}\hfill +{E}_i{I}_{3i}\left({U}_i^{\prime }+{\dot{U}}_i^{\prime }{\delta}^i/\pi \omega \right)\delta {U}_{i+1}^{\prime }+{E}_i{I}_{3i}\left({U}_{i+1}^{\prime }+{\dot{U}}_{i+1}^{\prime }{\delta}^i/\pi \omega \right)\delta {U}_i^{\prime}\hfill \\ {}\hfill +{G}_i\left({U}_{i+1}-{U}_i+{\dot{U}}_{i+1}{\delta}_c^i/\pi \omega -{\dot{U}}_i{\delta}_c^i/\pi \omega \right)\left(\delta {U}_{i+1}-\delta {U}_i\right)\hfill \\ {}\hfill +{G}_i\left(W^{\prime }+\dot{W}^{\prime }{\delta}_c^i/\pi \omega \right)\delta W^{\prime }{h}_i+{G}_i\left({U}_{i+1}-{U}_i+{\dot{U}}_{i+1}{\delta}_c^i/\pi \omega -{\dot{U}}_i{\delta}_c^i/\pi \omega \right)\delta W^{\prime}\hfill \\ {}\hfill \left.+{G}_i\left(W^{\prime }+\dot{W}^{\prime }{\delta}_c^i/\pi \omega \right)\left(\delta {U}_{i+1}-\delta {U}_i\right)\right]dx+m{\displaystyle \underset{0}{\overset{L}{\int }}\ddot{W}\kern0.5em \delta W\kern0.5em dx=0,}\hfill \\ {}\hfill m={\rho}_1{A}_1+{\rho}_2{A}_2+{\rho}_3{A}_3.\hfill \end{array} $$
(2.21)

Here, the following designations have been introduced:

$$ \begin{array}{c}\hfill \begin{array}{cc}\hfill {I}_{1i}={\displaystyle \underset{y_i}{\overset{y_{i+1}}{\int }}\left(y-{y}_{i+1}\right)/{h}_i^2\kern0.5em dy,}\hfill & \hfill {I}_{2i}={\displaystyle \underset{y_i}{\overset{y_{i+1}}{\int }}{\left(y-{y}_i\right)}^2/{h}_i^2\kern0.5em dy,}\hfill \end{array}\hfill \\ {}\hfill {I}_{3i}={\displaystyle \underset{y_i}{\overset{y_{i+1}}{\int }}\left(y-{y}_i\right)\left({y}_{i+1}-y\right)/{h}_i^2\kern0.5em dy.}\hfill \end{array} $$

As earlier, for the unknowns U i (x,t), W(x,t), we assumed approximations in the form of polynomials

$$ \begin{array}{c}\hfill {U}_i\left(x,t\right)={U}_{i,0}(t)+{U}_{i,1}(t)x+\dots {U}_{i,n}(t){x}^n,\hfill \\ {}\hfill W\left(z,t\right)={W}_0(t)+{W}_1(t)x+\dots {W}_{n+1}(t){x}^{n+1},\hfill \end{array} $$
(2.22)

where U i,0, U i,1,…,W 0,…,W n+1 are the required functions of time, whereas the degree of the polynomial for W is taken by one unity higher than for the polynomials for the unknowns U i .

Inserting Eqs. (2.22) into Eq. (2.21), we come to the equations of motion composed with respect to the functions U i,n and W n in the standard way. In their solution and calculations, the minimum number of unknowns, corresponding to the approximations

$$ W={W}_2(t){x}^2+{W}_3(t){x}^3\kern0.5em {U}_i={U}_{i,1}(t)x+{U}_{i,2}(t){x}^2, $$

were used.

To define the initial conditions, we first solved the static problem on cylindrical bending of a plate with a given w 00 deflection for its right end and determined the values of U i,1(0), U i,2 (0), W 2 (0), and W 3 (0). As earlier, the first derivatives of the sought-for functions at the initial instant of time were equal to zero. As a result, Eq. (2.21), in a combination with the initial conditions, leads to the initial problem relative to the functions U i,1,U i,2, W 2, and W 3, which is solved by the same method as in Sect. 2.1.

2.2. Identification of the logarithmic decrement of vibrations of materials. Let experimental results for vibrations of the plate shown in Figs. 9 and 10 be known. Then, it can be considered that the time dependences of vibration amplitude of its right free end are found. In the general case, we assume that the experiments were carried out for different relations of layer thicknesses and different lengths of the plate. Hence, we can determine experimental values of the logarithmic decrements of vibrations of different test specimens, δ exp1 , δ exp2 , … δ exp n , for different amplitude ( n is the total number of experimental values of the logarithmic decrement of vibrations).

The identification problem consists in search for the functions for layer materials

$$ \begin{array}{c}\hfill {\delta}^i\left(\varepsilon \right)={\delta}_0^i+{\delta}_1^i\left|\varepsilon \right|+{\delta}_2^i{\varepsilon}^2+{\delta}_3^i\left|{\varepsilon}^3\right|+\dots, \hfill \\ {}\hfill {\delta}^{\gamma}\left(\gamma \right)={\delta}_0^{\gamma }+{\delta}_1^{\gamma}\left|\gamma \right|+{\delta}_2^{\gamma }{\gamma}^2+{\delta}_3^{\gamma}\left|{\gamma}^3+\dots \right|\hfill \end{array} $$

from the condition that the results of computational experiments differ only slightly from the results of physical tests. For this purpose, the problems on vibrations of plates with the same sizes as in experiments, but with trial values δ i0 , δ i1 , δ i2 , …, have to be solved. Then, the vibration decrements δ cal1 , δ cal2 , …, δ cal n of a sandwich plate can be calculated. To compare the results obtained, the norm of discrepancy of the quantities to be compared must be introduced, for example, in the form

$$ \Delta =\frac{1}{n}\sqrt[2k]{{\left(\frac{\delta_1^{\mathrm{cal}}-{\delta}_1^{\exp }}{\delta_1^M}\right)}^{2k}+{\left(\frac{\delta_2^{\mathrm{cal}}-{\delta}_2^{\exp }}{\delta_2^M}\right)}^{2k}+\dots } $$
(2.23)

Minimizing the quantity Δ by choosing various values of δ i0 , δ i1 , δ i2 , …, we find the values of δ cal1 , δ cal2 , …, δ cal n which best agree with experimental data.

In order to exclude the influence of environment caused by the aerodynamic forces of air resistance, the calculation results for the vibration decrement were obtained by using expression (1.8). As the norm (2.23), the quadratic discrepancy was employed. Its minimum was found by using the method consisting in the following. A base point of δ i0 , δ i1 , δ i2 , … is chosen, and the value of the objective function Δ is estimated at points surrounding the base one. If the point giving a minimum of the objective function is new, it is taken for the next base point. Otherwise, the region of search is narrowed and the procedure is repeated.

In what follows, some results of identification of damping characteristics for a base made of St3 steel and for a rubber are presented. First, the experimental data for steel single-layer test specimens with L = 200, 250, and 300 mm were processed. The results are shown in Fig. 11. An analysis of these relationships shows that, up to a strain of 0.08%, the characteristic δ st in tension-compression can be regarded as a linear function of strains.

Fig. 11
figure 11

Graphs of relations between the damping characteristic δ st and strain ε for steel obtained in different experiments.

Full size image

Next, the experimental data for sandwich test specimens of the same length L = 200, 250, and 300 mm, with a 1.2-mm-thick outer rubber layers, were processed. The results obtained are illustrated in Fig. 12.

Fig. 12
figure 12

Relations between the damping characteristic δ r and strain ε for rubber obtained in different experiments.

Full size image

An analysis of these relations showed that, up to strains of the order of 0.3%, the characteristic δ r in tension-compression could be considered constant.

However, in the case of shear deformations, quite a different picture is observed — the vibration decrement of resin considerably depends on shear strains, as seen from Fig. 13. The solution of the corresponding identification problem makes it possible to assume the following relation between the vibration decrement δ sh and the shear strain γ :

Fig. 13
figure 13

Damping characteristic δ sh of rubber as a function of shear strain γ.

Full size image
$$ {\delta}_{\mathrm{sh}}=0.0014+103.3\left|\gamma \right|-2360{\gamma}^2. $$

Comparing the results presented in Figs. 12 and 13, it can be seen that, for the material examined, the use of the formula δ sh = δ r /[2(1 + μ r )], similar to the formula G r  = E r /[2(1 + μ r )], allows one to estimate the effect of damping properties of a material on the dynamic processes of its deformation in shear only with a significant error.