The concept of measurement uncertainty [1–4] is used in metrology along with error estimates [5]. The question of which approach is preferable in these metrological problems remains open. Error calculations are, however, widely used in the calibration of means of measurement. During calibration, the systematic error of a measuring instrument is often determined as the deviation of the readings from a reference value of the measured quantity that is reproduced or obtained from a suitable standard.

The following are taken into account when calculating measurement uncertainty: uncertainty in the calibration characteristics of the standard measurement instruments or in the current values of the standard gauges, as well as their instability; nonlinearity of the calibration characteristic of the measurement instruments; random errors in the standards, the instrument being calibrated, and the calibration technique; and uncertainty in the corrections for the deviations from standard conditions specified for each type of measurement and in the method for transfer of the unit of the measured quantity.

This article discusses a simplified model for the systematic error B of a measuring instrument that is being calibrated:

$$ B=X={X}_{\mathrm{ref}}, $$
(1)

where X is the average reading of the instrument being calibrated for a number of repeated measurements that approaches infinity, and X ref is the reference value of the measured quantity.

For a specific form of measurement and calibration technique, model (1) becomes more complicated with the introduction of corrections for influence factors and the approach discussed below can be generalized for any particular case.

For measurements with the aid of a standard, an estimate of the measured quantity is obtained with the corresponding uncertainty {x ref, u(x ref)} or with an indication of the limits of error {x ref, θ}. In the former case, information on the measured quantity can be represented by a normal density distribution p ref(x) with mathematical expectation x ref and standard deviation u(x ref) and in the latter case, by a uniform distribution with center x ref and symmetric boundaries ±θ [6].

Usually, repeated measurements x 1, …, x n are made during calibration in order to evaluate the combined random error owing to the standards, the instruments to be calibrated, and the calibration technique. Here it is assumed that the unit readouts of the measurement instrument are distributed normally with unknown parameters {X ref + B, σ}, where σ is a precision (repeatability) parameter for the measurement results during calibration. Thus, in this problem there are three unknown parameters X ref, B, and σ. The joint probability distribution for these parameters is found using Bayes’ theorem on the basis of the available a priori information, as well as the information obtained during the measurements. We assume that these parameters are independent. We also assume that there is no a priori information on the bias of the readings from the measurement instrument or the precision of the measurements and that these are described by an uninformative a priori density distribution p(b, σ) ∝ σ-1 for these parameters (the symbol ∝ denotes equality to within a normalization factor).

Let us consider the first of these cases. Here the a posteriori joint distribution is specified by

$$ \begin{array}{l}p\left(x,b,\sigma \mid {x}_1,\dots, {x}_n,{x}_{\mathrm{ref}},u\left({x}_{\mathrm{ref}}\right)\right)\propto {\sigma}^{-\left(n+1\right)} \exp \left\{-\frac{1}{2{\sigma}^2}{\displaystyle \sum \left({x}_1-b-{x}^2\right)}\right\}\times \\ {}\kern8em \times \exp \left\{-{\left(x-{x}_{\mathrm{ref}}\right)}^2/\left[2{u}^2\left({x}_{\mathrm{ref}}\right)\right]\right\}.\end{array} $$

Integrating with respect to the interfering parameter makes it possible to fi nd an a posteriori distribution for the systematic error:

$$ p\left(x,b,\mid {x}_1,\dots, {x}_n,{x}_{\mathrm{ref}},u\left({x}_{\mathrm{ref}}\right)\right)={\displaystyle \int p\left(x,b,\sigma \mid {x}_1,\dots, {x}_n,{x}_{\mathrm{ref}},u\left({x}_{\mathrm{ref}}\right)\right)} d\sigma dx $$

After some simple calculations, we obtain:

$$ \begin{array}{l}p(b)=\frac{1}{2^{\left(n-1\right)/2}\uppi}\frac{{\left(\left(n-1\right){S}^2\right)}^{\left(n-1/2\right)}}{u\left({x}_{\mathrm{ref}}\right)}\frac{\varGamma \left(n/2\right)}{\varGamma \left(n-1/2\right)}\frac{1}{\sigma^{n+1}}\times \\ {}\times {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\left(n{\left(b+x-\overline{x}\right)}^2+\left(n-1\right){S}^2\right)}^{-n/2} \exp \left\{\frac{-{\left(x-{x}_{\mathrm{ref}}\right)}^2}{2{u}^2\left({x}_{\mathrm{ref}}\right)}\right\}dx;}\end{array} $$
$$ {S}^2=\frac{1}{n-1}{\displaystyle \sum_1^n{\left({x}_i-\overline{x}\right)}^2},\overline{x}=\frac{1}{n}{\displaystyle \sum_1^n{x}_i}, $$
(2)

where Γ(n/2) and Γ (n – 1/2) are gamma functions, and x is the mean value for a finite sample.

Therefore, in the Bayesian approach the systematic error is described by the random quantity B in the distribution (2), for which the mathematical expectation and standard deviation are estimates of the error and standard uncertainty, respectively. An estimate for the systematic error can be obtained by substituting the estimates of the input quantities in Eq. (1):

$$ \widehat{b}=\overline{x}-{x}_{\mathrm{ref}} $$

According to [1], the corresponding standard uncertainty is calculated using the formula

$$ {u}^2(b)={u}_{\mathrm{A}}^2\left(\overline{x}\right)+{u}_{\mathrm{B}}^2\left({x}_{\mathrm{ref}}\right)={S}^2/n+{u}^2\left({x}_{\mathrm{ref}}\right) $$
(3)

The Bayesian approach, however, yields another formula for the standard uncertainty [7]:

$$ {\tilde{u}}^2(b)=\left(n-1\right){S}^2/\left[\left(n-3\right)n\right]+{u}^2\left({x}_{\mathrm{ref}}\right) $$
(4)

Equation (4) is meaningful only for n > 3. It is interesting to note that in [8], repeated measurements are also taken to have n > 3. Equation (4) decreases monotonically and approaches Eq. (3) with increasing n. For sufficiently large n, Eqs. (3) and (4) are essentially the same.

The purpose of this article is to calculate the expanded uncertainty of measurements for a probability (confidence level) P; it is given by the product of the combined standard uncertainty and the coverage factor k:

$$ {U}_p(b)=k\tilde{u}(b) $$

An expression for k with P = 0.95 has been found for the cases discussed above (B and σ independent, with no a priori information on their possible values). In this case, it is generally assumed that k = 2. Here we analyze the differences in the estimated uncertainty for k = 2 and for its exact value.

$$ \tilde{B}=\left[B-\left(\overline{X}-{X}_{\mathrm{ref}}\right)\right]\sqrt{n/S} $$

The distribution of A is determined by transforming Eq. (2) for B:

$$ p\left(\tilde{b}\right)\frac{1}{\uppi \sqrt{2\left(n-1\right)}}\frac{\varGamma \left(n/2\right)}{\varGamma \left(\left(n-1\right)/2\right)}{{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\left(\frac{1}{n-1}{\left(z\frac{\sqrt{nu\left({x}_{\mathrm{ref}}\right)}}{S}+\tilde{b}\right)}^2+1\right)}}^{-n/2} \exp \left\{-\frac{z^2}{2}\right\}dz $$
(5)

Equation (5) is the convolution of the normal distribution and the Student scaling distribution with n – 1 degrees of freedom, which depends on the parameter γ = n 1/2 u(x ref)/S. As γ → 0, the distribution (5) converges to the Student distribution, while for γ → ∞ it approaches the normal distribution. The parameter γ is the ratio of the standard uncertainty resulting from the standard that is used to the sample standard deviation of the averaged result, which characterizes the random error of the measurements during transfer of the unit of the quantity. Evidently, the values of this parameter are always limited in practice.

We have calculated the percentage points 〈0.95 of the (5) distribution for different values of γ and n and for symmetric probability intervals for P = 0.95. Accordingly, the expanded uncertainty of the initial quantity B is calculated using the formula

$$ {\varDelta}_{0.95}-{\alpha}_{0.95}S/\sqrt{n} $$

The final goal was to obtain the functions k(γ, n), which makes it possible to proceed from the standard to the expanded uncertainty of the measurement. When n > 3, Eq. (4) applies for the standard uncertainty, so the coefficient k is given by

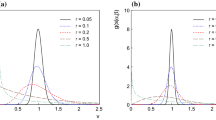
$$ {k}_{0.95}={\alpha}_{0.95}{\left[{\upgamma}^2+\left(n-1\right)/\left(n-3\right)\right]}^{-1/2} $$

Figure 1 is a plot of k 0.95 as a function of γ for different values of n.

Fig. 1
figure 1

k 0.95 (γ, n) for the case in which there is a reference value and a corresponding uncertainty

Full size image

k = 2 is an upper bound estimate for P = 0.95 if the standard uncertainty of the measurements is calculated using Eq. (4); for n > 5, k differs from 2 by less than 2%. Similar calculations of k were done for the case when estimates of the reference value and the limit on its permissible error {x ref, θ} are known. Here the information on the value of the measured quantity is formalized as a uniform distribution with center x ref and symmetric boundaries at ±θ. Values of k for calculating the expanded uncertainty were also obtained:

$$ {U}_p(b)=k\tilde{u}(b),{\tilde{u}}^2(b)=\left(n-1\right){S}^2/\left[\left(n-3\right)n\right]+{\uptheta}^2/3 $$
(6)

k 0.95 is plotted as a function of n and γ = n 1/2θ/S for P = 0.95 in Fig. 2. As opposed to the previous case, the values of k are significantly different for different γ. However, it should be noted that for P = 0.95 and n > 4, the k(γ) curves are essentially the same for different n.

Fig. 2
figure 2

k 0.95 (γ, n) for the case in which there is a reference value and a limit on the permissible error

Full size image

There is some interest in comparing these estimates for the expanded uncertainty with the confidence limits on the error given in [8]:

$$ {\varDelta}_p={\sqrt{\frac{S^2}{n}\frac{\theta^2}{3}\left[{t}_p\left(n-1\right)\frac{S}{\sqrt{n}}+0\right]\left[\frac{S}{\sqrt{n}}\frac{\theta }{\sqrt{3}}\right]}}^{-1} $$
(7)

We now denote r the ratio of the expanded measurement uncertainty given by Eq. (6) to the confi dence limits on the error given by Eq. (7). Figure 3 shows plots of r as a function of n and γ = n 1/2θ/S for p = 0.95. Figure 4 shows that the difference between the two estimates of the accuracy can approach 10%. For 0 < γ < 2, Eq. (7) gives a low estimate of the accuracy compared to the Bayesian estimate (6), and for γ > 2 the situation is the opposite.

Fig. 3
figure 3

The ratio r of the expanded measurement uncertainty calculated using Eq. (6) to the confidence limits on the error calculated using Eq. (7) as functions of n and γ = n 1/2θ/S for P = 0.95.

Full size image
Fig. 4
figure 4

The probability distributions for a normally distributed systematic error b (1) and for the Bayesian approach (2).

Full size image

We conclude with an example of estimating the measurement uncertainty during calibration of a liquid thermometer. The following measurement data for the temperature of the thermometer to be calibrated: {40.01; 40.018; 40.020; 40.017; 40.014; 40.014; 40.011; 40.016; 40.011; 40.017}, x = 40.016. A standard was used to find the measured value x ref = 39.999 with a permitted error limit of θ = 0.01. The systematic error of the thermometer was calculated using the formula b = x – x ref and found to be b = 0.017. Formal application of [1] gives

$$ \begin{array}{l}{u}_{\mathrm{A}}^2\left(\overline{X}\right)={S}^2/n={0.00307}^2/10=9.4\cdot {10}^{-6};\\ {}{u}_{\mathrm{B}}^2\left(\overline{X}\right)={\theta}^2/n={0.01}^2/3=3.33\cdot {10}^{-5};\\ {}{u}_{\sum}^2(b)={u}_{\mathrm{A}}^2\left(\overline{X}\right)+{u}_{\mathrm{B}}^2\left(\overline{X}\right)=3.4\cdot {10}^{-5};\\ {}{U}_{0.95}^{\left[1\right]}=2\sqrt{u_{\mathrm{A}}^2\left(\overline{X}\right)+{u}_{\mathrm{B}}^2\left(\overline{X}\right)}=0.012\end{array} $$

Fig. 4 The probability distributions for a normally distributed systematic error b (1) and for the Bayesian approach (2).

When the approach with k = 2 was used, a coverage interval of (0.005; 0.29) was found for b. The choice of k = 2 corresponds to the assumption of a normal distribution for the systematic error of the instrument. Figure 4 shows a normal distribution (curve 1). When a Bayesian estimate is used for the systematic error, the coverage interval is (0.006; 0.027). Curve 2 of Fig. 4 corresponds to the probability distribution for the systematic error. The points on curves 1 and 2 indicate the corresponding coverage intervals. The approach of Ref. 1 yields a wider coverage interval. It can be obtained using the curve of Fig. 3 for γ = 10.29 and n = 10. For these values, k = 1.7 and the corresponding coverage interval is (0.006; 0.027), in agreement with the interval obtained using the Bayesian approach. Finally, using Eq. (7) gives an interval of (0.006; 0.028) for the systematic error of the thermometer. At the same time, formal application of Ref. 1 yields an excessive estimate of the measurement uncertainty.

In this article, we have examined the problem of estimating measurement uncertainty during calibration, when the measurement equation is of the form (1). We have considered repeated measurements and two ways of representing the data on the reference value of the measured quantity. The coverage factor k and the expanded measurement uncertainty have been calculated using a Bayesian approach. The results have been compared with those obtained using [1] and the calculations of [8]. The conditions for using k = 2 for the standard combined uncertainty according to the Bayesian approach have been formulated.

These calculations of the expanded uncertainty in a determination of the systematic error of a measuring instrument during calibration can be used to calculate the measurement uncertainty in a situation where the following measurement data are available: the results of more than three repeated readouts from the instrument; a priori information on the accuracy of this instrument, which can be represented by the instrumental uncertainty uB or the measurement error limit θ. In this case, it is necessary to find the distribution of the measured quantity, which can be obtained in a way similar to the calculations of [9].

In this situation with two sources of uncertainty, Eq. (7) for the confidence limits of the combined error [8] is within 10% of the Bayesian estimate for the expanded measurement uncertainty (6).