In view of the widespread use of nanotechnologies in different fields, such as biology, medicine, energy, electronics, optics, and photonics, we wish to study the problem of taking measurements of the dispersion parameters of aerosols and particles of suspensions in the nanometer range. Following approval of State Primary Standard GET 163–2003 of the units of the dispersion parameters of aerosols, suspensions, and powdered materials, which had reproduced the dispersion parameters in the range of particle sizes 0.5–10 μm, studies designed to improve the standard and to create a state secondary standard intended for reproduction of the sizes of the units of the dispersion parameters of nanoparticles of suspensions were begun. In GET 163–2003 [1] the lower limits of measurements of the sizes of particles was expanded all the way down to 30 nm and the newly created State Secondary Standard of the units of the dispersion parameters of suspensions in the nanometer range VET 163–1–2010 assures a uniformity of measurements of nanoparticles in liquid media in the range of concentrations 108–1014 cm−3 and inspection and calibration of instruments for the measurement of the parameters of particles in the range down to 10 nm [2]. The measurements are based on the method of dynamic scattering of light, the primary method of analysis of the parameters of nanoparticles in liquid media.

Particles of both natural and technogenic origin exert a significant effect on the processes that occur in air [3, 4] and in liquid media, which, in turn, affect the climate and ecological situation, since a significant proportion of the particles transported by these media are found in the composition of the disperse phase of matter. In order to study and control the action of particles on processes that occur in natural and technogenic media, assurance of the uniformity and reliability of measurements of the basic parameters of these media, such as the size (in units of length), countable concentration (expressed in terms of the number of particles per unit volume), specific surface area (expressed in terms of units of area per unit volume), and the volumetric and mass concentration (expressed in terms of the volume and mass of particles per unit volume), as well as the form, structure, and chemical or biological composition of particles is of extraordinary importance.

Several standard methods of measuring the size of particles, such as a method that uses features of the diffraction of laser radiation by particles [5]; the method of dynamic light scattering in liquid media (in the range of sizes down to 3 nm) [6]; a method based on the differential electrical mobility of nanoparticles (in the range from 1 μm to 7 nm) [7]; and the method of diffusion spectroscopy [8], are used in standard equipment.

Devices that use these methods are manufactured by a number of foreign firms, such as Malvern (Great Britain), Fritsch (Germany), and others. For monodisperse particles, the estimates of the nonexcluded systematic error, the standard deviation, and the expanded uncertainty with 0.95 confidence probability are 4.0, 1.5, and 8.0%, respectively. The limitation of the lower limit of the measured particle sizes to 0.08–0.1 μm is a major drawback of these devices.

Dynamic light scattering is one of the most effective methods of determining the sizes of particles in liquid media [9]. The method is based on the analysis of the autocorrelation function of radiation that has been scattered by colloidal particles. The applicability of the method for the analysis of monodisperse solutions of particles in a broad range of sizes from several nanometers to several microns has been demonstrated in a host of experiments. However, there still does not exist a single algorithm by means of which complex mixtures containing groups of particles of different sizes could be analyzed with a sufficient degree of precision.

In a typical experiment in an analysis performed by means of dynamic light scattering, a test solution of particles is illuminated by a narrow beam of light from a monochromatic coherent source (laser) with wavelength λ0 [10]. The light scattered by the particles is detected coherently at an angle θ relative to the direction of initial propagation of the beam. It is assumed that the particles in the solution do not coalesce and do not expand. As a consequence of Brownian motion, the density of the particles in the medium fluctuates over time and, consequently, the laser radiation scattered by the particles fluctuates. The field created by the total wave constitutes a superposition of the fields scattered by the Brownian particles [11]:

$$ E(t)={\displaystyle \sum_{j=1}^n{E}_j{\mathrm{e}}^{i\left({\varphi}_j(t)-{\omega}_0t\right)}}, $$

where E j is the amplitude of the scattered wave, which depends on the form of the particle, its optical properties, the distance to the detector, and the scattering angle; N, number of particles; ω0, frequency of incident radiation; φ j (t) = qr j , phase advance associated with a random shift of the jth particle; r, radius vector of jth particle; and q = k 0 – k s , difference of wave vectors of incident and scattered waves. The modulus of the vector q is defined as

$$ q = 4\pi {n}_0/{\uplambda}_0 \sin \left(\uptheta /2\right), $$
(1)

where n 0 is the index of refraction of the medium filling the scattering volume and θ the scattering angle.

The intensity of the scattered radiation,

$$ I(t)={E}^{*}(t)E(t)={\displaystyle \sum_{j=1}^n{\displaystyle \sum_{k=1}^n{E}_j{E}_k{\mathrm{e}}^{i\left({\varphi}_j(t)-{\varphi}_k(t)\right)}}}, $$

where E and E * are the complex-conjugate values of the strength of the electrical field of the incident radiation, is the quantity we wish to measure.

The autocorrelation function of the intensity:

$$ {G}_I\left(\uptau \right)=\left\langle I(t)I\left(t+\uptau \right)\right\rangle $$

is constructed in order to obtain valuable information about the scattering particles. Here 〈〉 denotes averaging over time.

If we are given a discrete series of measured values of the intensity I(t i ), the autocorrelation function for a given value of τ′ may be calculated by the formula

$$ {G}_I\left({\tau}^{\prime}\right)=\frac{1}{N_{\tau^{\prime }}}{\displaystyle \sum_{i=1}^{N_{\tau^{\prime }}}I\left({t}_i\right)I\left({t}_i+{\tau}^{\prime}\right)}. $$

For spherical particles of identical size (degenerate distribution), the correlation function assumes the form:

$$ G\left(\tau \right)={\beta}^2{E}_0^4\left({N}^2+\left({N}^2-N\right){\mathrm{e}}^{-\varGamma \tau}\right), $$

where β = E 1 2/E 0 2; E 1 and E 0 are the strengths of the electrical field of the scattered and incident waves, respectively; N, number of scattering particles; and Γ, damping factor. The term N in the coefficient of the exponential expression is negligible by comparison with N 2 (we are assuming that the number of scattering particles is always great). Thus, the problem of determining the diameter of the particles reduces to that of finding the factor Γ, which is related to the diameter of a particle d by the diffusion coefficient D:

$$ \varGamma ={q}^2D={q}^2{k}_BT/\left(3\uppi \upeta d\right), $$
(2)

where k B is Boltzmann’s constant; T, temperature; and η, dynamic viscosity of the liquid. The modulus of the wave vector of the fluctuations of the concentrations of particles is described in (1).

The correlation function of the intensity of scattered light, which has the form

$$ G\left(\tau \right)=a{\mathrm{e}}^{-2\tau /{t}_{\mathrm{c}}}+b, $$

where a and b are empirical constants and t c the correlation time, is analyzed in the course of implementing this method of measurement, which is regulated by the standard [6].

In accordance with the solution of the diffusion equation, the inverse correlation time t c −1 = Γ.

If there exists a discrete series of values of the intensities I(t i ) obtained as a result of measurements, the correlation function for a given value of τ is calculated by means of the formula

$$ G\left(\tau \right)=\underset{N_{\tau}\to \infty }{ \lim}\frac{1}{N_{\tau }}{\displaystyle \sum_{i=1}^{N_{\tau }}I\left({t}_i\right)I\left({t}_i+\tau \right)}, $$

where N τ is the number of measurement points.

In the case of a polydisperse distribution of particles by size, the problem of determining the diameter of the particles becomes complicated. Where the particles that are being investigated do not interact and where scattering of light is single scattering, the correlation function may be represented in the form [10]:

$$ G\left(\tau \right)=A+{\left({\displaystyle \sum_i{B}_i{\mathrm{e}}^{-{\varGamma}_i\tau }}\right)}^2, $$

where B i ≅ β i N i E 0 2 = 〈I i 〉; 〈I i 〉 is the time-averaged intensity of the light scattered by particles of the same type and A is the base line.

Usually, in the analysis of obtained data it is not the correlation function of the intensity G(τ) which is used, but instead the function g 1(τ), the correlation function of the field, defined as g 1(τ) = [G(τ) – A]1/2. For a polydisperse distribution with A = 0, the function g 1(τ) assumes the following form in integral form

$$ {g}_1\left(\tau \right)={\displaystyle \underset{0}{\overset{\infty }{\int }}B\left(\varGamma \right){\mathrm{e}}^{-\varGamma \tau }d\varGamma }; $$
(3)

and in the form of a discrete series,

$$ {g}_1\left(\tau \right)={\displaystyle \sum_i{B}_i{\mathrm{e}}^{-{\varGamma}_i\tau }}. $$
(4)

The dimensionless coefficients B i contain information about the distribution of the particles by size.

Problems of the form (4) belong to the class of ill-posed problems. There are methods for processing data by means of which as much information as desired may be extracted from the correlation function (4). Below, we present several general methods used for the analysis of dynamic light scattering data in the case of a polydisperse distribution of particles by size [12].

Using the method of cumulants [13, 14], information may be obtained concerning the disperseness of the system in the following way:

$$ {g}_1\left(\tau \right)={\mathrm{e}}^{-\overline{\varGamma}\tau}\left[1+\frac{\mu_2}{2!}{\tau}^2-\frac{\mu_3}{3!}+\dots \right], $$
(5)

where

$$ {\mu}_m={\displaystyle \underset{0}{\overset{\infty }{\int }}B\left(\varGamma \right)\left(\varGamma -\overline{\varGamma}\right)d\varGamma }. $$

In this method the correlation curve is approximated by one and only one exponential curve, which is characterized by the damping factor G. From (2) we find the harmonic mean of the size (average hydrodynamic diameter of the system). By means of this method it is also possible to determine the relative width of the distribution from the relationship

$$ PI={\mu}_2/{\overline{\varGamma}}^2. $$

This method functions effectively whenever the sizes of the particles possess a smooth distribution around a single mean value. In the multimodal (more than a single maximum) case, it does not yield real information about the sizes of the particles.

With the use of the nonnegative method of least squares [15] it is possible calculate the distribution histogram of the particles by size for a given set of damping factors through minimization of the expression

$$ {\chi}_1^2={{\displaystyle \sum_{j=1}^M\left[{g}_1\left({\tau}_j\right)-{\displaystyle \sum_{i=1}^N{B}_i{\mathrm{e}}^{-{\varGamma}_i{\tau}_j}}\right]}}^2\to \min, $$

where g(τ j ) is an experimental autocorrelation function.

An exponential sample [16] is an alternative method of determining the damping factors, the distribution functions of which are specified by the set {B i , Γ i }. The set of damping factors Γ i is defined as

$$ {\varGamma}_{i+1}={\varGamma}_i{\mathrm{e}}^{\pi /{\omega}_{\max }}, $$

where ωmax is an empirical parameter. The coefficients B i are calculated by means of minimization of expression (4).

The general-purpose CONTIN algorithm of constrained regularization for inverting noisy linear algebraic and integral equations [17, 18] is based on the Laplace transformation of the correlation function g(τ), where the distribution function of the damping factors B(Γ) is calculated by means of minimization of the expression

$$ {\chi}_2^2\left(\alpha \right)={\displaystyle \sum_i\left(1/{\sigma}_i^2\right)}{\left[{g}_1\left({\tau}_i\right)-{\displaystyle \underset{0}{\overset{\infty }{\int }}B\left(\varGamma \right){\mathrm{e}}^{-\varGamma \tau }d\varGamma}\right]}^2+\alpha \left\Vert LB{\left(\varGamma \right)}^2\right\Vert, $$

where σ i is the standard deviation of an experimental point of given g(τ i ) and αhLB(Γ)h2 a regularizing term with regularizing coefficient 0 < α < 1 and operator L, where the second derivative is usually selected as the latter. By means of this method it is possible to easily describe a polydisperse system by approximating its monomodal distribution over the entire range of sizes of the particles present in the mixture.

In the dual exponential, or bimodal method [19], a sample consisting of two clearly distinct modes of monodisperse particles is represented, i.e., the correlation function is represented in the form of a sum of two exponential functions with different sets of free parameters B 1,2 and Γ1,2,

$$ {g}_1\left(\tau \right)={B}_1{\mathrm{e}}^{-{\varGamma}_1\tau }+{B}_2{\mathrm{e}}^{-{\varGamma}_2\tau }, $$
(6)

which are determined by the nonnegative method of least squares through minimization of an experimental correlation function and a model function (6).

Experimental Testing of Different Methods of Processing the Data. Results obtained by these methods for three monodisperse latex samples s 1–s 3 of different size and three samples s 4–s 6 with bimodal distribution fabricated from different combinations of monodisperse substances are shown in Table 1.

Table 1 Results of a Study of the Parameters of Latex Particles by Different Dynamic Light Scattering Methods of Processing Data [20]
Full size table

From the data of Table 1 (samples s 1, s 2, and s 3) it follows that in a cumulative analysis PI < 0.01, which corresponds to a polydispersivity size less than 5% (samples s 2 and s 3). Consequently, for the bimodal samples s 4, s 5, and s 6 cumulative analysis yields a value PI > 0.05 in all cases. The average diameter of the particles determined in a cumulative analysis for the bimodal samples s 4 and s 5 is less than the theoretical value. In sample s 6 the value of the average size of the particle approaches the expected value. In order to achieve an exact measurement of the size distribution of the bimodal samples by means of dynamic light scattering, sample s 5 is quite difficult to analyze, since the ratio between the diameters of the two types of particles is close to the critical value of 2 and the limit of the resolution for this method. In this case, the nonnegative method of least squares yields two inaccurate average particle sizes, whereas both the exponential sample method and dual exponential method yield similar results within a 5% error from the true values as well as a more precise size for fractions of large particles. The basic problem in the description of bimodal particles measured by means of dynamic light scattering lies in the precision with which the size of small particles is determined where there are large particles present. For sample s 4, the scattering intensity is much greater be, 〈I〉 ~ d 6, and the bimodality resolution will not affect the problems due to the value of the size coefficient of the particles (4.8), whereas the nonnegative method of least squares yields a less precise result. On the other hand, the bimodality of sample s 6 with ratio of particle sizes less than 2 is found outside the range of capability of measurements performed by means of dynamic light scattering.

The exponential sample and dual exponential methods are more efficient from the point of view of the precision with which particle size is determined. The algorithm of the nonnegative method of least squares is the most reproducible method and makes it possible to track different combinations of monodisperse components present in the solution (under the condition stipulated above).

New algorithms possessing the advantages of those we have discussed have now been developed. One such study is that of [20], in which the algorithm is based on the use of additional data obtained in static light scattering at several angles. But none of these methods function if the examples of the particles differ less than three-fold.

It should be noted that the process of solving the problem is substantially complicated by the presence of a noise-contaminating nonzero base line A in (4).

Equation (3) is a Laplace transformation, which is a special case of the general class of linear integral Fredholm equations of the first kind with common kernel e–Γτ. However, there exist two constraints [18] that arise in a dynamic light scattering experiment which renders the transformation ill-posed. The first constraint is related to all the different types of noise that do not exhibit the nature of exponential descent and frequently distort the autocorrelation function due to the nonideal conditions of the experiment, e.g., nonuniform profile of the laser beam, insufficient resolution of the quantization signal and other base errors.

The second constraint is related to the fact that the bandwidth (range of delay times) in the correlator is always limited, i.e., the limits of integration in (3) are bounded from Γmin to Γmax.

The essence of the algorithm of the nonnegative method of least squares consists in predetermination of the system by addition of an a priori assumption concerning the value of the unknown vector x n and subsequent minimization of the rate of discrepancy by the method of least squares in order to obtain a unique stable solution. We have complemented the algorithm of the nonnegative method of least squares with yet one more a priori component, the thesis that multimodal components containing a group of particles of different sizes are present in the form of combinations of discrete Heaviside functions the direct Laplace transformation of which constitutes a correlation function g 1(τ) as follows:

$$ {g}_1\left(\tau \right)={\displaystyle \sum_i\left[{B}_i\left({\mathrm{e}}^{-{\varGamma}_i\tau }-{\mathrm{e}}^{-\left({\varGamma}_i+\varDelta \right)\tau}\right)/\tau \right]}, $$
(7)

where the parameter Δ is selected arbitrarily based on a given range of measurements of particle sizes and the noise component of the correlation function, while the coefficients B i are determined by means of minimization of the difference of the experimental correlation function and the sum of model functions with given damping factor:

$$ {\chi}_3^2={{\displaystyle \sum_{j=1}^M\left[{g}_1\left({\tau}_j\right)-{\displaystyle \sum_{i=1}^K{B}_i\left({\mathrm{e}}^{-{\varGamma}_i{\tau}_j}-{\mathrm{e}}^{-\left({\varGamma}_i+\varDelta \right){\tau}_j}\right)/{\tau}_j}\right]}}^2\to \min . $$
(8)

Here g 1(τ) is an experimental autocorrelation function; M, number of points of correlation times or number of channels forming the experimental correlation function; and K, number of damping factors being considered.

Performing the operation of the inverse Fourier transformation on the function g 1(τ) with the coefficients B i that have been found, we determine one-component distribution functions for a mixture of particles of different sizes present in the solution:

$$ {g}_1\left(\tau \right)={\displaystyle \sum_{j=1}^M\left[{\displaystyle \sum_{i=1}^K{B}_i\left({\mathrm{e}}^{-{\varGamma}_i{\tau}_j}-{\mathrm{e}}^{-\left({\varGamma}_i+\varDelta \right){\tau}_j}\right)/{\tau}_j}\right]}. $$

In order to verify the proposed approach, we carried out a series of experiments with the dynamic light scattering method using polydisperse mixtures consisting of monodisperse latex particles with sizes differing less than three-fold. The results of processing the experimental correlation functions for such mixtures are presented in Fig. 2.

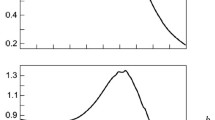
Theoretical autocorrelation functions calculated by means of (4) and (6) and an experimental autocorrelation function obtained on a dynamic light scattering analyzer for a mixture consisting of three types of monodisperse latex particles 20, 40, and 80 nm in size are shown in Fig. 1. From Fig. 1 it follows that the autocorrelation function obtained by means of numerical modeling using formula (4) repeats the features of the function modeled by means of formula (8). This fact may indicate that the two descriptions (5) and (8) of the autocorrelation function of the signal in the case of a polydisperse distribution of particles by size are equivalent.

Fig. 1
figure 1

Correlation function for a polydisperse mixture: —) experiment; – – –) modeling using (5);⋯) modeling using (8).

Full size image

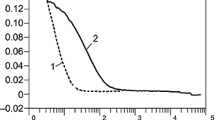
Results found by processing an experimental autocorrelation function for a mixture of latex particles with sizes 20, 40, and 80 nm by means of the CONTIN algorithm and the algorithm of the nonnegative method of least squares are presented in Fig. 2a . An example illustrating the processing of this autocorrelation function by means of the approach proposed by the present authors is presented in Fig. 2b .

Fig. 2
figure 2

Results of processing an experimental autocorrelation function of a polydisperse mixture by means of: a) CONTIN and the nonnegative method least squares, curves 1 and 2, respectively; b) proposed approach.

Full size image

Six latex suspensions of particles with nominal sizes of 20, 60, 100, 200, and 1000 nm and nanoparticles of gold 10, 30, and 60 nm in size produced by NIST (United States) were prepared and experimentally investigated as the model object. The suspensions were prepared directly in a measurement dish by dissolving 200 μl of a test sample in 1.4 ml distilled water. The results of the measurements are summarized in Table 2 and typical histograms of the distribution of the particles by size are shown in Fig. 3.

Table 2 Results of Measurements of the Sizes of the Components of Mixtures of Particles of Latex and Nanoparticles of Gold
Full size table
Fig. 3
figure 3

Examples of disperse distributions of nanoparticles by size: a) nanoparticles of spherical latex 21 and 105.7 nm in diameter; b) nanoparticles of gold 13.5, 32.6, and 68.1 nm in size.

Full size image

Note that the mixture of latex particles 63.3 and 100.4 nm in size (cf. Table 2) does not possess any resolution, that is, the analyzer yields a unimodal distribution of the particles by size. This may be due to the rather broad disperse distribution of the latex components. At the same time, mixtures of nanoparticles of gold the components of which have a narrower disperse distribution possess total resolution.

Thus, by complementing the algorithm used to process the data of the nonnegative method of least squares with one more a priori component (representation of multimodal components containing a group of particles of different sizes in the form of a combination of discrete Heaviside functions) , we are able to substantially increase the resolution of the dynamic light scattering method.

In order to obtain an estimate and confirmation of the characteristics of the dispersion parameters obtained through inclusion of a dynamic light scattering spectrometer in the set of standard equipment, an independent method of determining these characteristics is needed. A new interferometric method of determining the size of particles in the nanometer and submicron ranges on the basis of a Fabry–Perot interferometer was proposed and developed by the present authors [21, 22]. The method also makes it possible to determine the index of refraction of the material of these particles.

Interferometric methods of measuring the index of refraction of different media have long been known [23]. However, the integral characteristics of the index of refraction are measured by means of these methods. Thus, for example, if the index of refraction of a suspension of particles in liquid is measured, the result of the measurement will be a combination of the indices of refraction of the particles and of the medium, and the greater the number of particles that are present in the liquid, the closer the result will be to the index of refraction of the particles, i.e., the result will depend on the concentration of the particles N. To avoid this dependence, we wish to suggest calculating the index of refraction of the particles using the dependence of the index of refraction n on the ratio N Re S(0)/N Im (S(0), where S(0) is the extinction cross-section of a particle with a known diameter of the particles, Re S(0) and Im S(0) its real and imaginary parts, and N the concentration of the particles. The index of refraction of diamond nanoparticles 106 and 854 nm in size suspended in water was determined by this method and found to be 1.78 and 1.79, respectively [22].

Table 3 presents results of measurements of the size of latex spheres in pure deionized water obtained by an interferometric method and the method of diffraction of laser radiation.

Table 3 Results of Measurements of the Size of Latex Spheres in Deionized Water
Full size table

The obtained data are in agreement with the nominal particle sizes determined by the dynamic light scattering method and, despite the fact that the error of the nominal sizes is not normalized, these results are not inferior to the results of measurements found by means of diffraction of laser radiation. The countable concentration of the particles N is computed for a given diameter of the particles. A countable concentration of 50 μm−3 is a limiting value for this method, since the measurement of phase and the amplitude relationships then become difficult.

Conclusion. The measurement methods and instruments that have been described here have been implemented in the equipment of the State Secondary Standard of the units of the dispersional parameters of suspensions of nanometer-range nanoparticles VET 162–1–2010 [25] in a newly developed and certified technique of measurement of the parameters of nanoparticles in liquid media under the conditions of a polydisperse multimodal distribution [26] and have also been used in comparisons carried out as part of COOMET Project No. 575/RU/12, “Pilot Comparisons in the Field of Measurements of the Size and Concentration of Nanoparticles” [27]. Through the use of the measurement methods and instruments that have been developed at VNIIFTRI it has become possible to assure the uniformity of measurements in the production of nanoproducts at enterprises in the electronic, pharmaceutical, and astronautic industries and also in the development of such critical technologies as the technology underling the creation of new generations of space-rocket, aviation, and marine equipment, nanotechnologies and nanomaterials, technologies of mechanotronics and the creation of microsystems instruments, the technology underlying the creation of electronic microcircuitry, biomedicine, and veterinarian technologies of life support and the protection of man and animal.

The use of these methods in standard equipment has made it possible to assure a uniformity of measurements of nanoparticles in liquid media in the range of concentrations 108–1014 cm−3, inspection and calibration of instruments for the measurement of the dispersion parameters of nanoparticles in the range of sizes all the way down to 10 nm as well as COOMET pilot comparisons in the range of measurements of the size and concentrations of nanoparticles.