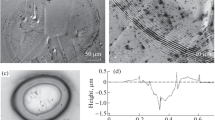
Selective laser processing of thin surface layers of metallic alloys selectively affects certain defective areas, such as stress concentrators, fracture nuclei, crack tips, and nanoscale particles. The rest of the material is practically unaffected. The method of selective laser processing increases both the microhardness and fracture toughness of, particularly, thin ribbons of hard and brittle amorphous- nanocrystalline metal alloys. It is essential that the initial amorphous-nanocrystalline structure of the material is preserved. The impact of a nanosecond laser pulse of high power density on the surface of a metal alloy is accompanied by laser-induced breakdown plasma, shock wave, and impulsive heating. The heating of the material is preceded by the passage of a compression shock wave capable of initiating local deformations and damages. The uneven heating of the material is primarily manifested in the defective areas and can lead to the relaxation of mechanical stresses due to plastic deformation. To study the interaction between the thermal front initiated by a laser pulse and defects in the surface layer of a metal alloy, it is necessary to improve the physical and mathematical models of these processes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The surface layer of amorphous metal alloys contains highly dense defects because of the redundant and structurally dependent free volume [1, 2]. Defects can be process-induced [3,4,5]. Pores are mainly filled with air. All this leads to either negative or positive change in the physical and mechanical properties [6,7,8,9,10]. To predict the effect of defects during further heat treatment, it is necessary to understand the physics behind the processes in the structure of the material.
The physical, mechanical, and chemical characteristics of defects differ substantially from those of the alloy the product is made of [11, 12]. Defect areas are usually no larger than 100 nm in length. Defect areas’ growing to larger dimensions leads to the nucleation of cracks, followed by the embrittlement and fracture of the whole specimen.
Our goal here is to study the physics of the effect of high-temperature impulsive heating on defects in the surface layer of a metal alloy. To achieve this goal, it is necessary to study the heat conductivity of metal films of 50 μm thickness with defects uniformly distributed over the volume (the gas phase in pores).
Materials and Methods
A nanosecond laser pulse exerts a local thermal effect on the alloy volume. The mean values of the thermal conductivity λ of different materials under normal conditions can differ by several orders of magnitude: ≈ 2.5∙10–2 W/(m∙К) for air, ≈ 1.8∙10–1 W/(m·К) for hydrogen, 10–500 W/(m∙К) for metals and alloys [13,14,15].
Assume that heat conduction is the major heat-transfer process, convective heat transfer being neglected. Let us apply the splitting principle to approximate numerical solutions. For example, the one-dimensional heat- transfer equation in a Cartesian coordinate system contains two terms:
The first term on the right-hand side describes heat conduction, while the second term, convection. Using the splitting principle, we write the separate equations for these processes:
Assuming that the effect of convective heat transfer is weak, we will set up an elementary heat-conduction equation whose solution is nontrivial if nanoscale topological defects are accounted for.
In the general case, the temperature field at the microlevel is described by the heat-conduction equation
where
c is specific heat, J/(kg∙К);
T is temperature, K;
t is time, sec;
λ is thermal conductivity, W/(m∙К);
q is the power of near-surface heat sources, W/m3;
ρ is density, kg/m3.
The temperature gradient shows the direction of increase in temperature. However, since the heat source is on one side of the specimen, and the temperature decreases with depth of the alloy, we consider that the right- hand side of the equations is negative.
The temperature gradient in the Cartesian coordinate system:
The expanded heat-conduction equation in the alloy volume in the Cartesian coordinate system has the form
Let the heat sources on the upper boundary of the surface be defined as the temperature on the model edge.
We will calculate temperature T and heat flux density F = –λ ∙ grad (T) in the three-dimensional case for a positive heat source:
Assume that the length of the specimen (for example, a metal ribbon) is much greater than its width and thickness. Then we can neglect the z-coordinate tensor and solve the two-dimensional problem.
Boundary-Value Problem and Problem-Solving Method in Cartesian Coordinate System
The solution of the two-dimensional problem is also nontrivial because of the possible significant difference between the heat conductivities of metal and nanoparticles. The heat conductivity at the point with coordinates (x, y) depends on the material and time. Assume that the components of the thermal-conductivity tensor are equal: λx = λy.
Thus, it is necessary to solve a nonstationary problem. If we use the mesh method, then it is reasonable to solve the two-dimensional problem layerwise (coordinate-wise). The heat-conduction equation for the coordinate y has the form
where
a = λ/c is thermal diffusivity, m2 /sec.
Following the geometry of the problem, we introduce boundary conditions:
where
α is the heat-transfer factor, W/(m2 ·К);
Tα is the temperature of the ambient medium (for example, air), K.
Due to the local thermal effect, the given heat flow condition Ff = – qs on the external boundary is assumed to be qs = 0.
Let us define the initial condition on the boundary L. Assume that at the initial time t = 0, the specimen is not heated and its temperature T is equal to Ta:
The presence of nanoscale particles and the use of a numerical method do not allow continuous variables, and the problem should be solved layerwise in increments smaller than the mean linear dimension of particles.
Thus, the problem for the temperature T,
takes the following form for the i th layer:
Let us find the solution for the temperature in the i th layer for the coordinate y by solving a series of problems. In this case, the coordinate x can take values from 0 to H in, for example, increments Δx = Δy.
The adjusted values of the temperature T are denoted by T*. Applying linear interpolation of temperature in the range from Ti to Ti +1,
we arrive at a boundary-value problem for the solution of the series:
When choosing the step of solving the problem by, for example, the explicit mesh method, it is necessary to consider that the time and coordinate steps for the heat-conduction equation with thermal diffusivity a [m2 /sec] are related by a ∙ ∆t ≤ 0.5∆y. In cases of a complex configuration of particles, it is possible to use nonlinear approximation and a variable step or to use simplex methods.
The nonstationary problem for the temperature T with boundary conditions that account for a local, limited thermal effect can be represented by a system of differential equations:
The discrete representation of the problem differs from the layerwise one in that the i th layer is replaced with discrete values of the angle φi in the range from φ1 to φ2:
The problem should be solved by numerical methods of solving Poisson’s equation in domains with circular boundaries. It is also possible to apply difference methods of high order with an adaptive rectangular mesh with irregular cells on the boundary of the domain [16,17,18,19].
The general solution of the problem includes the solutions of the subproblems for heat conductivity in the domains y ∈ ξ and r ∈ ξ. The nonstationary problem is considered as quasistationary, i.e., a set of stationary problems solved in a certain number of time slots.
In this case, in each iteration, the derivative of temperature with respect to time is equal to zero, and the equation in Cartesian coordinates takes the form
If a topological defect or a nanoparticle is rectangular and easily fits into the coordinate system (x, y), then knowing the heat conductivity of the material, we can replace the linear approximation of the mesh with known analytical relations T = f (y). For example, in the case being considered,
for y = 0 , T = T1 for the upper boundary and y = δ , T = T2 for the lower boundary, after integration, we get
The constants are determined from the conditions
Substituting the values of the constants, we obtain the temperature distribution
According to the Fourier law, the heat coming through a topological defect along the axis 0Y is
It should be noted that it was assumed that the heat conductivity is constant and the initial temperature distribution is uniform. Real systems are subject to more complex processes and are not considered in this model.
Discussion of the Results
A simplified model of heating of the material can show typical changes in defective surface layers on a rather short time interval. Figure 1 shows the result of modeling the effect of impulsive heating on defects. The area affected by a nanosecond laser pulse (≈ 20 nsec) on the surface of the material has the form of a hemisphere of constant radius. Inside the hemisphere, constant temperature can be maintained due to the radiation of the gas plasma. The duration of such a flame can vary within 100–200 nsec. The specimen is heated due to heat transfer from the boundaries of the hemispherical molten layer. The time of heating is 0.1 sec in Figs. 1 and 2. This time corresponds to the maximum temperature gradient. The first pore at a distance of 3 μm from the surface has a considerable effect on the isotherms. The temperature of the heated area is 1293 K, and the initial temperature is 293°C. The dimensions of the specimen are 50 × 50 μm. The radius of the heated hemisphere is 6 μm. In Fig. 1, the pore diameter is 2.5 μm.
The temperatures on the upper and lower boundaries of the first pore are 1077 and 721 K, respectively (∆T = 356 K). If there is no pore, the temperatures at the same points will be 1001 and 799 K, respectively (∆T = 201 K). Thus, the pore increases the temperature before it and decreases the temperature under it. This creates conditions for plastic flow and pore healing.
The first pore and isotherms are shown in Fig. 2 at high magnification. The model demonstrates that heating (movement of the isotherms) accelerates before the upper part of the pore, compared with the faultless material. Simultaneously, the temperature gradient increases and the movement of the isotherms slows down under the pore.
Due to the formation of a specific temperature gradient, the temperature of the material in the upper part of the pore is much higher than under the pore. That is, since the material in the upper part of the specimen is heated to higher temperatures, it deforms easier. A laser pulse not only produces a thermal effect but also exerts a shock pressure of up to 100 kbar. The peak of the shock wave can occur in advance of the maximum temperature. However, a heated material, especially under repeated radiation, is affected by pressure and, as a result, fills pores. This promotes either partial or full healing of defects. The exact solution of this problem requires the modeling of the plastic flow of the material under a laser pulse. However, as shown in this problem, the temperature distribution around a pore promotes such processes.
The results of modeling are validated against experimental hardening of the surface of a material by selective laser processing. In [20], it was established that after selective laser processing of a layer of VT9 titanium alloy, its nanohardness increased four times (from 6.3 to 27.5 GPa) and Young’s modulus increased approximately twice (from 163.5 to 362.4 GPa). Also, the microhardness of the surface increased by 40% (360 MPa). The expectation of the probability of cracking of the raw surface indented with a Vickers pyramid is 52% (a load of 0.49 N). The Vickers pyramid did not cause cracking in the areas processed by laser. These processes are mainly caused by defect healing, followed by an increase in the nano- and microhardness and crack resistance of the surface.
Conclusions
The physics of the selective effect of laser radiation on topological defects can be clarified using the method of sequential quasistationary problems. The heat conductivity of defects and nanoparticles can vary over a wide range, while the geometry of defects can be either simple or irregular.
The nonuniformity of the heating by an impulsive thermal load such as selective laser processing can accurately be determined by computer modeling, using the method proposed here.
Computer modeling has demonstrated that impulsive laser processing heats the material before the pore to a higher temperature than in the faultless area of the specimen. The material under the pore is heated to a lower temperature than in the faultless area. Since laser plasma also exerts shock pressure on the material, the pore can be filled with viscous metal heated to premelting temperatures.
The physical model of the selective effect of laser radiation on nano- and microdefects consistently explains the experimental data on the simultaneous increase in the hardness and crack resistance of the surface affected by nanosecond laser pulses.
References
R. A. Andrievskii and A. V. Ragulya, Nanostructured Materials [in Russian], Akademiya, Moscow (2005).
A. M. Glezer and N. A. Shurygina, Amorphous-Nanocrystalline Alloys [in Russian], Fizmatlit, Moscow (2013).
I. V. Ushakov and I. S. Safronov, “Directed changing properties of amorphous and nanostructured metal alloys with help of nanosecond laser impulses,” CIS Iron and Steel Review, 22, 77–81 (2021).
I. V. Ushakov and A. D. Oshorov, “Viscosity of microdestruction of multilayer composite and method of its revealing,” Mater. Sci. Forum, 1052, 110–115 (2022); https://doi.org/10.4028/p-5q4060.
N. A. Chichenev, S. M. Gorbatyuk, O. A. Kobelev, and A. N. Pashkov, “Improving the thermal fatigue strength of hot-working tools by laser treatment,” Mater. Res. Proc., 21, 43–50 (2022); https://doi.org/10.21741/9781644901755-8
M. G. Isaenkova, Yu. A. Perlovich, A. E. Rubanov, and A. V. Yudin, “Anisotropy of the mechanical properties of austenitic steel products obtained by selective laser melting,” CIS Iron and Steel Review, 18, 64–68 (2019).
M. S. Bolkhovitin and A. V. Ionov, “Improving the quality of manufacture of die tooling for gas-turbine engine compressors,” Tr. MAI, No. 71, 15 (2013).
I. S. Safronov, I. V. Ushakov, and V. I. Minaev, “Influence of environment at laser processing on microhardness of amorphous nano crystalline metal alloy,” Mater. Sci. Forum, 1052, 50–55 (2022).
V. N. Shinkin, “Influence of non-linearity of hardening curve on elasticoplastic bend of rectangular rod,” CIS Iron and Steel Review, 17, 39–42 (2019).
A. V. Bronz, D. E. Kaputkin, L. M. Kaputkina, V. E. Kindop, and A. G. Svyazhin, “Influence of the composition on the lattice and physical properties of ferromanganese alloys with high aluminum content,” Metalloved. Term. Obrab. Metall., No. 12 (702), 11–15 (2013).
N. A. Chichenev, S. M. Gorbatyuk, M. G. Naumova, and I. G. Morozova, “Using the similarity theory for description of laser hardening processes,” CIS Iron and Steel Review, 19, 44–47 (2020).
A. A. Dmitrievskii, N. Yu. Efremova, and D. G. Guseva, “Quantitative assessment of the content of metastable phases of silicon Si-XII, Si-III, and α-Si in the indentation,” Izv. RAN, Ser. Fiz., 81, No. 11, 1522–1525 (2017).
A. V. Bronz, D. E. Kaputkin, L. M. Kaputkina, V. E. Kindop, and A. G. Svyazhin, “Mechanical and physical properties of cast Fe–Mn–Al–C–N alloys,” Izv. VUZov, Chern. Metallurg., 57, No. 11, 43-47 (2014).
N. B. Vargaftik, Handbook of Thermophysical Properties of Gases and Fluids [in Russian], Nauka, Moscow (1972).
W. S. Cleveland, “Robust locally weighted regression and smoothing scatterplots,” J. Amer. Stat. Assoc., 74, No. 368, 829–836 (1979).
A. V. Bokov, M. A. Korytova, and A. B. Samarov, “Numerical simulation of convective heat and mass transfer in spherical coordinates,” Vestn. YuUrGU, Ser. Mat. Model. Program., 12, 96–109 (2019).
E. V. Vorozhtsov and V. P. Shapeev, “Numerical solution of Poisson’s equation in polar coordinates by the method of collocations and minimum residuals,” Model. Analiz. Inform. Sist., 22, No. 5, 648–664 (2015).
A. A. Samarskii and A. V. Gulin, Numerical Methods of Mathematical Physics [in Russian], Nauchnyi Mir, Moscow (2003).
A. A. Samarskii and P. N. Vabishchevich, Numerical Methods for Solving Convection–Diffusion Problems [in Russian], URSS, Moscow (2009).
I. V. Ushakov and Yu. V. Simonov, “Using short-pulse laser radiation to control the physical and mechanical properties of the surface of titanium alloys,” Vestn. Moskov. Gos. Obl. Univ., Ser. Fiz.-Mat., No. 4, 30–42 (2019).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Metallurg, Vol. 67, No. 7, pp. 74–79, July, 2023.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Ushakov, I.V., Safronov, I.S., Oshorov, A.D. et al. Physics of the Effect of High-Temperature Pulse Heating On Defects in the Surface Layer of a Metal Alloy. Metallurgist 67, 986–994 (2023). https://doi.org/10.1007/s11015-023-01588-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11015-023-01588-z