Deviatoric stress waves due to rheology in incompressible thermoviscoelastic solid medium with small strain, small deformation physics

Abstract

This paper demonstrates existence of deviatoric stress waves in thermoviscoelastic (TVE) solid continua due to rheology in addition to the presence of usual deviatoric stress waves purely due to elasticity of the solid continua. The physical mechanisms that enable existence of deviatoric stress waves due to rheology in TVE solid continua are identified. Evolutions of deviatoric stress waves due to rheology are presented. Propagation, reflection, transmission, and interaction of such waves in conjunction with usual elastic stress waves are presented. The parameters controlling the rheological deviatoric stress waves and the speed of propagation of composite deviatoric stress waves due to rheology and elasticity are identified, discussed and illustrated through model problem studies. Mathematical model for the TVE solids in $\mathbb {R}^{1}$ is constructed using conservation and balance laws of classical continuum mechanics in $\mathbb {R}^{3}$ and the constitutive theories that are derived using entropy inequality and representation theorem. Model problems and their solutions are also presented to illustrate the validity of the concepts presented in the paper.

1 Introduction, literature review, and scope of work

The subject of stress waves in elastic solids has been of interest for a long time. Small deformation, small strain and finite deformation, finite strain studies related to elastic wave propagation are well published. In case of the TVE solid continua with dissipation mechanism, it is considered sufficient to determine influence of dissipation on wave amplitude attenuation and base elongation. It is believed that presence of dissipation mechanism and rheology does not appreciably alter the elastic waves. In case of TVE solid continua, we have physics of elasticity, dissipation as well as memory or rheology. In such solids upon cessation of external disturbance, the deformed matter takes finite amount of time to resume unstressed or relaxed state. This is called stress relaxation phenomenon and is characterized by relaxation time. For larger relaxation times, TVE solid continua take more time to resume an unstressed state. In published works, this physics is incorporated in the mathematical model either phenomenologically or using CBL of CCM and the constitutive theories.

The linear and nonlinear mathematical models, the analytical and/or numerical solutions of the boundary value problems (BVPs) and the initial value problem (IVPs) for elastic, thermoviscoelastic solid continua with and without memory are documented in various published works [1, 2, 4,5,6,7,8, 13,14,15,16,17,18, 20, 21, 36,37,38]. We simply cite these here for convenience of interested readers, but these works do not have direct bearing on the research presented in this paper, but provide background material. A good discussion of the published works in these references can be found in [9, 31].

The mathematical models and the concepts used in deriving them for TVE solid continua are largely borrowed from polymeric fluids for which experiments are relatively easier to perform and easier to observe (under microscopic photography) the deformation details. Just like polymeric fluid, a polymeric solid is also synthesized using a solvent consisting of short chain molecules and a polymer consisting of long chain molecules. The resulting solid is referred to as polymeric solid or thermoviscoelastic solid. When the composition of the polymeric solid is dominated by the short chain molecules i.e. solvent, the polymeric solid behaves more like a solid with short chain molecule material. On the other hand, if the composition of the polymeric solid is dominated by long chain molecules of the polymer, the polymeric solid behaves more like long chain polymeric solid continua with prominent rheology. Microscopic photography of deforming polymeric fluids reveal complex Brownian motion of the long chain molecules at the molecular level. In the relaxed unstressed state, the long chain polymer molecules are observed mostly in a coiled state either by themselves or collectively in a colony of long-chain molecules. These colonies of long chain molecules are observed to be interconnected with the neighboring colonies. The solvent and polymer have their own properties (like viscosities) that contributes to the properties of the TVE solid continua. But the synthesized polymeric solid has its own viscosity, conductivity and other material properties. These obviously must be determined experimentally for the polymeric solid.

Upon applying disturbance to a TVE solid continua the short chain molecules collectively behave like usual short chain molecule solids (such as a monolithic material). The long chain molecules on the other hand, begin to uncoil primarly in the direction of the disturbance. This requires that they overcome the viscous resistance (drag) offered by the solvent as well as viscous resistance offered by the polymer molecules. Thus, the motion of the polymer molecules is like one dimensional springs. Collectively the polymer molecules act like one dimensional springs in the direction of the disturbance. Just like a one dimensional spring is only active in its axial direction and has no resistance or response normal to this direction, the polymer molecules behave in a similar fashion. That is, normal to the direction of disturbance the polymer molecules response is quite weak, but not zero due to random orientation and arrangement of the polymer molecules in the TVE solid continua. At scales lower than macroscale, the polymeric solids are not homogenous and isotropic (the Brownian motion confirms this), but at macroscale TVE solids can be considered isotropic and homogenous. This allows us to use CBL of CCM in deriving mathematical models for deformation physics of TVE solid continua. Surana [28, 29] and Surana et.al [11] have presented the derivations of mathematical models for TVE solid continua using CBL of CCM as well as derivation of constitutive theories using entropy inequality and representation theorem.

There is vast amount of published work on deviatoric stress wave propagation in elastic solid continua. Existence and propagation of such waves require presence of strain i.e. elasticity. This stress wave propagation phenomenon is due to mechanism of vibrational energy transfer between neighboring material points, hence requires presence of strain and elasticity. To our knowledge the existence and propagation of deviatoric stress waves purely due to rheology have never been reported in the published works on TVE solids. This in fact is the incentive and motivation for the work presented in this paper.

In any deforming solid continua, the total deformation can be additively decomposed into volumetric and distortional. Volumetric deformation results in change of volume if the matter is compressible and the distortional deformation results in only the change of shape of the volume of matter. The volumetric deformation can result in pressure waves only if the matter is compressible. Distortional deformation results in deviatoric stress waves. Existence and propagation of these waves require stiffness and mass. For example, in incompressible solid continua that has stiffness and mass, deviatoric stress waves can exist and propagate but pressure waves are not possible due to lack of volumetric deformation. Likewise, in a compressible gas that has virtually no stiffness only pressure waves can exist and propagate. In TVE solids, the deviatoric stress waves due to elasticity (strain) co-exist with deviatoric stress waves due to rheology. In a recent paper Surana et al. [10] demonstrated existence of deviatoric stress waves in polymeric fluids. In such fluids due to absence of elasticity (strains) the stiffness due to elasticity is absent. The authors identified viscosity and relaxation time as sources of dynamic stiffness in such fluids that permit existence, propagation, transmission, reflection and interaction of deviatoric stress waves purely due to rheology. Authors showed that increasing viscosity and decreasing relaxation time results in increasing dynamic stiffness hence result in faster deviatoric stress wave speed. The authors also presented results showing dependence of deviatoric wave speed on viscosity and relaxation time. The work presented in the present paper is motivated by the work of reference [19].

1.1 Motivation and scope of present work

We consider isotropic, homogeneous, incompressible TVE solid continua with elasticity, dissipation and memory mechanism. Due to incompressibility, pressure waves cannot exist in such solid continua, but deviatoric stress waves that require stiffness and mass can exist and propagate. In TVE solid continua considered here there are two mechanisms of deviatoric stress waves that co-exist: (1) The first type of deviatoric stress waves are due to elasticity (strain) and mass or in general due to static stiffness because of elasticity and mass. These are commonly studied in solid continua (2) The second type of deviatoric stress waves are due to rheology. These have never been studied and reported to our knowledge. We explain the rheology mechanisms that makes existence of such stress waves possible. When a TVE solid continua is subjected to disturbance, the viscous resistance offered to the motion of polymer molecules by the solvent and the neighboring polymer molecules in the direction of the disturbance can be collectively viewed as one dimensional springs acting in the direction of the disturbance. This is additional source of dynamic stiffness in TVE solids with memory, and since TVE solids naturally have mass, additional deviatoric stress wave can exist due to this rheology in TVE solids. This mechanism of additional dynamic stiffness exists regardless of whether the TVE solid continua is compressible or incompressible but requires motion of the polymer molecules. Thus, it is straight forward to conclude the existence of deviatoric stress waves in TVE solid continua due to rheology regardless of whether the TVE solid is compressible or incompressible. A complete study of deviatoric stress waves due to rheology in TVE solids with memory is the objective of the research presented in this paper. The investigations considered in this paper are outlined in the following:

• (1) Existence of the deviatoric stresses due to rheology and the composite stress waves due to rheology and elasticity of solid continua.

• (2) Purely elastic deviatoric stress waves and their propagation.

• (3) Physics of propagation of deviatoric stress waves due to rheology.

• (4) Parameters influencing the deviatoric stress waves due to rheology and their speed of propagation.

• (5) Physics of propagation of composite deviatoric stress waves due to elasticity and rheology.

• (6) Propagation, reflection, transmission and interaction of composite deviatoric stress waves.

The mathematical model considered in the present work consists of CBL of CCM in $\mathbb {R}^{1}$ in lagrangian description derived from CBL in $\mathbb {R}^{3}$ and the linear constitutive theories that are derived using entropy inequality and the representation theorem. For noncyclic loading (as considered here) the entropy production due to dissipation is not significant, hence the deformation process can be assumed isothermal, thus energy equation need not be considered as part of the mathematical model. We consider simple linear viscoelastic solid with small deformation, small strain physics. The mathematical model is nondimensionalized and the solutions of the IVP described by the mathematical model are obtained using space-time coupled finite element method based on space-time residual functional, also referred to as space-time least squares method for a space-time strip with time marching [12]. The space time differential operator in the present study is linear.

2 Mechanisms of static and dynamic stiffness in TVE solid continua with memory

TVE solids possess elasticity due to strains, dissipation physics due to viscosity and rheology due to long chain molecules of the polymer. Such solids naturally possess static (same as dynamic) stiffness due to elasticity (strains). This permits existence and propagation of deviatoric elastic (or non elastic) stress waves in such solids. In solid continua presence of strain during deformation is essential for existence and propagation of deviatoric stress waves.

Additionally, in TVE solid continua with memory, the long chain molecules provide rheology or memory. Uncoiling and stretching of long chain molecules during loading and the viscous drag (resistance) experienced by the polymer molecules in this process is similar to stretching of one dimensional springs. This is additional source of dynamic stiffness in TVE solids with memory. Since viscous drag is dependent on viscosity of the polymeric solid, viscosity is naturally a parameter that controls the dynamic stiffness due to rheology in TVE solids. Higher values of viscosity naturally result in more pronounced viscous drag, thus higher dynamic stiffness.

The second source of dynamic stiffness due to rheology is because of relaxation physics. A smaller relaxation time implies less physical time for the polymer molecules to revert back to relaxed state, hence increased viscous resistance and higher stiffness during relaxation process compared to longer relaxation time that requires longer physical time for the relaxation process. Thus, in this case the relaxation process is spread over a longer time implying decreased dynamic stiffness. The stiffness due to rheology is naturally dynamic stiffness i.e. its existence requires motion. For a stationary TVE solid continua, the elastic stiffness dependent on elastic properties is always nonzero, but the dynamic stiffness due to rheology is zero when the continua does not have time dependent deformation as it requires motion of the polymer molecules.

In a deforming TVE solid the deviatoric stress waves due to elasticity and due to rheology always co-exist. We shall see that in general the deviatoric stresses due to elasticity are much more dominant in TVE solid continua with memory compared to the deviatoric stresses due to rheology. Separating the two effects in the study of deviatoric stress wave propagations in TVE solids is somewhat difficult. This is due to two reasons: (i) Physics of stress wave propagation in solid continua (ii) and secondly due to the fact that the deviatoric stress waves due to rheology are quite weak compared to purely elastic waves hence, in the composite wave the influence of rheology is not dominant, hence may not be detectable.

3 Deviatoric stress wave propagation in TVE solid continua

The physics of deviatoric stress wave propagation in solid continua requires elasticity but more specifically presence of strain. The purely elastic waves naturally have strain physics but the deviatoric stress waves due to rheology do not contain strain physics. Instead, the deviatoric stress wave due to rheology have strain rate physics (convected time derivatives of strain tensor(s)). Thus, composite deviatoric stress wave and purely elastic deviatoric stress waves can propagate in TVE solids due to presence of strain physics in both cases. However, a deviatoric stress wave purely due to rheology can exist but cannot propagate due to the absence of strain physics. Thus, in the model problem studies it is possible to demonstrate existence of deviatoric stress waves due to rheology but their propagation during evolution is not possible. Instead, the only alternative is to compare purely elastic wave with the composite wave to study their propagation, reflection, transmission, interaction and their propagation speeds.

Regarding composite wave speed, we know that effective total dynamic stiffness increases due to presence of rheology, thus in principle the composite wave speed must be influenced by viscosity and relaxation time. However, the change in stiffness due to rheology is small compared to the stiffness due to elasticity, thus a quantitative measure of change in wave speed due to rheology is also quite difficult, nonetheless in model problem studies we clearly demonstrate the existence of this physics.

4 Mathematical model

The mathematical model consists of CBL of CCM and the constitutive theories derived based on entropy inequality and representation theorem for small deformation, small strain physics. Explicit form of the partial differential equations (PDEs) constituting the mathematical model in ${\mathbb {R}}^{1}$ (used in present work) are obtained as a special case of the mathematical model in ${\mathbb {R}}^{3}$. Thermoviscoelastic solids with memory (rubber like material) have been studied for longtime [19]. Most approaches used in deriving constitutive theories have been phenomenological, primarily based on 1D spring and 1D dashpot, dumbbell models [3]. More recently CCM principles are slowly being used for constitutive theories for TVE solids with memory [11, 28, 29]. At macroscale TVE solids are assumed isotropic and homogeneous. This allows us to use CBL of CCM and constitutive theory methodologies for isotropic and homogeneous matter based of entropy inequality and the representation theorem [22,23,24,25,26,27, 32,33,34,35, 39, 40].

4.1 Conservation and balance laws and constitutive theories

The rate of entropy production in such solids is relatively small (when the loads are not repeated cyclic loads), thus thermal effects are almost negligible, hence can be neglected. Thus, the mathematical model consists of conservation of mass (CM), balance of linear momenta (BLM), balance of angular momenta (BAM) and the constitutive theory for the stress tensor. Furthermore, in case of small deformation, small strain the determinant of the jacobian of deformation is one ($| \pmb {\varvec{J }}|=1$), hence the density remains constant during the deformation process. Thus, CM is not part of mathematical model considered here. Density $\rho _{_{_{\!\!0}}}$ used in BLM is the constant density in the reference or initial configuration that does not change during deformation.

In case of small deformation, small strain, the initial (same as reference) configuration and the deformed configurations are virtually the same due to the fact that deformed coordinates ${\bar{x}}_{i}$ of the material point can be considered to be the same as the undeformed coordinates ${x}_{i}$. Thus, in this case, whether we use ${x}_{i}$ coordinates and time t or ${\bar{x}}_{i}$ coordinates and time t, the resulting mathematical model will be the same. Since we are considering solid medium, we prefer to use ${x}_{i}$ and t in the mathematical model, hence the Lagrangian description.

Using notations of references [28, 29], we have the following for BLM and BAM of CCM in $\mathbb {R}^{3}$ in Lagrangian description.

$$\begin{aligned}{} & {} \rho _{_{_{\!\!0}}}\frac{D \pmb {\varvec{v }}}{Dt} - \rho _{_{_{\!\!0}}} \pmb {\varvec{F }}^b - \pmb {\varvec{\nabla }} \pmb {\varvec{\cdot }} \pmb {\varvec{\sigma }}= 0 \qquad \qquad \text {(BLM)} \end{aligned}$$

(1)

$$\begin{aligned}{} & {} [ \pmb {\varvec{\sigma }}] = [ \pmb {\varvec{\sigma }}]^T \qquad \qquad \text {(BAM)} \end{aligned}$$

(2)

$$\begin{aligned}{} & {} \pmb {\varvec{v }} = \frac{D \pmb {\varvec{u }}}{Dt} = \frac{\partial \pmb {\varvec{u }}}{\partial t} \end{aligned}$$

(3)

in which ${\rho _{_{_{\!\!0}}}}$ is density in the reference configuration, ${ \pmb {\varvec{v }}}$ is velocity, ${ \pmb {\varvec{u }}}$ is displacement, vector ${ \pmb {\varvec{F }}^b}$ is body force vector per unit mass, ${ \pmb {\varvec{\sigma }}}$ is cauchy stress tensor (basis independent due to small deformation, small strain)

Constitutive Theories

We decompose ${ \pmb {\varvec{\sigma }}}$ into ${{}^{e} \pmb {\varvec{\sigma }}}$ and ${{}^{d} \pmb {\varvec{\sigma }}}$, equilibrium and deviatoric stress tensors (additive decomposition).

$$\begin{aligned} \pmb {\varvec{\sigma }} = {}^{e} \pmb {\varvec{\sigma }}+ {}^{d} \pmb {\varvec{\sigma }}\end{aligned}$$

(4)

Constitutive theory for ${}{}^{e} \pmb {\varvec{\sigma }}$ describes volumetric deformation and the constitutive theory for ${}{}^{d} \pmb {\varvec{\sigma }}$ addresses distortional deformation physics [29]. Since the matter is assumed incompressible, the constitutive theory for ${}{}^{e} \pmb {\varvec{\sigma }}$ is much simplified and is given by [29]

$$\begin{aligned} {}^{e} \pmb {\varvec{\sigma }}= -p \pmb {\varvec{\delta }} \end{aligned}$$

(5)

in which p is the mechanical pressure, assumed positive when compressive. Derivation of the constitutive theory for ${}{}^{d} \pmb {\varvec{\sigma }}$ begins with the conjugate pair ${}^{d} \pmb {\varvec{\sigma }}: \pmb {\varvec{\varepsilon }}$ in the entropy inequality [21,22] in which $\pmb {\varvec{\varepsilon }}$ is the linear part of Green’s strain tensor. Thus, for incompressible, isothermal physics we can write

$$\begin{aligned} {}^{d} \pmb {\varvec{\sigma }}= {}^{d} \pmb {\varvec{\sigma }}( \pmb {\varvec{\varepsilon }}) \end{aligned}$$

(6)

Due to physics of dissipation, Eq. (6) must be modified to include strain rate $\overset{\,{{\textbf {.}}}}{ \pmb {\varvec{\varepsilon }}}$ in the argument tensors of ${}^{d} \pmb {\varvec{\sigma }}$.

$$\begin{aligned} {}^{d} \pmb {\varvec{\sigma }}= {}^{d} \pmb {\varvec{\sigma }}( \pmb {\varvec{\varepsilon }},\overset{\,{{\textbf {.}}}}{ \pmb {\varvec{\varepsilon }}}) \end{aligned}$$

(7)

Let ${}^{(i)} \pmb {\varvec{\gamma }}$; i=1,2,...,n be the rates of strain tensor $\pmb {\varvec{\varepsilon }}$ of up to order n. ${}^{(i)} \pmb {\varvec{\gamma }}$ are naturally basis independent, then we can generalize (7) and instead use

$$\begin{aligned} {}^{d} \pmb {\varvec{\sigma }}= {}^{d} \pmb {\varvec{\sigma }}( \pmb {\varvec{\varepsilon }},{}^{(i)} \pmb {\varvec{\gamma }}) \quad ; \quad i=1,2,...,n \end{aligned}$$

(8)

From published works on polymeric fluids [3, 28,29,30], we know that a constitutive theory for deviatoric cauchy stress tensor must at least use the first convected time derivative of the deviatoric cauchy stress tensor as a constitutive variable with deviatoric cauchy stress tensor as its argument tensor. Otherwise, it is not possible to show the existence of memory modulus, hence lack of rheology and relaxation physics. The same concept apply to polymeric solids as well. That is, we must at least consider the following instead of Eq. (8)

$$\begin{aligned} {}^{d} \pmb {\varvec{\sigma }}^{(1)} = {}^{d} \pmb {\varvec{\sigma }}^{(1)}({}^{d} \pmb {\varvec{\sigma }}, \pmb {\varvec{\varepsilon }},{}^{(i)} \pmb {\varvec{\gamma }}) \quad ; \quad i=1,2,...,n \end{aligned}$$

(9)

Let ${}^{d} \pmb {\varvec{\sigma }}^{(j)}$; j=1,2,...,m be material or time derivatives of the cauchy stress tensor up to orders m (same as the convected time derivatives due to Lagrangian description and small strain, small deformation assumption), then we can generalize Eq. (9).

$$\begin{aligned}{} & {} {}^{d} \pmb {\varvec{\sigma }}^{(m)} = {}^{d} \pmb {\varvec{\sigma }}^{(m)}( \pmb {\varvec{\varepsilon }},{}^{d} \pmb {\varvec{\sigma }}, {}^{d} \pmb {\varvec{\sigma }}^{(j)},{}^{(i)} \pmb {\varvec{\gamma }}) \nonumber \\{} & {} \quad ; \quad i=1,2,...,n \quad ; \quad j=1,...,m-1 \end{aligned}$$

(10)

Using (10), we can derive a most general constitutive theory for ${}^{d} \pmb {\varvec{\sigma }}^{(m)}$ based on integrity and representation theorem.

Surana [28, 29] has presented the details of the derivation as well as derivation of material coefficients. These constitutive theories are called theories of order (n,m). In the present work we consider a simplified constitutive theory of up to orders m=1 and n=2 that resembles the constitutive theories for Maxwell, Oldroyd-B and Giesekus constitutive models for viscoelastic polymeric fluids [28, 29].

$$\begin{aligned}{} & {} {}^{d} \pmb {\varvec{\sigma }}+ \lambda _{1}({}^{d} \pmb {\varvec{\sigma }}^{(1)}) = 2\mu \pmb {\varvec{\varepsilon }} + \lambda (tr( \pmb {\varvec{\varepsilon }})) \pmb {\varvec{I }} \nonumber \\{} & {} \quad + 2\eta {}^{(1)} \pmb {\varvec{\gamma }} + 2\eta \lambda _{2}{}^{(2)} \pmb {\varvec{\gamma }} + \alpha \frac{{\lambda }_{1}}{\eta }({}^{d} \pmb {\varvec{\sigma }})^{2} \end{aligned}$$

(11)

in which $\lambda _{1}$ is relaxation time, $\mu$ and $\lambda$ are Lamé’s constants, $\eta$ is viscosity, $\lambda _{2}$ is retardation time and $\alpha$ is mobility factor (see references [3, 28, 29] for more details). Using Eq. (11) we define three different constitutive theories that are parallel to the constitutive theories for Maxwell, Oldroyd-B and Giesekus polymeric fluids, hence are denoted so.

Maxwell model:

$\lambda _{2}$=0, $\alpha$=0 in Eq. (11)

Oldroyd-B model:

$\alpha$=0 in Eq. (11)

Giesekus model:

$\lambda _{2}$=0 in Eq. (11)

4.2 Complete mathematical model

Complete mathematical model consists of (1)–(3) in which we substitute additive stress decomposition Eq. (4) and constitutive theory for equilibrium stress tensor ${}^{e} \pmb {\varvec{\sigma }}$ given by (5) and the constitutive theory for deviatoric stress tensor ${}^{d} \pmb {\varvec{\sigma }}$ given by (11)

$$\begin{aligned}{} & {} \rho _{_{_{\!\!0}}}\frac{\partial {v}_{i}}{\partial {t}} - \rho _{_{_{\!\!0}}} \pmb {\varvec{F }}^b_{i} + \frac{\partial {p}}{\partial {x_{i}}} - \frac{\partial ({}^{d} \pmb {\varvec{\sigma }}_{ji})}{\partial {x_{j}}} = 0 \end{aligned}$$

(12)

$$\begin{aligned}{} & {} {}^{d} \pmb {\varvec{\sigma }}+ \lambda _{1}\frac{\partial ({}^{d} \pmb {\varvec{\sigma }})}{\partial {t}} = 2\mu \pmb {\varvec{\varepsilon }} + {\lambda }tr( \pmb {\varvec{\varepsilon }}) \pmb {\varvec{I }} \nonumber \\{} & {} \quad + 2\eta \frac{\partial ( \pmb {\varvec{\varepsilon }})}{\partial {t}} + 2\eta \lambda _{2}\frac{\partial ^{2}( \pmb {\varvec{\varepsilon }})}{\partial {t}^{2}} + \alpha \frac{{\lambda }_{1}}{\eta }({}^{d} \pmb {\varvec{\sigma }}^{(0)})^{2} \end{aligned}$$

(13)

$$\begin{aligned}{} & {} {v}_{i} = \frac{\partial {u_{i}}}{\partial {t}} \end{aligned}$$

(14)

4.3 Dimensionless form of the mathematical model in ${\mathbb {R}}^{3}$

Let $L_{0}$, $v_{0}$, $t_{0}$, $(\rho _{_{_{\!\!0}}})_{ref}$, $\tau _{0}$, $p_{0}$, $\eta _{0}$ be reference length, velocity, time, density, stress, pressure and viscosity respectively. First we express Eq. (12)–(14) using hat ( $\hat{}$ ) on all quantities which implies that all these quantities have their usual dimensions or unit, then we define the following dimensionless variables

$$\begin{aligned} \left. \begin{array}{c} {x} = \dfrac{{\hat{x}}}{L_{0}} \text { }, \text { } {v} = \dfrac{{\hat{v}}}{v_{0}} \text { }, \text { } {u} = \dfrac{{\hat{u}}}{L_{0}} \text { }, \text { } {t} = \dfrac{{\hat{t}}}{t_{0}} \text { }, \text { } \\ {{}^{d}{\sigma }} = \dfrac{\hat{{}^{d}\sigma }}{\tau _{0}} \text { }, \text { } {p} = \dfrac{{\hat{p}}}{p_{0}} \text { }, \text { } {\eta } = \dfrac{\hat{\eta }}{\eta _{0}} \text { }, \text { } {E} = \dfrac{{\hat{E}}}{E_{0}} \text { }, \text { } {\rho _{_{_{\!\!0}}}} = \dfrac{\hat{\rho _{_{_{\!\!0}}}}}{(\rho _{_{_{\!\!0}}})_{ref}} \\ with \text { } t_{0}=\dfrac{L_{0}}{v_{0}} \text { }, \text { } v_{0}=\sqrt{\dfrac{E_{0}}{(\rho _{_{_{\!\!0}}})_{ref}}}, \\ \text { } \tau _{0}=p_{0}=(\rho _{_{_{\!\!0}}})_{ref}v_{0}^{2} \text { }; \text { } characteristic \text { } kinetic \text { } energy \\ Then \text { } E_{0}=\tau _{0}=p_{0}=(\rho _{_{_{\!\!0}}})_{ref}v_{0}^{2} \text { }, \text { } we \text { } also \text { } use \text { } \dfrac{\hat{F_{i}^{b}}}{{F_{0}}} = F_{b}. \end{array}\quad \right\} \end{aligned}$$

(15)

The dimensionless form of Eqs. (12)–(14) are given by

$$\begin{aligned} & \rho _{0} \frac{{\partial v_{i} }}{{\partial t}} - \left( {\frac{{L_{0} F_{0} }}{{v_{0}^{2} }}} \right)\rho _{0} \varvec{F}_{i}^{b} \\ & \; + \left( {\frac{{p_{0} }}{{(\rho _{0} )_{{ref}} v_{0}^{2} }}} \right)\frac{{\partial p}}{{\partial x_{i} }} - \left( {\frac{{\tau _{0} }}{{(\rho _{0} )_{{ref}} v_{0}^{2} }}} \right)\frac{{\partial (^{d} \varvec{\sigma }_{{ji}} )}}{{\partial x_{j} }} = 0 \\ \end{aligned}$$

(16)

$$\begin{aligned} & ^{d} \varvec{\sigma } + \left( {\frac{{\hat{\lambda }_{1} }}{{t_{0} }}} \right)\frac{{\partial (^{d} \varvec{\sigma })}}{{\partial t}} = \frac{{E_{0} }}{{\tau _{0} }}(2\mu \varvec{\varepsilon } + \lambda tr(\varvec{\varepsilon })\varvec{I}) \\ & \; + 2\eta \left( {\frac{{\eta _{0} }}{{\tau _{0} t_{0} }}} \right)\frac{{\partial (\varvec{\varepsilon })}}{{\partial t}} + 2\eta \left( {\frac{{\eta _{0} }}{{\tau _{0} t_{0} }}} \right)\frac{{\hat{\lambda }_{2} }}{{t_{0} }}\frac{{\partial ^{2} (\varvec{\varepsilon })}}{{\partial t^{2} }} + \left( {\frac{\alpha }{\eta }} \right)\left( {\frac{{\tau _{0} t_{0} }}{{\eta _{0} }}} \right)\left( {\frac{{\hat{\lambda }_{1} }}{{t_{0} }}} \right)(^{d} \varvec{\sigma }^{{(0)}} )^{2} \\ \end{aligned}$$

(17)

$$\begin{aligned}{} & {} {v}_{i} = \frac{\partial {u_{i}}}{\partial {t}} \end{aligned}$$

(18)

$$\left. {\begin{array}{*{20}c} {If{\text{ }}we{\text{ }}choose{\text{ }}F_{0} = \frac{{v_{0}^{2} }}{{L_{0} }}{\text{ }},{\text{ }}then{\text{ }}\frac{{F_{0} L_{0} }}{{v_{0}^{2} }} = 1{\text{ }}and{\text{ }}\frac{{P_{0} }}{{(\rho _{0} )_{{ref}} v_{0}^{2} }} = 1{\text{ }},} \\ {\frac{{\tau _{0} }}{{(\rho 0)_{{ref}} v_{0}^{2} }} = 1{\text{ }},{\text{ }}De = \frac{{\hat{\lambda }_{1} }}{{t_{0} }}{\text{ }},{\text{ }}De_{2} = \frac{{\hat{\lambda }_{2} }}{{t_{0} }}{\text{ }},{\text{ }}Re = \frac{{\tau _{0} t_{0} }}{{\eta _{0} }}} \\ \end{array} } \right\}$$

(19)

we can write Eqs. (16)–(18) as

$$\begin{aligned}{} & {} \rho _{_{_{\!\!0}}}\frac{\partial {v}_{i}}{\partial {t}} - \rho _{_{_{\!\!0}}} \pmb {\varvec{F }}^b_{i} + \frac{\partial {p}}{\partial {x_{i}}} - \frac{\partial ({}^{d} \pmb {\varvec{\sigma }}_{ji})}{\partial {x_{j}}} = 0 \end{aligned}$$

(20)

$$\begin{aligned} & ^{d} \varvec{\sigma } + De\frac{{\partial (^{d} \varvec{\sigma })}}{{\partial t}} = 2\mu \varvec{\varepsilon } + \lambda tr(\varvec{\varepsilon })\varvec{I} \\ & \; + \left( {\frac{{2\eta }}{{Re}}} \right)\frac{{\partial (\varvec{\varepsilon })}}{{\partial t}} + 2\eta \left( {\frac{{De_{2} }}{{Re}}} \right)\frac{{\partial ^{2} (\varvec{\varepsilon })}}{{\partial t^{2} }} + \alpha \frac{{DeRe}}{\eta }(^{d} \varvec{\sigma }^{{(0)}} )^{2} \\ \end{aligned}$$

(21)

$$\begin{aligned}{} & {} {v}_{i} = \frac{\partial {u_{i}}}{\partial {t}} \end{aligned}$$

(22)

where Re is the Reynolds number and De and $De_{2}$ are Deborah numbers.

Equations Eqs. (20)–(22) are the final form of the dimensionless BLM, and the constitutive equation.

4.4 Dimensionless form of the mathematical model in ${\mathbb {R}}^{1}$

We consider pure axial deformation in $x_{1}$ direction.

For 1D in ${\mathbb {R}}^{1}$ ($O-x_{1}$ of x-frame), we can obtain the following mathematical model using (20)-(22). For simplicity we choose $\lambda _{2}=0$ and $\alpha =0$ i.e. we consider mathematical model parallel to Maxwell polymeric fluid.

We obtain the following

$$\begin{aligned}{} & {} \rho _{_{_{\!\!0}}}\frac{\partial {v}_{1}}{\partial {t}} - \rho _{_{_{\!\!0}}}{F}^b_{1} + \frac{\partial {p}}{\partial {x_{1}}} - \frac{\partial ({}^{d}{\sigma _{11}})}{\partial {x_{1}}} = 0 \end{aligned}$$

(23)

$$\begin{aligned}{} & {} {}^{d}{\sigma _{11}} + De\frac{\partial ({}^{d}{\sigma _{11}})}{\partial {t}} = E\frac{\partial {u_{1}}}{\partial {x_{1}}}+(\frac{2\eta }{Re}){\frac{\partial {v_{1}}}{\partial {x_{1}}}} \end{aligned}$$

(24)

$$\begin{aligned}{} & {} {v}_{1} = \frac{\partial {u_{1}}}{\partial {t}} \end{aligned}$$

(25)

In which E is module of elasticity. We choose mechanical pressure $p=0$ and $F_{1}^{b}=0$ for the model problem studies presented in the paper.

Secondly, since the main thrust of this work is to investigate the deviatoric stress waves due to rheology, this requires that we vary De, E and $\eta$. For this reason we can recast Eq. (24) in a more convenient form. Thus, finally we have the following mathematical model that is suitable for 1D deviatoric stress wave studies in the viscoelastic polymeric solid with memory.

$$\begin{aligned}{} & {} \rho _{_{_{\!\!0}}}\frac{\partial {v}_{1}}{\partial {t}} - \frac{\partial ({}^{d}{\sigma _{11}})}{\partial {x_{1}}} = 0 \end{aligned}$$

(26)

$$\begin{aligned}{} & {} {}^{d}{\sigma _{11}} + De\frac{\partial ({}^{d}{\sigma _{11}})}{\partial {x_{1}}} = {C_{1}}\frac{\partial {u_{1}}}{\partial {x_{1}}}+{C_{2}}{\frac{\partial {v_{1}}}{\partial {x_{1}}}} \quad \forall \quad x,t \in \Omega _{xt} \end{aligned}$$

(27)

$$\begin{aligned}{} & {} {v}_{1} = \frac{\partial {u_{1}}}{\partial {t}} \end{aligned}$$

(28)

In the mathematical model Eqs. (26)–(28), varying De number represents varying rheology and $C_{1}$,$C_{2}$ represent presence of elasticity due to strain and the presence of dissipation due to viscosity respectively.

5 Solution of the mathematical model

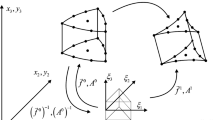
The mathematical model Eqs. (26)–(28) is a system of linear partial differential equations in space coordinate $x_{1}$ and time t, hence is an initial value problem (IVP) in which the space-time differential operator is linear but not self-adjoint [12]. We seek solution of this IVP using space-time finite element method in which space-time integral form is space-time variationally consistent [12]. Based on reference [12], the space-time integral form based on space-time residual functional is the only space-time integral form that is space-time variationally consistent, hence ensures unconditional stability of the computations during entire evolution, hence is used in the present work. We divide space-time domain ${{\bar{\Omega }}_{xt}}$ into space time strips, ${{\bar{\Omega }}_{xt}^{T}}=\underset{j=1}{\overset{}{{\textstyle \cup }} }{}^{j}{{\bar{\Omega }}_{xt}^{T}}$ in which ${{\bar{\Omega }}_{xt}^{T}}$ is discretization of ${{\bar{\Omega }}_{xt}}$ in space time strips ${}{}^{j}{{\bar{\Omega }}_{xt}^{T}}$ (Fig. 1a). A typical $n^{th}$ space-time strip is divided into nine-node p-version hierarchical space-time finite elements for which the local approximations are of higher order global differentiability in space x and time t.

Fig. 1b shows discretization ${}{}^{1}{{\bar{\Omega }}_{xt}^{T}}=\underset{e}{\overset{}{{\textstyle \cup }} }{{\bar{\Omega }}_{xt}^{e}}$ of the first space-time strip $(0\le {t}\le {\Delta {t}})$, using BCs and ICs for the first space-time strip, a converged solution is obtained (h,p-refinements, with minimally conforming approximation space [12]) for the first space-time strip. Using the converged calculated solution at $\Delta {t}$, initial conditions are obtained for the second space-time strip $({\Delta {t}}\le {t}\le {2\Delta {t}})$ followed by computation of solution for the second space-time strip. We call this procedure; space-time strip with time marching. This procedure is continued until the desired time is reached. In this approach of calculating evolution the residual functional I [12] for each space-time strip is an accurate measure of solution accuracy when the approximation space is minimally conforming. Thus, the solutions reported in the paper are nearly time accurate (within computational roundoffs).

5.1 Space-time residual functional for a space-time strip

Consider discretization ${}{}^{n}{{\bar{\Omega }}_{xt}^{T}}=\underset{e}{\overset{}{{\textstyle \cup }} } {{\bar{\Omega }}_{xt}^{e}}$ of $n^{th}$ space-time strip of ${}{}^{n}{{\bar{\Omega }}_{xt}}$. Let $(u_{1})^{e}_{h}$, $(v_{1})^{e}_{h}$ and $({}{}^{d}\sigma _{11})^{e}_{h}$ be the local approximation of $u_{1}$, $v_{1}$ and ${}{}^{d}\sigma _{11}$ over an element ${{\bar{\Omega }}_{xt}^{e}}$ and $(u_{1})_{h}$, $(v_{1})_{h}$ and $({}{}^{d}\sigma _{11})_{h}$ be approximations of u, v and ${}{}^{d}\sigma _{11}$ over discretization ${}{}^{n}{{\bar{\Omega }}_{xt}^{T}}$ such that

$$\begin{aligned} (u_{1})_{h}=\underset{e}{\overset{}{{\textstyle \cup }} }(u_{1})_{h}^{e} \text { };\text { } (v_{1})_{h}=\underset{e}{\overset{}{{\textstyle \cup }} }(v_{1})_{h}^{e}\text { };\text { } ({}{}^{d}\sigma _{11})_{h}=\underset{e}{\overset{}{{\textstyle \cup }} }({}^{d}\sigma _{11})^{e}_{h} \end{aligned}$$

(29)

Upon substituting (29) we obtain residual functions $E_{1}$,$E_{2}$ and $E_{3}$ over ${}{}^{n}{{\bar{\Omega }}_{xt}^{T}}$.

$$\begin{aligned}{} & {} E_{1}=\rho _{_{_{\!\!0}}}\frac{\partial ({v}_{1})_{h}}{\partial {t}} - \frac{\partial ({}^{d}{\sigma _{11}})_{h}}{\partial {x_{1}}} \end{aligned}$$

(30)

$$\begin{aligned}{} & {} E_{2}=({}^{d}{\sigma _{11}})_{(h)}+ De\frac{\partial ({}^{d}{\sigma _{11}})_{(h)}}{\partial {t}} = {C_{1}}\frac{\partial ({u_{1}})_{h}}{\partial {x_{1}}}+{C_{2}}{\frac{\partial ({v_{1}})_{h}}{\partial {x_{1}}}} \end{aligned}$$

(31)

$$\begin{aligned}{} & {} E_{3}=({v}_{1})_{h} - \frac{\partial ({u_{1}})_{h}}{\partial {t}} \end{aligned}$$

(32)

Space-time residual functional I over ${}^{n}{{\bar{\Omega }}_{xt}^{T}}$ is defined as

$$\begin{aligned} I=\sum _{i=1}^{3}I_{i}=\sum _{i=1}^{3}(E_{i},E_{i})_{{}^{n}{\bar{\Omega }}_{xt}^{T}} \end{aligned}$$

(33)

If I is differentiable in its arguments i.e. in $(u_{1})_{h}$, $(v_{1})_{h}$ and $({}{}^{d}\sigma _{11})_{h}$, then $\delta {I}$ is unique and $\delta {I}=0$ is a necessary condition for an extremum functional I in (33)

$$\begin{aligned} \delta {I}=\sum _{i=1}^{3}2(E_{i},\delta {E_{i}})=\{g\}=0 \end{aligned}$$

(34)

and

$$\begin{aligned} \delta ^{2}{I}=\sum _{i=1}^{3}2(\delta {E_{i}},\delta {E_{i}}) > 0 \text { } \forall \text { } \delta {E_{i}} \text { }; \text { } i=1,2,3 \end{aligned}$$

(35)

Hence, (35) is sufficient condition or extremum principle that ensure unique $(u_{1})_{h}$, $(v_{1})_{h}$ and $({}{}^{d}\sigma _{11})_{h}$ from Eq. (34) and this solution minimizes I in (33) (due to Eq. (35)). Let

$$\begin{aligned} \begin{aligned}{} & {} (u_{1})_{h}^{e} = [N^{u_{1}}]\{\delta _{e}^{u_{1}}\} \text { }, \text { } (v_{1})_{h}^{e} = [N^{v_{1}}]\{\delta _{e}^{v_{1}}\}\\{} & {} ({}{}^{d}\sigma _{11})_{h}^{e} = [N^\sigma ]\{\delta _{e}^{\sigma }\} \end{aligned} \end{aligned}$$

(36)

In the local approximation Eq. (36), $[N^{u_{1}}]$,$[N^{v_{1}}]$ and $[N^\sigma ]$ are approximation functions and $\{\delta ^{u_{1}}_{e}\}$, $\{\delta ^{v_{1}}_{e}\}$ and $\{\delta ^{\sigma }_{e}\}$ are nodal degrees of freedom for $(u_{1})^{e}_{h}$, $(v_{1})^{e}_{h}$ and $({}{}^{d}\sigma _{11})^{e}_{h}$ and

$$\begin{aligned} \{\delta ^{u_{1}}\}=\underset{e}{\overset{}{{\textstyle \cup }} }\{\delta ^{u_{1}}_{e}\} \text { }; \text { } \{\delta ^{v_{1}}\}=\underset{e}{\overset{}{{\textstyle \cup }} }\{\delta ^{v_{1}}_{e}\} \text { }; \text { } \{\delta ^{\sigma }\}=\underset{e}{\overset{}{{\textstyle \cup }} }\{\delta ^\sigma _{e}\} \end{aligned}$$

(37)

are degrees of freedom for ${}^{n}{{\bar{\Omega }}_{xt}^{T}}$ for $u_{1}$,$v_{1}$ and ${{}^{d}\sigma _{11}}$ and

$$\begin{aligned} \{\delta \}^{T}= [\{\delta ^{u_{1}}\}^{T}, \{\delta ^{v_{1}}\}^{T}, \{\delta ^{\sigma }\}^{T}] \end{aligned}$$

(38)

and

$$\begin{aligned} \{{\delta }^{e}\}^{T}= [\{{\delta ^{u_{1}}_{e}}\}^{T}, \{{\delta ^{v_{1}}_{e}}\}^{T}, \{{\delta ^{\sigma }_{e}}\}^{T}] \end{aligned}$$

(39)

are total dofs for ${}^{n}{{\bar{\Omega }}_{xt}^{T}}$ and ${{\bar{\Omega }}_{xt}^{e}}$.

We can write the following using Eq. (33)

$$\begin{aligned}{} & {} I=\sum _{i=1}^{3}I_{i}=\sum _{e}^{}(\sum _{i=1}^{3}(E_{i}^{e},E_{i}^{e})_{{{\bar{\Omega }}_{xt}^{e}}}) \end{aligned}$$

(40)

$$\begin{aligned}{} & {} \pmb {\varvec{\therefore }}\quad \delta {I}=\sum _{e}^{}(\sum _{i=1}^{3}2(E_{i}^{e},\delta {E_{i}^{e}})_{{{\bar{\Omega }}_{xt}^{e}}})=\sum _{e}^{}(\sum _{i=1}^{3}\{g_{i}^{e}\})=\{g(\{\delta \})\}=0 \end{aligned}$$

(41)

$\{g^{e}(\{\delta ^{e}\})\}$ and $\{g(\{\delta \})\}$ are linear functions of $\{\delta ^{e}\}$ and $\{\delta \}$ respectively, hence we can write the following:

$$\begin{aligned} \sum _{i=1}^{3}(E_{i}^{e},\delta {E_{i}^{e}})_{{{\bar{\Omega }}_{xt}^{e}}} = [K^{e}]\{\delta ^{e}\}-\{f^{e}\} \end{aligned}$$

(42)

and

$$\begin{aligned} \delta {I} = 2\sum _{e}([K^{e}]\{\delta ^{e}\}-\{f^{e}\})=0 \end{aligned}$$

(43)

or

$$\begin{aligned}{}[K]\{\delta \}=\{F\} \end{aligned}$$

(44)

in which

$$\begin{aligned}{} & {} [K] = \sum _{e}[K^{e}] \; \ assembly \ of \ [K^{e}]\nonumber \\{} & {} \quad \{F\} = \sum _{e}[f^{e}] \; \ assembly \ of \ \{f^{e}\} \end{aligned}$$

we impose BCs and ICs in Eq. (44) and solve for remaining $\{\delta \}$. After calculating solution for a space-time strip, we calculate residual functional I using Eq. (33). Its proximity to zero is a measure of accuracy. In the present work I values of the order of $O(10^{-8})$ or lower are considered zero and are achieved in all solutions reported in the paper.

6 Model problem studies

In this section we present model problem studies using mathematical model in $\mathbb {R}^{1}$ for 1D axial deformation to demonstrate existence and evolution of deviatoric stress waves purely due to rheology. We also present studies for composite deviatoric stress waves, their propagation, reflection, transmission and interaction. Composite wave speed, its dependence on viscosity and De are illustrated in the numerical studies. Dependence of dynamic stiffness on viscosity and De is also shown in the model problem studies. The assumptions used in deriving the conservation and the balance laws remain valid here as well.

Figure 2a shows a rod of constant cross section of polymeric solid with dissipation and memory. The left end of the rod is clamped (impermeable) and the right end ($x_{1}=1$) is subjected to a deviatoric stress or a velocity pulse of duration $2\Delta {t}$ (Fig. 2d). Assuming that the rod deformation is purely 1D, we can idealize the rod of Fig. 2(a) by a line representation shown in Fig. 2b. Figure 2c shows a space-time finite element discretization ${}^{1}{{\bar{\Omega }}_{xt}^{T}}$ of the first space-time strip ${}^{1}{{\bar{\Omega }}_{xt}}$ using nine node p-version hierarchical space-time elements with higher order global differentiability in $x_{1}$ and t. Boundary conditions and initial conditions are also shown in Fig. 2c. Figure 2d shows the stress or velocity pulse (shown as deviatoric stress pulse in Fig. 2d) applied at $x_{1}=L=1$.

Values of De, elastic coefficient $C_{1}$ and dissipation coefficient $C_{2}$ are given in the graphs of the calculated results. In all numerical studies the space-time domain ${}^{n}{{\bar{\Omega }}_{xt}}$ of the $n^{th}$ space-time strip is discretized into ${}^{n}{{\bar{\Omega }}_{xt}^{T}}$ = $\underset{e}{\overset{}{{\textstyle \cup }} }{{\bar{\Omega }}_{xt}^{e}}$ using uniform discretization consisting of 10 nine node p-version space-time elements ${{\bar{\Omega }}_{xt}^{e}}$. Since the mathematical model in $u_{1}$, ${}^{d}{\sigma _{11}}$ and ${v_{1}}$ is a system of first order PDEs in space and time, local approximation of class $C^{11}$ for all three variables in space and time constitute minimally conforming approximations, hence are used in the numerical studies.

p convergence studies are conducted for the first space-time strip to ensure that choice of p-level in space and time always yields residual functional I of the order of $O(10^{-8})$ or lower, confirming good accuracy of the computed solution. $p-$level of 9 in space and time is found to be adequate, hence is used in all studies for all space-time strips.

6.1 Existence of the deviatoric stress wave due to rheology

Since the deviatoric stress wave due to elasticity and due to rheology co-exist in deforming TVE solids with memory, application of deviatoric stress wave at $x=L$ implies application of total deviatoric stress at $x_{1}=L$ due to elasticity and rheology. Thus, with applied ${}^{d}{\sigma _{11}}$ at $x_{1}=L$ it is not possible to separate ${}^{d}{\sigma _{11}}$ due to elasticity and rheology. In order to demonstrate existence of ${}^{d}{\sigma _{11}}$ purely due to rheology we set $C_{1}$ (elastic constant) to zero. This eliminates elasticity all together, secondly, instead of ${}^{d}{\sigma _{11}}$ pulse of base $2\Delta {t}$ at $x_{1}=L$, we apply a pulse of velocity $v_{1}$ of duration $2\Delta {t}$ with peak value of $v_{1}=0.1$ (can be applied by impact in the experiment). This impacts certain amount of energy to the rod at $x=L$. Since $C_{1}=0$, the resistance offered to the deformation of the rod is purely due to rheology. We monitor evolution of ${}^{d}{\sigma _{11}}$ in the rod with time. An important point to remember here is that since $C_{1}=0$ (no elasticity) deviatoric stress waves can not propagate as time elapses. The medium has viscosity, thus we expect base elongation and amplitude decay of the ${}^{d}{\sigma _{11}}$ due to velocity pulse as time elapses, but no propagation of ${}^{d}{\sigma _{11}}$ wave as evolution proceeds. For these studies we consider $De=0.004$ and $C_{1}=0$ and $C_{2}=0.01$. Figure 3 shows evolution of ${}^{d}{\sigma _{11}}$ along the length of the rod for various increments of time. The first time step shows the maximum possible magnitude of ${}^{d}{\sigma _{11}}$ ($- 0.03$) for this choice of De and $C_{2}$ and for velocity pulse of duration [0,$\Delta {t}$]. In the second time step, the velocity pulse is discontinued, instead half stress pulse of magnitude ${}^{d}{\sigma _{11}}=-0.03$ at $\Delta {t}$ and ${}^{d}{\sigma _{11}}=0$ at $2\Delta {t}$ with continuous and differentiable distribution is applied. For $t\ge 2\Delta {t}$, the boundary at $x_{1}=L$ is free boundary. Switching the half velocity pulse to half stress pulse for $\Delta {t}\le {t}\le 2\Delta {t}$ is essential to ensure that the boundary at $x_{1}=L$ is not a stress free boundary for $\Delta {t}\le {t}\le 2\Delta {t}$, as a stress free boundary will result in reflection of compressive ${}^{d}{\sigma _{11}}$ for $0\le {t}\le {\Delta {t}}$ into a tensile wave for $t>\Delta {t}$. We observe the following:

• (1) The existence of deviatoric stress wave purely due to rheology for all values of time.

• (2) The peak value ${}^{d}{\sigma _{11}}$ is clearly at $t=\Delta {t}$ for the first increment of time. Upon further evolution, the peak values of the subsequent waves progressively diminish, accompanied by base elongation due to dissipation physics.

• (3) We note that waves for all values of time are anchored at $x_{1}=L$, confirming that these deviatoric stress waves due to rheology are unable to propagate due to lack of elasticity (as $C_{1}=0$).

• (4) This study conclusively confirm existence of deviatoric stress wave purely due to rheology, attenuation and dispersion of the stress waves due to viscosity and their inability to propagate due to absence of elasticity are clearly demonstrated

• (5) We note that when $De=0$, $C_{2}=0$ and $C_{1}=1.0$ (pure elastic case) ${}^{d}{\sigma _{11}}$=0.1 at $t=\Delta {t}$ for the same velocity pulse. This magnitude is much higher than the magnitude of ${}^{d}{\sigma _{11}}$ purely due to rheology, confirming weaker resistance offered by rheology physics compared to elastic behavior due to strain physics.

Fig. 1

Discretization of space-time domain into space-time strips, discretization of $n^{th}$ space-time strip into space-time elements

Fig. 2

1D solid domain, idealization of 1D solid domain, discretization of first space-time strip with space-time finite elements and applied disturbance

6.2 Influence of viscosity on deviatoric stress waves due to rheology

In this study also we choose $C_{1}=0$ (absence of elasticity) and $De=0.004$. We compute evolutions for $C_{2}=0.01$ and 0.015 using the same discretization and $p-$levels used in Sect. 6.1. Thus the ${}^{d}{\sigma _{11}}$ waves in this case are purely due to rheology. We apply velocity pulse of duration $2\Delta {t}$, but switch it to a stress pulse for $\Delta {t}\le {t}\le 2\Delta {t}$ of same peak magnitude as obtained in the first time step. ${}^{d}{\sigma _{11}}$ is zero beyond $t=2\Delta {t}$. This procedure is same as in described in 6.1. Evolution is computed for both values of $C_{2}$. Higher dissipation must result in higher magnitude of ${}^{d}{\sigma _{11}}$ as it offers more resistance to the polymer molecules during their motion, but also causes more amplitude decay and base elongation. For $0\le {t}\le {\Delta {t}}$, ${}^{d}{\sigma _{11}}$ versus $x_{1}$ plots for $C_{2}=0.01$ and 0.015 are shown in Figs. 3 and 4. We clearly observe higher values of ${}^{d}{\sigma _{11}}$ over the length of the rod at $t=\Delta {t}$ for $C_{2}=0.015$ (Figs 4) compared to ${}^{d}{\sigma _{11}}$ versus x at $t=\Delta {t}$ shown in Figs. 3 for $C_{2}=0.01$. This confirms increased resistance to motion for $C_{2}=0.015$ compared to $C_{2}=0.01$, hence increased dynamic stiffness due to rheology. In general we also observe higher values of ${}^{d}{\sigma _{11}}$ for $C_{2}=0.015$ for all values of time compared to $C_{2}=0.01$. However, we keep in mind that for $C_{2}=0.015$, amplitude decay and base elongation are more pronounced compared to $C_{2}=0.01$, hence it is entirely possible that for some values of time ${}^{d}{\sigma _{11}}$ amplitudes for $C_{2}=0.015$ may become lower than those for $C_{2}=0.01$. This aspect is not investigated in this particular study. As expected for both values of $C_{2}$, the ${}^{d}{\sigma _{11}}$ wave due to rheology experiences base elongation and amplitude decay due to dissipation physics.

This study demonstrates that dynamic stiffness due to rheology increases with increasing dissipation coefficient, implying that ${}^{d}{\sigma _{11}}$ increases with increasing dissipation (as shown here) and that total stiffness (sum of purely elastic and due to rheology) increases as well. A consequence of this is of course increased speed of the composite deviatoric stress wave. Studies presented in a later section confirm this.

Remarks

This study again confirms:

• (1) Existence of ${}^{d}{\sigma _{11}}$ waves due to rheology alone (in the absence of elasticity).

• (2) Higher dissipation coefficient yields higher magnitude of ${}^{d}{\sigma _{11}}$ but more pronounced amplitude decay and base elongation compared to lower dissipation.

• (3) It is worth noting that the maximum value of ${}^{d}{\sigma _{11}}$ due to rheology is much lower than ${}^{d}{\sigma _{11}}$ due to pure elasticity (${}^{d}{\sigma _{11}}=0.1$) when the same disturbance is applied at $x_{1}=L$.

6.3 Influence of De on deviatoric stress waves due to rheology

In this study we illustrate the influence of De on deviatoric stress wave purely due to rheology as well on the composite deviatoric stress wave due to elasticity and rheology. As we have seen in TVE solids with memory deviatoric stress wave can only propagate in the presence of elasticity. Thus, influence of De on the deviatoric stress wave depends upon whether the wave is propagating (i.e. $C_{1}\ne {0}$) i.e. whether the elasticity is present ($C_{1}\ne {0})$ or absent ($C_{1}=0$).

First, we consider study in which $C_{1}=0$ (absence of elasticity), $C_{2}=0.01$ and $De=0.004$, 0.006 and 0.008. We apply half velocity pulse of magnitude (0.1) at $x_{1}=L=1.0$. Figure 5a shows evolution of ${}^{d}{\sigma _{11}}$ at $t=\Delta {t}$ for all three values of De. Figure 5b shows an exploded view of the evolution of ${}^{d}{\sigma _{11}}$ in the vicinity of $x_{1}=1.0$. We clearly note that higher Deborah number (De) results in higher values of ${}^{d}{\sigma _{11}}$. ${}^{d}{\sigma _{11}}$ stress wave in this case is purely due to rheology but the deviatoric stress waves are unable to propagate due to absence of elasticity. Without motion, rheology is absent, thus De in this case merely offers resistance to the motion, hence the reason to higher ${}^{d}{\sigma _{11}}$ for higher De.

In the second study we choose $C_{1}=1.0$ (presence of elasticity), $C_{2}=0.01$ and $De=0.004$, 0.006 and 0.008 (same $C_{2}$ and De values as in the previous study without elasticity). In this case also we apply half velocity pulse of peak magnitude (0.1) at $x_{1}=L=1.0$. Figure 6a shows evolution ${}^{d}{\sigma _{11}}$ at $t=\Delta {t}$ for all three values of De. Figure 6b shows an exploded view of ${}^{d}{\sigma _{11}}$ in the vicinity of $x_{1}=1.0$. We clearly observe that ${}^{d}{\sigma _{11}}$ magnitude increases with decreasing Deborah number. This behavior is exactly opposite when compared with the study for $C_{1}=0.0$ presented in Fig 5. We discuss results of Figs. 5 and 6 in the following.

Remarks:

• (1) The relaxation phenomenon and rheology requires propagation of the disturbance which is only possible when $C_{1}\ne {0}$. In this case lower De implies lower time for the stress relaxation, hence higher resistance to the motion of the polymer molecules during relaxation which results in higher values of ${}^{d}{\sigma _{11}}$ for decreasing De as shown in Fig. 6b.

• (2) When $C_{1}=0$, there is no elasticity, hence the ${}^{d}{\sigma _{11}}$ wave is merely diffusing but not propagating, thus in this case De only offers resistance to motion but not rheology. As a consequence higher De results in higher ${}^{d}{\sigma _{11}}$ values.

• (3) We note that when $C_{1}\ne {0}$ (as in (1)) the physics of rheology is identical to deviatoric stress waves physics in polymeric fluids reported by Surana et. al [10].

6.4 Composite deviatoric stress $({}^{d}{\sigma _{11}})$, wave speed and its propagation

In a purely elastic medium the reference wave speed $v_{0} = \sqrt{\frac{E_{0}}{{(\rho _{_{_{\!\!0}}})_{ref}}}}$ is precisely deterministic. However in TVE solids with memory the wave speed changes due to additional dynamic stiffness because of rheology. We have seen in the model problems presented in Sects. 6.1–6.3 that in TVE solids with memory the resistance offered to the time dependent disturbance increases with increasing viscosity and decreasing De. Thus the dynamic stiffness consists of elastic stiffness (independent of time) and the dynamic stiffness due to viscosity and De. Increased dynamic stiffness must promote faster deviatoric stress wave propagation. As we have seen in Sects. 6.1–6.3, deviatoric stress wave propagation in TVE solids requires presence of elasticity. Thus, in TVE solids with memory, we can only study the speed of propagation of a composite wave, that contains influence of elasticity as well as rheology. Furthermore, we have seen that contribution to total ${}^{d}{\sigma _{11}}$ due to rheology is small compared to elasticity.

However, there are some facts that we have clearly observed (when elasticity and rheology both are present): (1) increasing dynamic stiffness with increasing $C_{2}$; (2) increasing dynamic stiffness with decreasing De. Thus, we can conclude the following: (a) increasing ${}^{d}{\sigma _{11}}$ wave speed with increasing $C_{2}$; (b) increasing ${}^{d}{\sigma _{11}}$ wave speed with decreasing De. We present numerical studies to illustrate these. In both of the following two studies a velocity pulse of duration $2\Delta {t}$ with peak value of 0.1 is applied at $x_{1}=1.0$. For $t\ge {2\Delta {t}}$, $x_{1}=1.0$ is a free boundary.

Case I: varying $C_{2}$ for fixed $C_{1}$ and De.

In the first study we consider $C_{1}=1$, $De=0.004$ and choose $C_{2}=0.01,0.015,0.02.$

Case II: varying De for fixed $C_{1}$ and $C_{2}$

In the second study we consider $C_{1}=1$, $C_{2}=0.01$ and choose $De=0.004,0.006,0.008.$

Discussion of results: Case I

The computed evolution for this case for $t=3\Delta {t}$, $7\Delta {t}$, $15\Delta {t}$ and $18\Delta {t}$ are shown in Figs. 7a–d. In all graphs in Fig. 7, the peak magnitude of ${}^{d}{\sigma _{11}}$ is determined and is clearly identified for all four values of time. Time values, $t=3\Delta {t}$ and $7\Delta {t}$ correspond to before the reflection of ${}^{d}{\sigma _{11}}$ waves from the impermeable boundary at $x_{1}=0$. Time values, $t=15\Delta {t}$ and $18\Delta {t}$ correspond to time after the reflection of ${}^{d}{\sigma _{11}}$ waves from the boundary at $x_{1}=0$. We note the following from the results presented in Figs. 7a–d.

• (i) Progressively larger values of $C_{2}$ result in:

  • (a) Progressively increasing composite wave speed. This is confirmed by noting that peaks of ${}^{d}{\sigma _{11}}$ for $C_{2}=0.015$ and $C_{1}=0.01$ trail the peak of ${}^{d}{\sigma _{11}}$ for $C_{2}=0.02$. This holds true before reflection (Fig. 7a and b) as well as after reflection (Figs. 7c and d)

  • (b) Progressively increased amplitude decay and base elongation. Figures 7a and b clearly show that for $C_{2}=0.02$, we have the smallest amplitude and largest base of the wave.

• (ii) Since ${}^{d}{\sigma _{11}}$ purely due to rheology is quite weak (very low amplitude) compared to purely elastic wave, the waves shown in Fig 7 are dominated by elasticity. Thus, increasing ${}^{d}{\sigma _{11}}$ due to rheology for increasing $C_{2}$ is not observed in these graphs but only the progressively increasing dissipative effect of progressively increasing $C_{2}$ is observed.

• (iii) These studies confirm that the composite deviatoric stress wave speed increases with progressively increasing dissipation coefficient but at the expense of base elongation and amplitude decay.

Discussion of results: Case II

The computed evolutions for $t=3\Delta {t}$, $8\Delta {t}$, $14\Delta {t}$ and $18\Delta {t}$ are shown in Figs. 8a–d. In all graphs in Figs. 8a–d, the peak magnitude of ${}^{d}{\sigma _{11}}$ is determined and is clearly identified for all four values of time. Times, $t=3\Delta {t}$ and $8\Delta {t}$ are before the reflection of ${}^{d}{\sigma _{11}}$ waves from the boundary at $x_{1}=0$ whereas times, $t=14\Delta {t}$ and $18\Delta {t}$ are the values of time after the reflection of ${}^{d}{\sigma _{11}}$ waves from the impermeable boundary at $x_{1}=0$. We can observe the following from the results presented in Figs. 8a–d.

• (i) Progressively reducing Deborah numbers result in:

  • (a) Progressively increasing composite wave speed. ${}^{d}{\sigma _{11}}$ wave with smaller De is always ahead of the ${}^{d}{\sigma _{11}}$ waves with larger De. This holds true before as well as after reflection of ${}^{d}{\sigma _{11}}$ waves from the boundary at $x_{1}=0.0$.

  • (b) Since $C_{2}=0.01$ for all three De, the dissipation mechanism is identical for all three De. Higher De corresponds to larger relaxation time hence more time is required for the relaxation process. Thus, at an instant of time (as in graphs 8(a)-(d)), higher De would result in higher stress values. Support of the wave is effected likewise, i.e. higher De would yield smaller base of the wave as we can observe in Fig. 8a–d.

• (ii) As in case I, here also ${}^{d}{\sigma _{11}}$ due to rheology is weak compared to pure elastic ${}^{d}{\sigma _{11}}$ wave, hence its impact on composite wave is not observable in Figs. 8a–d.

• (iii) These studies confirm that the composite deviatoric stress wave speed increases with progressively decreasing De. Higher De, naturally results in higher peak value of composite ${}^{d}{\sigma _{11}}$ wave accompanied with smaller support compared to lower De

6.5 Composite deviatoric stress (${}^{d}{\sigma _{11}}$) wave propagation, reflection, transmission and interaction

In this study we consider the dimensionless spatial domain of length two units $(\text { } [0,L]=[0,2]\text { } )$. The domain is divided in two subdomains [0, 1] and [1, 2] referred to as $M_{1}$ and $M_{2}$. We assign different values of $C_{1}$ to each of subdomains $M_{1}$ and $M_{2}$.

Case I:

For subdomain $M_{1} \text { } (0\le {x_{1}}\le {1})$, we consider $C_{1}=1.0$ and for sudomain $M_{2} \text { } (1\le {x_{1}}\le {2})$, we choose $C_{1}=2.0.$

Case II:

In this study, for subdomain $M_{1}$, we choose $C_{1}=2.0$ and for subdomain $M_{2}$ we consider $C_{1}=1.0.$

In both cases we consider $De=0.0015$ and $C_{2}=0.004$. For case I, the stress wave speed in subdomain $M_{2}$ is faster than the one in subdomain $M_{1}$ due to higher value of $C_{1}$ for $M_{2}$. In case II $C_{1}$ values are interchanged for $M_{1}$ and $M_{2}$, hence in this case wave speed is faster in subdomain $M_{1}$. Domain [0, 2] is discretized (uniform discretization) using 30 nine node p-version space-time elements. p-level of 9 with equal order, equal degree local approximations of class $C^{1}$ in space and time are found adequate to yield residual functional values I of the order of $O(10^{-8})$, confirming that the equations in the first order mathematical model are satisfied accurately in the point wise sense. In both studies, we apply a velocity pulse of duration $2\Delta {t}$ at $x_{1}=2.0$ with peak value of 0.5 of the velocity pulse.

For t$\ge {2\Delta {t}}$, $x_{1}=2.0$ is a free boundary. In both cases evolution of ${}^{d}{\sigma _{11}}$ is calculated for $0\le {t}\le {30\Delta {t}}$. Plots of the evolution of ${}^{d}{\sigma _{11}}$ i.e. graphs of ${}^{d}{\sigma _{11}}$ versus $x_{1}$ for various values of time are shown in Figs. 9a–b and 10a–b. We discuss the results in the following.

Discussion of results: case I

At $t=2\Delta {t}$, the ${}^{d}{\sigma _{11}}$ stress wave enters in the domain completely. At $t=8\Delta {t}$, the wave reaches the bimaterial interface and the reflection, transmission process initiates. At $t=9\Delta {t}$, we observe transmission of compressive wave in material $M_{1}$ and reflected tensile wave in material $M_{2}$. Since $C_{1}$ for $M_{1}$ is lower than for $M_{2}$, the interface for the reflected wave behaves like a free boundary. At $t=10\Delta {t}$, the transmitted and the reflected waves are propagating to the left and the right of the interface. At $t=14\Delta {t}$, the tensile wave in material $M_{2}$ reaches free boundary at $x_{1}=2.0$ first (due to faster wave speed in $M_{2}$). At $t=18\Delta {t}$, the tensile wave in $M_{2}$ is reflected from the free boundary at $x_{1}=2.0$ as a tensile wave and begins to propagate towards the interface. The compressive wave in $M_{1}$ reflects from the impermeable boundary at $x_{1}=0$ (magnitude doubles at the reflection).

At $t=22\Delta {t}$ the reflected wave in $M_{1}$ recovers as a steady propagating wave toward the interface while the tensile wave in $M_{2}$ is at the interface and has already gone through partial transmission. At $t=24\Delta {t}$ we observe transmission of tensile wave (from $M_{2}$) into $M_{1}$ as a tensile wave, but reflected wave from the interface is a compressive wave. We note that wave amplitudes are progressively decreasing as evolution proceeds. This of course is due to dissipation. At $t=25\Delta {t}$ the reflected wave in $M_{1}$ from boundary at $x_{1}=0$ and the transmitted tensile wave in $M_{1}$ from $M_{2}$ interact and combine into a single wave with lower peak amplitude (as the two waves are compressive and tensile). At $t=26\Delta {t}$ the transmitted tensile wave and the reflected compressive wave resume their identity they had before the interaction. At $t=27\Delta {t}$, the compressive wave in $M_{1}$ reaches the interface, while the other waves continue to propagate. This process continues till the dissipation mechanism has completely converted the energy in the waves into entropy. At this stage both materials $M_{1}$ and $M_{2}$ are stress free, hence resume their original undeformed state.

Discussion of results: case II

In this case the wave speeds are reversed between $M_{1}$ and $M_{2}$ compared to Case I, hence the wave evolution is quite different compared to Case I. At time $t=2\Delta {t}$, the entire wave is in the spatial domain. At $t=11\Delta {t}$ the wave has gone through partial transmission in domain $M_{1}$ and ready for reflection at the interface between $M_{1}$ and $M_{2}$. At $t=13\Delta {t}$, both transmitted and reflected waves are compressive as expected. Both transmitted and reflected waves continue to propagate ($t=14\Delta {t}$). At $t=18\Delta {t}$ the wave in $M_{1}$ reaches impermeable boundary, the wave in $M_{2}$ has not reached free boundary at $x_{1}=2.0$. At $t=22\Delta {t}$ the reflected wave in $M_{1}$ from the impermeable boundary at $x_{1}=0$ continues to propagate towards the bimaterial interface while the reflected wave from the interface in $M_{2}$ reaches the free boundary at $x_{1}=2.0$. At $t=25\Delta {t}$ the wave in $M_{2}$ reflects from the free boundary as a tensile wave while the compressive wave in $M_{1}$ reaches interface with partial transmission. At $t=26\Delta {t}$, tensile wave from the free boundary at $x_{1}=2.0$ continues to move towards the interface, while the wave in $M_{1}$ approaching interface goes through reflection as a tensile wave (as $C_{1}$ in $M_{2}$ is lower than $C_{1}$ in $M_{1}$) and transmits as a compressive wave ($t=27\Delta {t}$). At $t=28\Delta {t}$, compressive and tensile waves in $M_{2}$ interact to form a single wave which splits into original waves before interaction at $t=29\Delta {t}$. At $t=30\Delta {t}$ the tensile wave moving to the left is ready to reach the interface. This process of reflection, transmission and interaction continues till wave magnitude reduce to zero due to dissipation. At this stage both $M_{1}$ and $M_{2}$ are stress free.

7 Summary and conclusion

In the following we summarize the work presented in this paper and draw some conclusions.

• 1. The mathematical model in Lagrangian description consisting of balance of linear momenta in $x_{1}$ and the constitutive theory for deviatoric Cauchy stress similar to Maxwell fluid (Eulerian description) but containing elasticity is used to study deviatoric stress waves purely due to rheology as well as composite deviatoric stress waves due to elastic part and due to rheology.

  • (i) It is shown that drag or viscous resisting forces experienced by the uncoiling of the polymer molecules results in additional dynamic stiffness over and above the stiffness due to elasticity. Thus, motion of the polymer molecules is similar to a one dimensional spring. When a TVE solid is disturbed the polymer molecules collectively behave like 1D springs in the direction of the disturbance. This dynamic stiffness does not exist in a stationary TVE solid.

  • (ii) Since viscous drag is proportional to viscosity, increasing viscosity results in increasing dynamic stiffness.

  • (iii) Another mechanism of dynamic stiffness in TVE solid continua is due to De number. It is shown that in TVE solids decreasing Deborah number results in increasing dynamic stiffness.

• 2. It is shown that in the absence of elasticity, the deviatoric stress waves due to rheology exist and evolve as time elapses, but can not propagate as stress wave propagation in solid continua requires presence of elasticity. Thus, in the absence of elasticity the deviatoric stress waves due to rheology can exist, but can only experience base elongation and amplitude decay (due to dissipation) without propagation.

• 3. Magnitudes of the deviatoric stress waves due to rheology increase with increasing viscosity of the medium due to increased resistance to motion. Higher values of viscosity yield higher values of ${}_{d}{\sigma _{11}}$ but accompanied by faster wave attenuation and base elongation.

• 4. In the absence of elasticity, increasing values of De yield increasing peak values of deviatoric stress waves as in this case De is merely a source of resistance as shown in Fig. 5

• 5. In the presence of elasticity, the deviatoric stress wave propagates, hence the physics is similar to deviatoric stress wave propagation in polymeric fluids (Surana et al. [10]), thus for this case decreasing De produces increasing composite deviatoric stress values as shown in Fig. 6.

• 6. Since the deviatoric stress wave magnitude due to rheology are much smaller compared to elastic deviatoric stress wave magnitudes, the composite wave magnitude is naturally dominated by the elasticity.

• 7. Increased total dynamic stiffness (due to elasticity as well as rheology) due to increasing dissipation coefficient and decreasing De must result in increasing wave speed. This can be observed in Figs. 7 and 8. Since the additional stiffness due to rheology is small, the wave speed of the composite ${}^{d}{\sigma _{11}}$ does not show appreciable visible increase compared to pure elastic case. We note from Figs. 7 and 8 that with prolonged evolution composite ${}^{d}{\sigma _{11}}$ wave speed increases with increasing dissipation and decreasing De is clearly observed.

• 8. In rubber like materials, more like gels, the elasticity is low but rheology is dominant. In such applications ${}^{d}{\sigma _{11}}$ due to rheology will obviously be dominant.

• 9. We remark that deviatoric stress wave due to rheology and dynamic stiffness due to rheology require motion, hence obviously for a stationary rod these are absent.

• 10. The work presented in this paper on:

  • (a) deviatoric stress waves due to rheology, their existence, their dependence on dissipation and relaxation time,

  • (b) the composite deviatoric stress waves, their propagation, reflection, transmission and interaction, their dependence on dissipation and relaxation time,

  • (c) dependence of wave speed on dissipation and relaxation time,

  • (d) increase in composite wave speed with increasing dissipation and decreasing relaxation time,

  to our knowledge is the first and the only presentation in the published literature.

Fig. 3

Existence of ${}^{d}{\sigma _{11}}$ purely due to rheology: $C_{1}=0$, $De=0.004$, $C_{2}=0.01$

Fig. 4

Existence of ${}^{d}{\sigma _{11}}$ purely due to rheology: $C_{1}=0$, $De=0.004$, $C_{2}=0.015$

Fig. 5

Evolution of ${}^{d}{\sigma _{11}}$ for $C_{1}=0$, $C_{2}=0.01$ and $De=0.004$, 0.006, 0.008 a^dσ₁₁versus x₁ b^dσ₁₁versus x₁(exploded view of circled area shown in Fig. 5a

Fig. 6

Evolution of ${}^{d}{\sigma _{11}}$ for $C_{1}=1$, $C_{2}=0.01$ and $De=0.004$, 0.006, 0.008 a^dσ₁₁versus x₁ b^dσ₁₁versus x₁(exploded view of circled area shown in Fig. 6a

Fig. 7

a ${}^{d}{\sigma _{11}}$ versus $x_{1}$ at $t=3\Delta {t}$. b ${}^{d}{\sigma _{11}}$ versus $x_{1}$ at $t=7\Delta {t}$. c ${}^{d}{\sigma _{11}}$ versus $x_{1}$ at $t=15\Delta {t}$. d ${}^{d}{\sigma _{11}}$ versus $x_{1}$ at $t=18\Delta {t}$

Fig. 8

a ${}^{d}{\sigma _{11}}$ versus $x_{1}$ at $t=3\Delta {t}$. b ${}^{d}{\sigma _{11}}$ versus $x_{1}$ at $t=8\Delta {t}$. c ${}^{d}{\sigma _{11}}$ versus $x_{1}$ at $t=14\Delta {t}$. d ${}^{d}{\sigma _{11}}$ versus $x_{1}$ at $t=18\Delta {t}$

Fig. 9

a Evolution of ${}^{d}{\sigma _{11}}$, Case I. b Continued evolution of ${}^{d}{\sigma _{11}}$, Case I

Fig. 10

a Evolution of ${}^{d}{\sigma _{11}}$, Case II. b Continued evolution of ${}^{d}{\sigma _{11}}$, Case II