1 Introduction

The traditional dynamic models of precision multi-link press mechanism usually ignore the influence of the clearance in kinematic pair on its dynamic behavior, which results in low analysis accuracy. However, in engineering practice, due to the influence of manufacturing error and other factors, the clearance of the kinematic pair is inevitable. The existence of clearance will cause wear between the elements of kinematic pair, and the irregular change of clearance after wear makes the dynamics characteristics more complex, which leads to motion accuracy of mechanism sharply decrease. Therefore, in order to ensure the motion accuracy of press mechanism, it is of great significance to accurately predict the dynamic behavior of multi-link press mechanism with non-uniform wear clearances.

Recently, many scholars have done a series of research on dynamics characteristics of mechanism with clearance. However, most of these researches focus on dynamic analysis of mechanism with fixed clearance, while the research on mechanism with wear clearance is less, and the dynamic analysis of mechanism with non-uniform wear clearance is even less. Bai et al. [1] conducted the dynamic response of satellite antenna with joint clearance, and reduced the impact of joint clearance on motion accuracy of mechanism through optimization. Marques et al. [2] proposed a modeling method of spherical clearance joint and applied it to spatial four-bar mechanism, which proved the feasibility of this method. Miao et al. [3] established a model for the locking mechanism with clearance, and the dynamics performance and motion stability of system are studied. Brogliato [4] studied the feedback control of mechanism with clearance in detail through a series of examples. Li et al. [5] carried out the flexible model of planar composite solar array, considering the influence of the coupling of thermal environment and overall motion on dynamic performance of mechanism with joint clearance. Qian et al. [6] established a three-dimensional model of translational clearance joint, and discussed the nonlinear dynamic characteristics of mechanism through numerical calculation, simulation and experiment. Wang [7] used the difference method to simulate the collision process of rotating joint clearance, and verified the correctness of this model by crank slider mechanism. Amiri et al. [8] used tuned mass damper to reduce the impact of revolute joint clearance on multibody system dynamics. Farahan et al. [9] researched the nonlinear dynamics of a four-bar mechanism with joint clearance, and analyzed the bifurcation of the mechanism under different influence factors. Muvengei et al. [10] studied the rigid body dynamics of slider-crank mechanism with multiple clearances based on MATLAB software. It is found that there is a strong dynamic interaction between joint clearance. Chen et al. [11] explored the dynamic response of planar complex mechanisms with mixed clearances. Bai et al. [12] considered 3D rotary clearance joint for satellite antenna system, established clearance rigid body dynamic model based on normal and tangential contact force model. Xiang et al. [13] conceived the dynamic performance of space robot manipulator based on joint clearance and parameter uncertainty. And the relationship between the response and parameters of mechanism was explained by Chebyshev polynomials. Xu et al. [14] analyzed the dynamics characteristics of planar parallel mechanism with clearance. Guo et al. [15] performed the dynamic model of the secondary motion of piston with clearance, and found that the joint clearance and the secondary motion of piston are closely related. Akhadkar et al. [16] used nonsmooth set-valued contact models and used the so-called NSCD method and the time-stepping Moreau-Jean algorithm to perform numerical simulations for 3D revolute joints with clearances, and verified the correctness of the model by experiments. Especially the sticking modes induced by Coulomb friction are taken into account in the framework of the paper.

In practical engineering, frequent collision and friction will inevitably occur between the elements of kinematic pair, which will lead to the occurrence of wear phenomenon. Wear will reduce the accuracy and shorten the service life of mechanism. Currently, the researches on wear clearance mainly focus on dynamic characteristics of simple mechanism with single wear clearance, while the research on dynamic characteristics of planar complex linkage with multiple wear clearances are less. Machado et al. [17] presented a numerical model to describe the wear between bearing and shaft, and analyzed the effect of wear on dynamics of rotor-bearing system. Zhuang et al. [18] conducted the abrasion phenomenon of the rotary joint clearance of the aircraft locking mechanism. Zhu et al. [19] performed the NLCP method that combines dynamic analysis and wear calculation. The correctness of this method is proved by experimental research on crank-slider mechanism with wear clearance. Flores [20] presented a method to quantify the wear phenomenon of revolute clearance, and verified it with a four-bar mechanism. Lai et al. [21] proposed an effective method for calculating the wear of low-speed planar rotary joints, which was verified by wear tests of typical mechanisms. Zhao et al. [22] conceived a numerical modeling and prediction method for crank-slider mechanism considering the clearance and wear of rotating joint. Wang et al. [23] explored the impact of spherical joint wear on dynamic behavior of space four-bar mechanism. Zhao [24] et al. proposed a numerical method for modeling and predicting the wear of rotating clearance joints in flexible multi-body mechanical systems, and verified this method by crank-slider mechanism. Mukras [25] et al. predicted the wear function at the clearance by Archard wear model, and then verified this model by comparing the wear prediction and wear test of crank slider with clearance. Mukras [26] et al. compared two methods of analyzing the planar multi-body system worn at the rotating joints, and compared the performance of the two methods through experiments on crank-slider mechanism. Ordiz [27] et al. explored the influence of the wear in rotating clearance joints on life of slider-crank mechanism. Alves [28] et al. analyzed the influence of bearing wear on the response of rotating mechanism, and discussed the vibration phenomenon in the presence of bearing wear. Machado [29] et al. discussed the influence of journal bearing wear on dynamic characteristics of rotating system under different conditions. Singh [30] et al. investigated the effect of non-Newtonian lubricants on the bearing characteristics of wear bearings.

Based on above analysis, the researches on mechanism with wear clearance is less, and most of the researches on wear clearance mainly focus on simple mechanism with single clearance, but on dynamics characteristics of complex planar mechanisms with multiple wear clearances is even less. Thus, so as to accurately predict the dynamic response of complex mechanism with multiple wear clearances, this paper takes the hybrid drive seven-bar press mechanism as an example, and makes a detailed study on it. The layout of the paper is as follows. In chapter 2, based on L-N model and modified Coulomb friction model, the normal contact force and the tangential friction force of the revolute clearance are established respectively. In chapter 3, based on Lagrange multiplier method, the dynamic model of hybrid seven-bar press mechanism with clearances is developed. In chapter 4, according to Archard wear model, the non-uniform wear model at the learance is constructed. In chapter 5, the wear times, friction coefficient and driving velocities on wear characteristics of kinematic pair and the dynamic response of press mechanism are analyzed respectively.

2 Establishment of clearance model

2.1 Establishment of clearance model

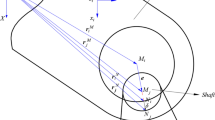
The mathematical model of joint clearance of revolute pair is established, which has shown in Fig. 1.

Fig. 1
figure 1

The clearance model

Full size image

The eccentricity vector is

$$ {\mathbf{e}}_{ij} = {\mathbf{r}}_{i}^{P} - {\mathbf{r}}_{j}^{P} $$
(1)

where \(P_{i}\) and \(P_{j}\) represent the position vectors of the bearing and shaft centers in the coordinate system, and \({\mathbf{r}}_{i}^{P}\) and \({\mathbf{r}}_{j}^{P}\) represent the position vectors of the bearing and shaft respectively.

The unit eccentricity vector is

$$ {\mathbf{n}}_{ij} = \frac{{{\mathbf{e}}_{ij} }}{{e_{ij} }} $$
(2)

where \(e_{ij} = \sqrt {{\mathbf{e}}_{ij}^{\text{T}} {\mathbf{e}}_{ij} }\) is the size.

The position vector of the collision point is

$$ \left\{ \begin{gathered} {\mathbf{r}}_{i}^{{Q_{i} }} = {\mathbf{r}}_{i}^{{P_{i} }} + R_{i} {\mathbf{n}}_{ij} \hfill \\ {\mathbf{r}}_{j}^{{Q_{j} }} = {\mathbf{r}}_{j}^{{P_{j} }} + R_{j} {\mathbf{n}}_{ij} \hfill \\ \end{gathered} \right. \, $$
(3)

where \(Q_{i}\) and \(Q_{j}\) represent the collision points of the bearing and the shaft in the coordinate system, respectively.

The velocity at \(Q_{i}\) and \(Q_{j}\) can be used for the first-order derivation of their positions

$$ \left\{ \begin{gathered} {\dot{\mathbf{r}}}_{i}^{{Q_{i} }} = {\dot{\mathbf{r}}}_{i}^{{P_{i} }} + R_{i} {\dot{\mathbf{n}}}_{ij} \hfill \\ {\dot{\mathbf{r}}}_{j}^{{Q_{j} }} = {\dot{\mathbf{r}}}_{j}^{{P_{j} }} + R_{j} {\dot{\mathbf{n}}}_{ij} \hfill \\ \end{gathered} \right. \, $$
(4)

where \({\dot{\mathbf{n}}} = \frac{{{\dot{\mathbf{e}}}_{ij} e_{ij} - \dot{e}_{ij} {\mathbf{e}}_{ij} }}{{e_{ij}^{2} }}\)

The normal and tangential relative velocities of the impact point are

$$ \left\{ \begin{gathered} v_{n} = ({\mathbf{r}}_{i}^{{Q_{i} }} - {\mathbf{r}}_{j}^{{Q_{j} }} )^{{\text{T}}} {\mathbf{n}}_{ij} \hfill \\ v_{t} = ({\mathbf{r}}_{i}^{{Q_{i} }} - {\mathbf{r}}_{j}^{{Q_{j} }} )^{{\text{T}}} {\mathbf{t}}_{ij} \hfill \\ \end{gathered} \right. $$
(5)

The penetration depth is

$$ \delta_{ij} = e_{ij} - r $$
(6)

where \(r = R_{i} - R_{j}\) is the clearance value.

The collision conditions are as follows

$$ \left\{ \begin{gathered} \delta_{ij} = e_{ij} - r < {0 } \hfill \\ \delta_{ij} = e_{ij} - r = {0} \hfill \\ \delta_{ij} = e_{ij} - r > {0} \hfill \\ \end{gathered} \right. $$
(7)

When \(\delta_{ij} = e_{ij} - r < {0}\), no collision; When \(\delta_{ij} = e_{ij} - r = {0}\), contact or separation; When \(\delta_{ij} = e_{ij} - r > {0}\), collision and elastic deformation.

2.2 Establishment of normal contact force model

In the actual collision process, the contact collision force will aggravate the vibration and wear of the mechanism. L-N model, as a nonlinear viscoelastic model, can be applied to general mechanical contact and collision problems, especially when the recovery coefficient is high and the energy dissipation in the collision process is relatively small. Moreover, the influence of parameters such as stiffness and damping on the mechanism is fully considered in the model. Therefore, the L-N model is used to represent the contact force at the clearance. According to the literature [2], the expression is

$$ F_{n} = K_{{\text{n}}} \delta_{ij}^{n} + D_{\bmod } \dot{\delta }_{ij} \, $$
(8)

where \(K_{{\text{n}}}\) is the nonlinear stiffness coefficient,\(K_{{\text{n}}} = \frac{{4}}{{{3}(\delta_{i} + \delta_{j} )}}\sqrt {\frac{{R_{i} R_{j} }}{{R_{i} + R_{j} }}}\), \(\delta_{i} = \frac{{1 - v_{i}^{2} }}{{E_{i} }}\), \(\delta_{j} = \frac{{1 - v_{j}^{2} }}{{E_{j} }}\), \(\delta_{i} ,\delta_{j}\) are the collision depth of shaft and bearing respectively. \(D_{{{\text{mod}}}}\) is the modified damping coefficient, \(D_{{{\text{mod}}}} = \frac{{{3}K(1 - c_{{\text{e}}}^{2} )\delta_{ij}^{n} }}{{4\dot{\delta }_{0} }}\), \(c_{{\text{e}}}\) represents coefficient of recovery, \(\dot{\delta }_{ij}\) and \(\dot{\delta }_{0}\) represent relative collision velocity and initial impact velocity respectively, \(n\) represents metal surface power exponent.

2.3 Establishment of tangential friction model

The modified Coulomb friction model is widely used to solve the tangential friction of two-dimensional revolute clearance[3,5,8], which can be expressed as

$$ F_{t} = - c_{f} c_{d} F_{n} \frac{{v_{t} }}{{\left| {v_{t} } \right|}} = \left\{ {\begin{array}{*{20}l} {0\;\left| {v_{t} } \right| \le v_{0} } \hfill \\ { - c_{f} \frac{{\left| {v_{t} } \right|{\text{ }} - {\text{ }}v_{0} }}{{v_{1} {\text{ }} - {\text{ }}v_{0} }}F_{n} sign(v_{t} )\;v_{0} \le \left| {v_{t} } \right| \le v_{1} } \hfill \\ { - c_{f} F_{n} sign(v_{t} )\;\left| {v_{t} } \right| > v_{1} } \hfill \\ \end{array} } \right. $$
(9)

where \(c_{f}\) is the friction coefficient, \(c_{d}\) is the dynamic correction coefficient and expresses as \(c_{d} = \left\{ {\begin{array}{*{20}c} {0} & {\left| {v_{t} } \right| \le v_{{0}} } \\ {\frac{{\left| {v_{t} } \right|{ - }v_{{0}} }}{{v_{1} { - }v_{{0}} }}} & {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} v_{{0}} \le \left| {v_{t} } \right| \le v_{1} } \\ 1 & {\left| {v_{t} } \right| \ge v_{1} } \\ \end{array} } \right.\), \(v_{0}\) and \(v_{1}\) are the static and dynamic friction velocities respectively.

The impact force and moment can be obtained by normal contact force and tangential friction force, expressed as follows

$$ \left\{ \begin{gathered} F_{ij} = F_{n} n + F_{t} t = \left[ {\begin{array}{*{20}c} {F_{ij}^{x} } & {F_{ij}^{y} } \\ \end{array} } \right]^{{\mathbf{T}}} \hfill \\ M_{ij} = - (y_{i}^{{Q_{i} }} - y_{i} )f_{ij}^{x} + (x_{i}^{{Q_{i} }} - x_{i} )f_{ij}^{y} \hfill \\ M_{ji} = - (y_{j}^{{Q_{j} }} - y_{j} )f_{ji}^{x} + (x_{j}^{{Q_{j} }} - x_{j} )f_{ji}^{y} \hfill \\ \end{gathered} \right. $$
(10)

3 Dynamic modeling of mechanism with multi clearances

3.1 Structural characteristics of mechanism

As the main body of the hybrid driven press, the structure diagram is shown in Fig. 2. The seven-bar linkage with multiple clearances is composed of frame, crank 2 and 7, connecting rod 3, triangle plate 4, connecting rod 5,and slider 6. The clearance A is located at the joint of crank 2 and connecting rod 3, and the clearance C is located at the joint of triangle plate 4 and connecting rod 5. Because the research of multiple clearances is mostly concentrated on the crank, the research on triangle plate is less, and all the key parts of the mechanism should be included as much as possible. Therefore, the clearance A and clearance C are selected to study and analyze. The mechanism has 2 degrees of freedom. In order to make the mechanism have definite motion, the hybrid drive mode is adopted, that is, crank 1 is driven by direct-current electromotor and crank 4 is driven by servo motor. The advantages of hybrid drive can make the mechanism realize the movement of multiple tracks.

Fig. 2
figure 2

The structure diagram of press mechanism

Full size image

3.2 Dynamic modeling of mechanism

According to Fig. 2, the corresponding global generalized coordinates are as follows

$$ {\varvec{q}}_{j} = \left( {\begin{array}{*{20}c} {x_{j} } & {y_{j} } & {\theta_{j} } \\ \end{array} } \right)^{\text{T}} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {j = 2 \cdots 7} \right) $$
(11)

where \(x_{j}\) and \(y_{j}\) represent the centroid coordinates and \(\theta_{j}\) represents the included angle.

The corresponding generalized velocity and acceleration are expressed as follows

$$ \dot{\varvec{q}}_{j} = \left( {\begin{array}{*{20}c} {\dot{x}_{j} } & {\dot{y}_{j} } & {\dot{\theta }_{j} } \\ \end{array} } \right)^{\text{T}} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {j = 2 \cdots 7} \right) \, $$
(12)
$$\ddot{ \varvec{q}}_{j} = \left( {\begin{array}{*{20}c} {\ddot{x}_{j} } & {\ddot{y}_{j} } & {\ddot{\theta }_{j} } \\ \end{array} } \right)^{\text{T}} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {j = 2 \cdots 7} \right) $$
(13)

When the Lagrange multiplier method is used to establish the dynamic model of mechanism, two constraints will be introduced into each plane motion pair. Ideally (that is, when only bilateral constraints is considered), the planar seven-bar mechanism has seven revolute pairs, one moving pair and two driving constraints, so eighteen constraint equations will be introduced.

When the existence of clearance is considered at both revolute joint A and revolute joint C, the bilateral constraints of the two revolute pairs are removed, so the constraint equations are reduced by four. Therefore, the constraint equation of planar seven-bar mechanism with two clearances is shown in Eq. 14.

$$ {{\varvec{\Phi}}}({\varvec{q}},t) = \left[ {\begin{array}{*{20}c} {hx - (x_{2} + L_{s2} \cos \theta_{2} )} \\ {hy - (y_{2} + L_{s2} \sin \theta_{2} )} \\ {x_{3} - L_{s3} \cos \theta_{3} - (x_{4} - L_{s41} \cos (\theta_{4} + \beta_{1} - \pi ))} \\ {y_{3} - L_{s3} \sin \theta_{3} - (y_{4} - L_{s41} \sin (\theta_{4} + \beta_{1} - \pi ))} \\ {x_{7} + L_{s7} \cos \theta_{7} - (x_{4} + L_{s42} \cos (\theta_{4} - \beta - \pi ))} \\ {y_{7} + L_{s7} \sin \theta_{7} - (y_{4} + L_{s42} \sin (\theta_{4} - \beta - \pi ))} \\ {x_{6} - (x_{5} - L_{s5} \cos \theta_{5} )} \\ {y_{6} - (y_{5} - L_{s5} \sin \theta_{5} )} \\ {x_{6} - hx} \\ {\theta_{6} - 90^\circ } \\ {x_{7} - L_{s7} \cos \theta_{7} } \\ {y_{7} - L_{s7} \sin \theta_{7} } \\ {\theta_{7} - \omega_{7} t + 51.18^\circ } \\ {\theta_{2} - \omega_{2} t + 119.27^\circ } \\ \end{array} } \right] = {\mathbf{0}} $$
(14)

The corresponding velocity can be acquired by calculating the first derivative of time by constraint Eq. (14), which is expressed as follows

$$ {{\varvec{\Phi}}}_{q} \dot{\varvec{q}} = - {{\varvec{\Phi}}}_{t} \equiv {\varvec{\upsilon}} $$
(15)

where \({{\varvec{\Phi}}}_{q}\) is Jacobian matrix.

The corresponding acceleration can be obtained by calculating the second derivative of time by constraint Eq. (14), which is expressed as follows

$$ {{\varvec{\Phi}}}_{q} \ddot{\varvec{q}} = - \left( {{{\varvec{\Phi}}}_{q} \dot{\varvec{q}}} \right)_{q} \dot{\varvec{q}} - 2{{\varvec{\Phi}}}_{qt} \dot{\varvec{q}} - {{\varvec{\Phi}}}_{tt} \equiv {\varvec{\gamma}} $$
(16)

According to Eq. (15) and Eq. (16), the dynamic equation is obtained as follows

$$ \varvec{M}\ddot{\varvec{q}} + {{\varvec{\Phi}}}_{q}^{\text{T}} {\varvec{\lambda}} = {\varvec{g}} $$
(17)

where \({\varvec{M}}\) is the mass matrix, \({\varvec{\lambda}}\) is the Lagrange multiplier column vector, and \({\varvec{g}}\) is the generalized external force column vector.

The dynamic equation of rigid body is expressed as follows

$$ \left( {\begin{array}{*{20}c} {\varvec{M}} & {{{\varvec{\Phi}}}_{\varvec{q}}^{\text{T}} } \\ {{{\varvec{\Phi}}}_{q} } & {\mathbf{0}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\varvec{\ddot{q}}} \\ {\varvec{\lambda}} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\varvec{g}} \\ {\varvec{\gamma}} \\ \end{array} } \right)^{\text{T}} $$
(18)

The stability of the calculation results is ensured by introducing displacement and velocity constraints, which are expressed as follows

$$ \varvec{\gamma^{\prime}} = {\varvec{\gamma}} - 2\alpha {\dot{\mathbf{\Phi }}} - \beta^{2} {{\varvec{\Phi}}} $$
(19)

\(\alpha { = }\beta { = }20\) is the stability coefficient, \({\dot{\mathbf{\Phi }}} = \frac{{d{{\varvec{\Phi}}}}}{dt}\).

Thus, the stable dynamic equation can be expressed as follows

$$ \left( {\begin{array}{*{20}c} \varvec{M} & {{\mathbf{\Phi }}_{q}^{\text{T}} } \\ {{\mathbf{\Phi }}_{q} } & {\mathbf{0}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\ddot{\varvec{q}}} \\ \varvec{\lambda } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} \varvec{g} \\ {\varvec{\gamma ^{\prime}}} \\ \end{array} } \right)^{\text{T}} $$
(20)

4 Establishment of wear model with clearance

4.1 Archard wear model

According to a large number of references, the Archard wear model is widely used for the calculation and modeling of revolute clearance between the bearing and shaft. Since the wear amount in the Archard wear model can be related to the physical and geometric properties of the sliding body, more accurate calculation results can be obtained. The expression is as follows

$$ \frac{V}{s} = \frac{{K_{m} F_{n} }}{H} $$
(21)

where \(V\) and \(s\) are volume wear and relative slip distance, \(F_{n}\) represents normal collision forces, \(K_{m}\) represents dimensionless wear coefficients, and \(H\) represents hardness of softer materials.

Because the wear depth is more convenient, and the dimensionless wear coefficient can be obtained by the materials and wear conditions of moving pair, Archard wear model can be expressed as

$$ \frac{V}{s} = K_{m} A = \frac{{K_{m} F_{n} }}{H} \, $$
(22)

where \(A\) is the actual contact area.

Both sides of the formula are divided by area \(A\), and the result is as follows

$$ \frac{h}{s} = \frac{{K_{m} p}}{H} \, = K_{d} p $$
(23)

where \(h\) is the wear depth, \(K_{d}\) is the linear wear coefficient and \(p\) is the contact stress.

4.2 Calculation of slip distance

When dynamic wear model is established, continuous contact process needs to be discretized. Discretization of slip distance is shown in Fig. 3, \(\Delta s\) is slip distance within \(\Delta t_{i}\), so \(\Delta s\) can be expressed as

$$ \Delta s_{i} = (R_{j} + \delta )\Delta \varphi (t_{i} ) $$
(24)
Fig. 3
figure 3

The discretization of slip distance

Full size image

where \(R_{J}\) is the radius of the shaft, \(\delta\) is the deformation of the bearing, and \(\Delta \varphi (t_{i} )\) is the angle of \(\Delta t_{i}\) axis movement in time.

4.3 Calculation of approximate contact area

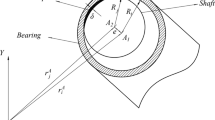
The contact diagram of revolute pair is shown in Fig. 4, and the geometric relationship between the clearance elements is shown in Fig. 5.

Fig. 4
figure 4

The contact diagram of revolute pair

Full size image
Fig. 5
figure 5

Geometric relations of elements in clearance

Full size image

In Figs. 4 and 5, \(P_{i}\) and \(P_{j}\) are the center of bearing and shaft respectively, \(\overline{\beta }\) is the contact angle, \(\overline{DC}\) is the contact chord length, \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{CE} \) is the contact height and \(E\) is the position of the maximum contact deformation.

The contact angle can be obtained by cosine theorem

$$ \overline{\beta }\,{ = }\arccos \frac{{{\text{e}}_{{}}^{2} {\text{ + R}}_{j}^{2} {\text{ - R}}_{i}^{2} }}{{2{\text{e}}_{{}} {\text{R}}_{j} }} $$
(25)

The contact arc length along the circumferential direction is

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{CE} = R_{j} \sin (\pi - \overline{\beta }) $$
(26)

When collision occurs, the actual contact area can be expressed as

$$A = 2 * \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{CE} * b $$
(27)

where \(b\) is the axial contact.

4.4 Calculation of contact stress

At present, the calculation methods of contact stress of contact surface mainly include finite element method, experimental method, Winkler elastic foundation theory, boundary element method and direct method. This chapter uses the direct method to calculate the contact force. The expression is as follows

$$ P_{n} = \frac{{{\text{F}}_{{{\text{n}}{\kern 1pt} }} }}{{\text{A}}} $$
(28)

4.5 Calculation of wear depth

Because the wear process is dynamic, and the differential coefficient expression of the actual solution equation is expressed as

$$ \frac{dh}{{ds}} = K_{d} p \, $$
(29)

The dynamic wear is the change rate of the wear depth relative to the slip distance. Thus, the wear depth can be obtained by integrating the slip distance. When a mechanism moves, a discrete area will produce multiple contact and wear. The wear depth in this area can be expressed as

$$ h = \sum {h_{n} } = h_{n - 1} + \Delta h_{n} $$
(30)

where \(h_{n}\) means wear depth of \(n\) period, \(h_{n - 1}\) means wear depth of last period and \(\Delta h_{n}\) means wear depth of n-th period.

4.6 Calculation of surface reconstruction

The surface discretization is used to discretize the geometric surface profile of shaft and bearing. Then the incremental method is used to determine the specific position of the shaft and bearing in each integration step and store it in the corresponding discrete area. Finally, the sum of each integral time step in the discrete area is the area based on the wear depth, the geometric surface of the worn can be obtained. The discrete analysis diagram of geometric surface is shown in Fig. 6.

Fig. 6
figure 6

The discrete analysis diagram of geometric surface

Full size image

Therefore, the total wear depth can be expressed as

$$ h = \sum {h_{m} } $$
(31)

where \(m\) is the code for dividing the discrete area of shaft and bearing surface, and \(h_{m}\) is the wear depth in the discrete area with code \(m\).

According to the geometric characteristics of the clearance between the rotating pair, each discrete interval of the radius obtained after wear can be expressed as

$$ \left\{ \begin{gathered} R_{i}^{*} = R_{i} { + }\frac{h}{2} \hfill \\ R_{j}^{*} = R_{j} - \frac{h}{2} \hfill \\ \end{gathered} \right. $$
(32)

where, \(R_{{_{i} }}^{*}\) means initial radius of bearing, \(R_{{_{j} }}^{*}\) means initial radius of shaft, and \(h\) means total wear and even distribution (the wear depth is the same, that is, the shaft and bearing wear half).

5 Analysis of wear characteristics of kinematic pair and dynamic response of mechanism

5.1 Solution flow chart

Assuming that the mechanism runs for 200 cycles to calculate the wear depth once, because the wear amount is too small, the surface wear of the shaft and bearing is not obvious. Therefore, in order to reduce the calculation cost and improve the calculation efficiency, the wear depth of 200 cycles is enlarged by 20,000 times to approximate the wear depth of the bearing for 2 million cycles, which is first wear. After the first wear, reconstruct the surface of the shaft and bearing and repeat the above steps. This is second wear. The detailed solution flow chart of the dynamic model is shown in Fig. 7.

Fig. 7
figure 7

The flow chart of dynamic solution

Full size image

5.2 System parameters

Geometric parameters and inertia parameters are shown in Table 1. Clearance parameters are shown in Table 2.

Table 1 Geometric Parameters and Inertial Parameters
Full size table
Table 2 Clearance parameters
Full size table

5.3 The influence of different parameters on wear characteristics of kinematic pair

5.3.1 Wear characteristics of different wear times

The clearance values at clearance A and C are set to 0.8 mm, the driving velocities are set to \(\omega_{{2}} = - 3.5\pi (\text{rad/s}),\omega_{{7}} = {3}{\text{.5}}\pi (\text{rad/s})\), and the friction coefficient is set to 0.02. The wear depth at clearance A and clearance C is shown in Fig. 8. The wear characteristics of kinematic pair at clearance A and clearance C are shown in Fig. 9 and Fig. 10 respectively.

Fig. 8
figure 8

Wear depth

Full size image
Fig. 9
figure 9

Wear characteristics of clearance A

Full size image
Fig. 10
figure 10

Wear characteristics of clearance C

Full size image

According to Fig. 8 (a), the wear depth of clearance A increases from \(1.221 \times 10^{ - 6}\) m to \(1.178 \times 10^{ - 3}\) m after considering second wear, and the angle of peak value changes from \(100.7^{{\text{o}}}\) to \(132.7^{{\text{o}}}\). In Fig. 8 (b), the wear depth of clearance C increases from \(2.044 \times 10^{ - 6}\) m to \(4.548 \times 10^{ - 6}\) m, and the angle of peak value changes from \(225.1^{{\text{o}}}\) to \(297.4^{{\text{o}}}\). Based on the analysis, the wear phenomenon of clearance is more severe when the second wear is considered. And the wear degree of clearance A is more serious, but the wear range of clearance C is wider.

According to Figs. 9a, c and 10a, c, there is slight wear at the clearance. The wear surface is locally enlarged to clearly express the wear phenomenon, as shown in Figs. 9b, d and 10b, d. According to the local enlarged drawing that non-uniform wear occurs on the surface of shaft and bearing, and the second wear is more serious. Compared with clearance C, the wear phenomenon of clearance A is more obvious.

5.3.2 Wear characteristics of different friction coefficient

The driving velocities are set to \(\omega_{{2}} = - 6\pi (\text{rad/s}),\omega_{{7}} = {6}\pi (\text{rad/s})\), the clearance value is set to 0.6 mm, and the friction coefficients of 0.05 and 0.1 are used for analysis. The wear depth at the clearance A and clearance C is shown in Fig. 11. The wear characteristics of kinematic pair at clearance A and clearance C are shown in Figs. 12 and 13 respectively.

Fig. 11
figure 11

Wear depth

Full size image
Fig. 12
figure 12

Wearcharacteristics of clearance A

Full size image
Fig. 13
figure 13

Wearcharacteristics of clearance C

Full size image

According to Fig. 11a, the main wear area of clearance A is [\(71^{{\text{o}}} ,90^{{\text{o}}}\)], when the friction coefficient is 0.05, the peak value of wear depth appears at \(84.52^{{\text{o}}}\) and the value is \(4.406 \times 10^{ - 5}\) m. When the friction coefficient is 0.1, the peak value of wear depth appears at \(86.31^{{\text{o}}}\) and the value is \(2.468 \times 10^{ - 5}\) m. In Fig. 11b, the main wear area of clearance C are [\( 102^{{\text{o}}}, 187^{{\text{o}}}\)] and [\( 246.7^{{\text{o}}}, 360^{{\text{o}}}\)], when the friction coefficient is 0.05, the peak value of wear depth appears at \(122.6^{{\text{o}}}\) and the value is \(9.531 \times 10^{ - 6}\) m. When the friction coefficient is 0.1, the peak value of wear depth appears at \(115.4^{{\text{o}}}\) and the value is \(7.559 \times 10^{ - 6}\) m. Based on the above analysis, the wear depth at the friction coefficient of 0.05 is much greater than that of the friction coefficient of 0.1, and the wear degree of clearance A is more serious, but the wear range of clearance C is wider.

According to Figs. 12a, c and 13a, c, there will be a small amount of wear at clearance A and clearance C. In order to clearly reflect the wear phenomenon, the wear surface is locally enlarged. According to the enlarged drawing of shaft and bearing surface that the smaller the friction coefficient is, the more serious the non-uniform wear of shaft and bearing surface is.

5.3.3 Wear characteristics of different driving velocities

The clearance value at the clearance is set to 0.8 mm, and the friction coefficient is set to 0.03. The driving velocities of the two cranks are set to \(\omega_{{2}} = - 4\pi (\text{rad/s}),\omega_{{7}} = {4}\pi (\text{rad/s})\) and \(\omega_{{2}} = - 8\pi (\text{rad/s}),\omega_{{7}} = {8}\pi (\text{rad/s})\) respectively. The wear depth at clearance A and clearance C is shown in Fig. 14. The wear characteristics of kinematic pair at clearance A and clearance C are shown in Figs. 15 and 16 respectively.

Fig. 14
figure 14

Wear depth

Full size image
Fig. 15
figure 15

Wear characteristics of clearance A

Full size image
Fig. 16
figure 16

Wear characteristics of clearance C

Full size image

According to Fig. 14, when the driving velocities of two cranks increase from \(\omega_{{2}} = - 4\pi (\text{rad/s}),\omega_{{7}} = {4}\pi (\text{rad/s})\) to \(\omega_{{2}} = - 8\pi (\text{rad/s}),\omega_{{7}} = {8}\pi (\text{rad/s})\), the peak value of wear depth of clearance A increases from \(1.414 \times 10^{ - 6}\) m to \(5.502 \times 10^{ - 5}\) m, and the angle of peak value changes from \(95.76^{{\text{o}}}\) to \(65.52^{{\text{o}}}\).The peak value of wear depth of clearance C increases from \(2.835 \times 10^{ - 6}\) m to \(2.117 \times 10^{ - 5}\) m, and the angle of peak increases from \(310.3^{{\text{o}}}\) to \(312.8^{{\text{o}}}\). Based on the above analysis, the driving velocities are greater, the wear depth is greater, and the wear degree at clearance A is more serious, but the wear range at clearance C is wider.

According to Figs. 15a, c and 16a, c, there is a small amount of wear at clearance A and clearance C. In order to clearly reflect the wear phenomenon, the wear surface is locally enlarged, as shown in Figs. 15b, d and 16b, d. According to the enlarged drawing of shaft and bearing surface that the higher the driving velocities, the more serious the non-uniform wear of shaft and bearing surface is.

5.4 The influence of different parameters on dynamic response of mechanism

5.4.1 The influence of wear times on dynamic response

The clearance values at clearance A and C are set to 0.8 mm, the driving velocities are set to \(\omega_{{2}} = - 3.5\pi (\text{rad/s}),\omega_{{7}} = {3}{\text{.5}}\pi (\text{rad/s})\), and the friction coefficient is set to 0.02. The dynamic response of mechanism is shown in Fig. 17. The collision force and center trajectory at clearance A and clearance C are shown in Figs. 18 and 19 respectively.

Fig. 17
figure 17

Dynamic response of mechanism

Full size image
Fig. 18
figure 18

Collision force at clearance

Full size image
Fig. 19
figure 19

Center trajectory of shaft

Full size image

According to Fig. 17a, the actual displacement curve of slider lags behind after wear. After the first wear, the displacement curve is not smooth, and the peak value increases to 0.1076 m. When the second wear occurs, the actual displacement curve of slider shows obvious vibration, and the peak value increases to 0.1079 m. In Fig. 17b, when considering no wear, first wear and second wear at the clearance, the peak values of velocity of slider are 0.9925, 1.005 and 1.106 m/s respectively. And the velocity curve of slider fluctuates obviously after the second wear. In Fig. 17c, when considering no wear, first wear and second wear at the clearance, the peak values of acceleration of slider are 1221, 1523 and 3629 m/s2 respectively. And the acceleration curve of slider fluctuates obviously after the second wear. Therefore, with the increase of wear times, the errors of slider output response is also increasing.

According to Fig. 18a, the peak value of collision force at clearance A increases from 206.9 N to 406.7 N after first wear, and that increases from 406.7 N to 2847 N after second wear. In Fig. 18b,the peak value of collision force at clearance A increases from 206.9 N to 310.3 N after first wear, and that increases from 310.3 N to 1176 N after second wear. In addition, the collision force at clearance A increases more serious than that at clearance C after wear.

According to Fig. 19, with the increase of wear times, the movement of center trajectories at clearance A and C becomes more chaotic and the collision range becomes more wide. The reason is that the non-uniform wear leads to the missing of the elements of kinematic pair, which makes the surface of the shaft and the bearing no longer smooth. So the shaft and bearing will collide more disorderly, resulting in more chaotic of center trajectory of shaft.

5.4.2 The influence of different friction coefficients on dynamic response

The driving velocities are set to \(\omega_{{2}} = - {6}\pi (\text{rad/s}),\omega_{{7}} = {6}\pi (\text{rad/s})\), the clearance value is set to 0.6 mm, and the friction coefficient is 0.05 and 0.1.The dynamic response of mechanism is shown in Fig. 19. The collision force and center trajectory at clearance A and clearance C are shown in Figs. 20 and 21 respectively.

Fig. 20
figure 20

Dynamic response of mechanism

Full size image
Fig. 21
figure 21

Collision force at clearance

Full size image

According to Fig. 20a, different friction coefficients have little effect on displacement response of mechanism. In Fig. 20b, when the friction coefficient changes from 0.05 to 0.1, the velocity curve of slider fluctuates more violently. In Fig. 20c, when the friction coefficient changes from 0.05 to 0.1, the peak value of acceleration of slider changes from 4671 to 1244 m/s2, and can be seen that the smaller the friction coefficient is, the larger the acceleration fluctuation range is.

According to Fig. 21a, when the friction coefficient changes from 0.05 to 0.1, the peak value of acceleration of slider changes from 2363 N to 448.5 N. In Fig. 21b, when the friction coefficient changes from 0.05 to 0.1, the peak value of acceleration of slider changes from 650.3 N to 258.8 N. In addition, the collision force at clearance A increases more serious than that at clearance C.

According to Fig. 22, with the increase of friction coefficient, the center trajectory of shaft at the clearance becomes stable. This is because the greater the friction coefficient at the clearance, the more energy the shaft and bearing consume during the collision, which makes the center trajectory of shaft more stable.

Fig. 22
figure 22

Center trajectory of shaft

Full size image

5.4.3 The influence of different driving velocities on dynamic response

The clearance value is set to 0.8 mm, and the friction coefficient is set to 0.03. The driving velocities are set to \(\omega_{{2}} = - 4\pi (\text{rad/s}),\omega_{{7}} = {4}\pi (\text{rad/s})\) and \(\omega_{{2}} = - 8\pi (\text{rad/s}),\omega_{{7}} = {8}\pi (\text{rad/s})\) respectively. The dynamic response of mechanism is shown in Fig. 23. The collision force and center trajectory at clearance A and clearance C are shown in Figs. 24 and 25 respectively.

Fig. 23
figure 23

Dynamic response of mechanism

Full size image
Fig. 24
figure 24

Collision force at clearance

Full size image
Fig. 25
figure 25

Center trajectory of shaft

Full size image

According to Fig. 23a, when the drive velocities are \(\omega_{{2}} = - 4\pi (\text{rad/s}),\omega_{{7}} = {4}\pi (\text{rad/s})\), the displacement curve of slider is close to the ideal curve when considering no wear and first wear. When the drive velocities are \(\omega_{{2}} = - 8\pi (\text{rad/s}),\omega_{{7}} = {8}\pi (\text{rad/s})\), the displacement curve shows obvious deviation from 0.2 s to 0.25 s when considering no wear and first wear. In Fig. 23b, the velocity curve of slider shows significant fluctuations when considering no wear and first wear. And the greater the drive velocity, the greater the speed curve fluctuates. In Fig. 23c, when the drive velocities are \(\omega_{{2}} = - 4\pi (\text{rad/s}),\omega_{{7}} = {4}\pi (\text{rad/s})\), the peak value of acceleration of slider is 1789 and 2378 m/s2 when considering no wear and first wear respectively. When the drive velocities are \(\omega_{{2}} = - 8\pi (\text{rad/s}),\omega_{{7}} = {8}\pi (\text{rad/s})\), the peak value of acceleration of slider is 2877 and 5391 m/s2 when considering no wear and first wear respectively. Therefore, compared with no wear, the peak value of acceleration of first wear is larger. And the larger the driving velocities are, the larger the peak value of acceleration is.

The collision force at clearance A is shown in Fig. 24a, when the driving velocities are \(\omega_{{2}} = - 4\pi (\text{rad/s}),\omega_{{7}} = {4}\pi (\text{rad/s})\) and \(\omega_{{2}} = - 8\pi (\text{rad/s}),\omega_{{7}} = {8}\pi (\text{rad/s})\) respectively, the peak values of the collision force of no wear are 366.8 N, 574.6 N respectively and that of first wear are 420.6 N 1278 N respectively. The collision force at clearance A is shown in Fig. 24b, when the driving velocities are \(\omega_{{2}} = - 4\pi (\text{rad/s}),\omega_{{7}} = {4}\pi (\text{rad/s})\) and \(\omega_{{2}} = - 8\pi (\text{rad/s}),\omega_{{7}} = {8}\pi (\text{rad/s})\) respectively, the peak values of the collision force of no wear are 321.2 N, 424 N respectively and that of first wear are 466.2 N and 1957 N respectively. In summary, the collision force at the clearance considering first wear is much greater than no wear. And the greater the driving velocities, the greater the collision force at the clearance.

According to Fig. 25a and b, with the increase of driving velocities, the movement of center trajectory of shaft at the clearance becomes chaotic. The reason is that the greater the drive velocity, the higher the collision frequency between the shaft and bearing, resulting in a more chaotic center trajectory of shaft.

6 Conclusions

In this paper, the wear characteristics prediction of kinematic pair and the dynamic response of mechanism with non-uniform wear clearances are studied. The results are as follows:

  1. 1.

    The Archard wear model and the clearance model are embedded into ideal rigid body dynamics, and the dynamic model of seven-bar press mechanism with multiple non-uniform wear clearances is developed.

  2. 2.

    The wear characteristics prediction of kinematic pair was carried out and the influence of wear times, friction coefficient and driving velocities on wear characteristics are studied. The results show that when wear times or driving velocities are lager, the wear degree of geometry surface is more serious. However, when friction coefficient is larger, the wear degree and wear range are reduced and relatively concentrated. In addition, the wear degree of clearance A is more serious than that of clearance C, which indicates that the closer the clearance is to the driving rod, the more obvious the wear phenomenon is.

  3. 3.

    The influence of important parameters on dynamic response of press mechanism with non-uniform wear clearances is studied. The results show that when wear times and driving velocities increase, the frequency and amplitude of the displacement, velocity, acceleration and collision force oscillation increase, and the center trajectory of shaft become more disordered. However, when the friction coefficient is larger, the frequency and amplitude of response of mechanism decreases, and the center trajectory of shaft becomes relatively stable.