On Λ-fractional elastic solid mechanics

Abstract

After defining the fractional Λ-derivative, having all the requirements for corresponding to a differential, the fractional Λ-strain is established. Contrary to the common strain, that has a local character, fractional strain access a non-local character, quite important for expressing deformations in non-homogeneous media with microcracks and inhomogeneities, that may change during deformation. The purpose of the present work is the establishement of the principles and laws of the non-linear Λ-fractional Elasticity. The Λ-fractional non-linear stress–strain relations are derived. The restriction into the linear fields is presented. Further, fractional deformation of a fractal bar is discussed. The Fractional deformations and fractional elastic problems are set up with the definition of stresses and displacements in the initial space. Further, the Λ-fractional analysis with its conjugate Λ-fractional space is presented, considering fractional derivatives of both sides in the bending of a cantilever beam under uniform continuously distributed loading.

1 Introduction

The Non-linear elasticity theory [16, 17] is a mathematical theory concerning with the large deformations of an elastic body. Various deformation, strain and stress tensors are defined connecting the initial (at ease) placement to the current one. The main problem is that the current geometry of the elastic body differs from the initial (unloaded) one. The linear elasticity differs from the non-linear one, because the geometry of the current placement is considered as a perturbation around the initial placement. The basic axiom of the non-linear elasticity is Noll’s axiom of local action [13, 33]. That means that only local derivatives are considered in the analsis of elasticity theory. The non-linear theory has been applied to biomechanics, polymerics, rubbers, thin structures and elastic stability problems.

Eringen [29] in his excellent treatment concerning the Non-local theories of continua states in the introduction of his treatment Non-local continuum field theories are concerned with the physics of material bodies whose behavior of a material point is influenced by the state of all points of the body. The non-local theory generalizes the classical field theory in two respects (i) the energy balance law is considered valid globally (for the entire body) and (ii) the state of the body at a material point is described by the response functionals.

Fractional Calculus is a blooming mathematical tool for various applications in physics and engineering. Machado et al. [1] have presented a historical retrogression for fractional calculus originated by Leibniz [2], Liouville [3], and established by Riemann [4] and others. The main advantage of fractional calculus is the non-local character, contrary to the common derivatives that have inherited by their definition a strong local property. Fractional calculus has been an indispensable tool in various branches in physics, mechanics, control theory, engineering, economics, Baleanu [5], Atanackovic [6]. Classical references are the books [7,8,9,10,11] including also various applications.

Non-local continuum theories are important when nonlocal intermolecular attractions are considerable. It is well known that a large class of problems in physics and continuum mechanics may not be described in the context of classical field theories, such as problems of fracture of solids, the various fields of stresses at the crack tips and around dislocation fields. Moreover, singularities that may be present at the application points of concentrated loads fail to be described by the conventional local theories. Of course, there are many other situations where the classical field theories fail to describe the phenomena.

Although fractional calculus was intensively used for the last 50 years, it was referred only to time non-locality. Lazopoulos [12] turned the attention from time to space, just to include non-local properties in space due to inhomogeneities, microcracks, etc. Further, there exist some efforts for using fractional derivatives in fractal materials, see Carpinteri et al. [19, 35]. However, the used fractional derivatives are local. Relations between fractal dimensions and fractional orders are discussed in Refs.[30,31,32]. Lazopoulos [12] established the fractional strain with strong non-local character, contrary to the local character of the conventional strain, Truesdell [13]. Nevertheless, all the well known fractional derivatives have mainly an operative character, Adda [23], instead of a derivative’s one since they do not satisfy the properties of a derivative demanded by Differential Topology, Chillingworth [26]

$$ 1.\quad {\text{Linearity}}\quad D\left( {af\left( x \right) + bg\left( x \right)} \right) = aDf\left( x \right) + bDg\left( x \right) $$

(1.1)

$$ 2.\quad {\text{Leibnizrule}}\quad D\left( {f\left( x \right) \cdot g\left( x \right)} \right) = Df\left( x \right) \cdot g\left( x \right) + f\left( x \right) \cdot Dg\left( x \right) $$

(1.2)

$$ 3.\quad {\text{Chain}}\;{\text{rule}}\quad D\left( {g\left( f \right)} \right)\left( x \right) = Dg(f\left( x \right) \cdot Df\left( x \right) $$

(1.3)

Those conditions are necessary for defining a differential corresponding to the derivative. Since no differential geometry, mechanics and physics may mathematically be established without mathematically defined derivative, the use of the well known fractional derivatives in mathematics and physics is questionable. Hence their use was not mathematically established, but it has an ad-hoc character. Lazopoulos [14, 24, 25] trying to fill that gap, proposed the fractional L-derivative. Nevertheless, that effort was not successful, since again the conditions demanded by differential topology were not satisfied. Let us point out the various efforts of combining fractal structures with fractional derivatives, just to generate geometry necessary to physics and various other branches like economy, biology etc. [38,39,40,41]. Nevertheless, those homogenisation approaches are ad hoc and easily proved they lack of the geometrical bases they adopt. Lately, Lazopoulos [15] proposed the fractional Λ-derivative, a modification of the fractional L-derivative, along with the conjugate fractional Λ-space, where the fractional Λ-derivative behaves with conventional derivative rules. The proposed non-local procedure has already been applied to the bending problem of a beam, Lazopoulos [37], and the linear plane elasticity, Lazopoulos [38].

Further definitions of fractional strain have been presented in [19,20,21,22], using the well known fractional derivatives, that have more the properties of an operator than a derivative. With the establishment of the fractional Λ-derivative and the conjugate fractional Λ-space, the fractional Λ-strain is proposed exhibiting a local character. The Λ-fractional deformations, along with the Λ-fractional Cauchy-Green deformation tensors [13, 16, 17] are also defined. Further, the Λ-fractional Green–Lagrange strain tensor, along with the Λ-fractional Euler-Almansi tensor will also be formulated. Let us point out that the strain, having the character of a derivative, exists only in the Λ-space, where the local derivation is allowed and geometry exists. The strain in the initial space may be defined only as a function of the transferring of the strain from the Λ-space to the initial one. On the contrary, the stresses and the displacements may be transferred from the conjugate Λ-space to the initial one.

The formulation of the Λ-space is presented, where geometry and physics are valid in a conventional way. Further, the solution of the elasticity problem in the Λ-space, such as the deformation and the stress, is transferred in the initial space. The simple problem of a fractional bar under axial load is presented, just to show how the proposed Λ-strain may be used. Interestingly, the solution reveals the size effect as it has been exhibited in the strain gradient theories, Aifantis [34].

The fractional deformation of a fractal rod is also discussed just to show that fractional calculus and fractal fractal geometry are quite different fields without interconnection as it has been presented in various places [38,39,40,41], suggesting the homogenization of the fractal geometries, through fractional calculus, lacking of differentials to generate geometry.

Although the analysis, up to that point, has been based upon the left fractional derivatives, the last section concerning linearly elastic plane problems has been formulated. Just to show how an elastic problem may be set up with the help of both side fractional derivatives.

It is again pointed out that the present methodology tries to conform with the 6th Hilberts’ problem, concerning the Mathematical treatment of the axioms in Physics concerning: “The rigorous theory of limiting processes which lead from the Atomistic view to the laws of motion of continua”.

2 The Λ-fractional derivative

A very brief outline of fractional calculus is presented in this chapter, while the interested reader is referred to Refs. [7,8,9,10,11] for further information. The left and right fractional integrals are defined by,

$$ {}_{\alpha }I_{x}^{\gamma } f(x) = \frac{1}{\Gamma (\gamma )}\int\limits_{\alpha }^{x} {\frac{f(s)}{{(x - s)^{1 - \gamma } }}ds} $$

(2.1)

$$ {}_{x}I_{b}^{\gamma } f(x) = \frac{1}{\Gamma (\gamma )}\int\limits_{x}^{b} {\frac{f(s)}{{(s - x)^{1 - \gamma } }}ds} $$

(2.2)

γ is the order of fractional integrals where Γ(x) = (x-1)! with Γ(γ) Euler’s Gamma function. Also, the left and right Riemann–Liouville (RL) derivatives are defined by:

$$ {}_{a}^{RL} D_{x}^{\gamma } f(x) = \left( \frac{d}{dx} \right)^{m} ({}_{{\text{a}}}I_{x}^{m - \gamma } \;f(x)) $$

(2.3)

and

$$ {}_{x}^{RL} D_{b}^{\gamma } f(x) = \left( { - \frac{d}{dx}} \right)^{m} ({}_{x}I_{b}^{m - \gamma } \;f(x)) $$

(2.4)

Let us point out that for the left fractional integrals and derivatives

$$ {}_{a}^{RL} D_{x}^{\gamma } \left( {{}_{a}{\rm I}_{x}^{\gamma } f\left( x \right)} \right) = f\left( x \right) $$

(2.5)

A similar relation is valid for the right RL-fractional derivative and right fractional integral. Considering only the left space, the Λ-fractional derivative (Λ-FD) has been defined as

$$ {}_{a}^{\Lambda } D_{x}^{\gamma } f(x) = \frac{{{}_{\alpha }^{RL} D_{x}^{\gamma } f(x)}}{{{}_{a}^{RL} D_{x}^{\gamma } x}} $$

(2.6)

Recalling the definition of the Riemann–Liouville fractional derivative, Eq. (2.3), the Λ-FD is expressed by,

$$ {}_{a}^{\Lambda } D_{x}^{\gamma } f\left( x \right) = \frac{{\frac{{d{}_{a}I_{x}^{1 - \gamma } f(x)}}{dx}}}{{\frac{{d{}_{a}I_{x}^{1 - \gamma } x}}{dx}}} = \frac{{d{}_{a}I_{x}^{1 - \gamma } f(x)}}{{d{}_{a}I_{x}^{1 - \gamma } x}} $$

(2.7)

Further, if

$$ X = {}_{a}I_{x}^{1 - \gamma } x\quad {\text{and}}\quad F(X) = {}_{a}I_{x}^{1 - \gamma } f(x), $$

(2.8)

the Λ-FD appears to behave like a conventional derivative in the fractional Λ-space (X, F(X)) with local properties. The Fractional Differential Geometry may be developed as a conventional differential geometry in the Λ-fractional space, (X, F(X)).

Indeed, Eq. (2.8a) yields

$$ X = \frac{{x^{2 - \gamma } }}{{\Gamma \left( {3 - \gamma } \right)}} $$

(2.9)

It should be pointed out that the present analysis concerns only real X spaces. Possible complex X spaces are not included. In addition, Eqs. (2.8b, 2.9) suggest that:

$$ F\left( x \right) = {}_{\alpha }I_{x}^{1 - \gamma } f\left( x \right) = \frac{1}{{\Gamma \left( {1 - \gamma } \right)}}\mathop \smallint \limits_{\alpha }^{x} \frac{f\left( s \right)}{{\left( {x - s} \right)^{\gamma } }}ds $$

(2.10)

Inverting Eq. (2.9) it appears,

$$ x = \left( {\Gamma \left( {3 - \gamma } \right){\rm X}} \right)^{{1/\left( {2 - \gamma } \right)}} = x\left( X \right) $$

(2.11)

Proceeding further to the definition of the fractional Λ-space, inserting x(X) into Eq. (2.10), the function F(x) may be expressed as a function of X.

$$ F\left( X \right) = F\left( {x\left( X \right)} \right) $$

(2.12)

It is evident that, in the just presented Λ-fractional derivatives, only left fractional integrals and RL fractional derivatives were considered. If we were to involve the right fractional integrals and RL derivatives, then the Λ-Fractional derivatives should be defined by

$$ {}_{{}}^{\Lambda } D_{{}}^{\gamma } f\left( x \right) = \frac{{d{}_{a}I_{x}^{1 - \gamma } f(x) - d{}_{x}I_{b}^{1 - \gamma } f(x)}}{{2\,d{}_{a}I_{x}^{1 - \gamma } x}} = \frac{dF(X)}{{dX}} $$

(2.13a)

with

$$ \left( x \right) = \frac{{\left( {{}_{\alpha }I_{x}^{1 - \gamma } f\left( x \right) - {}_{x}I_{b}^{1 - \gamma } f\left( x \right)} \right)}}{2} = \frac{1}{{\Gamma \left( {1 - \gamma } \right)}}\left( {\mathop \smallint \limits_{\alpha }^{x} \frac{f\left( s \right)}{{\left( {x - s} \right)^{\gamma } }}ds - \mathop \smallint \limits_{x}^{b} \frac{f\left( s \right)}{{\left( {s - x} \right)^{\gamma } }}ds} \right) = F\left( {x\left( X \right)} \right) $$

(2.13b)

It will be clarified in the application, how from the initial space (x, f(x)) the fractional Λ-space (X, F(X)) is defined. Further, the pullback of the results in the initial space will also be demonstrated. For simplicity reasons, only the left fractional integrals and derivatives will be taken into consideration in the first chapters. In the last chapter 9, the plane linear elastic problem is formulated considering fractional derivatives of both sides. Applications with both side fractional derivatives may be found in Lazopoulos [37].

3 Geometry in the Λ-fractional space

Just to understand the analysis in the Λ-fractional space, the geometry of the surface,

$$ z = x^{2} y^{2} ,\quad 0 < x < 1,\quad 0 < y < 1 $$

(3.1)

will be discussed (Fig. 1).

Fig. 1

The surface z

The conjugate fractional Λ-space (X, Y, Z) to the initial space is defined by,

$$ X = \frac{{x^{2 - \gamma } }}{{\Gamma \left( {3 - \gamma } \right)}} $$

(3.2)

$$ Y = \frac{{y^{2 - \gamma } }}{{\Gamma \left( {3 - \gamma } \right)}} $$

(3.3)

$$ Z = {}_{b}I_{y}^{1 - \gamma } {}_{\alpha }I_{x}^{1 - \gamma } z\left( {x,y} \right) = \frac{1}{{\left( {\Gamma \left( {1 - \gamma } \right)} \right)^{2} }}\mathop \smallint \limits_{b}^{y} \left( {\mathop \smallint \limits_{\alpha }^{x} \frac{{z\left( {s,t} \right)}}{{\left( {x - s} \right)^{\gamma } }}ds} \right)\frac{dt}{{\left( {y - t} \right)^{\gamma } }} $$

(3.4)

With a = b = 0, Eq. (3.4) yields,

$$ Z = \frac{{2\left( {X{\Gamma }\left[ {3 - \gamma } \right])^{{\frac{3 - \gamma }{{2 - \gamma }}}} } \right)}}{{{\Gamma }\left[ {4 - \gamma } \right]}}Y $$

(3.5)

For γ = 0.6, the surface Z in the Λ-fractional space is defined by

$$ Z = 0.947X^{1.714} Y^{1.714} $$

(3.6)

and it is shown in Fig. 2.

Fig. 2

The surface Z in the Λ-fractional space

Further, the tangent space of the surface with γ = 0.6, at the point X = Y = 0.6 is defined by,

$$ Z = \left( {0.947X^{1.714} Y^{1.714} } \right)_{{\left( {X = Y = 0.6} \right)}} + \frac{{dZ\left( {X = Y = 0.6} \right)}}{dX}\left( {{\rm X} - 0.6} \right) + \frac{{dZ\left( {X = Y = 0.6} \right)}}{dY}\left( {Y - 0.6} \right) $$

(3.7)

and finally the equation of the tangent space in the Λ-fractional space,

$$ Z = 0.164 + 0.469\left( {{\rm X} - 0.6} \right) + 0.469\left( {\Upsilon - 0.6} \right) $$

(3.8)

The corresponding surface in the initial space to the tangent plane in the Λ-fractional space is defined by (Fig. 3),

$$ \begin{aligned} z & = x^{2} y^{2}_{{\left( {x = y = 0.81} \right)}} + \left( {\left( {{}_{0}^{RL} D_{y = 0.81}^{1 - \gamma } {}_{0}^{RL} D_{x = 0.81}^{1 - \gamma } \left( {\frac{dZ}{{dX\left( x \right)}}} \right)} \right)\left( {X\left( x \right) - 0.6} \right)} \right) \\ & \quad + \left( {({}_{0}^{RL} D_{y = 0.81}^{1 - \gamma } {}_{0}^{RL} D_{x = 0.81}^{1 - \gamma } \left( {\frac{dZ}{{dY}}} \right))\left( {Y\left( y \right) - 0.6} \right)} \right) \\ \end{aligned} $$

(3.9)

Fig. 3

The surface with the tangent space in the Λ-fractional space

The surface defined by Eq. (3.9) is shown in Fig. 4.

Fig. 4

The surface with its tangent surface at the point (x = y = 0.8106) at the initial space

It seems that the initial surface and the tangent surface, corresponding to the tangent space at the Λ-space, have almost a common tangent plane in the initial space since their mathematical expressions are different, but they are quite close.

The transferring of the geometry from the Λ-space to the initial one is quite important, since the real space is the initial space. Let us consider that the bending problem is studied. The elastic line in the Λ-space is defined through its curvature, existing only in the Λ-space. The real elastic line lies in the initial space through transferring the Λ-space elastic line to the initial one. It is clearly explaned in the chapter 9, where the bending of a cantilever beam with two-side fractional derivatives is discussed.

4 Conventional deformation versus Λ-fractional deformation geometry

Consider a material body b with its boundary $\partial \mathbf{b}$ at its undeformed initial placement. Its current (deformed) configuration is δ with the boundary $\partial$ δ. Α material point x in the reference placement b takes the placement ψ in the current configuration δ, see Fig. 5. Hence, the local deformation is defined by, [13, 16, 17],

$$ {\mathbf{F}}\left( {{{\varvec{\uppsi}}}({\mathbf{x}})} \right) = \frac{{\partial \left( {{\varvec{\uppsi}}} \right)}}{{\partial {\mathbf{x}}}} $$

(4.1)

Fig. 5

The initial and deformed placements at the initial space

The right Cauchy-Green deformation tensor is defined by,

$$ {\mathbf{C}} = {\mathbf{F}}^{{\mathbf{T}}} {\mathbf{F}} $$

(4.2)

whereas the left Cauchy-Green deformation tensor is expressed by,

$$ {\mathbf{B}} = {\mathbf{FF}}^{{\mathbf{T}}} $$

(4.3)

where ()^T denotes the transpose matrix.

Then, the Euler–Lagrange strain tensor is defined by,

$$ {\mathbf{E}} = 1/2({\mathbf{C}} - {\mathbf{I}}) $$

(4.4)

and the Euler–Almansi strain tensor:

$$ {\mathbf{e}} = 1/2\left( {{\mathbf{I}} - {\mathbf{B}}^{ - 1} } \right) $$

(4.5)

Besides, the linear strain tensor is defined by:

$$ {\mathbf{E}}^{{\mathbf{l}}} = \frac{1}{2}\left( {{\mathbf{F}} + {\mathbf{F}}^{{\mathbf{T}}} } \right) - {\mathbf{I}} = \frac{1}{2}\left( {{\mathbf{H}} + {\mathbf{H}}^{{\mathbf{T}}} } \right) $$

(4.6)

where H = F-I is the displacement gradient tensor.

Proceeding to define the deformation and strain in the fractional Λ-space, the reference placement b and the deformed one δ are represented by the configurations B and Δ in the Λ-space through the transformation, see Eq. (3.2),

$$ {\mathbf{X}} = \frac{{x_{i}^{2 - \gamma } {\mathbf{e}}_{i} }}{{\Gamma \left( {3 - \gamma } \right)}},\quad i = 1, \cdot ,3 $$

(4.7)

recalling the tensor contraction and the vectors e_i are the unit ones. It is pointed out that the present theory is restricted only to real X values. Possible complex values of X are not valid in the present context of the theory.

Also, the transformation Ψ of the current placement ψ(x) in the fractional Λ-space (Fig. 6.) is defined through the help of transformations similar to Eqs. (3.2, 3.4) by,

$$ {\mathbf{\bar{\Psi }}}\left( {\mathbf{x}} \right) = \frac{{{\mathbf{E}}_{i} }}{{\Gamma \left( {1 - \gamma } \right)^{3} }}\mathop {\iiint}\limits_{{\alpha _{3} \alpha _{2} \alpha _{1} }}^{{x_{3} x_{{2~}} x_{3} }} \frac{{\psi _{\iota } \left( {s,t,u} \right)~ds~dt~du}}{{\left( {\left( {x_{1} - s} \right)\left( {x_{2} - t} \right)\left( {x_{3} - u} \right)} \right)^{\gamma } }} $$

(4.8)

where Ε_ι, i = 1,2,3, are the unit vectors in the conjugate Λ-space. Equation (4.8) defines the transformed current placement in the Λ-space, with coordinates of the initial space. Substituting x_i from Eq. (4.7), the current placement is defined through the equation

$$ {{\varvec{\Psi}}} = {{\varvec{\Psi}}}({\mathbf{\rm X}}) $$

(4.9)

with the Χ vector defining the initial placement in the conjugate Λ-fractional space.

Fig. 6

The initial and the deformed placements at the Λ-space

Hence, the Λ-fractional deformation tensor is defined by

$$ {}^{{\varvec{\varLambda}}}{\mathbf{F}}\left( {{{\varvec{\Psi}}}\left( {\mathbf{\rm X}} \right)} \right) = \frac{{\partial \left( {{\varvec{\Psi}}} \right)}}{{\partial {\mathbf{\rm X}}}} $$

(4.10)

The Λ-fractional right Cauchy-Green deformation tensor is defined by,

$$^{{{\varvec{\Lambda}}}} {\mathbf{C}} =^{{{\varvec{\Lambda}}}} {\mathbf{F}}^{{\mathbf{T}}} \;^{{{\varvec{\Lambda}}}} {\mathbf{F}} $$

(4.11)

whereas the left Λ-fractional Cauchy-Green deformation tensor is expressed by,

$$^{{{\varvec{\Lambda}}}} {\mathbf{B}} =^{{{\varvec{\Lambda}}}} {\mathbf{F}}\;^{{{\varvec{\Lambda}}}} {\mathbf{F}}^{{\mathbf{T}}} $$

(4.12)

with ()^T denoting the transpose matrix.

Then, the Λ-fractional Euler–Lagrange strain tensor is defined by,

$$^{{{\varvec{\Lambda}}}} {\mathbf{E}} = 1/2\left( {^{{{\varvec{\Lambda}}}} {\mathbf{C}} - {\mathbf{I}}} \right) $$

(4.13)

where I is the identity matrix. Yet the Λ-fractional Euler–Almansi strain tensor:

$$ {}^{{{\varvec{\Lambda}}}}{\mathbf{e}} = 1/2\left( {{\mathbf{I}} - {}^{{{\varvec{\Lambda}}}}{\mathbf{B}}^{ - 1} } \right) $$

(4.14)

Further, the Λ-fractional linear strain tensor is defined by:

$$ {}^{{{\varvec{\Lambda}}}}{\mathbf{E}}^{{\mathbf{l}}} = \frac{1}{2}\left( {{}^{{{\varvec{\Lambda}}}}{\mathbf{F}} + {}^{{{\varvec{\Lambda}}}}{\mathbf{F}}^{{\mathbf{T}}} } \right) - {\mathbf{I}} = \frac{1}{2}\left( {{}^{{\varvec{\varLambda}}}{\mathbf{H}} + {}^{{{\varvec{\Lambda}}}}{\mathbf{H}}^{{\mathbf{T}}} } \right) $$

(4.15)

with ${}^{{\varvec{\varLambda}}}{\mathbf{H}}$ the Λ-fractional displacement gradient in the Λ-fractional space.

Let us point out that strains may not be transferred in the initial space with the notion of derivatives but only as functions.

The various deformation tensors in the Λ-fractional space may be transferred back to the original space through the transformation,

$$ {\mathbf{q}}\left( {\mathbf{x}} \right) = {}_{a}^{RL} D_{{{\mathbf{x}}\left( {\mathbf{X}} \right)}}^{1 - \gamma } \left( {{\mathbf{Q}}\left( {\mathbf{X}} \right)} \right) $$

(4.16)

In the case of both sides, two fractional Λ-spaces should be considered the left and the right one. The transformation Ψ(X) of the displacement function ψ, Eq. 4.8 for the right fractional Λ-space becomes,

$$ {\overline{\mathbf{\Psi }}}\left( {\varvec{x}} \right) = \frac{{{\mathbf{E}}_{i} }}{{(2\Gamma \left( {1 - \gamma } \right))^{3} }}\mathop \smallint \limits_{{x_{3} }}^{{b_{3} }} \left( {\mathop \smallint \limits_{{x_{2} }}^{{b_{2} }} \left( {\left( { \mathop \smallint \limits_{{x_{1} }}^{{b_{1} }} \frac{{\psi_{\iota } \left( {s,t,u} \right) ds }}{{\left( {\left( {x_{1} - s} \right)\left( {x_{2} - t} \right)\left( {x_{3} - u} \right)} \right)^{\gamma } }}} \right)dt} \right)du} \right) $$

(4.17)

Further, the X space, see Eq. (4.7), in the right fractional space, is expressed by,

$$ {\mathbf{X}}^{{\mathbf{r}}} = \frac{{(l_{i} - x_{i} )^{1 - \gamma } \left( {l_{i} - l_{i} \gamma + x_{i} } \right) {\mathbf{e}}_{i} }}{{\Gamma \left( {3 - \gamma } \right)}} $$

(4.18)

Without restricting the problem but rather trying to make it more accessible, the left fractional derivative is only considered in the following first chapters. That does not restrict the problem but the interested reader may formulate the complete problem, considering the left and right fractional derivatives. The last application, concerning the fractional cantilever beam problem, has been formulated considering left and right fractional derivatives. In that application, the conjugate Λ-fractional space is formulated with the help of both side fractional derivatives. Further ways for considering both side fractional derivatives may be found in [37].

5 The non-linear elasticity problem

According to the conventional theory of elasticity, the strain energy density function [16, 17, 27],

$$ W = W\left( {\mathbf{C}} \right) $$

(5.1)

where C is the right Cauchy-Green deformation tensor, Eq. (4.2). Further for isotropic materials,

$$ W = W\left( {I_{1} ,I_{2} ,I_{3} } \right) $$

(5.2)

where ${I}_{1},{I}_{2},{I}_{3}$ are the principal invariants of the tensor C or B. Then the stress tensor T is defined by, Atkin and Fox [27],

$$ {\mathbf{T}} = \chi_{0} {\mathbf{\rm I}} + \chi_{1} {\mathbf{B}} + \chi_{ - 1} {\mathbf{\rm B}}^{ - 1} $$

(5.3)

where $\mathbf{\rm I}$ is the unit 3 × 3 matrix and if ${W}_{i}=\frac{\partial W}{\partial {I}_{i}}$,

$$ \chi_{0} = \frac{2}{{{\rm I}_{3}^{1/2} }}\left( {{\rm I}_{2} W_{2} + {\rm I}_{3} W_{3} } \right),\quad \chi_{1} = \frac{2}{{I_{3}^{1/2} }}W_{1} ,\quad \chi_{ - 1} = - 2I_{3}^{1/2} W_{2} $$

(5.4)

Yet, for incompressible isotropic materials with I₃ = 1, the stress tensor is expressed by,

$$ {\mathbf{T}} = - p{\mathbf{\rm I}} + 2W_{1} {\mathbf{B}} - 2W_{2} {\mathbf{\rm B}}^{ - 1} $$

(5.5)

where p is the pressure due to the constraint of incompressibility.

Let us point out that for neo-Hookean materials

$$ W = C_{1} \left( {I_{1} - 3} \right) $$

(5.6)

With

$$ {\mathbf{T}} = - p{\mathbf{\rm I}} + 2C_{1} {\mathbf{\rm B}}_{1} $$

(5.7)

Besides, for the Mooney–Rivlin incompressible materials with,

$$W={C}_{1}\left({I}_{1}-3\right)+{C}_{2}({I}_{2}-3)$$

the stress tensor is expressed by,

$$\mathbf{T}=-p\mathbf{\rm I}{+2C}_{1}\mathbf{B}-{2C}_{2}{\mathbf{\rm B}}^{-1}$$

(5.8)

Likewise, for linear elasticity with infinitesimal deformations,

$${T}_{KL}=2\mu {\rm E}_{KL}+\lambda {\rm E}_{{\rm M}{\rm M}}{\delta }_{KL}$$

(5.9)

where,

$${E}_{KL}=\frac{1}{2}\left({u}_{K,L}+{u}_{L,K}\right)$$

(5.10)

is the linear deformation tensor.

The coefficients (λ,μ) are the well known Lame coefficients. Further, the various results may be transferred as functions to the original space through the transformation of Eq. (4.16). Also, the equation expressing the balance of linear momentum is defined by,

$$ div[{\mathbf{T}}^{{}} ] + \rho {\mathbf{b}} = 0 $$

(5.11)

where b is the body loading and ρ is the material density. Following similar steps as in the conventional case, the balance of rotational momentum yields the symmetry of Cauchy stress tensor.

$$ {\mathbf{T}} = {\mathbf{T}}^{T} $$

(5.12)

The present section is referred to the conventional elasticity. In the case of the Λ-space, all the functions will be considered with the Λ-upper left index.

6 Application

Let us consider a material point (x,y) displaced after deformation to the current placement (χ,ψ) = ξ(x + x²y, y + y²x), with $\left|\xi \right|\ll 1$, in the initial plane (x,y). Then the point (x,y) in the initial space corresponds to the point (X, Y) of the Λ-fractional space, where, see Eq. (4.7),

$$X=\frac{{x}^{2-\gamma }}{\Gamma (3-\gamma )}$$

(6.1)

$$Y=\frac{{y}^{2-\gamma }}{\Gamma (3-\gamma )}$$

(6.2)

Since the algebra becomes quite lengthy, the application from this very point will be discussed considering the fractional dimension γ = 0.6. Furthermore, taking into consideration Eq. (4.8), the current displacement (u,v) in the initial plane corresponds to the displacement (U, V) in the Λ-fractional space with,

$$U=0.973\xi {\rm X}^{1.71}Y$$

$$V=0.973{\xi {\rm X}Y}^{1.71}$$

(6.3)

Recalling that in the Λ-fractional space the derivation follows the conventional rules, the Λ-fractional (non-local) displacement gradient ${}^{\Lambda }\mathbf{H}$ is defined by,

$${}^{\Lambda }\mathbf{\rm H}=\frac{\partial \left(U,V\right)}{\partial \left(X,Y\right)}$$

(6.4)

With the help of the computerized Mathematica pack [18], the Λ-fractional linear strain tensor, Eq. (4.6), has been defined. In that case,

$${}^{{\varvec{\Lambda}}}{\mathbf{E}}^{\mathbf{l}}\left(X,Y\right)=\xi \left[\begin{array}{cc}1.668{\rm X}^{0.714}Y& 0.487({\rm X}^{0.714}+{Y}^{0.714})\\ 0.487({\rm X}^{0.714}+{Y}^{0.714})& 1.668{{\rm X}Y}^{0.714}\end{array}\right]$$

(6.5)

All the various Λ-fractional deformation and strain tensors may be defined using similar procedures with the help of the Mathematica [18] computerized algebra. Trying to pull back to the initial space the various deformation tensors, the following method should be followed:

First the variables X and Y should be expressed in x and y through the Eqs. (6.1, 6.2, 4.15). Then the Eq. (4.16) yields,

$$\mathbf{q}\left(x,y\right)={{}_{a}{}^{RL}D}_{{\varvec{y}}}^{1-\gamma }{{}_{a}{}^{RL}D}_{{\varvec{x}}}^{1-\gamma }\left(\mathbf{Q}(X(x),Y(y))\right)$$

(6.6)

Expressing the fractional Riemann–Liοuville derivatives in Eq. (6.6), it appears

$$\mathbf{q}\left(x,y\right)=\frac{1}{{\left(\Gamma (\gamma )\right)}^{2}}\frac{{\partial }^{2}}{\partial x\partial y}\underset{0}{\overset{y}{\int }}\frac{1}{{\left(y-t\right)}^{1-\gamma }}\left(\underset{0}{\overset{x}{\int }}\frac{\mathbf{Q}\left(s,t\right)}{{\left(x-s\right)}^{1-\gamma }}ds\right)dt$$

(6.7)

Applying Eq. (6.7) to the Λ-fractional deformation and Λ-strain matrices, the corresponding matrices in the original space (x,y) may be revealed. Indeed, the fractional linear strain ${\mathbf{e}}^{\mathbf{l}}$ in the initial space may be computed through the relation,

$${\mathbf{e}}^{\mathbf{l}}\left(x,y\right)={{}_{a}{}^{RL}D}_{{\varvec{y}}}^{1-\gamma }{{}_{a}{}^{RL}D}_{{\varvec{x}}}^{1-\gamma }\left({}^{{\varvec{\Lambda}}}{\mathbf{E}}^{\mathbf{l}}(X(x),Y(y))\right)$$

(6.8)

Performing the computation with the help of Mathematica [18] computerized algebra, it is found:

$${\mathbf{e}}^{\mathbf{l}}\left(x,y\right)=\xi \left[\begin{array}{cc}1.599{x}^{0.6}y& 0.335\left(\frac{{x}^{2}}{{y}^{0.4}}+\frac{{y}^{2}}{{x}^{0.4}}\right)\\ 0.335\left(\frac{{x}^{2}}{{y}^{0.4}}+\frac{{y}^{2}}{{x}^{0.4}}\right)& 1.599{xy}^{0.6}\end{array}\right]$$

(6.9)

Following that procedure, the various deformation and strain tensors will be computed in the Λ-fractional space and the initial as well. It is pointed out that Eq. (6.9) may be considered as the transformation of the strain in the Λ-space and not as the strain in the initial space since the notion of strain includes the idea of derivative and derivatives do not exist in the initial space. Proceeding to the definition of the stresses in the Λ-space,

$$\frac{{\Sigma }_{11}}{\left(2\mu +\lambda \right)\xi }={\rm E}_{11}+\frac{\mu }{2\mu +\lambda }{\rm E}_{22}$$

(6.10)

$$\frac{{\Sigma }_{22}}{\left(2\mu +\lambda \right)\xi }={\rm E}_{22}+\frac{\mu }{2\mu +\lambda }{\rm E}_{11}$$

(6.11)

$$\frac{{\Sigma }_{12}}{\left(2\mu +\lambda \right)\xi }=\frac{2\mu }{2\mu +\lambda }{\rm E}_{12}$$

(6.12)

Further, the stresses have been transferred to the original space (x,y) through the transformation, Eq. (6.7). With the help of Mathematica computerized algebra pack [18] the stresses $\frac{{\sigma }_{ij}}{\left(2\mu +\lambda \right)\xi }$ in the original space have been computed for.

7 $\frac{\mu }{2\mu +\lambda }=0.30$.

In Figs. 7, 8, 9 the stresses in the initial space are shown for γ = 0.5, 0.8, 1.0. The contribution of the fractional-order γ is highly important.

Fig. 7

The (dimensionless) stress σ₁₁ in the initial space for γ = 0.5, 0.8, 1.0

Fig. 8

The (dimensionless) stress σ₁₂ in the initial space for γ = 0.5,0.8,1.0

Fig. 9

The (dimensionless) stress σ₂₂ in the initial space for γ = 0.5,0.8,1.0

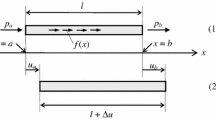
8 The bar extension

The present section concerns the discussion of the simple problem of the bar extension and its purpose is to show how the Λ-strain may be implemented in solving deformation problems. Let us suppose that a bar, of initial length l and fixed at the one end, is fractionally deformed through the application of the extensional force p at its free end, see Fig. 10.

Fig. 10

The bar in the initial space

In the fractional Λ-space, the corresponding force P applied at the free end is defined by the relation,

$${\varvec{P}}=\frac{1}{\Gamma (1-\gamma )}{\int }_{0}^{l}\frac{{\varvec{p}}}{{(l-s)}^{\gamma }}ds=\frac{{\varvec{p}}{l}^{1-\gamma }}{\Gamma (2-\gamma )}$$

(7.1)

Further, the length l of the bar in the initial space becomes,

$$L=\frac{{l}^{2-\gamma }}{\Gamma (3-\gamma )}$$

(7.2)

in the Λ-space, see Fig 11.

Fig. 11

The bar in the fractional Λ-space

Likewise, the constant cross-section area a of the bar in the initial space is transferred to the fractional Λ-space by,

$${A}=\frac{1}{\Gamma (1-\gamma )}{\int }_{0}^{x}\frac{a}{{(l-s)}^{\gamma }}ds=\frac{a{x}^{1-\gamma }}{\Gamma (2-\gamma )}$$

(7.3)

Hence, the strain in the Λ-space, following the linear Hook’s law is defined by,

$$\frac{dY}{dX}=\frac{P}{EA}=\frac{p{l}^{1-\gamma }}{{\rm E}{ax}^{1-\gamma }}$$

(7.4)

where E is Young’s modulus of Elasticity in the Λ-space. At this point, I should stress that either Young’s modulus is constant at the Λ-space, as it is considered here, or it is constant in the initial space and should be transferred as a non-constant one in the Λ-space and that is a different fractional elastic problem. Further,

$$x={\left(\Gamma \left(3-\gamma \right){\rm X}\right)}^{\frac{1}{2-\gamma }}$$

(7.5)

Hence, Eq. (7.4) yields,

$$Y\left({\rm X}\right)=\underset{0}{\overset{X}{\int }}\frac{p{l}^{1-\gamma } d{\rm X}}{{\rm E}a{{\left(\Gamma \left(3-\gamma \right){\rm X}\right)}^{\frac{1-\gamma }{2-\gamma }} }}=\frac{(2-\gamma )p{l}^{1-\gamma }{\rm X}^{\frac{1}{2-\gamma }}}{{\rm E}a}$$

(7.6)

where Υ(Χ) denotes the displacement in the fractional Λ-space. The elastic modulus E is considered constant in the conjugate Λ-fractional space.

Further, the displacement Y may be defined as a function of the initial placement x through Eq. (6.1). Indeed,

$$Y\left(x\right)=\frac{p{x}^{2-\gamma }{\left(l{\left({x}^{2-\gamma }\right)}^{\frac{1}{-2+\gamma }}\right)}^{1-\gamma }}{{\rm E}a\Gamma \left(1-\gamma \right)}$$

(7.7)

Recalling Eq. (4.16), the displacement y(x) in the initial plane (x,y) is transferred through,

$$y\left(x\right)=\frac{1}{\Gamma (\gamma )}\frac{d}{dx}\underset{0}{\overset{x}{\int }}\frac{Y(s)}{{(x-s)}^{1-\gamma }}ds$$

(7.8)

Performing the algebra, the displacement in the initial space x is defined by,

$$y\left(x\right)=\frac{\left(-2+\gamma \right){l}^{1-\gamma }p{x}^{\gamma }}{{\rm E}\alpha \Gamma (1+\gamma ){\Gamma (3-\gamma )}^{\frac{1}{2-\gamma }}}$$

(7.9)

Figure 12 shows the displacement functions for o bar of length l = 2 and γ = 0.6, 0.8, 1.

Fig. 12

The (dimensionless) bar displacement y(x) for various values of the fractional-order γ

The displacements become higher for smaller values of the fractional-orders γ.

Likewise, considering that in the Λ-space the conventional mechanics' rules are valid, the axial force is constant and equal to P, see Eq. (7.1), the axial stress Σ(Χ), along the bar in the Λ-space, is defined through the relation,

Σ(Χ)=$\frac{P}{A}=\frac{P\Gamma \left(2-\gamma \right)}{a{\left(\Gamma \left(3-\gamma \right){\rm X}\right)}^{\frac{1-\gamma }{2-\gamma }}}$ (7.10).

Further, the stress Σ(Χ) in the Λ-space may be expressed in the x variable of the initial space by,

Σ(Χ(x))$=\frac{p{l}^{1-\gamma }}{\alpha {x}^{1-\gamma }}$ (7.11).

Yet, the stress in the initial space is defined through the transformation,

$$\sigma \left(x\right)={}_{0}{}^{RL}{D}_{x}^{1-\gamma }\Sigma \left({\rm X}\left(x\right)\right)=\frac{1}{\Gamma (\gamma )}\frac{d}{dx}\underset{0}{\overset{x}{\int }}\frac{p{l}^{1-\gamma }}{{\alpha {s}^{1-\gamma }(x-s)}^{1-\gamma }}ds=\frac{p{l}^{1-\gamma }\Gamma (\gamma ){x}^{-2+2\gamma }}{\alpha \Gamma (2\gamma -1)}$$

(7.12)

It is evident that the present method exhibits the size effect phenomenon, well known by gradient theories, see Aifantis [34].

Next, the variation of stresses in the initial space for various values of the fractional-order γ, for a bar of initial length l = 2 is shown in Fig. 13.

Fig. 13

Variation of (dimensionless) stresses in the initial space with for various fractional orders γ

Let us point out, that many discussions and topics may be included even in the simple problem of extension of a fractional bar under axial loading. However, the present analysis has been added, just to show how the Λ-strain may be manipulated, to yield reliable results.

9 The fractal bar extension

The application of the fractional Λ-derivative and the use of the Λ-fractional space will be implemented to fractals. Let us consider the extension problem of the bar under tension, just the same as in the preceding section, but with variable cross-section area. The various diagrams have been found with the help of the Mathematica computerized algebra. The cross-section area a(x) in the initial space is defined by the fractal function with Hausdorff dimension d_H = 1.5,

$$a\left(x\right)=1+\sum_{n=1}^{\infty }{n}^{-0.5n}sin\left({n}^{n}x\right)$$

(8.1)

Just for computing economy the cross-sectional area a(x) may be approximated by,

$$a\left(x\right)\approx 1+\sum_{n=1}^{5}{n}^{-0.5n}sin\left({n}^{n}x\right)$$

(8.2)

Then, the corresponding cross-sectional area in the Λ-space is defined by,

$$A\left(x\right)=\frac{1}{\Gamma \left(1-\gamma \right)}\underset{0}{\overset{x}{\int }}\frac{a(s)}{{(x-s)}^{\gamma }}ds$$

(8.3)

Further, according to Eq. (6.1),

$$X=\frac{{x}^{2-\gamma }}{\Gamma (3-\gamma )}$$

Solving for x from Eq. (2.9), see Εq. (2.11),

10 $x={(\Gamma \left(3-\gamma \right)X)}^{\frac{1}{2-\gamma }}$.

According to Liang et al. [28, 30,31,32] and Yao et al.[36], there exists a simple connection between the Hausdorff dimension and fractal order. Introducing x from Eq. (2.11) into Eq. (8.3), the corresponding cross-sectional area function Α(Χ) in the Λ-space is shown for the initial cross-sectional area a(x) for γ = 0.6 in Fig. 14.

Fig. 14

The (dimensionless) fractal cross-sectional area a(x) in the initial space of the bar with unit length

Besides, the axial length l in the initial space becomes L in the Λ-space by:

$$L=\frac{1}{\Gamma (1-\gamma )}{\int }_{0}^{l}\frac{1}{{(l-s)}^{\gamma }}ds=\frac{{l}^{1-\gamma }}{\Gamma (2-\gamma )}$$

Then the force p applied at the free end of the bar in the initial space, becomes

$$P=\frac{1}{\Gamma (1-\gamma )}{\int }_{0}^{l}\frac{p}{{(l-s)}^{\gamma }}ds=\frac{p{l}^{1-\gamma }}{\Gamma (2-\gamma )}$$

in the conjugate Λ-space (Fig. 15). Since in the Λ-space everything works conventionally, the equilibrating axial stress in the Λ-space is defined by,

Fig. 15

The (dimensionless) cross-sectional area A(X) versus the axial coordinate X in the Λ-space

$$\Sigma \left({\rm X}\right)=\frac{P}{A(X)}=\frac{p{l}^{1-\gamma }}{\Gamma \left(2-\gamma \right){\rm A}({\rm X})}$$

(8.3)

The axial stress Σ(Χ) depends upon the initial length l, revealing the size effect phenomenon (Fig. 16), well known by gradient theories, see Aifantis [34].

Fig. 16

The diagram of the (dimensionless) fractional stress Σ(Χ) versus the axial coordinate X in the Λ-space for unit initial axial length and γ = 0.6

Also, considering the elastic modulus E constant in the initial space, the fractional strain in the Λ-space is defined by,

$$E\left(X\right)=\frac{\Sigma ({\rm X})}{{E}^{\Lambda }}=\frac{P}{{E}^{\Lambda }{\rm A}({\rm X})}=\frac{p{l}^{1-\gamma }}{{\rm E}{x}^{1-\gamma }{\rm A}({\rm X})}$$

(8.4)

Further, considering Eq. (8.3), the fractional strain E(X) is defined by,

$$E\left(X\right)=\frac{p{l}^{1-\gamma }}{{\rm E}{(\Gamma \left(2-\gamma \right){\rm X})}^{\frac{1-\gamma }{2-\gamma }}{\rm A}({\rm X})}$$

(8.5)

where E is the common Young’s modulus in the initial space. In Fig. 17 the fractional strain versus the X coordinate has been indicated.

Fig. 17

The (dimensionless) fractional strain Ε(Χ) in the fractional Λ-space with unit initial length and γ = 0.6

Since, the strain in the Λ-space,

$$\frac{dY(X)}{dX}=E(X)$$

(8.6)

the displacement Υ(Χ) in the Λ-space is defined by,

$$Y\left(X\right)=\underset{0}{\overset{X}{\int }}E\left(X\right)dX$$

(8.7)

For the fractal bar of initial unit length, the displacement function in the Λ-space for the order γ = 0.6 is shown in Fig. 18.

Fig. 18

The (dimensionless) fractional displacement field for the bar of unit initial length with γ = 0.6 in the Λ-fractional space

Transferring the stress function into the initial space, the axial stress, along the bar in the initial space, is defined through the relation,

$$\sigma (x)=\frac{1}{\Gamma (\gamma )}\frac{d}{dx}\underset{0}{\overset{x}{\int }}\frac{\Sigma (s)}{{(x-s)}^{1-\gamma }}ds$$

(8.8)

where Σ(x) is the stress function in the fractional Λ-space expressed in the variable x of the original space. With the help of Mathematica, the stress function versus the axial distance x of the bar, Eq. (8.8), for the considered example has been shown in Fig. 19.

Fig. 19

The (dimensionless) fractional stress field for the bar of unit initial length with γ = 0.6 in the initial space

Further, the displacement in the initial space may be defined through the relation,

$$y(x)=\frac{1}{\Gamma (\gamma )}\frac{d}{dx}\underset{0}{\overset{x}{\int }}\frac{Y(s)}{{(x-s)}^{1-\gamma }}ds$$

(8.9)

Indeed, the displacement in the initial space has been calculated with the help of the Mathematica computerized pack. Figure 20 indicates the displacement function.

Fig. 20

The (dimensionless) fractional displacement field for the bar of unit initial length with γ = 0.6 in the initial space

11 Bending of a cantilever beam with two-side fractional derivatives.

The present chapter deals with the interaction of both side fractional derivatives. The cases with the interaction of the left fractional derivatives are considered as separate problems and the same holds for the interaction of the right side fractional derivatives. The final result is the mean value from the left and right solutions. As a simple problem for exhibiting the interaction of the two-side fractional derivatives, the bending of a uniform cantilever under the action of uniformly distributed loading is studied.

11.1 The left fractional Λ-space

First, the beam deflection will be defined in the left Λ-fractional space. If the beam (x,y(x)) is defined in the initial space, the deflection y(x) of the beam is derived, through the γ-order Λ-fractional derivative. At first, the simply supported beam is transferred from the initial space (x,y) to the Λ-fractional space (X, Y(Χ)). Hence, in the Λ-fractional space variable X is defined by:

$$ X = I^{1 - \gamma } x = \frac{1}{{\Gamma \left( {1 - \gamma } \right)^{{}} }}\int\limits_{0}^{x} {\frac{sds}{{\left( {x - s} \right)^{\gamma } }}} = \frac{{x^{2 - \gamma } }}{{\Gamma \left( {3 - \gamma } \right)}} $$

(9.1)

_{And consequently:}

$$ x = [X \cdot \Gamma \left( {3 - \gamma } \right)]^{{\frac{1}{2 - \gamma }}} $$

(9.2)

_{Accordingly, for the axis Y(X)}

$$Y\left(x\right)={{}_{0}{\rm I}}_{x}^{1-\gamma }y\left(x\right)=\frac{1}{\Gamma (1-\gamma )}\underset{0}{\overset{x}{\int }}\frac{y(s)}{{(x-s)}^{\gamma }}ds$$

(9.3)

Using Eq. (9.2), the x variable may be substituted and the elastic line Y(X) in the Λ-fractional space is defined. Recalling that derivation in the Λ-fractional space is valid, contrary to the initial space, the derivative in the fractional Λ-space is defined by,

$$ Y^{\prime}\left( X \right) = \frac{dY\left( X \right)}{{dX}} = \frac{{\frac{dY\left( x \right)}{{d\left( x \right)}}}}{{\frac{{d\left( {X\left( x \right)} \right)}}{dx}}} = \frac{{Y^{\prime}\left( x \right)}}{X^{\prime}\left( x \right)} $$

(9.4)

It is reminded that the Λ-fractional derivative is local in the conjugated fractional Λ-space and corresponds to a differential. Hence differential geometry is generated using that derivative.

Let us consider a cantilever beam with stiffness EI, length l, loaded by a uniformly distributed loading q. Then the corresponding stiffness in the Λ-space EI^Λ is defined by, see Eq. (2.10),

$${EI}^{\Lambda }=\frac{1}{\Gamma (1-\gamma )}\underset{0}{\overset{x}{\int }}\frac{EI}{{(x-s)}^{\gamma }}ds=\frac{EI{x}^{1-\gamma }}{\Gamma (2-\gamma )}$$

(9.5)

The corresponding bending moment in the conjugate fractional Λ-space is further defined by,

$${\rm M}^{\Lambda }=-\frac{1}{\Gamma (1-\gamma )}\underset{0}{\overset{x}{\int }}\frac{0.5q{\left(l-s\right)}^{2}}{{(x-s)}^{\gamma }}ds=-q\frac{{x}^{1-\gamma }\left(3-\gamma \right)\left(2-\gamma \right){l}^{2}+2\left(-3+\gamma \right)lx+2{x}^{2}}{2\left(4-\gamma \right)}$$

(9.6)

Also, the beam elastic curve, in the Λ-space is described by the equation,

$$ EI^{\Lambda } \Upsilon^{\prime\prime}\left( {\rm X} \right) = - {\rm M}^{\Lambda } $$

(9.7)

Recalling Eq. (9.4), the curvature,

$$ Y^{\prime\prime}\left( X \right) = \frac{1}{X^{\prime}}\frac{d}{dx}\left( {\frac{{Y^{\prime}\left( x \right)}}{{X^{\prime}\left( x \right)}}} \right) = \frac{{Y^{\prime\prime}\left( x \right)X^{\prime}\left( x \right) - Y^{\prime}\left( x \right)X^{\prime\prime}\left( x \right)}}{{\left( {X^{\prime}\left( x \right)} \right)^{3} }} $$

(9.8)

the beam governing equation, Eq. (9.7), yields

$$ \frac{{EI(l - x)^{1 - \gamma } }}{{\Gamma \left( {2 - \gamma } \right)}} \frac{{Y^{\prime\prime}\left( x \right)X^{\prime}\left( x \right) - Y^{\prime}\left( x \right)X^{\prime\prime}\left( x \right)}}{{\left( {X^{\prime}\left( x \right)} \right)^{3} }} = q\frac{{\left( {l - x} \right)^{2 - \gamma } \left( {3 - \gamma } \right)\left( {2 - \gamma } \right)l^{2} + 2\left( { - 3 + \gamma } \right)lx + 2x^{2} }}{{\Gamma \left( {4 - \gamma } \right)}} $$

(9.9)

Since,

$$ X^{\prime}\left( x \right) = \frac{dX\left( x \right)}{{dx}} = \frac{{x^{1 - \gamma } }}{{\Gamma \left( {2 - \gamma } \right)}} $$

(9.10)

and

$$ X^{\prime\prime}\left( x \right) = \frac{{dX^{\prime}\left( x \right)}}{dx} = \frac{{x^{ - \gamma } }}{{\Gamma \left( {1 - \gamma } \right)}} $$

(9.11)

the governing equation for the elastic curve of the beam is given by,

$$ EIx^{ - 2 + 2\gamma } \Gamma \left( {2 - \gamma } \right)^{2} \left( { - \frac{{x^{ - \gamma } Y^{\prime}\left( x \right)}}{{\Gamma \left( {1 - \gamma } \right)}} + \frac{{x^{1 - \gamma } Y^{\prime\prime}\left( x \right)}}{{\Gamma \left( {2 - \gamma } \right)}}} \right) - q\frac{{x^{1 - \gamma } \left( {3 - \gamma } \right)\left( {2 - \gamma } \right)l^{2} + 2\left( { - 3 + \gamma } \right)lx + 2x^{2} }}{{2\left( {4 - \gamma } \right)}} = 0 $$

(9.12)

with the boundary conditions,

$$ Y\left( 0 \right) = Y\prime \left( 0 \right) = 0 $$

(9.13)

The solution Y(x) to the Eq. (9.12) with the b.cs (9.13) has been solved numerically with EI/q = 1 and for γ = 0.6 and γ = 0.8. The solution refers to the displacement in the Λ-space and the variable x expressed in the initial space. Therefore the elastic curve in the initial space may be transferred from the Λ-space to the initial one by the relation,

$$y\left(x\right)={}_{0}{}^{RL}{D}_{x}^{1-\gamma }\left({Y}^{l}(x)\right)$$

(9.14)

11.2 The right fractional Λ-space

A similar procedure may be followed considering the right fractional derivatives. The right Λ-fractional space is separate and does not have any connection with the left one.

_{Hence, in the right Λ-fractional space variable X is defined by:}

$$ X = I^{1 - \gamma } x = \frac{1}{{\Gamma \left( {1 - \gamma } \right)^{{}} }}\int\limits_{x}^{l} {\frac{sds}{{\left( {s - x} \right)^{\gamma } }}} = \frac{{(l - x)^{1 - \gamma } (l - l\gamma + x)}}{{\Gamma \left( {3 - \gamma } \right)}} $$

(9.15)

_{Besides, the Y(X) in the right fractional Λ-space it is expressed by,}

$$Y\left(x\right)={{}_{x}{\rm I}}_{l}^{1-\gamma }y\left(x\right)=\frac{1}{\Gamma (1-\gamma )}\underset{x}{\overset{l}{\int }}\frac{y(s)}{{(s-x)}^{\gamma }}ds$$

(9.16)

Further, any constant number θ assigned at any point x of the initial space is transferred to the right Λ-fractional space through the relation,

$$\Theta \left(x\right)={{}_{x}{\rm I}}_{l}^{1-\gamma }\theta =\frac{\theta }{\Gamma (1-\gamma )}\underset{x}{\overset{l}{\int }}\frac{1}{{(s-x)}^{\gamma }}ds$$

(9.17)

Further, the bending moment for the right fractional Λ-space is defined by,

$${\rm M}^{\Lambda }=-\frac{1}{\Gamma (1-\gamma )}\underset{x}{\overset{l}{\int }}\frac{0.5q{\left(l-s\right)}^{2}}{{(s-x)}^{\gamma }}ds=-q\frac{}{\Gamma (4-\gamma )}$$

(9.18)

Also, the beam elastic curve, in the right fractional Λ-space is given by,

$$ \frac{{EI(l - x)^{1 - \gamma } }}{{\Gamma \left( {2 - \gamma } \right)}} \frac{{Y^{\prime\prime}\left( x \right)X^{\prime}\left( x \right) - Y^{\prime}\left( x \right)X^{\prime\prime}\left( x \right)}}{{\left( {X^{\prime}\left( x \right)} \right)^{3} }} = q\frac{{(l - x)^{3 - \gamma } }}{{\Gamma \left( {4 - \gamma } \right)}} $$

(9.19)

with the boundary conditions,

$$ Y\left( 0 \right) = Y\prime \left( 0 \right) = 0 $$

(9.20)

Again the solution of Eqs. (9.19, 9.20) may be transferred to the initial space through the relation,

$$ y\left( x \right) = {}_{x}^{RL} D_{l}^{1 - \gamma } \left( {Y^{r} \left( x \right)} \right) $$

(9.21)

11.3 The interaction of the left and right fractional Λ-spaces

The final elastic curve is defined as the average of the left and right elastic curves, Eqs. [9.14, 9.21],

$$y\left(x\right)=1/2({}_{0}{}^{RL}{D}_{x}^{1-\gamma }\left({Y}^{l}(x)\right)+{}_{x}{}^{RL}{D}_{l}^{1-\gamma }\left({Y}^{r}(x)\right))$$

(9.22)

The solution Y^l(x) to the Eq. (9.12) with the b.cs (9.13) has been solved numerically with EI/q = 1 and for γ = 0.6 and γ = 0.8. The solution refers to the displacement in the left fractional Λ-space and the variable x expressed in the initial space. Therefore the elastic curve in the initial space may be transferred from the left fractional space Λ-space to the initial one by the relation, Eq. (9.14). Solving numerically the Eqs. (9.19, 9.20) with EI/q = 1 and l = 1, the elastic curve y(x) in the initial space has been found, applying also Eq. (9.22). The elastic curve y(x) in the right fractional space has been defined for γ = 0.6 and γ = 0.8. Finally, considering that the elastic curve is defined as the average of the left and right elastic curves, for the same fractional orders the elastic curves are shown in Fig. 21.

Fig. 21

The (dimensionless) final fractional elastic curve of the cantilever beam for fractional orders γ = 0.6 and 0.8 and 1, considering the average of the left and right curves

The present chapter may be served as a model for consideration of two side fractional derivatives. Similar procedures may be followed for discussing multidimensional problems into the context of non-local mechanics, working with two side fractional derivatives.

12 Conclusion-further research

The present work tries to initiate the Fractional Continuum Mechanics in a strictly mathematical basis, since the Continuum Mechanics area demands accurate mathematical formulation. The fractional deformation tensor, along with the fractional stress and strain tensors in the Λ-fractional space are defined. The fractional derivatives operate conventionally in the Λ-space, satisfying all the requirements demanded by Differential Topology. In fact the elastic problem is solved in the Λ-space. Stresses and displacements are defined there. The stresses along with the current placement geometry (shape) may be pulled back into the initial space. Strains as derivatives may not be transferred. The applications indicate the procedure that a fractional mechanics problem should follow, for having reliable and mathematically correct results in fractional analysis. Especially the fractional deformation of a bar exhibits the size-effect, well known from the strain gradient problems, classified also in the non-local problems. The theory was applied to the simplest case of the extension of a bar since the solution required mathematical and computing approaches that could be performed through the Mathematica computing pack. Also the extension of a fractional bar is discussed just to show that fractional calculus and fractal geometries are quite different branches, having no interconnection through homogeneization procedures. Of course they could interact as in the extension of the fractal bar is indicated. They could not be substituted. Further, a problem of bending of a fractional cantilever beam has been presented, formulating the conjugate Λ-space dependent upon fractional derivatives of both sides. All those examples may serve as models for further analysis in mechanics and physics problems. The proposed method may be considered as a basic theory for discussing fractional problems with horizon in the left and right fractional regions.

One might ask, is there any experimental evidence for the proposed non-local theory? The answer is given by Truedell in [33] on page 4 of Sect. 2 in the Non-linear theories of Continuum Mechanics. Truesdell states, of course physical theory must be based on experience, but experiment comes after, rather than before theory. Without theoretical concepts, one would neither know what experiments to perform nor be able to interpret their outcome.