1 Introduction

Misalignment and unbalance are common disturbance sources in rotating machines that promote anticipated faults in oil-film journal bearings. While the misalignment comes from the mechanical assembly of rotating shafts, like the coupling of a driver to a driven rotating system, the unbalance is always present after the machine turning or milling of a manufactured rotating part. Both defects can generate oscillations of the shaft inside the oil-film journal bearing resulting in variations of the pressure distribution and consequently in bearing reaction forces and moments. Recently magnetorheological (MR) fluids have been developed to be incorporated in journal bearings with the promise of controlling these rotor oscillations by changing stiffness and damping coefficients with an applied external magnetic field.

It is important to take in account the nonlinear phenomena caused by fluid-film dynamic instability. The occurrence of rotor lateral self-excited vibrations like whirl and whip arises from the nonlinear behavior of the fluid [1, 2], where the unstable operation or the high-level vibration of the system contributes to the potential damage of the rotating machinery. Castro et al. [3] studied these instabilities in rotor-bearing system considering a nonlinear force model. Jing et al. [4] considered the nonlinear model proposed by Capone to analyze the nonlinear dynamic behavior of bearings, taking into account the oil-whip phenomenon. Wang et al. [5] analyzed the bifurcation behavior of a flexible rotor supported by two fluid-film journal bearing. Irannejad and Ohadi [6] have expressed the pressure distribution with the effects of the squeeze film and obtained the hydrodynamic forces by the use of numerical integrations in axial and circumferential directions. Adiletta [7] observed the appearance of chaotic motions for rigid rotors supported by short journal bearings.

Considering the dynamic behavior promoted by the mechanical coupling misalignment Xu and Marangoni [8, 9] developed a complete model of a driver shaft coupled to a driven system using the method of component mode synthesis and compared the results with experimental ones. In another analysis of this problem, Al-Hussain [10] considered the angular misalignment of a flexible coupling to connect two rotor segments supported by hydrodynamic bearings. Sekhar and Prabhu [11] evaluated the force and moment due to standard parallel and angular misalignments at coupling locations using a higher order finite element model. The presence of a second order harmonic in the response was demonstrated in their work by performing a linear finite element analysis. Pennacchi et al. [12] studied the ratios between higher order harmonic components and synchronous vibrations. They observed that superharmonic components are the most remarkable nonlinear effects caused by coupling misalignment in rotors.

The nonlinearity of the complete rotor-bearing-coupling system arises from the oil film forces acting on the bearing. Although these nonlinear oil film forces act locally at the bearing positions on the rotor, their effects are global due to the general coupling of the system [13]. Aiming at analysing the nonlinear behavior of the complete rotor-bearing-coupling system a finite element (FE) model is proposed in this research. The radial and angular misalignments of a rigid coupling cause nonlinear vibrations to the rotor due to the reaction forces produced by the squeeze film bearings. In this work, the change in dynamic responses due to the use of magnetorheological squeeze films (MRSF) in the bearings is also analyzed, as presented by the authors in a previous work [14]. The modified Reynolds equations for a viscoplastic Bingham material are derived to determine the fluid-film pressure distribution as previously done by Wang et al. [15]. The magnetic pull force is calculated considering the behavior of MRSF as described by Tichy [16]. In this work the FE model of the shaft-line considers the Timoshenko beam theory and allows different sections for the shaft segments. Masses and inertias of a disk are added to the node where it is positioned. Centrifugal forces are calculated for the disk unbalanced mass considering the orientation with respect to the turning phase reference. Newmark’s implicit method is used in this work to numerically solve the equations of motion. Due to the nonlinear reaction forces from the MRSF in the bearings the common Newmark method could not guarantee the rotor dynamic equilibrium and a correction process was done by the Newton–Raphson method for each time step.

2 Finite element model of the rotor system

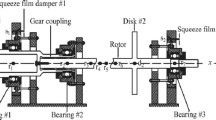
The complete rotor-bearing-coupling system is composed of two shaft segments connected by the rigid coupling and supported by squeeze film journal bearings. The one-dimensional finite element formulation is considered for the shafts allowing different properties to be chosen in the case of a stepped rotor modeling. The beam finite element having only flexural deformations are formulated and implemented to obtain the stiffness, mass and gyroscopic matrices. The Timoshenko beam theory is considered by taking into account the shear deformation and rotary inertia effects. In this work, analysis of axial and torsional deformations are not considered.

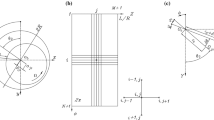
As depicted in Fig. 1, elevation and plan views are represented by the orthogonal planes y-z and x-z, respectively, with z-axis being the spinning axis. Each finite element node along the shaft has four degrees of freedom (DOFs), being two of them the transverse displacements u, v, along the x- and y-axes, respectively, and more two angular displacements \(\frac{\partial {v}}{\partial {z}}\), \(\frac{\partial {u}}{\partial {z}}\), about the x- and y-axes, respectively.

The displacement vector \({\mathbf {q}}^e\) for each element is

$$\begin{aligned} \mathbf {q}^e = \left[ u_{1},\frac{\partial {u_{1}}}{\partial {z}}, v_{1},\frac{\partial {v_{1}}}{\partial {z}},u_{2},\frac{\partial {u_{2}}}{\partial {z}},v_{2}, \frac{\partial {v_{2}}}{\partial {z}} \right] ^T \end{aligned}$$
(1)

where the superscript e stands for the element number.

Fig. 1
figure 1

One-dimensional finite element description with local coordinate planes x-z and y-z

Full size image

The assumption of small shaft bending in rotordynamics problems brings linearized equations of motion for the beam finite element applied to the rotating shaft. For the constant rotational speed \(\dot{{\varphi }}\), these equations of motion are

$$\begin{aligned} \mathbf {M}^e \, \ddot{\mathbf {q}}^e + ( \dot{{{\varphi }}} \, \mathbf {G}^e + \mathbf {C}^e ) \dot{\mathbf {q}}^e + \mathbf {K}^e \mathbf {q}^e = \mathbf {Q}^e + \mathbf {W}^e\, \end{aligned}$$
(2)

where \({\mathbf {q}}^e\) and \({\mathbf {Q}}^e\) are 8x1 vectors and \({\mathbf {M}}^e\), \(\dot{{\varphi }} \, {\mathbf {G}}^e\), \({\mathbf {C}}^e\) and \({\mathbf {K}}^e\) are 8x8 matrices.

The expression (2) is derived from energy principles as documented in previous publications [17, 18] and not repeated here. The matrices and vectors are typical for one-dimensional elements: \({\mathbf {M}}^e\) is a positive definite symmetric matrix derived from the kinetic energy representing the mass/inertia; \(\dot{{\varphi }} \, {\mathbf {G}}^e\) is a real skew-symmetric matrix derived from the rotational kinetic energy representing the conservative gyroscopic effect; \({\mathbf {K}}^e\) is a positive semi-definite symmetric matrix derived from the strain energy representing the elastic stiffness; \({\mathbf {C}}^e\) is proportional to the stiffness matrix representing the damping; \({\mathbf {Q}}^e\) is a force vector, which includes all the excitation forces acting on the shaft element; \({\mathbf {W}}^e\) is the element static weight.

For calculating the static weight, gravity acceleration values are considered for the translational shaft element DOFs in the form

$$\begin{aligned} \mathbf {W}^e = \mathbf {M}^e \, \left[ g_x, \, 0,\, g_y,\, 0,\, g_x,\, 0,\, g_y,\, 0 \right] ^T \end{aligned}$$
(3)

The system equations of motion are obtained by assembling the equations from the shaft elements together with the ones from other essential components. The rotor disc is modeled as a simple lumped mass element with properties of mass and polar moments of inertia. The coupling that connects two shaft segments has also the properties of mass and polar moments of inertia, but it is considered a special element due to the additional properties required, such as misalignment of the angular and radial coupling, which will be better described later in the Sect. 4. The lumped masses calculated from the disc or coupling properties are added directly to the degrees of freedom of the corresponding model nodes. In this work, the bearing is defined as an interconnection component between a shaft element node and the ground. It does not introduce additional DOFs to the model, but promote the rotor system support with forces which are nonlinear in nature. Besides the bearing nonlinear forces, the global mathematical model have also forces coming from the mechanical coupling misalignment, mass unbalance and static weight of the rotor.

The assembled equations of motion for the rotor-bearing-coupling system is represented by

$$\begin{aligned} \mathbf {M} \, \ddot{\mathbf {q}} + ( \dot{{\varphi }} \, \mathbf {G} + \mathbf {C} ) \dot{\mathbf {q}} + \mathbf {K} \, \mathbf {q} = \mathbf {F}_{b} + \mathbf {F}_{coupl} + \mathbf {F}_{unb} + \mathbf {W} \, \end{aligned}$$
(4)

where all the global matrices are real and assembled from the associated components. The global displacement vector is denoted by \(\mathbf {q}\) in expression (4), \(\dot{{\varphi }}\) represents the rotational speed of the rotor, and \({\mathbf {F}}_{b}\), \({\mathbf {F}}_{coupl}\), \({\mathbf {F}}_{unb}\) and \(\mathbf {W}\) are, respectively, the vectors of the nonlinear forces of the oil film, excitation forces due to misalignments of the rigid coupling, unbalance forces and rotor weight.

3 Nonlinear forces of hydrodynamic bearing

The fluid pressure of the squeeze film bearing prevents contact between the rotating journal and the bearing surface. A short journal-bearing scheme is considered and the calculation of the distributed pressure in the cylindrical journal is performed by solving the simplified Reynolds equation. It is necessary to consider the imposed variational inequalities for nonlinear problems like elastic contact, fluid lubrication, etc. For fluid lubrication of the journal bearing the solution must satisfy certain restricted requirements in the solution domain, i.e. if negative values are calculated for the fluid film pressure, representing the cavitation, a restriction of null values may be applied.

The integration of the pressure distribution along the circumferential coordinate and the width is a procedure used to obtain the equivalent reaction forces of the bearing in the x and y directions. These forces depend on the radial displacements and velocities of the journal inside the bearing, what demands an iterative process to determine the dynamic equilibrium of the moving parts. The accuracy of nonlinear oil-film forces and their derivatives affects not only the convergence of the numerical solutions, but also the analysis of stability and bifurcation.

Fig. 2
figure 2

Bingham fluid biviscosity model adapted from [15]

Full size image

Wada et al. [19] used mathematical models and experiments to state that an electrorheological (ER) fluid can be described by the Bingham material model since it presents a viscoplastic characteristic represented by two parameters: yield shear stress and viscosity. The yield shear stress \(\tau _0\) is proportional to the square of the applied electric field. When the magnitude of the deviatoric stress tensor is below this shear stress, the material behaves as rigid. On the other hand, above the yield shear stress, the ER behaves like a quasi-Newtonian fluid.

Provided that this work deals with magnetorheological fluid (MR), it is important to give some attention regarding the differences and similarities between ER and MR fluids. MR fluids often exhibit field-induced shear stress with two times magnitude compared with the ER fluid [20]. Additionally, it is stated that conductivity and electric breakdown can be neglected in MR fluids, whilst in ER such effects are of great relevance. However, Ginder et al. discussed that when the magnetic field is in the linear or low-field regime, the calculation of fields and forces in MR fluids is analogous to that for ER fluids.

Given that context, this work proceeds with the modification of Reynolds equation in the velocity profile and pressure distribution by treating the MR as a Bingham viscoplastic fluid in the same sense as done by Zapomel and Ferfecki [21]. This analysis is also detailed for a rigid rotor by Wang et al. [22], where the mathematical model considers the short bearing approach with embedded MR fluid and different configurations for electric currents induced in the bearings. In another research Wang et al. [15] presented the whole Reynolds equation deduction and the particularization to the viscoplastic Bingham material. The expressions for the pressure distribution were deduced concerning the short bearing approach to construct the finite element model of a rotating system supported by a single MR squeeze film journal bearing.

According to literature [15, 16], the MR fluid viscosity is considered as depicted in Fig. 2. Thus, the dynamic viscosity of the MR fluid is written as

$$\begin{aligned} \mu&= \mu _{p} \, , \qquad \text{if } \ \ \dot{\gamma } \le \frac{\tau _{0}}{\mu - \mu _{p}} \\ \mu&= \mu _{f} + \frac{\tau _{0}}{\dot{\gamma }}, \qquad \text{if } \ \ \dot{\gamma } > \frac{\tau _{0}}{\mu - \mu _{p}} \, \end{aligned}$$
(5)

where \(\mu _{p}\) is the plastic viscosity and \(\mu _{f}\) is the Newtonian viscosity.

The yield shear stress \(\tau _{0}\) is nearly proportional to the square of the applied electric field H in the journal. For a thin gap, H is the applied voltage difference between the two surfaces of rotor and bearing divided by the gap [16]. An estimation is given by \(\tau _{0} = A \, H^2\), where A is the electrorheological fluid property, with values in the range of \(10^{-10}\) to \(10^{-9}\) \(N/V^2\).

It is remarked by Wang et al. [15] that \(\mu _{p} \gg \mu _{f}\). During the simulations performed by Bompos and Nikolakopoulos [23], \(\mu _{p} = 100 \, \mu _{f}\) has been adopted. The authors of the present work could not find any reference regarding a lower limit between the \(\mu _{p}\) and \(\mu _{f}\) relation. That said, in order to avoid convergence issues for the simulations in this work it has instead adopted \(\mu _{p} = 20 \, \mu _{f}\) since this proportion still covers the relation proposed by Wang et al. [15]. H is approximated by \(H = I N / 2 h\), where I is the electric current, N is the number of coil turns and h is the film thickness.

Fig. 3
figure 3

Cross-sectional view of the journal bearing and the auxiliary coordinate system X-Y

Full size image

The Reynolds equation for journal bearings can be expressed as

$$\begin{aligned} \left( \frac{R}{L} \right) ^2 \frac{\partial {}}{\partial {z}} \left( h^3 \frac{\partial {p}}{\partial {z}} \right) = \frac{\partial {h}}{\partial {\varphi }} + 2 \frac{\partial {h}}{\partial {\tau }} \end{aligned}$$
(6)

where p is the fluid film pressure, \(\varphi\) is the circumferential angle, z is the axial coordinate of calculation, \(\tau = \dot{\varphi } \, t\) is the dimensionless time.

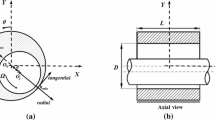
The necessary bearing parameters are the radial clearance c, bearing length L, bearing radius R and fluid film dynamic viscosity as presented in expression (5). As depicted in Fig. 3, the auxiliary coordinate system X-Y is positioned with the Y axis in the same direction where the maximum and minimum fluid film thickness are measured. The journal movement inside the bearing produces different trajectories depending on the dynamics of the rotating shaft. Any orbit described by the journal center are inside the whirl circle. The rotation of the auxiliary coordinate system relative to x-y is measured by the angle \(\theta\). The position of the journal inside the bearing is described by the eccentricity \(e_b\) and the angle \(\theta\).

Solving the Reynolds equation for the MR squeeze film journal bearing the fluid film pressure p is written as

$$\begin{aligned} p (\theta ,z)&= - \frac{6 \, \mu \, \dot{\varphi } \, e_b \sin {\theta }}{c^2 \left( 1 + e_b \cos {\theta } \right) ^3} \left( z^2 - \frac{L^2}{4} \right) ,\\ \text{if } \ \ \dot{\gamma } &\le \frac{\tau _{0}}{\mu - \mu _{p}} \, \\ p (\theta ,z)&= - \frac{6 \, \dot{\varphi } \, e_b \sin {\theta } [ \dot{\gamma } \, \mu _f + \tau _{0}(H) ]}{c^2 \left( 1 + e_b \cos {\theta } \right) ^3} \left( z^2 - \frac{L^2}{4} \right) , \\ \text{if } \ \ \dot{\gamma } &> \frac{\tau _{0}}{\mu - \mu _{p}} \end{aligned}$$
(7)

In this work the pressure distribution is expressed as presented by Wang et al. [15] by adopting the Gumbel boundary conditions, but neglecting the cavitations effects. Based on Irannejad’s conclusions [6], the atmospheric pressure can be considered as the minimum value for the pressure distribution of squeeze oil films. Then the dynamic pressure presented in expression (7) is considered in the form

$$\begin{aligned} \begin{array}{ll}p= p_{atm} , &\quad \text{if } \ \ 0 \le \theta< \pi \\ p= p (\theta ,z) , &\quad \text{if } \ \ \pi \le \theta < 2 \pi \end{array}\end{aligned}$$
(8)

The hydrodynamic forces in radial and tangential directions are

$$\begin{aligned} F_r&= \left| R \int ^{L/2}_{-L/2} \int ^{2 \pi }_{\pi } p (\theta ,z) \cos {\theta } \, d \theta \, dz \right| \, \\ F_t&= \left| R \int ^{L/2}_{-L/2} \int ^{2 \pi }_{\pi } p (\theta ,z) \sin {\theta } \, d \theta \, dz \right| \end{aligned}$$
(9)

In addition, the magnetic pull force appears due to eccentricity between the two magnetic poles: the rotating shaft and the bearing [16]. The magnetic pull force direction aligns with the radial hydrodynamic forces. Then, the expression of the magnetic pull force is written as

$$\begin{aligned} F_m = \mu _f \, U^2_m \frac{\pi R \,L \,e_b}{\sqrt{(c^2 - e^2_b )^3}} \end{aligned}$$
(10)

where \(U_m\) the magnetic motion force.

Neglecting the magnetic field outer the journal bearing, the magnetic motion force can be calculated by \(U_m = I N\). Besides, the eccentricity \(e_b\) is a function of the relative positions (horizontal and vertical) between the shaft and the bearing, which can be determined by \(e_b = \sqrt{x^2+y^2}\).

Thereby, the radial effective force can be calculated by subtracting the hydrodynamic radial force and the magnetic pull force

$$\begin{aligned} F_{r_{eff}} = F_r - F_m \end{aligned}$$
(11)

Calculating the forces \(F_x\) and \(F_y\) from the radial effective force and the tangential hydrodynamic forces in accordance with the coordinate system depicted in Fig. 3, it follows

$$\begin{aligned} F_x&= - F_{r_{eff}} \cos {\psi } - F_t \sin {\psi } \, \\ F_y&= - F_{r_{eff}} \sin {\psi } + F_t \cos {\psi } \end{aligned}$$
(12)

where, \(\psi = \arctan { ( y / x )}\).

The Jacobians of hydrodynamic forces \(F_x(x, y, \dot{x}, \dot{y})\) and \(F_y(x, y, \dot{x}, \dot{y})\) with respect to the journal displacements x, y and velocities \(\dot{x}, \dot{y}\) are calculated firstly, and the computational cost spent on the Jacobians is much less than those spent on the oil film forces themselves.

4 Modeling of rigid coupling misalignment

The term angular misalignment is easily understood in the literature, although the term offset is not always clear and correct as used [12]. Related to the misalignment concept, offset does not represent the distance between two parallel shafts not coaxial, which could be understood as fixed in the space. The offset occurs when there is a wrong static alignment between the two rotors to be coupled, many times due to the flanges that are wrongly machined and have wrong distributed bolt holes. In this case, when both flanges are mounted a radial rotating misalignment is imposed. As a consequence, it is necessary to take into account the effect of rigid coupling misalignment on the static centerline and consider that the reaction forces of the bearing are changing owing to the rotation of the shaft, or in other words, to the orientation of the misalignment with respect to the phase reference.

Fig. 4
figure 4

a Draft with angular and radial measurements of the flange faces considering the same plane of reference. b Correspondent wrong mounting for the coupling

Full size image

In the finite element model of the connected shafts, the mounted coupling flanges are represented in the connection node between both shaft segments. Looking for imperfections in this coupling one possible representation of an imperfect machining causing angular and radial misalignments is drafted schematically in Fig. 4a and a wrong mounting of the coupling flanges in Fig. 4b. The draft views are too much simplified and cannot give the idea of all possibilities for the imperfect machining or the wrong mounting of the flanges. The machining of one flange of the coupling is not necessarily executed together with the other one. Then it is possible to have bolt holes machined in any axial angle when comparing one flange to the other. Therefore, not only the magnitudes of the misalignments \(\Delta r\) and \(\Delta \alpha\) have to be considered, but also the angles \(\phi _r\) and \(\phi _\alpha\), where the radial and angular magnitudes occur relative to an angular reference. Then radial and angular misalignments are conveniently formulated to impose the generalized displacements \(\Delta {\mathbf {q}}_{\, coupl}\), which are function of the angular position \(\theta = \dot{\varphi } t\) of the shaft as follows

$$\begin{aligned} \Delta {\mathbf {q}}_{\, coupl} (\theta ) = \Delta {\mathbf {q}}_{\, coupl} (\dot{\varphi } t) = \left[ \begin{array}{ccc} 1 &{} 0 \\ 0 &{} i \\ i &{} 0 \\ 0 &{} 1 \end{array} \right] \, \left\{ \begin{array}{ccc} \Delta r \, e^{i \phi _r} \\ \Delta \alpha \, e^{i \phi _\alpha } \end{array} \right\} \, e^{i \varphi t} \end{aligned}$$
(13)

The imposed generalized displacements cause static reaction forces \(\mathbf {R} (\theta )\) on the bearings that can be calculated by the static equilibrium of the free-body composed by shaft segments and coupling as

$$\begin{aligned} \mathbf {R} (\theta ) = \mathbf {K} \left[ \mathbf {q} + \Delta {\mathbf {q}}_{\, coupl}(\theta ) \right] + \mathbf {W} = \mathbf {K} \mathbf {q} + {\mathbf {F}}_{coupl}(\theta ) + \mathbf {W} \end{aligned}$$
(14)

where \({\mathbf {F}}_{coupl}(\theta )\) is the equivalent force vector due to the coupling misalignment.

The static reactions are then calculated considering the partitioning of the stiffness matrix [24] and re-ordering the degrees of freedom of the nodes and grouping the free and the constrained ones as

$$\begin{aligned} \left\{ \begin{array}{ccc} \mathbf {0} \\ \mathbf {R} (\theta ) \end{array} \right\} = \left[ \begin{array}{ccc} \mathbf {K}_{ff} &{} \mathbf {K}_{fc} \\ \mathbf {K}_{cf} &{} \mathbf {K}_{cc} \end{array} \right] \, \left\{ \begin{array}{ccc} \mathbf {q}_f \\ \mathbf {q}_c \end{array} \right\} + \left\{ \begin{array}{ccc} \mathbf {F}_{coupl}(\theta )_f \\ \mathbf {0} \end{array} \right\} + \left\{ \begin{array}{ccc} \mathbf {W}_f \\ \mathbf {W}_c \end{array} \right\} \end{aligned}$$
(15)

where \({\mathbf {F}}_{coupl}(\theta )_c = \mathbf {0}\), because the coupling is not in the same position of bearings.

Firstly, considering the expression (15), the static free displacements of the rotor shall be solved as function of its angular position \(\theta\). Then the reaction forces actuating on the rotor at the bearing positions are calculated. Due to the presence of the coupling misalignment, these bearing reactions have generally both x and y components which are 1x periodical.

5 Dynamical behavior of the rotor-bearing-coupling system

The nonlinear equations of motion of the rotor-bearing-coupling system at the operating speed are rewritten as

$$\begin{aligned} \mathbf {M} \, \ddot{\mathbf {q}} + ( \dot{{\varphi }} \mathbf {G} + \mathbf {C} ) \dot{\mathbf {q}} + \mathbf {K} \mathbf {q} - {\mathbf {F}}_b (\mathbf {q}, \dot{\mathbf {q}}) = {\mathbf {F}}_{coupl} + {\mathbf {F}}_{unb} + \mathbf {W} \, \end{aligned}$$
(16)

where, in the right side of expression (16), the sum of forces is also considered as \({\mathbf {F}}_{ext}\).

The response of the state variables for any time t considers the equilibrium of all forces actuating on the nonlinear dynamic system. Typically, responses of the highest vibration modes of the numerical model are physically meaningless, insignificantly small, but potentially lightly damped. However, the shortest natural period governs the stability of numerical integration methods. The explicit numerical integration methods can artificially add numerical damping to suppress instabilities with the higher vibration mode responses while the implicit numerical methods can be unconditionally stable [25].

The Newmark method is used in this work for solving the nonlinear equations numerically. This implicit method is quite popular for the numerical integration of linear equations of motion in structural dynamics [24]. However the nonlinear behavior of the system brings some known difficulties for implicit methods. Note that since differentiation amplifies high frequencies of the dynamic model, changes in the displacements \(\mathbf {q}\) and velocities \(\dot{\mathbf {q}}\) from time \(t_{i}\) to time \(t_{i+1}\) will be much smoother than the corresponding changes in the accelerations \(\ddot{\mathbf {q}}\). Therefore, it is not sufficient to consider the equilibrium for each time step of calculation, but the differential equilibrium of the system considering the time step \(\Delta t\), in the form

$$\begin{aligned} \mathbf {M} \, \Delta \ddot{\mathbf {q}}^{i} + ( \dot{{\varphi }} \, \mathbf {G} + \mathbf {C} ) \Delta \dot{\mathbf {q}}^{i} + \mathbf {K} \Delta \mathbf {q}^{i} - \Delta \mathbf {f}^{i}_{\, nl} = \Delta \mathbf {F}^{i}_{ext} \, \end{aligned}$$
(17)

where the finite difference relationships are

$$\begin{aligned} \Delta \mathbf {f}^{i}_{\, nl}&= \mathbf {F}_b (\mathbf {q}^{i+1}, \dot{\mathbf {q}}^{i+1}) - \mathbf {F}_b (\mathbf {q}^{i}, \dot{\mathbf {q}}^{i}) = \mathbf {F}_b (\mathbf {q}^{i} + \Delta \mathbf {q}^{i}, \dot{\mathbf {q}}^{i} + \Delta \dot{\mathbf {q}}^{i}) - \mathbf {F}_b (\mathbf {q}^{i}, \dot{\mathbf {q}}^{i}) \\ \Delta \ddot{\mathbf {q}}^{i}&= \ddot{\mathbf {q}}^{i+1} - \ddot{\mathbf {q}}^{i} \\ \Delta \dot{\mathbf {q}}^{i}&= \dot{\mathbf {q}}^{i+1} - \dot{\mathbf {q}}^{i} \\ \Delta \mathbf {q}^{i}&= \mathbf {q}^{i+1} - \mathbf {q}^{i} \end{aligned}$$
(18)

The incremental acceleration and velocity are evaluated as

$$\begin{aligned} \Delta \ddot{\mathbf {q}}^{i}&= \frac{1}{\beta \, \Delta t^2} \Delta \mathbf {q}^{i} - \frac{1}{\beta \, \Delta t} \dot{\mathbf {q}}^{i} - \frac{1}{2 \, \beta } \ddot{\mathbf {q}}^{i} \\ \Delta \dot{\mathbf {q}}^{i}&= \frac{\Gamma }{\beta \, \Delta t} \Delta \mathbf {q}^{i} - \frac{\Gamma }{\beta } \dot{\mathbf {q}}^{i} + \Delta t \left( 1 - \frac{\Gamma }{2 \, \beta } \right) \ddot{\mathbf {q}}^{i} \end{aligned}$$
(19)

The Newmark parameters \(\beta = 1/4\) and \(\Gamma = 1/2\) were considered because of the numerical stability [26]. The substitution of expression (19) into expression (17), then re-grouping terms and solving for the increment in displacements, it follows

$$\begin{aligned}&\left[ \frac{1}{\beta \, \Delta t^2} \mathbf {M} + \frac{\Gamma }{\beta \, \Delta t} ( \dot{{\varphi }} \, \mathbf {G} + \mathbf {C} ) \right] \Delta \mathbf {q}^{i} = \left[ \frac{1}{\beta \, \Delta t} \mathbf {M} + \frac{\Gamma }{\beta } ( \dot{{\varphi }} \, \mathbf {G} + \mathbf {C} ) \right] \dot{\mathbf {q}}^{i} \\&+ \left[ \frac{1}{2 \, \beta } \mathbf {M} - \Delta t \left( 1 - \frac{\Gamma }{2 \, \beta } \right) ( \dot{{\varphi }} \, \mathbf {G} + \mathbf {C} ) \right] \ddot{\mathbf {q}}^{i} + \Delta \mathbf {f}^{i}_{\, nl} + \Delta \mathbf {F}^{i}_{ext} \, \end{aligned}$$
(20)

The incremental displacement \(\Delta \mathbf {q}^{i}\) is then obtained as follows

$$\begin{aligned} \Delta \mathbf {q}^{i} = \hat{\mathbf {K}}^{-1} \left( \hat{\mathbf {C}} \dot{\mathbf {q}}^{i} + \hat{\mathbf {M}} \ddot{\mathbf {q}}^{i} + \Delta \mathbf {f}^{i}_{nl} + \Delta \mathbf {F}^{i}_{ext} \right) = \hat{\mathbf {K}}^{-1} \mathbf {f}^{i} \end{aligned}$$
(21)

where,

$$\begin{aligned} {\hat{\mathbf {K}}}&= \left[ \frac{1}{\beta \,\Delta t^2} \mathbf {M} + \frac{\Gamma }{\beta \,\Delta t} ( \dot{{\varphi }} \,\mathbf {G} + \mathbf {C} ) + \mathbf {K} \right] \\ {\hat{\mathbf {C}}}&= \left[ \frac{1}{\beta \,\Delta t} \mathbf {M} + \frac{\Gamma }{\beta } ( \dot{{\varphi }} \,\mathbf {G} + \mathbf {C} ) \right] \\ {\hat{\mathbf {M}}}&= \left[ \frac{1}{2 \,\beta } \mathbf {M} - \Delta t \left( 1 - \frac{\Gamma }{2 \,\beta } \right) ( \dot{{\varphi }} \,\mathbf {G} + \mathbf {C} ) \right] \end{aligned}$$
(22)

The dynamic system described in expression (17) has a local nonlinearity due to the not negligible nonlinear bearing force increment \(\Delta \mathbf {f}^{i}_{\, nl}\). This fact is observed by the dependence of \(\mathbf {f}^{i}\) on the incremental displacement \(\Delta \mathbf {q}^{i}\) and the incremental velocity \(\Delta \dot{\mathbf {q}}^{i}\), as described in the expressions (18). The common Newmark method cannot obtain the response of the system at time \(t_{i+1}\) directly, but is possible to improve it. The prediction value for the next step can be taken as the initial value and then a correcting process is done by the NewtonRaphson method. Here, the Newton–Raphson algorithm is an efficient method to solve the expression (21), calculating the incremental displacement. The iterative algorithm proceeds as follows:

Step 1 The initial value for \(\Delta \mathbf {q}^{i}\) is denoted \(\Delta \mathbf {q}^{i}_{\ 0}\) and is arbitrarily set to zero. The corresponding value for \(\mathbf {f}^{i}\) is

$$\begin{aligned} {\hat{\mathbf {f}}}^{i} \left( \Delta \mathbf {q}^{i}_{\ 0} \right) = \Delta \mathbf {F}^{i}_{ext} + \hat{\mathbf {C}} \dot{\mathbf {q}}^{i} + \hat{\mathbf {M}} \ddot{\mathbf {q}}^{i} \, \end{aligned}$$
(23)

Step 2 The Newton–Raphson recurrence relation is simply

$$\begin{aligned} \Delta \mathbf {q}^{i}_{\, n+1} = {\hat{\mathbf {K}}}^{-1} \hat{\mathbf {f}}^{i} \left( \Delta \mathbf {q}^{i}_{\, n} \right) \, \end{aligned}$$
(24)

where,

$$\begin{aligned} {\hat{\mathbf {f}}}^{i} \left( \Delta \mathbf {q}^{i}_{\, n} \right) = {\hat{\mathbf {f}}}^{i} \left( \Delta \mathbf {q}^{i}_{\, 0} \right) + \mathbf {F}_b \left( \mathbf {q}^{i} + \Delta \mathbf {q}^{i}_{\, n}, \dot{\mathbf {q}}^{i} + \Delta \dot{\mathbf {q}}^{i}_{\, n} \right) - \mathbf {F}_b \left( \mathbf {q}^{i}, \dot{\mathbf {q}}^{i} \right) \, \end{aligned}$$
(25)

and

$$\begin{aligned} \Delta \dot{\mathbf {q}}^{i}_{\, n} = \frac{\Gamma }{\beta \, \Delta t} \Delta \mathbf {q}^{i}_{\, n} - \frac{\Gamma }{\beta } \dot{\mathbf {q}}^{i} + \Delta t \left( 1 - \frac{\Gamma }{2 \, \beta } \right) \ddot{\mathbf {q}}^{i} \, \end{aligned}$$
(26)

Step 3 Expression (24) is iterated upon until \(\left\| \Delta \mathbf {q}^{i}_{\, n+1} - \Delta \mathbf {q}^{i}_{\, n} \right\| < \epsilon\), with \(\epsilon\) representing the tolerance for the convergence. In this work, \(\epsilon\) was selected as \(1 \times 10^{-6} m\), which is very low in comparison with the bearing dimensions or clearance. The convergence of this form of the Newton-Raphson method depends on the local smoothness of \(\mathbf {F}_b \left( \mathbf {q}^{i}, \dot{\mathbf {q}}^{i} \right)\). Convergence can be improved, for a particular time step, by making \(\Delta t\) smaller.

After obtaining the solution for \(\Delta \mathbf {q}^{i}\), the displacements and velocities are updated with

$$\begin{aligned} \begin{array}{lll} \mathbf {q}^{i+1} = \mathbf {q}^{i} + \Delta \mathbf {q}^{i} \,\\ {\dot{\mathbf {q}}}^{i+1} = \left( 1 - \frac{\Gamma }{\beta } \right) \dot{\mathbf {q}}^{i} + \Delta t \left( 1 - \frac{\Gamma }{2 \, \beta } \right) + \frac{\Gamma }{\beta \, \Delta t} \Delta \mathbf {q}^{i} \, \end{array} \end{aligned}$$
(27)

The accelerations are updated with the expression (16) as

$$\begin{aligned} {\ddot{\mathbf {q}}}^{i+1} = \mathbf {M}^{-1} \, \left[ \mathbf {F}_{b} \left( \mathbf {q}^{i+1}, \dot{\mathbf {q}}^{i+1} \right) + \mathbf {F}^{i+1}_{ext} - ( \dot{{\varphi }} \,\mathbf {G} + \mathbf {C} ) \dot{\mathbf {q}}^{i+1} - \mathbf {K} \mathbf {q}^{i+1} \right] \, \end{aligned}$$
(28)

In this work the rotor has proper boundary conditions and the rigid body motions are disabled. Then the finite element model of the constrained structural rotor system has positive definite matrices for stiffness and mass [24]. Also, it is important to note that \(\mathbf {K}\) does not depend on \(\Delta \mathbf {q}^{i}\). The matrices \(\mathbf {K}\) and \(\mathbf {M}\) may be inverted or factorized only once at the beginning of the simulation. The equilibrium of the nonlinear system is obtained by iteration with the NewtonRaphson method where the prediction value of the next step is taken as the initial values, and then the correcting process is implemented.

6 Numerical results

In this work, two simulations are performed using the numerical methods described in Sect. 5. In the first one the radial and angular misalignments of a rigid coupling promote nonlinear responses using common squeeze film journal bearings to emphasize the efficacy of the numerical method. In the second analysis the MR fluid properties are considered and differences in nonlinear responses for an unbalance mass are noticed when considering or not the electromagnetic induction in the journal bearings. In order to promote the best performance to the simulations the rotors are modified geometrically from one case to the other. However, the two rotors are composed by flexible shafts, for which the density of mass is \(7800 \, \mathrm{{kg/m}}^3\), the Youngs elastic modulus is \(206.7\, \mathrm{{GPa}}\), the Poisson ratio is 0.3 and the proportional damping to stiffness value is \(25 \times 10^{-5}\).

Table 1 Rotor dimensions and parameters for misalignment analysis
Full size table
Fig. 5
figure 5

Two segments of rotors connected by rigid coupling

Full size image

6.1 Radial and angular misalignment

The rotor configuration proposed to the first analysis is showed in Fig. 5, where two segments with the same length are connected by a rigid coupling. The shaft and bearing dimensions and parameters are presented in Table 1. All the four cylindrical bearings have the same dimensions.

Different amounts of radial and angular misalignment for the rigid coupling have been proposed. One simulation of the dynamic response of the rotor-bearing-coupling system is performed at the rotating speed of \(100 \, rad/s\). Figure 6a, b depict the stationary orbits of the journal near the first bearing, considering the radial and angular misalignments, respectively. It is important to highlight that there is no imbalance present in this first simulation case. In both figures the stationary orbits start as periodic and reach the double period behavior. Moreover, even for a small amount of misalignment, it is possible to preview the existence of higher order harmonics, either by the deformations of the orbit or by the vertical displacement variations. Experiments showing these harmonics have been presented by Xu and Marangoni [9]. It is possible to observe the influence of gravity by the small vertical displacement and the elongated shape of the orbits when the low misalignment intensity is applied. In opposite, for higher misalignment intensity the vertical displacement of the orbit increases in comparison to the horizontal one changing drastically the orbit geometric form.

Fig. 6
figure 6

a Radial and b angular misalignment in bearing 1 for \(\dot{\varphi } = 100 \, \mathrm{{rad/s}}\)

Full size image
Fig. 7
figure 7

Bifurcation diagram for radial misalignment considering \(\dot{\varphi } = 500 \, \mathrm{{rad/s}}\)

Full size image

To extend the demonstration of the nonlinear behavior the bifurcation analysis was performed as showed in Fig. 7. The bifurcation diagram was obtained with the variation of the radial misalignment intensity from \(\Delta r = 0.1 \, \mu m\) to \(\Delta r = 12 \, \mu m\), considering the rotating speed of \(500 \, rad/s\). In this figure, the maximum positive horizontal displacements for the stationary orbits were taken, considering the shaft position near the first bearing. The periodic orbit behavior occurs for low intensity values of radial misalignment. A bifurcation appears with \(\Delta r = 3.8 \, \mu m\), approximately. Above this intensity value the period-doubling bifurcation is observed. The quasi-periodic regime of the journal is denoted for the intensity range between \(\Delta r = 9.7 \, \mu m\) and \(\Delta r = 12.0 \, \mu m\). By increasing this intensity above \(\Delta r \ge 12.0 \, \mu m\), the quasi-periodic regime turns to a periodic behavior again.

6.2 Unbalance mass

In this second analysis the two segments of the rotor are uncoupled and only the left segment is considered. The dimensions were changed too. The two bearings are specified as MR squeeze film journal bearings. The shaft is discretized with five elements instead of three in the former analysis and supports a rigid disk at the right end, as depicted in Fig. 8. The dimensions and parameters are presented in Table 2.

Fig. 8
figure 8

One segment of rotor with a rigid disk

Full size image
Table 2 Rotor dimensions and parameters for analysis with MR bearings
Full size table
Fig. 9
figure 9

Waterfall diagram with no current applied Nonlinear effects

Full size image

The waterfall diagram in Fig. 9 has been determined for the Bearing 2. Over the \(1.0 \times\) line there is a peak at \(1600 \, \mathrm{{rpm}}\) or \(27 \, \mathrm{{Hz}}\), corresponding to the critical speed of the system. However, the \(0.5 \times\) line presents higher displacements above \(3600 \, \mathrm{{rpm}}\) with values at least 3 times the ones observed in the critical speed.

Fig. 10
figure 10

Run-up frequency response with no current applied Nonlinear effects

Full size image

For a better understanding of the dynamic behavior of the rotor it has been done a run-up simulation, when the angular speed is increased systematically. Figure 10 shows the vertical displacement in Bearing 2 as a function of the rotation speed. The first peak occurs at 27 Hz (1600 rpm) approximately, which is the critical speed previously demonstrated in the waterfall diagram. After that, the system stabilizes in a rotation speed window corresponding 40–70 Hz. However, when the rotation speed reaches 70 Hz (4200 rpm) the vertical displacements starts to increase, reaching the whip instability above 80 Hz (4800 rpm).

Fig. 11
figure 11

Time response for the node 4 (\(I = 1.0 \, A\) and \(800 \, \mathrm{{rpm}}\))

Full size image
Fig. 12
figure 12

Detail of the nonlinear transient response for the node 4 (\(I = 1.0 \, A\) and \(800 \, rpm\))

Full size image

The time response has been determined at 800 rpm for 1.0 A of electric current. The vertical displacements of bearing 2, which represent the MR squeeze film journal bearing is shown in Fig. 11. The response represents a nonlinear behavior, since presents a variable period. On the other hand, the displacement amplitude demonstrates stabilization in \(0.8 \times 10^{-6} \, \mathrm{{m}}\) after 0.3 s. The time scale in Fig. 11 has been expanded as depicted in Fig. 12 to see details of the nonlinear transients.

Fig. 13
figure 13

Stationary orbits for the node 4 (800 rpm)

Full size image

For the same bearing operating with no electric current, the orbit with a quasi-elliptical shape is concentrated in the fourth quadrant, as showed in Fig. 13. When the electric current equals to \(1.0 \, \mathrm{{A}}\) the orbit takes a circular shape and its center is placed at the origin of the coordinate system. A reduction in horizontal and vertical displacements is also observed when electrical currents are applied to the MR system.

Fig. 14
figure 14

Run-up frequency response with \(I = 1.0 \, \mathrm{{A}}\)

Full size image

Finally, a run-up frequency response with I = 1.0   A and the unbalance increased of 10 kg m is demonstrated in Fig. 14. An increase of the system critical speed to 33 Hz or 2000 rpm is noted with the application of the electric current, which is \(23 \%\) higher than the value observed when no electric current applied. Thus, it can be assumed that the electromagnetic induction contributed to the increase of the system stiffness. In addition, the oil whip instability is no longer noticeable in the frequency range of 0 to 100 Hz.

7 Conclusions

In this work, the nonlinear responses of a rotor system due to the radial and angular misalignments in the rigid coupling were performed by an improved Newmark method, with a local iteration using the NewtonRaphson method. The proposed method is considered as unconditionally stable and had the iteration executed only on the degrees of freedom related to the nonlinear forces acting on the bearings. The nonlinear steady-state shaft orbits were obtained for different intensities of radial and angular misalignments and the bifurcation analysis was used to identify the complex nonlinear behaviors such as periodic, period-doubling and quasi-periodic. Therefore, it is necessary to take into account the effect of rigid coupling misalignment on the reaction forces of the bearings, considering that these forces are changing owing to the rotation of the shaft, i.e. to the orientation of the misalignment with respect to the phase reference.

When supported by MR squeeze film journal bearings the rotor was analyzed for unbalance forces. Without the electric current the cascading diagrams show the critical speed at 1600 rpm and the emergence of whip instability at 3200 rpm. The presence of gravity acceleration delays the onset of fluid-induced instability. In the sequence the electromagnetic induction in the MR squeeze film bearings demonstrate the systematic reduction of the displacement amplitudes. Also the shape of the orbits is no longer elliptical as in the current-free case, but circumferential after the actuation of electric currents. The higher the applied electric current the lower are the displacement amplitudes as well as the orbits shape become more circumferential. This behavior is noted in the experimental results obtained by Wang, Meng and Hahn [22]. Finally, the simulation of the run-up in this work shows that current of 1.0 A provides an increase in critical rotation to 33.3 Hz and a reduction in response amplitudes. Furthermore, this phenomena can be observed in the simulations performed by Zapomel and Ferfecki [21].