Dynamics of cable truss via polynomial shape functions

Abstract

A model for the in-plane dynamic behaviour of a biconcave cable structure, subject to large static deformations and potentially slack harnesses is proposed, based on polynomial shape functions, in line with the classical Ritz method. The model provides a semi-analytical approach to the calculation of natural frequencies and modal shapes of the structure. The proposed formulation leads to an eigenvalue problem, based on a reduced number of degrees of freedom compared with equivalent FEM solutions, providing the basis for fast and accurate sensitivity analysis. The behaviour of the deformed structure is analysed in detail to understand the non-linear effects of non-symmetric mass and load distribution and slack harnesses on natural frequencies and corresponding modal shapes. Results confirm the relevance of the non-linear effects, due to the statically loaded configuration, on the linear vibrations of the structure, in particular evidencing the influence of the slackening of harnesses on modal shapes. Results are compared to analytical models, where available (single sagged cable), and to FEM solutions (for cable trusses with non-uniform mass and load distribution and potentially slack harnesses), providing good agreement.

1 Introduction

Objective of this paper is to provide a simplified and accurate model for the dynamic response of a class of cable structures (e.g. cable-suspended roofs and pedestrian, cable-suspended, pre-stressed bridges with vertical harnesses) subject to both operating and exceptional static loading conditions.

The dynamic behaviour of this class of structures is significantly affected by the geometrical configuration and stress distribution they assume under initial static loading, in particular the partial slackening of harnesses (a situation in which, due to exceptional static loads, part of the harnesses are slack, while the sagging cable and remaining harnesses are still in tension, contributing to the stiffness of the structure) influences their response (in terms of modal shape evolution) to increasing loading conditions. The proposed model is based on a simple description of the statically loaded configuration, involving a reduced number of degrees of freedom, and leads to a simplified but accurate description of the dynamics of the structure.

A simplified, semi-analytical model is desirable because it provides a reference for cross-checking results obtained with FEM analysis, it can be the tool for a fast and accurate preliminary analysis of a number of different geometrical configurations, loading and pre-tension conditions, avoiding the need for re-meshing of different structural configurations, as required by the FEM approach.

A semi-analytical approach provides the means for a synthetic and more intuitive description of the inner mechanical structure of the problem, in particular the present simplified model provides the basis for further developments in the non-linear dynamics regime, where approximate solutions can provide more in-depth understanding of the basic phenomena.

Although semi-analytical models have been developed for the static behaviour of cable trusses, we have no evidence of semi-analytical models for the dynamic response of this class of structures, taking into account both a non-symmetrically loaded deformed geometry and the slackening phenomenon.

The dynamic analysis of vibrating strings dates back to the beginning of the eighteenth century, with the experimental works of Sauveur and with the famous dispute involving Euler, Daniel Bernoulli, and d’Alembert. The problem was finally resolved by the work of Fourier (1807) and Dirichlet (1829). The problem of the dynamic behaviour of a sagged cable proved more elusive: von Kàrmànn et al. [1], in their relation over the collapse of the Tacoma Narrow bridge (1941), studied the natural modes of a three-span inextensible cable structure with flexible supports, but only in 1974 Irvine [2,3,4,5] proposed an analytical model able to correctly simulate the dynamic behaviour of a single sagged cable in the linear domain (and of a symmetrical bi-concave cable truss). Irvine introduced the $\lambda$ coefficient explaining the coalescence of the first and second mode of the single sagged cable. Rega et al. [6] analyse large amplitude free vibrations of a suspended cable. Triantafyllou and Triantafyllou [7] provide a geometric theory for the description of frequency coalescence and mode localization phenomena. Further analysis has been conducted (both analytical and experimental) to address the behaviour of single cables with different boundary and loading conditions. Rega [8, 9] provides a comprehensive review of the research on non-linear vibrations of suspended cables. Srinil et al. [10] investigate the multi-modal dynamics of horizontal/inclined cables. Lepidi and Gattulli [11] analyse thermal effects on the static and dynamic response of elastic suspended cables. Recently Mansour et al. [12] presented an analytical solution for the catenary-induced non-linear effects on cable linear vibrations. Regarding cable trusses dynamic behaviour, an analytical approach has been proposed by Mesarovic and Gasparini [13, 14], in a well-designed series of papers (1992) aimed at modelling the behaviour of an 8-element cable truss (representing a simplified model for understanding the behaviour of a cable dome structure) through generalised coordinates. Brownjohn [15] studies the vibration characteristics of a suspension footbridge. Chen et al. [16] propose a simplified model for the linear dynamic behaviour of cable-truss footbridges. Wang et al. [17] provide a new model for the in-plane dynamics of a suspension bridge, including the hangers’ elastic properties, through the transfer matrix method. The majority of the analysis on 2 and 3-dimensional cable trusses is conducted through the Finite Element Method. To our knowledge no semi-analytical approach has been proposed to date for the dynamic analysis of statically deformed, partially slack cable structures. The present paper provides a simplified (in the following pages the majority of numerical tests is performed with a 10th degree polynomial expansion), semi-analytical model for accurately describing the dynamic behaviour of biconcave cable trusses, starting from different initial static loading conditions (including non-symmetrical loads) and relevant deformed configurations. The approach takes into account both geometric (large displacements) non-linearity and slackening (unilateral, tension-only constraints) of the vertical harnesses (while no material non-linearity is currently included). The solution is based on the approximation of the vertical displacement of the cables through nth degree polynomial shape functions.

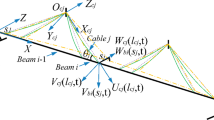
A recent paper [18] proposes a non-linear model for the static analysis of biconcave cable trusses, based on polynomial shape functions and energy approach. The (statically loaded) reference structure is described in Fig. 1. The present paper extends the polynomial shape-function approach to the in-plane dynamic behaviour of the cable truss. As described in detail in the previous paper, the static solution is found through minimisation of total potential energy. Regarding the dynamic behaviour of the structure, the application of the Lagrange equation to the model leads to a polynomial system, in which the coefficients of the shape functions represent the generalized coordinates. The linear components of the system define an eigenvalue problem, the solution of which provides frequencies and modal shapes of the linear problem from the statically deformed configuration. The numerical tests performed aim at both validating the approach (the results are compared to Irvine’s solution and to a FEM approach) and at highlighting the non-linear influence of the initial geometry (including slackening of harnesses) on the linear vibrations of the structure.

Fig. 1

Biconcave cable structure—deformed geometry under non-symmetric load

2 Problem description and assumptions

Biconcave cable structures with vertical harnesses (see Fig. 1) are constituted by a weight-bearing cable (bracing cable) and a stabilising cable (sagging cable). The two cables are connected with vertical harnesses (equally spaced in most applications). The structure is pre-tensioned in order to ensure the required rigidity and to limit the deformations when affected by external loads. Under static vertical loads, these structures present a rich non-linear behaviour. In particular, when subject to exceptional loads, part of the harnesses can become slack, while the sagging cable and other harnesses are still in tension. The non-linear static problem has been analysed in a previous paper [18] while, in the present paper, we will focus on the modal behaviour of the deformed structure. The following assumptions are used: horizontal displacements of both cables are considered negligible, cable length is approximated with the first three terms of its series expansion, material behaviour is linear, harnesses are simulated with inextensible, tension-only constraints for the static solution while, for the linear dynamic case, tensioned harnesses are, more conveniently, simulated through a continuous displacement constraint between bracing and sagging cable. The hypothesis of inextensible harnesses is widely adopted for analytical models (e.g. Irvine, Brownjohn, Kmet) and provides a realistic first approximation for the behaviour of most biconcave cable structures. A more detailed simulation of the structural behaviour can be obtained by considering the elastic properties of harnesses, as demonstrated by Wang et al. It is worth noticing that the present approach can be easily modified to include the elastic contribution of harnesses. Finally, static condensation is adopted.

3 Static equilibrium

Bracing and sagging cable (and their displacements) are described with polynomial shape functions of the form:

$$y\left( x \right) = l\mathop \sum \limits_{i = 1}^{n} b_{i} \left[ {\left( {\frac{x}{l}} \right)^{i + 1} - \left( {\frac{x}{l}} \right)^{i} } \right]$$

(1)

The statically loaded configuration, and relevant cable tension, can be calculated [18] minimising total potential energy under unilateral displacement constraints, representing the effect of inextensible, tension-only harnesses.

In the following pages we will denote the statically deformed configuration, obtained by minimizing the total energy, with $b\left( x \right)$ for the bracing cable and $s\left( x \right)$ for the sagging cable. The relevant vectors of the coefficients of the polynomial shape functions being, respectively, $\varvec{b}$ and $\varvec{s}$, the corresponding tensions in the bracing and sagging cable are denoted with $\hat{H}_{b}$ and $\hat{H}_{s}$. In favour of simplicity, we will omit noting vector transposition. We express the dynamic displacements, respectively for the bracing and sagging cable, as:

$$v\left( x \right) = l\mathop \sum \limits_{i = 1}^{n} v_{i} \left[ {\left( {\frac{x}{l}} \right)^{i + 1} - \left( {\frac{x}{l}} \right)^{i} } \right] \quad and\quad w\left( x \right) = l\mathop \sum \limits_{i = 1}^{n} w_{i} \left[ {\left( {\frac{x}{l}} \right)^{i + 1} - \left( {\frac{x}{l}} \right)^{i} } \right]$$

(2)

In the following, in order to describe the linear dynamic response of the structure, we will retain only quadratic terms in the calculation of the Lagrangian of the problem.

4 Kinetic energy

Supposing the mass is uniformly distributed on the span $\alpha_{1} l \le x \le \alpha_{2} l$ of the bracing cable (as in the case of most cable-suspended roofs) or directly transmitted to the bracing cable by inextensible connections (as for the mass of the deck and loads in the case of pedestrian cable-suspended bridges), neglecting the mass of the sagging cable (negligible when compared with the mass of the suspended loads) and neglecting horizontal displacements, the kinetic energy $E_{K}$ can be written as:

$$E_{K} = \frac{1}{2}\mathop \int \limits_{{\alpha_{1} l}}^{{\alpha_{2} l}} m\dot{v}^{2} \left( {x,t} \right)dx$$

(3)

and, in terms of shape functions:

$$E_{K} = \frac{1}{2}ml^{2} \mathop \int \limits_{{\alpha_{1} l}}^{{\alpha_{2} l}} \left\{ {\mathop \sum \limits_{i = 1}^{n} \dot{v}_{i} \left[ {\left( {\frac{x}{l}} \right)^{i + 1} - \left( {\frac{x}{l}} \right)^{i} } \right]} \right\}^{2} dx$$

(4)

Integrating:

$$E_{K} = \frac{1}{2}ml^{3} \mathop \sum \limits_{i,j = 1}^{n} \dot{v}_{i} \dot{v}_{j} \left[ {\left( {\frac{1}{i + j + 3}\alpha_{2}^{i + j + 3} - \frac{2}{i + j + 2}\alpha_{2}^{i + j + 2} + \frac{1}{i + j + 1}\alpha_{2}^{i + j + 1} } \right) - \left( {\frac{1}{i + j + 3}\alpha_{1}^{i + j + 3} - \frac{2}{i + j + 2}\alpha_{1}^{i + j + 2} + \frac{1}{i + j + 1}\alpha_{1}^{i + j + 1} } \right)} \right]$$

(5)

In matrix form:

$$E_{K} = \frac{1}{2}ml^{3} {\dot{\varvec{v}}}{\varvec{K}}{\dot{\varvec{v}}}$$

(6)

where $\varvec{K}$ is the mass matrix, with

$$K_{i,j} = \left( {\frac{1}{i + j + 3}\alpha_{2}^{i + j + 3} - \frac{2}{i + j + 2}\alpha_{2}^{i + j + 2} + \frac{1}{i + j + 1}\alpha_{2}^{i + j + 1} } \right) - \left( {\frac{1}{i + j + 3}\alpha_{1}^{i + j + 3} - \frac{2}{i + j + 2}\alpha_{1}^{i + j + 2} + \frac{1}{i + j + 1}\alpha_{1}^{i + j + 1} } \right)$$

(7)

Differentiating with respect to $\dot{\varvec{v}}$ we obtain:

$$\frac{{\partial E_{K} }}{{\partial \dot{v}}} = ml^{3} {\varvec{K}}{\dot{\varvec{v}}}$$

(8)

and, again differentiating with respect to $t$:

$$\frac{d}{dt}\left( {\frac{{\partial E_{K} }}{{\partial \dot{v}}}} \right) = ml^{3} {\varvec{K}}{\ddot{\varvec{v}}}$$

(9)

For the calculation of the other terms of the Lagrangian, two cases must be distinguished:

• the statically loaded configuration does not present slack harnesses, therefore $\varvec{v} = \varvec{w}$ (under the commonly adopted assumption that vertical harnesses can be represented through a continuum constraint on relative vertical displacements of the two cables)

• the statically loaded configuration presents slack harnesses along the span $0 \le x \le \mu l$ and therefore $\varvec{v} \ne \varvec{w }\,for\, 0 \le x \le \mu l$ and $\varvec{v} = \varvec{w }\,for\, \varvec{ }\mu l \le x \le l$

5 Fully-tensioned harnesses

In case of fully-tensioned harnesses, the expression for cable elongation is derived, approximated to the third term of its series expansion. A simplified formulation, with cable elongation calculated to the second term, can be easily obtained and is given in Eqs. 29 and 30; a comparison between the results of the two approximations is provided in results’ Sect. 8.6.

$$\begin{aligned} \Delta L & \cong \mathop \int \limits_{0}^{l} \left[ {1 + \frac{1}{2}\left( {b^{\prime} + v^{\prime}} \right)^{2} - \frac{1}{8}\left( {b^{\prime} + v^{\prime}} \right)^{4} } \right]dx \\ & \quad - \mathop \int \limits_{0}^{l} \left[ {1 + \frac{1}{2}b^{'2} - \frac{1}{8}b^{'4} } \right]dx \\ & = \mathop \int \limits_{0}^{l} \left[ {b^{\prime}v^{\prime} + \frac{1}{2}v^{'2} - \frac{1}{8}\left( {4b^{'3} v^{\prime} + 6b^{'2} v^{'2} + 4b^{\prime}v^{'3} + v^{'4} } \right)} \right]dx \\ \end{aligned}$$

(10)

where $b$ is the initial configuration of the cable and $v$ represents a vertical displacement from the initial configuration. In matrix form, Eq. 10 can be expressed as follows (see “Appendix 1” for details):

$$\Delta L \cong \frac{1}{8}l\left[ {8 \varvec{bBv} + 4 \varvec{vBv} - 4 \varvec{b}\left( {\varvec{bGb}} \right)\varvec{v} - 6\varvec{ v}\left( {\varvec{bGb}} \right)\varvec{v} - 4 \varvec{v}\left( {\varvec{bGv}} \right)\varvec{v} - \varvec{ v}\left( {\varvec{vGv}} \right)\varvec{v}} \right]$$

(11)

where $\varvec{B}$ is [18] a square matrix, with: $B_{ij} = \frac{ij + i + j + 1}{i + j + 1} - \frac{2ij + i + j}{i + j} + \frac{ij}{i + j - 1}$ and $\varvec{G}$ is the 4-dimensional tensor resulting from integration of Eq. 10 (see “Appendix 1”).

Introducing the square matrices ${\varvec{\Gamma}}$ and ${\varvec{\Upsilon}}$, defined as: ${\varvec{\Gamma}} = \varvec{ bGb}$ and ${\varvec{\Upsilon}} = \varvec{ sGs}$, Eq. 11 can be more conveniently written, respectively for the bracing and sagging cable, as:

$$\Delta L \cong \frac{1}{8}l\left[ {8 \varvec{bBv} + 4 \varvec{vBv} - 4 \varvec{b}{\varvec{\Gamma}}\varvec{v} - 6\varvec{ v}{\varvec{\Gamma}}\varvec{v} - 4 \varvec{v}\left( {\varvec{bGv}} \right)\varvec{v} - \varvec{ v}\left( {\varvec{vGv}} \right)\varvec{v}} \right]$$

(12)

$$\Delta L \cong \frac{1}{8}l\left[ {8 \varvec{sBv} + 4 \varvec{vBv} - 4 \varvec{s}{\varvec{\Upsilon}}\varvec{v} - 6\varvec{ v}{\varvec{\Upsilon}}\varvec{v} - 4 \varvec{v}\left( {\varvec{sGv}} \right)\varvec{v} - \varvec{v}\left( {\varvec{vGv}} \right)\varvec{v}} \right]$$

(13)

The elastic energy for the bracing cable can be approximated as $E_{E} \cong \frac{1}{2}\left( {\frac{EA}{l}} \right)_{b} \Delta L^{2}$ and it can be written (retaining only quadratic terms) as:

$$E_{E} \cong \frac{1}{2}\left( {\frac{EA}{l}} \right)_{b} \Delta L^{2} \cong \frac{1}{8}\left( {\frac{EA}{l}} \right)_{b} l^{2} \left[ {4 \varvec{bBv} \cdot \varvec{bBv} + \varvec{b}{\varvec{\Gamma}}\varvec{v} \cdot \varvec{b}{\varvec{\Gamma}}\varvec{v} - 4 \varvec{bBv} \cdot \varvec{b}{\varvec{\Gamma}}\varvec{v}} \right]$$

(14)

Differentiating with respect to $\varvec{v}$ we obtain:

$$\frac{{\partial E_{E} }}{\partial v} = \frac{1}{4}\left( {\frac{EA}{l}} \right)_{b} l^{2} \left[ {4 \varvec{bB} \otimes \varvec{bB} + \varvec{b}{\varvec{\Gamma}} \otimes \varvec{b}{\varvec{\Gamma}} - 4 \varvec{bB} \otimes \varvec{b}{\varvec{\Gamma}}} \right]\varvec{v}$$

(15)

where $\otimes$ denotes the Kronecker product. Proceeding with the same approach for pre-tension energy and, again, retaining only quadratic terms:

$$E_{H} = \hat{H}_{b} \Delta L \cong \frac{1}{8}l\hat{H}_{b} \left[ {4 \varvec{vBv} - 6\varvec{ v}{\varvec{\Gamma}}\varvec{v}} \right]$$

(16)

Differentiating with respect to $\varvec{v}$:

$$\frac{{\partial E_{H} }}{\partial v} = l\hat{H}_{b} \left[ { \varvec{B} - \frac{3}{2}{\varvec{\Gamma}}} \right]\varvec{v}$$

(17)

Neglecting the potential energy of loads, because it is linear with respect to the generalised coordinates, the Lagrangian of the problem is:

$$L = E_{K} - E_{E} - E_{H}$$

(18)

Substituting the derivatives obtained from Eqs. 9, 15 and 17 in the Lagrange equation $\frac{d}{dt}\left( {\frac{\partial L}{{\partial \dot{v}_{j} }}} \right) = \frac{\partial L}{{\partial v_{j} }}$ and extending the approach to the sagging cable, we obtain:

$$\begin{aligned} \omega^{2} \varvec{Kv} & = - \frac{1}{{ml^{3} }}\left\{ {\left( {\frac{EA}{l}} \right)_{b} l^{2} \left[ {\varvec{bB} \otimes \varvec{bB} + \frac{1}{4} \varvec{b}{\varvec{\Gamma}} \otimes \varvec{b}{\varvec{\Gamma}} - \varvec{bB} \otimes \varvec{b}{\varvec{\Gamma}}} \right]} \right. \\ & \quad + \,\left( {\frac{EA}{l}} \right)_{s} l^{2} \left[ {\varvec{sB} \otimes \varvec{sB} + \frac{1}{4}\varvec{s}{\varvec{\Upsilon}} \otimes \varvec{s}{\varvec{\Upsilon}} - \varvec{sB} \otimes \varvec{s}{\varvec{\Upsilon}}} \right] \\ & \quad \left. { +\, l\hat{H}_{b} \left[ { \varvec{B} - \frac{3}{2} {\varvec{\Gamma}}} \right] + l\hat{H}_{s} \left[ { \varvec{B} - \frac{3}{2} {\varvec{\Upsilon}}} \right]} \right\}\varvec{v} \\ \end{aligned}$$

(19)

The solution of Eq. 19 provides the eigenvalues and eigenvectors for the loaded truss with fully-tensioned harnesses.

Equation 19 is linear with respect to the dynamic displacement $\varvec{v}$ while it has a non-linear dependence on the initial geometry, described through the vectors $\varvec{b}$ and $\varvec{s}$.

The matrix $\varvec{B}$ and the 4-dimensional tensor $\varvec{G}$ are invariants for the problem, while the two-dimensional matrices: ${\varvec{\Gamma}} = \varvec{ bGb}$ and ${\varvec{\Upsilon}} = \varvec{sGs}$ depend on the initial conditions (i.e. the geometrical configuration of the statically loaded structure) through the coefficients of the shape functions of, respectively, the bracing and sagging cable $\varvec{b}$ and $\varvec{s}$.

The square matrices $\varvec{bB} \otimes \varvec{bB}$ and $\varvec{sB} \otimes \varvec{sB}$ describe the contribution of the first term of Eq. 10$\left( { {\hbox{i.e.}}\; b^{'} v^{\prime} } \right)$ to the elastic component of the stiffness matrix. This term depends on the initial deformation $\varvec{b}$.

The matrix $\varvec{B}$ describes the contribution of the second term of Eq. 10$\left( { {\hbox{i.e.}}\; \frac{1}{2}v^{\prime 2} } \right)$ to the pre-tension component of the stiffness matrix. This term is independent from the initial configuration of the structure.

It is interesting to notice that the reduced equation $\omega^{2} \varvec{Kv} = l\hat{H}_{b} \varvec{ Bv}$ (obtained in the case the initial configuration is linear and the relevant vector $\varvec{b}$ is null) is the equation of a vibrating string of length $l\varvec{ }$ and tension $H_{b}$, approximated via polynomial shape functions.

The square matrices $\frac{1}{4} \varvec{b}{\varvec{\Gamma}} \otimes \varvec{b}{\varvec{\Gamma}}$ and $\frac{1}{4}\varvec{s}{\varvec{\Upsilon}} \otimes \varvec{s}{\varvec{\Upsilon}}$ describe the contribution of the fourth term, of Eq. 10, ${\hbox{i.e.}} - \frac{1}{8}\left( {6b^{\prime 2} v^{\prime 2} } \right)$, to the elastic component of the stiffness matrix.

The square matrices $- \varvec{bB} \otimes \varvec{b}{\varvec{\Gamma}}$ and $- \varvec{sB} \otimes \varvec{s}{\varvec{\Upsilon}}$ describe the combined contribution of the second and third term of Eq. 10, ${\hbox{i.e.}} \;b^{'} v^{\prime}\;and\; - \frac{1}{8}\left( {4b^{\prime 3} v^{\prime}} \right)$, to the elastic component of the stiffness matrix.

Finally, the square matrices $- \frac{3}{2} {\varvec{\Gamma}}$ and $- \frac{3}{2} {\varvec{\Upsilon}}$, with ${\varvec{\Gamma}} = \varvec{bGb}$ and ${\varvec{\Upsilon}} = \varvec{ sGs}$, represent the contribution of the third term of Eq. 10, ${\hbox{i.e.}} \; - \frac{1}{8}\left( {4b^{\prime 3} v^{\prime}} \right)$, to the pre-tension component of the stiffness matrix.

6 Slack harnesses, $\varvec{ v} \ne \varvec{w}$

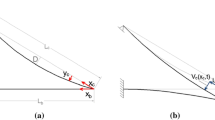
In case of slack harnesses, the sagging cable deformed configuration can, more conveniently, be described through a piecewise function, the function is linear where the harnesses are slack while, where the harnesses are in tension, the function (in line with the hypothesis of inextensible harnesses) corresponds to the initial sagging cable configuration plus the vertical displacement of the bracing cable (see Fig. 2). Let’s $\mu \cdot l$ be the abscissa of the first non-slack harness, obtained via static loading analysis. In this case, in correspondence to the span $0 - \mu \cdot l$ where the harnesses are slack, the bracing and sagging cable displacement functions are independent.

Fig. 2

Biconcave cable structure, slack harnesses—sagging cable geometry (not to scale)

In order to calculate the energy contribution of the sagging cable, the sagging cable elongation is derived. The value of $\hat{s} = s\left( {\mu l} \right)$ is immediately derived by substitution. The piecewise deformed configuration of the sagging cable, in case of slack harnesses, follows:

$$\left\{ {\begin{array}{*{20}l} {s_{dyn} \left( x \right) = s\left( x \right) + v\left( x \right) \quad for\quad \mu l < x \le l} \hfill \\ {s_{dyn} \left( x \right) = \frac{x}{\mu l}\left[ {s\left( {\mu l} \right) + v\left( {\mu l} \right)} \right] \quad for\quad 0 < x \le \mu l} \hfill \\ \end{array} } \right.$$

(20)

$s_{dyn} \left( x \right)$ being the dynamically deformed configuration of the structure; $\mu$ and, consequently, $s\left( {\mu l} \right)$ are constant terms for a given statically deformed configuration. Denoting, for simplicity of notation $\hat{s} = s\left( {\mu l} \right)$ The corresponding cable length is (see “Appendix 2” for detailed calculation):

$$\begin{aligned} \Delta L & \cong \sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} + 2\hat{s}v + v^{2} } - \sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } \\ & \quad + \frac{1}{2}\int_{\mu l}^{l} {\left[ {2\hat{s}^{'} v^{\prime} + v^{\prime 2} - \frac{1}{8}\left( {4s^{\prime 3} v^{\prime} + 6s^{\prime 2} v^{\prime 2} + 4s^{\prime}v^{\prime 3} + v^{\prime 4} } \right)} \right]dx} \\ & = \sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } \left\{ {\frac{1}{2}\frac{{2\hat{s}v + v^{2} }}{{\left( {\mu l} \right)^{2} + \hat{s}^{2} }} - \frac{1}{8}\frac{{\left( {2\hat{s}v + v^{2} } \right)^{2} }}{{\left[ {\left( {\mu l} \right)^{2} + \hat{s}^{2} } \right]^{2} }}} \right\} \\ & \quad + \frac{1}{2}\mathop \int \limits_{\mu l}^{l} \left[ {2\hat{s}^{'} v^{\prime} + v^{\prime 2} - \frac{1}{8}\left( {4s^{\prime 3} v^{\prime} + 6s^{\prime 2} v^{\prime 2} + 4s^{\prime}v^{\prime 3} + v^{\prime 4} } \right)} \right]dx \\ \end{aligned}$$

(21)

and in matrix form, neglecting higher order terms, we obtain:

$$\Delta L \cong \frac{{\hat{s}l}}{{\sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } }}\varvec{\mu v} + \frac{1}{2}\left\{ {\frac{{l^{2} }}{{\sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } }} - \frac{{ \hat{s}^{2} l^{2} }}{{\left[ {\left( {\mu l} \right)^{2} + \hat{s}^{2} } \right]^{{\frac{3}{2}}} }}} \right\}\varvec{\mu v} \cdot \varvec{\mu v} + \frac{1}{8}l\left[ {8 \varvec{sMv} + 4 \varvec{vMv} - 4 \varvec{s}{\varvec{\Phi}}\varvec{v} - 6\varvec{ v}{\varvec{\Phi}}\varvec{v}} \right]$$

(22)

where ${\varvec{\Phi}} = \left( {\varvec{sHs}} \right)$ and $\varvec{H}$ is a 4-dimensional tensor, resulting from integration in Eq. 21 (see “Appendix 1”):

Substituting Eq. 22 in the expression for elastic energy, and maintaining only second order terms we obtain:

$$E_{Es} = \frac{1}{2}\left( {\frac{EA}{l}} \right)_{s} \Delta l_{s}^{2} = \frac{1}{2}\left( {\frac{EA}{l}} \right)_{s} \left[ {\frac{{\hat{s}l}}{{\sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } }}\varvec{\mu v} + l \varvec{sMv} - \frac{l}{2} \varvec{s}{\varvec{\Phi}}\varvec{v}} \right]^{2}$$

(23)

$$\begin{aligned} E_{Es} & = \frac{1}{2}\left( {\frac{EA}{l}} \right)_{s} l^{2} \left\{ {\frac{{\hat{s}^{2} }}{{\left( {\mu l} \right)^{2} + \hat{s}^{2} }}\varvec{\mu v} \cdot \varvec{\mu v} + \varvec{sMv} \cdot \varvec{sMv} + \frac{1}{4} \varvec{s}{\varvec{\Phi}}\varvec{v} \cdot \varvec{s}{\varvec{\Phi}}\varvec{v}} \right. \\ & \quad \left. { + \,2\frac{{\hat{s}}}{{\sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } }}\varvec{\mu v} \cdot \varvec{sMv} - \frac{{\hat{s}}}{{\sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } }}\varvec{\mu v} \cdot \varvec{s}{\varvec{\Phi}}\varvec{v} - \varvec{sMv} \cdot \varvec{s}{\varvec{\Phi}}\varvec{v}} \right\} \\ \end{aligned}$$

(24)

Differentiating we obtain:

$$\frac{{\partial E_{Es} }}{{\partial \varvec{v}}} = \left( {\frac{EA}{l}} \right)_{s} l^{2} \left\{ {\frac{{\hat{s}^{2} }}{{\left( {\mu l} \right)^{2} + \hat{s}^{2} }}\varvec{\mu}\otimes\varvec{\mu}+ \frac{{\hat{s}}}{{\sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } }}\varvec{\mu}\otimes \varvec{ }\left[ {2\varvec{ sM} - \varvec{s}{\varvec{\Phi}}} \right] + \varvec{sM} \otimes \varvec{s}\left[ {\varvec{M} - {\varvec{\Phi}}} \right] + \frac{1}{4}\varvec{s}{\varvec{\Phi}} \otimes \varvec{s}{\varvec{\Phi}}} \right\}\varvec{v}$$

(25)

A similar approach for pre-tension energy leads to the following expression for energy (again, only quadratic terms):

$$E_{Hs} = H\Delta L = \hat{H}_{s} \left\{ {\frac{1}{2}\left[ {\frac{{l^{2} }}{{\sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } }} - \frac{{ \hat{s}^{2} l^{2} }}{{\left[ {\left( {\mu l} \right)^{2} + \hat{s}^{2} } \right]^{3/2} }}} \right]\varvec{\mu v} \cdot \varvec{\mu v} + \frac{1}{8}l\left[ {4 \varvec{vMv} - 6\varvec{ v}{\varvec{\Phi}}\varvec{v}} \right]} \right\}$$

(26)

Differentiating and keeping only linear terms (no constant and no higher order terms), we obtain:

$$\frac{{\partial E_{Hs} }}{{\partial \varvec{v}}} = \hat{H}_{s} \left\{ {\left[ {\frac{{l^{2} }}{{\sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } }} - \frac{{ \hat{s}^{2} l^{2} }}{{\left[ {\left( {\mu l} \right)^{2} + \hat{s}^{2} } \right]^{3/2} }}} \right]\varvec{\mu}\otimes\varvec{\mu}+ l\left( { \varvec{M} - \frac{3}{2}\varvec{ }{\varvec{\Phi}}} \right)} \right\}\varvec{v}$$

(27)

Finally, substituting in the Lagrange equation, we can write:

$$\begin{aligned} \omega^{2} \varvec{Kv} & = - \frac{1}{{ml^{3} }}\left\{ {\left( {\frac{EA}{l}} \right)_{b} l^{2} \left[ {\varvec{bB} \otimes \varvec{bB} + \frac{1}{4}\varvec{ b}{\varvec{\Gamma}} \otimes \varvec{ b}{\varvec{\Gamma}} - \varvec{bB} \otimes \varvec{b}{\varvec{\Gamma}}} \right]} \right. \\ & \quad + \,l\hat{H}_{b} \left[ { \varvec{B} - \frac{3}{2} {\varvec{\Gamma}}} \right] + \left( {\frac{EA}{l}} \right)_{s} l^{2} \left[ {\frac{{\hat{s}^{2} }}{{\left( {\mu l} \right)^{2} + \hat{s}^{2} }}\varvec{\mu}\otimes\varvec{\mu}} \right. \\ & \quad \left. { + \,\frac{{\hat{s}}}{{\sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } }}\varvec{\mu}\otimes \varvec{ s}\left[ {2\varvec{ M} - {\varvec{\Phi}}} \right] + \varvec{sM} \otimes \varvec{sM} + \frac{1}{4} \varvec{s}{\varvec{\Phi}} \otimes \varvec{s}{\varvec{\Phi}} - \varvec{sM} \otimes \varvec{s}{\varvec{\Phi}}} \right] \\ & \quad \left. { + \,l\hat{H}_{s} \left[ {\left[ {\frac{l}{{\sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } }} - \frac{{ \hat{s}^{2} l}}{{\left[ {\left( {\mu l} \right)^{2} + \hat{s}^{2} } \right]^{3/2} }}} \right]\varvec{\mu}\otimes\varvec{\mu}+ \left( { \varvec{M} - \frac{3}{2}\varvec{ }{\varvec{\Phi}}} \right)} \right]} \right\}\varvec{v} \\ \end{aligned}$$

(28)

The solution of the previous system (Eq. 28) provides frequencies and mode shapes for the linear vibration of a biconcave cable truss from its statically loaded configuration ($\varvec{b}, \varvec{s})$ in the case of slack harnesses in the interval $0 \le x \le \mu l$. When compared with Eq. 19 it is worth noticing that:

• As expected the terms related to the bracing cable contribution to the stiffness matrix do not change.

• The sagging cable terms $\left( {\frac{EA}{l}} \right)_{s} l^{2} \left[ {\varvec{sB} \otimes \varvec{sB} + \frac{1}{4}\varvec{s}{\varvec{\Upsilon}} \otimes \varvec{s}{\varvec{\Upsilon}} - \varvec{sB} \otimes \varvec{s}{\varvec{\Upsilon}}} \right] + l\hat{H}_{s} \left[ { \varvec{B} - \frac{3}{2} {\varvec{\Upsilon}}} \right]$ have been substituted with the analogous $\left( {\frac{EA}{l}} \right)_{s} l^{2} \left[ {\varvec{sM} \otimes \varvec{sM} + \frac{1}{4} \varvec{s}{\varvec{\Phi}} \otimes \varvec{s}{\varvec{\Phi}} - \varvec{sM} \otimes \varvec{s}{\varvec{\Phi}}} \right] + l\hat{H}_{s} \left[ {\left( { \varvec{M} - \frac{3}{2}\varvec{ }{\varvec{\Phi}}} \right)} \right]$, relating to the $\mu l \le x \le l$ portion of the sagging cable; in case $\mu l = 0$, we have $\varvec{M} = \varvec{B}$, ${\varvec{\Upsilon}} = {\varvec{\Phi}}$, and the two terms coincide.

• New terms have been added to the sagging cable component of the stiffness matrix: $\left( {\frac{EA}{l}} \right)_{s} l^{2} \left[ {\frac{{\hat{s}^{2} }}{{\left( {\mu l} \right)^{2} + \hat{s}^{2} }}\varvec{\mu}\otimes\varvec{\mu}+ \frac{{\hat{s}}}{{\sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } }}\varvec{\mu}\otimes \varvec{ s}\left[ {2\varvec{ M} - {\varvec{\Phi}}} \right]} \right]$ describing the contribution of the portion of the sagging cable with slack harnesses $\left( {0 \le x \le \mu l} \right)$ to the elastic component of the stiffness matrix and $l\varvec{ }\hat{H}_{s} \left[ {\left[ {\frac{l}{{\sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } }} - \frac{{ \hat{s}^{2} l}}{{\left[ {\left( {\mu l} \right)^{2} + \hat{s}^{2} } \right]^{3/2} }}} \right]\varvec{\mu}\otimes\varvec{\mu}} \right]$, describing the contribution of the portion of the sagging cable with slack harnesses $\left( {0 \le x \le \mu l} \right)$ to the pre-tension component of the stiffness matrix.

7 Problem formulation: summary

In summary, two equations (Eqs. 19, 28) for the linear dynamic behaviour of biconcave cable trusses subject to large static deformations have been derived under rather general assumptions (i.e. static condensation, horizontal displacements are neglected and the calculation of cable elongation is approximated to the first three terms of its series expansion). The two equations address, respectively, the case of fully tensioned and of partially slack harnesses

Equations 19 and 28 can be further simplified by truncating the series expansion for the cable length to the second term, obtaining respectively, for fully-tensioned and partially slack harnesses, the following expressions:

$$\omega^{2} \varvec{Kv} = - \frac{1}{{ml^{3} }}\left[ {\left( {\frac{EA}{l}} \right)_{b} l^{2} \varvec{ bB} \otimes \varvec{bB} + \left( {\frac{EA}{l}} \right)_{s} l^{2} \varvec{ sB} \otimes \varvec{sB} + l\hat{H}_{b} \varvec{B} + l\hat{H}_{s} \varvec{B}} \right]\varvec{v}$$

(29)

$$\begin{aligned} \omega^{2} \varvec{Kv} & = - \frac{1}{{ml^{3} }}\left\{ {l^{2} \left( {\frac{EA}{l}} \right)_{b} \varvec{bB} \otimes \varvec{bB} + l\hat{H}_{b} \varvec{B}} \right. \\ & \quad + \,\left( {\frac{EA}{l}} \right)_{s} l^{2} \left[ {\frac{{\hat{s}^{2} }}{{\left( {\mu l} \right)^{2} + \hat{s}^{2} }}\varvec{\mu}\otimes\varvec{\mu}+ \varvec{sM} \otimes \varvec{sM} + 2\frac{{\hat{s}}}{{\sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } }}\varvec{\mu}\otimes \varvec{sM}} \right] \\ & \quad \left. { + \,l\varvec{ }\hat{H}_{s} \left[ {\frac{l}{{\sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } }}\varvec{\mu}\otimes\varvec{\mu}+ \varvec{M}} \right]} \right\}\varvec{v} \\ \end{aligned}$$

(30)

In the following Sect. 8.6 we compare the results provided by Eq. 19 (three terms of the series expansion) and Eq. 29 (two terms of the series expansion).

8 Results

Five series of simulations have been performed, with the aim of both validating the approach and describing the non-linear effects of different initial loading conditions and initial geometries on natural frequencies and corresponding modal shapes.

• 1. Single sagged cable, uniform load and mass distribution The present approach (simplified 2-terms model, Eq. 29) is compared with analytical results (Irvine) for symmetric loading and mass distribution conditions.

• 2. Biconcave cable truss with increasing uniform loading The present approach is compared with the results obtained through a FEM model.

• 3. Biconcave cable truss with non-symmetric, increasing loading conditions, including slackening of harnesses The results of the present approach are compared to the results of a FEM model.

• 4. Biconcave cable truss with non-symmetric loading conditions and different sag of the sagging cable The results of the present approach are analysed for increasing sag of the sagging cable.

• 5. Biconcave cable truss with non-symmetric loading conditions The results of 2-terms and 3-terms models are compared to a FEM reference model.

The following Table 1 provides a synthetic description of the numerical experiments.

Table 1 Numerical experiments

The reference structure used for numerical experiments is derived from a 60-m, previously studied biconcave cable truss [18,19,20,21] with the following parameters:

• Span = 60 m.

• Sag of the bracing cable = 4.02 m.

• Sag of the sagging cable = 4.02, 3.52, 3.02, 2.52, 2.02 m.

• E = 1.40 * 10¹¹.

• Area of the bracing cable, A_b = 0.0019995 m².

• Area of the sagging cable, A_s = 0.0012996 m².

• Distributed mass = 907.796 kg/m * LF, were LF is a load multiplication factor.

The finite element model used for testing is a simplified, 22-nodes (44 d.o.f.), geometrically non-linear truss model, with tension-only elements representing cables and harnesses; equivalent loads are concentrated on the nodes of the bracing cable.

8.1 Test series 1: single sagged cable—uniform load

A first series of numerical tests is performed, on a uniformly loaded, single sagged cable (the bracing cable of the 60-m reference structure), to compare the results obtained with the present approach (with the expression for elongation limited to the second term) to the results obtained using the analytical solution provided by Irvine. The polynomial expansion has been truncated at the 10th term.

Figures 3 and 4 describe the behaviour of the first five modal components (and relevant frequencies) subject to two different uniformly distributed load conditions and relevant mass distribution (respectively with load factor 2 and 8). The dotted lines represent the modal components according to the present approach while diamonds represent the corresponding values derived from Irvine’s analytical solution. The numbers on the lines represent the vibrating periods expressed in seconds. As expected, the form of the first symmetric modal component shifts (with increasing load) from a two-node shape to a zero-node shape, and the lower frequency shifts from the one-node asymmetric form to the zero-node symmetric form.

Fig. 3

Modal shapes—uniform load and mass distribution, load factor 2

Fig. 4

Modal shapes—uniform load and mass distribution, load factor 8

The results of the two approaches are totally consistent, the difference in both frequencies and modal shapes being negligible; the following Table 2 shows the difference between period of vibration T (s) as calculated via Irvine’s analytical solution and via present approach with load factors ranging from 1 to 8: the values practically coincide (maximum error 0.1%).

Table 2 Comparison between Irvine’s approach and present solution—period of vibration (s)

Figure 5 describes the change in the first vibration periods with increasing load (from load factor 1 to load factor 10). It is worth noticing that the first mode is antisymmetric up to a load factor of 9, when a crossover between the first symmetric and antisymmetric mode takes place (Irvine’s ${\text{elastogeometric}}\;{\text{parameter}}\;\lambda^{2} = 4\pi^{2}$).

Fig. 5

Period (s)—uniform load and mass distribution, load factor increasing from 1 to 10

8.2 Test series 2: cable truss—increasing uniform loading

A second series of tests has been performed on the reference cable truss for increasing uniform loading (load factor 0.04, 0.2, 0.5, 1.0, 1.5). Due to inextensible harnesses hypothesis, in absence of slackening, the shape functions of bracing and sagging cable coincide.

The following Fig. 6 represents the mode shapes obtained from the present approach (lines) and from a FEM model (markers) for a load factor of 1. The numbers on the lines represent the vibration period expressed in seconds. The modal shapes obtained with the present approach are very close to the results obtained with FEM.

Fig. 6

Modal shapes—uniform load and mass distribution, load factor 1

Table 3 presents the results in terms of vibration periods for load factor 1, again, the results are very close for the first three modes (all less than 1% difference in vibration period). The fourth mode presents a difference of about 3% between the vibration period obtained with present model and with FEM. This can be partly explained by the different load and mass distribution (continuous for the present model and concentrated in the 11 nodes of the bracing cable for the FEM model).

Table 3 Uniform load and mass distribution, load factor 1—periods (s), first 4 modes

The following Fig. 7 presents the results of the experiments conducted with the present approach (lines) and a comparison with FEM results (calculated for load factor 0.4 and 1.0). As expected the increase in load factor determines a (non-linear) increase in the vibration period.

Fig. 7

First 4 periods (s) for increasing uniform load (LF 0.04, 0.2, 0.5, 1.0, 1.5)

8.3 Test series 3: cable truss—increasing non-symmetric loading

A fourth series of tests is performed, on the reference structure, to understand the impact of increasing non-symmetrical loading on frequencies and modal shapes. The cable truss is loaded with a uniform load on the entire span (load factor = 1) and a second uniform load on the left-hand half-span (progressively reaching load factor 8). Figure 8 describes the loading and relevant deformed configuration for load factor 2_1 (solid line: shape functions, markers FEM).

Fig. 8

Non-symmetric load and mass distribution, load factor 2_1 (not to scale)

Figures 9, 10, 12 and 13 depict the results of modal analysis resulting from the present approach (dotted lines, the labels represent vibration period T in seconds) and resulting from FEM model (markers), corresponding to different left-hand uniform load. From load factor 1_1 to load factor 4.5_1 the harnesses remain fully tensioned. From load factor 5_5 harnesses start to become slack.

Fig. 9

Modal shapes—non-symmetric load and mass distribution, load factors 2_1

Fig. 10

Modal shapes—non-symmetric load and mass distribution, load factors 4_1

The two models provide very close results in terms of modal shape. Regarding vibration periods, as expected, the models provide close results for lower frequencies, with an increase in the differences between shape function and FEM for higher frequencies (see Table 4).

Table 4 Non-symmetric load and mass distribution, load factors 2_1—periods (s), first 4 modes

With increasing, non-symmetric loading, the two models continue to provide close results both in terms of shape functions (see Fig. 10) and of vibration periods (Table 5).

Table 5 Non-symmetric load and mass distribution, load factors 4_1—periods (s), first 4 modes

A further increase of loading leads to the slackening of left-hand hangers, as described in Fig. 11, were the slackening is evident from the straight-line configuration assumed by the left-hand segment of the sagging cable (no vertical load transmitted by hangers).

Fig. 11

Statically deformed configuration—non-symmetric load and mass, load factor 6_1 (not to scale)

In this case, due to slack harnesses, eigenvalues and eigenvectors are calculated based on Eq. 28 and the shape functions of bracing and sagging cable are independent in the span $0 - \mu \cdot l$. The resulting modal shapes (for load factor 6_1) are described in Figs. 12 and 13 (respectively for the bracing and sagging cable) and relevant vibrating periods are described in Table 6.

Fig. 12

Modal shapes—non-symmetric load and mass, load factors 6_1—bracing cable

Fig. 13

Modal shapes—non-symmetric load and mass, load factors 6_1—sagging cable

Table 6 Non-symmetric load and mass distribution, load factors 6_1—periods (s), first 4 modes

The results from the shape function approach are very close to the FEM results in terms of vibration periods of the first two modes, the difference increases with increasing frequencies (third and fourth mode). Notwithstanding the fact that the difference in modal shapes is more pronounced, compared with the examples with fully tensioned harnesses, the shape function model and FEM continues to provide substantially consistent results.

The following Fig. 14 provides a comparison between shape function and FEM results in terms of vibration periods (first four modes), for increasing load factor, from 1_1 (symmetric) to 8_1. The load factor increase step is 0.5 for shape function (15 samples) and 1.0 for FEM (8 samples). The red lines and red markers denote initial loading conditions leading to slack harnesses.

Fig. 14

First 4 periods (s) for increasing non-symmetric load (LF from 1_1 to 8_1). (Color figure online)

The comparison between present approach and FEM demonstrates a good agreement, both in mode shape and in frequency. The difference in frequency increases for higher frequencies; this can be partly explained by the fact that the two models are based on a different representation of load and mass distribution (uniformly distributed for the present approach and mass and load concentrated in the 11 nodal points of the bracing cable for the FEM model).

8.4 Test series 3: non-linear effects of initial geometry on modal shapes

The following Figs. 15, 16, 17, 18, 19, 20, 21 and 22 represent the change in the first four modal shapes of bracing and sagging cable for increasing load factor (from 1_1 to 8_1). Vertical displacements are plotted on the vertical axis as a function of span and increasing non-symmetric loading. The non-linear effect of increasing loads is evident; in particular, from load factor of 5_1 (initial slackening), the modal shape evolution is markedly affected by the slackening of left-side harnesses, the most evident effect being a less pronounced change in modal shape with increasing load.

Fig. 15

Increasing non-symmetric load (LF from 1_1 to 8_1)—first mode, bracing cable, modal shape

Fig. 16

Increasing non-symmetric load (LF from 1_1 to 8_1)—first mode, sagging cable, modal shape

Fig. 17

Increasing non-symmetric load (LF from 1_1 to 8_1)—second mode, bracing, modal shape

Fig. 18

Increasing non-symmetric load (LF from 1_1 to 8_1)—second mode, sagging, modal shape

Fig. 19

Increasing non-symmetric load (LF from 1_1 to 8_1)—third mode, bracing, modal shape

Fig. 20

Increasing non-symmetric load (LF from 1_1 to 8_1)—third mode, sagging, modal shape

Fig. 21

Increasing non-symmetric load (LF from 1_1 to 8_1)—fourth mode, bracing, modal shape

Fig. 22

Increasing non-symmetric load (LF from 1_1 to 8_1)—fourth mode, sagging, modal shape

For all four modes the modal shapes undergo a relatively fast change up to load factor 5_1 (slackening), then the rate of change in the modal shape suddenly decreases.

8.5 Test series 4: cable truss—increasing non-symmetric loading, variable sag

Five numerical experiments are run to understand the influence of the geometry of the sagging cable on frequencies and modal shapes. The sagging cable sag is increased at intervals of 0.5 m, from 2.02 to 4.02 m.

The bracing cable initial (unloaded) tension is kept the same (5.88E5 KN) for the five cases, therefore the decrease of sag corresponds to an increase in the initial pre-tensioning of the sagging cable to ensure the same pre-tension of the bracing cable.

Results are represented in Figs. 23, 24 and 25.

Fig. 23

Increasing sag of sagging cable, non-symmetric load (LF 2_1)—first 4 periods (s)

Fig. 24

Increasing sag of sagging cable, non-symmetric load (LF 2_1)—first 4 modal shapes

Fig. 25

Increasing sag of sagging cable, non-symmetric load (LF 2_1)—average curvature

An increase in sag of the sagging cable corresponds to an increase in the period of each mode. This can be explained by the fact that an increase in sag requires a decrease in pre-tension of the sagging cable (in order to maintain a constant tension in the bracing cable), therefore it results in a decrease of the sagging cable contribution to total pre-tension energy and an overall decrease in the rigidity of the stiffness matrix. The following Fig. 24 presents the evolution of the first four modal shapes with the progressive increase in sag of the sagging cable, for the same energy content (the arrows indicate the increase in sag), while Fig. 25 presents the evolution of the curvature of the modal shapes.

An increase of the sag of the sagging cable generates an increase of the average curvature for first, second and fourth mode. The third mode presents a different response to the change in the sag, with a decrease in curvature when the sag reaches about 2.5 m. The second mode gradually shifts from a one-node to a two-node configuration, with a related increase in the average curvature. For sag slightly over 3.5 m, the curvature of the second mode intersects the curvature of the third mode.

8.6 Test series 5: cable truss, half span load, 2nd and 3rd-term model comparison

Numerical experiments have been performed, to understand the behaviour of the simplified model (Eqs. 29, 30) including only the first 2 terms of the series expansion, compared with the 3-term model and the FEM solution.

The following Table 7 and Fig. 26 compare the results of the two models and the relevant FEM results in the case of load factor 2_0.

Table 7 Cable truss loaded on half span—period (s) for the first four vibration modes

Fig. 26

Cable truss loaded on half span—first four vibration modes. (Color figure online)

For the first and second mode both 2-term and 3-term models provide results in line with the FEM simulation. As expected the three-terms model performs closer to the FEM model. For higher modes both models gradually diverge from the results obtained with FEM simulation. The reason of relatively larger differences among the results for the fourth mode can be explained by the fact that the actual dynamic response to the particular load configuration analysed (only half span loaded) determines (for higher modes) increasing horizontal displacements, not considered by the present model. This leads to an under-estimation of the kinetic energy and, consequently, to an under-estimation of the relevant period.

Figure 26 shows the first four vibration modes of the bracing cable as calculated with the FEM model (dots), 2-term shape function model (black lines) and 3-terms shape function model (red lines). The plot confirms a good fit between the shape function models and FEM, demonstrating how the simplified 2-terms model can provide a reasonable approximation of both frequency and shape functions, suitable for preliminary analysis of the impact of exceptional loads on the dynamic response of the structure.

9 Summary and conclusions

A model has been developed for the modal analysis of cable trusses from their statically deformed configuration, involving large deformations and potentially slack harnesses. The model provides the tools for the simplified modal analysis of the structure, generating accurate results with a reduced number of degrees of freedom (the examples in this paper are based on a 10th order polynomial shape function), while an equivalent FEM model requires the solution of an eigenvalue problem involving 44 degrees of freedom. The model provides a semi-analytical approach able to explain the rich non-linear effects of geometry and loading conditions on dynamic response of biconcave cable trusses with vertical harnesses.

The present approach can be extended, without major modifications, to biconcave cable trusses, with the obvious exclusion of the slackening of harnesses.

A series of tests has been performed to understand the influence of different loading conditions, initial shape of the structure (different sag of sagging cable) and accuracy in the model (2nd and 3rd term of the expression for cable elongation).

Numerical results demonstrate an almost perfect agreement with previous analytical work by Irvine (limited to symmetrical sagged cable) and substantial agreement with FEM simulations (for cable trusses, both symmetric and non-symmetric load distribution, fully-tensioned and partially slack harnesses).

The numerical simulation highlights some characteristics of the modal behaviour of this class of cable structures, in particular:

• The impact of slack harnesses, providing a discontinuity in the evolution of modal shapes.

• The influence of sagging cable geometry on frequency and modal shape.

The relative simplicity of the approach makes it a useful tool for the sensitivity analysis of cable trusses under different initial geometries and loading conditions and a promising tool for the analysis of more complex cable structures (e.g. suspension bridges, cable stayed roofs, cable domes).

Furthermore, its simplicity makes it a useful tool to test and provide an interpretation to FEM dynamic models.

Finally, the present simplified model provides the basis for further development in the non-linear regime, where approximate solutions can provide more in-depth understanding of the basic phenomena.

Further research is under course to extend the approach to non-linear dynamics.

Appendices

Appendix 1: Expression for cable elongation. Polynomial segment

Cable geometry is expressed via polynomial shape functions:

$$y\left( x \right) = l\mathop \sum \limits_{i = 1}^{n} b_{i} \left[ {\left( {\frac{x}{l}} \right)^{i + 1} - \left( {\frac{x}{l}} \right)^{i} } \right]\quad \text{and}\quad y^{\prime}\left( x \right) = \mathop \sum \limits_{i = 1}^{n} b_{i} \left[ {\left( {i + 1} \right)\left( {\frac{x}{l}} \right)^{i} - i\left( {\frac{x}{l}} \right)^{i - 1} } \right]$$

(31)

From Eq. 10, the general expression for elongation in the segment $\mu l \le 0 \le l$ reads:

$$\Delta L \cong \mathop \int \limits_{\mu l}^{l} \left[ {b^{\prime}v^{\prime} + \frac{1}{2}v^{\prime 2} - \frac{1}{8}\left( {4b^{\prime 3} v^{\prime} + 6b^{\prime 2} v^{\prime 2} + 4b^{\prime}v^{\prime 3} + v^{\prime 4} } \right)} \right]dx$$

(32)

For simplicity of notation lets’ pose:

$$\vartheta_{i} \left( x \right) = \left[ {\left( {i + 1} \right)\left( {\frac{x}{l}} \right)^{i} - i\left( {\frac{x}{l}} \right)^{i - 1} } \right]$$

(33)

Substituting expression 33 in expression 32, we obtain:

$$\begin{aligned} \Delta L & \cong \mathop \int \limits_{\mu l}^{l} \mathop \sum \limits_{i,j = 1}^{n} b_{i} v_{j} \vartheta_{i} \vartheta_{j} dx + \frac{1}{2}\mathop \int \limits_{\mu l}^{l} \mathop \sum \limits_{i,j = 1}^{n} v_{i} v_{j} \vartheta_{i} \vartheta_{j} dx \\ & \quad - \,\frac{1}{8}\mathop \int \limits_{\mu l}^{l} 4\mathop \sum \limits_{i,j,k,m = 1}^{n} b_{i} b_{j} b_{k} v_{m} \vartheta_{i} \vartheta_{j} \vartheta_{k} \vartheta_{m} dx \\ & \quad - \,\frac{1}{8}\mathop \int \limits_{\mu l}^{l} 6\mathop \sum \limits_{i,j,k,m = 1}^{n} b_{i} b_{j} v_{k} v_{m} \vartheta_{i} \vartheta_{j} \vartheta_{k} \vartheta_{m} dx \\ & \quad - \,\frac{1}{8}\mathop \int \limits_{\mu l}^{l} 4\mathop \sum \limits_{i,j,k,m = 1}^{n} b_{i} v_{j} v_{k} v_{m} \vartheta_{i} \vartheta_{j} \vartheta_{k} \vartheta_{m} dx \\ & \quad - \,\frac{1}{8}\mathop \int \limits_{\mu l}^{l} \mathop \sum \limits_{i,j,k,m = 1}^{n} v_{i} v_{j} v_{k} v_{m} \vartheta_{i} \vartheta_{j} \vartheta_{k} \vartheta_{m} dx \\ \end{aligned}$$

(34)

The vectors of coefficients $\varvec{v} \,\,and \,\,\varvec{b}$ are independent from the integration variable $x$, and the problem is reduced to the evaluation of two tensors of integrals: the matrix $\varvec{M}$ with elements:

$$M_{ij} = \mathop \int \limits_{\mu l}^{l} \vartheta_{i} \left( x \right)\vartheta_{j} \left( x \right)dx$$

(35)

and the 4-dimensional tensor $\varvec{H}$, with elements:

$$H_{ijkm} = \mathop \int \limits_{\mu l}^{l} \vartheta_{i} \left( x \right)\vartheta_{j} \left( x \right)\vartheta_{k} \left( x \right)\vartheta_{m} \left( x \right)dx$$

(36)

Integrating $M_{ij}$:

$$M_{ij} = \mathop \int \limits_{\mu l}^{l} \vartheta_{i} \left( x \right)\vartheta_{j} \left( x \right)dx = \mathop \int \limits_{\mu l}^{l} \left[ {\left( {i + 1} \right)\left( {\frac{x}{l}} \right)^{i} - i\left( {\frac{x}{l}} \right)^{i - 1} } \right]\left[ {\left( {j + 1} \right)\left( {\frac{x}{l}} \right)^{j} - j\left( {\frac{x}{l}} \right)^{j - 1} } \right]dx$$

(37)

$$M_{ij} = \left[ {\frac{ij + i + j + 1}{i + j + 1}\left( {1 - \mu^{i + j + 1} } \right) - \frac{2ij + j + i}{i + j}\left( {1 - \mu^{i + j} } \right) + \frac{ij}{i + j - 1}\left( {1 - \mu^{i + j - 1} } \right)} \right]$$

(38)

In a similar way, integrating $H_{ijkm}$:

$$H_{ijkm} = \mathop \int \limits_{\mu l}^{l} \vartheta_{i} \left( x \right)\vartheta_{j} \left( x \right)\vartheta_{k} \left( x \right)\vartheta_{m} \left( x \right)dx = \mathop \int \limits_{\mu l}^{l} \left[ {\left( {i + 1} \right)\left( {\frac{x}{l}} \right)^{i} - i\left( {\frac{x}{l}} \right)^{i - 1} } \right]\left[ {\left( {j + 1} \right)\left( {\frac{x}{l}} \right)^{j} - j\left( {\frac{x}{l}} \right)^{j - 1} } \right]\left[ {\left( {k + 1} \right)\left( {\frac{x}{l}} \right)^{k} - k\left( {\frac{x}{l}} \right)^{k - 1} } \right]\left[ {\left( {m + 1} \right)\left( {\frac{x}{l}} \right)^{m} - m\left( {\frac{x}{l}} \right)^{m - 1} } \right]dx$$

(39)

$$\begin{aligned} H_{ijkm} & = \frac{ijkm + ijk + ijm + ij + ikm + ik + im + i + jkm + jk + jm + j + km + k + m + 1}{i + j + k + m + 1}\left( {1 - \mu^{i + j + k + m + 1} } \right) \\ & \quad - \,\frac{4ijkm + 3ijk + 3ijm + 3ikm + 2ik + 2im + 3jkm + 2jk + 2jm + 2km + k + m + 2ij + j + i}{i + j + k + m}\left( {1 - \mu^{i + j + k + m} } \right) \\ & \quad + \,\frac{6ijkm + 3ikm + 3jkm + km + 3ijk + 3ijm + jk + jm + ik + im + ij}{i + j + k + m - 1}\left( {1 - \mu^{i + j + k + m - 1} } \right) \\ & \quad - \,\frac{4ijkm + jkm + ikm + ijk + ijm}{i + j + k + m - 2}\left( {1 - \mu^{i + j + k + m - 2} } \right) + \frac{ijkm}{i + j + k + m - 3}\left( {1 - \mu^{i + j + k + m - 3} } \right) \\ \end{aligned}$$

(40)

In the particular case in which $\mu = 0$, matrix $\varvec{M}$ reduces to matrix $\varvec{B}$, with elements $B_{ij}$:

$$B_{ij} = \frac{ij + i + j + 1}{i + j + 1} - \frac{2ij + i + j}{i + j} + \frac{ij}{i + j - 1}$$

(41)

And the 4-dimensional tensor $\varvec{H}$ reduces to the 4-dimensional tensor $\varvec{G}$, with elements $G_{ij}$:

$$\begin{aligned} G_{ij} & = \frac{ijkm + ijk + ijm + ij + ikm + ik + im + i + jkm + jk + jm + j + km + k + m + 1}{i + j + k + m + 1} \\ & \quad - \,\frac{4ijkm + 3ijk + 3ijm + 3ikm + 2ik + 2im + 3jkm + 2jk + 2jm + 2km + k + m + 2ij + j + i}{i + j + k + m} \\ & \quad + \,\frac{6ijkm + 3ikm + 3jkm + km + 3ijk + 3ijm + jk + jm + ik + im + ij}{i + j + k + m - 1} \\ & \quad - \,\frac{4ijkm + jkm + ikm + ijk + ijm}{i + j + k + m - 2} + \frac{ijkm}{i + j + k + m - 3} \\ \end{aligned}$$

(42)

Appendix 2: Expression for cable elongation. Linear segment

The length of the cable in the linear segment $0 \le x \le \mu l$ is:

$$L = \sqrt {\left( {\mu l} \right)^{2} + s^{2} \left( {\mu l} \right)}$$

(43)

and the total cable elongation can be calculated as:

$$\Delta L \cong \sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} + 2\hat{s}v + v^{2} } - \sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } + \frac{1}{2}\mathop \int \limits_{\mu l}^{l} 2\hat{s}^{'} v^{\prime} + v^{\prime 2} - \frac{1}{8}\left( {4s^{\prime 3} v^{\prime} + 6s^{\prime 2} v^{\prime 2} + 4s^{\prime}v^{\prime 3} + v^{\prime 4} } \right)dx$$

(44)

$$\begin{aligned} & \sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} + 2\hat{s}v + v^{2} } - \sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } \\ & = \sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } \sqrt {1 + \frac{{2\hat{s}v + v^{2} }}{{\left( {\mu l} \right)^{2} + \hat{s}^{2} }}} - \sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } \\ & = \sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } \left( {\sqrt {1 + \frac{{2\hat{s}v + v^{2} }}{{\left( {\mu l} \right)^{2} + \hat{s}^{2} }}} - 1} \right) \\ & \cong \sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } \left\{ {\frac{1}{2}\frac{{2\hat{s}v + v^{2} }}{{\left( {\mu l} \right)^{2} + \hat{s}^{2} }} - \frac{1}{8}\frac{{\left( {2\hat{s}v + v^{2} } \right)^{2} }}{{\left[ {\left( {\mu l} \right)^{2} + \hat{s}^{2} } \right]^{2} }}} \right\} \\ \end{aligned}$$

(45)

and in matrix form, neglecting higher order terms, we obtain:

$$\begin{aligned} \Delta L & \cong \frac{{\hat{s}l}}{{\sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } }}\varvec{\mu v} + \frac{1}{2}\frac{{l^{2} }}{{\sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } }}\varvec{\mu v\mu v} - \frac{1}{8}\frac{{4 \hat{s}^{2} l^{2} }}{{\left[ {\left( {\mu l} \right)^{2} + \hat{s}^{2} } \right]^{{\frac{3}{2}}} }}\varvec{\mu v\mu v}\Delta L \\ & = \frac{{\hat{s}l}}{{\sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } }}\varvec{\mu v} + \frac{1}{2}\left\{ {\frac{{l^{2} }}{{\sqrt {\left( {\mu l} \right)^{2} + \hat{s}^{2} } }} - \frac{{ \hat{s}^{2} l^{2} }}{{\left[ {\left( {\mu l} \right)^{2} + \hat{s}^{2} } \right]^{3/2} }}} \right\}\varvec{\mu v\mu v} \\ \end{aligned}$$

(46)