1 Introduction

The use of gears is widespread in mechanical industry since they allow high efficiency and high power density for a wide range of speeds and torques and their applications span from everyday life to very dedicated solutions. In spite of the long track of gears application and usage, the complex phenomena in which gears are involved in the meshing process still constitute an active research topic.

Fig. 1
figure 1

Semi-analytic gear contact model

Full size image

1.1 Analytical models for gear contact problems

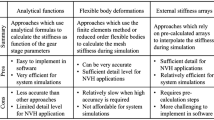
First attempts to tackle gear contact problems have been done using analytical models, which offer a high computational speed yet require the need of a priori assumptions to simplify meshing condition and system complexity [4, 9, 14, 16]. Most of these formulations are derived by a series of numerical or experimental results in order to extrapolate stiffness relationships in function of basic manufacturing gear parameters. However due to weight and mounting restrictions as well as more stringent functional requirements, modern gear transmission designs correspond less to the situations for which these modelling techniques were designed and the underlying assumptions become questionable [25].

1.2 Finite element-based models for gear contact problems

On the other hand, the finite element (FE) method is the most powerful general numerical method to simulate gear contact problem. However the need for highly refined mesh near the contact zone implies large number of degrees of freedom (DOFs). The contact width is typically one order of magnitude smaller than the other gear characteristic dimensions and its location varies in three directions during the gear meshing. Therefore the large number of DOFs, together with the relatively high cost of imposing the non-penetrability condition, yields a feasible computational time only for static simulations. Its very high computational cost makes it impractical to treat dynamic problems, especially when a long time-stable simulation is requested. Evaluating quantities such as tooth deflections, gear meshing stiffness or stress distribution in dynamic conditions is still too time expensive with the FE method.

In order to reduce the computational cost of standard FE simulations for gear contact problems, many authors [1, 5, 26] have proposed semi-analytic contact models, where the tooth deformation is calculated by combining a numerical (FE) and an analytic solution. As shown in Fig. 1, this approach splits the total gear deformation into a local and a global contribution, described respectively by an analytic and a numerical solution. The former describes the local displacement field close to the contact point, while the latter captures the remaining deformation defined as global.

Fig. 2
figure 2

The approach of Andersson and Vedmar

Full size image

This approach assumes that the gear teeth flank is subjected to a load distribution for which a corresponding analytic expression of the deformation field is available (for example the Hertz’s pressure distribution [10, Chapter 6.3] or a combination of Boussinesq’s point loads [12, Chapter 2.1]). Moreover semi-analytic approaches make it possible to use a relatively coarse mesh to compute the numerical displacement field since the FE model does not capture the local deformation. This aspect means a consequent consistent gain in memory storage and computational time. Although these approaches reduce significantly the size of the model as compared to traditional FE based contact simulations, the procedure of matching the analytic and the FE solutions at a certain depth below the contact surface is computationally involved and it does not ensure a continuous displacement and stress field within the gear tooth. This fact is not discussed in the literature.

In this context, it is relevant to mention the work of Andersson–Vedmar [1], who introduced a method to calculate the tooth deformation under a known load applied on the gear teeth flanks: synthesized in Fig. 2, their approach exploits a finite element model in the pre-processing phase to extrapolate a stiffness function of the gear flank. This FE-based stiffness is combined with an analytic stiffness derived by the formula of Weber and Banaschek [27]. More conspicuously, in order to obtain the global (numerical) deformation field of Fig. 1 (and from that to derive the global stiffness), Andersson and Vedmar propose to perform two FE static analyses at each possible contact node. Both FE analyses are carried out under a unitary point load acting on the same FE model with different boundary conditions (BC). The two cases are shown on the right-hand side of Fig. 2, where the second element represents the partial model used to eliminate the local deformation from the total model (first element). Such partial model is obtained by clamping a tooth section located at a distance h underneath the tooth flank.

A similar approach has been proposed by Chang [5], who combines a global linear deformation (captured by a FE model) with a non linear local contact deformation described by means of an analytic formula for finite length line contact (proposed by Ding and Zhang [7]). The main difference with respect to the method [1] lays in the boundary conditions of the partial FE model used to correct for the local deformation. As shown in Fig. 3, the surfaces in orange are clamped while the load is applied on the right tooth flank. The dependency of the local deformation from mesh size and partial model boundary conditions remain an unsolved issue in [1, 5].

Differently from [1] or [5], Vijayakar [26] proposes a method where the FE solution and the analytic contact model are solved simultaneously at each time step. Numerical and analytic solutions are matched at the matching surface by solving a least-squares problem. Between the matching surface and the force location, Vijayakar uses the Boussinesq’s analytic solution for point load to describe the displacement field, while the numerical solution is considered to be valid in the remaining part of the gear.

1.3 Flexible multibody models for gear contact problems

Other authors modelled gears as flexible bodies in a multibody environment, where the use of conventional FE to represent flexible bodies can be rendered practical with the aid of model order reduction (MOR) techniques. Using the floating frame of reference formulation [20, Chapter 5.6], the linear elastic deformation of a flexible body is separated from the gross non-linear motion of its body reference, thus allowing linear MOR techniques to be applied for reducing the number of elastic DOFs of the body. However, these methods cannot readily be applied to general contact problems to yield computationally efficient reduced-order models (ROM): contact problems in multibody dynamics are characterized by significant variations in the location and size of the contact area and for a flexible body discretized using FE, this implies a multitude of possibly although not necessarily simultaneously loaded DOFs. Furthermore, as contact interactions generally involve steep stress gradients and relatively small volumes of stressed material, highly refined meshes are mandatory to capture correctly these stress fields. The multiple input–multiple output (MIMO) behaviour of the multibody-contact problem poses considerable difficulties to classical model reduction techniques, such as the traditional CMS [6].

Fig. 3
figure 3

The approach of Chang

Full size image

In this respect, some authors have proposed new procedures for the analysis of dynamic contact problems: the first successful attempt has been done with the static modes switching (SMS) method [11] where a discontinuous reduction space has been used to achieve accurate contact forces with a limited computational burden. Such method has been applied to the gear contact problems by Tamarozzi et al. [24] showing the applicability to examples of industrial relevance but posing some questions regarding the discontinuous behaviour of the reduction space. Particularly suitable to deal with loads moving across model boundaries are parametric model order reduction (PMOR) techniques, where the location of the contact force is parametrized in the full-order model and the parameter dependency is preserved throughout the reduction process. Relevant is the work of Blockmans et al. [3], where a PMOR scheme is developed and applied to gear contact problems. [3] uses a reduction space that consists of a truncated set of eigenvectors augmented with a parameter dependent set of static shape vectors. The static shape is computed by interpolating among a set of displacement modes of the interacting bodies obtained from a series of static contact analyses. The interpolation of these displacement modes is based on the parameter(s) describing the rigid-body configuration of the multibody system. In the field of bearing analysis, Fiszer et al. [8] proposes to combine the aforementioned PMOR technique with a semi-analytic contact model similar to the one described in [1]. The total deformation is separated in the global deformation of the rings and their support, represented by a parametrically reduced order model, and the non-linear local Hertzian deflections at the contact zone.

1.4 Contribution and structure

This work proposes a parametric model order reduction technique combined with a semi-analytic contact model. The combination of these two methods allows to overcome the main limitations of a standard penalty approach for describing the contact condition. First, we can describe the bodies’ deformation using a much lower number of DOFs since the local contact deformation is described by means of an analytic formulation. This allows to assemble particularly light reduced order models, with a significant gain in computational speed. Second, the dynamic contact problem using a semi-analytic model is characterised by a lower numerical stiffness as compared to standard non-linear FE with penalty formulation. As consequence, we can use a larger simulation time step while maintaining the same level of accuracy. Since in literature a systematic study on the assumptions which lay as foundations of semi-analytic contact model is not present and several key-issues remain not answered, in this paper we propose a novel approach that respects the physic of the contact problems. We compare the methodology with the semi-analytic methods often applied to gear contact problems, questioning their assumptions. We also implement a semi-analytic contact model in MUTANT (MUltibody Transient ANalysis of Transmissions—a code for gear dynamic problems) [13] and we apply it to spur and helical gears simulations. We validate static results against experimental data available in the literature, showing an excellent capability of capturing quantitative relevant behaviour such as static transmission error for different torque levels. Finally, we compare the obtained dynamic results with numerical results of the same parametric reduction scheme combined with standard penalty approach. The method used as reference in this case has been already presented and validated in [3].

The remainder of this paper is structured as follows. In Sect. 2, we describe the semi-analytic contact model: we discuss in detail how to combine analytic and numerical solution, comparing the proposed method with the models available in literature. In Sect. 3, we present the PMOR scheme, focusing on the definition of the reduction space and the interpolation of the static vectors. Sect. 4 deals with the integration of the semi-analytic contact model in the PMOR technique and Sect. 5 with its numerical implementation strategy. Finally, in Sect. 6, we propose the results of the novel methodology validated by means of comparison with both numerical and experimental data.

2 Semi-analytic contact model

Fig. 4
figure 4

Combined analytic-numerical model

Full size image

In this section we discuss the combination of an analytic formula with a numerical model for describing the contact condition. The section is divided in two parts as follows. The first part presents a novel theoretical method for combining analytic and numerical models: such a solution not only respects the boundary conditions of the given structural problem but also ensures continuity with respect to stresses and displacements. The second part addresses the method implemented in this work for combining analytic and numerical model. The method is compared against the novel theoretical approach as well as other solutions proposed in literature in order to analyse its physical limitations and accuracy.

2.1 Theoretical method for combining analytic and numerical model

The basic idea of combined numerical-analytic methods [1, 5, 26] consists in describing the solution of a given structural problem as combination of a numerical and an analytic solution allowing to obtain continuous displacement and stress fields which respect the boundary conditions of the original problem. The example shown in Fig. 4 can be taken as reference study case to illustrate the procedure: the actual problem on the left-hand side of the Fig. 4, shows the reference body, subjected to a contact force on the left face and essential boundary conditions on the bottom surface. The consequent deformation can be modelled as sum of a numerical and an analytic displacement field (Fig. 4—right side). This approach is shared by several authors [1, 5] and differs mainly for the spatial region extension where the analytic solution domain is considered valid (i.e. how far from the contact force location the analytic solution is still valid). Indeed one key-issue of the method consists in avoiding that the numerical solution describes the same deformation effect captured by the analytic model and that the sum of numerical and analytic solutions correctly represent the initial deformation field.

Closed form expressions of displacement and stress fields under an applied load are available in the literature (analytic models), but they are mathematically derived assuming that the body is of infinite extension. When such analytic expressions have to be combined with a numerical model of finite dimension, their domain has to be relegated to a finite region as well. It may be noticed that, when a finite (analytic) sub-region is cut out from the initial infinite (analytic) domain (Fig. 4 right), the analytic stress and displacement functions do not respect the new domain boundaries any more: for example stresses or displacements are identified also on surfaces respectively free or clamped in the actual problem.

The aim of the proposed method, inspired by acoustic applications, is to allow combining numerical and analytic models (Fig. 4—right side) while respecting the (physical) initial problem boundary conditions and to ensure continuity of displacement and stress fields.

2.1.1 Steps for implementing a combined numerical-analytic contact model.

  1. 1.

    Identify and isolate the two bodies in contact. The element shown in Fig. 4 (left side) represents schematically one of the two bodies in contact, i.e. one of the two gears, where the “physical” boundary conditions are applied (see point 4).

  2. 2.

    Choose the analytic formula to describe contact load and deformation field. In a semi-analytic contact model, one assumption consists in the a priori known load distribution on the body during contact. The analytic formula that describes the applied force and the consequent body deformation field must be known, but the process steps remain the same regardless the chosen specific formula.

  3. 3.

    Create the FE model. The body of Fig. 4 is discretized by means of FE mesh: the total displacement field of the actual problem is evaluated at the FE nodes locations and it is identified by the vector \(\mathbf {u}\). It can be calculated as follows:

    $$\begin{aligned} \mathbf {u} = \mathbf {u}^\mathrm {fe} + \mathbf {u}^\mathrm {an} \end{aligned}$$
    (1)

    where the vector \(\mathbf {u}^\mathrm {fe}\) represents the nodal displacements of the FE model, while \(\mathbf {u}^\mathrm {an}\) describe the analytic displacement field \(\mathbf {u}^\mathrm {an}(\mathbf {x})\), function of the spatial coordinate \(\mathbf {x}\), evaluated at the FE nodes location. Similar to the calculation of the displacement field, the stress field can be calculated as following:

    $$\begin{aligned} {\varvec{\sigma }} = {\varvec{\sigma }}^\mathrm {fe} + {\varvec{\sigma }}^\mathrm {an} \end{aligned}$$
    (2)
  4. 4.

    Impose the bodies boundary conditions. The boundary conditions for a body subjected to contact forces can be represented by the example of Fig. 5: here the element boundary domain \({\varvec{\Omega }}\) has been divided in three regions as follows:

    • \({\varvec{\Gamma }}\), where the essential boundary conditions on displacements are applied ;

    • \({\varvec{\Pi }}\), where the natural boundary conditions on loads are applied;

    • \({\varvec{\Theta }}\), identified as \(\varOmega - (\varGamma \cup \varPi )\).

    The natural boundary conditions on the loaded surfaces are imposed by the chosen contact formula (see point 2.), while the essential boundary conditions are dictated by the physics of the problem. Regardless of the particular analytic contact formulation, the following system of equations describes the developed approach and its solution provides a continuous displacement and stress field:

    $$\begin{aligned} \textit{Model}&{\left\{ \begin{array}{ll} \mathbf {u} &= \mathbf {u}^\mathrm {fe} + \mathbf {u}^\mathrm {an} \\ {\varvec{\sigma }} &= {\varvec{\sigma }}^\mathrm {fe} + {\varvec{\sigma }}^\mathrm {an} \end{array}\right. } \\ \textit{B.C.}&{\left\{ \begin{array}{ll} \mathbf {u}_\varGamma = \mathbf {\widehat{u}}_{imposed} \\ \qquad \textit{imposed disp. (essential B.C.)}\\ {\varvec{\sigma }}_\varPi = \mathbf {\widehat{\sigma }}_{imposed} \\ \qquad \textit{imposed loads (natural B.C.)} \\ \mathbf {\sigma _n}_\varTheta = \mathbf {0} \\ \qquad \textit{normal stresses null on} \\ \qquad \textit{external (free) surfaces} \end{array}\right. } \end{aligned}$$
    (3)
  5. 5.

    Derive the numerical boundary conditions. In this example the numerical model is a linear FE model, characterized by constant mass \(\mathbf {M}^\mathrm {fe}\) and stiffness \(\mathbf {K}^\mathrm {fe}\) matrices. Since the analytic displacement and stress fields (\(\mathbf {u}^\mathrm {an}\) and \(\ {\varvec{\sigma }}^\mathrm {an}\), respectively) are known from the chosen contact formula, the unknown \(\mathbf {u}^\mathrm {fe}\) is calculated solving the equations system 3 as following:

    $$\begin{aligned} \textit{Model}_{fe}&{\left\{ \begin{array}{ll} \mathbf {u}^\mathrm {fe} = \mathbf {u} - \mathbf {u}^\mathrm {an} \\ {\varvec{\sigma }}^\mathrm {fe} = {\varvec{\sigma }} - {\varvec{\sigma }}^\mathrm {an} \end{array}\right. } \\ \textit{B.C.}_{fe}&{\left\{ \begin{array}{ll} \mathbf {u}^\mathrm {fe}_{\varGamma } = \mathbf {u}_\varGamma - \mathbf {u}_{\varGamma }^\mathrm {an} \\ {\varvec{\sigma }}_{\varPi }^\mathrm {fe} = {\varvec{\sigma }}_{\varPi } - {\varvec{\sigma }}_{\varPi }^\mathrm {an} \\ {\varvec{\sigma }}_{n\varTheta }^\mathrm {fe} = \mathbf {0} - {\varvec{\sigma }}_{n\varTheta }^\mathrm {an} \end{array}\right. } \end{aligned}$$
    (4)

    Without loss of generality and for sake of exposition, we can assume that the initial model of Fig. 5 is clamped at \(\varGamma\), so \(\mathbf {u}_\varGamma = \mathbf {\widehat{u}}_{imposed}\,=\, \mathbf {0}\):

    $$\begin{aligned} \mathbf {u}_{\varGamma }^\mathrm {fe} = \mathbf {u}_\varGamma - \mathbf {u}_{\varGamma }^\mathrm {an} = - \mathbf {u}_{\varGamma }^\mathrm {an} \end{aligned}$$
    (5)

    In this way, the numerical model boundary conditions \(\mathbf {u}_{\varGamma }^\mathrm {fe}\), once combined with the analytic displacement field calculated on \(\varGamma\), respect the original model boundary conditions \(\mathbf {u}_{\Gamma }\). The same concept is applied to the natural boundary conditions and since the load in the original model coincides with the analytic forces distributions (\({\varvec{\sigma }}_{\varPi } = {\varvec{\sigma }}_{\varPi }^\mathrm {an}\)), the load on the numerical model \({\varvec{\sigma }}_{\varPi }^\mathrm {fe}\) is:

    $$\begin{aligned} {\varvec{\sigma }}_{\varPi }^\mathrm {fe} = {\varvec{\sigma }}_{\varPi } - {\varvec{\sigma }}_{\varPi }^\mathrm {an} = \mathbf {0} \end{aligned}$$
    (6)

    Finally, the numerical stress field on the free surfaces \(\varTheta\) can be calculated from the last equation of system 4. The numerical stress field is necessary to balance the analytic stress field on the analytic domain boundaries and will cause the FE model to deform (see Fig. 4). As result, the initial model physical condition of null normal stress on the free surfaces are satisfied.

    $$\begin{aligned} {\varvec{\sigma }}_{n\varTheta }^\mathrm {fe} = - {\varvec{\sigma }}_{n\varTheta }^\mathrm {an} \end{aligned}$$
    (7)

    By integrating \(\mathbf {\sigma _n}_{\varTheta }^\mathrm {fe}\) on the surface we can calculate the nodal forces \(\mathbf {F}_{\varTheta }^\mathrm {fe}\) of the numerical model. With these forces and the boundary conditions of Eq. (5) we can solve the numerical model and obtain as a solution the part of the deformation of the initial problem (Fig. 4) not captured by the analytic model.

  6. 6.

    Solve the numerical displacements field. From Eqs. (5), (6) and (7), the following set of Eq. (8) can be derived:

    $$\begin{aligned} \underbrace{ \begin{bmatrix} \mathbf {K}_{\varGamma \varGamma }&\mathbf {K}_{\varGamma \varPi }&\mathbf {K}_{\varGamma \varTheta }\\ \mathbf {K}_{\varPi \varGamma }&\mathbf {K}_{\varPi \varPi }&\mathbf {K}_{\varPi \varTheta }\\ \mathbf {K}_{\varTheta \varGamma }&\mathbf {K}_{\varTheta \varPi }&\mathbf {K}_{\varTheta \varTheta }\\ \end{bmatrix}}_{\mathbf {K}^\mathrm {fe}} \underbrace{ \begin{Bmatrix} \mathbf {u}_{\varGamma }^\mathrm {fe}\\ \mathbf {u}_{\varPi }^\mathrm {fe}\\ \mathbf {u}_{\varTheta }^\mathrm {fe} \end{Bmatrix}}_{\mathbf {u}^\mathrm {fe}} = \begin{Bmatrix} \mathbf {F}_{\varGamma }^\mathrm {fe}\\ \mathbf {F}_{\varPi }^\mathrm {fe}\\ \mathbf {F}_{\varTheta }^\mathrm {fe}\\ \end{Bmatrix} \end{aligned}$$
    (8)

    where the unknown displacement vector \(\mathbf {u}^\mathrm {fe}\) and the matrix \(\mathbf {K}^\mathrm {fe}\) have been partitioned following the surfaces definition above. The vector \(\mathbf {u}_{\varGamma }^\mathrm {fe}\) is directly solved by using Eq. (5) while the forces vector \([ \mathbf {F}_{\varPi }^{\mathrm {fe}T} \ \mathbf {F}_{\varTheta }^{\mathrm {fe}T}]^\mathrm{T}\) of system 8 is computed from Eqs. (6) and (7) by integrating on the FE surfaces. The unknown part of \(\mathbf {u}^\mathrm {fe}\) (\([ \mathbf {u}_{\varPi }^{\mathrm {fe}T} \ \mathbf {u}_{\varTheta }^{\mathrm {fe}T}]^\mathrm{T}\)) can be computed by:

    $$\begin{aligned} \begin{Bmatrix} \mathbf {u}_{\varPi }^\mathrm {fe}\\ \mathbf {u}_{\varTheta }^\mathrm {fe} \end{Bmatrix} =&\begin{bmatrix} \mathbf {K}_{\varPi \varPi }&\mathbf {K}_{\varPi \varTheta }\\ \mathbf {K}_{\varTheta \varPi }&\mathbf {K}_{\varTheta \varTheta }\\ \end{bmatrix}^{-1} \begin{Bmatrix} \mathbf {F}_{\varPi }^\mathrm {fe}\\ \mathbf {F}_{\varTheta }^\mathrm {fe}\\ \end{Bmatrix} \nonumber \\&-\begin{bmatrix} - \mathbf {K}_{\varPi \varGamma }\\ \mathbf {K}_{\varTheta \varGamma } \end{bmatrix} \begin{Bmatrix} \mathbf {u}_{\varGamma }^\mathrm {fe}\\ \end{Bmatrix} \end{aligned}$$
    (9)

    The displacements vector \(\mathbf {u}^\mathrm {fe} = [\mathbf {u}_{\varGamma }^{\mathrm {fe}T} \ \mathbf {u}_{\varPi }^{\mathrm {fe}T} \ \mathbf {u}_{\varTheta }^{\mathrm {fe}T}]^\mathrm{T}\) is computed from Eqs. (5) and (9). Such vector, combined with the analytic displacement vector \(\mathbf {u}_{an}\), respects the initial problem boundary conditions ensuring continuous displacement and stresses fields (see Eqs. 1, 2) and is such that \(\mathbf {u} = \mathbf {u}^\mathrm {fe} + \mathbf {u}^\mathrm {an}\) as requested.

Fig. 5
figure 5

Boundary conditions scheme of the actual problem

Full size image

In the case of dynamic gear contact problems, the presented method implies the numerical integration of the stress field of Eq. (7) on a geometrically complex domain where the force distribution changes in time. This makes the computational cost particularly high. Moreover the contact forces and hence the surface stresses that need to be integrated (Eq. 7) depend on the actual position and deformation of the body in space, which in turn depend on the inertia and damping forces [not included in Eq. (8), see Eq. (25)]. However the method remains suitable for problems where the body domain is regular and it is the only method that assures a continuous stress and displacement field.

2.2 Global attachment modes set

Fig. 6
figure 6

Total and partial model used to compute the global displacement field of Eq. (10)

Full size image

An attachment mode is defined by Craig [6] as the displacement vector obtained by applying a unit load to a selected degree of freedom. In this work, we define as Global Attachment Mode the deformation patter obtained by applying a unit load to a certain degree of freedom and discarding the local deformation that occurs in proximity of the force location. In order to extract only the global displacement field, the method proposed by Chang [5] has been used in this work and further developed within the MOR technique (see Sect. 4.3). Therefore the global displacement vector \(\mathbf {u}_{fe}\) of Eq. (1) is calculated as

$$\begin{aligned} \mathbf {u}^\mathrm {fe} = \mathbf {u}^\mathrm {fe}_{total} + \mathbf {u}^\mathrm {fe}_{partial} \end{aligned}$$
(10)

Looking back at the system of Eq. (3), it is already clear that this approach does not ensure a continuous stress field. The two displacement fields \(\mathbf {u}^\mathrm {fe}_{total}\) and \(\mathbf {u}^\mathrm {fe}_{partial}\) are calculated using the FE model shown in Fig. 6, which has the base clamped in the total model and a clamped vertical section in the plane YZ in the partial model, perpendicular to the force direction and located at a distance h from the force application point. When the two FE deformation fields, total and local, are summed together, the displacement gradient present in the local model nearby the clamped section, introduces a stress field in the global model that has no physical meaning. The global model should indeed capture stress and deformation due to the body bending and no residual of the local deformation should be present. However, by moving the clamped section further from the force location, the stresses introduced in proximity of the clamped surface have a lower magnitude than in the other cases. It is indeed one of the goal of this article to evaluate quantitatively the influence of the clamped section in the partial model. Nevertheless also by varying the position of the clamped section, the method does not respect the condition of Eq. (3) necessary for obtaining a continuous stress field. By means of model shown in Fig. 6 we evaluate the influence of the distance h between the force location and the clamped section in the partial model. The position of the clamped surface determines indeed the main difference between the methods proposed by Chang and Andersson–Vedmar.

Figures 7 and 8 illustrate the effects on the stress field of the position of the clamped section used in the partial model. In particular we propose three cases where the clamped section is gradually moved further from the force location and we plot the stresses in the same direction of the applied force as well as the von Mises stresses. In each plot we can observe the the stress field of the globally deformed body that should have a component only in proximity of the body base (due to the bending). However, the use of a sub-model to eliminate the local deformation component implies the presence of a residual stress in proximity of the vertical clamped section. The magnitude of such induced stress becomes less relevant compared to the bending stress value by increasing the distance h between the clamped section and the force location.

Fig. 7
figure 7

Stress field in the globally deformed body calculated in x-direction varying the position of the clamped vertical section

Full size image
Fig. 8
figure 8

Stress field in the globally deformed body calculated at the element centres (von Mises) varying the position of the clamped vertical section

Full size image

It can be concluded that the accuracy of the method on a stress level depends on the distance of the clamped section from the force application point and from the mesh size. Neither the solution proposed by Vijayakar [26] ensures a continuous stress field and its computational time, although less expensive than high-fidelity FE models, is much higher than the approaches proposed by Andersson [1] or Chang [5]. In term of accuracy on the stress field, the limitations of the method proposed by Chang [5] are overtaken by the numerical advantages in the gear application case. Moreover, the level of introduced von Mises stress in correspondence of the clamped surfaces is less than 5% of the stress level at the tooth root (due to the bending). This makes the former negligible even if non-physical. Finally, von Mises stress analysis is generally used in gear applications for evaluating durability and failure prediction during a post-processing phase. However, in the final part of this work, we assess the accuracy of the combination of semi-analytic contact model with MOR technique through the analysis of Transmission Error. This quantity is influenced mainly by the accuracy on a displacement level of the contacting tooth. In this respect, we show in Sect. 6 that Eq. (10) provides a sufficient level of accuracy.

3 Paramentric model order reduction technique

The PMOR technique considered in this section has been developed by Blockmans et al. [3], starting from the work of [23], as an adaptation of the traditional CMS approach. The method exploits a reduction space consisting of a truncated set of eigenvectors augmented with a parameter-dependent set of static shape vectors. Such static vectors are obtained by interpolating among a set of global contact shapes, which represent the displacement modes of the interacting bodies obtained from a series of static contact analyses.

3.1 Reduction space

The PMOR scheme adopted here belongs to the class of projection-based methods. In general, the aim of MOR techniques is to reduce the number of DOFs of the full-order model. In this case, the number n of nodal DOFs of the Full Order Model (FOM) of the gears, discretized by means of the Finite Element Method, can easily reach up to \(n \approx 10^{5-6}\), far too high to be integrated dynamically in an efficient manner. In order to alleviate the computational cost, the nodal displacements vector of the ith gear, indicate by \(\mathbf {u}_f^i \in \mathbb {R}^{n \times 1}\), is approximated by a vector of lower dimension as follows:

$$\begin{aligned} \mathbf {u}_f^i \approx \mathbf {V}^i {\varvec{{\eta }}}^i \end{aligned}$$
(11)

where \(\mathbf {V}^i \in \mathbb {R}^{n \times n_{\eta }}\) is the model reduction space and \({\varvec{{\eta }}}^i \in \mathbb {R}^{n_{\eta } \times 1}\) is the generalized elastic coordinates vector. The reduction space \(\mathbf {V}^i\), used to reduce the model, is composed by two components:

$$\begin{aligned} \mathbf {V}^i = {[{{\varvec{{\Phi }}}^i } \ \ {\varvec{{\Psi }}}^i ]} \end{aligned}$$
(12)

where \({\varvec{\Phi }}^i\) indicates a set of eigenvectors, truncated in order to capture the dominant physic of the problem, while the computation and interpolation (based on the rigid-body configuration of the multibody system) of the parameter-dependent set of static shape vectors \({\varvec{\Psi }}^i\) are explained in the next paragraph.

3.2 Global contact shape calculation

A global contact shape \(\mathbf {S}^i\) is defined as the displacement mode of the ith meshing gear obtained from a static contact analysis of the gear pair, locked at a certain configuration and experiencing a defined external torque. At each angular position and applied torque will correspond a certain global contact shape. In order to calculate a global contact shape, the following non-linear system has to be solved:

$$\begin{aligned} \begin{bmatrix} 0&\varvec{0}&\varvec{0}\\&\varvec{K}_{FE}^1&\varvec{0} \\ sym. &{} &\varvec{K}_{FE}^2 \end{bmatrix} \begin{Bmatrix} \theta _1\\ \varvec{u}_f^1\\ \varvec{u}_f^2 \end{Bmatrix} = \begin{Bmatrix} T^1\\ \varvec{0}^\mathrm{T}\\ \varvec{0}^\mathrm{T} \end{Bmatrix} + \varvec{Q}_C \end{aligned}$$
(13)

where \(\varvec{S}^1 = \varvec{u}_f^{1}\) and \(\varvec{S}^2 = \varvec{u}_f^{2}\), \(\varvec{Q}_C\) represent the contact force vectors and it is calculated by means of a penalty contact formulation. Finally \(\varvec{K}_{FE}\) identifies the FE stiffness matrix of the ith gear. The solution of the system of Eq. (13) corresponds to the static equilibrium of the two gears in contact with each other, given their angular positions (in cinematic condition) and the applied external torque (\(T^1\)). The unknowns \(\theta _1\), \(\varvec{u}_f^1\) and \(\varvec{u}_f^2\) correspond respectively to the angle of the gear 1 (driving gear) and the displacement modes of gear 1 and 2 at static equilibrium. When the static equilibrium is reached, the unknown \(\theta _1\), due to the gears deformation, is different from the cinematic angle of gear 1; the angle \(\theta _2\) of gear 2 (driven gear) is instead held fixed.

By evaluating the system of Eq. (13) for different angular positions \(n_\theta\) of the gear pair and different torques \(n_t\) applied to the driven gear, the set of static shape vectors \(\varvec{S}^i\) is assembled. Multiple levels of torque ensure that the non-linear relationship between applied torque and resulting nodal displacements is properly captured. The result is a set of \(n_s = n_\theta \times n_t\) global contact shapes. For more details about the choice of \(n_\theta\) and \(n_t\) we refer the interested reader to [3]. Finally, in order to obtain dynamic decoupling between the elastic coordinates corresponding to \(\varvec{S}^i\) and \(\varvec{\varPhi }^i\), the global contact shapes obtained from the system of Eq. (13) must be made residual with respect to the vectors \(\varvec{\varPhi }^i\). In such case it can be shown [24] that the resulting global contact shapes satisfy the following relations:

$$\begin{aligned} \varPhi ^{i \ T} M_{FE}^{i} S^i = 0 \ , \ \varPhi ^{i \ T} K_{FE}^{i} S^i = 0 \end{aligned}$$
(14)

where \(M_{FE}\) represents the FE mass of the ith gear.

3.2.1 Interpolation of the global contact shapes

The static shape vectors \(\varvec{\varPsi }^i\) are obtained by interpolating among the set of global contact shapes \(\varvec{S}^i\), based on the current configuration of the gear pair.

The PMOR method is not restricted to a specific interpolation scheme. In this work a linear interpolation scheme has been used to construct the static shape vectors. Denoting the global contact shapes corresponding to \(\theta ^{i}=\theta ^{i}_{s}\) by \(\varvec{S}^{i}_{s}\) and the ones corresponding to \(\theta ^{i}=\theta ^{i}_{s+1}\) by \(\varvec{S}^{i}_{s+1}\), the matrix of static shape vectors \(\varvec{\varPsi }^{i}\) at an intermediate angle \(\bar{\theta }^{i}\) can be defined by using the following linear interpolation formula:

$$\begin{aligned} \varvec{\varPsi }^{i}=(1-p)\varvec{S}^{i}_{s} + p\varvec{S}^{i}_{s+1} \in \mathbb {R}^{n \times n_t} \end{aligned}$$
(15)

where p is a parameter depending only on the angular position \(\theta ^{i}\) of the gear. The relation between p and \(\bar{\theta }^{i}\) is linear and can be written explicitly as

$$\begin{aligned} p=\frac{\bar{\theta }^{i}-\theta ^{i}_{s}}{\theta ^{i}_{s+1}-\theta ^{i}_{s}}=\frac{\bar{\theta }^{i}-\theta ^{i}_{s}}{\Delta \theta ^{i}} \end{aligned}$$
(16)

where the angular increment \(\triangle \theta ^{i}\) is defined as \(\Delta \theta ^{i} = \theta ^{i}_{s+1}-\theta ^{i}_{s}\). Hence, the parametric reduction space \(\varvec{V}^{i}\) that underlies the presented PMOR technique is composed of a constant set of eigenvectors \(\varvec{\varPhi }^{i}\) and a configuration -dependent set of interpolated global contact shapes \(\varvec{\psi }^{i}(\theta ^{i})\):

$$\begin{aligned} \varvec{V}^{i}(\theta ^{i}) = \begin{bmatrix} \varvec{\varPhi }^{i} \, \varvec{\varPsi}^{i}(\theta ^{i}) \end{bmatrix} \\ = \begin{bmatrix} \varvec{\varPhi}^{i} \, (1-p(\theta ^{i}))\varvec{S}^{i}_{s} + p(\theta ^{i})\varvec{S}^{i}_{s+1} \end{bmatrix}\end{aligned}$$
(17)

4 Semi-analytic contact model in a parametric model order reduction scheme

This section illustrates the procedure for combining the semi-analytic contact model together with the PMOR technique presented in the previous section. In the first part, an overview on the calculation of the standard global contact shapes by means of a ROM is given; such ROM problem is modified in the second part in order to separate the local contact deformation from the gear total deformation. Finally, the ROM is combined with a Hertzian contact model for calculating the contact forces and a new basis for the PMOR scheme is assembled.

4.1 The ROM for calculating the global contact shapes

In the standard PMOR technique, the system of non-linear equations (Eq. 13) necessary for calculating the set of global contact shapes is solved by means of a statically complete ROM in order to limit the overall cost of the computation [23]. The reduction of the FOM is performed with a standard CMS method, where the reduction space \({\varvec{{\psi }}}_{CMS}^i \in \mathbb {R}^{n \times n_{c}}\) contains one static attachment mode for each nodal degree of freedom j \((j=1\ldots n_{c})\) that can be possibly loaded during the computation of the shapes (hence all the nodes on the gears flanks that can go in contact). Each attachment mode represents the displacement vector calculated when the corresponding degree of freedom is loaded.

The matrix \(\varvec{\psi }_{CMS}^i\) is used to transform Eq. (13) to an equivalent system of reduced dimension as follow:

$$\begin{aligned} \left[ \begin{array}{ccc} 0 &{} \varvec{0} &{} \varvec{0}\\ &{} \varvec{K}_{CMS}^1 &{} \varvec{0}\\ sym. &{} &{} \varvec{K}_{CMS}^2\\ \end{array}\right] \left\{ \begin{array}{c} \theta _1\\ \varvec{u}_{CMS}^1\\ \varvec{u}_{CMS}^2\\ \end{array}\right\} = \left\{ \begin{array}{c} T^1\\ \varvec{0}^\mathrm{T}\\ \varvec{0}^\mathrm{T}\\ \end{array}\right\} + \tilde{\varvec{Q}}_{pen} \end{aligned}$$
(18)

where

$$\begin{aligned} \varvec{K}_{CMS}^i = \varvec{\psi }_{CMS}^{iT} \varvec{K}_{FE}^i \varvec{\psi }_{CMS} ^{i} \in \mathbb {R}^{n_c \times n_{c}} \end{aligned}$$
(19)

and the vector \(\varvec{u}_{CMS}^i\) represents the modal participation factors of the reduction space \(\varvec{\psi }_{CMS}\). The projected contact forces \(\tilde{\varvec{Q}}_{pen}\) are calculated by projecting the physical contact forces on the reduced space; the physical forces are calculated by means of a standard penalty formulation, so by multiplying the penetration gap between the teeth in contact by a chosen penalty factor. Indications about how to choose the penalty factor are given in [24], that generally should be 2 order of magnitude stiffer than the bodies involved into contact. Finally the linear combination of the modal participation factors \(\varvec{u}_{CMS}^i\), calculated by solving the system of Eq. (18) at a certain angular position and torque level, is used to compute one displacement mode \(\varvec{S}^i_s = \varvec{\psi }_{CMS}^i \varvec{u}_{CMS}^i\).

4.2 The new reduction space for the ROM problem

In the proposed method, the calculation of contact forces and reduction space of the ROM are modified with respect to the scheme illustrated previously. The procedure to calculate the new reduction space of the ROM consists in the following steps:

  1. 1.

    Calculate \(\varvec{\psi }_{glob}^{i}\), the global attachment modes set. A global attachment mode is defined as the static displacement vector of the system when a certain DOF is subjected to a unit load but excluding the local deformation close to the load application point. The procedure to extract the local deformation is explained in Sect. 2.2. Then the new set includes one mode for each nodal DOF that can possibly be loaded during the computation of the shapes (for each gear). The result is a mode set that describes the tooth bending and shearing for each possible force input location.

  2. 2.

    Calculate the new reduction space \(\varvec{\psi }_{sv}^i\) of the ROM. The matrix \(\varvec{\psi }_{glob}^i\) contains all the global attachment modes but, in this case, the displacement vectors represented by such modes describe “almost” the same physical phenomena. Therefore a singular values decomposition (SVD) is performed in order to avoid having badly conditioned reduced matrices. The result is the matrix \(\varvec{\psi }_{sv}^i \in \mathbb {R}^{n \times n_{sv}}\), whose dimensions are significantly lower with respect to the above -mentioned standard \(\varvec{\psi }_{CMS}^i \in \mathbb {R}^{n \times n_{c}}\), reducing drastically the numerical complexity of solving Eq. (18). The procedure to assemble the new reduction space \(\varvec{\psi }_{sv}^i\) is illustrated in Table 1.

The number \(n_{sv}\) of retained SVs is selected by means of an energy-based criterion (as explained in Table 1) in order to conserve a user-defined percentage \(p_{en}\) of the system deformation energy.

Table 1 SVD process
Full size table

The new projection matrix \(\varvec{\psi }_{sv}^i\) is used to reduce the FOM problem, obtaining an equivalent system of reduced dimension shown in Eq. (23). By solving such system, the unknown modal participation factors \(\varvec{u}_{sv}^i\) can be calculated for a certain angular position and torque level. Finally they will be used to construct a new displacement modes set as \(\varvec{S}_{s,sv}^i = \varvec{\psi }_{sv}^i \varvec{u}_{sv}^i\) and the new global contact shape is calculated by interpolating within the displacement modes set.

4.3 Contact force calculation

As first step of the implemented semi-analytic contact model within the PMOR technique, the local contact deformation has been separated from the numerical solution. Hence, the new global contact shape, calculated from Eq. (23), describes the gear body deformation as well as the teeth bending and shearing, without taking into consideration the local deformation in correspondence of the contact points. This part of the deformation is described by the contact model and used to calculate contact forces and local stress field.

In this case the contact forces cannot be calculated by imposing a non-penetration condition for the teeth flanks, like in the classical penalty approach for contact problem (by using for example the Signorini’s condition [28, Chapter 5.1]). If so, the two gears would be able neither to penetrate each other nor locally deform, resulting in an overestimation of the total contact stiffness. Therefore the contact model has to allow a certain penetration between the teeth flanks: such penetration gap has to match the local deformations of the teeth flanks that are not captured by the numerical ROM (and represented by the red area on the right-hand side of Fig. 9).

Fig. 9
figure 9

Classic penalty approach (left) and semi-analytic contact method (right)

Full size image

The output contact forces are calculated starting from the penetration gap between the teeth flanks. The contact model uses a formula (Eq. 20) derived from the Hertz theory by Harris and Kotzalas [10, Chapter 6.3] in case of parallel axes cylinders in contact with each others (with ideal line contact)Footnote 1 :

$$\begin{aligned} \alpha =&\frac{2P }{\pi l} \Big (\frac{1-\nu _1^2}{E_1} + \frac{1-\nu _2^2}{E_2}\Big ) \cdot \nonumber \\&\ln \Big [ \frac{\pi l^2}{P } \Big (\frac{1}{R_1} + \frac{1}{R_2}\Big ) \Big (\frac{1-\nu _1^2}{E_1} + \frac{1-\nu _2^2}{E_2}\Big )^{-1} \Big ] \end{aligned}$$
(20)

where \(\alpha\) represents the amount of penetration due to the force P, \(R_1 \text { and } R_2\) the curvature radii of the cylinders at the contact location, l the contact length while \((\nu _1,E_1) \text { and } (\nu _2,E_2)\) identify respectively the Poisson’s ratio and the Young’s modulus of the two cylinders materials (Fig 10).

Fig. 10
figure 10

Contact between two cylinders with parallel axes [18]

Full size image

Moreover it has to be underlined that the method proposed in this paper is not restricted to the analytic formula described by Eq. (20) to represent the local contact deformations. The latter has however been selected due to its rather limited number of assumptions, hence it can be used for different gear meshing scenarios. In the implemented method, the Eq. (20) is numerically inverted in order to find from the penetration gap \(\alpha\) the output force P. The amount of penetration gap is computed by a contact detection algorithm that is illustrated in Sect. 5.1. Moreover the teeth axial width is divided in sections according to the axial sections of the finite elements model and the contact forces are calculated on all the sections where the contact occurs. Therefore in this model there is no coupling between the slices in the local effect, which is a fair assumption due to the exponential decay of the local deformation from the location of the applied force [12, Chapter 2.1]. Finally the contact force distribution can be calculated according to the Hertz hypothesis:

$$\begin{aligned} p = \sqrt{\frac{2P}{\pi l }\left( \frac{1-\nu _1^2}{E_1} + \frac{1-\nu _2^2}{E_2}\right) ^{-1} \left( \frac{1}{R_1} + \frac{1}{R_2}\right) } \end{aligned}$$
(21)

The distribution p is integrated in the numerical model along a rectangular domain of size \(l \times 2\beta\), where l is the half-section length and \(\beta\) is the semi-width of the contact surface. The latter is calculated from [10, Chapter 6.3] as following:

$$\begin{aligned} \beta = \sqrt{ \frac{4P}{\pi l} \left( \frac{1-\nu _1^2}{E_1} + \frac{1-\nu _2^2}{E_2}\right) \left( \frac{1}{R_1} + \frac{1}{R_2}\right) ^{-1} } \end{aligned}$$
(22)

In such manner there are no a-priori assumptions of constant pressure distribution along the whole tooth flank, but only within each axial slice in contact. The result is a set of nodal physical contact forces. As final remark, the variables of the contact Eq. (20), such as radii of curvature and contact length that depends on the current contact location, are evaluated considering the geometry of the globally deformed bodies.

4.4 New reduction space

The new global contact shape can be calculated by solving the ROM problem of Eq. (23).

$$\begin{aligned} \begin{bmatrix} 0&\varvec{0}&\varvec{0}\\&\varvec{K}_{sv}^1&\varvec{0}\\ sym.&\varvec{K_{sv}}^2 \end{bmatrix} \begin{Bmatrix} \theta _1\\ \varvec{u}_{sv}^1\\ \varvec{u}_{sv}^2 \end{Bmatrix} = \begin{Bmatrix} T^1\\ \varvec{0}^\mathrm{T}\\ \varvec{0}^\mathrm{T} \end{Bmatrix} + \tilde{\varvec{Q}}_{hertzian} \end{aligned}$$
(23)

The system has been reduced with the matrix \(\varvec{\psi }_{sv}\), that together with \(\varvec{K}_{sv}^i\) and \(\varvec{u}_{sv}^i\), is presented in Sect. 4.2. The projected contact forces are calculated as \(\tilde{\varvec{Q}}_{hertzian} = \varvec{\psi }_{sv}^\mathrm{T} \varvec{Q}_{hertzian}\), where the computation of the physical contact forces \(\varvec{Q}_{hertzian}\) is illustrated in Sect. 4.3. The results is a new set of displacement modes, each calculated as \(\varvec{S}_{s,sv}^i = \varvec{\psi }_{sv}^i \varvec{u}_{sv}^i\), varying angular position and torque level. As in Eq. (12), the reduction space can be written as by interpolating among the displacement modes set \(\varvec{S}_{sv}^i\):

$$\begin{aligned} \tilde{\varvec{V}}^i = {[ \varvec{\varPhi }^i \ \varvec{\varPsi }_{sv}^i(s) ]} \end{aligned}$$
(24)

The number of DOFs of \(\tilde{\varvec{V}}^i\) is the same as \(\varvec{V}^i\) of the PMOR scheme presented initially (Eq. 12), but there are consistent computational advantages in both assembling (pre-processing) and using (processing) the new proposed reduction matrix that will be illustrated in the next section.

5 Computer implementation

The implementation of the PMOR technique combined with a semi-analytic contact model is discussed. The main features of the method are illustrated in this section, and applied to two gear pairs in Sects. 6.1 and 6.2. In order to perform a dynamic simulation using such scheme, a phase of pre-processing, processing and post-processing is required. During pre-processing phase the basis matrices \(\tilde{\varvec{V}}^i\) of Eq. (24) are computed and, making use of such matrices, the equation of motions are reduced and solved in the subsequent processing phase.

5.1 Pre-processing phase: computing the basis matrices

In the pre-processing phase the basis matrices \(\tilde{\varvec{V}}^i\) of Eq. (24) are assembled after calculating eigenvectors and global contact shapes of the two gears. The required steps to their computation are illustrated in the flowchart of Fig. 11. The inputs to this phase are the FE mass and stiffness matrices (\(\varvec{M}^i_{FE}\) and \(\varvec{K}^i_{FE}\)) and the corresponding vectors of the undeformed nodal coordinates (\(\varvec{u}_0^i\)), while the inner bores of the two gears are constrained to the center points by means of rigid multipoint constraints. The eigenvectors \(\varvec{\varPhi }^i \in \mathbb {R}^{n \times n_{k}}\) of the two gears correspond to the \(n_k\) lowest eigenfrequency retaining their center point fixed. The global contact shape \(\varvec{S}^i\) is defined as the gear static deformation for a fixed angular configuration and under an applied torque: each combination of \(T^i\) and \(\varTheta ^i\) represents a sampling point of the parametric model order reduction scheme. In the present work, the global contact shapes are computed for a set of external torques, typically 2 or 3, while the angular sampling points are selected equidistantly along one angular pitch of the driving gear, taking advantage of the symmetry of the gears. The set of global contact shape is computed using a ROM model and a semi-analytic contact model (see Sect. 4.2). Due to the use of the modified CMS approach proposed in this work, the local deformation is separated by the rest of the deformation of the ROM (and captured by the analytic contact model), further reducing the computational effort of solving the FOM. Eq. (23), that corresponds to the ROM problem, is solved iteratively for a particular combination of \(T^i\) and \(\theta ^i\). Within each iteration a sub-loop is necessary to compute the contact forces due to the non-linear nature of the analytic contact model. The loop starts from the position of the non-locally deformed gears for evaluating the local contact parameters characteristic of Eq. (20), such as curvature radii and length of contact. Then, using Eqs. (20) and (22), the contact pressure distribution is calculated and integrated on the FE model to obtain the nodal contact forces of the FOM. Such forces are projected on the ROM space and Eq. (23) can be solved.

Once the global contact shapes have been computed, a mass orthonormalization procedure is performed to make these vectors residual with respect to the set of kept eigenvectors, \(\varvec{\varPhi }^i\), in order to allow faster inversions of the reduced matrices in the processing phase. A detailed description of this procedure can be found in [3], as well as the procedure to calculate the mass and stiffness invariants of the gears. These data, along with the eigenvectors and global contact shapes of the gears, are sent to the processing phase of the simulation.

Fig. 11
figure 11

Flowchart for the offline calculation of the reduction basis \(\varvec{V}^i\)

Full size image

5.2 The processing phase: solving the equations of motion

The steps for efficiently solve this system have been illustrated by Blockmans et al. [3], hence only the new implemented contact model will be explained in this section. The equations of motion of the gear pair have the form of a system of non-linear second-order ordinary differential equations and they can be written in the following form:

$$\begin{aligned} \varvec{M}^{i}(\varvec{q}) \ddot{\varvec{q}}^{i} + \varvec{K}^{i} \varvec{q}^{i} = \varvec{Q}^{i}_{e}(\varvec{q},t) + \varvec{Q}^{i}_{c}(\varvec{q}) + \varvec{Q}^{i}_{v}(\varvec{q},\dot{\varvec{q}}) \end{aligned}$$
(25)

where \(\varvec{q}^{i}\) represents the vector of generalized coordinates of the ith gear, defined as:

$$\begin{aligned} {\varvec{q}^{i}}^\mathrm{T} = \{\theta ^{i}\;{\varvec{\eta }^{i}}^\mathrm{T}\} \in \mathbb {R}^{1\times n_{q}} \end{aligned}$$
(26)

The vectors \(\varvec{Q}^{i}_{e}, \ \varvec{Q}^{i}_{c}\) represent respectively the external and the contact forcesFootnote 2, while the quadratic velocity vector, which contains the gyroscopic and Coriolis force components, is defined as

$$\begin{aligned} \varvec{Q}^{i}_{v} = -\dot{\varvec{M}}^{i} \dot{\varvec{q}}^{i} + \frac{1}{2} \left[ \frac{\partial }{\partial \varvec{q}^{i}} \left( \dot{\varvec{q}}^{i^\mathrm{T}} \varvec{M}^{i} \dot{\varvec{q}}^{i}\right) \right] ^\mathrm{T} \end{aligned}$$
(27)

The inputs to this phase consist of the initial conditions \(q_i(0)\) and \(\dot{q}_i(0)\), the external loads \(Q_e^i(t)\) and the data computed during the pre-processing phase, that is the mass invariants and basis vectors [20, Chapter 5.6]. In order to solve system of Eq. (25) by means of an explicit fourth-order Runge–Kutta solver [2, Chapter 4.2], the previous equations are converted into a first-order system as following:

$$\begin{aligned} \dot{\varvec{y}}^{i} = \left\{ \begin{array}{c} \dot{\varvec{q}}^{i} \\ \ddot{\varvec{q}}^{i} \end{array} \right\} = \left\{ \begin{array}{c} \dot{\varvec{q}}^{i} \\ \varvec{M}^{i^{-1}} \{ \varvec{Q}^{i}_{e} + \varvec{Q}^{i}_{c} + \varvec{Q}^{i}_{v} - \varvec{K}^{i} \varvec{q}^{i}\} \end{array} \right\} \nonumber \\ \in \mathbb {R}^{2 n_{q} \times 1} \end{aligned}$$
(28)

where the state vector \(y^{i}\) is twice the size of the vector of generalized coordinates \(q^{i}\).

During the processing phase, the rigid-body parameters needed for interpolating among the set of pre-computed global contact shapes are calculated. By means of those parameters the reduction basis V of Eq. (11) is interpolated. Next, the right-hand side of Eq. (28) is constructed. The contact forces \(\varvec{Q}^{i}_{c}\) are computed by using the contact model presented in Sect. 4.3. The presented method requires the inversion of a non-linear equation to find from the penetration gaps the corresponding distributed contact forces. As consequence, the computational cost for solving each time-step is higher with respect to a standard penalty-based contact algorithm. Despite this, the numerical stiffness of the problem, the ratio between contact force and penetration gap in the new contact model is much lower (at least two orders of magnitude) than the penalty factor generally used in a standard penalty approach. The ratio between contact force and penetration gap could be defined as a new penalty factor, that is in this case based on the physic of the problem and derived by the Hertz theory and it is not a numerical expedient to approximate the Signorini’s conditions. The lower magnitude of the physic-based penalty factor allows the use of an higher time step for the solver with a consequent consistent gain in the computational time required in dynamic simulations. An example is shown in Sect. 6.2, where the proposed approach is compared with the method developed by Blockmans et al. [3] and already validated by means of numerical comparison against full order FE simulations. In both cases, the dimensions of the dynamic problem are dictated by the reduction basis \(\varvec{V}\) of Eq. (11), so they do not depend on the chosen method (standard-penalty approach or Hertz based penalty formulation) but on the selected number of global contact shapes and retained normal modes (as explained in Sect. 3.1).

6 Numerical results

In this section the proposed PMOR technique combined with a semi-analytic contact model (combined PMOR-Hertz) is applied to several gear contact examples. Results are analyzed with respect to accuracy and computational time, providing both experimental and numerical comparisons. The combined PMOR-Hertz strategy is implemented in the KU Leuven code MUTANT (MUltibody Transient ANalysis of Transmissions—a code for gear dynamic problems) [13]. MUTANT has been already used by Blockmans et al. [3] to numerically validate the PMOR technique presented in Sect. 3 (and referred to as PMOR-standard). Concerning validations, the experimental data obtained by a single flank gear-testing machine developed by Kurokawa in [15] are used to compare Static Transmission Error (STE) results. Both spur and helical gears are analyzed providing a very valuable experimental validation of both the PMOR techniques analyzed. The two proposed methods are briefly compared in Table 2.

Table 2 Numerical codes characteristics
Full size table

6.1 Static results

Example 1

The first example case concerns a series of static simulations of a spur gear pair. Manufacturing parameters and operating conditions of the studied gears are taken by the work of Kurokawa [15] and displayed respectively in Tables 3 and 4. For this gear pair Kurokawa measured the STE in function of the rotational angle of the driven gear, varying the applied load. In particular, the specific load varies from 22 N/mm until 392 N/mm and it identifies the applied load per unit of length at the operating pitch point in a normal direction with respect to the tooth involute.

Table 3 Gears manufacturing parameters
Full size table
Table 4 Performed static analyses
Full size table

The conditions detailed in Tables 3 and 4 have been reproduced numerically using both the PMOR standard and the combined PMOR-Hertz. A series of static simulations for different angular configurations of the gears has been performed covering the full length of the path of contact for each loading condition. Practically the series of static analyses is obtained by locking gear 2 at discrete angular configurations and applying the desired torque to gear 1 (see Table 4). The equilibrium solution is obtained thanks to a relatively standard Newton based non-linear solver.

Figures 12 and 13 show the FE mesh of the driving gear and a detail of the FE mesh of the driven gear. For sake of memory requirement and without any loss of generality, only the teeth involved in the contact during the prescribed rotation are finely meshed while the rest of the teeth and the gear blank are coarsely meshed but correctly represent the stiffness distribution of the gear. As far as the transition between the fine and the coarse mesh is concerned, we use a surface-based constraint. The latter ties the active DOFs on the slave surface to the active DOFs of the master surface through the use of position-based interpolation formula that derives from the element’s shape functions.

Fig. 12
figure 12

Finite element model of the driver generated in Matlab

Full size image
Fig. 13
figure 13

Teeth mesh of the driven gear

Full size image

Static analyses are performed to create the reduction spaces needed to apply the combined PMOR-Hertz and standard-PMOR. In order to speed up this preparation phase each global contact shape (which is by definition the solution of a static contact problem) is solved by means of a reduced order model. One of the benefits of the combined PMOR-Hertz strategy is that it allows to have a much shorter computational time and memory requirement during the computation of the global contact shapes (see also Sect. 4.1). In Example 1 if the standard PMOR approach is used, a static shape (attachment mode) has to be computed for each DOF that can possibly be loaded during the meshing cycle. Therefore the reduction space adopted to evaluate the global contact shapes (see \(\psi _{CMS}\) in Eq. 18) can remain very large. As shown in Table 5, the ROM used to create the global contact shapes maintains a very large dimensionality and includes 14850 shapes (as opposed to the 264762 DOFs of the FOM). On the contrary by using the combined PMOR-Hertz method, the dimension of the ROM after SVD decreases to only 21 shapes (by choosing \(p_{en}\) of Table 1 equals to \(99\%\)). As consequence, the time required to solve the static analysis decreases significantly and so the memory requirements. The gain in computational time for calculating each each static analysis can be appreciated in Fig. 14, where the computational time for the six levels of selected torque (y-axis) is presented in logarithmic scale against the static simulations along the sampled angular pitch (x-axis). In case of spur gears, for each torque level, the time required for calculating 41 static simulations is 1461 s (35.61 s for each simulation) with standard-PMOR approach, while it decreases to 44.20 s (1.078 s for each simulation) if the combined PMOR-Hertz method is employed. Moreover Fig. 14 shows the achieved speed-up, defined as the ratio between the reference execution time (standard-PMOR method) and the execution time of the proposed approach. It is worth noting that the complexity of the contact formulations is proportional to the number of nodes in contact. In case of aligned spur gears, the number of gear axial sections (and therefore nodes) in contact is proportional to the number of engaging tooth pairs. Therefore we normalize the speed-up with respect to the number of tooth pairs in contact and we obtain an average normalized speed-up of 18.03 times. It has to be underlined that the amount of global contact shapes needed in the processing phase (see Sect. 6.2) remains the same for both the methods presented.

Table 5 Characteristics of the FE models and reduced models
Full size table
Fig. 14
figure 14

Preprocessing computational time and speed-up: comparison between standard-PMOR and combined PMOR-Hertz methods for spur gears

Full size image

Figure 15 compares the experimetal STE curves measured by Kurokawa [15] against the results obtained with the combined PMOR-Hertz approach. The results are properly matching both along the line of action and with respect to the varying torque. Shape and peak-to-peak value present a very similar behaviour both during the period of single tooth in contact as well as during the period of two teeth in contact.

Fig. 15
figure 15

Comparison with experimental data for spur gears [15]

Full size image

As expected, the period of single tooth contact, identified by the number 1 in Fig. 15, is shorter according to the load increase. Conversely, the period of double tooth contact, represented by the number 2 in Fig. 15, is longer due to the tip-involute-contact that is induced by the tooth deformation. Finally the load induced stiffening effect typical of gear contact problems is properly matched by the numerical strategy. Figure 16 shows a comparison between the two modelling techniques. The degree of similarity is satisfactory and the combined PMOR-Hertz approach is able to closely match the performance of the standard PMOR method. However a slight worsening of the degree of similarity occurs with increasing the input torque level. Indeed the STE peak-to-peak value is slightly underestimated by the combined PMOR-Hertz approach and this difference increases with increasing load.

Example 2

Similarly to Example 1, this second example proposes a series of static simulations of a helical gear pair based on the work of Kurokawa [15]. As compared to spur gears, the main advantage of helical gear transmission consists in a more gradual and smoother engagement as well as a better capability to carry high loads and a smoother pressure distribution over the teeth flanks. For this reason the combined PMOR-Hertz method is expected to perform to the best of its capacities since the boundaries of validity of Hertz theory are usually not approached. The analysis of the contact interactions for helical gears is significantly more complicated than for spur gears. During the engagement of a helical gear pair, the contact starts at one end of the tooth root and then gradually spreads over the complete tooth flank throughout the rotation to finally gradually exit plane of contact. In this situation the contact width of the tooth flank is not constant and the corresponding contact pressure present a more complex shape and variation during the relative motion of the 2 gears. From a modeling standpoint, such loading conditions require an accurate description of the teeth and gear flexibility. In particular the tooth bending and torsion during the partial loading of the teeth flanks is of particular importance and requires a fine axial discretization of the FE model. This translated into a larger number of DOFs included in the FOM as compared to spur gears

The parameters and working conditions of the gear pair examined [15] are presented in Tables 6 and 7. The measurement data include STE values over path of contact of the driven gear 1 for several operating conditions ranging from 8 to 784 N/mm

Fig. 16
figure 16

STE comparison between the combined PMOR-Hertz approach and the standard PMOR method for different torque levels - spur gears

Full size image

Figure 17 shows a front 2-D view of the gear pair at the start of engagement while Fig. 18 shows a view of the FE model of the driven gear.

Table 6 Gears manufacturing parameters
Full size table
Table 7 Performed static analyses
Full size table

Other information about the modeling choices are displayed in Table 8 while Fig. 20 underlines the potential of the combined PMOR-Hertz in reducing the pre-processing effort with respect to the standard PMOR approach. As already shown for the case of spur gear pair, also in case of helical gears the required computational time for calculating each each static contact analysis can be observed in Fig. 20: here the computational time for the six levels of selected torque (y-axis) is presented in logarithmic scale against the static simulations along the sampled angular pitch (x-axis). In case of helical gears, for each torque level, the time required for calculating 31 static simulations is 5208 s (168.0 s for each simulation) with standard-PMOR approach, while it decreases to 347.5 s (11.21 s for each simulation) if the combined PMOR-Hertz method is employed. Figure 20 illustrates also the speed-up of the proposed approach with respect to the standard-PMOR method. The speed-up is in this case 15.73 times as average along an angular pitch.Footnote 3

Table 8 Characteristics of the FE models and reduced models
Full size table
Fig. 17
figure 17

Engagement of the helical gear pair

Full size image
Fig. 18
figure 18

Mesh detail of the driven gear

Full size image
Fig. 19
figure 19

Comparison with experimental and numerical data for helical gears [15]

Full size image
Fig. 20
figure 20

Preprocessing computational time and speed-up: comparison between standard-PMOR and combined PMOR-Hertz methods for helical gears

Full size image

Figure 19 shows the comparison between numerical and experimental STE at different torque levels during three angular pitches. The numbers 2 and 3 at the bottom of the figure identifies the period of double and triple tooth contact respectively. The results clearly show that the a very high degree of similarity between the experimental and the numerical results. As it can be noticed the behaviour of the STE curve with respect to both angular rotation and torque is strongly non-linear but despite this fact is correctly captured by the proposed numerical approach. In particular the delay in the transit from 3 to 2 teeth in contact with increasing torque is well capture together with a more prolonged period of triple tooth contact. This phenomenon is particularly relevant in the analysis of helical geared transmission and is usually hard to capture numerically. Finally it can be noticed that the two proposed methods present a higher degree of similarity as compared to the Example 1 as anticipated. Helical gears generally present a lower peak-to-peak value for the STE even for higher external torques. This is due to the generally higher contact ratio that is characteristic of helical pairs. In this specific case the contact ratio remains between 2 and 3 under any loading.

6.2 Dynamic results

In order to finalize the analysis regarding the potential of the method, a highly transient dynamic simulation of a spur gear pair is presented. The results of the combined PMOR-Hertz method are compared against the standard PMOR method that is taken as reference.

Example 3

The gear pair starts to spin with an initially zero velocity. During the time simulation an external torque ramp-up is applied to the driving gear and reaches a constant value of \(185 \left[ Nm\right]\) after 5 ms. The driven gear reacts to the external load with a viscous torque of 20 Nm s/rad such that a steady-state angular velocity of about 13.63 (rad/s) is reached. The duration of the simulation is 25 ms. More details about the simulation can be found in Table 9. The manufacturing parameters of the spur gear pair used in this simulation are the same of Example 1 and are shown in Table 3; The FE mesh used presents a larger amount of elements along the involute flank, 53, leading to a total number of DOFs equals to 264762 for the FOM of the two meshing gears. The projection space, used to reduce Eq. (25), has been assembled following the procedure explained in Sect. 5.1. The number of precomputed global contact shapes is 40 along one angular pitch for each of the two precomputed torque levels, respectively 150 and 250 Nm. During the dynamic simulation, the amount of DOFs retained in the combined PMOR-Hertz and the standard PMOR is the same and amount to 42 divided in 40 eigenmodes and 2 global contact shapes (one for each level of torque) obtained by interpolation as explained in Sect. 3.2.1.

The accuracy of the proposed method during transient simulation is assessed by analysing the dynamic transmission error (DTE). The standard PMOR method is kept as a reference since already validated in [3, 21, 22]. The DTE of a gear pair is fundamental in order to properly study the noise and vibrations performances of geared transmissions. The DTE is defined in literature as the difference between the actual position of the driven gear and the theoretical position it would occupy if the gears were infinitely stiff and no micro-geometry modification with respect to the ideal involute teeth profile were present. Until recently, accurate DTE simulations have not been achievable in reasonable computational times due to the complexity of the this problem. Despite this fact, a drive-train design based on the study of dynamic transient simulations and DTE would significantly improve its NVH and durability performances.

Figure 21 illustrates a comparison of the DTE results of the gear pair, computed using the standard PMOR technique and the combined PMOR-Hertz method. A steep transition in the DTE appears around 12.09 ms of simulation: This phenomena is noticeable also in the static analysis of example 1 and is caused by the varying number of teeth in contact during the meshing. The proposed combined PMOR-Hertz approach matches the reference simulation very closely. In contrast, the computational cost of the two methods is substantially different, as Table 10 shows: such difference can be explained by analysing how the dynamic problem is solved. In this example but without loss of generality with respect to any integrator adopted, the equations of motion are solved by using an explicit four-stage Runge–Kutta solver with constant time-step. The computational performances scale linearly with respect to the selected time-step. It is well known that, in contact problems in general in particular for penalty based contact methods, the strictest condition for the stability of an explicit integrator is dictated by contact stiffness. This is to say that is the penalty factor could be reduced in absolute value, the computational benefits would significant since the region of stability of the integrator would be significantly broadened. In shorter terms the problem would become numerically less stiff. Generally, such penalty factor is selected to be around two orders of magnitude higher than the physical stiffness of the bodies in contact [24]. In this way the error induced by the regularization of the Signorini conditions can be reduced significantly at the expenses of a more stiff numerical problem. If the penalty factor is chosen properly, the residual and not physical penetration between the contacting bodies can be brought to negligible terms. The proposed combined PMOR-Hertz approach can be seen as physic-based penalty approach. In this respect the two contacting bodies are meant to maintain a certain level of penetration that correspond to the combined local deformation effects of both bodies (and here described by Hertz theory). To further expand this concept to the gear pair example, it is possible to say that, when the force equilibrium is reached, a penetration corresponding to the teeth local deformation has to be present between the gear teeth. By writing and deriving the dependency of the applied force in Eq. (20) with respect to the penetration, we can obtain the value for an ’equivalent’ penalty factor to be compared with the numerical penalty factor used in the standard PMOR approach. The ratio between a numerical penalty factor and a Hertz-based penalty factor is highly case dependent. In Example 3 we obtained a ratio between the penalty factor used for the standard PMOR approach and the combined PMOR-Hertz approach of around 7. This allowed to maintain a stable solution, for the latter case, using a time step that is up to 6 times larger than the standard method with a subsequent computational gain without compromising in accuracy.

Table 9 Parameters of the dynamic simulation
Full size table
Fig. 21
figure 21

Dynamic transmission error of spur gear pair

Full size image
Table 10 Dynamic simulation results
Full size table

A few extra remarks are needed regarding the computational performances. Firstly, it has to be said that, despite the deceased numerical stiffness of the problem obtained with the proposed approach, a small time step is always required in contact problems due to their impulsive nature: the relevant dynamic phenomena happen at a small time-scale. Secondly, as it can be seen in Table 10 the computational performances of the new approach are only 4.5 times better as compared to the standard method despite a 6 times larger time step. The combined PMOR-Hertz approach adopts a non-linear relationship between penetration and contact force. This calls for a solution of multiply scalar non-linear problems at each time-step and causes a slight performance decrease as compared to the theoretical one. It has to be noticed that the relation between penetration and contact forces in the Hertz model is load, geometry and material dependent, with the consequence that also the maximum allowed time steps and computational gain is problem specific.

7 Conclusion and future work

Starting from a theoretical analysis of the existing and most often used semi-analytic contact methods, we originally highlight the most critical aspects of such methodologies. In particular, our investigation clarifies why the model presented by Chang [5] outperforms the model proposed by Andersson and Vedmar [1], by demonstrating that the error arising from the non- physical underlying assumptions of the above-mentioned methods is negligible.

Strengthened by the gained theoretical insight, this paper proposes an original method that combines an advanced parametric model order reduction method and a Hertz based contact model. As confirmed by our results, the method can be applied to solve dynamic gear contact problems more efficiently and without sacrificing accuracy.

Static numerical simulations of both spur and helical gear contact analyses showed very accurate agreement with experimental data (Transmission Error curves) measured by Kurokawa [15]. However the STE comparison between the proposed Hertz-based approach and penalty-based contact methods showed a different peak-to-peak value at high input torque levels. This emerges very clearly during the period of single pair in contact which corresponds to high local contact pressure applied to the teeth flanks. Further investigations are needed to assess if this effect is due to the limitations of the Hertz theory, which assumes the area of contact to remain much smaller than the characteristic dimensions of the contacting bodies.

Dynamic simulations confirm that the paradigm shift from penalty-based contact model towards the proposed Hertz based allows to achieve a dramatic reduction of the overall computational complexity: lower pre- processing time and reduced memory usage requirements due to smaller number of necessary degrees of freedom and a faster execution due to a lower penalty factor are considerable advantages of the proposed method.

Taking advantage of the performance delivered by the proposed methodology, upcoming research will focus on the following aspects: (1) investigation of the Hertz-based contact model accuracy for high specific load as well as gears with micro-geometry modifications; (2) dynamic experimental validation of the method will be carried out by using the set-up of [17] for measuring dynamic Transmission Error curves; (3) lubricated contact problems will be studied by taking into account the lubricant properties within the semi-analytic contact model and the results validated against [19]; (4) more complex system level cases will be investigated and the method will be integrated in a 1D environment to efficiently capture geared transmission torsional behaviour.