1 Introduction

In order to improve the mechanical efficiency of internal combustion engines, the friction between the piston rings and the cylinder liner needs to be reduced. It is widely known that surface texturing may enhance the tribological properties of sliding surfaces [1, 2]. With well-designed features on the surface, the interfacial friction and wear of friction pairs can be effectively reduced. Meanwhile, the energy loss can be minimized and the operational life of the components can be prolonged. The possible mechanisms behind the improvement of tribological properties for surface texturing can be described as follows: (a) secondary lubrication [3], (b) tripping wear debris [3], and (c) micro-hydrodynamic effect [3–5].

For the piston ring/liner conjunction, mixed lubrication is inevitable during engine cycles. In the mixed-lubrication regime, the asperities support a great share of the load. In particular, most of the load is shared by the asperities when the piston ring is located at the top dead center (TDC) or the bottom dead center (BDC). To predict the asperity contact, two types of approaches are available in the literatures, including the deterministic approach [6, 7] and the stochastic approach [8–10]. In the deterministic approach, the measured actual surface roughness profiles of the surfaces are required as an input to characterize the rough surface. While, in the stochastic approach, a range of statistical parameters is employed to represent the characteristics of the rough surfaces. Between them, the statistical approach is the most convenient, and it can meet the need for approximate models in practical applications [11]. It is also the focus of the current paper. One of the earliest statistical rough surface contact models was proposed by Greenwood and Williamson [12]. The model is known as the GW model, and is suitable for the engineering applications. Based on the Greenwood and Williamson approach, Greenwood and Tripp [13] proposed an equivalent rough surface model for two rough surfaces. The model is known as the GT model. It is one of the most popular and convenient methods for the simulation of piston ring lubrication.

However, when sliding pairs run under the condition of being overloaded or at the start and stop phases, the tribology system is usually under the mixed or starved lubrication condition, and the asperity contact undertakes the most of the load. Under some severe lubrication conditions, there are local high compressive stresses at each asperity pair contact. This can induce asperity level yielding, possibly resulting in the plastic deformation and wear at the interface. However, both the GW model and the GT model mentioned above are developed on the assumption of elastic Hertzian contact for asperity pairs. The elastic Hertizian contact assumption may cause prediction results for rough surface contact to be inaccurate in some situations [14].

In recent years, many researchers have paid attention to the statistical elasto-plastic contact and friction. The elasto-plastic contact for the flat surfaces was first studied by Archard [15]. Chang et al. [16] proposed a model to consider the elasto-fully plastic deformation of asperities. Nonetheless, the model has a discontinuity in the expression of the contact pressure at the critical interface [8]. To overcome this limitation, Zhao et al. [17] considered the intermediate regime of deformation and provided an elastic-elasto/plastic-fully plastic model. In this model, the elastic and plastic behaviors of the asperity were bridged using an analytical function. In this way, Zhao’s model resolved the continuity problem in Chang’s model. However, overcoming the discontinuity was based on the mathematical manipulations rather than the physical considerations. Later, Kogut and Etsion [18, 19] proposed the convenient empirical expressions by carrying out the corresponding finite-element simulations for the deformation of a single asperity. The proposed expressions included different asperity deformation regimes. The model proposed by Kogut and Etsion is known as the KE model. Meanwhile, finite-element analysis was also used by Jackson and Green [20–22]. In their model, the effects of material properties and geometry during the deformation were taken into account. The model developed by the Jackson and Green is known as the JG model. In fact, both the KE and the JG models contributed significantly toward the development of the convenient empirical elasto-plastic model. It should be noted that the derivation of all of the above elasto-plastic contact models was based on the contact of an equivalent rough surface against an ideally smooth flat surface. However, the asperity contact result for an equivalent surface against a plane is different from that for two rough surfaces [13]. For the contact between two rough surfaces, the asperity peaks may overlap, and result in no contact, owing to the misalignment [13]. Therefore, it is meaningful to study an improved elasto-plastic asperity contact model for two rough surfaces.

In order to predict the performance of the textured ring-liner system more accurately, an integrated Reynolds equation with a statistical elasto-plastic contact model for two rough surfaces is proposed in this paper. After considering the transition of the asperity contact deformation from elastic to elastoplastic and finally to be fully plastic state, the asperity contact model is suitable for the asperity interactions of two rough surfaces. Based on the proposed model, the tribological properties of surface texturing under the mixed lubrication are analyzed.

2 Mathematical model

2.1 Contact conjunction

Figure 1 illustrates the mathematical model of the ring/liner system. The two-dimensional Reynolds equation with corrective flows is employed as follows [3, 23, 24]:

Fig. 1
figure 1

Mathematical model of the piston ring/cylinder liner system

Full size image
$$\frac{\partial }{\partial x}\left( {\phi_{x} \frac{{h^{3} }}{\mu }\frac{\partial p}{\partial x}} \right) + \frac{\partial }{\partial y}\left( {\phi_{y} \frac{{h^{3} }}{\mu }\frac{\partial p}{\partial y}} \right) = 6U\phi_{c} \frac{\partial h}{\partial x} + 6U\sigma \frac{{\partial \phi_{s} }}{\partial x} + 12\phi_{c} \frac{\partial h}{\partial t}$$
(1)

where p is the hydrodynamic pressure, h is the mean film thickness, σ is the composite roughness of the piston ring and the cylinder liner, and U is the sliding velocity of the piston ring. ϕ x and ϕ y are the pressure flow factors, which can be calculated according to Patir and Cheng [25, 26]. ϕ s is the shear flow factor. ϕ c is the contact factor, which is defined by Wu and Zheng [27]. Using this Reynolds equation, the influence of surface irregularities on the lubricant flow under the mixed lubrication conditions can be taken into account.

In simulation of surface texturing, the textures should be well expressed. The textures can be designed and machined into different shapes [28, 29]. Since micro-dimples have the advantages of easy fabrication and superior tribological characteristics, the piston ring with semi-ball shaped micro-craters is studied in this paper. The local film thickness equation h(x, y) can be expressed as follows:

$$h_{S} \left( {x,y} \right) = 4\delta x^{2} /b^{2}$$
(2)
$$h_{R} \left( {x,y} \right) = {{h_{p} \sqrt {r_{p}^{2} - x^{\prime 2} - y^{\prime 2} } } \mathord{\left/ {\vphantom {{h_{p} \sqrt {r_{p}^{2} - x^{\prime 2} - y^{\prime 2} } } {r_{p} }}} \right. \kern-0pt} {r_{p} }}\quad x,y \in \varOmega$$
(3)
$$h\left( {x,y} \right) = h_{0} + h_{R} \left( {x,y} \right) + h_{S} \left( {x,y} \right)$$
(4)

where δ is the ring crown height, b is the ring axial width, h p is the dimple depth, r p is the dimple radius, h 0 is the minimum oil film thickness, and Ω is the area occupied by the dimples. Because the textures are periodically distributed along the circumferential direction Y, it is sufficient to use one column of textures as the research object in the simulation. Besides, the terms x and \(x^{\prime }\) in the above equations are different in the coordinate system, as well as the terms y and \(y^{\prime }\). As shown in Fig. 2c, x and y are in the global coordinate system, while, \(x^{\prime }\) and \(y^{\prime }\) are located in the local coordinate system. It should be noticed that the originating point of the local coordinate system is at the center of each textures.

Fig. 2
figure 2

a Geometrical model of a textured piston ring, b detail of a group of dimples, c one column of dimples

Full size image

2.2 Boundary conditions

In the lubricant problem, cavitation will take place if the absolute local pressures of the lubricant fall below the cavitation pressure. As the Swift-Stieber boundary condition is the most widely used boundary condition for considering the cavitation effect, this boundary condition is also used here. It can be described as follows:

$$\frac{\partial p}{\partial x} = 0$$
(5)
$$p \to p_{cav} = 0$$
(6)

In addition, as only one column of textures is studied in the simulation, the following boundary conditions should be also adopted (owing to the symmetry and continuity of the pressure distribution):

$$\left. {\frac{\partial p}{\partial y}} \right|_{y = 0} = \left. {\frac{\partial p}{\partial y}} \right|_{y = l}$$
(7)
$$p\left( {x,0} \right) = p\left( {x,l} \right)$$
(8)

2.3 Asperity contact model

For the mixed-lubrication case, the load is shared by both the asperity contact and the hydrodynamic support. It is important to consider how to calculate the asperity contact pressure. The most common and convenient method for calculating the asperity contact is with a stochastic model. According to the work of Greenwood and Tripp [13], the total contact force F asp_T and the total actual contact area A asp_T are defined as:

$$F_{asp\_T} \left( h \right) = \eta A\int\limits_{0}^{\infty } {F_{asp\_T0} \left( {\omega ,r} \right)\phi \left( z \right)dz}$$
(9)
$$A_{asp\_T} \left( h \right) = \eta A\int\limits_{0}^{\infty } {A_{asp\_T0} \left( {\omega ,r} \right)\phi \left( z \right)dz}$$
(10)

where η is the asperity density, A is the entire apparent contact area, ω is the interference, r is the misalignment factor considering the misalignments between the asperities of two rough surfaces, and ϕ refers to the asperity distribution.

Meanwhile, the terms F asp_T0 and A asp_T0 can be calculated as:

$$F_{asp\_T0} \left( h \right) = 2\pi \eta \int\limits_{0}^{\infty } {P_{asp} \left( {\omega ,r} \right)rdr}$$
(11)
$$A_{asp\_T0} \left( h \right) = 2\pi \eta \int\limits_{0}^{\infty } {A_{asp} \left( {\omega ,r} \right)rdr}$$
(12)

where

$$\omega = z - h - 2f\left( {r/2} \right) = \omega_{p} - 2f\left( {r/2} \right)$$
(13)
$$2f\left( {r/2} \right) = r^{2} /4\beta$$
(14)

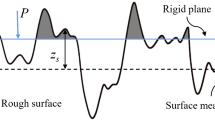
The term z is the height of the asperity from the mean of asperity heights, which is set to z = z 1 + z 2. As shown in Fig. 3, ω p is the overlap between the peaks of asperities pairs. Because of misalignment, the peaks of asperities may overlap, leading to no contact [13].

Fig. 3
figure 3

Contact of two rough surfaces: height of the asperities is z 1 and z 2, and horizontal distance is r

Full size image

It should be noticed that the terms P asp and A asp in Eqs. (11) and (12) are the load carrying capacity and the actual contact area of a single asperity pair, respectively. In the GT model, the Hertzian contact theory is applied to calculate these two parameters by assuming that the asperity contact is fully elastic [13]. However, for the ring/liner system or other high load friction pairs, if the value of the oil-film thickness is small, an asperity contact with plastic deformation may occur. In this sense, the purely elastic contact model may not be suitable for the case of mixed lubrication. Hence, in this study, the terms P asp and A asp will be predicted based on the elasto-plasticity model by Kogut and Etsion [18, 19]. In the KE model, the elasto-plasticity transition of contact deformation is considered instead of assuming a purely elastic asperity deformation. It is worth mentioning that the results predicted by the KE model were in good agreement with the experimental results, according to the work of Ovcharenko et al. [30].

For marking the transition from the elastic to the elastic–plastic deformation regime, the critical interference, ω c , is defined as [16]:

$$\omega_{c} = \left( {\frac{\pi KH}{{2E^{\prime } }}} \right)^{2} \beta_{e}$$
(15)
$$\omega_{c}^{*} = \frac{{\omega_{c} }}{\sigma } = \left( {\frac{\pi KH}{{2E^{\prime } }}} \right)^{2} \left( {\frac{{\beta_{e} }}{\sigma }} \right)$$
(16)

where K is the hardness factor between the maximum contact pressure and the hardness at the onset of plastic deformation. In the work of Chang et al., the hardness factor is related to the Poisson ratio by K = 0.454 + 0.41υ [31]. H is the hardness of the softer material and is typically taken to equal 2.8 times the yield strength S y for untreated surfaces. β e is the effective mean asperity curvature by 1/β e  = 1/β 1 + 1/β 2. When two rough surfaces have the same asperity radiuses (β 1 = β 2 = β), β e is equal to β/2. Meanwhile, \(E^{\prime }\) is the effective modulus of elasticity, which is defined as:

$$E^{\prime } = \frac{1}{{\left( {1 - \upsilon_{1}^{2} } \right)/E_{1} + \left( {1 - \upsilon_{2}^{2} } \right)/E_{2} }}$$
(17)

where E 1, E 2 and υ 1, υ 2 are the Young’s modulus and Poisson’s ratios of the two materials, respectively.

According to the KE model, the single asperity pair contact force and area can be calculated in the piecewise forms [19] as follows:

$$P_{asp} \left( \omega \right) = \left\{ {\begin{array}{*{20}l} {P_{c} \left( {\frac{\omega }{{\omega_{c} }}} \right)^{1.5} ,} & {\omega \le \omega_{c} } \\ {1.03P_{c} \left( {\frac{\omega }{{\omega_{c} }}} \right)^{1.425} , } & {\omega_{c} < \omega \le 6\omega_{c} } \\ {1.40P_{c} \left( {\frac{\omega }{{\omega_{c} }}} \right)^{1.263} , } & { 6\omega_{c} < \omega \le 110\omega_{c} } \\ {\frac{3}{K}P_{c} \left( {\frac{\omega }{{\omega_{c} }}} \right)^{1} ,} & {110\omega_{c} < \omega } \\ \end{array} } \right.$$
(18)
$$A_{asp} \left( \omega \right) = \left\{ {\begin{array}{*{20}l} {A_{c} \left( {\frac{\omega }{{\omega_{c} }}} \right)^{1} ,} & {0 < \omega \le \omega_{c} } \\ {0.93A_{c} \left( {\frac{\omega }{{\omega_{c} }}} \right)^{1.136} , } & { \omega_{c} < \omega \le 6\omega_{c} } \\ {0.94A_{c} \left( {\frac{\omega }{{\omega_{c} }}} \right)^{1.146} ,} & {6\omega_{c} < \omega \le 110\omega_{c} } \\ {2A_{c} \left( {\frac{\omega }{{\omega_{c} }}} \right)^{1} ,} & {110\omega_{c} < \omega } \\ \end{array} } \right.$$
(19)

where

$$P_{c} = 4E^{\prime } {{\sqrt {\beta_{e} } (\omega_{c} )^{{\frac{3}{2}}} } \mathord{\left/ {\vphantom {{\sqrt {\beta_{e} } (\omega_{c} )^{{\frac{3}{2}}} } 3}} \right. \kern-0pt} 3} = {{2KH\pi \beta_{e} \omega_{c} } \mathord{\left/ {\vphantom {{2KH\pi \beta_{e} \omega_{c} } 3}} \right. \kern-0pt} 3}$$
(20)
$$A_{c} = \pi \beta_{e} \omega_{c}$$
(21)

By combining the above equations (Eqs. 9–21), the improved elasto-plastic asperity contact model for two rough surfaces can be obtained as:

$$\begin{aligned} F_{asp\_T} \left( h \right) & = \frac{2}{3}KH\left( {\pi \eta \beta } \right)^{2} A\left\{ {\frac{2}{2.5}\omega_{c}^{ - 0.5} \int\limits_{d}^{{d + \omega_{c} }} {\omega^{2.5} \phi \left( z \right)dz} } \right. \\ & \quad + \frac{2}{2.425}1.03\omega_{c}^{ - 0.425} \int\limits_{{d + \omega_{c} }}^{{d + 6\omega_{c} }} {\omega^{2.425} \phi \left( z \right)dz} \\ & \quad + \frac{2}{2.263}1.4\omega_{c}^{ - 0.263} \int\limits_{{d + 6\omega_{c} }}^{{d + 110\omega_{c} }} {\omega^{2.263} \phi \left( z \right)dz} \\ & \quad \left. { +\, \frac{3}{K}\int\limits_{{d + 110\omega_{c} }}^{\infty } {\omega^{2} \phi \left( z \right)dz} } \right\} \\ \end{aligned}$$
(22)
$$\begin{aligned} A_{asp\_T} \left( h \right) & = \left( {\pi \eta \beta } \right)^{2} A\left\{ {\frac{2}{2}\int\limits_{d}^{{d + \omega_{c} }} {\omega^{2} \phi \left( z \right)dz} } \right. \\ & \quad + \frac{2}{2.136}0.93\omega_{c}^{ - 0.136} \int\limits_{{d + \omega_{c} }}^{{d + 6\omega_{c} }} {\omega^{2.136} \phi \left( z \right)dz} \\ & \quad + \frac{2}{2.146}0.94\omega_{c}^{ - 0.146} \int\limits_{{d + 6\omega_{c} }}^{{d + 110\omega_{c} }} {\omega^{2.146} \phi \left( z \right)dz} \\ & \quad \left. { +\, 2\int\limits_{{d + 110\omega_{c} }}^{\infty } {\omega^{2} \phi \left( z \right)dz} } \right\} \\ \end{aligned}$$
(23)

In particular, the height of the asperities at the contact surfaces can be assumed to have a Gaussian distribution. The term ϕ can be described as follow [32, 33]:

$$\phi^{*} \left( s \right) = e^{{ - \frac{1}{2}s^{2} }} /\sqrt {2\pi }$$
(24)

Thus,

$$F_{n} \left( u \right) = \int\limits_{u}^{\infty } {\left( {s - u} \right)^{n} \phi^{*} \left( s \right)ds} = \frac{1}{{\sqrt {2\pi } }}\int\limits_{u}^{\infty } {\left( {s - u} \right)^{n} e^{{ - \frac{{s^{2} }}{2}}} ds}$$
(25)

Then, the current model for two rough surfaces can be rewritten as follows:

$$\begin{aligned} F_{asp\_T} \left( {H_{\sigma } } \right) & = \pi \left( {\eta \beta \sigma } \right)^{2} A\left\{ {\underbrace {{\frac{16}{15}\sqrt 2 E^{\prime } \sqrt {\frac{\sigma }{\beta }} \left[ {F_{2.5} \left( {H_{\sigma } } \right) - F_{2.5} \left( {H_{\sigma } + \omega_{c}^{*} } \right)} \right]}}_{{{\text{Elastic}}\;{\text{deformation}}}}} \right. \\ & \quad + \underbrace {{\frac{2}{3}\frac{2}{2.425}1.03\pi KH\omega_{c}^{* - 0.425} \left[ {F_{2.425} \left( {H_{\sigma } + \omega_{c}^{*} } \right) - F_{2.425} \left( {H_{\sigma } + 6\omega_{c}^{*} } \right)} \right]}}_{{{\text{Elastoplastic}}\;{\text{deformation }}\left( {1{\text{st}}\;{\text{stage}}} \right)}} \\ & \quad + \underbrace {{\frac{2}{3}\frac{2}{2.263}1.4\pi KH\omega_{c}^{* - 0.263} \left[ {F_{2.263} \left( {H_{\sigma } + 6\omega_{c}^{*} } \right) - F_{2.263} \left( {H_{\sigma } + 110\omega_{c}^{*} } \right)} \right]}}_{{{\text{Elastoplastic}}\;{\text{deformation}}\;\left( {2{\text{nd}}\;{\text{stage}}} \right)}} \\ & \quad \left. { + \underbrace {{2\pi HF_{2} \left( {H_{\sigma } + 110\omega_{c}^{*} } \right)}}_{{{\text{Fully}}\;{\text{plastic}}\;{\text{deformation}}}}} \right\} \\ \end{aligned}$$
(26)
$$\begin{aligned} A_{asp\_T} \left( {H_{\sigma } } \right) & = \pi^{2} \left( {\eta \beta \sigma } \right)^{2} A\left\{ {\underbrace {{\left[ {F_{2} \left( {H_{\sigma } } \right) - F_{2} \left( {H_{\sigma } + \omega_{c}^{*} } \right)} \right]}}_{{{\text{Elastic}}\;{\text{deformation}}}}} \right. \\ & \quad + \underbrace {{\frac{2}{2.136}0.93\sigma \omega_{c}^{* - 0.136} \left[ {F_{2.136} \left( {H_{\sigma } + \omega_{c}^{*} } \right) - F_{2.136} \left( {H_{\sigma } + 6\omega_{c}^{*} } \right)} \right]}}_{{{\text{Elastoplastic}}\;{\text{deformation}} \left( {1{\text{st}}\;{\text{stage}}} \right)}} \\ & \quad + \underbrace {{\frac{2}{2.146}0.94\omega_{c}^{* - 0.146} \left[ {F_{2.146} \left( {H_{\sigma } + 6\omega_{c}^{*} } \right) - F_{2.146} \left( {H_{\sigma } + 110\omega_{c}^{*} } \right)} \right]}}_{{{\text{Elastoplastic}}\;{\text{deformation}}\;\left( {2{\text{nd }}\;{\text{stage}}} \right)}} \\ & \quad \left. { + \underbrace {{2F_{2} \left( {H_{\sigma } + 110\omega_{c}^{*} } \right)}}_{{{\text{Fully}}\;{\text{plastic}}\;{\text{deformation}}}}} \right\} \\ \end{aligned}$$
(27)

where \(H_{\sigma } = {\raise0.7ex\hbox{$h$} \!\mathord{\left/ {\vphantom {h \sigma }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\sigma $}}\) is the ratio of the mean film thickness h to the composite roughness σ. Moreover, the derivation process of Eqs. (26) and (27) is given in “Appendix 1” section. Meanwhile, in “Appendix 2” section, the values of F n (H σ ) for the varying term H σ are provided, as well as the corresponding fitting formulas.

It should be noticed that four stages are included in the equations of the asperity contact force and asperity contact area. The first and the last ones in Eqs. (26) and (27) describe the elastic and fully plastic deformation. The middle two parts (the second and the third ones) are used to characterize the elastoplastic deformation of asperities. When the modeled asperity contact is under the elastic deformation, only the equation involving the elastic deformation is used, and the equations of the elastoplastic deformation and fully plastic deformation are invalid. When the fully plastic deformation is experienced, all equations are active. Moreover, it is interesting to point out that the equation involving the elastic deformation in current model is same to the equation of GT model. In other words, the current model would provide the same results as the popular GT model, when the asperities of the contact surfaces only experience the elastic deformation. This point can used to demonstrate the validity of this model.

2.4 Lubricant viscosity on the liner

In the lubrication system, the lubricant viscosity is sensitive to the temperature change and is an important factor of determining the lubrication performance. According to the work of Morris et al. [34], the oil temperature can be assumed to be equal to the liner temperature at the corresponding position. Meanwhile, according to the work of Guo et al. [35], the temperature distribution along the liner (T liner ) can be calculated using the following expression:

$$T_{liner} = T_{TDC} - \left( {T_{TDC} - T_{BDC} } \right)\sqrt {x_{L} /S_{L} }$$
(28)

where T TDC is the liner temperature at the position of the top compression ring at the TDC, T BDC is the liner temperature at the position of the oil ring at the BDC, x L is the liner location relative to the position of the top compression ring at the TDC, and S L is the distance between the two measured points.

The lubricant viscosity is influenced by the lubricant temperature. This relationship can be expressed as [36]:

$$\mu = a_{0} \exp \left( {\frac{{T_{1} }}{{T_{2} + T_{m} }}} \right)$$
(29)

where a 0, T 1, and T 2 are the correlation parameters in the calculation of the lubricant viscosity, and T m is the lubricant temperature. Table 1 gives some parameters of the viscosity [36].

Table 1 Viscosity parameters [36]
Full size table

2.5 Friction model

For the lubrication of the ring/liner system, viscous friction dominates when the lubricant film is thick. However, when the lubricant film is thin, asperity interaction cannot be avoided. The presence of asperity interaction leads to the boundary friction. The total friction force is a combination of the hydrodynamic friction force and the boundary friction force. The total friction force can be calculated as follows:

$$\tau = - \mu \frac{U}{h}\left( {\phi_{f} + \phi_{fs} } \right) + \phi_{fp} \frac{h}{2}\frac{\partial p}{\partial x}$$
(30)
$$F_{frc,oil} = \iint {\tau dxdy}$$
(31)
$$F_{frc,asp} = \tau_{0} \iint {A_{asp\_T} dxdy} + C_{f} \iint {F_{asp\_T} dxdy}$$
(32)
$$F_{frc,total} = F_{frc,oil} + F_{frc,asp}$$
(33)

where ϕ fs and ϕ fp are the shear stress factors. These two factors and the term ϕ f can be calculated according to the work of Patir and Cheng [25, 26]. C f is the coefficient of friction for asperity contact. In the simulation, C f  = 0.12 is adopted based on the previous work on the ring/liner system [37]. τ 0 is the Eyring shear stress of the lubricant [14]. The terms A asp_T and F asp_T are the total contact area and the contact force, respectively. They can be obtained according to the improved contact model presented in this study, including both the elastic and elasto-plastic parts.

3 Method of solution

In the ring/liner system, several forces act on the ring. As shown in Fig. 4, the term F g is the gas pressure load acting behind the ring. It is changed with the crank angle. The term F e is the ring tension force. This tension force is due to the elastic response of the ring to the deformation needed to fit its placement. It is assumed as a constant. W h is the load-carrying capacity of the hydrodynamic force. The value of W a is obtained by the integral of the hydrodynamic pressure. The governing Eqs. (1)–(8) are discretized and solved to predict the pressure and the film distributions. W a is the asperity contact force. Its value can be calculated by the integral of the asperity contact pressure. The distribution of asperity contact pressure is obtained by Eqs. (9)–(27). Meanwhile, the terms ηβσ = 0.05 [38] and σ/β = 0.01 [38] are used in this study. The numerical solution procedure for the mixed lubrication involves the following steps:

Fig. 4
figure 4

An overview of the domain in the piston movement direction, with several forces acting on the ring

Full size image

  • Step 1 At each time step, the outward force (adhering the ring to the liner surface) should be calculated with the following expression:

    $$F = F_{e} + F_{g}$$
    (34)

    where F g is the gas force, and F e is the ring tension force. Meanwhile, some parameters should be given initial values, such as the pressure distribution, minimum film thickness, etc.

  • Step 2 Using Eqs. (28) and (29), the lubricant viscosity for each time step can be obtained. It is worth mentioning that the temperature at each time step is uniform.

  • Step 3 The oil film pressure distribution is obtained from Eq. (1) using the boundary conditions in Eqs. (5)–(8). The asperity contact force is calculated by Eqs. (26) and (27).

  • Step 4 The applied load obtained from Eq. (34) is assumed to equilibrate the support induced by the hydrodynamic pressure and the asperity contact. Thus, the following convergence criterion is applied at each time step:

    $$\left| {\frac{{W_{h} + W_{a} - F}}{F}} \right| \le \varepsilon$$
    (35)

    where the term ɛ is equal to 10−6. W h is the load-carrying capacity of the hydrodynamic force, while, W a denotes the load-carrying capacity of the asperity contact. The time step can be advanced once the convergence criterion is satisfied. Otherwise, the minimum oil film thickness h 0 is adjusted and steps 3 and 4 are repeated.

  • Step 5 When the convergence criterion is satisfied, the crank angle is advanced by one time step. The entire procedure is repeated until the whole engine cycle is completed and reaches a periodic state.

4 Results and discussion

4.1 Model tests

Before applying the improved elasto-plastic model to the problem of the textured ring/liner system, it is necessary to compare the improved elasto-plastic contact model with other models. Some steady cases are carried out. In these cases, the apparent contact area is set to 1 mm × 1 mm, as shown in Fig. 5a. Varying forces are loaded at the upper sample. In order to investigate the influence of different contact models, three models are compared, including the GT model, the KE model and the current model.

Fig. 5
figure 5

a Schematic diagram of two contact samples and b comparison of the KE model with the current model

Full size image

In the first case, the current model is compared with the KE model. As mentioned above, the KE model is an elasto-plastic model, in which an ‘equivalent’ single rough surface is assumed. For the equivalent single rough surface, the asperity curvature is the sum of the two curvatures and the height distribution of asperities is the sum of the heights of the original pair. In fact, when the asperities of the friction pair are aligned, the assumption of the equivalent surface is reasonable. Moreover, it is worth mentioning that the elasto-plastic model developed in this paper can be regarded as an improved KE model, which is based on the Greenwood and Tripp approach. Thus, the comparison of these two models in this case is a study on the effect of permitting misalignment. As shown in Fig. 5b, the trends of the two curves obtained by the current model and the KE model are the same, but the corresponding values are different, showing the effect of permitting misalignment. The reasons can be explained as follows: since the algorithm in current model is derived based on the KE model, it leads to the generation of same trends. Meanwhile, the current model takes into account the effect of the permitting misalignment, while the KE model does not. It results in the different values. The similar results was also found in the comparison results between the GW model (equivalent surface against a plane) and the GT model (two rough surfaces) conducted by Greenwood and Tripp [13]. Considering the permitting misalignment, the current model is suitable for the contact problem of two rough surfaces.

In addition, anther comparison is made, in which the common used GT model is compared with the current model. As the effect of the permitting misalignment is considered by both two model, the following comparison analysis is used to find the effect of the plastic deformation of asperities. Figure 6a shows the relationship of the real contact area fraction and the clearance between two samples. The real contact area fraction is the ratio of the actual contact area to the apparent contact area. It is observed that a larger real contact area fraction is generated along with decreasing clearance, in the current model, as compared with the GT model. Figure 6b shows the relationship of the contact load and the ratio of the clearance to the combined surface roughness. It appears that the load-carrying capacity of the asperity contact decreases once plasticity is initiated. Figure 6c illustrates the relationship of the real contact area fraction and the contact load. It is worth mentioning that two curves are coincidence in the starting position. It is because the deformation of asperities is at the range of elastic when the load is limited. Meanwhile, the equation describing the elastic deformation in current model is equal to that in GT model. This leads to the coincidence of two curves. When the given applied load is high, the real contact area fraction predicted by the current model is larger than that predicted by the GT model. This shows that the actual contact area is underestimated by the elastic deformation assumption under the high load condition. The underestimation of actual contact area would result in an inaccurate prediction of the frictional characteristics for the contact of two rough surfaces. Therefore, by comparing the current model with the GT and KE models, both the effect of the permitting misalignment and the influence of plastic deformation of asperities have been addressed. The effectiveness of this model is guaranteed from the view of the mathematics.

Fig. 6
figure 6

a Relationship of the real contact area fraction and the ratio of the clearance to the combined surface roughness, b relationship of the contact load and the ratio of the clearance to the combined surface roughness, and c relationship of the real contact area fraction and the contact load

Full size image

4.2 Application in analysis of the textured piston ring

The effect of surface texturing on the reduction of friction and wear has been recognized [39–42]. When the engine works at the end of a stroke, the textured ring/liner conjunction runs at mixed lubrication, even at the boundary lubrication. Thus, the accurate prediction of the metal-to-metal interaction is important. Since the current asperity contact model contributes to predicting the metal-to-metal interaction more accurately, the average flow Reynolds equation and the presented asperity contact model are employed together to analyze the effect of surface texturing on the performance of the internal combustion engine. The case considered in the following analysis is a four-stroke gasoline engine. Table 2 provides the necessary data for the current analysis. Figure 7a, b show the combustion pressure variation and the piston sliding speed, respectively. The measured temperatures of the liner at the TDC and BDC are 180 and 130 °C, respectively. According to Eqs. (28) and (29), the temperature distribution along the liner can be obtained. Since the oil temperature corresponds to the liner temperature, the relationship between the oil temperature and the crank angle can be shown as Fig. 7c. Besides, it should be noticed that the contact deflection is ignored in the simulation. In other words, the macroscopic (or rather mesoscopic) deformation is not considered in this simulation. Only the micro-scale asperity deformation is considered using the presented model. The stress concentration at the edge of textures cannot be captured by the presented asperity contact models. However, in certain conditions, the limited local macroscopic deformation can affect the contacts and lubrication. Therefore, the limitations should be acknowledged.

Table 2 Parameters of the gasoline engine
Full size table
Fig. 7
figure 7

Input conditions for the analysis: a gas pressure in the combustion chamber, b piston sliding speed, and c the relationship between the oil temperature and the crank angle

Full size image

4.2.1 Comparison of asperity contact models

Figure 8 shows some simulation results for the first ring. In the simulations, both the GT asperity contact model and the current asperity contact model are used. Notice that the film thickness ratio is the ratio of the minimum film thickness to the composite roughness. It is defined in accordance with Stribeck’s proposition and can be calculated by h 0/σ. When the film thickness ratio is >4, the ring/liner system is in the hydrodynamic lubrication regime. Otherwise, the ring/liner system is under the mixed lubrication. No asperity contact happens when the hydrodynamic lubrication is experienced. Therefore, as shown in Fig. 8, no difference can be found in the results of the different contact models when the film thickness ratio is large. When the ring/liner tribological conjunction is in the mixed lubrication, along with a decreasing oil film thickness ratio, the surfaces of the ring and the liner are close to each other. With the change in the clearance between the ring and the liner, the asperity contact deformation would transform from elastic to elasto-plastic and finally to the fully plastic state. As shown in Fig. 8, at the end of each stroke, the minimum film thickness of the current model is thinner than that of the GT model. At the TDC, the asperity contact force accounts for 94 % of the load, when the GT model is adopted. At the same crank angle, the share of asperity contact predicted by the current model is 84.5 %. For the asperity contact at the TDC, a greater amount of plastic deformation of the asperity would happen. In fact, because the elastic deformation of asperities dominates in most strokes of the engine, the difference in the results predicted by the two models is limited. This is why the GT model is preferred in the ring/liner simulation, particularly when the lubrication condition is not severe and the load is not high. As discussed above, owning to the features of the piecewise function, the presented elastoplastic model can provide the same result as the GT model, when only elastic deformation of asperities is induced. When the plastic deformation of asperities is involved, a more accurate prediction can be made by the presented elastoplastic model by considering the effect of the plastic deformation of asperities. Therefore, the presented model can be regarded as a universal asperity contact model, no matter the plastic deformation of asperities is induced or not.

Fig. 8
figure 8

The simulation results of the film thickness ratio using the Greenwood and Tripp model and the current model for the textured ring/liner system

Full size image

4.2.2 State of contact at reversal

Since the current asperity contact model contributes to predicting the asperity contact force more accurately, it would be meaningful to investigate the state of contact at the reversal points. It is well known that the contact area would be reduced after surface texturing. Meanwhile, the distribution of textures also influences the contact interface. Figure 9 shows the change in the hydrodynamic and asperity supports with or without surface texturing during the whole working cycle. As shown in Fig. 9, the difference between the untextured and textured results is not obvious, except near the TDC. In the vicinity of the TDC, it seems that the textured surface provides a larger hydrodynamic support than the untextured surface does. It is also observed that the asperity contact force is reduced after texturing, which contributes to the reduction in friction.

Fig. 9
figure 9

The variation in hydrodynamic and asperity supports over the whole working cycle: a for the untextured ring and b for the textured ring

Full size image

When the ring is at TDC or BDC, the inlet reversal leads to thin films and more asperity contacts. Therefore, the status at the centers requires special attention. Figure 10 shows the predicted pressure distributions when the piston ring is near TDC. It is worth mentioning that the dimensionless X is obtained by the expression X = (2x − b)/b, while, the expression Y = (2y − l)/l is adopted to obtain the dimensionless Y. When the piston speed is zero at TDC, the hydrodynamic lubrication effect generated by the textured region is weak, as the hydrodynamic pressure is induced by the squeeze effect. Therefore, the ring is at mixed lubrication. When the crank angle is between 359° and 361°, the inlet of oil reverses. It is observed that there is a larger pressure peak after surface texturing. It seems that the introduction of surface texturing on the ring results in a wider influence area and a larger pressure peak, when the ring is at reversal. It seems that surface texturing with suitable dimensions can produce a positive influence on the tribological behaviors.

Fig. 10
figure 10

2D contour plots of hydrodynamic pressure distribution: a for the untextured ring at 359°, b for the untextured ring at 360°, c for the untextured ring at 361°, d for the textured ring at 359°, e for the textured ring at 360°, and f for the textured ring at 361°

Full size image

Figure 11a, b show the predicted results about the distributions of asperity contact pressure for untextured and textured rings when the rings are at TDC. Since the ring is barrel-shaped, the peaks of the asperity contact pressure are located at the center region. With textures on the ring face, it is observed that the asperity contact pressure at the textured zone is reduced. When the crank angle is ranging from 358° to 362°, the contact pressure peaks change with the crank angles. At 361°, the contact pressure peaks reach their maximum values. The result of the contact pressure peaks in the case of the textured ring is smaller than that from the untextured ring. This is mainly due in large part to the texture-induced hydrodynamic lift sharing more of the load.

Fig. 11
figure 11

a 2-D contour plots of asperity contact pressure for the untextured ring, b 2-D contour plots of asperity contact pressure for the textured ring, and c variation of the peaks in asperity contact pressure with the crank angle (from 358° to 362°)

Full size image

4.2.3 Friction and wear

The purpose for applying surface texturing to the ring/liner is to obtain a better tribological performance. Figure 12a shows the results about the ratio of the frictional traction to the contact load for the untextured and the textured rings. Notice that the ratio of the frictional traction to the contact load is calculated by dividing the applied load by the total friction force. As shown in Fig. 12a, by comparing the result about the ratio of the frictional traction to the contact load with and without surface texturing, it can be seen that there is a reduction in friction force after texturing. The results show that surface texturing can be used as a means of reducing friction loss to obtain the promising tribological properties.

Fig. 12
figure 12

a Variation in the ratio of the frictional traction to the contact load with the crank angle, b variation in asperity load ratio with the crank angle

Full size image

The phenomenon of wear in an engine, which is induced by asperity contact, is also one most interesting topic. Figure 12b shows the change of asperity load ratio throughout an engine cycle. The asperity load ratio is the ratio of the load carried by the asperities to the total load. According to the result, the application of surface texturing has a significant effect on the reduction in asperity contact. The reduction trend is obvious both in the power stroke and near dead centers. Both the high gas pressure in the combustion chamber and the low sliding speed cause the ring/liner system to be under the mixed lubrication. With the help of surface texturing, it appears that the wear of the ring/liner system is reduced.

To characterize the phenomenon of wear more clearly, the parameter wear load is computed for the liner and each ring face. As defined in the work of Gulwadi [43], the wear load parameter can be calculated as follows:

$$Wear\;load = \frac{1}{T}\int\limits_{0}^{T} {P_{asp} \left| U \right|dt}$$
(36)

where U is the piston velocity and T is the period of the engine cycle. Notice that, the wear load parameter is based on the calculation of the asperity pressure, and is influenced by the sliding speed of the piston ring.

Figure 13 shows the wear load profiles on the top compression ring face with and without surface texturing. As shown in Fig. 13, the values of peak wear load are different for the untextured and textured rings. Lower values of peak wear load are observed at the center region of the ring face when surface texturing is introduced. This shows that surface texturing on the ring can reduce wear.

Fig. 13
figure 13

Wear load profiles: a for the untextured ring and b for the textured ring

Full size image

5 Conclusions

In this study, based on the Greenwood and Tripp approach, an improved statistical elasto-plastic asperity contact model for two rough surface was established. Unlike the GT model, which assumes a purely elastic asperity deformation, the current model takes the elasto-plasticity transition of contact deformation into account. In this way, the contact force and actual contact area can be predicted more accurately, especially for the high-load condition. Meanwhile, compared with the KE model, the presented model is more suitable for solving the contact problem of two rough surfaces, by considering the permitting misalignment. It also meets the need for approximate models in practical applications. The improved asperity contact model can be integrated into the mixed-lubrication model to understand the influence of surface texturing.

In the simulation of the textured ring under engine like conditions, the reductions of friction and wear for surface texturing are demonstrated. The results using the mixed-lubrication model highlighted above are compared with the prediction made by the combination of the Reynolds equation and the purely elastic asperity model. It is shown that, the presented elastoplastic asperity contact model can provide the same result as the GT model, when only elastic deformation of asperities is involved. Meanwhile, a more accurate prediction can be provided based on the presented model, once the plastic deformation of asperities is induced. The presented asperity contact model can deal with different scenarios, no matter the plastic deformation of asperities is induced or not, which is a universal asperity contact model. Furthermore, according to the wear load results, it is observed that suitable surface texturing on the ring can reduce the wear. The main mechanism for such an effect may be attributed to the surface texturing inducing hydrodynamic lift.