Inviscid instability of two-fluid free surface flow down an incline

Abstract

The inviscid temporal stability analysis of two-fluid parallel shear flow with a free surface, down an incline, is studied. The velocity profiles are chosen as piecewise-linear with two limbs. The analysis reveals the existence of unstable inviscid modes, arising due to wave interaction between the free surface and the shear-jump interface. Surface tension decreases the maximum growth rate of the dominant disturbance. Interestingly, in some limits, surface tension destabilises extremely short waves in this flow. This can happen because of the interaction with the shear-jump interface. This flow may be compared with a corresponding viscous two-fluid flow. Though viscosity modifies the stability properties of the flow system both qualitatively and quantitatively, there is qualitative agreement between the viscous and inviscid stability analysis when the less viscous fluid is closer to the free surface.

1 Introduction

Motivated by different applications, a large number of inviscid instability studies have been carried out on parallel shear flows that include flows between parallel plates [1–5], flows bounded by two free surfaces or wall bounded flows bounded by a free surface from above [6–12]. These investigations have employed various piecewise linear velocity profiles in their models and analysis, with different aims. As we shall describe below, one of the recurrent aims has been to represent viscous flows by selecting the closest inviscid flow profiles, to evaluate the inviscid nature of the instabilities in viscous flows. Our aim here is the same, and the viscous flow we would like to make a correspondence with is that of a two-fluid film flow on an inclined surface. The two fluids have different viscosities but the same density, with viscosity varying from one fluid’s value to the next within a thin layer of mixed fluid.

This study is in fact motivated by the recent study on the linear stability of miscible two-fluid free-surface flows of varying viscosity down an inclined substrate examined by Usha et al. [13]. The results reveal the occurrence of new instability modes when the critical layer of dominant disturbance overlaps the viscosity gradient. A configuration with a less viscous wall layer is identified to be the most stable configuration at moderate miscibility, with respect to both overlap and surface modes. However, when a less viscous fluid is adjacent to the free surface, the configuration is unstable which is in contrast with the immiscible interface dominated two-fluid free surface flow [14]. An increase in the inclination angle enhances the destabilization. It is of interest to understand the physical mechanism responsible for flow instabilities in the above flow system and one needs to find out whether the instabilities arise due to viscosity stratification and/or diffusivity and/or inviscid mechanism. In view of this, in the present study, an inviscid flow model of the above free surface flow problem is developed and the instability of two-fluid parallel shear flow down an incline separated by a jump in viscosity is analyzed. For the inviscid model, we consider base velocity profiles as continuous piecewise linear profiles with a slope change across the viscosity interface such that the asymptotic behaviour of the viscous velocity profile is maintained (see Fig. 2).

It is worth mentioning that a similar analysis was performed by Sahu and Govindarajan [15], in which they have investigated the viscous instability of free shear layer in the vicinity of a viscous stratified mixed layer. Their results show that diffusivity has no influence on the stability of this class of shear flows but viscosity stratification has a significant role on the stability characteristics. This requires an explanation as to why there is no influence of diffusivity on the stability in this system. The authors have pointed out that “it could be due to viscosity stratification acting on the stability in an inviscid nondiffusive way”. In order to understand this, they have considered an inviscid model flow with a slope change across the interfaces where viscosity is stratified. The ratio of the slopes across the middle interface represents the inverse of the viscosity ratio. The existence of an unstable inviscid mode for small wave numbers has been shown. In addition, a qualitative agreement between viscous and inviscid results through the trend of growth rate and the influence of the location of the slope change on the dominant growth rate have been observed. These authors have concluded that this broad qualitative agreement between the viscous and the inviscid model results indicate that an inviscid non-diffusive mechanism has a role to play through a change in the velocity profile above and below the stratified layer.

In line with the above investigation, our goal in the present study is to understand the mechanism by which viscosity stratification acts in free surface flows. It is important to note that viscosity stratification across two different fluid phases can give rise to instabilities that are neither inviscid nor of the TS type [16–21]. There are also inviscid models of two-phase flows or free-shear layer flows which are inviscidly unstable to infinitesimal perturbations, under certain conditions. The inviscid framework is sufficient to describe the disturbance evolution at large Reynolds numbers [22–24]. In addition, the present study provides information on the inviscid analysis on wall bounded flows bounded by a free surface from above.

It is to be noted that, in spite of a number of engineering applications such as spilling breakers [6, 7], coating of a substrate or manufacture of photographic films [25, 26] and environmental flows such as rock glaciers [8, 27] in which one comes across instabilities in a film with a free surface, there are only few inviscid studies on flows bounded by a free surface. Bakas and Ioannou [10] have studied modal and non-modal growth of inviscid planar perturbations in shear flows with a free surface by approximating the mean flow with one kind of piecewise linear profile. They have examined the interaction of edge waves that arise at the density discontinuity at the surface and vorticity waves that are supported at the mean vorticity gradient discontinuities in the interior. Renardy’s investigation [11] on plane parallel shear flows bounded by two free surfaces shows that the flow system has long-wave instabilities for all types of velocity profiles that are not uniform. Kaffel and Renardy [12] have considered the linear stability of plane Poiseuille flow between two parallel free surfaces and the analysis reveals that there are short wave instabilities for a velocity profile with a shear rate increasing towards the free surface. However, a broad class of wall bounded flows are stable and there is no smooth velocity profile that is unstable to short waves.

Rayleigh’s criterion for wall bounded flows states that the base flow profile must have an inflection point for instabilities to exist. Yih [28] and Hur and Lin [29] have extended Rayleigh’s criterion for wall bounded flows to free surface flows. They have claimed that all monotonic profiles with inflection points have long-wave instabilities. Correcting the errors in the arguments presented by Yih [28] and Hur and Lin [29], Renardy and Renardy [30] in their investigation on the linear stability of inviscid parallel shear flow in a geometry bounded by a wall at the bottom and with a free surface subject to gravity show that the stability characteristics of a free surface flow are different from those for wall bounded flows. Their conclusions are based on the three specific flows U(y) namely, Poiseuille flow (with no inflection point but has velocity extremum), flow with a hyperbolic tangent shear layer (has an inflection point at $y = 0$, U and $U''$ have opposite signs), and a cubic base profile (has an inflection point at $y = 0$, U and $U''$ have same signs). The results show that while neutral limiting modes must have a wave speed equal to an inflection value of the base flow profile for wall bounded case, a shear flow with a free surface can have a wave speed equal to either the velocity at the bottom or to an extremum value of velocity. Furthermore, short waves are destabilized as the shear rate increases towards the free surface.

Instabilities in shear flows have also been studied in detail for base flows without inflection point, [12, 30–32] for flows with piecewise linear profiles [33, 34] and for continuous profiles [35]. The stability of gravitational-capillary waves in the presence of vertically non-uniform current analysed by Voronovich et al. [34] shows that long waves are stable. In their study, the bottom layer is infinite and a vortex sheet is located at a fixed depth below the surface. The velocity profile in the top layer is linear. If however, it is constant, then, in the absence of a vortex sheet, the long waves are unstable for an infinite depth (Theorem 1.2 in Bresch and Renardy [36]).

Bresch and Renardy [36] have revisited the problem analyzed by Voronovich et al. [34] for a configuration with a finite bottom layer, relaxing the assumption of an irrotational flow and by including the gravity effects. They have examined Kelvin–Helmholtz instability with a free surface. The velocities of two-fluid layers are different. Long-wave stability for sufficiently small gravity is shown for smooth monotone velocity profiles of base flow. The scenario in the wall bounded case is different; the flow is unstable to all wavenumbers. Instabilities existing at large wavenumbers are localized and are independent of the boundary conditions.

Concerning shear flows without an upper free surface, the classical inviscid problem considered by Kelvin and Helmholtz that involves a vortex sheet (an infinite surface of discontinuity) separating two unbounded fluid layers of different velocity and density is always unstable provided a velocity difference exists and it has largest growth rate in the absence of density discontinuity. Following this, numerous studies have attempted to understand the instability characteristics of unbounded parallel inviscid flows [37–41].

There are investigations on two-fluid flows stratified by gravity and also between two rigid plates [1–5, 36]. The inviscid instability of immiscible fluids in a shear layer examined by Pouliquen et al. [42] revealed the existence of Holmboe waves for symmetric broken-line profile. Though they ignored the viscosity effects, the chosen velocity profile satisfied the condition of continuity of shear stress at the interface. When the symmetry is broken (the two fluids have different densities with zero velocity at the interface), they observed a single mode propagating in the same direction as the less viscous fluid at high wavenumbers. The linear stability of inviscid density-stratified shear layer flows are discussed in detail by Redekopp [43]. The effects of surface tension, density and velocity profile on inviscid instability of an unbounded shear layer are examined by Alabduljalil and Rangel [44]. In this study, they have taken the background velocity profiles as (a) piecewise linear profile and (b) error-function profile. The results reveal that surface tension has a destabilizing effect and that the unstable mode induced by surface tension is weak as compared to the dominant mode. Instabilities at large wavenumbers are observed with a background viscosity jump at the interface. Although the above studies deal with inviscid stability analysis of an unbounded shear layer of two fluids, the viscosity has its role to play on the background flow and influences the stability characteristics of the flow. In the inviscid analysis presented, the effect of viscosity appears through its influence on the background velocity profile.

There are also some earlier work relevant to the present study [45–48]. The viscous temporal stability problem of a planar gas–liquid mixing layer with a single interface and without confinement is analyzed by Yecko et al. [45] and Boeck and Zaleski [46] for basic velocity profiles characterized by boundary layers adjacent to the interface. Boeck and Zaleski [46] performed the inviscid computations for a piecewise linear velocity profile with slopes corresponding to the boundary layers associated with the viscosity profile. When the base velocity profiles are smooth and monotonic, the above investigations show that there are three characteristic unstable modes in different bandwidth of wavenumbers. These modes arise due to (i) the difference in free-stream velocity responsible for inviscid Kelvin–Helmholtz mechanism, (ii) the TS mechanism in the gas boundary layer and (iii) the viscosity contrast mechanism. These modes occur distinctly in the limiting case of large Reynolds numbers. They have observed difference between the viscous and inviscid computations and they have attributed this to the viscosity-contrast instability mechanism. The instability that arises due to viscosity contrast occurs at the interface between the two fluids, occurs for short-wavelengths when viscosity rather than inertia is the dominant physical effect. The instability mechanism for the short-wavelength instability due to viscosity contrast was analysed by Hinch [47], who postulated that this instability requires a large viscosity contrast and a significant vorticity diffusion (i.e. a high Schmidt number).

The viscous linear stability analysis of the gas–liquid mixing layers considered by Otto et al. [48] depends on the basic velocity profiles, the density ratio and on the Reynolds number. Their inviscid computations for growth rates is only favourable for low air velocities when the experimental frequencies are used and a small or moderate velocity deficit is incorporated. Their spatial stability analysis predicts results that agree very well with measured growth rates obtained in air–water experiments.

The above investigations [45, 46, 48] indicate that it is possible to gain insight into the perturbation growth mechanism in the present study by understanding the modal instabilities in terms of the interaction between the interfaces, namely the free surface with or without surface tension and the liquid–liquid interface with viscosity jump. The paper is organized as follows: Sect. 2 presents the governing equations, the base state profiles and the derivation of the dispersion relation. The results are discussed in Sect. 3; the equation for the total rate of disturbance kinetic energy is derived in Sect. 3.4; and the concluding remarks are given in Sect. 4. The present study is only a model to check if inviscid mechanism is important and hence the focus is on investigating a base state which is just a profile mimicking the viscous base state. In other words, we perform the stability analysis of an inviscid base profile which follows the characteristics and asymptotic behaviour of viscous base profile.

Fig. 1

Schematic of the geometry for the flow system considered. Fluids ‘1’ and ‘2’ occupy the regions near the inclined plane (y = H) and near the free surface ($y = h_2(x,t)$) respectively. $y = h_1(x,t)$ represents the liquid–liquid interface and $\theta$ is the angle of inclination

Fig. 2

Base velocity profiles: a for inviscid two-fluid free surface flow with slope change interface located at $d = 0.4$ and b for the corresponding viscous miscible two-fluid flow in Fig. 2 of Usha et al. [13]; curves with star symbols represent base viscosity profiles

2 Mathematical formulation

2.1 Base state

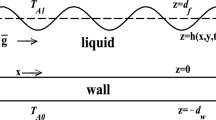
As mentioned before, the idea is to investigate whether viscosity change across a film flow can have an inviscid effect on the stability, via changes in the velocity profile. An inviscid and non-diffusive analogue of the miscible two-fluid viscosity stratified flow down an inclined substrate (Usha et al. [13]) is constructed (Fig. 1). As is common in inviscid analyses [15, 46], continuous piecewise linear velocity profiles are used as base flow as shown in Fig. 2a. The jump in shear stress at the interface is taken to be equal to the inverse of the viscosity jump we are interested in comparing with. The corresponding velocity profiles in a viscous film are constructed by the approach described in Usha et al. [13], and are shown in Fig. 2b. The viscosity jump across the mixed layer is modelled by a corresponding jump in the slope of the velocity profile at $y = d$ for the inviscid analysis. The inviscid flow now supports two sets of waves, one at the liquid–liquid interface ($y = d$) and another at the free surface ($y=0$).

Let $U_{1B}(y)$ and $U_{2B}(y)$ denote the base velocity profiles in fluid layers 1 and 2 respectively. Taking the base profiles as piecewise linear and using the conditions $U_{1B}(y = 1) = 0$, $U_{2B}(y = 0) = 1$ and $U_{1B}(y = d) = U_{2B}(y = d)$, these are obtained as

$$U_{1B}(y)= \frac{K_1}{Y}(1-y),$$

(1)

$$U_{2B}(y)= \frac{K_2}{Y} (d - y) + \frac{K_1}{Y}(1-d),$$

(2)

where the factor $Y = K_2d +1 -d$ appears upon scaling the velocity with its value at the free surface. In what follows, $K_1$ is fixed as $K_1 = 1$ without loss of generality. For comparing with a viscous flow of viscosity ratio $m = \mu _2/\mu _1$, an appropriate choice of $K_2$ is 1 / m (as $m = 1/K_2$ makes the shear stress continuous in the viscous case with viscosity ratio m). The base velocity profiles for different values $K_2$ (0.5, 1, 1.5) in the upper layer are presented in Fig. 2a. Figure 2a suggests that, when $K_2<1$ ($K_2>1$), the velocity profile is convex (concave) function of y. $K_2 = 1$ presents a single fluid flow with linear velocity profile. The value $K_2 > 1$ corresponds to $m<1$ and $K_2 < 1$ to $m > 1$ profiles in Fig. 2b for the viscous case.

It is worth mentioning here that according to the inviscid theory, a flow system with convex base velocity profile is more inviscidly stable [2]. Our goal is to develop an inviscid model for the miscible two-fluid flow system to check if inviscid mechanism is important or not.

2.2 Linear stability equations

The equations and the boundary conditions governing the inviscid instability of the gravity-driven free surface flow of two-fluids down an incline on $0 \le y \le H$ (Fig. 1) are non-dimensionalized using the following scales:

$$\begin{aligned} x^{*} &= \frac{x}{H},\quad y^{*} = \frac{y}{H},\quad t^{*} = \frac{V}{H}t, \quad (u_n^{*},v_n^{*}) = \frac{1}{V}(u_n,v_n),\, \\ p^{*} &= \frac{p}{\rho V^{2}},\quad d^{*} = \frac{d}{H},\quad h_n^{*} = \frac{h_n}{H}, \end{aligned}$$

(3)

where V is the characteristic velocity at the free surface, H is the height of the unperturbed film and $\rho$ is the fluid density; the sub-index $n = 1, 2$ denotes to the flow variables in fluid layers ‘1’ ($d \le y \le 1$) and ‘2’ ($0 \le y \le d$) respectively; $u_n$, $v_n$ are the velocity components in the x and y directions, respectively; $p_n$ and t correspond to the pressure and time. $h_1(x,t)$, $h_2(x,t)$ are the deflections of the liquid–liquid interface and the free surface with respect to $y = d$ and $y = 0$, respectively (see Fig. 1).

The boundary conditions are the no-slip condition at the inclined plane ($y=1$), the continuity of normal velocity, pressure and kinematic condition at the fluid–fluid interface ($y = h_1(x,t)$) together with the kinematic condition and the balance of pressure at the free surface ($y = h_2(x,t)$). They are linearized about the base flow and in terms of disturbances $\tilde{u}_n, \tilde{v}_n, \tilde{p}_n$ and $\tilde{h}_n$ ($n = 1, 2$) proportional to ${\mathrm {e}}^{{\mathrm {i}}\left( \alpha x - \omega t \right) }$ with proportionality constants $\hat{u}_n, \hat{v}_n, \hat{p}_n$ and $\hat{h}_n$ ($n = 1, 2$) respectively, where $\, {\mathrm {i}}\equiv \sqrt{-1}$, $\alpha$ and $\omega = \alpha c$ are the wave number and the frequency of the infinitesimal two-dimensional disturbances; c is the complex wave speed. This results in the following eigenvalue problem in the form of Rayleigh equations for the two-dimensional perturbations on the domain $0 \le y \le 1$ [after suppressing hat $(\;\hat{}\;)$ symbols]:

$$(U_{nB}-c)(D^2 - \alpha ^2)v_n - U_{nB}'' v_n = 0.$$

(4)

Note that since the velocity profiles are linear, $U_{nB}'' = 0$. The boundary conditions are given by

$$v_1= 0 \quad \text { at }\, y = 1,$$

(5)

$$v_1 = v_2 \quad \text { at }\, y = d,$$

(6)

$$p_1 = p_2 \quad \text { at }\, y = d,$$

(7)

$$v_1 = {\mathrm {i}} \alpha h_1(U_{1B} - c) \quad \text { at }\, y = d ,$$

(8)

$$v_2 = {\mathrm {i}} \alpha h_2(U_{2B} - c) \quad \text { at }\, y = 0 ,$$

(9)

$$p_2 = - \alpha ^2 S h_2 - G\cot (\theta ) \quad \text { at }\, y = 0.$$

(10)

In the above, $G = \frac{g H \sin (\theta )}{V^2}$ is the dimensionless gravity parameter, $S = \frac{\sigma }{\rho V^2 H}$ is the dimensionless surface tension parameter, where $\sigma$, g are the surface tension coefficient between fluid-2 and air, and acceleration due to gravity, respectively.

The solutions of Eq. (4) are

$$v_1(y)= P_1 {\mathrm {e}}^{\alpha y} + Q_1 {\mathrm {e}}^{- \alpha y},$$

(11)

$$v_2(y)= P_2 {\mathrm {e}}^{\alpha y} + Q_2 {\mathrm {e}}^{- \alpha y},$$

(12)

where $P_1$, $Q_1$, $P_2$, $Q_2$ are arbitrary constants to be determined. Substitution of $v_1$, $v_2$ in the boundary conditions (5)–(10) yields the following dispersion relation in wave speed ‘c’ and wave number ‘$\alpha$’:

$$\begin{aligned}&\left[ \alpha (c - U_{1B}^d)({\mathrm {e}}^{\alpha d}+{\mathrm {e}}^{\alpha (2-d)}) + U_{1By}^d ({\mathrm {e}}^{\alpha d}-{\mathrm {e}}^{\alpha (2-d)})\right] \\&\quad ={M_3} \left[ \alpha (c - U_{2B}^d) ({\mathrm {e}}^{\alpha d}-{M_2} {\mathrm {e}}^{-\alpha d}) \right. \\&\qquad \left. +U_{2By}^d({\mathrm {e}}^{\alpha d}+M_2 {\mathrm {e}}^{-\alpha d})\right] , \\ \end{aligned}$$

(13)

where

$$\begin{aligned} M_1 &= \alpha (c - U_{2B}^0),\\ M_2 &= \left[ \frac{M_1(M_1 + U_{2By}^0) + (\alpha ^3 S + \alpha G \cot (\theta ))}{M_1(M_1 - U_{2By}^0) - (\alpha ^3 S + \alpha G \cot (\theta ))}\right] , \\ M_3 &= \left[ \frac{{\mathrm {e}}^{\alpha d}-{\mathrm {e}}^{\alpha (2-d)}}{{\mathrm {e}}^{\alpha d}+{M_2} {\mathrm {e}}^{-\alpha d}}\right] . \end{aligned}$$

and $U_{nB}^d$ and $U_{nB}^0$ ($n = 1,2$) represent the values of base velocity at $y = d$ and $y = 0$ respectively. The dispersion relation (13) is cubic in c for a given value of $\alpha$. Equation (13) can be simplified since the base velocity profiles are piecewise linear and $U_{2B}^0=1$, $K_1=1$. Also, from equations (1) and (2), one obtains $U_{1B}^d = U_{2B}^d = (1-d)/Y$, $U_{1By}^d =-1/Y$, $U_{2By}^d =-K_2/Y$, $U_{2By}^0 =-K_2/Y$. Defining

$$f \equiv G\cot {\theta } + S \alpha ^2,$$

(14)

and for ease of algebra, setting $~ q \equiv \sinh [\alpha (1-2d)]/$ $(\cosh \alpha )$, $r \equiv \cosh [\alpha (1-2d)]/(\cosh \alpha )$, $x = 1-d$, $K_2 = k$, $y = kd$ and $t = \tanh (\alpha )$, Eq. (13) is rewritten after some algebra as

$$c^3 + B c^2 + C c + D = 0,$$

(15)

where

$$B= \frac{1}{(x+y)}\left[ -3x- 2y + \frac{( k + 1)t + q ( 1-k)}{2\alpha }\right] ,$$

(16)

$$\begin{aligned} C &= \frac{1}{(x+y)^2}\bigg [ (x+y)(3x+y) \\&\quad-\frac{t}{\alpha } \left[ x + k - f+ 2( x+y)f + d^2 (k-1)^2 f \right] \\&\quad+\frac{( k - 1)}{2\alpha ^2} \left[ k ( r-1) + 2\alpha (x+y) q\right] \bigg ], \end{aligned}$$

(17)

$$\begin{aligned} D &= -\frac{1}{(x+y)}\left\{ x - \frac{kxt}{\alpha (x+y)}\right.\\&\quad\left.+\frac{1}{2\alpha }\left[ ( k - 1 - 2x f)t + q(k-1)\right] \right. \\&\quad\left.+\frac{(r-1)(k-1)}{2\alpha ^2}\left[ f + \frac{k}{(x+y)}\right] \right\} . \end{aligned}$$

(18)

For a cubic equation with real coefficients, the only two possibilities are that either all roots are real, or that one root is real and the other two are complex conjugates of each other. Therefore, the flow system is stable (unstable) accordingly as the discriminant,

$${\varDelta }= {C}^2({B}^2 - 4 C) - 4 {B}^3 D - 27 {D}^2 + 18 B C D$$

(19)

is positive (negative).

3 Stability results

3.1 Limiting cases

Before presenting the complete solution, it is revealing to obtain some limiting solutions of this problem. First, when $d=0$ and $k=1$, Eq. (15) reduces to that for a single fluid, which, upon regrouping, can be written as

$$\begin{aligned} (c-1)\left[ -\alpha c^2 + c (2 \alpha - \tanh (\alpha ))\right] \\ \quad + (c-1)\left[ (f + 1) \tanh (\alpha ) - \alpha \right] = 0. \end{aligned}$$

(20)

The roots of Eq. (20) are

$$\begin{aligned} &c_1 = 1,\\ &c_{2,3} = \frac{(2\alpha - \tanh (\alpha )) \mp \sqrt{\tanh ^2(\alpha ) + 4 \alpha f \tanh (\alpha ) }}{2\alpha }, \end{aligned}$$

which may be seen to be all real, since $\alpha \ge 0$. Thus, a film of a single fluid with a linear profile flowing down an incline is inviscidly stable at all wavenumbers for any surface tension and any inclination. We return to the piecewise linear velocity profile, with $k \ne 1$.

3.1.1 Vertical wall, no surface tension

We notice that gravity and surface tension appear in the problem only as the combination f, given by Eq. 14. For a vertical wall ($\theta = 90^{\circ }$), in the absence of surface tension ($S = 0$), we have $f=0$. It may be checked that $1+B+C+D = 0$, showing that $c = 1$ is a root of the cubic equation (15). The other two roots are those of the quadratic equation

$$c^2 + (1+B)c - D = 0.$$

(21)

The discriminant of Eq. (21) becomes (after some algebra),

$$\begin{aligned} {\varDelta } &= \frac{(1-k)}{(x+y)^2}\left[ \frac{2k}{\alpha ^2}(r-1) + \frac{y}{\alpha } (t+q)+\frac{t^2}{4\alpha ^2}(1+3k)\right. \\&\quad\left. + \frac{q^2}{4\alpha ^2}(1-k) + \frac{tq}{2\alpha ^2}(1+k) \right] + \frac{1}{(x+y)^2}\left[ y - \frac{kt}{\alpha }\right] ^2 \end{aligned}$$

Case (i) Short waves $({\alpha \rightarrow \infty })$: Here, ${\varDelta }= k^2 d^2/(kd + 1 - d)^2$ which is positive, showing that the roots of Eq. (21) are real. Therefore, there is no short wave instability for $f = 0$.

Case (ii) Long waves $({\alpha \rightarrow 0})$: In this case, ${\varDelta }= (1 - d)^2/(kd + 1 - d)^2$ and it is positive again, so long-waves too are stable for any k when $f = 0$.

3.1.2 Horizontal wall or large surface tension

In the limit of either $\cot \theta$ or S becoming extremely large, f becomes very large. An examination of the discriminant makes it evident that stability is decided in this limit by the sign of $-4C^3$. In this limit,

$$C = -\left( \frac{tf}{\alpha }\right) .$$

(22)

It is immediately evident that the discriminant is always positive, which makes the flow always stable when either the wall inclination goes to 0 or surface tension is very large.

For the case when $f \ne 0$ but is finite, we examine below the limits of diverging and vanishing shear ratios.

3.1.3 Diverging shear ratio k

As the ratio of the slopes of the linear velocity profiles tends to infinity ($k \rightarrow \infty$), we have the velocity of the lower fluid going to 0. One obtains from Eqs. (16)–(18),

$$\begin{aligned} B_{k\rightarrow \infty } &= -2 + \frac{t - q}{2 d \alpha },\\ C_{k\rightarrow \infty } &= 1 + \frac{1}{2\alpha ^2 d^2} ( r + 2\alpha d q-1) - \frac{tf}{\alpha },\\ D_{k\rightarrow \infty } &= \frac{1}{2\alpha ^2 d^2} \left[ (1-r)(1 + df) - \alpha d(q+t) \right] . \end{aligned}$$

Case (i) Short waves: We note that,

$$\begin{aligned} \lim _{\alpha \rightarrow \infty } \frac{t}{\alpha } = 0, \quad \lim _{\alpha \rightarrow \infty } \frac{q}{\alpha } = 0, \quad \lim _{\alpha \rightarrow \infty } \frac{q}{\alpha ^2} = 0, \quad \lim _{\alpha \rightarrow \infty } \frac{r-1}{\alpha ^2} = 0. \end{aligned}$$

For short waves, in the absence of surface tension, $B_{k\rightarrow \infty }$ $= -2$, $C_{k\rightarrow \infty } = 1$ and $D_{k\rightarrow \infty } = 0$. The discriminant ${\varDelta }$ (Eq. 19) is zero in this case, showing that short waves are stabilized as $k \rightarrow \infty$ and $S = 0$. On the other hand, when surface tension is present but small, i.e., in the limit $S\ne 0$ but $\alpha S<< 1$, then, for short waves $B_{k\rightarrow \infty } = -2$, $C_{k\rightarrow \infty } = 1 - tS\alpha$ and $D_{k\rightarrow \infty } = \frac{S(1-r)}{2d}$ and the discriminant (19) becomes,

$${\varDelta }= -\frac{1}{4d^2}\left[ 8dS(1-r) + 27 S^2 (1-r)^2\right] .$$

Since $1-r > 0$ for large $\alpha$, ${\varDelta }< 0$ showing that short waves are unstable in the presence of surface tension as $k \rightarrow \infty$. This result shows that surface tension has a destabilising effect on short waves in this inviscid flow. The reason for this counter-intuitive effect is the fact that there is an interaction with the layer of shear jump, which can phase-lock the waves on the two layers in an unstable configuration. Such phase locking will be seen below in the solution of the complete problem.

Case (ii) Long waves: For long waves, we have

$$\lim _{\alpha \rightarrow 0} \frac{t}{\alpha } = 1, \quad \lim _{\alpha \rightarrow 0} \frac{q}{\alpha } = 1-2d, \quad \lim _{\alpha \rightarrow 0} \frac{r-1}{\alpha ^2} = 2d(d-1),$$

the coefficients are $B_{k\rightarrow \infty } = -1$, $C_{k\rightarrow \infty } = -G\cot {\theta }$ and $D_{k\rightarrow \infty } = G\cot {\theta }(1-d)$. The discriminant ${\varDelta }$ is then,

$$\begin{aligned} {\varDelta } &= 4G^3 \cot ^3 {\theta } + G^2 \cot ^2 {\theta }(3d-2)^2\\&\quad- 12G^2 \cot ^2 {\theta }(3d-1)(d-1) + 4G\cot {\theta }(1-d). \end{aligned}$$

The stability properties are independent of surface tension for long waves. Now, for a vertical wall ($\theta = 90^{\circ }$), ${\varDelta }= 0$ and the system is stable. For any $\theta \ne 90^{\circ }$, the system is stable for $\frac{1}{3}<d<1$, while at other d the flow may be stable or unstable.

3.1.4 Vanishing shear ratio k

Fig. 3

Real and imaginary parts of eigenmodes as a function of wave number $\alpha$ when $K_1 = 1, K_2 = 1.5, d = 0.4$ and $G = 5/6$: a, b for $\theta = 90^{\circ },\, S = 0$; c, d for $\theta = 45^{\circ },\, S = 0$. e, f For surface tension parameter $S = 0.02$ with $\theta = 90^{\circ }$. Here $c_r$ and $c_i$ represent real and imaginary parts of the eigenmodes

Fig. 4

Influence of upper layer slope ($K_2$) and effect of distance between the two interfaces (d) on the growth rate $\omega _i = \alpha c_i$ for $K_1 = 1, \, \theta = 90^{\circ },\, G = 1/Y$. a, b without surface tension ($S = 0$) and in c, d surface tension $S = 0.02$. In a, c, $d = 0$ and in b, d, $K_2 = 1.5$

We note that due to the presence of a no penetration surface at $y=H$ and a free surface at $y=0$, the limits $k \rightarrow \infty$ and $k \rightarrow 0$ will not yield the same result. We therefore consider the latter case separately here, where the upper fluid is at a constant velocity of 1. When $k \rightarrow 0$, we have from Eqs. (16)–(18),

$$\begin{aligned} B_{k\rightarrow 0} &= -3 + \frac{1}{2\alpha x}(t + q), \\ C_{k\rightarrow 0} &= 3-\frac{1}{\alpha x}(t + q) - \frac{tf}{\alpha }, \\ D_{k\rightarrow 0} &= -1 + \frac{1}{2\alpha x}(t + q) +\frac{tf}{\alpha } - \frac{f}{2\alpha ^2x}(r-1). \end{aligned}$$

(23)

Case (i) Short waves: In the case of short waves,

$$\begin{aligned} B_{k\rightarrow 0} &= -3,\, C_{k\rightarrow 0} = 3-tS\alpha ,\\ D_{k\rightarrow 0} &= -1 + tS\alpha + \frac{S}{2x}(r-1). \end{aligned}$$

The inclination of wall has no influence on the stability properties. In the absence of surface tension, $B_{k\rightarrow 0} = -3,\, C_{k\rightarrow 0} = 3,\,D_{k\rightarrow 0} = -1$ and ${\varDelta }= 0$; hence the short waves are stable.

If surface tension is present but $S \alpha<< 1$ then $B_{k\rightarrow 0} = -3$, $C_{k\rightarrow 0} = 3,\,D_{k\rightarrow 0} = -1+ \frac{S}{2x}(r-1)$. The discriminant is

$${\varDelta }= - \frac{27}{4}\left( \frac{S^2}{x^2}\right) (r-1)^2 ,$$

and is negative for all x and r. Therefore, in the presence of small surface tension, the short waves ($\alpha \rightarrow \infty$) are destabilized.

Case (ii) Long waves: For long waves, $B_{k\rightarrow 0} = -2$, $C_{k\rightarrow 0} = 1-G \cot {\theta }$ and $D_{k\rightarrow 0} = G \cot {\theta } (1-d)$. The discriminant in this case is

$${\varDelta }= 4G\cot {\theta }(G\cot {\theta } - 1)^2 + 9 G^2 \cot ^2 {\theta }(1+3d)(1-d),$$

which is zero for a vertical wall ($\theta = 90^{\circ }$) and positive for any other wall inclination ($\theta$) less than $90^{\circ }$. Therefore there is no long wave instability when $k \rightarrow 0$.

Although the configurations and base state profiles are different, it is worth mentioning the different limiting cases examined by Bresch and Renardy [36] for the Kelvin–Helmholtz instability with a free surface for the wall bounded case. The authors exhibit scenarios similar to the limiting cases of the present study for long and short wavelengths for constant-shear base velocity profiles. They have shown that there is no long-wave instability ($\alpha \rightarrow 0$) when gravity (G) satisfies the condition $0 \le G \le 1/2$. In the case of short waves ($\alpha \rightarrow \infty$) there is Kelvin–Helmholtz type instability and it is independent of gravity. Farther, the results reveal that stability of long waves for small gravity generally holds for monotone profiles. The base velocity profiles in the present study are always monotone.

Having examined these limiting cases for long and short waves for extreme values of k, we move on to the stability results for finite k and moderate wave numbers. These are obtained numerically from the dispersion relation and presented in the next section.

3.2 Numerical results

The Eq. (15) describes the stability problem for the two layer inviscid fluid flow system. It is an equation for the wave speed c with real coefficients. The stability of the base flow, approximated by a piecewise linear profile is considered. The behaviour of eigenmodes for the case when surface tension $S = 0, \, 0.02$ and gravitational parameter $G \ne 0$ is first examined.

Figure 3 provides a typical result showing the real ($c_r$) and imaginary ($c_i$) parts of the eigenvalues of Eq. (13) as functions of wavenumber $\alpha$, when $K_1 = 1, K_2 = 1.5 \ (m<1), d = 0.4, \,G = 5/6$, for two different values of $S = 0$ (Fig. 3a, b for $\theta = 90^{\circ }$ and Fig. 3c, d for $\theta = 45^{\circ }$) and $S = 0.02$ (Fig. 3e, f for $\theta = 90^{\circ }$). Figure 3a, b shows the three modes for the case when $f = 0$ (zero surface tension and vertical wall). In this case the existence of the third mode with $c_r=1$ and $c_i=0$ has been shown in the Sect. 3.1.1. When surface tension is non-zero or the wall is not vertical, this third mode displays a phase speed different from 1, but is always neutrally stable. In each case instability occurs in a window of wave numbers, where two of the eigenvalues occur in a complex conjugate pair, with one decaying and the other growing. Outside this window, the modes are all neutrally stable and travel with different phase speeds. The figure thus suggests that both long and short waves are inviscidly stable for a vertically falling two-fluid film. Surface tension dampens the maximum growth rate for the unstable mode (compare Fig. 3b, f) for a vertical wall. In the configuration with $\theta = 45^{\circ }$, surface tension has a strong stabilising effect, and $S = 0.02$ is stable for all wave numbers (as we shall see in Fig. 7c).

The dimensionless disturbance growth rates $\omega _i = \alpha c_i$ as a function of wave number $\alpha$ are presented in Fig. 4, when $S = 0$ (Fig. 4a, b) and $S = 0.02$ (Fig. 4c, d) for different upper layer slopes ($K_2$) (Fig. 4a, c; $d = 0.4$) and for different distances between two interfaces d (Fig. 4b, d; $K_2 = 1.5$). The other parameters are $K_1 = 1,\, \theta = 90^{\circ }$ and G. Here G is taken as $G = 1/(K_2d + 1 -d)$. Figure 4a reveals that an increase in slope discontinuity ($K_2$) enhances the growth rate and widens the bandwidth of unstable wave numbers for a vertically falling film in the absence of surface tension. As the location of the liquid-liquid interface (d) approaches the solid substrate, the unstable region is shifted towards the smaller wave numbers (Fig. 4b; $K_2 = 1.5$). The long-wave cut-off emerges and reveals the bandwidth of unstable wave numbers in the long-wave regime. The wavelength of the dominant perturbation scales with the distance d between the liquid–liquid interface and the free surface. There is diminishing of growth rate, destabilization of long waves and stabilization of short waves. The $\alpha _{max}$ in the range of unstable wave numbers $[\alpha _{min},\alpha _{max}]$ decreases as the lower layer/upper layer thickness decreases/increases. This may be due to the weak wave interaction between the liquid–liquid interface and free surface when the distance between them (d) increases.

Fig. 5

a Influence of surface tension on the growth rate ($\omega _i$) and b Phase lag between the waves, at the free surface ($h_2$) and the liquid–liquid interface ($h_1$) for different surface tension parameter (S) value. The other parameters are $K_2 = 1.5,\, d = 0.4,\, \theta = 90^{\circ },\, G = 5/6$

When $S = 0.02$ (Fig. 4c), the bandwidth of unstable wave numbers $[\alpha _{min},\alpha _{max}]$ is such that $\alpha _{min}$ decreases with an increase in $K_2$ indicating destabilization of long waves and $\alpha _{max}$ has non-monotonic behaviour. When $d = 0.2$, the growth rate is zero (for all $\alpha$ values considered) for $S = 0.02$ (Fig. 4d), while it is positive for $S = 0$ (Fig. 4b). On the other hand, for $d = 0.4$, the short waves are destabilized when $S = 0.02$ in contrast to the stabilization of this configuration for $S = 0$. There is dampening of maximum growth rate for $S \ne 0$ as compared to $S = 0$ for each value of d.

The influence of surface tension (S) on the growth rate as a function of wave number ($\alpha$) is evident from Fig. 5a, when $K_2 = 1.5,\, d = 0.4,\, \theta = 90^{\circ },\, G = 5/6$. Recall from the previous section that in the limit of high surface tension, this flow was expected to be stable under all circumstances. Consistent with this, we see that increasing surface tension has a significant stabilising effect, with the wave-number range and growth rate of instability at $S=0.03$ much lower than that at $S=0$. The limiting case of short waves above had given us to expect that surface tension could have an interesting and counter-intuitive destabilising effect on short waves. Consistent with this, we see that the growth rate of the instability displays a non-monotonic behaviour at higher wave numbers. Increasing the surface tension from zero has a significant destabilising effect on the short waves.

That this counterintuitive effect is caused by the interaction with the shear-jump interface is seen in Fig. 5b, which shows the phase lag/phase shift between the maxima in disturbance heights, $h_2$ of the free surface, and $h_1$ of the shear-jump interface, as a function of wave number ($\alpha$). We may check that in the range of wave numbers where the phase lag locked into a positive value, the flow has positive growth rate (see Fig. 5a). It is clear that at small values of surface tension, short waves are destabilised by the increase of surface tension, but as the surface tension is further increased, the phase-locking into a positive value is restricted to a small range of wavenumbers, and short waves are stabilised. The mechanism for instability in the inviscid system may thus be attributed to the interaction between the waves at the two interfaces (The positive phase lag (more than $0^{\circ }$ and less than $180^{\circ }$) corresponds to the inviscid interaction between the waves at the free surface and the liquid–liquid interface. On the other hand, zero phase lag indicates that there is no wave–wave interaction). The effect of the magnitude and the location of the slope change, as well as surface tension, on the most unstable eigenmode is summarised in Fig. 6 by the contour plot of maximum growth rate $\omega _{i,max}$ in the $K_2 - d$ plane. Fig. 6 presents results in the absence of surface tension ($S = 0$) (a) and in its presence (b). For a fixed d, as $K_2$ decreases (m increases), the flow becomes more stable. In addition, the flow is always more stable in the presence of surface tension. The strongest stabilisation due to surface tension is seen at low d, i.e. when the separation between the jump in shear stress and the free surface is small. We note that for $K_2 < 1$ ($m>1$), the configuration is inviscidly stable for all values of d in the range considered. At extremely small values of $K_2$, extremely short waves are destabilised by surface tension, but this limit is not shown here.

Fig. 6

Contour plot of maximum growth rate $\omega _{i,max}$ in $K_2 - d$ plane: a in the absence of surface tension ($S = 0$); b for surface tension parameter $S = 0.02$. The other parameters are $K_1 = 1,\, \theta = 90^{\circ },\, G = 1/Y$

Fig. 7

Influence of angle of inclination $\theta$ on the growth rate $\omega _i = \alpha c_i$ for $K_1 = 1, K_2 = 1.5,\, d = 0.4$: $S = 0$ in (a) and $S = 0.02$ in (b). The dimensionless gravity parameter, $G = 5/6$

As the slope of the inclined substrate is decreased (Fig. 7a; $S = 0$), the growth rate is decreased and the unstable region is shifted towards shorter wave lengths. However, the bandwidth of unstable wave numbers is decreased, indicating the stabilizing effect of decrease in inclination angle $\theta$. In the presence of surface tension (Fig. 7b; $S = 0.02$), a decrease in $\theta$ decreases the maximum growth rate, reduces the bandwidth of unstable wave numbers and stabilizes both long and short waves.

Fig. 8

Comparison of inviscid result (I) with viscous results (V): a $S = 0$ and b $S = 0.02$. In the inviscid case, $\omega _{i,max}$ is given as a function of the distance (d) between the liquid–liquid interface and free surface for different upper layer slopes ($K_2$). In the viscous case, $\omega _{i,max}$ is presented as a function of the distance (d) of the thin mixed layer from the free surface for different viscosity ratios (m). Here $m = 1/K_2$. The other parameters are, in the viscous case $Re = 100,\, \theta = 90^{\circ },\, Sc = 100$ and in the inviscid case $\theta = 90^{\circ },\, K_1 = 1,\, G = 1/Y$

3.3 Comparison to viscous results

Having examined various aspects of the inviscid instability, we return to the flow which motivated this study, namely the viscous miscible two-fluid film flow on an inclined wall, whose base state was seen in Fig. 2b. It is not possible to make a firm statement on whether the instability due to viscosity stratification is caused by inviscid means or not. We therefore restrict ourselves to pointing out, by means of Fig. 8, that the two instability growth rates display a qualitative similarity in terms of the range of unstable wavenumbers, and in terms of the increase in growth rate with increasing viscosity contrast 1 / m (or $K_2$), when $\theta = 90^{\circ }$ ($S = 0$ in Fig. 8a and $S = 0.02$ in Fig. 8b).

Fig. 9

Comparison of eigenvalues (a, b) and growth rates (c, d) between viscous and inviscid flow. In a, $\theta = 90^{\circ },\, S = 0$ and in b, $\theta = 45^{\circ },\, S = 0.02$. The other parameters are $m = 0.67,\,Re = 100,\, \theta = 90^{\circ },\, Sc = 100$ in the viscous case and in the inviscid case $K_2 = 1.5,\,\theta = 90^{\circ },\, K_1 = 1,\, G = 5/6$. The curves with circle symbols in c (for $S = 0.0$) and d (for $S = 0.02$) present the inviscid results

The present inviscid analysis shows the existence of an unstable mode, with $c_r<1$ at moderate wave numbers for a wide range of parameters (Fig. 3). The growth rate of this mode decreases with an increase in the distance between the liquid–liquid interface and the free surface (Fig. 4). These results are observed for the configuration with $K_2>1$ which corresponds to $m<1$ in the viscous case (see Fig. 8 for comparison). As the slope ($K_2$) of the upper layer increases from one, maximum growth rate ($\omega _{i,max}$) increases (Fig. 8). Moreover, the stabilizing effect of $\theta$ and S observed in the inviscid model are also seen in the viscous case (Fig. 12 in Usha et al. [13]). Another inviscid mode, with phase speed $c_r>1$, that is shown to exist in this study, may be associated with the inviscidly stable free surface mode of the viscous case [13], since the phase speed $c_r$ for both the modes is greater than one. However, the viscous forces destabilized this mode as shown by Usha et al. [13].

Figure 9 presents comparison of eigenmodes for $\theta =90^{\circ }$ (Fig. 9a) and $\theta =45^{\circ }$ (Fig. 9b) between the viscous case (filled circles) and the inviscid case (square symbols). We observe from Fig. 9a that the overlap modes ($O_1$ and $O_2$ modes) in viscous case and the Modes-1, 2 of the inviscid case have phase speed $c_r<1$. The surface mode (S-mode) in the viscous case and the Mode-3 in the inviscid case have $c_r>1$. A similar scenario is observed in Fig. 9b for $\theta =45^{\circ }$. While both the inviscid (Mode-2) and viscous modes (overlap modes) are unstable for $\theta =90^{\circ }$; we see that when $\theta =45^{\circ }$, only viscous overlap modes are unstable. Figure 9c and d present growth rate curves for different angle of inclinations when $S = 0$ and $S = 0.02$ respectively. The other parameters are $K_1 = 1.0, K_2 = 1.5, G = 5/6$ and $d = 0.4$. Curves with symbols are for inviscid case and other curves are for viscous case. Without surface tension (Fig. 9c), in the viscous case, the $O_2$ overlap mode is the most unstable mode, and this mode is relatively unaffected by inclination angle. In the inviscid case, the most unstable mode (Mode-2) is heavily affected by inclination angle both in terms of growth rate and wavelength. In the presence of surface tension (Fig. 9d), the inviscid modes are heavily stabilized for most inclinations lower than 90 degrees, while viscous modes remain unstable for all inclinations shown. Hence, while the inviscid Mode-2 shows qualitative similarity with viscous $O_2$ for $\theta =90^{\circ }$ inclination (Fig. 8), we conclude that viscosity modifies the stability properties of the flow quantitatively and qualitatively for most other inclinations.

3.4 Kinetic energy of disturbances

The disturbance kinetic energy is examined through an energy budget analysis. The analysis explains how the unstable disturbances extract their energy growth from the base flow or the opposite for the stable disturbances. The energy budget equation is derived using a standard procedure [2].

Fig. 10

Energy terms for different S when $\theta = 30^{\circ }$. The other parameters are taken as $K_1 = 1, K_2 = 1.5, d = 0.4$ and $G = 0.02$

The x and the y momentum equations for the perturbed quantities are multiplied by the respective components of velocity perturbations; the resulting equations are added and integrated over one wavelength $\lambda = \frac{2\pi }{\alpha }$ of the disturbance in a domain bounded by the free surface at $y = 0$ and the wall at $y = 1$. Using all the boundary conditions, the following energy disturbance equation for the two-fluid inviscid free surface flow down an incline is obtained [after substituting the normal modes for the perturbations and suppressing hat $(\hat{}\,)$ symbols]:

$$KEN = RES + STE + HYD,$$

(24)

where,

$$\begin{aligned} KEN &= \frac{\omega _i}{2}{\int _0}^d (|u_2|^2 + |v_2|^2)dy + \frac{\omega _i}{2}{\int _d}^1 (|u_1|^2 + |v_1|^2)dy,\\ RES &= -\frac{1}{4}{\int _0}^d U_{2B}^{'}(\bar{u}_2 v_2 - u_2 \bar{v}_2)dy\\&\quad-\frac{1}{4}{\int _d}^1 U_{1B}^{'}(\bar{u}_1 v_1 - u_1 \bar{v}_1)dy,\\ STE &= -\frac{\alpha ^2S}{4}\left[ \left( v_2 \bar{h}_2 + \bar{v}_2 h_2\right) {\Big |}_{\text {at}\,\, y=0}\right] ,\\ HYD &= -\frac{G\cot (\theta )}{4} \left[ \left( v_2 \bar{h}_2 + \bar{v}_2 h_2\right) {\Big |}_{\text {at}\,\, y=0}\right] . \end{aligned}$$

In the above, an over-bar $(\bar{}\,)$ represents the complex conjugate; KEN is the time rate of change of the total disturbance energy and RES is the rate of energy transfer between the base flow and the disturbance (commonly known as “Reynolds stress” term); STE and HYD respectively correspond to the surface energy due to surface tension at the free surface and the gravity potential energy. The terms in Eq. (24) are plotted as a function of wave number $\alpha$ for different surface tension parameter (S) values, after scaling by the factor ‘SKL’ given by

$$SKL = {\int _0}^d (|u_2|^2 + |v_2|^2)dy + {\int _d}^1 (|u_1|^2 + |v_1|^2)dy,$$

for $\theta = 30^{\circ }$ (Fig. 10). The other parameters are taken as $K_1 = 1,\, K_2 = 1.5, \, d = 0.4$ and $G = 0.02$ (Fig. 10). When $\theta = 90^{\circ }$ the term HYD has no contribution to the energy budget for any value of G (since $\cot {\theta } = 0$). Also, the term STE has no contribution to the energy budget if surface tension parameter $S = 0$.

Figure 10a shows the KEN term which corresponds to the scaled growth rate ($\omega _i/2$) for the indicated parameters. So, the flow system is stable or unstable if $KEN<0$ or $KEN>0$. Figure 10a reveals that, the long-waves are stabilized by the presence of surface tension and the maximum growth rate decreases with an increase in surface tension parameter (S) value. However, the presence of surface tension ($0 < S \le 0.025$) at the free surface ($y=0$) creates a disturbance and new set of damped and unstable short wave modes exist at large wave numbers (for $\alpha > 4$ when $S = 0.02$; Fig. 10a). Beyond this S value, the short waves are also stabilized.

The contribution to the energy transfer from the Reynolds stress (RES) is presented in Fig. 10b. When $S = 0$, Eq. (24) has KEN, RES and HYD terms, and so $KEN = RES+HYD$. In this case, the instability arises due to the production of energy by Reynolds stress (RES) and there is contribution to the energy transfer from HYD term in Eq. (24), but it is small as compared to other energy terms. It produces negative energy for all S values considered indicating its stabilizing role (Fig. 10d). When S is increased, contribution to the energy transfer comes also from the STE term and it is negative for all unstable wave numbers (Fig. 10c).

For moderate wave numbers, the surface tension displays a stabilizing effect by overcoming the destabilizing effect of Reynolds stress. The rate of kinetic energy disturbance decreases due to the contribution of negative energy from surface tension at the free surface. As S increases, this stabilizing effect is enhanced for this range of moderate wave numbers. Short waves are destabilized for small surface tension value ($S = 0.02$) as the destabilizing effect of Reynolds stress overcomes the stabilizing effect of surface tension (for $\alpha \ge 4$). However, as S increases in addition, the destabilizing effect of RES is suppressed by the damping effect of surface tension and the flow becomes neutrally stable beyond $S \ge 0.03$.

4 Conclusions

The inviscid temporal stability of two-fluid parallel shear flow in the presence of a free surface down an inclined substrate is analyzed. The base velocity profiles in the two layers are approximated by piecewise linear profiles. The choice of base velocity profile for the inviscid case ensures that its characteristic features such as asymptotic velocity values in each layer match with that of the viscous case. The viscosity stratification of the background flow is thus incorporated through a slope change in the base profiles, at the interface between the two fluids. The analytical results of the limiting cases of the dispersion relation reveal that:

• In the absence of surface tension, for any inclination of the wall, the short waves are stabilized as $K_2 \rightarrow \infty$. But, surface tension destabilizes short waves.

• For a vertical wall, in the presence or absence of surface tension, there is no long-wave instability as $K_2 \rightarrow \infty$. In fact, long-wave instability is independent of surface tension effects, when $K_2 \rightarrow \infty$.

• In the absence of surface tension and for a vertical wall, $K_2 \rightarrow 0$ limiting case is inviscidly stable for any position of the interface.

• Also, when $K_2 \rightarrow 0$ there is no long-wave (short-wave) instability for a vertical wall in the presence (absence) of surface tension. But, the presence of small surface tension (with $S\alpha<< 1$) destabilizes the short waves as $K_2 \rightarrow 0$. However, the inclination of the wall has no influence, in this case.

• In the absence of surface tension ($S = 0$), for a vertical wall ($\theta = 90^{\circ }$), there is no long or short-wave instabilities for any value of upper layer slope ($K_2$).

In the above $K_2 \rightarrow 0$ corresponds to the case where the velocity of the upper layer is very high as compared to the lower layer. On the other hand $K_2 \rightarrow \infty$ implies that the upper layer has a uniform constant velocity.

The numerical solution of the dispersion relation produces results consistent with the limiting cases above. In addition, it shows that in the absence of surface tension ($S = 0$), for a vertically falling film ($\theta = 90^{\circ }$), two inviscid modes occur with phase speed less than the free surface velocity ($c_r<1$), when the upper layer slope is greater than one ($K_2>1$) and one of the modes is unstable for moderate wave numbers. In this case, the long and short waves are inviscidly stable. As the inclination of the substrate is decreased, a new neutrally stable mode is found with phase speed $c_r>1$. This scenario is also observed when $S \ne 0$. The unstable mode is destabilized by increasing the upper layer slope and stabilized by placing the liquid–liquid interface closer to the wall (Fig. 4). Although surface tension (S) dampens the maximum growth rate of the dominant disturbance, the system is unstable for short waves when S is small (Fig. 3; $S = 0.02$). This may be due to the interaction of the inviscid waves at the free surface and the liquid–liquid interface. A detailed wave interaction approach [49, 50] is required for a complete and thorough understanding and will be pursued in future. In order to understand the disturbance evolution and the role of surface tension, we have performed an energy budget analysis. The energy transfer from the base flow to the disturbances (through the Reynolds stress term) is responsible for the inviscid instability and surface tension has a non-monotonic effect on the energy transfer depending on the wave number.

When $m>1$ ($K_2<1$), we observe the existence of unstable modes due to viscosity stratification in viscous flow [13]. The inviscid analysis shows that for $K_2 < 1$, the flow system is inviscidly stable. This suggests that the unstable modes that occur for $m>1$ in the viscous case arise due to viscosity stratification and diffusivity mechanism. On the other hand, for $K_2 > 1$, the inviscid analysis has identified two modes: one unstable mode with phase speed $c_r < 1$ and another neutrally stable mode with $c_r > 1$. In the viscous flow system, for $m<1$, Usha et. al. [13] have shown the existence of two types of unstable modes namely, the overlap modes with $c_r<1$ and a surface mode with $c_r > 1$. This indicates that, for a flow configuration with the less viscous fluid adjacent to the free surface ($m < 1$; $K_2 > 1$), the inviscid mechanism is also responsible for the occurrence of unstable modes. This is evident from the qualitative agreement between the inviscid model results and the viscous case ($m < 1$; $K_2 > 1$ as shown in Fig. 8). Viscous effects modify the stability properties of the flow system quantitatively.