1 Introduction

Two-fluid problems, in which the motion of two different fluids interacts through an interface, have been extensively studied in the past. In many practical situations, both in nature and engineering, two different immiscible fluids are moving almost parallel to each other at different speeds. Lock [1], for instance, obtained similarity solutions in terms of a fluid property parameter and the ratio between the velocity of the lower and upper fluid. That situation was also examined by Wang [2], but in his case the upper fluid exhibited a uniform shear rate rather than a uniform velocity as in [1]. Herczynski et al. [3] found similarity solutions for two-fluid jets and wakes by matching the fluid velocity and shear stresses at the two-fluid interface. In these and other two-fluid problems, the two fluids have different densities and viscosities, but both fluids exhibit Newtonian, i.e. linear, rheology.

Non-Newtonian fluids are, however, frequently studied in one-fluid problems. Of particular relevance here is the sheet-driven boundary layer problem which originates from the works of Sakiadis [4] and Crane [5] and recently was revisited by Al-Housseiny and Stone [6] to include the sheet mechanics via the stress balance in the sheet. The Crane-problem was generalized to non-Newtonian power-law fluids by Andersson et al. [7] and further analysed by Andersson and Kumaran [8]. The velocity profiles turned out to vary with the fluid properties, i.e. the so-called power-law index n. The shearing stress at the moving sheet as well as the thickness of the momentum boundary layer exhibited significant n-dependence. More recently Guedda [9] considered the shear-driven flow of a power-law fluid along a plane solid surface. Power-law fluids are also encountered in many industrial processes [10] as well as in nature [11], but such other applications are outside the scope of the present study.

The popular power-law model is known to be unrealistic at high and low shear rates. These shortcomings can be remedied by more elaborate, but yet purely viscous, non-Newtonian fluid models; see e.g. Chapter 6 in Irgens [12]. Unsteady boundary layer flows over moving walls, i.e. the classical Stokes’ first and second problems, were analysed for power-law fluids by Pascal [13] and Pritchard et al. [14], respectively, and subsequently extended to generalized Newtonian fluids by Duffy et al. [15].

The purpose of this paper is to show that similarity solutions exist also for two-fluid problems in which one of the fluids exhibits non-Newtonian rheology. More specifially, we consider the shear-driven motion of a Newtonian fluid above an otherwise still non-Newtonian fluid. The motion of the lower fluid is induced solely by the interfacial shear stress exerted by the upper fluid. One may therefore conjecture that the resulting flow resembles that of the sheet-driven boundary layers by Sakiadis [4] and Crane [5] and the more recent extension to power-law fluids by Andersson and Kumaran [8]. However, the generalized Newtonian fluid model is adopted herein to represent the non-Newtonian rheology. The investigation will therefore apply for any purely viscous fluid, similarly as the recent analysis of Stokes’ first problem by Duffy et al. [15]. A power-law fluid is thereafter chosen to illustrate both shear-thinning and shear-thickening effects.

To this end we consider an incompressible purely viscous and potentially non-Newtonian fluid. The rheological equation of state for a generalized Newtonian fluid reads:

$$\tau_{ij} = + 2\mu \left\{ {\dot{\gamma }} \right\}D_{ij} \quad {\text{where}}\quad \dot{\gamma } = (2D_{ij} D_{ij} )^{1/2}$$
(1)

in Cartesian tensor notation; see e.g. Irgens [12]. The extra stress tensor τ ij depends non-linearly on the deformation rate tensor \(D_{ij} = (\partial u_{i} /\partial x_{j} + \partial u_{j} /\partial x_{i} )/2\) whenever the viscosity function \(\mu \left\{ {\dot{\gamma }} \right\}\) varies with the magnitude of the shear rate \(\dot{\gamma }\). The constitutive Eq. (1) simplifies to that of a Newtonian fluid when the viscosity function is independent of the shear rate and the constant μ is then referred to as the dynamic viscosity of the fluid.

While the boundary-layer flow of a power-law fluid along a solid surface studied by Guedda [9] was driven by an external free-stream exhibiting a prescribed power-law shear, the present boundary-layer flow of an underlying non-Newtonian fluid is driven by the a priori unknown shear imposed by the overlying Newtonian boundary-layer flow. The coupling between the upper Newtonian fluid and the lower non-Newtonian fluid is at the interface, i.e. through the interfacial boundary conditions. This coupling is linear in the case of two different Newtonian fluids, but becomes non-linear when the lower fluid is non-Newtonian. In spite of this non-linear boundary condition, along with the non-linearity introduced in the momentum boundary layer equation, similarity solutions can be found, as we will show in Sect. 3. Although the self-similar solutions can be obtained for any generalized Newtonian rheology, we adopt the power-law fluid in Sect. 4 with the view to illustrate such solutions. A direct numerical integration approach based on a double shooting technique is described in Sect. 5. Numerical solutions of the two-fluid problem are presented in Sect. 6 and further discussed in Sect. 7 in order to elucidate the influence of the non-Newtonian rheology on the shear-driven fluid motion.

2 Formulation of the two-fluid problem

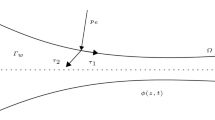
We consider the boundary layer flow of a non-Newtonian fluid driven solely by the shearing motion of a Newtonian fluid as depicted in Fig. 1. Let u′ and v′ be the velocity components of the upper fluid in the x′ and y′ directions, respectively. The Newtonian fluid has density ρ u and kinematic viscosity ν u  = μ/ρ u . The upper fluid has a linear shearing velocity u′ = by′ for x′ < 0 and for large y′; see Fig. 1. The lower non-Newtonian fluid is quiescent at large distances away from the two-fluid interface at x′ = X′ > 0; y′ = Y′ = 0. It should be noted that the vertical coordinate axes y′ and Y′ are in opposite directions. We assume that the Froude number is sufficiently large so that the interface remains horizontal.

Fig. 1
figure 1

Sketch of the flow problem. The origins of the coordinate system (x′, y′) for the Newtonian upper fluid and (X′, Y′) for the non-Newtonian lower fluid are co-located. The x′- and X′-axes are aligned whereas the Y′-axis points in the opposite direction of the y′-axis

Full size image

After normalization with the length scale \(\left( {\nu_{u} /b} \right)^{1/2}\) and the velocity scale \(\left( {\nu_{u} b} \right)^{1/2}\) the momentum boundary layer equation for the upper fluid becomes:

$$\frac{{\partial \psi_{u} }}{\partial y}\,\frac{{\partial^{2} \psi_{u} }}{\partial x\partial y} - \frac{{\partial \psi_{u} }}{\partial x}\,\frac{{\partial^{2} \psi_{u} }}{{\partial y^{2} }} = \,\frac{{\partial^{3} \psi_{u} }}{{\partial y^{3} }}.$$
(2)

Here ψ u is the stream function defined in terms of the velocity components as \(u = \partial \psi_{u} /\partial y\) and \(v = - {\kern 1pt} \partial \psi_{u} /\partial x\).

The lower non-Newtonian fluid is modelled as a generalized Newtonian fluid (1) for which the extra stress tensor \(\tau_{ij}\) depends non-linearly on the shear rate \(\dot{\gamma }\). In two-dimensional boundary layers, \({\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}\partial U^{\prime} /\partial Y^{\prime}\) is by far the largest component of the deformation rate tensor D ij and the magnitude of the shear rate simplifies to:

$$\dot{\gamma } = \left( {\left[ {\frac{{\partial U^{\prime} }}{{\partial Y^{\prime} }}} \right]^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} = \left| { - \frac{{\partial U^{\prime} }}{{\partial Y^{\prime} }}} \right|.$$
(3)

The motion of the lower non-Newtonian fluid is driven by the interfacial shear caused by the upper Newtonian fluid. The second part of Eq. (3) is therefore based on the assumption that \(\partial U^{\prime} /\partial Y^{\prime} \le 0\). The only stress component of dynamic significance becomes

$$\tau_{xy} = \tau_{yx} = 2\mu \left\{ {\dot{\gamma }} \right\}D_{xy} = \mu \left\{ {\dot{\gamma }} \right\}\frac{{\partial U^{\prime} }}{{\partial Y^{\prime} }}$$
(4)

where the shear rate \(\dot{\gamma }\) is given in Eq. (3).

Similarly as for the upper fluid, a dimensionless stream function \(\psi_{\ell }\) is defined in terms of the normalized velocity components U and V of the lower fluid as \(U = \partial \psi_{\ell } /\partial Y\) and \(V = - {\kern 1pt} \partial \psi_{\ell } /\partial X\). Note that the same length and velocity scales defined for the upper Newtonian fluid are used also for the lower non-Newtonian fluid. The normalized momentum boundary layer equation for the lower generalized Newtonian fluid becomes:

$$\frac{{\partial \psi_{\ell } }}{\partial Y}\,\frac{{\partial^{2} \psi_{\ell } }}{\partial X\partial Y} - \frac{{\partial \psi_{\ell } }}{\partial X}\,\frac{{\partial^{2} \psi_{\ell } }}{{\partial Y^{2} }} = \,\frac{\partial }{\partial Y}\left[ {\tilde{\mu }\left\{ {\frac{{\partial^{2} \psi_{\ell } }}{{\partial Y^{2} }}} \right\}\frac{{\partial \psi_{\ell } }}{\partial Y}} \right].$$
(5)

Here, \(\tilde{\mu } = \mu \left\{ {\dot{\gamma }} \right\}/\rho_{u} \nu_{u}\) is the normalized viscosity function and the fluid pressure has been assumed to be constant, just as in the upper fluid.

The upper and lower flow problems governed by Eqs. (2) and (5), respectively, are subjected to the six boundary conditions:

$$y \to \infty ,\quad \partial \psi_{u} /\partial y \to y;$$
(6a)
$$Y \to \infty ,\quad \partial \psi_{\ell } /\partial Y \to 0;$$
(6b)
$$y = Y = 0,\quad \psi_{u} = \psi_{\ell } = 0;$$
(6c)
$$y = Y = 0,\;\;\partial \psi_{u} /\partial y = \partial \psi_{\ell } /\partial Y;$$
(6d)
$$y = Y = 0,\;\;\partial^{2} \psi_{u} /\partial y^{2} = \tilde{\mu }\,\partial^{2} \psi_{\ell } /\partial Y^{2} .$$
(6e)

Here, the boundary condition (6a) states that the horizontal velocity component u varies linearly high above the interface at y = Y = 0, whereas U should decay to zero (6b) deep below the interface. The conditions (6c) primarily serve to set the level of the two stream functions ψ u and ψ ℓ , but as a consequence also assure that the vertical velocity components v and V in each of the two fluids vanish at the interface. The velocities and the shear stresses match at the interface y = Y = 0 according to (6d) and (6e), respectively.

3 Similarity transformations

We now introduce the similarity variable η u and the dimensionless stream function f for the upper fluid as follows:

$$\eta_{u} = \frac{y}{{x^{1/3} }}\;;\;\psi_{u} = x^{2/3} f(\eta_{u} ).$$
(7)

The momentum boundary layer Eq. (2) and the boundary condtions (6a, 6c) for the upper Newtonian fluid then become:

$$(f^{\prime} )^{2} - 2ff^{\prime\prime} = 3f^{\prime\prime\prime}$$
(8)
$$f^{\prime\prime} (\eta_{u} ) \to 1\quad as\quad \eta_{u} \to \infty ;\;\quad f(0) = 0.$$
(9)

The prime signifies differentiation with respect to the similarity variable \(\eta_{u}\).

Similarly for lower non-Newtonian fluid, the similarity transformation

$$\eta_{\ell } = \frac{Y}{{X^{1/3} }}\;;\;\psi_{\ell } = X^{2/3} g(\eta_{\ell } )$$
(10)

transforms the partial differential Eq. (5) and the accompanying boundary conditions (6b, 6c) into

$$(g^{\prime} )^{2} - 2gg^{\prime\prime} = 3\left( {\tilde{\mu }g^{\prime\prime} } \right)^{\prime}$$
(11)
$$g^{\prime\prime} (\eta_{\ell } ) \to 0\;\;as\quad \eta_{\ell } \; \to \infty ;\quad g(0) = 0.$$
(12)

It is essential to remember that the normalized viscosity function \(\tilde{\mu }\) depends on the normalized shear rate, i.e. \(\tilde{\mu } = \tilde{\mu }\left\{ {g^{\prime\prime} } \right\}\). At the interface, i.e. η u  = η ℓ  = 0, the boundary conditions (6d, e) become:

$$f^{\prime} (0) = g^{\prime} (0)$$
(13a)
$$f^{\prime\prime} (0) = \tilde{\mu }\left\{ {g^{\prime\prime} (0)} \right\}g^{\prime\prime} (0).$$
(13b)

The governing momentum boundary layer equations and the accompanying boundary conditions defined in Eqs. (2), (5), and (6) have thus been recast into a set of two non-linear ordinary differential Eqs. (8) and (11) for f and g subjected to the boundary conditions (9), (12), and (13). The upper Newtonian boundary layer problem and the lower non-Newtonian bounder layer problem are only coupled through the two interface conditions (13).

In Newtonian fluid mechanics, transformations which exactly transform the governing partial differential equations into ordinary differential equations are relatively rare, mainly due to the non-linear convection terms. The additional non-linearity introduced by the constitutive equation for generalized Newtonian fluids generally prohibits self-similarity. The present flow problem is therefore one of the exceptions.

4 Example: power-law fluids

The mathematical formulation of the two-fluid problem in Sect. 2 and the coupled self-similar problem in Sect. 3 are valid for any generalized Newtonian lower fluid. The shear flow over a still Newtonian fluid was recently explored by Andersson and Mukhopadhyah [16] who demonstrated that that problem could be expressed in terms of two independent parameters. Rheological models for generalized Newtonian fluids inevitably involve more than one fluid property. In order to avoid a multi-dimensional parameter space, the remaining parts of this paper is confined to power-law fluids.

The lower non-Newtonian fluid is modelled as a power-law (Ostwald-de-Waele), fluid which is a special case of generalized Newtonian fluids defined by the rheological equation of state (1) with viscosity function:

$$\mu = K\dot{\gamma }^{n - 1} = K(2D_{ij} D_{ij} )^{(n - 1)/2}$$
(14)

where \(K\) and \(n\), i.e. the consistency coefficient and the power-law index, are fluid properties; see e.g. Irgens [12]. Equation (14) represents shear-thinning (pseudo-plastic) fluids for n < 1, shear-thickening (dilatant) fluids for n > 1, and the special case of a Newtonian fluid is obtained for n = 1. In two-dimensional boundary layers where \({\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}\partial U/\partial Y\) is the dominant element of the strain rate tensor D ij , the viscosity function (14) simplifies to:

$$\mu = K\left( {\left[ {\frac{\partial U}{\partial Y}} \right]^{2} } \right)^{{{{(n - 1)} \mathord{\left/ {\vphantom {{(n - 1)} 2}} \right. \kern-0pt} 2}}} = K\left( { - \frac{\partial U}{\partial Y}} \right)^{n - 1} .$$
(15)

The only stress component of dynamic significance (4) is therefore

$$\tau_{xy} = \tau_{yx} = 2\mu D_{xy} = - K\left( { - \frac{\partial U}{\partial Y}} \right)^{n} ;$$
(16)

see e.g. Andersson and Kumaran [8].

For the power-law fluid, the normalized momentum boundary layer Eq. (5) reads:

$$\frac{{\partial \psi_{\ell } }}{\partial Y}\,\frac{{\partial^{2} \psi_{\ell } }}{\partial X\partial Y} - \frac{{\partial \psi_{\ell } }}{\partial X}\,\frac{{\partial^{2} \psi_{\ell } }}{{\partial Y^{2} }} = \,n\widehat{\lambda }\left( { - \frac{{\partial^{2} \psi_{\ell } }}{{\partial Y^{2} }}} \right)^{n - 1} \frac{{\partial^{3} \psi_{\ell } }}{{\partial Y^{3} }}$$
(17)

and the continuity of the shear stress at the interface (6e) becomes

$$y = Y = 0,\;\;\partial^{2} \psi_{u} /\partial y^{2} = - \sigma \widehat{\lambda }\,{\kern 1pt} \left( { - \,\partial^{2} \psi_{\ell } /\partial Y^{2} } \right)^{n} .$$
(18)

The ratio between the density of the lower and upper fluids is denoted \(\sigma \equiv \rho_{\ell } /\rho_{u} \ge 1\) and the non-dimensional parameter

$$\hat{\lambda } \equiv \frac{{{K \mathord{\left/ {\vphantom {K {\rho_{\ell } }}} \right. \kern-0pt} {\rho_{\ell } }}}}{{\nu_{u} }}b^{n - 1}$$
(19)

simplifies to the ratio between the kinematic viscosities of the two different fluids for n = 1. For \(n \ne 1\), however, \(\hat{\lambda }\) depends not only on the properties of the two fluids but also on the shear rate b driving the upper fluid.

By means of the similarity transformations in the previous section, the resulting ordinary differential Eq. (11) governing the momentum transport in the lower fluid becomes

$$(g^{\prime} )^{2} - 2gg^{\prime\prime} = 3n\hat{\lambda }\left( { - g^{\prime\prime} } \right)^{n - 1} g^{\prime\prime\prime}$$
(20)

and the interfacial stress condition (13b) is:

$$f^{\prime\prime} (0) = \sigma \hat{\lambda }\left[ { - g^{\prime\prime} (0)} \right]^{n} .$$
(21)

The two-fluid problem consisting of an upper shear-driven Newtonian fluid above an otherwise quiescent power-law fluid accordingly constitutes a three-parameter problem in σ, \(\hat{\lambda }\), and n. If the lower fluid happens to be Newtonian, i.e. n = 1, the two-parameter problem studied by Andersson and Mukhopadhyay [16] is recovered.

5 A direct integration approach

We proceed to solve the coupled similarity problems in a direct manner as described by Andersson and Mukhopadhyay [16], i.e. for given parameter values σ, \(\hat{\lambda }\), and n. The two third-order ordinary differential Eqs. (8) and (20) are written as a set of six first-order equations:

$$f' = z;\;z' = p;\;p' = (z^{2} - 2fp)/3$$
(22a)
$$g' = w;\;w' = q;\;q' = \left( {w^{2} - 2gq} \right)/\left( {3n\hat{\lambda }\left[ { - q} \right]^{n - 1} } \right).$$
(22b)

The six required initial conditions can be written as:

$$f(0) = g(0) = \,0;\;z(0) = w(0) = \beta ;\quad p(0)\, = \alpha ;\,\;q(0) = - \left( {\alpha /\sigma \hat{\lambda }} \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} .$$
(23)

However, the interfacial values α and β are a priori unknown and will be determined as a part of the numerical solution for given combinations of the parameters σ, \(\hat{\lambda }\), and n.

In order to integrate Eqs. (22) as an initial value problem, initial values for z and p, i.e. \(f'(0) = \beta\) and \(f''(0) = \alpha\), are required. These initial values are first guessed and then serve also as initial values for w and q in accordance with Eq. (23). In this double-shooting approach, it is essential to determine appropriate finite values of \(\eta_{u}\) and \(\,\,\eta_{\ell }\) where the far-field boundary conditions (9) and (12) as \(\eta_{u} \to \infty ,\,\,\eta_{\ell } \to \infty\) can be enforced. Proper finite values of the extent of the integration domain depend on the actual flow problem and also on the rheological properities of the fluids. For the boundary layer flow of a power-law fluid along a linearly stretching sheet Andersson and Kumaran [8] reported an extreme thickening of the boundary layer for highly shear-thinning fluids, i.e. n < 0.5. Here, however, the power-law index is within the range \(0.6 \le n \le 1.4\) and η u  = 14 and η ℓ  = 14 appeared to be adquate choices for the domain sizes in the upper and lower fluid, respectively. These values were based on earlier experiences [7, 8] and sensitivity tests using some different domain sizes. The six differential Eqs. (22) are therefore integrated by means of a classical fourth-order Runge–Kutta method with step size 0.01 up to η u  = η ℓ  = 14. The unknown interface values α and β are successively adjusted by means of Newton’s method until the outer boundary conditions \(f^{\prime\prime} (\eta_{u} = 14) = 1\) and \(g^{\prime} (\eta_{\ell } = 14) = 0\) are satisfied to within the desired accuracy of 1·10−5.

6 Results

The present two-fluid problem involves three different dimensionless parameters σ, \(\widehat{\lambda }\), and n. Here, σ and n are fluid properties, whereas \(\widehat{\lambda }\) combines both fluid properties and the shear rate b into one single parameter. The three-parameter problem simplifies to a two-parameter problem in the particular case of a Newtonian fluid (n = 1.0) and \(\widehat{\lambda }\) becomes equal to the ratio between the viscosities of the lower and upper fluids. If so, the dimensionless flow problem in Sect. 4 becomes independent of the imposed shear rate b. For the sake of simplification, the density ratio σ is taken as 1.0 in this paper, whereas \(\widehat{\lambda } = 0.5, \, 1.0,\) and 2.0 and n is varied in the range from 0.6 to 1.4, i.e. from a shear-thinning to a shear-thickening power-law fluid.

The resulting flows of the upper and lower fluids for \(\widehat{\lambda } = 0.5\) are shown in Figs. 2 and 3, respectively. The velocity \(f^{\prime} (\eta_{u} )\) increases monotonically upwards from the interface and gradually approaches the imposed linear shear rate, i.e. \(f^{\prime\prime} (\eta_{u} ) = 1\). Although the upper fluid is Newtonian, the boundary layer adjacent to the interface is affected by the non-Newtonian rheology of the lower fluid such that the interface velocity \(f^{\prime} (\eta_{u} = 0)\) decreases with increasing power-law index and the interface shear \(f^{\prime\prime} (\eta_{u} = 0)\) increases with n. The dependence of the motion of the upper fluid on the power-law index n of the lower fluid is brought about only by the interfacial boundary conditions (13a) and (21).

Fig. 2
figure 2

Profiles of the streamwise velocity and shear rate in the upper fluid for σ = 1.0 and \(\widehat{\lambda } = 0.5\) and five different values of the power-law index n. a Streamwise velocity \(f^{\prime} (\eta_{u} )\). b Shear rate \(f^{\prime\prime} (\eta_{u} )\). The solid lines correspond to a Newtonian lower fluid (n = 1)

Full size image
Fig. 3
figure 3

Profiles of the streamwise velocity and shear rate in the lower fluid for σ = 1.0 and \(\widehat{\lambda } = 0.5\) and five different values of the power-law index n. a Streamwise velocity \(g^{\prime} (\eta_{\ell } )\). b Shear rate \(g^{\prime\prime} (\eta_{\ell } )\). The solid lines correspond to a Newtonian lower fluid (n = 1)

Full size image

In the following we will focus on the flow of the underlying power-law fluid and the interface velocity and shear stress. The motion of the lower fluid is driven solely by the interfacial shear. The velocity profiles in Fig. 3b show that the velocity \(g^{{\prime }} (\eta_{\ell } )\) decays asymptotically to zero below the interface. At a given depth, however, \(g^{{\prime }} (\eta_{\ell } )\) increases with decreasing values of n and the higher velocity is accompanied by an increasing boundary layer thickness. The shear-induced motion seems to penetrate about twice as deep into the shear-thinning fluid with n = 0.7 as in the shear-thickening fluid (n = 1.3). This is consistent with the trend observed by Andersson et al. [7] for boundary layer flow over a linearly stretching sheet.

The magnitude of the shear rate \(- g^{{\prime \prime }} (\eta_{\ell } )\) is highest at the interface between the Newtonian and the non-Newtonian fluids and decays downwards and eventually approaces zero. It is noteworthy that the most shear-thinning fluid (n = 0.7) gives rise to the highest shear rate not only in the immediate vicinity of the interface but also at large depths, but surprisingly not at intermediate depths \(0.7 \le \eta_{\ell } \le 2\). The inset in Fig. 3b shows that the shear-rate profiles intersect such that the monotonically decreasing trend of the shear rate with increasing n next to the interface reverses beyond \(\eta_{\ell } \approx 0.8\).

To illustrate the effect of the non-dimensional parameter \(\widehat{\lambda }\) defined in Eq. (19), computed profiles of the fluid velocities and shear rates for \(\widehat{\lambda } = 2.0\) are presented in Figs. 4 and 5. The results for the upper fluid in Fig. 4 show the same qualitative behaviour as the profiles in Fig. 2 for \(\widehat{\lambda } = 0.5\), but the influence of the power-law index of the underlying non-Newtonian fluid is now more accentuated. The significant effect of n is even more pronounced in the profiles for the lower fluid in Fig. 5. In particular, the shear rate distributions for different n-values do no longer intersect as they did for \(\widehat{\lambda } = 0.5\) in Fig. 3b. The highest shear rate \(- g^{{\prime \prime }} (\eta_{\ell } )\) is obtained for the most shear-thinning fluid all through the boundary layer. It is furthermore noteworthy that the thickness of the power-law fluid boundary layer is significantly larger for \(\widehat{\lambda } = 2.0\) in Fig. 5 than for \(\widehat{\lambda } = 0.5\) in Fig. 3.

Fig. 4
figure 4

Profiles of the streamwise velocity and shear rate in the upper fluid for σ = 1.0 and \(\widehat{\lambda }\) = 2.0 and five different values of the power-law index n. a Streamwise velocity \(f^{\prime} (\eta_{u} )\). b Shear rate \(f^{\prime\prime} (\eta_{u} )\). The solid lines correspond to a Newtonian lower fluid (n = 1)

Full size image
Fig. 5
figure 5

Profiles of the streamwise velocity and shear rate in the lower fluid for σ = 1.0 and \(\widehat{\lambda } = 2.0\) and five different values of the power-law index n. a Streamwise velocity \(g^{\prime} (\eta_{\ell } )\). b Shear rate \(g^{\prime\prime} (\eta_{\ell } )\). The solid lines correspond to a Newtonian lower fluid (n = 1)

Full size image

7 Discussion

The trends observed from Figs. 2, 3, 4 and 5 were based on five different values of the power-law index. However, the two-fluid problem was solved for altogether 9 different values of n in the range from 0.6 to 1.4. The most essential parts of the results are presented graphically in Fig. 6, from which the following trends can be seen: The interface velocities \(f^{{\prime }} (0) = g^{{\prime }} (0)\) decrease with \(\widehat{\lambda }\) in the range from 0.5 to 2.0. The interfacial shear rate \(f^{{\prime \prime }} (0)\) increases with \(\widehat{\lambda }\) whereas the strain rate \(- g^{{\prime \prime }} (0)\) in the lower fluid decreases. The displacement thickness \(\delta_{\ell }\) of the power-law fluid boundary layer increases with \(\widehat{\lambda }\) from 0.5 to 2.0. It is noteworthy that these trends are the same for all values of the power-law index n considered, i.e. for shear-thinning as well as for shear-thickening fluids.

Fig. 6
figure 6

Interfacial velocities, shear rates, and displacement thickness for σ = 1.0 with \(\widehat{\lambda }\) and n as parameters. Dotted lines \(\widehat{\lambda } = 0.5\). Solid lines \(\widehat{\lambda } = 1.0\). Dashed lines \(\widehat{\lambda } = 2.0\). a Interfacial velocity \(f^{\prime} (\eta_{u} = 0)\) and shear rate \(f^{\prime\prime} (\eta_{u} = 0)\) in the upper fluid. The upper circle identifies results for \(f^{\prime} (\eta_{u} = 0)\) and the lower circle corresponds to results for \(f^{\prime\prime} (\eta_{u} = 0)\). b Interfacial shear rate \(- g^{\prime\prime} (\eta_{\ell } = 0)\) in the lower fluid. c Displacement thickness \(\delta_{\ell }\) of the power-law fluid boundary layer

Full size image

Of particular relevance in the present study is the effect of the power-law index n which represents the rheology of the lower non-Newtonian fluid. Irrespective of the value of \(\widehat{\lambda }\), the interfacial velocities \(f^{{\prime }} (0) = g^{{\prime }} (0)\) decrease monotonically with n all through the parameter range from 0.6 to 1.4. The interfacial shear rate \(f^{\prime\prime} (0)\) increases with n whereas \(- g^{\prime\prime} (0)\) decreases. A normalized displacement thickness for the lower power-law fluid can be defined in the same way as suggested by Andersson et al. [7]:

$$\delta_{\ell } \equiv \int\limits_{0}^{\infty } {g^{\prime} (\eta_{\ell } )d\eta_{\ell } = \mathop {\lim \,}\limits_{{\eta_{\ell } \to \infty }} } g - \underbrace {g(0)}_{ = 0}.$$
(24)

In the present two-fluid problem this displacement thickness is a measure of the thickness of the viscous boundary layer in the underlying non-Newtonian fluid. Figure 6c exhibits a substantial reduction of \(\delta_{\ell }\) from the most shear-thinning fluid with n = 0.6 to the highly shear-thickening fluid with n = 1.4.

The most striking observation made is probably the gradual thinning of the shear-driven boundary layer in the lower fluid with increasing values of the power-law index n, as seen in Fig. 6c. This may at first sight seem to be in contrast with the monotonically increasing interfacial shear stress which is proportional to f″(0) in Fig. 6a. However, the viscosity function μ in Eq. (15) varies with the local shear rate \({\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}\partial U/\partial Y\) in the power-law fluid. In the present shear-driven boundary layer, the shear rate decays with depth from the interface and downwards, as can be seen in Fig. 3b and Fig. 5b. As long as \(- g^{{\prime \prime }} (\eta_{\ell } )\) is smaller than unity, but yet larger for shear-thinning fluids than for shear-thickening fluids, μ reduces with increasing n-values. Since the viscosity function appears as a variable diffusion coefficient in the momentum boundary layer Eqs. (5) and (11) for the non-Newtonian fluid, the reduction of μ tends to make the boundary layer thinner. This is consistent with our observation from Fig. 6c that the thickness of the shear-driven power-law boundary layer is reduced with increasing values of n. The thinning of the underlying non-Newtonian boundary layer in the present two-fluid problem is in qualitive agreement not only with the behavior of the sheet-driven steady boundary layer in a power-law fluid reported by Andersson et al. [7] and Andersson and Kumaran [8], but also with the unsteady boundary layer flow studied by Duffy et al. [15].

The boundary layer displacement thickness \(\delta_{\ell }\) and the interfacial shear rate \(- g^{{\prime \prime }} (0)\) both increase as the power-law n reduces, i.e. with increasing shear-thinning of the lower fluid. The high shear rate in the vicinity of the two-fluid interface tends to lower the viscosity function μ whereas the lower shear rate at larger depths makes the fluid relatively more viscous. This explains why the shear rate profile for n = 0.7 in Fig. 3b twice intersects the profile for the Newtonian fluid (n = 1).

For the sake of reducing the parameter space from three to two dimensions, the density ratio σ was kept equal to unity in Sect. 6. The parameter \(\widehat{\lambda }\) turned out to have a major effect on the computed results and, indeed, \(\widehat{\lambda }\) controls the ratio between the interfacial shear stresses in the upper Newtonian and the lower power-law fluid in accordance with Eq. (21) and thereby explains why the shear rate \(- g^{\prime\prime} (0)\) decreases with increasing values of \(\widehat{\lambda }\). At first sight this seems to be conflicting with the observation that the displacement thickness \(\delta_{\ell }\) increases as \(\widehat{\lambda }\) increases in Fig. 6c. However, the diffusion term in the momentum boundary layer Eq. (20) is proportional with n \(\widehat{\lambda }\). Therefore the increasing diffusion of streamwise momentum more than outweighs the reduction of the driving interfacial shear.

The effect of the density ratio σ has been explored for the simpler case when also the lower-lying fluid is Newtonian and the non-dimensional parameter \(\widehat{\lambda }\) defined in Eq. (19) becomes independent of the shear rate b which drives the upper fluid. Wang [2] showed that the shear-driven upper boundary layer could be formulated as a one-parameter problem in \(\sigma^{2} \widehat{\lambda }\), whereas Andersson and Mukhopadhyah [16] demonstrated that the underlying boundary layer flow not only depended on the parameter combination \(\sigma^{2} \widehat{\lambda }\) but also on \(\sigma \widehat{\lambda }\). The interfacial velocity \(f^{\prime} (\eta_{u} = 0) = g^{\prime} (\eta_{\ell } = 0)\) was observed to decrease monotonically from ≈0.9343 for \(\sigma^{2} \widehat{\lambda } = 1\) to zero with increasing values of \(\sigma^{2} \widehat{\lambda }\). For values of \(\sigma \gg 1\) also the present two-fluid problem simplifies such that the simple analytical solutions:

$$f = \frac{1}{2}\eta^{2} ;\;f^{{\prime }} = \eta ;\quad f^{{\prime \prime }} = 1$$
(25a)
$$g = 0;\;g^{{\prime }} = 0;\quad g^{{\prime \prime }} = 0$$
(25b)

apply in the limit as σ → ∞. This implies that shearing motion in the upper fluid is unable to set the lower fluid in motion. Such situations arise only when the underlying fluid is much heavier than the upper fluid, for instance a gas above a liquid, and the higher inertia suffices to keep the liquid in rest. Indeed, for airflow above water (\(\sigma = 833\)) the numerical solution by Andersson and Mukhopadhyah [16] was surprisingly close to the analytic solutions (25).

8 Concluding remarks

We have considered the shear flow of a Newtonian fluid over an otherwise quiescent non-Newtonian fluid. The rheology of the lower fluid was modelled as a generalized Newtonian fluid, similarly as in the one-fluid problem studied by Duffy et al. [15].

In spite of the non-linearity which arose from the rheological equation of state, also the coupled two-fluid problem allowed for similarity solutions. The coupled self-similarity formulation of the two-fluid problem in Sect. 3 is therefore applicable for any generalized Newtonian fluid, for instance Casson and Herschel-Bulkley fluids which both are three-parameter models and the Carreau fluid which is a four-parameter model.

The popular power-law fluid model was adopted for illustrative purposes and two coupled two-point boundary value problems were solved numerically by means of a double shooting technique. The interfacial coupling (13b) made the shear-layer of the upper Newtonian fluid dependent on the non-linear dependence of the viscosity function μ on the shear rate \(\dot{\gamma }\) in the underlying non-Newtonian fluid. The interfacial velocities decreased monotonically with increasing values of the power-law index n in the range from 0.6 to 1.4. The shear-induced motion of the lower non-Newtonian fluid penetrated far deeper into a shear-thinning than into a shear-thickening fluid. This phenomenon can be ascribed to the non-linear dependence of the viscosity function μ on the power-law index n.