Dynamic stability in parametric resonance of axially excited Timoshenko microbeams

Abstract

The dynamic stability in parametric resonance of a Timoshenko microbeam subject to a time-dependent axial excitation load (comprised of a mean value along with time-dependent variations) is analysed in the subcritical regime. Based on the modified couple stress theory, continuous expressions for the elastic potential and kinetic energies are developed using kinematic and kinetic relations. The continuous model of the system is obtained via use of Hamilton’s principal. A model reduction procedure is carried out by applying the Galerkin scheme, in conjunction with an assumed-mode technique, yielding a high-dimensional second-order reduced-order model. A liner analysis is carried out upon the linear part of this model in order to obtain the linear natural frequencies and critical buckling loads. For the system in the subcritical regime, the parametric nonlinear responses are analysed by exciting the system at the principal parametric resonance in the first mode of transverse motion; this analysis is performed via use of a continuation technique, the Floquet theory, and a direct time integration method. Results are shown in the form of parametric frequency–responses, parametric force–responses, time traces, phase-plane diagrams, and fast Fourier transforms. The validity of the numerical simulations is tested via comparing our results, for simpler models for buckling response, with those given in the literature.

1 Introduction

1.1 Fundamentals and applications

Microscale elements, such as microbeams and microplates, can be found in various microdevices and micromachine components, for example in biosensors, microswitches, and electrical microactuators [1–3]. The experimental investigations reported that microscale continuous elements display size-dependent deformation behaviour [4, 5]; this is beyond the capability of the classical continuum theory to predict. In order to overcome this drawback of the classical continuum theory, new continuum theories such as the modified couple stress [6, 7] and strain gradient theories have been developed, which are capable of capturing size effects; the modified couple stress theory is employed in this paper.

1.2 Time-dependent axial load

As is well-known, there are many applications where microbeams are subject to axial loads; in real-life microdevices, under dynamic operating conditions, these axial loads are time-dependent. Here, the time-varying axial load is modelled by superimposing time-dependent harmonic variations over a constant (mean) value. This class of systems are classified as parametrically excited. The class features include the occurrence of resonances in the vicinity of twice any linear natural frequency.

1.3 Literature review

The literature concerning the statics and dynamics of microbeams may be classified into two general groups in terms of the model being considered. The first class employed the Euler–Bernoulli beam theory while the second group employed shear deformable, such as Timoshenko and Reddy, beam theories.

Reviewing the studies which fall into the first class, for instance, Kong et al. [8] analysed the dynamics of an Euler–Bernoulli microbeam in order to obtain the size-dependent natural frequencies. Asghari et al. [9] obtained the size-dependent dynamical response of functionally graded microbeams via use of the modified couple stress theory. Akgöz and Civalek [10, 11] examined the free dynamics and buckling of a microbeam using both the strain gradient and modified couple stress theories. Ghayesh et al. [7, 12] examined the size-dependent nonlinear dynamics of microbeams based the modified couple stress theory.

Reviewing the second class, for example, Ma et al. [13] examined the size-dependent dynamical behaviour of a Timoshenko microbeam based on the modified couple stress theory. Nateghi and Salamat-talab [14] examined the effect of thermal variations on the size-dependent dynamics of functionally graded microbeams. Ansari et al. [15, 16] analysed the bending and thermal post-buckling of a functionally graded Timoshenko microbeam by means of the strain gradient theory. Based on the modified couple stress theory, Ke et al. [17] investigated the thermal effect on free vibration and buckling of Timoshenko microbeams. Ramezani [18] and Asghari et al. [19] solved the equations of motion of a Timoshenko microbeam via the method of multiple scales via a single-mode truncation. Mohammad-Abadi and Daneshmehr [20] contributed to the field by analysing the size-dependent buckling of microbeams employing the modified couple stress theory. Şimşek and Reddy [21] developed a higher order beam theory, in the framework of modified couple stress theory, for buckling analysis of functionally graded microbeams.

1.4 Contributions of this paper to the field

To the authors’ best knowledge, the nonlinear size-dependent parametric resonant dynamics of Timoshenko microbeams subject to time-dependent axial loads has not been investigated in the literature yet. The main contribution of the current paper is to include a time-dependent term in the axial load, which substantially changes the dynamic class of Timoshenko microbeams. More specifically, continuous models for the kinetic and potential energies are developed using the modified couple stress theory and constitutive relations, taking into account small-size effects. The continuous model of the system is developed by means of Hamilton’s principle. A model reduction procedure is carried out via use of the Galerkin scheme, in conjunction with an assumed-mode technique. A high-dimensional reduced-order model is considered in the nonlinear analysis, capable of capturing almost all modal interactions and internal energy transfer [22] between different modes. The second-order reduced-order model is recast into a double-dimensional first-order model, which is treated using four different numerical techniques. The first technique is on the basis of a continuation technique in order to analyse the parametric dynamics of the system near the principal parametric resonance; in other words, for the system in the subcritical regime, the nonlinear parametric response, due to the time-dependent axial load, is obtained by means of the pseudo-arclength continuation technique. The second method is an eigenvalue analysis, which is employed to determine the linear natural frequencies as well as critical buckling loads, due to the mean value of the axial force. Third method is direct time integration via use of the variable step-size modified Rosenbrock scheme. The fourth technique uses the Floquet theory to determine the stability of solution branches. The linear and nonlinear numerical results show that this parametrically excited system displays various interesting and rich dynamics even in the subcritical regime.

2 Continuous and reduced-order models and solution methods

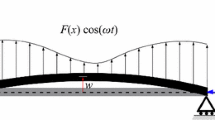
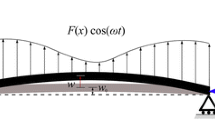
Figure 1 shows a Timoshenko microbeam of length L, cross sectional area A, and second moment of area I; E and μ represent the Young’s modulus and the shear modulus, respectively. The mass density of the microbeam is denoted by ρ. The displacements in the x and z directions (which define the longitudinal and transverse displacements) are represented by u(x, t) and w(x, t), respectively; ϕ(x, t) denotes the rotation of the transverse normal, where t is time. The microbeam is subject to a time-dependent longitudinal excitation force in the form of P ₀ + P ₁ cos (ωt).

Fig. 1

a Schematic representation of a Timoshenko microbeam subject to a time-dependent axial load. b An element of the microbeam before and after deformation

The equations for the longitudinal, transverse, and rotational motions are obtained via the following assumptions: (1) the source of the geometric nonlinearity is mid-plane stretching; (2) the Timoshenko beam theory is employed; (3) cross-sectional area is uniform along the entire length of the beam; (4) there is no warping in the system.

Under the above assumptions, the components of the displacement field, in x, y and z directions, for a Timoshenko beam is given by the following components [23]

$$ \begin{aligned} u_{x} = & u(x,t) + z\phi (x,t), \\ u_{y} = & 0, \\ u_{z} = & w(x,t). \\ \end{aligned} $$

(1)

The relation between the displacement vector u and the rotation vector θ can be expressed as [24]

$$ {\varvec{\uptheta}} = \frac{1}{2}\nabla \times {\mathbf{u}}. $$

(2)

The symmetric curvature tensor χ can be expressed as a function of the rotation vector θ such that [24]

$$ {\varvec{\upchi}} = \frac{1}{2}\left( {\nabla {\varvec{\uptheta}} + (\nabla {\varvec{\uptheta}})^{\text{T}} } \right). $$

(3)

Simplification of Eqs. (1–3) gives the following non-zero components of the symmetric curvature tensor as functions of the displacement field

$$ \chi_{xy} = \chi_{yx} = \frac{1}{4}\left( {\frac{\partial \phi }{\partial x} - \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right). $$

(4)

The components of the strain tensor ε are related to the displacement field components through the following relations [25]

$$ \varepsilon_{xx} = \frac{\partial u}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2}\,+\, z\frac{\partial \phi }{\partial x}, $$

(5)

$$ \varepsilon_{xz} = \varepsilon_{zx} = \frac{1}{2}\left( {\frac{\partial w}{\partial x} + \phi } \right). $$

(6)

For an isotropic linear elastic material, the stress tensor σ and the deviatoric part of the symmetric couple stress tensor m can be expressed as [24]

$$ {\varvec{\upsigma}} = \lambda {\text{tr}}({\varvec{\upvarepsilon}} ){\mathbf{I}} + 2\mu {\varvec{\upvarepsilon}}, $$

(7)

$$ {\mathbf{m}} = 2l^{2} \mu {\varvec{\upchi}}, $$

(8)

where λ and μ denote the Lamé constants, l is the material length-scale parameter, I is the second-order identity tensor, tr is the trace of a matrix.

Based on the modified couple stress theory [24], the elastic strain energy of a system occupying volume V is given by

$$ U = \frac{1}{2}\int_{V} {\left( {{\varvec{\upsigma}}:{\varvec{\upvarepsilon}} + {\mathbf{m}}:{\varvec{\upchi}}} \right){\text{d}}V} . $$

(9)

The size-dependent strain energy of the system can be obtained by inserting Eqs. (4–8) into Eq. (9) as follows [25]

$$ U = \frac{1}{2}EI\int_{0}^{L} {\left( {\frac{\partial \phi }{\partial x}} \right)^{2} } {\text{d}}x + \frac{1}{2}EA\int_{0}^{L} {\left[ {\frac{\partial u}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right]}^{2} {\text{d}}x + \frac{1}{2}\mu A\int_{0}^{L} {\left[ {\left( {\frac{\partial w}{\partial x} + \phi } \right)^{2} + \frac{{l^{2} }}{4}\left( {\frac{\partial \phi }{\partial x} - \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)^{2} } \right]} \;{\text{d}}x. $$

(10)

The kinetic energy of the system is given as a function of the displacement field by [25]

$$ T = \frac{1}{2}\rho A\int_{0}^{L} {\left[ {\left( {\frac{\partial u}{\partial t}} \right)^{2} + \left( {\frac{\partial w}{\partial t}} \right)^{2} } \right]} \;{\text{d}}x + \frac{1}{2}\rho I\int_{0}^{L} {\left( {\frac{\partial \phi }{\partial t}} \right)^{2} } {\text{d}}x. $$

(11)

Application of Hamilton’s principle to Eqs. (10) and (11) results in the following equations for the longitudinal, transverse, and rotational motions [25]

$$ \rho A\frac{{\partial^{2} u}}{{\partial t^{2} }} - EA\left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{\partial w}{\partial x}\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) = 0, $$

(12)

$$ \begin{aligned} & \rho A\frac{{\partial^{2} w}}{{\partial t^{2} }} - EA\left[ {\frac{\partial u}{\partial x}\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial x^{2} }}\frac{\partial w}{\partial x} + \frac{3}{2}\frac{{\partial^{2} w}}{{\partial x^{2} }}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right] \\ & \quad - \mu A\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{\partial \phi }{\partial x}} \right) + \frac{{\mu Al^{2} }}{4}\left( {\frac{{\partial^{4} w}}{{\partial x^{4} }} - \frac{{\partial^{3} \phi }}{{\partial x^{3} }}} \right) = 0, \\ \end{aligned} $$

(13)

$$ \rho I\frac{{\partial^{2} \phi }}{{\partial t^{2} }} - EI\frac{{\partial^{2} \phi }}{{\partial x^{2} }} + \mu A\left( {\frac{\partial w}{\partial x} + \phi } \right) + \frac{{\mu Al^{2} }}{4}\left( {\frac{{\partial^{3} w}}{{\partial x^{3} }} - \frac{{\partial^{2} \phi }}{{\partial x^{2} }}} \right) = 0. $$

(14)

The microbeam is constrained axially at the left end; an axial load, in the form of P(t) = P ₀ + P ₁cos(ωt), is applied to the right end of the microbeam (see Fig. 1). The boundary conditions for the longitudinal motion of such a system are given by [26]

$$ \left. u \right|_{x = 0}\, =\, 0,\;\left. u \right|_{x = L}\, =\, - \frac{P(t)L}{EA}. $$

(15)

The boundary conditions for the transverse and rotational motions are given by [27]

$$ \left. w \right|_{x = 0}\,=\,\left. w \right|_{x = L}\,=\,0, $$

(16)

$$ \left. {\frac{\partial \phi }{\partial x}} \right|_{x = 0} = \left. {\frac{\partial \phi }{\partial x}} \right|_{x = L} = 0. $$

(17)

Neglecting fast dynamics in Eq. (12) while employing Eq. (15), one can obtain the following equations for the transverse and rotational motions, respectively

$$ \begin{aligned} & \rho A\frac{{\partial^{2} w}}{{\partial t^{2} }} - \frac{EA}{L}\frac{{\partial^{2} w}}{{\partial x^{2} }}\int_{0}^{L} {\left[ {\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right]} {\text{d}}x - \mu A\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{\partial \phi }{\partial x}} \right) \\ & \quad +\,\frac{{\mu Al^{2} }}{4}\left( {\frac{{\partial^{4} w}}{{\partial x^{4} }} - \frac{{\partial^{3} \phi }}{{\partial x^{3} }}} \right) + \left( {P_{0} + P_{1} \cos (\omega t)} \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} + c\frac{\partial w}{\partial t} = 0, \\ \end{aligned} $$

(18)

$$ \rho I\frac{{\partial^{2} \phi }}{{\partial t^{2} }} - EI\frac{{\partial^{2} \phi }}{{\partial x^{2} }} + \mu A\left( {\frac{\partial w}{\partial x} + \phi } \right) + \frac{{\mu Al^{2} }}{4}\left( {\frac{{\partial^{3} w}}{{\partial x^{3} }} - \frac{{\partial^{2} \phi }}{{\partial x^{2} }}} \right) + c_{r} \frac{\partial \phi }{\partial t} = 0, $$

(19)

where a term for viscous damping, which is a common and effective damping model used widely in the literature, has been added. c denotes the damping coefficient for the transverse motion and c _r represents that for rotation; moreover, c _r = c(I/A).

Time-dependent coefficients in Eqs. (18) and (19), due to the time-variant axial load (P ₀ + P ₁ cos (ωt)), make the system parametrically excited. An interesting feature of this class of systems is the occurrence of principal parametric resonance in the vicinity of the twice the first natural frequency of the linear system. There is also a zero response throughout the solution space, both stable and unstable [28–31].

The continuous models for the transverse and rotational motions, given in Eqs. (18) and (19), are reduced using the Galerkin method, resulting in a second-order nonlinear reduced-order model, to be solved numerically.

Introducing the following series expression

$$ w(x,t) = \sum\limits_{k = 1}^{M} {q_{k} (t)\varphi_{k} (x),} $$

(20)

$$ \phi (x,t) = \sum\limits_{k = 1}^{N} {p_{k} (t)\psi_{k} (x),} $$

(21)

in which q _k (t) and p _k (t) are the kth generalized coordinates of the transverse and rotational motions, respectively; φ _k (x) = sin(kπx/L) is the kth eigenfunction for the transverse motion of a hinged–hinged linear beam and ψ _k (x) = cos(kπx/L).

Application of the Galerkin scheme by inserting the series expansions [i.e. Eqs. (20, 21)] into the continuous models for the transverse and rotational motions [i.e. Eqs. (18, 19)], multiplying the resultant expressions by the corresponding eigenfunctions, and integrating over x from 0 to L results in the second-order nonlinear reduced-order model of the system. This model is first transformed to a double-dimensional first-order reduced-order model via use of a change of variables. The following techniques are used to solve the new model and analyse the results: (1) a continuation technique for determining the principal parametric dynamics of the system; (2) an eigenvalue analysis so as to determine the linear natural frequencies; (3) direct time integration by means of the variable step-size modified Rosenbrock scheme; (4) the Floquet theory to determine the stability of solution branches. The numerical simulations have been performed for an epoxy microbeam of l = 17.6 µm, h = 6.0 l, b = 2 h, L = 50 h, E = 1.44 GPa, µ = 521.7 MPa, and ρ = 1220 kg/m³ [13, 32].

Moreover, the following dimensionless parameters are used throughout the numerical simulations

$$ \begin{aligned} w^{*} = & \frac{w}{h},\quad \varOmega = \omega \sqrt {\frac{{\rho AL^{4} }}{EI}} ,\quad t^{*} = t\sqrt {\frac{EI}{{\rho AL^{4} }}} ,\quad P_{0}^{*} = \frac{{P_{0} L^{2} }}{EI},\quad P_{1}^{*} = \frac{{P_{1} L^{2} }}{EI}, \\ c_{d} = & \frac{{cL^{4} }}{EI}\sqrt {\frac{EI}{{\rho AL^{4} }}} ,\quad \omega_{i}^{*} = \omega_{i} \sqrt {\frac{{\rho AL^{4} }}{EI}} \quad i = 1,2, \\ \end{aligned} $$

(22)

where ω _i denotes the ith natural frequency of the transverse motion. In what follows, the system parameters and the numerical results are reported only in the dimensionless forms and the asterisk notation is dropped for briefness.

3 Validation of the model for the case of static buckling

Figure 2 shows the variation of the critical static buckling load of a microbeam obtained by the numerical simulations of the present study and that obtained based on the formula presented by Reddy [33] for a Timoshenko beam model; the length-scale parameter is set to zero, while the thickness and width of the microbeam are chosen the same as those used in this study. The solid line represents the results obtained using the formula in Ref. [33] and the symbols show that obtained via the present nonlinear analysis. It is seen that the results of both studies match. Figure 3 shows the bifurcation diagram of a microbeam obtained by the numerical simulations of the present study and that obtained by Xia et al. [34]; the system parameters are set to values given in Ref. [34]. It is seen that the results of both studies almost match which prove the validity of the numerical simulations employed in this paper. It is worthwhile noting that the small differences between the results are due to the fact that the present study employs the Timoshenko beam theory while Xia et al. [34] employed Euler–Bernoulli beam theory.

Fig. 2

The variation of the critical buckling load with microbeam length: solid line represents the results obtained using the formula in Ref. [33] and the symbols show that obtained by the present study

Fig. 3

The bifurcation diagram of a microbeam: solid line represents the result obtained by the present study and symbols shows that obtained in Ref. [34]

4 Results and discussions

4.1 Natural frequencies

Based on the solution procedure explained in Sect. 2, an eigenvalue analysis is applied to the linear part of the reduced-order model. This results in eigen frequencies (and hence natural frequencies) of the system. For the analysis of this section, the time-dependent component of the axial load P ₁ is set to zero.

Table 1 shows the variations of the first two linear natural frequencies of the transverse motion as P ₀ (i.e. the mean value of the axial load) is varied. As seen in this table, both the first and second linear natural frequencies decrease as P ₀ is increased. Moreover, for each P ₀, the model based on the modified couple stress theory predicts larger values for the first and second linear natural frequencies of the transverse motion of the linear system. It is also seen that, as P ₀ is increased, the percentage difference between the predicted natural frequencies by the two theories increases.

Table 1 The first two dimensionless natural frequencies of the transverse motion as functions of the amplitude of the mean axial load

4.2 Principal parametric response in subcritical regime

This section examines the principal parametric resonance of the system in the subcritical regime. In other words, the mean value of the axial force is set to a value below the critical value and the principal parametric response is analysed; this response is due to the time-dependent component of the axial load. An interesting feature of this system, classified as a parametrically excited system, is that parametric resonances occur in the vicinity of twice any natural frequency of the linear system, as opposed to externally excited (e.g. a microbeam subject to a transverse load). Another interesting feature of this class of systems is that there is always a trivial solution throughout the solution space. Moreover, as opposed to transversely excited systems, there are period-doubling bifurcations present. In what follows, the modal damping ratio ζ is set to 0.017; ζ is related to c _d through c _d = 2ζω ₁.

Figure 4 shows the size-dependent principal resonant response of the system; a frequency sweep is conducted around twice the first linear natural frequency of the transverse motion, when P ₀ = 4.0, P ₁ = 4.0, and ω ₁ = 8.34. Sub-figures (a) and (b) correspond to the transverse displacement at the mid-point and rotation at x = 0, respectively. Theoretically, as the frequency ratio (Ω/ω ₁) is increased from 1.95, the system stays at rest until reaching Ω = 1.9853ω ₁, where the first period-doubling bifurcation occurs, and a non-trivial stable solution branch bifurcates. It is worth noting that sharp increase in the transverse amplitude (from zero) hints the occurrence of a buckling. A second period-doubling bifurcation occurs at point PD₂ (Ω = 2.0138ω ₁); the trivial solution branch is unstable between the two period-doubling bifurcations. At the second period-doubling bifurcation point, a non-trivial unstable solution branch emerges. The two stable and unstable solution branches coincide at Ω = 2.1995ω ₁, where a limit point bifurcation occurs. Figure 5 shows the details of the dynamic response of the system at Ω = 2.10ω ₁, through (a, b) time traces, (c, d) phase-plane portraits, (e, f) fast Fourier transforms (FFTs), of the transverse motion and rotation, respectively. The time histories of the transverse motion at several excitation frequencies are depicted in Fig. 6. It is seen that, as a result of increased amplitude of oscillation, the nonlinear frequency of the oscillation increases as well.

Fig. 4

Frequency–response curves of the system: a the maximum amplitude of the transverse motion at the centre of the microbeam; b the maximum amplitude of the rotation at x = 0; P ₀ = 4.0, P ₁ = 0.52, and ω ₁ = 8.34

Fig. 5

The details of the dynamics of the system of Fig. 4 at Ω = 2.10ω ₁: a, b time traces, c, d phase-plane portraits, and e, f FFTs of the transverse motion and rotation, respectively

Fig. 6

Time histories of the transverse motion of the system of Fig. 4 at a Ω = 2.03ω ₁ and Ω = 2.06ω ₁, b Ω = 2.09ω ₁ and Ω = 2.12ω ₁, and c Ω = 2.15ω ₁ and Ω = 2.18ω ₁

When P ₀ is set to 4.0, which is lower than the critical value, and also Ω is set to 2.05ω ₁, the system response is plotted in Fig. 7 as the amplitude of axial load variations, P ₁, is varied. There are two bifurcation points. The first one is of a period-doubling type (P ₁ = 0.8617); this bifurcation is responsible for bifurcating the unstable non-trivial solution (of subcritical type). The second bifurcation is a limit point type, which occurs at P ₁ = 0.4896; this bifurcation is responsible for regaining stability. An important feature of the response is the occurrence of the limit point bifurcation earlier than the period-doubling bifurcation, i.e. the system displays subcritical bifurcation. From design perspective, this is crucial, since, when P ₁ is increased, a jump (from rest at zero to a non-zero amplitude) could occur at values lower than P ₁ corresponding to the period-doubling bifurcation, and thus the system may experience a large-amplitude motion prior to reaching the period-doubling bifurcation point.

Fig. 7

Force–response curves of the system: a the maximum amplitude of the transverse motion at the centre of the microbeam; b the maximum amplitude of the rotation at x = 0; P ₀ = 4.0, Ω = 2.05ω ₁, and ω ₁ = 8.34

The principal parametric resonant responses obtained based on the modified couple stress and classical continuum theories are shown in Fig. 8. As seen in this figure, based on the modified couple stress theory, the peak-amplitude occurs at a smaller excitation frequency (i.e. the frequency of the axial load variations); the peak-amplitude is also smaller based on the modified couple stress theory. Both the theories predict a hardening-type nonlinear behaviour.

Fig. 8

Frequency–response curves of the system obtained via the modified couple stress and classical continuum theories: a the maximum amplitude of the transverse motion at the centre of the microbeam; b the maximum amplitude of the rotation at x = 0; P ₀ = 4.0 and P ₁ = 0.52

The principal parametric response of the system for several values of P ₀ (i.e. the constant component of the axial load) is plotted in Fig. 9, illustrating that for larger values of P ₀, the non-trivial response emerges at lower frequency ratios. Moreover, the peak-amplitude is larger for larger values of P ₀ and occurs at larger frequency ratios.

Fig. 9

Frequency–response curves of the system for several values of P ₀: a the maximum amplitude of the transverse motion at the centre of the microbeam; b the maximum amplitude of the rotation at x = 0; P ₁ = 0.52

Figure 10 demonstrates the relation between the amplitude of axial load variations, P ₁, and the frequency ratios corresponding to the period-doubling bifurcations in the frequency–response curves. As seen in this figure, as P ₁ is increased, the first period-doubling bifurcation (PD₁) occurs at smaller frequency ratios and the second one (PD₂) occurs at larger frequency ratios.

Fig. 10

The variations of the excitation frequencies corresponding to the period-doubling bifurcations in the frequency–response curves of the system with P ₁; P ₀ = 4.0 and ω ₁ = 8.34

The principal parametric response of the system, when P ₁ is varied as the control parameter (i.e. the force–response curve), is illustrated in Fig. 11 for several values of P ₀. It is seen that as the value of P ₀ is increased, the period-doubling bifurcation occurs at larger values of P ₁, and the subcritical behaviour becomes stronger (i.e. the difference between the period-doubling and limit point bifurcations increases). Figure 12 shows a closer look at the variation of the amplitude of P ₁ corresponding to the period-doubling bifurcation with P ₀, illustrating that as the amplitude of P ₀ is increased, a larger P ₁ is required to reach the period-doubling bifurcation (instability).

Fig. 11

Force–response curves of the system for several values of P ₀: a the maximum amplitude of the transverse motion at the centre of the microbeam; b the maximum amplitude of the rotation at x = 0; Ω = 16.80

Fig. 12

The variations of the amplitude of the dynamic axial load (P ₁) corresponding to the period-doubling bifurcation in the force–response curves of the system with P ₀; Ω = 16.80

The effect of the frequency ratio on the force–responses of the system is depicted in Fig. 13, showing that for higher value of Ω/ω ₁, the amplitude of oscillation is larger at sufficiently large P ₁. Moreover, it is seen that for frequency ratios less than or equal to 2.0, no limit point bifurcation occurs after the occurrence of the period-doubling bifurcation. Figure 14 demonstrates the variation of the amplitude of P ₁ corresponding to the period-doubling bifurcation with Ω/ω ₁. It is seen that as the frequency ratio is increased from 1.90, the amplitude of P ₁ corresponding to the period-doubling bifurcation decreases until reaching a minimum value at Ω/ω ₁ = 2.0. The amplitude of P ₁ corresponding to the period-doubling bifurcation increases thereafter with increasing frequency ratio.

Fig. 13

Force–response curves of the system for several excitation frequencies: a the maximum amplitude of the transverse motion at the centre of the microbeam; b the maximum amplitude of the rotation at x = 0; P ₀ = 4.0

Fig. 14

The variations of the amplitude of the dynamic axial load (P ₁) corresponding to the period-doubling bifurcation in the force–response curves of the system with excitation frequency ratio; P ₀ = 4.0

5 Conclusions

The nonlinear dynamic stability in parametric resonant response of axially excited Timoshenko microbeams has been examined numerically; the microbeam was subject to a time-dependent axial load. A continuous model based on the modified couple stress theory was constructed and reduced via Galerkin’s method. The pseudo-arclength continuation method, a direct time integration method based on the modified Rosenbrock scheme, an eigenvalue extraction method, and the Floquet method were employed to obtain the system response and its stability.

The linear analysis showed that as the amplitude of mean axial load is increased, the natural frequencies of the system decrease. Moreover, it was shown that the modified couple stress theory predicts a larger natural frequency, compared to the classical continuum theory, at arbitrary amplitude of the mean axial load.

The nonlinear principal parametric response of the system showed that: (1) as the frequency of the axial load variations is varied around twice the first linear natural frequency of the transverse motion, non-trivial solution branches bifurcate, due to occurrences of period-doubling bifurcations; (2) the force–response of the system displays a sub-critical behaviour, with the possibility of jumping to the non-trivial branch at amplitudes of the axial load variations prior to the occurrence of period-doubling bifurcation; (3) the modified couple stress theory predicts the occurrence of non-trivial solution branch at larger excitation frequencies; (4) as a result of increased amplitude of the axial load variations, the unstable region between the two period-doubling bifurcations becomes larger; (5) the minimum amplitude of the axial load variation corresponding to the period-doubling bifurcation in the force–response of the system occurs at Ω/ω ₁ = 2.0.