1 Introduction

Graphite materials are widely used as structural materials for load-bearing applications in different branches of technique, so the studies of fracture properties of these materials are important. These heterogeneous materials are multiphase, polygranular and contain pores, micro-cracks and other defects of structure to considerable extent, which cannot be eliminated by supplementary treatment, such as high temperature pressing and impregnation with pitch, or some other methods. Many graphite materials have small non-linearity of stress–strain curves [1–5] but they possess another type of physical non-linearity concerned the dependence of their mechanical properties on the type of loading [6–10]. For these materials, the stress–strain curves under uniaxial tension, uniaxial compression, shear and other types of loading differ noticeably. Instead of a single curve of dependence between von Mises equivalent stress and equivalent strain, there is a set of equivalent stress–strain curves for different loading conditions that is caused by heterogeneous structures of materials. In these materials, the process of bulk deformation is related to shear deformations. These effects are different for isotropic and anisotropic materials according to their structures. Some features of the behavior of anisotropic materials were considered in [9].

The constitutive relations to describe these features of the behavior of heterogeneous materials were proposed [6–9]. Different crack problems for plane stress and plane strain conditions were considered [11, 12]. It was shown that in some cases, the traditional approaches to the solution of crack problems cannot be used and corresponding methods for the solution of these problems were proposed.

The crack growth behavior in graphite materials was investigated for different loading conditions and at various temperatures [13–17] including the study of the formation of damage zones near the tips of notches in the process of loading [1, 18, 19]. The graphite materials are quasi-brittle aggregate materials and they have microstructural features similar to many other porous, aggregate and other heterogeneous materials and in the first instance such as concrete and composites [20–24]. Similar effects are observed in structural materials, such as alloys, under long-term creep conditions at elevated temperature when the nucleation and development of damage take place and materials can fail in quasi-brittle manner [25, 26].

The investigation of post-cracking and post-critical behavior of solids and structural elements are important both from the theoretical point of view and for practical purposes [27–29] to predict the character of failure of structures and the crack behavior in cases of different overloads. The objectives of this study are to compare the strength and fracture toughness characteristics of different grades of graphite materials and to investigate the crack growth behavior in structural members working under bending conditions. The method for the determination of fracture toughness of the materials during crack growth is proposed, which can be used to study crack growth rate and its possible influence on the values of fracture toughness. The process of post-critical crack growth in graphite is studied and the values of fracture toughness are determined. It has been shown that crack growth under bending conditions can be stable, equilibrium, or unstable. The condition of unstable crack growth is determined. When unstable crack growth in structural members in bending is observed, it is important to investigate some features of this process. The corresponding analysis of unstable crack growth is carried out, which can be equally used not only for quasi-brittle materials but for elastic–plastic ones, too, if the requirements of linear fracture mechanics are satisfied. Many structures work under bending conditions and it is important to investigate when the crack growth can be stable or unstable. The results of the performed studies have broad-range significance and can be applied to various classes of materials.

2 Elastic and strength properties of graphite materials

The elastic and fracture properties of three grades of graphite materials, which were formed with the use of isostatic pressing method, were studied. All tested graphite materials were practically isotropic. The coarse grained dense graphite VPPFootnote 1 (bulk density ~1.85 × 103 kg m−3) formed under multiple alternation of impregnation with pitch binder and roasting before graphitization had maximum coal coke grain size of 2.3 × 103 μm. This graphite is used for manufacture of large-sized multi-purpose structures. The other two fine grained dense graphite materials MPG-61 (bulk density ~1.75 × 103 kg m−3) and MPG-81 (bulk density ~1.91 × 103 kg m−3) had mean grain size of about 90 μm. The fine-grained structure of these materials in conjunction with strength properties allow to reach high degree of surface finish of products and to produce structural parts with the thickness of less than 0.8 mm. These graphite materials are widely used in nuclear engineering, in the equipment for high temperature testing, metallurgy, the manufacture of nozzles and parts of turbines, electronic equipment and many others.

The polished samples of graphite materials MPG-6, MPG-8 and VPP were tested at the temperature of 23 °C. The Young’s modulus, Poisson’s ratio and strength properties of graphite materials were determined based on the tests of smooth plane specimens under conditions of tension. The specimens had the thickness of 5 mm, the width of 9 mm and the gage length of 40 mm. Plates of wood were glued to the ends of samples surface to prevent the destruction of samples in the testing machine’s pneumatic gripes. Instron extensometers were used to determine longitudinal and lateral deformations. The stress–strain diagrams were linear with small deviation from the linearity near the breaking stress. The strength properties were determined under the conditions of bending, too. The experimental values of elastic and strength properties of graphite materials are given in Table 1.

Table 1 Elastic and strength properties of graphite materials
Full size table

The considerable difference between tensile and flexural strength properties was observed that is natural for graphite and other semi-brittle materials, such as cast-iron, rocks, refractory ceramics and many other materials. For the determination of material’s properties, the stress and strain distributions have to be uniform in a specimen and these conditions are satisfied in tests under uniaxial tension. Under conditions of bending, the stress and strain fields are not uniform and the values of strength obtained under these conditions cannot be regarded the material properties, especially for materials, which properties are susceptible to the stress state type.

3 Fracture toughness characteristics

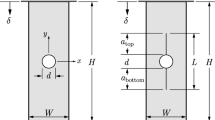
For the determination of the fracture toughness characteristics of graphite materials, three-point bending tests of cracked specimens with different depth of cuts were carried out (Fig. 1).

Fig. 1
figure 1

Specimen for crack toughness testing

Full size image

The specimens had the following dimensions: b = 14.80–15.00 mm, B = 14.92–15.00 mm, L = 80 mm, S = 60 mm. Surfaces of specimens were polished before the tests. The cuts were made by a special slitting saw with the thickness equal to 0.1 mm that gives the possibility to achieve the crack tip sharpness of the radius not more than 0.01 mm.

The value of elastic strain energy release rate can be determined with the use of the compliance method and the corresponding analytical formula for energy release [30–32]

$$G = \frac{{P_{c}^{2} }}{2Bb}\frac{dC}{d\omega },$$
(1)

where ω = a/b is the relative crack length, P C is a critical load corresponding to the initiation of crack growth and C is the compliance of notched specimen, C = υ/P, where υ is the load line displacement. For this type of loading, we have the following formula for stress intensity factor [33]

$$K_{I} = \frac{6M\sqrt a }{{Bb^{2} }}Y(\omega ),{\text{ where}}\quad Y\left( \omega \right) = A_{0} + A_{1} \omega + A_{2} \omega^{2} + A_{3} \omega^{3} + A_{4} \omega^{4} .$$
(2)

For the conditions of three-point bending M = PS/4, the coefficients A i have the following values for S/b = 4:

$$A_{0} = 1.93,\quad A_{1}=-3.07,\quad A_{2} =14.53,\quad A_{3}= -25.11,\quad A_{4} = 25.80.$$

There is a simple relation between the elastic strain energy release rate and the critical value of stress intensity factor \(K_{{I_{C} }}\), which is a material characteristic:

$$G = \frac{{1 - \nu^{2} }}{E}K_{{I_{C} }}^{2} ,\quad K_{{I_{C} }} = \frac{{3P_{c} S\sqrt a }}{{2Bb^{2} }}Y(\omega )$$
(3)

The tests were carried out at constant cross-head speed of α = 3.33 × 10−5 mc−1. The specimen’s surfaces were polished before the tests. The load variation in time was registered during the test and simultaneously the load–displacement diagram was determined, too. The diagrams were linear almost up to the maximum load corresponding to crack growth initiation. Two of these diagrams obtained for MPG-6 are shown in Fig. 2. The diagrams obtained for other graphite materials were similar.

Fig. 2
figure 2

Typical load–displacement curves for different initial crack lengths

Full size image

The set of five specimens were tested for each initial crack length. The experimental values of fracture toughness are given in Table 2. Four sets of specimens of graphite MPG-6 with different crack length were tested. The mean values of crack length, critical load and fracture toughness are given in Table 2. The values of initial crack length were determined with the use of optical microscope Carl Zeiss Discovery V12. The mean value of critical stress intensity factor is \(K_{{I_{C} }} = 12.78 \times 10^{5} \;{\text{Nm}}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0pt} 2}}}\) with the variation of 8 %. The mean value of elastic strain energy release rate is G = 1.83 × 102 Nm−1.

Table 2 Mean values of fracture toughness for different graphite materials
Full size table

Two sets of specimens of MPG-8 were tested and the mean value of \(K_{{I_{C} }} = 16.31 \times 10^{5} \;{\text{Nm}}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0pt} 2}}}\) with the variation of 3 % and the mean value of G = 1.137 × 102 Nm−1 were obtained. Two sets of six specimens each of VPP graphite were tested. The mean value of \(K_{{I_{C} }} = 12.62 \times 10^{5} \;{\text{Nm}}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0pt} 2}}}\) with the variation of 10 % and the mean value of G = 1.686 × 102 Nm−1 were determined.

Based on the experimental data, we can compare the strength and fracture toughness characteristics of different grades of graphite materials. The strength of MPG-6 is about two times higher than the strength of VPP graphite but the fracture toughness or the resistance of the material to the crack growth is almost the same. The strength of MPG-8 is about 2.5 times higher than the strength of VPP but the value of fracture toughness is less than the value for VPP. Thus, these graphite materials have almost the same fracture toughness characteristics, despite the fact that their strength properties are quite different.

In the case when the length of the initial crack is not very short, it is possible to determine a number of values of fracture toughness during the test of a single specimen. Bending is a type of loading where cross-beam displacement is controlled. Therefore, the repeated loading of a specimen is possible and one can determine a number of values of critical loads for different crack lengths, which can be measured on the polished surface of a specimen. One of these diagrams for MPG-6 is shown in Fig. 3. This procedure was used for the analysis of the process of stable, equilibrium crack growth.

Fig. 3
figure 3

Load-displacement diagrams for repeated loading

Full size image

According to this procedure, fracture toughness can be determined during crack growth. Values of load under repeated loadings were almost the same as values of load before unloading. Values of fracture toughness determined during the test of a single specimen were in the range of experimental data scattering for all specimens.

According to Eqs. (1)–(3), there is the differential relation between the compliance and relative crack length:

$$\frac{dC}{d\omega } = \frac{{9S^{2} a(1 - \nu^{2} )}}{{2Bb^{3} E}}[Y(\omega )]^{2} .$$
(4)

The load is not entered into this equation. The compliance depends on two material properties—Young’s modulus and Poisson’s ratio, specimen dimensions and relative crack length. This equation can be integrated as follows:

$$C = C_{0} + \frac{{9S^{2} (1 - \nu^{2} )}}{{2Bb^{2} E}}[F(\omega ) - F(\omega_{0} )] .$$
(5)

where C 0 is the compliance of the specimen with initial relative crack length ω 0,

$$\begin{aligned} F(\omega ) = \omega^{2} \left[ {\frac{1}{2}A_{0}^{2} + \frac{2}{3}A_{0}^{{}} A_{1} \omega + \frac{1}{4}(A_{1}^{2} + 2A_{0}^{{}} A_{2} )\omega^{2} + } \right. \hfill \\ \frac{2}{5}(A_{1} A_{2} + A_{0} A_{3} )\omega^{3} + \frac{1}{6}(A_{2}^{2} + 2A_{0} A_{4} + 2A_{1} A_{3} )\omega^{4} + \hfill \\ \left. {\frac{2}{7}(A_{1} A_{4} + A_{2} A_{3} )\omega^{5} + \frac{1}{8}(2A_{2} A_{4} + A_{3}^{2} )\omega^{6} + \frac{2}{9}A_{3} A_{4} \omega^{7} + \frac{1}{10}A_{4}^{2} \omega^{8} } \right]. \hfill \\ \end{aligned}$$
(6)

It is possible to accept C 0 in (5) to be equal to the compliance of un-notched specimen (ω 0 = 0), in this case C 0 = S 3/4EBb 3. Then for the compliance of a notched specimen one can obtain the following equation:

$$C(\omega ) = \frac{{S^{2} }}{{2EBb^{2} }}\left[ {\frac{S}{2b} + 9(1 - \nu^{2} )F(\omega )} \right] .$$
(7)

A typical diagram for the test of notched specimen of brittle or quasi-brittle material under bending conditions is shown in Fig. 4. Assuming a certain crack length a, one can calculate the compliance of a specimen C for the given relative crack length ω = a/b using Eq. (7). Drawing straight lines corresponding to the calculated value of compliance C from the origin of coordinates to the intersection with P ∼ υ diagram (Fig. 4), one can obtain the critical value of load P c necessary to maintain crack growth. Substituting the obtained values of P c into Eq. (3), it is possible to determine the values of the stress intensity factor during the crack growth.

Fig. 4
figure 4

A diagram for the test of the notched specimen of brittle or quasi-brittle material under bending conditions

Full size image

This analysis of the results of experimental studies for different grades of graphite material was carried out, in particular, for the diagrams shown in Fig. 2 corresponding to the initial relative crack length ω 0 = 0.35 and ω 0 = 0.46 (MPG-6). Table 3 shows the values of K Ic during the crack growth obtained with the use of proposed method. The variation of the calculated values of K Ic is very small and does not exceed the bounds of experimental data scattering. The values of stress intensity factor is approximately constant during the crack growth under bending conditions except for the cases when the crack approaches the free boundary of a specimen.

Table 3 Values of K Ic during crack growth
Full size table

The error of Eq. (2) does not exceed 0.2 % for values of ω ≤ 0.6 but it increases rapidly for ω > 0.7, and this is shown in Table 3.

The mean value of the stress intensity factor in the range of ω ≤ 0.7 is equal to 15.99 × 105 Nm−3/2 with a variation of 4 % for ω 0 = 0.35 and 14.38 × 105 Nm−3/2 with a variation of 3 % for ω 0 = 0.46. As a consequence of the heterogeneous structure of graphite materials, the process of crack growth is uneven and sometimes interrupted. The values of K Ic for crack growth initiation were less in comparison with ones for growing cracks that was caused by the secondary cracking near the notch tips developed during the loading that usually is not taken into account.

The described method can be used not only to determine the values of the stress intensity factor during crack growth, but to study the influence of the crack growth rate on the fracture toughness of a material, too.

During the test, the diagrams of P ∼ t and P ∼ υ usually can be determined. For the assigned crack length increment Δa, the values of load P can be determined for different values of ω. On the basis of the P ∼ t diagram, time interval Δt can be determined when the crack increases its length in Δa. Thus, the mean value of the crack growth rate in the interval Δt can be determined that is equal to Δa/Δt.

4 Stable and unstable crack growth

In the experiments, unstable non-equilibrium crack growth from short initial crack was observed. This effect can be analytically approved and the condition for stable crack growth under bending can be determined. Equation (3) establishes the relation between the critical load and the corresponding crack length. This dependence can be represented in a non-dimensional form:

$$\bar{P}_{c} = \frac{{3P_{c} S}}{{2K_{Ic} Bb^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} }} = [Y(\omega )\sqrt \omega ]^{ - 1} .$$
(8)

For each value of the critical load, we have a corresponding value of the critical load line displacement υ C according to the following relation

$$\upsilon_{C} = C(\omega )P_{c}$$
(9)

From Eqs. (7)–(9), the relation between non-dimensional critical displacement \(\bar{\upsilon }_{c}\) and relative crack length can be determined

$$\bar{\upsilon }_{c} = 3\frac{{\upsilon_{C} E\sqrt b }}{{SK_{Ic} }} = \left[ {\frac{S}{2b} + 9(1 - \nu^{2} )F(\omega )} \right][Y(\omega )\sqrt \omega ]^{ - 1}, \quad S = 4b.$$
(10)

Equations (8) and (10) can be regarded as parametric dependencies of the critical load and the critical displacement on relative crack length. The corresponding graphs for the non-dimensional critical load (curve 1) and the critical displacement (curve 2) are shown in Fig. 5. On the base of (7) and (9) or using these two graphs, the relation between the critical load and the critical displacement can be established, which is shown in Fig. 6. The dependence of the critical load on the critical displacement is not even and it is not simple either. From these graphs, the condition of the unstable crack growth can be determined.

Fig. 5
figure 5

Diagrams of dependencies of non-dimensional critical load (curve 1) and critical displacement (curve 2) on the relative crack length

Full size image
Fig. 6
figure 6

Dependence of critical load on critical displacement

Full size image

The straight line corresponds to the dependence between load and load line displacement for an un-notched specimen. Point A corresponds to the relative crack length equal to ω = 0.27. If the test is carried out under the control of displacement alteration and the initial relative crack length ω 0 = a 0/b is less than 0.27, unstable crack growth is to begin after the load reaches its critical value, as it was observed in experiments, too. This result is referred not only to graphite materials but to other semi-brittle materials, such as concretes, refractory ceramics, cast-iron and others. It is valid for elastoplastic materials, too, if the requirements of linear fracture mechanics are fulfilled. The unstable crack growth is very dangerous because usually there is no pre-failure indication of it. Similar qualitative results were obtained in the case of tension of a plate with a central crack under the conditions of hard loading [34, 35]. The processes of stable and unstable crack growth were studied with the use of the strain energy theory for different loading conditions, namely the uniaxial tension of a plate with inclined crack, tension of a plate with central crack and two notches, a circular disc subjected to two equal and opposite forces [36].

5 Analysis of kinetic energy

In the case of unstable crack growth, some part of stored energy is expended not only on the formation of new crack surface but on the kinetic energy of the beam, too. The studies of values of these expenditures and variation of kinetic energy during the unstable crack growth under different loading conditions are of scientific and practical interest. This analysis can be performed with the use of energy balance equation that for a solid with a moving crack without heat flux can be represented in the following form:

$$\Delta {\text{U}} +\Delta {\text{K}} +\Delta \Pi =\Delta {\text{A}} .$$
(11)

where \(\Delta {\text{U}}\) is the increment of elastic energy, \(\Delta {\text{K}}\) is the increment of kinetic energy, \(\Delta \Pi\) is the change of energy in consequence of the formation of a new crack surface and \(\Delta {\text{A}}\) is the increment of the work of external force. For a linear elastic material or when the most part of a solid is in an elastic state, the relation between the displacement and the load is represented in the form υ = CP, where C is the compliance, which is the function of a relative crack length ω. The elastic energy stored in a solid under the loading is

$${\text{U}} = \frac{1}{2}P\upsilon .$$
(12)

The energy loss due to the formation of the new crack surface for the specimen shown in Fig. 1 can be represented in the following form:

$$\Delta \Pi = GB\Delta a.$$
(13)

The increment of the work of external force is

$$\Delta {\text{A}} = P\Delta \upsilon .$$
(14)

Substituting (12)–(14) into (11) and using the relation Δυ = PΔC + CΔP, we can obtain the following energy equation:

$$\Delta {\text{K}} + GB\Delta a - \frac{{P^{2} }}{2}\Delta C = 0.$$
(15)

Substituting increments by differentials, we can obtain a differential equation for kinetic energy

$$\frac{{d{\text{K}}}}{{{\text{d}}\omega }} = \frac{{P^{2} }}{2}\frac{dC}{d\omega } - GBb.$$
(16)

Equation (16) can be used for the analysis of crack behavior in different materials.

6 Crack growth at constant displacement

Equation (16) can be applied to different loading conditions. Let us consider the case when displacement remains constant after the load reaches the critical value for some initial crack length (Fig. 7).

Fig. 7
figure 7

Diagram of P ∼ υ in the case of constant displacement when the critical state is reached

Full size image

In this case, Eq. (16) can be represented in the following form:

$$\frac{{d{\text{K}}}}{{{\text{d}}\omega }} = \frac{{\upsilon_{c}^{2} }}{{2C^{2} }}\frac{dC}{d\omega } - GBb.$$
(17)

The integral of Eq. (17) corresponding to initial conditions ω = ω 0, K = 0, has a simple form

$$K = \frac{{\upsilon_{c}^{2} }}{2}\left[ {\frac{1}{{C(\omega_{0} )}} - \frac{1}{C(\omega )}} \right] - GBb(\omega - \omega_{0} ).$$
(18)

The critical value of displacement and the compliance are characterized by Eqs. (10) and (7), respectively. Substituting Eqs. (3), (7) and (10) into (18), we obtain the following equation for kinetic energy:

$${\bar{\text{K}}} = \frac{{{S \mathord{\left/ {\vphantom {S {2b}}} \right. \kern-0pt} {2b}} + 9(1 - \nu^{2} )F(\omega_{0} )}}{{9(1 - \nu^{2} )Y(\omega_{0} )\omega_{0} }}\left[ {1 - \frac{{{S \mathord{\left/ {\vphantom {S {2b}}} \right. \kern-0pt} {2b}} + 9(1 - \nu^{2} )F(\omega_{0} )}}{{{S \mathord{\left/ {\vphantom {S {2b}}} \right. \kern-0pt} {2b}} + 9(1 - \nu^{2} )F(\omega )}}} \right] - (\omega - \omega_{0} ).$$
(19)

where \({{{\bar{\text{K}}} = {\text{K}}E} \mathord{\left/ {\vphantom {{{\bar{\text{K}}} = {\text{K}}E} {BbK_{{I_{C} }}^{2} (1 - \nu^{2} )}}} \right. \kern-0pt} {BbK_{{I_{C} }}^{2} (1 - \nu^{2} )}}\) is non-dimensional kinetic energy.

The diagrams of variation of kinetic energy during crack growth corresponding to different initial crack lengths ω 0 are shown in Fig. 8.

Fig. 8
figure 8

Change of kinetic energy during crack growth at constant displacement

Full size image

The process of fracture can be characterized as follows (Fig. 7). After the critical conditions are reached at point A, the accelerating crack growth begins. The kinetic energy increases from zero and reaches its maximum value at point B and then decreases to zero when the crack stops at point M. Kinetic energy is represented by the area between the graph P c  ∼ υ c and straight line AB. At point M all the kinetic energy transforms into the energy required for the formation of a new crack surface. Thus the area of ADB equals to the area of MNB.

7 Analysis of kinetic energy at a constant load line displacement rate

On the basis of Eq. (16), it is possible to study the variation of kinetic energy in the case of unstable crack growth at an arbitrary change of displacement υ = υ(t). For this analysis, it is necessary to use the corresponding load-time dependence P = P(t) obtained during the test. Using Eq. (5) and the known variations of displacement and the load as the functions of time, it is possible to determine the dependence P = P(ω) in the process of crack growth. The kinetic energy variation is described by the following equation:

$$\overline{\text{K}} = \int\limits_{{\omega_{0} }}^{\omega } {\left( {\frac{{9S^{2} P^{2} (\omega )}}{{2B^{2} b^{3} K_{{I_{C} }}^{2} }}\frac{dF}{d\omega } - 1} \right)d\omega } .$$
(20)

Let us consider a particular case of the constant load line displacement rate equal to cross-head speedα. This condition was met in the performed experimental studies. If the load decreases with some overall rate β, as shown in Fig. 9, the change of compliance in the process of crack growth can be represented by the following equation: C = (υ c  + αt)/(P c  − βt). The initial value of compliance is C 0 = υ c /P c . Introducing non-dimensional time \(\bar{t} = {t \mathord{\left/ {\vphantom {t {t_{C} }}} \right. \kern-0pt} {t_{c} }}\), where t c  = υ c /α, one can obtain the following equation for compliance:

$$C = C_{0} \frac{{1 + \bar{t}}}{{1 - \beta_{1} \bar{t}}},$$
(21)

where β 1 = βC 0/α. Equation (21) can be solved for non-dimensional time \(\bar{t} = {{(C - C_{o} )} \mathord{\left/ {\vphantom {{(C - C_{o} )} {(\beta_{1} C + C_{o} )}}} \right. \kern-0pt} {(\beta_{1} C + C_{o} )}}\), and as a result we can obtain the relation between the load and the compliance during crack growth:

$$P = P_{c} \frac{{1 + \beta_{1} }}{{1 - \beta_{1} \frac{C}{{C_{0} }}}}.$$
(22)

For these loading conditions, we can also obtain the analytical formula for kinetic energy, as in the previous case of constant displacement. Equation (16) can be integrated with initial conditions ω = ω 0, C = C 0, K = 0, and for kinetic energy we obtain the following equation:

$${\text{K}} = \int\limits_{{C_{0} }}^{C} {\frac{{P^{2} }}{2}dC - \frac{{(1 - \nu^{2} )}}{E}} K_{{I_{C} }}^{2} Bb(\omega - \omega_{0} ).$$
(23)

Using Eqs. (22) and (23) one can obtain the following formula for kinetic energy:

$${\text{K}} = \frac{{(1 + \beta_{1} )\upsilon_{C}^{2} }}{{2\beta_{1} C_{0} }}\left( {1 - \frac{{1 + \beta_{1} }}{{1 + \beta_{1} \frac{C(\omega )}{{C_{0} }}}}} \right) - \frac{{(1 - \nu^{2} )}}{E}K_{{I_{C} }}^{2} Bb(\omega - \omega_{0} ).$$
(24)

The dependence of compliance on relative crack length is determined by Eq. (5), which can be used to obtain the corresponding formula for non-dimensional kinetic energy:

$$\overline{\text{K}} = \frac{{(1 + \beta_{1} )\upsilon_{C}^{2} E}}{{2\beta_{1} C_{0} Bb(1 - \nu^{2} )K_{{I_{C} }}^{2} }}\left( {1 - \frac{1}{{1 + \frac{{9\beta_{1} (1 - \nu^{2} )S^{2} }}{{2(1 + \beta_{1} )EBb^{2} C_{0} }}\left[ {F(\omega ) - F(\omega_{0} )} \right]}}} \right) - (\omega - \omega_{0} ).$$
(25)

From Eq. (21), the dependence of the relative crack length on time can be determined:

$$\bar{t} = \frac{{\frac{{9(1 - \nu^{2} )S^{2} }}{{2EBb^{2} C_{0} }}(F(\omega ) - F(\omega_{0} ))}}{{1 + \beta_{1} \left[ {1 + \frac{{9(1 - \nu^{2} )S^{2} }}{{2EBb^{2} C_{0} }}(F(\omega ) - F(\omega_{0} ))} \right]}}.$$
(26)

Using Eq. (22), one can obtain the relation between the load P and the relative crack length ω during crack growth:

$$P = P_{c} \frac{{1 + \beta_{1} }}{{1 + \beta_{1} \left[ {1 + \frac{{9(1 - \nu^{2} )S^{2} }}{{2EBb^{2} C_{0} }}(F(\omega ) - F(\omega_{0} ))} \right]}}.$$
(27)

The values of parameters of Eqs. (24)–(27), which obtained for tested specimens, are shown in Table 4. The diagrams of the load variation during the tests obtained for two particular specimens of MPG-6 with the initial crack lengths of ω 0 = 0.155 and ω 0 = 0.215, and the limit diagram of the dependence P C  ∼ υ C are shown in Fig. 9.

Fig. 9
figure 9

Load-time diagrams (left) and load–displacement diagrams (right) for different initial crack lengths

Full size image
Table 4 Test parameters in the case of unstable crack growth
Full size table

It can be seen that the dependence of the load on time in the falling parts of the diagrams are approximately linear with the parameters β 1 = 4.44 for ω 0 = 0.155 and β 1 = 5.05 for ω 0 = 0.215. Using these parameters and Eq. (25), the graphs of kinetic energy variation in the process of crack growth can be obtained (Fig. 10).

Fig. 10
figure 10

Change of kinetic energy during crack growth under a constant displacement rate

Full size image

Calculations were carried out up to ω ≈ 0, 8 because Eq. (2) for the stress intensity factor is valid in a limited range of relative crack lengths. In this case, the kinetic energy increases with ω and reaches its maximum value at ω ≈ 0, 8. Similar behavior was observed in the tests of specimens with short initial cracks under the conditions of a constant load line displacement rate (Fig. 9) and the correspondence between the results of experimental studies and theoretical analysis is quite satisfactory.

8 Conclusions

The elastic, strength and fracture toughness properties of structural graphite materials are investigated in this work. The theoretical analysis and the experimental studies of crack growth are carried out for the bending conditions. The stable crack growth is observed for the initial relative crack length ω 0 ≥ 0.27 and unstable, non-equilibrium, growth—for ω 0 < 0.27. Under a crack’s stable behavior, fracture toughness is determined during the process of crack growth, and the critical value of the stress intensity factor is approximately constant for such a heterogeneous material as graphite. The crack growth rate can also be determined during the test. Cases of unstable crack growth are analyzed for different loading conditions. It has been shown that in the cases of unstable crack growth under the conditions of quasi-static loading, the stored energy is spent not only on the formation of a new crack surface but on kinetic energy of a beam, too, and these parts of energy can be comparable. The same conclusion is referred to the tests on impact strength where noticeable part of energy is spent on kinetic energy of sample’s parts but not only on the formation of new fracture surface. The variation of kinetic energy can be described by corresponding equation that is obtained in a general form and can be used for arbitrary conditions of hard loading where cross-beam displacement is controlled. The results of this analysis can be equally applied not only to quasi-brittle materials, such as graphite, but to elastoplastic ones, too, in the cases when the requirements of linear fracture mechanics are satisfied.