Ritz method for slip flow in curved micro-ducts and application to the elliptic duct

Abstract

Slip flow is essential for micro-fluidics. Due to its difficulty, there are few reports on the slip flow in a curved duct. This paper introduces a new, highly efficient, semi-analytic Ritz method to treat slip flow in a general curved duct. The method is then applied to the curved elliptic duct which includes the important curved circular duct. Surface slip of a curved duct not only promotes the flow rate, but also shifts the maximum velocity towards the outer boundary and the minimum velocity towards the inner boundary.

1 Introduction

Slip flow has become prevalent in micro-fluidics which has numerous applications in MEMS, biotechnology, micro-assay, medical diagnosis, drug delivery etc. See e.g. Nguyen and Wereley [1]. There are many reports on slip flow in straight ducts, but curved ducts are necessary for mixing or redirecting the flow. Previous literature for slip flow in a curved duct include the analytic series solution for the curved rectangular duct of Wang [2], who also gave the solution for a curved channel. The stability of the flow was determined by Avramenko and Kuznetsov [3]. The slip flow in a curved circular tube was studied by Wang [4] using a small perturbation from the straight tube solution.

There is no information on slip flow through a curved ducts other than the above sources. In this paper we shall first develop a powerful Ritz method to to treat slip flow in curved ducts of arbitrary cross section. Then the method will be applied to the curved elliptic duct, which includes the important curved circular duct as a special case.

For rarefied gases, the basic partial slip condition is [1]

$$\Delta u\left| {_{wall} } \right. = \frac{2 - \sigma }{\sigma }\lambda_{f} \frac{\partial u}{{\partial n}}\left| {_{wall} } \right.$$

(1)

Here u is the tangential velocity, $\sigma \le 1$ is the accommodation coefficient which depends on the surface material and roughness, $\lambda_{f}$ is the mean free path and n is the unit normal. On the other hand, for liquid flow the boundary condition is

$$\Delta u\left| {_{wall} } \right. = L_{s} \frac{\partial u}{{\partial n}}\left| {_{wall} } \right.$$

(2)

where $L_{s}$ is the slip length, or the distance into the wall where the velocity is extrapolated to zero. The slip length depends on the amount and distribution of the low viscosity fluid trapped in the micro grooves of the wall.For both gas or liquid slip flows, the partial slip conditions may be described by the generic Navier’s condition. Normalize lengths by a characteristic length L, Eqs. (1, 2) can be written as

$$\Delta u\left| {_{wall} } \right. = \lambda \frac{\partial u}{{\partial n}}\left| {_{wall} } \right.$$

(3)

where $\lambda$ is the important non-dimensional slip factor, assumed to be constant for the range of our study.

$$\lambda = Kn\frac{{D_{h} }}{L}\frac{(2 - \sigma )}{\sigma }\,\,{\text{for}}\,{\text{gases}}$$

(4)

$$\lambda = \frac{{L_{s} }}{L}{\text{ for liquids}}$$

(5)

Here Kn is the Knudsen number $\lambda_{f} /D_{h}$, where $D_{h}$ is the hydraulic diameter. The no slip boundary condition is recovered when $\lambda = 0$. For rarefied gases, $\lambda$ is of the order of $10^{ - 3}$ to $10^{ - 1}$. For superhydrophobic microchannels, $\lambda$ could be as large as 10 [5].

For ducts of micron sizes, the Reynolds number is of the order of $10^{ - 3} - 10^{ - 5}$ and thus the nonlinear convection terms are negligible. There are two consequences of such low Reynolds number Stokes flow. Firstly, the entrance length is of the order of one diameter [6], and the velocity and pressure gradient in the curved tube are independent of axial distance. Secondly, the secondary flow due to centrifugal force is of the order of the Reynolds number, and thus negligible.

2 Formulation

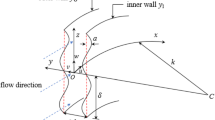
Consider fully developed flow in a long curved duct of constant cross section with a characteristic width of 2L. The curved centerline has a radius of cL. Normalize the longitudinal velocity by $GL^{2} /\mu$ where G is the pressure gradient along the centerline and $\mu$ is the viscosity of the fluid. The Stokes equation in cylindrical coordinates $(r,\,\theta ,\,z)$ reduces to

$$\frac{{\partial^{2} \upsilon }}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial \upsilon }{{\partial r}} - \frac{\upsilon }{{r^{2} }} + \frac{{\partial^{2} \upsilon }}{{\partial z^{2} }} = - \frac{c}{r}$$

(6)

where $\upsilon (r,z)$ is the azimuthal velocity in the $\theta$ direction, and r is the normalized radial distance from the symmetry axis shown in Fig. 1.

Note that for curved ducts Eq. (3) should be replaced by

$$\Delta \upsilon \left| {_{wall} + \lambda \tau_{n\theta } = 0} \right.$$

(7)

where $\tau_{n\theta }$ is the shear stress normalized by GL and $\vec{n}$ is the unit outward normal to the boundary. Let $n_{r} ,\,n_{z}$ be the direction cosines in the r, z directions respectively. Then

$$\frac{\partial \upsilon }{{\partial n}} = \vec{n} \cdot \nabla \upsilon = n_{r} \frac{\partial \upsilon }{{\partial r}} + n_{z} \frac{\partial \upsilon }{{\partial z}}$$

(8)

On the other hand, in cylindrical coordinates

$$\tau_{r\theta } = \frac{\partial \upsilon }{{\partial r}} - \frac{\upsilon }{r},\,\,\,\,\tau_{z\theta } = \frac{\partial \upsilon }{{\partial z}}$$

(9)

and using Eq. (8)

$$\tau_{n\theta } = n_{r} \tau_{r\theta } + n_{z} \tau_{rz} = \frac{\partial \upsilon }{{\partial n}} - \frac{{n_{r} }}{r}\upsilon$$

(10)

Thus if the boundary is stationary, the appropriate Navier slip boundary condition in cylindrical coordinates is

$$\upsilon + \lambda \left( {\frac{\partial \upsilon }{{\partial n}} - \frac{{n_{r} }}{r}\upsilon } \right) = 0$$

(11)

For given boundary described by $H(r,z) = 0$ the radial direction cosine is

$$n_{r} = \left[ {1 + \left( {\frac{\partial H/\partial z}{{\partial H/\partial r}}} \right)^{2} } \right]^{ - 1/2}$$

(12)

Equations (6, 11) are to be solved.

Fig. 1

The curved elliptic duct. The dash-dot line is the symmetry line of the curved duct. All lengths have been normalized by half lateral width of the duct cross section

3 The Ritz method

The Ritz method for Stokes no-slip flow in a curved duct was established by Wang [7]. The problem is much more involved for slip flow due to Navier’s boundary conditions. The derivation is as follows.

Theorem

Let $\varOmega$ be the cross sectional domain of the duct and P be its perimeter and $\lambda \ne 0$. Construct the functional

$$J = \iint {\left[ {r\left( {\frac{\partial \upsilon }{{\partial r}}} \right)^{2} + \frac{{\upsilon^{2} }}{r} + r\left( {\frac{\partial \upsilon }{{\partial z}}} \right)^{2} - 2c\upsilon } \right]}d\varOmega + \oint {\left( {\frac{r}{\lambda } - n_{r} } \right)\upsilon^{2} dP}$$

(13)

Then the extremum of J leads to Eqs. (6, 11) where there are no restrictions on $\upsilon$ inside $\varOmega$ and also on the boundary P.

Proof

Taking the variation of Eq. (13) we find [8]

$$\begin{array}{l} \delta J = \iint {2r\frac{\partial \upsilon }{{\partial r}}d(\delta \upsilon )}dz + \iint {\frac{2\upsilon }{r}\delta \upsilon drdz + \iint {2r\frac{\partial \upsilon }{{\partial z}}d(\delta \upsilon )dr}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\, - \iint {2c\delta \upsilon drdz + \oint {\left( {\frac{r}{\lambda } - n_{r} } \right)2\upsilon \delta \upsilon dP} } = 0 \hfill \\ \end{array}$$

(14)

Integration by parts give

$$\begin{array}{l} - 2\iint {\left[ {\frac{\partial }{\partial r}\left( {r\frac{\partial \upsilon }{{\partial r}}} \right) + \frac{\partial }{\partial z}\left( {r\frac{\partial \upsilon }{{\partial z}}} \right) - \frac{\upsilon }{r} + c} \right]}\delta \upsilon drdz \hfill \\ + 2\oint {\left[ {r\frac{\partial \upsilon }{{\partial n}} + \left( {\frac{r}{\lambda } - n_{r} } \right)\upsilon } \right]} \delta \upsilon dP = 0 \hfill \\ \end{array}$$

(15)

Now if $\upsilon$ is arbitrary inside $\varOmega$ and also on the boundary P, the brackets in Eq. (15) must be zero, which is exactly Eqs. (6) and (11).

Next we construct a Ritz method which is a semi-numerical method to minimize J. Let

$$\upsilon = \sum\limits_{i = 1}^{\infty } {a_{i} \varphi_{i} }$$

(16)

where $\{ \varphi_{i} \}$ is a set of Ritz functions which span the domain. Substitute Eq. (16) into (13). The necessary condition for extremum is

$$\frac{\partial J}{{\partial a_{i} }} = 0$$

(17)

After some work, algebraic equations are obtained

$$\sum\limits_{j = 1}^{N} {\left( {A_{ij} + \frac{{C_{ij} }}{\lambda } - D_{ij} } \right)c_{j} } = cB_{i} ,\,\,i = 1 \, {\rm to} \, N$$

(18)

where the series have been truncated to N terms and

$$\begin{array}{l} A_{ij} = \iint {\left[ {r\left( {\frac{{\partial \varphi_{i} }}{\partial r}\frac{{\partial \varphi_{j} }}{\partial r} + \frac{{\partial \varphi_{i} }}{\partial z}\frac{{\partial \varphi_{j} }}{\partial z}} \right) + \frac{1}{r}\varphi_{i} \varphi_{j} } \right]}drdz,\,\,\,\,\,B_{i} = \iint {\varphi_{i} drdz} \hfill \\ C_{ij} = \oint {r\varphi_{i} \varphi_{j} dP,\,\,\,\,\,D_{ij} = \oint {n_{r} \varphi_{i} \varphi_{j} dP} } \hfill \\ \end{array}$$

(19)

Equation (18) is inverted for the N unknowns $c_{j}$. Let the area of the cross section be A. The average velocity is the sum

$$V = \frac{1}{A}\iint {\upsilon drdz} = \frac{1}{A}\sum\limits_{1}^{N} {c_{i} B_{i} }$$

(20)

The average velocity is used to quantify the flow, since the Poiseuille number or friction factor- Reynolds number product are inappropriate indices for curved ducts.

4 The curved elliptic duct

The Ritz method in the previous section can be applied to curved ducts of any constant cross section. To illustrate, we apply the method to the curved elliptic duct. Let

$$r = c + x$$

(21)

and the boundary be described by

$$H(x,z) = 1 - x^{2} - (z/b)^{2} = 0$$

(22)

The length of the major axis is 2 and that of the minor axis is 2b, or b is the aspect ratio. The area is $\pi b$ and

$$n_{r} = \frac{{\text{sgn} (x)}}{{\sqrt {1 + (\partial H/\partial z)^{2} /(\partial H/\partial x)^{2} } }} = \frac{{\text{sgn} (x)}}{{\sqrt {1 + (z/x)^{2} /b^{4} } }}$$

(23)

Due to symmetry in z, the Ritz functions are chosen to be

$$\{ \varphi_{i} \} = \{ 1,x,x^{2} ,z^{2} ,x^{3} ,xz^{2} ,x^{4} ,x^{2} z^{2} ,z^{4} ,x^{5} ,x^{3} z^{2} ,xz^{4} \cdots \}$$

(24)

The number of terms N retained can be 1, 2, 4, 6, 9, 12, etc., including the highest homogeneous powers. For a given b and c, Eq. (19) are integrated and Eq. (18) solved. Table 1 shows some typical convergence rates. We see that N = 12 is adequate for a four- digit accuracy.

Table 1 Convergence for the average velocity V

Having established the convergence of the method, we compare our results with existing literature. First consider the slip flow in a straight elliptic duct. Table 2 shows a comparison with Wang [9] who used eigenfunction expansion and collocation. The difference is <0.1 %. Other sources include Spiga and Vocale [10] who used finite elements, and Duan and Muzychka [11] found an exact series solution in elliptic coordinates, but only three analytic terms are obtained. Table 3 shows a comparison of the average velocity. The results of Refs [10, 11]., which are in terms of Knudsen number and accommodation coefficient, are condensed into a single slip factor through Eq. (4). We used c = 1000 to approach the straight duct.

Table 2 Comparison of the average velocity for slip flow in a 1:2 (b = 0.5) straight elliptic duct

Table 3 Comparison of the average velocity for slip flow in a 1:2 straight elliptic duct

Another comparison is the slip flow in a curved circular duct, which was studied by Wang [4] by perturbing the flow through a circular tube about the small curvature. His analytic result, for zero Reynolds number, is

$$V = \frac{1}{8}\left[ {1 + 4\lambda + \frac{1}{{c^{2} }}\left( {\frac{{1 + 7\lambda - 288\lambda^{2} }}{48(1 + \lambda )}} \right) + O(c^{ - 4} )} \right]$$

(25)

Table 4 shows a comparison. The perturbation solution Eq. (25) deviates for low c (high centerline curvature) or large slip.

Table 4 Comparison of slip flow in a curved circular duct (b = 1)

5 Results and discussions

Figure 2 shows the constant velocity lines of a curved circular duct. We see that at low slip, the location of the maximum velocity is off centered, closer to the symmetry line of the curved duct (the dash-dot line of Fig. 1). The is also true for no-slip flow in a curved rectangular duct [7]. At high slip, the maximum velocity moved away from the symmetry line. The phenomenon persists for curved elliptic ducts. Figure 3 is a 1:2 elliptic duct with major axis perpendicular to the symmetry line. Figure 4 shows the elliptic duct with major axis parallel to the symmetry line.

Fig. 2

Constant velocity lines for a curved circular duct, b = 1, c = 2. a $\lambda =$ 0.001 from inside, $\upsilon$ = 0.25, 0.225, 0.2, 0.175, 0.15, 0.125, 0.1, 0.075, 0.05, 0.025. b $\lambda =$ 2 from inside, $\upsilon$ = 1.039, 1, 0.95, 0.9, 0.85, 0.8, 0.75, 0.7, 0.65. The symmetry line (dash-dot line in Fig. 1) is on the left

Fig. 3

Constant velocity lines for a curved elliptic duct, b = 0.5, c = 2. a $\lambda =$ 0.01 from inside, $\upsilon$ = 0.1, 0.08, 0.06, 0.04, 0.02. b $\lambda =$ 2 from inside, $\upsilon$ = 0.65, 0.625, 0.6, 0.575, 0.55, 0.525, 0.5, 0.475, 0.45, 0.425

Fig. 4

Constant velocity lines for a curved elliptic duct, b = 2, c = 4. a $\lambda =$ 0.01 from inside, $\upsilon$ = 0.4, 0.35, 0.3, 0.25, 0.2, 0.15, 0.1, 0.05. b $\lambda =$ 2 from inside, $\upsilon$ = 1.6, 1.5, 1.4, 1.3, 1.2

Tables 5, 6, 7 and 8 give our results for slip flow in curved elliptic ducts. Aside from average velocity, we also tabulated the maximum velocity and its location (negative means closer to the symmetry line than the centroid) and the minimum velocity, which is located on the surface either closest or furthest from the symmetry line.

Table 5 Results for slip flow in curved elliptic ducts, c = 2

Table 6 Results for slip flow in curved elliptic ducts, c = 3

Table 7 Results for slip flow in curved elliptic ducts, c = 5

Table 8 Results for slip flow in curved elliptic ducts, c = 10

Form Tables 5, 6, 7 and 8 we can conclude the following. If slip (represented by the slip factor$\lambda$) and/or the aspect ratio b increase, the average velocity, together with the maximum and minimum velocities, all increase. The interaction of the radius curvature of the duct centerline c and boundary slip is interesting. The average velocity decreases with increased c for small $\lambda$ but the opposite is true for large $\lambda$. This means, for the same centerline length, cross sectional geometry and pressure difference, the flow rate is larger for a straight duct than a curved duct if the slip factor is large. But the flow rate is larger for a curved duct than a straight duct if the slip factor is small. Also, the location of the maximum velocity moves towards the far boundary when slip is increased. The velocity and the shear stress on the boundary are not constant for slip flow in a curved duct, as seen from Figs. 2, 3 and 4.

6 Conclusions

Despite the importance of slip flow in curved ducts, research on this topic is scarce. This paper presents a powerful semi-analytic Ritz method to treat slip flow in arbitrary curved ducts. The method is versatile, accurate and efficient as evidenced in Tables 2, 3 and 4.

The method is applied to the slip flow in a curved elliptic duct. Our results would be very useful in the design of such curved micro-ducts. Tables are given (instead of graphs) and level lines are shown (instead of 3D plots) so that our results can be utilized in practice and also facilitate comparison with future reports on this important research