Finite element simulation of coating-induced heat transfer: application to thermal spraying processes

Abstract

Thermal spraying is a widely applied coating technique. The optimisation of the thermal spraying process with respect to temperature or temperature induced residual stress states requires a numerical framework for the simulation of the coating itself as well as of the quenching procedure after the application of additional material. This work presents a finite element framework for the simulation of mass deposition due to coating by means of thermal spraying combined with the simulation of nonlinear heat transfer of a rigid heat conductor. The approach of handling the dynamic problem size is highlighted with focus on the thermodynamical consistency of the derived model. With the framework implemented, numerical examples are employed and material parameters are fitted to experimental data of steel as well as of tungsten-carbide–cobalt-coating.

1 Introduction

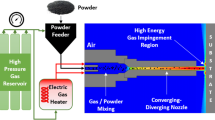
Thermal spraying is, amongst other techniques, widely used in order to produce wear-resistant surfaces for metal sheet forming tools. Thereby, hard materials are thermally fused, e.g., by a flame or an electric arc and accelerated to the surface of a substrate where a hard material coating is deposited. An overview on different thermal spraying processes and their application in the automobile industry is given in [10]. Regarding to wear-resistance, tungsten carbide (WC) and cobalt (Co) coatings are preferable compared to other coating systems consisting, e.g., of chrome and nickel [22]. Typically, for the spraying of WC-Co coatings, the High Velocity Oxygen Fuel (HVOF) thermal spraying process is used. The HVOF thermal spraying process is depicted in Fig. 1 and further details about the process can be found in, e.g., [12, 24].

Fig. 1

HVOF spraying process. The photograph is kindly provided by LWT, TU Dortmund

Naturally, the HVOF thermal spraying process induces thermal energy into the usually heterogeneous coating as well as the substrate. Since the coating has in general different properties than the substrate, the coating process represents an advanced, transient thermo-mechanical problem. Thereby, residual stress states arise during the process and during the quenching procedure thereafter [16, 17]. The quality of the produced coatings decreases with increasing residual tensile stresses which may have a significant influence, particularly on complex workpiece geometries with, e.g., sharp radii and high curvatures. Figure 2 illustrates the delamination of a WC-Co coating from two differently shaped workpieces due to thermal spraying induced residual stresses. More details on delamination due to thermally induced residual stresses can be found in, e.g., [4]. For the prediction of the cooling procedure and the resulting residual stress state during and after the quenching, a simulation tool is required that covers on the one hand the simulation of the material deposition and on the other hand the simulation of the quenching.

Fig. 2

Delamination of a WC-Co coating from a a workpiece with a sharp radius, b a plain surface with a ridge. The samples are kindly provided by LWT, TU Dortmund

Towards a thermo-mechanical coupled simulation tool, a finite element based software tool for the simulation of heat transfer during thermal spraying was recently proposed [2]. This work further extends the results established in [2]. Beside the thermo-mechanical coupling, the mass deposition of hot coating material was not previously covered within the simulation. When temperature is considered to be a degree of freedom in a finite element approach, adding elements to an existing system with a different temperature formally leads to a temperature jump. Two promising methods for the thermodynamically consistent simulation of mass deposition by means of the finite element method were proposed in the literature. One option is the use of discontinuous Galerkin methods. Finite element implementations of discontinuous Galerkin methods are used for many different applications such as gas dynamics [1], the solution of Hamilton-Jacobi equations [13] or solid mechanics [7]. In the framework of continuous Galerkin methods, another possibility is the use of interface elements which are well established for thermo-mechanical analysis [8, 9, 23].

This article presents a novel approach for thermodynamical consistent modeling of mass deposition for a rigid heat conductor in the framework of continuous Galerkin methods. The analysis is restricted to the temperature and newly added mass has to satisfy a continuous temperature distribution. We encounter this problem by the introduction of internal heat sources which shall ensure conservation of energy. The following section describes the underlying equations of continuum thermodynamics which result in the finite element discretisation described in Sect. 3. Section 4 presents academic examples in order to show the capabilities of the developed framework. The material parameters are fitted to experimental data.

2 Continuum thermodynamics framework

From a continuum thermodynamics point of view, the underlying problem represents an open system where mass is deployed on a surface of a body ${\mathscr {B}}$. Thus, the configuration of the considered body may change with time t. Since temperature is the only physical field considered within the presented framework, we do not distinguish between reference placements ${{ {\varvec{ X }}}}$ and current placements ${{ {\varvec{ x }}}}$ in the context of continuum mechanics. Specifically speaking, we consider a rigid heat conductor with a time dependent configuration that may expand by mass application.

A global physical quantity g at time t is determined by

$$\begin{aligned} g(t) = \int _{{\mathscr {B}}} \gamma ({{ {\varvec{ x }}}}, t) \, {\text {d}}v \; , \end{aligned}$$

(1)

where $\gamma$ is the density of the respective quantity at ${{ {\varvec{ x }}}}$ and t. The rate of g can be expressed as

$$\begin{aligned} \dfrac{{\text {d}}g}{{\text {d}}t} = \dfrac{{\text {d}}}{{\text {d}}t} \int _{{\mathscr {B}}} \gamma ({{ {\varvec{ x }}}}, t) \, {\text {d}}v= & \int _{{\mathscr {B}}} [\, \pi ({{ {\varvec{ x }}}}, t)+ \xi ({{ {\varvec{ x }}}}, t) \, ] \, {\text {d}}v \nonumber \\&- \int _{\partial {\mathscr {B}}} {{ {\varvec{ \phi }}}}({{ {\varvec{ x }}}}, t) \cdot {{ {\varvec{ n }}}} \, {\text {d}}a \; . \end{aligned}$$

(2)

Here, $\pi$ denotes the production and $\xi$ represents the supply of g within the body ${\mathscr {B}}$, whereas ${{ {\varvec{ \phi }}}}$ represents the flux of g via the surface $\partial {\mathscr {B}}$ of the body with surface normal ${{ {\varvec{ n }}}}$ [15]. Next, consider that the quantity g has a jump through a singular surface ${\mathfrak {s}}$ which divides the body ${\mathscr {B}}$ into ${\mathscr {B}}^+$ and ${\mathscr {B}}^-$ as illustrated in Fig. 3. Such a jump shall be denoted as $[\![g ]\!]:= g^+ - g^- \; .$ With this at hand, the change of g in time modifies (2) to

$$\begin{aligned} \dfrac{{\text {d}}g}{{\text {d}}t}= & \dfrac{{\text {d}}}{{\text {d}}t} \int _{{\mathscr {B}}^+} \gamma ({{ {\varvec{ x }}}}, t) \, {\text {d}}v + \dfrac{{\text {d}}}{{\text {d}}t} \int _{{\mathscr {B}}^-} \gamma ({{ {\varvec{ x }}}}, t) \, {\text {d}}v \nonumber \\= & \int _{{\mathscr {B}}^+} \dfrac{\partial \gamma }{\partial t} \, {\text {d}}v - \int _{{\mathfrak {s}}} \gamma ^+ {{{ {\varvec{ w }}}}}^+ \cdot {{ {\varvec{ n }}}}_{\mathfrak {s}} \, {\text {d}}a \nonumber \\&+ \int _{{\mathscr {B}}^-} \dfrac{\partial \gamma }{\partial t} \, {\text {d}}v + \int _{{\mathfrak {s}}} \gamma ^- {{{ {\varvec{ w }}}}}^- \cdot {{ {\varvec{ n }}}}_{\mathfrak {s}} \, {\text {d}}a \nonumber \\= & \int _{{\mathscr {B}}} \dfrac{\partial \gamma }{\partial t} \, {\text {d}}v - \int _{{\mathfrak {s}}} [\![\, \gamma \;{{ {\varvec{ w }}}} \cdot {{ {\varvec{ n }}}}_{\mathfrak {s}} \, ]\!]\, {\text {d}}a \; . \end{aligned}$$

(3)

Within the above equation ${{ {\varvec{ w }}}}$ denotes the interface velocity and ${{ {\varvec{ n }}}}_{\mathfrak {s}}$ represents the singular surface normal which points from the $^-$-side to the $^+$-side. For the computation of the flux of a physical quantity g, the surface $\partial {\mathscr {B}}$ is divided into positive $\partial {\mathscr {B}}^+ \cap {\mathfrak {s}}$ and negative $\partial {\mathscr {B}}^- \cap {\mathfrak {s}}$ parts. Application of the divergence theorem renders the flux relation

$$\begin{aligned} \int _{\partial {\mathscr {B}}} {{ {\varvec{ \phi }}}} \cdot {{ {\varvec{ n }}}} \, {\text {d}}a= & \int _{{\mathscr {B}}^+} \mathop {\hbox {div}}\nolimits {{ {\varvec{ \phi }}}} \, {\text {d}}v + \int _{{\mathscr {B}}^-} \mathop {\hbox {div}}\nolimits {{ {\varvec{ \phi }}}} \, {\text {d}}v \nonumber \\&+ \int _{{\mathfrak {s}}} [\![{{ {\varvec{ \phi }}}} \cdot {{ {\varvec{ n }}}} ]\!]\, {\text {d}}a \; , \end{aligned}$$

(4)

see [15]. In the case of vanishing production and supply terms within the singular surface, the general balance equation results in

$$\begin{aligned}&\int _{{\mathscr {B}}^+} \left[ \, \dfrac{\partial \gamma }{\partial t} + \mathop {\hbox {div}}\nolimits {{ {\varvec{ \phi }}}} - \pi - \xi \, \right] \, {\text {d}}v \nonumber \\&\quad \quad + \int _{{\mathscr {B}}^-} \left[ \, \dfrac{\partial \gamma }{\partial t} + \mathop {\hbox {div}}\nolimits {{ {\varvec{ \phi }}}} - \pi - \xi \, \right] \, {\text {d}}v \nonumber \\&\quad = \int _{\mathfrak {s}} [\![\, \gamma \; {{ {\varvec{ w }}}}_{\mathfrak {s}} \cdot {{{ {\varvec{ n }}}}}_{\mathfrak {s}} - {{ {\varvec{ \phi }}}} \cdot {{ {\varvec{ n }}}}_{\mathfrak {s}} \, ]\!]\, {\text {d}}a \; . \end{aligned}$$

(5)

Consider a part of the body ${\mathscr {B}}$ not containing the singular surface. Then the right hand side of the above equation vanishes and the equation reduces for each part, i.e. ${\mathscr {B}}^+$ and ${\mathscr {B}}^-$, to the local form

$$\begin{aligned} \dfrac{\partial \gamma }{\partial t} + \mathop {\hbox {div}}\nolimits {{ {\varvec{ \phi }}}} - \pi - \xi = 0 \; . \end{aligned}$$

(6)

On the singular surface, the left hand side of Eq. (5) vanishes and yields the local form

$$[\![\, \gamma \,{{ {\varvec{ w }}}}_{\mathfrak {s}} \, - {{ {\varvec{ \phi }}}} \, ]\!]\cdot {{{ {\varvec{ n }}}}}_{\mathfrak {s}} = 0\;. $$

(7)

This general representation of balance equation is next applied to different quantities of interest, such as mass and energy.

Fig. 3

Body ${\mathscr {B}}$ divided into ${\mathscr {B}}^+$ and ${\mathscr {B}}^-$ by the singular surface ${\mathfrak {s}}$

In view of the balance of mass, we use Eqs. (6) and (7) with $\gamma = \rho$, whereby $\rho$ represents the mass density. Moreover, we assume $\pi = \xi = 0$ and ${{ {\varvec{ \phi }}}} = {\mathbf {0}}$, so that the above mentioned equations related to balance of mass read

$$\begin{aligned}&\dfrac{\partial \rho }{\partial t} = 0 \; , \end{aligned}$$

(8)

$$\begin{aligned}&[\![\, \rho \,{{ {\varvec{ w }}}}_{\mathfrak {s}} \, ]\!]\cdot {{ {\varvec{ n }}}}_{\mathfrak {s}} = 0 \; . \end{aligned}$$

(9)

Concerning the energy balance, Eqs. (6) and (7) include the internal energy $\gamma = e$, the production of energy $\xi = q$ and the heat flux ${{ {\varvec{ \phi }}}} = {{ {\varvec{ q }}}}$. Note, that no energy production in form of radiation or chemical reactions is considered within the volume. Besides that, the kinetic part of the energy as well as surface tractions are neglected. Inserting these relations into the general representation of balance equations yields the local balance of energy as

$$\begin{aligned}&\rho \, \dfrac{\partial e}{\partial t} + \mathop {\hbox {div}}\nolimits {{ {\varvec{ q }}}} = q \; , \end{aligned}$$

(10)

$$\begin{aligned}&[\![\, \rho \,e\,{{ {\varvec{ w }}}}_{\mathfrak {s}} \, - {{ {\varvec{ q }}}} \, ]\!]\cdot {{{ {\varvec{ n }}}}}_{\mathfrak {s}} = 0 \; . \end{aligned}$$

(11)

Finally, the balance of entropy has to be taken into account. Application of Eqs. (6) and (7) now include the entropy $\gamma = \eta$, the production of entropy $\pi = {\mathscr {D}} \ge 0$, the entropy supply $\xi = q / \theta$ as well as the entropy flux ${{ {\varvec{ \phi }}}} = {{ {\varvec{ q }}}} / \theta$. Here, it is assumed that the entropy supply is proportional to the production of energy q and the entropy flux is proportional to the heat flux ${{ {\varvec{ q }}}}$ which is in line with Coleman and Noll [5]. For an outline about a different choice of the entropy flux the interested reader is referred to the text book of Müller [20], and the text book of Liu [19], as well as the references cited therein. In the present framework, the local form of entropy balance and entropy jump then read

$$\begin{aligned}&\rho \, \dfrac{\partial \eta }{\partial t} \, + \mathop {\hbox {div}}\nolimits \left( \dfrac{{{ {\varvec{ q }}}}}{\theta } \right) - q/\theta = {\mathscr {D}} \ge 0 \;, \end{aligned}$$

(12)

$$\begin{aligned}&[\![\, \rho \, \eta \, {{ {\varvec{ w }}}}_{\mathfrak {s}} - \dfrac{{{ {\varvec{ q }}}}}{\theta } \, ]\!]\cdot {{{ {\varvec{ n }}}}}_{\mathfrak {s}} = -{\mathfrak {p}}_{\mathfrak {s}} \le 0 \;. \end{aligned}$$

(13)

In the special case of a time depended configuration ${{ {\varvec{ x }}}} (t)$ of a rigid heat conductor, the interface velocities ${{ {\varvec{ w }}}}_{\mathfrak {s}}^+ = {{{ {\varvec{ w }}}}}_{\mathfrak {s}}^- = {{ {\varvec{ w }}}}_{\mathfrak {s}} = {\mathbf {0}}$ vanish such that the jump condition (9) is trivially fulfilled.

The balance of mass (8) ensures the mass to be constant for a given configuration. The entropy inequality (12) represents the second law of thermodynamics in terms of the Clausius−Duhem inequality. Carrying out the procedure outlined in [19], the Clausius–Duhem inequality reduces to

$$\begin{aligned} {\mathscr {D}}_{{\text {therm}}} = - \dfrac{{{ {\varvec{ q }}}} \cdot \mathop {\nabla _{\!\! {\varvec{ x }}}}\nolimits \theta }{\theta } \ge 0 \; . \end{aligned}$$

(14)

The above equation is known as the Fourier’s inequality which is fulfilled by Fourier’s law

$$\begin{aligned} {{ {\varvec{ q }}}} = - {{ {\varvec{ \kappa }}}}(\theta ) \cdot \mathop {\nabla _{\!\! {\varvec{ x }}}}\nolimits \theta \; , \end{aligned}$$

(15)

where ${{ {\varvec{ \kappa }}}}(\theta )$ is the temperature dependent positive semi-definite thermal conductivity tensor [19]. The energy balance (11) can be formulated in form of the temperature field equation

$$\begin{aligned} \rho \, c(\theta ) \, \dfrac{\partial \theta }{\partial t} + \mathop {\hbox {div}}\nolimits \left( - {{ {\varvec{ \kappa }}}}(\theta ) \cdot \mathop {\nabla _{\!\! {\varvec{ x }}}}\nolimits \theta \right) = q \; , \end{aligned}$$

(16)

where $c(\theta ) = \partial e / \partial \theta \ge 0$ is the temperature dependent heat capacity and Eq. (15) is inserted.

Solutions of Eq. (16) are automatically thermodynamical consistent as long as the restrictions for $c(\theta )$ and ${{ {\varvec{ \kappa }}}}(\theta )$ are satisfied. The considered initial boundary value problem requires the definition of an initial state of the body ${\mathscr {B}}$ and the definition of proper boundary conditions on $\partial {\mathscr {B}}$. Throughout this work, the only boundary conditions to be applied are adiabatic or Robin type boundary conditions, i.e.

$$\begin{aligned} - \, {{ {\varvec{ q }}}} \cdot {{ {\varvec{ n }}}}= & \,0 \quad {\text {on}} \quad \partial {\mathscr {B}}\;, \nonumber \\ - \, {{ {\varvec{ q }}}} \cdot {{ {\varvec{ n }}}}= &\, \bar{q}^{{{\text {R}}}}(\theta ) \quad {\text {on}} \quad \partial {\mathscr {B}} =\partial {\mathscr {B}}^{{{\text {R}}}} \; , \end{aligned}$$

(17)

which concern the heat flux ${{ {\varvec{ q }}}}$ on $\partial {\mathscr {B}} = \partial {\mathscr {B}}^{{{\text {R}}}}$.

3 Finite element implementation

In order to solve the balance of energy by means of the finite element method, the strong form given by Eq. (16) must be reformulated in weak form. Therefore, the energy balance is written in residual form, multiplied with the virtual temperature $\delta \theta$ as a test function and integrated over the volume of the body ${\mathscr {B}}$, i.e.

$$\begin{aligned} 0= & \int _{{\mathscr {B}}} \delta \theta \, \Big [ \rho \, c(\theta ) \, \dfrac{\partial \theta }{\partial t} \nonumber \\&+ \mathop {\hbox {div}}\nolimits \left( - {{ {\varvec{ \kappa }}}}(\theta ) \cdot \mathop {\nabla _{\!\! {\varvec{ x }}}}\nolimits \theta \right) - q \Big ]\, {\text {d}}v \;. \end{aligned}$$

(18)

The application of the divergence theorem and exploiting Eqs. (15) and (17) lead to

$$\begin{aligned} 0= & \int _{{\mathscr {B}}} \delta \theta \,\rho \, c(\theta ) \, \dfrac{\partial \theta }{\partial t}\, {\text {d}}v + \int _{\partial {\mathscr {B}}^{\text {R}}} - \, \delta \theta \, \bar{q}^{\text {R}}(\theta )\, {\text {d}}a \nonumber \\&- \int _{{\mathscr {B}}} - \mathop {\nabla _{\!\! {\varvec{ x }}}}\nolimits (\delta \theta ) \cdot {{ {\varvec{ \kappa }}}}(\theta ) \cdot \mathop {\nabla _{\!\! {\varvec{ x }}}}\nolimits \theta \, {\text {d}}v - \int _{{\mathscr {B}}} \delta \theta \, q \,{\text {d}}v \; . \end{aligned}$$

(19)

The different terms in the above equation can be interpreted as dynamic, volume, internal and surface contributions,

$$\begin{aligned} \text{w}_{\text {dyn}} & = \int _{{\mathscr {B}}} \delta \theta \,\rho \, c(\theta ) \, \dfrac{\partial \theta }{\partial t}\, {\text {d}}v \; ,\nonumber \\ \text {w}_{\text {vol}}= & \int _{{\mathscr {B}}} \delta \theta \, q \,{\text {d}}v \; ,\nonumber \\ \text {w}_{\text {int}}= & \int _{{\mathscr {B}}} - \mathop {\nabla _{\!\! {\varvec{ x }}}}\nolimits (\delta \theta ) \cdot {{ {\varvec{ \kappa }}}}(\theta ) \cdot \mathop {\nabla _{\!\! {\varvec{ x }}}}\nolimits \theta \, {\text {d}}v \; ,\nonumber \\ \text {w}_{\text {sur}}= & \int _{\partial {\mathscr {B}}^{\text {R}}} - \, \delta \theta \, \bar{q}^{\text {R}}(\theta )\, {\text {d}}a \; , \end{aligned}$$

(20)

such that Eq. (19) can be rewritten as

$$\begin{aligned} 0 = \text {w}_{\text {dyn}} - \text {w}_{\text {vol}} - \text {w}_{\text {int}} + \text {w}_{\text {sur}} \; . \end{aligned}$$

(21)

In this form, the energy balance is basically suitable for the solution by means of the finite element method. Since Robin boundary conditions represent a kind of temperature dependent loads, not only the considered body ${\mathscr {B}}$ but also the Robin boundary $\partial {\mathscr {B}}^{\text {R}}$ must be discretised, see e.g. [18] or [3] with application to deformation dependent loads such as pressure. Therefore, a finite number of $n_{el}^{{\mathscr {B}}}$ volume elements ${\mathscr {B}}_{\mathscr {B}}^e$ as well as a finite number of $n_{el}^{\partial {\mathscr {B}}^{{\text {R}}}}$ Robin boundary elements ${\mathscr {B}}_{\partial {\mathscr {B}}^{{\text {R}}}}^e$,

$$\begin{aligned} {\mathscr {B}} \approx {\mathscr {B}}^h= & \bigcup \limits _{e = 1}^{n_{el}^{{\mathscr {B}}}} {\mathscr {B}}_{{\mathscr {B}}}^{e} \;, \nonumber \\ \partial {\mathscr {B}}^{{{\text {R}}}} \approx \partial {\mathscr {B}}^{{{\text {R}}}\,h}= & \bigcup \limits _{e = 1}^{n_{el}^{\partial {\mathscr {B}}^{\text {R}}}} {\mathscr {B}}_{\partial {\mathscr {B}}^{\text {R}}}^{e} \;, \end{aligned}$$

(22)

approximate the body ${\mathscr {B}}$ and the Robin boundary $\partial {\mathscr {B}}^{{{\text {R}}}}$. Equation (22) can be rewritten as the sum over all element integrals

$$\begin{aligned} {\text {w}} \approx {\text {w}}^h = \sum \limits _{e = 1}^{n_{el}^{\mathscr {B}}} \left[ \, {\text {w}}_{\text {dyn}}^e - {\text {w}}_{\text {vol}}^e - {\text {w}}_{\text {int}}^e \, \right] + \sum \limits _{e = 1}^{n_{el}^{\partial {\mathscr {B}}^{\text {R}}}} \left[ \, {\text {w}}_{\text {sur}}^e \, \right] \; . \end{aligned}$$

(23)

By application of isoparametric finite elements, the spatial discretisation of the node positions ${{{ {\varvec{ x }}}}}^h \approx {{{ {\varvec{ x }}}}}$ as well as the dicretisation of the temperature $\theta ^h \approx \theta$ and the virtual temperature $\delta \theta ^h \approx \delta \theta$ is carried out by the same set of shape functions $N_{{ {\varvec{ x }}},\,{\mathscr {B}}}^{i}$ respectively $N_{{ {\varvec{ x }}},\,\partial {\mathscr {B}}^{\text {R}}}^{j}$ for $i = 1,...,n_{en}^{{\mathscr {B}}}$ volume element nodes and $j = 1,...,n_{en}^{\partial {\mathscr {B}}^{\text {R}}}$ boundary element nodes, i.e.

$$\begin{aligned} {{{ {\varvec{ x }}}}}^h_{{\mathscr {B}}}= & \displaystyle \bigcup \limits _{i = 1}^{n_{en}^{{\mathscr {B}}}} N_{{{ {\varvec{ x }}}},\,{\mathscr {B}}}^{i}\, {{ {\varvec{ x }}}}_i\;, \quad {{{ {\varvec{ x }}}}}^h_{\partial {\mathscr {B}}^{\text {R}}} = \displaystyle \bigcup \limits _{j = 1}^{n_{en}^{\partial {\mathscr {B}}^{\text {R}}}} N_{{ {\varvec{ x }}},\,\partial {\mathscr {B}}^{\text {R}}}^{j}\, {{{ {\varvec{ x }}}}}_j \;, \nonumber \\ {\theta }^h_{{\mathscr {B}}}= & \displaystyle \bigcup \limits _{i = 1}^{n_{en}^{{\mathscr {B}}}} N_{{{ {\varvec{ x }}}},\,{\mathscr {B}}}^{i}\, {\theta }_i\;, \quad {\theta }^h_{\partial {\mathscr {B}}^{\text {R}}} = \displaystyle \bigcup \limits _{j = 1}^{n_{en}^{\partial {\mathscr {B}}^{\text {R}}}} N_{{ {\varvec{ x }}},\,\partial {\mathscr {B}}^{\text {R}}}^{j}\, {\theta }_j \;, \nonumber \\ {\delta \theta }^h_{{\mathscr {B}}}= & \displaystyle \bigcup \limits _{i = 1}^{n_{en}^{{\mathscr {B}}}} N_{{{ {\varvec{ x }}}},\,{\mathscr {B}}}^{i}\, {\delta \theta }_i\;, \quad {\delta \theta }^h_{\partial {\mathscr {B}}^{\text {R}}} = \displaystyle \bigcup \limits _{j = 1}^{n_{en}^{\partial {\mathscr {B}}^{\text {R}}}} N_{{ {\varvec{ x }}},\,\partial {\mathscr {B}}^{\text {R}}}^{j}\, {\delta \theta }_j\;. \end{aligned}$$

(24)

Accordingly, the approximations of the gradients $\mathop {\nabla _{\!\! {\varvec{ x }}}}\nolimits {{{ {\varvec{ x }}}}} \approx \mathop {\nabla _{\!\! {\varvec{ x }}}}\nolimits {{{ {\varvec{ x }}}}}^h$, $\mathop {\nabla _{\!\! {\varvec{ x }}}}\nolimits {\theta } \approx \mathop {\nabla _{\!\! {\varvec{ x }}}}\nolimits {\theta }^h$ and $\mathop {\nabla _{\!\! {\varvec{ x }}}}\nolimits \delta \theta \approx \mathop {\nabla _{\!\! {\varvec{ x }}}}\nolimits {\delta \theta }^h$ are discretised.

The last level of discretisation of the problem is the time discretisation of Eq. (20)$_1$. The current state of the implementation of the presented framework makes use of the Backward Euler time integration scheme which reads

$$\begin{aligned} \dot{\theta } = \dfrac{\theta _{n+1} - \theta _{n}}{\Delta t} \end{aligned}$$

(25)

for the temperature with $\Delta t = t_{n+1} - t_n > 0$. The system of nonlinear equations that is to be solved at each discrete time step finally reads

(26)

In the above relation $\mathbf{w}^{h\Delta t}$ is an algebraic vector which depends on the nodal temperatures ${{ {\varvec{ \theta }}}}_{\,n+1}$ and ${{ {\varvec{ \theta }}}}_{\,n}$. The dimension of these vectors is $[\,n_{np}\times 1\,]$ where $n_{np}$ is the number of the (current) global node points. The symbol in Eq. (26) represents the assembly operator over all $e = 1,...,n_{el}^{\partial {\mathscr {B}}}$ volume elements and all $e = 1,...,n_{el}^{\partial {\mathscr {B}}^{\text {R}}}$ boundary elements. The equation $\mathbf{w}^{h\Delta t}{({{ {\varvec{ \theta }}}}_{\,n+1}, {{ {\varvec{ \theta }}}}_{\,n})} = \mathbf{0}$ is solved by means of a Newton–Raphson scheme [2], so that the update of the nodal temperatures at the current time step $\Delta {{ {\varvec{ \theta }}}}$ is calculated via

$$\begin{aligned} {\mathbf{K}}^{h\Delta t}\left( {{ {\varvec{ \theta }}}}_{\,n+1}, {{ {\varvec{ \theta }}}}_{\,n}\right) \,\cdot \Delta {{ {\varvec{ \theta }}}} = -\mathbf{w}^{h\Delta t}\left( {{ {\varvec{ \theta }}}}_{\,n+1}, {{ {\varvec{ \theta }}}}_{\,n}\right) \;. \end{aligned}$$

(27)

In the above equation, ${\mathbf{K}}^{h\Delta t}({{ {\varvec{ \theta }}}}_{\,n+1}, {{ {\varvec{ \theta }}}}_{\,n})$ represents the tangent matrix which is the derivative of the algebraic residual ${\mathbf{w}}^{h\Delta t}$ with respect to the current nodal temperatures ${{ {\varvec{ \theta }}}}_{\,n+1}$,

(28)

Compared to standard finite element implementations, a crucial detail of the presented framework is that the configuration ${{ {\varvec{ x }}}}(t)$ changes with time because of mass application such that $n_{np} \ne {\text{const}}$. This means that an existing discretisation $(\,{\mathscr {B}}^{h\Delta t}, \partial {\mathscr {B}}^{{{\text {R}}}\,{h\Delta t}}\,)_n$ at a discrete time step $t_n$ has to be updated to a discretisation $(\,{\mathscr {B}}^{h\Delta t}, \partial {\mathscr {B}}^{{{\text {R}}}\,{h\Delta t}}\,)_{n+1}$ at time step $t_{n+1}$ if the configuration has changed in that particular time step. In the particular case of adding particles with coating temperature $\theta _{\text {coat}}$ on a surface which possesses a different temperature, a method for the numerical treatment of the connection procedure must be chosen. At first, we assume that the total amount of stored energy within the existing body and the particles to be added to that body does not change by any dissipation effects during the assembly of the particles on the body’s surface. Thus, the energy of an adiabatic system has to remain conserved by the process of assembling.

As already mentioned in the introduction, there exist several options in order to handle the extension of an existing mesh of finite elements by additional finite elements. One possibility is the application of discontinuous Galerkin methods [1, 7, 13]. Another possibility is the use of interface elements [8, 9, 23, 26]. In contrast, the spirit of our current approach is to use continuous volume elements for the body and to use surface elements to capture the Robin boundary conditions. As a consequence, existing elements and added elements share connectivity nodes. However, existing nodes have a defined temperature which results from the solution path up to the moment of connecting new elements to existing elements. We resolve that problem by fixing the temperature value of each existing node that is occupied by a new element which can, of course, have a different temperature than the temperature of the newly connected existing node. Thus, in general, the energy conservation is violated by a change of the total thermal energy of an element which is computed by the expression

$$\begin{aligned} E^e = \int _{{\mathscr {B}}^e} \int _{\theta _0}^{\theta ^e} \rho \, c(\theta ) \; {\text {d}}\theta \, {\text {d}}v \;, \end{aligned}$$

(29)

wherein $\theta _0$ represents the reference temperature and $\theta ^e$ is the temperature of the element. This is illustrated by Fig. 4, where elements with different temperature distributions are connected.

Fig. 4

a Configuration of elements with different temperatures before the connection. b Configuration of the elements after the connection

As depicted, an energy source is introduced in order to conserve the energy. In each added element that shares one or more nodes with previously existing elements, an energy difference, $\Delta E_{*}^e = E^e - E^e_*$, occurs after its connection. This energy difference must be induced into the system in order to compensate the error in total thermal energy such that thermodynamical consistency is ensured. For this reason a heat supply term

$$\begin{aligned} \int _{{\mathscr {B}}^e} \rho \, \dfrac{q}{\Delta t}\, {\text {d}}v \,\doteq\, & \Delta E_{*}^e = E^e - E^e_*\nonumber \\= & \int _{{\mathscr {B}}^e} \,\rho \, \left[ \, \int _{\theta _0}^{\theta ^e} \, c(\theta ) \, {\text {d}}\theta - \int _{\theta _0}^{\theta ^e_*} \, c(\theta ) \, {\text {d}}\theta \, \right] {\text {d}}v\nonumber \\= & \int _{{\mathscr {B}}^e} \,\rho \, \int _{\theta _*^e}^{\theta ^e} \, c(\theta ) \, {\text {d}}\theta {\text {d}}v \end{aligned}$$

(30)

is introduced which is taken into account within the heat supply contribution of Eq. (16) or rather in its weak form (20), respectively the discritised weak form (26). In Eq. (30), $\theta _*^e$ is the temperature of an element after the assembling of elements and $\theta ^e$ is the temperature before the assembling. In the case of “old” elements, $\theta _*^e = \theta ^e$ holds true such that no heat supply term is induced. In the case of “new” elements $\theta _*^e \ne \theta ^e$ may occur such that a heat supply term is induced in the particular time step.

The solution procedure of the developed framework is not standard. Algorithm 1 provides a flow chart of the related finite element implementation. In each time step it is checked whether the configuration remains constant or not. Thus, in the first time step or if new elements are added, volume elements and surface elements are identified and the global system is either initialised (first time step) or reorganised. If new degrees of freedom are introduced, the values of the new degrees of freedom are set to the temperature $\theta _{\text {coat}}$ of the newly connected mass. With an updated configuration, the Newton–Raphson solution algorithm is applied in order to obtain a solution of the nonlinear system of equations.

4 Numerical examples

The proposed framework is applied to the simulation of initial boundary value problems in order to show the capabilities of the developed finite element software tool. For this purpose, the coating of an existing body with an initial temperature of $\theta _{\text {init}} = 293.15\,{\text {K}}$ is simulated. The temperature of the hot particles is assumed as $\theta _{\text {coat}} = 1873.15\,{\text {K}}$ which is in good agreement with particle temperatures during the HVOF thermal spraying process [12]. Some of the examples include the use of the aforementioned adiabatic boundaries (17)$_1$ whereas in the other examples Robin boundary conditions (17)$_2$ are involved.

Two different mechanisms are modeled with the help of Robin boundary conditions. The first mechanism is convection which is captured by a film condition

$$\begin{aligned} \bar{q}^{\text {R}}_{c} = - \, h_c \, [\theta - \theta _\infty ] \; . \end{aligned}$$

(31)

In the above equation, $h_c$ is the film condition coefficient, $\theta _\infty$ represents the environmental temperature and $\theta$ is the temperature of the modeled surface. Such boundary conditions are different for the case of an accelerated gun flame as for the case of quasi non-moving surrounding air. In order to capture this difference, $h_c^{\text {gun}}$ and $h_c^{\text {air}}$ are chosen differently as given in Table 1.

The second mechanism is radiation which is modeled by the expression

$$\begin{aligned} \bar{q}_{r}^{\text {R}} = - \, \varepsilon \,\sigma \,\left[ \theta ^4 - {\theta _{\infty }}^4\right] \;, \end{aligned}$$

(32)

wherein $\sigma$ denotes the Stefan Boltzmann constant and $\varepsilon$ is the emissivity which is chosen to model a grey body. The values chosen are summarised in Table 1. Note, that radiation inherently leads to a nonlinearity and therefore must be taken into account within the consistent linearisation of the finite element framework.

The heat conduction tensor is assumed to be isotropic

$$\begin{aligned} {{ {\varvec{ \kappa }}}}(\theta ) = \lambda (\theta ) \, {{ {\varvec{ I }}}} \;, \end{aligned}$$

(33)

where $\lambda (\theta )$ is the heat conduction coefficient and ${{ {\varvec{ I }}}}$ represents the second order identity. In order to capture the nonlinear temperature dependency of the heat capacity as well as the heat conduction coefficient, the same type of function

$$\begin{aligned} c(\vartheta )&= a_0 + a_1 \, \arctan \left( a_2 + a_3\,\vartheta \right) \end{aligned}$$

(34)

$$\begin{aligned} \lambda (\vartheta )&= b_0 + b_1 \, \arctan \left( b_2 + b_3\,\vartheta \right) \end{aligned}$$

(35)

in dependence of the temperature $\vartheta$ in $^\circ$C is chosen and fitted to experimental data for both steel and WC-Co [6, 14, 21, 25]. A summary of the parameters fitted is given in Table 2. For the purpose of illustration, the resulting functions are plotted with respect to the K-scale, whereby Fig. 5 refers to steel and Fig. 6 to WC-Co.

Some of the example simulations are carried out with constant values of the heat capacity as well as of the heat conduction coefficient. In these cases, the functions are evaluated at $293.15\,{\text {K}}$ $(20\,^\circ \hbox {C})$.

Fig. 5

a Fitted curve of the heat capacity of steel $c^{\text {S}}(\vartheta )$. b Fitted curve of the heat conduction coefficient of steel $\lambda ^{\text {S}}(\vartheta )$. The values are taken from [6, 14, 21, 25]

Fig. 6

a Fitted curve of the heat capacity of WC-Co $c^{\text {C}}(\vartheta )$. b Fitted curve of the heat conduction coefficient of WC-Co $\lambda ^{\text {C}}(\vartheta )$. The values are taken from [6, 14, 21, 25]

Table 1 Values for the convective heat transfer coefficients $h_c^{{\text {air}}}$ and $h_c^{{\text {gun}}}$, the emissivity $\varepsilon$, the Stefan–Boltzmann constant $\sigma$ and the mass densities of steel $\rho ^S$ as well as of WC-Co $\rho ^C$

Table 2 Parameters for $c(\vartheta )$ introduced in Eq. (34) and $\lambda (\vartheta )$ introduced in Eq. (35)

4.1 Two-element simulations—2d

A simple academic example to demonstrate the applicability of the developed framework is based on one element with a homogeneous initial temperature $\theta _1$ that is assembled to another element with a homogeneous temperature $\theta _2 \ne \theta _1$. The elements can represent either the same material or different materials. In total, four different scenarios are simulated. The first and second example involve two elements the underlying material of which refer to steel. Within the first example, $c^S$ and $\lambda ^S$ are chosen to be constant whereas for the second example $c^S$ and $\lambda ^S$ are temperature dependent as given by Eqs. (34) and (35). The third and fourth example each involve one steel-related element with $\theta _1$ and one WC-Co-related element with $\theta _2$. Analogously, $c^S$ and $\lambda ^S$ as well as $c^C$ and $\lambda ^C$ are constant within the third example and temperature dependent within the fourth example. For all four examples, an adiabatic boundary is modeled and the temperatures are set to $\theta _1 = 293.15\,{\text {K}}$ and $\theta _2 = 1873.15\,{\text {K}}$. The examples are carried out in two dimensional space with four-noded bilinear elements of $1\,$mm$^2$ size. The simulations start at time $t = 0$ and end at time $t = 5000\,$ms. The second element is assembled to the first at $t = 1000\,$ms. Furthermore, each of the four examples is simulated with two different time step sizes, namely $\Delta t = 10\,$ms and $\Delta t = 100\,$ms.

The results of the first two-element example are depicted in Fig. 9a–c. The energy of the system versus time is shown in part (a) of the figure. Evaluation of Eq. (29) gives the total energy of the system before (“A. low”) and after (“A. high”) the element assembly as analytic values. It can be seen that the stored energy which is computed by the finite element programme exactly hit these values for both time step sizes. Figure 9b shows the maximum and minimum temperatures for both time step sizes vs. time and, additionally, the analytically determined temperature value for $t \rightarrow \infty$. It is obvious that for both time step sizes the analytical temperature is computed by the finite element code for $t \ge 1800\,$ms. At time step $t = 1000\,$ms the simulation run with $\Delta t = 10\,$ms shows an underestimation of the lowest possible temperature and an overestimation of the highest possible temperature—there is no physical reason for $\theta _{\text {min}} \le 293.15\,$K or $\theta _{\text {max}} \ge 1873.15\,$K. For the larger time step size, the under- respectively overestimation is not observed. In Fig. 9c temperature plots of the one element before assembly and the two elements after assembly at specific time steps are depicted. As additional information, the minimum and maximum value of the temperature at each time step are listed. The time step size influences the temperature values at times that are close to the point in time of assembly. As already mentioned, the temperature tends, with increasing time, to exactly the same value for both time step sizes.

In Fig. 10a–c, the results of the second example simulation are shown. The difference to the first example is that $c^S$ and $\lambda ^S$ are now temperature dependent. The analytical value of the stored total energy in the system is higher than in the previous case since $c^S$ increases with increasing $\theta$. For this nonlinear case, the finite element code produces an error of $\approx 1.5 \%$ for $\Delta t = 10\,$ms and an error of $\approx 2 \%$ for $\Delta t = 100\,$ms. For $t \rightarrow \infty$, this results in a temperature of $1095\,$K for $\Delta t = 10\,$ms and a temperature of $1090\,$K $\Delta t = 100\,$ms. As above, for $\Delta t = 10\,$ms an underestimation of the lowest temperature as well as an overestimation of the highest temperature is observed at $t = 1000\,$ms. The loss in stored energy might result from the Backward Euler integration scheme that is known not to be energy conserving.

Figure 11 illustrates the results of the third two-element example. The total stored energy of the system vs. time plot shows that for this example the analytical total energy value is captured by the finite element programme for both time step sizes. Since $c^C < c^S$, the energy value is smaller than the one observed in the first example. For the example at hand, an underestimation of $\theta _{\text {min}}$ but no overestimation of $\theta _{\text {max}}$ occurs for $\Delta t = 10\,$ms. Both time step sizes lead to $\theta = 811\,$K for $t \rightarrow \infty$.

The results of the fourth example are depicted in Fig. 12a–c. Analogously to the error in the total energy value within the second example, the finite element code produces an error of $\approx 1.8 \%$ for $\Delta t = 10\,$ms and an error of $\approx 2.5 \%$ for $\Delta t = 100\,$ms. Since $c^C$ also increases with increasing $\theta$, the stored energy value is higher than for the third example with constant material parameters. In contrast to the third example, both an underestimation of $\theta _{\text {min}}$ and an overestimation of $\theta _{\text {max}}$ are observed for $\Delta t = 10\,$ms. For $t \rightarrow \infty$, a temperature of $\theta = 871\,$K is observed for $\Delta t = 10\,$ms as well as a temperature of $\theta = 865\,$K for $\Delta t = 100\,$ms.

4.2 Coating of a plate—2d

As a more complex academic example, the two dimensional problem which is depicted in Fig. 7a is considered. The 2d-representation of a plate is considered to be $30\,$mm wide and $3\,$mm high. The discretisation is performed with squared four-noded elements of $0.25\,$mm$^2$ size. The material is considered to represent steel and has an initial temperature of $\theta _{\text {init}} = 293.15\,$K. The time step size is $\Delta t = 10\,$ms and the material behaviour is supposed to be temperature dependent. Each $100\,$ms, a HVOF spray gun applies $6\,$mm by $0.5\,$mm—twelve by one elements—WC-Co-splats, the material behaviour of which is also considered to be temperature dependent, on the substrate. The temperature of the WC-Co-splats before the assembly with the existing system is $\theta _{\text {coat}} = 1873.15\,$K. Two different configurations of gun movement are simulated. In one setting, the HVOF gun always begins on the left hand side of the system and applies material until the right hand side is reached. This is called the “one-direction”-setting. For the other setting, the HVOF gun begins from left to right and continues mass application from the right to the left and so on. This is called the “two-direction”-setting. The arrows in Fig. 7b and c clarify the difference. The spray gun moves on for in total 6 paths such that finally half of the plate consists of “old” steel substrate and the other half consists of “new” applied WC-Co coating as depicted in Fig. 7d.

Fig. 7

Coating of a 2d plate. White elements are related to steel and blue elements are related to WC-Co. a Initial configuration of the steel substrate. b The first WC-Co-splat of the second path for the “one-direction”-setting is depicted. The arrows indicate the direction of the HVOF gun. c The first WC-Co-splat of the second path for the “two-direction”-setting is depicted. The arrows indicate the direction of the HVOF gun. d Configuration after the coating procedure. (Color figure online)

At first, the boundary of the system is considered adiabatic and simulations are carried out for both gun movement paths. The results of the simulation are depicted in Fig. 13 at which the temperature plots refer to time steps directly before the WC-Co-splat is applicated—after $t = 1090\,$ms, $t = 2090\,$ms and $t = 3090\,$ms—as well as at the final time step at 10,000 ms. As far as the eyes can catch, the temperature plots look “mirrored”. The only difference occurs when $\theta _{\text {min}}$ and $\theta _{\text {max}}$ of the two different gun movement paths are compared. Naturally, the “one-direction”-path leads to lower $\theta _{\text {min}}$ and higher $\theta _{\text {max}}$ but the difference is only a few Kelvin. At the end of the simulation, thermal equilibrium is almost reached in both cases ($\theta \approx 880\,$K).

In a second comparison, the boundary of the body is considered to be a Robin boundary with convective and radiative heat transfer via the surface. The environmental temperature of the surrounding air is the room temperature $\theta _\infty ^{\text {air}} = 293.15\,$K. The top side of the additionally applied (twelve by one) elements is occupied by the HVOF gun which is assumed to have a temperature of $\theta _\infty ^{\text {gun}} = 3073.15\,$K. The results are shown in Fig. 14. The points in time at which the results are visualised are chosen analogously to the previous example. Again, the temperature plots appear “mirrored” for the two gun movement paths. The comparison of $\theta _{\text {min}}$ and of $\theta _{\text {max}}$ for the two gun movement paths leads again to a slightly higher (only a few Kelvin) difference for the “one-direction” path. Since the boundary heat flux that is caused by convection and radiation leads to cooling of the body, the temperature plots show lower temperatures than those that are observed in Fig. 13. Obviously, the boundary heat flux that is induced by the gun flame during the coating procedure does not lead to a significant heating. Thermal equilibrium is expected for $t \rightarrow \infty$ when the temperature of the body is the same as the temperature of the surrounding air. At the final time step considered, the temperature of the body is in the range of ${\approx}[740;\,750]\,$K for both gun movement paths.

4.3 Coating of a plate—3d

The examples above involve application of mass in the same order of magnitude as the size of the initial configuration. Precisely, the added material occupies the same bulk as the initial configuration such that the total bulk was finally doubled. In reality, a comparatively small amount of hard material is deposited on an existing tool or workpiece. Therefore, in order to give a more realistic example, a three dimensional plate which is depicted in Fig. 8 is considered. The dimension of the plate is $180\,\text {mm}\times 180 \,\text {mm}\times 30\,\text {mm}$ in x-, y- and z-direction. The discretisation is performed with eight-noded hexahedral elements of different size. In z-direction, three layers of elements are used to discretise the range of $z=[0;\,29]\,\text {mm}$ and ten layers of elements discretise the range of $z=(29;\,30]\,\text {mm}$. This results in a fine discretisation near the surface at $z = 30\,$mm where the coating is applied. In x- and y-direction the discretisation is performed with $6\,$mm edge-length which results in comparatively strong distorted elements for $z>29\,$mm. This is a trade off, since the substrate is in this way discretised by 11,700 elements before any mass is newly applied. The initial temperature of the steel substrate is set to $\theta _{\text {init}} = 293.15\,$K. The material deposition is illustrated in Fig. 8b. In discrete time steps of $\Delta t = 100\,$ms, the HVOF gun applies $30\,\text {mm} \times 30\,\text {mm} \times 1\,\text {mm}$ WC-Co-splats with a temperature of $\theta _{\text {coat}} = 1873.15\,$K on the substrate. The material properties are chosen to be constant throughout the simulation. In order to model the surface heat flux, surrounding air with an ambient temperature of $\theta _{\text {air}} = 293.15\,$K is employed and a HVOF gun temperature of $\theta _{\text {gun}} = 3073.15\,$K is used in order to occupy the $z = 31\,$mm surface of the newly applied WC-Co splat. After 36 time steps, the coating is fully applied such that the configuration is discretised by in total 20,700 elements. Cooling in air is simulated until the final time step t = 10,000 ms.

Fig. 8

Coating of a 3d plate. White elements are related to steel and blue elements are related to WC-Co. a Initial configuration of the steel substrate. b The first WC-Co-splat is depicted. The arrows visualise the direction of the HVOF gun. (Color figure online)

In Fig. 15, the resulting temperature plots for four different time steps are depicted. Since the volume of the newly added material is small in relation to the substrate, it is plausible that the temperature increase is observed near the area of mass application, see Fig. 15a–b. Figure 15c shows the time step of the application of the last WC-Co-splat. At that time step, the temperature increase in deeper regions of the plate due to heat conduction can be observed in areas where the simulation of mass deposition started. Part (d) of Fig. 15 shows the temperature state of the plate after 10,000 ms. Due to heat conduction to the deeper regions of the plate as well as the cooling by the surrounding air, the maximum temperature is not more than ${\approx}380\,$K. During the simulation, under- and overestimation of the temperature occurs. Related to Figs. 15b and c, it can be observed that a newly applied WC-Co-splat leads to a drop of the temperature within the already applied splats next to it. As for the 2d example with Robin boundary, thermal equilibrium is expected for $t \rightarrow \infty$ when the temperature of the body is $\theta _{\text {air}} =293.15\,$K.

Fig. 9

a Total thermal energy versus time of two assembled elements which refer to steel ($\theta _1 = 293.15$ K and $\theta _2 = 1873.15$ K). Comparison of the total thermal energy for two different time step sizes ($\Delta t =$ 10 ms and $\Delta t =$ 100 ms) with the analytical values. b Maximum and minimum values of the temperature vs. time for two different time step sizes ($\Delta t = 10\,\hbox {ms}$ and $\Delta t = 100\,\hbox {ms}$). (c) Plot of the temperature of one element $(t = 100\,\hbox {ms})$ and of two assembled elements $(t \ge 1000\,\hbox {ms})$ at different time steps

Fig. 10

a Total thermal energy versus time of two assembled elements which refer to steel ($\theta _1 = 293.15$ K and $\theta _2 = 1873.15$ K). Comparison of the total thermal energy for two different time step sizes ($\Delta t =$ 10 ms and $\Delta t =$ 100 ms) with the analytical values. b Maximum and minimum values of the temperature versus time for two different time step sizes ($\Delta t =$ 10 ms and $\Delta t =$ 100 ms). c Plot of the temperature of one element ($t =$ 100 ms) and of two assembled elements ($t \ge$ 1000 ms) at different time steps

Fig. 11

a Total thermal energy versus time of two assembled elements which refer to steel and WC-Co respectively ($\theta _1 = 293.15$ K and $\theta _2 = 1873.15$ K). Comparison of the total thermal energy for two different time step sizes ($\Delta t =$ 10 ms and $\Delta t =$ 100 ms) with the analytical values. b Maximum and minimum values of the temperature versus time for two different time step sizes ($\Delta t =$ 10 ms and $\Delta t =$ 100 ms). c Plot of the temperature of one element ($t =$ 100 ms) and of two assembled elements ($t \ge$ 1000 ms) at different time steps

Fig. 12

a Total thermal energy versus time of two assembled elements which refer to steel and WC-Co respectively ($\theta _1 = 293.15$ K and $\theta _2 = 1873.15$ K). Comparison of the total thermal energy for two different time step sizes ($\Delta t =$ 10 ms and $\Delta t =$ 100 ms) with the analytical values. b Maximum and minimum values of the temperature versus time for two different time step sizes ($\Delta t =$ 10 ms and $\Delta t =$ 100 ms). c Plot of the temperature of one element ($t =$ 100 ms) and of two assembled elements ($t \ge$ 1000 ms) at different time steps

Fig. 13

Simulation of coating of a 2d-plate with adiabatic boundary with two different gun movement paths. Temperature distribution after a $1090\,$ms, b $2090\,$ms, c $3090\,$ms and d 10,000 ms

Fig. 14

Simulation of coating of a 2d-plate with Robin boundary (convection and radiation) with two different gun movement paths. Temperature distribution after a $1090\,$ms, b $2090\,$ms, c $3090\,$ms and d 10,000 ms

Fig. 15

Simulation of coating of a 3d-plate with Robin boundary conditions which cover convective and radiative heat transfer. Temperature distribution after a $100\,$ms, b $1600\,$ms, c $3700\,$ms and d 10,000 ms

5 Conclusions

This contribution presents a novel finite element tool for the simulation of material deposition and evolution of the workpiece temperature for thermal spraying processes. From the fundamental equations of continuum thermodynamics, the nonlinear finite element framework was derived and implemented. One of the main issues of this work is the introduction of an internal heat source in order to ensure conservation of energy in the framework of continuous Galerkin finite element methods. With this at hand, the proposed simulation approach can be implemented in established continuous Galerkin finite element codes. A set of example simulations demonstrates the numerical application of the implemented framework. The material parameters involved have been fitted to experimental data and the coefficients for convective and radiative heat transfer have been chosen to model conditions close to reality. The examples indicate that the time discretisation noticeably influences the solution of the temperature field near the point in time of mass deposition. For nonlinear simulations, comparatively small errors in the value of the total energy occur. A possible reason might be the use of the Backward Euler time integration scheme. With respect to energy consistency, the time integration scheme could be modified in future work, e.g, to a Galerkin-based time integrator. In the field of elastodynamics, i.e., energy-momentum consistent schemes are applied [11]. Nonetheless, in summary the present work contributes an easy-to-implement novel finite element approach for a nonlinear rigid heat conductor with mass deposition.

Future research will include a fully coupled thermo-mechanical framework in order to predict residual stresses due to the quenching induced by the thermal spraying process. Depending on the considered materials, the modeling of phase transformations should be taken into account. Another aspect of interest might be the analysis of damage behavior during the thermal spraying. In addition, experimental investigations for calibration, verification and validation should be carried out such that reliable real world applications can be simulated.