Abstract
The present paper deals with the homogenization problem of periodic composite materials, considering a Cosserat continuum at the macro-level and a Cauchy continuum at the micro-level. Consistently with the strain-driven approach, the two levels are linked by a kinematic map based on a third order polynomial expansion. Because of the assumed regular texture of the composite material, a Unit Cell (UC) is selected; then, the problem of determining the displacement perturbation fields, arising when second or third order polynomial boundary conditions are imposed on the UC, is investigated. A new micromechanical approach, based on the decomposition of the perturbation fields in terms of functions which depend on the macroscopic strain components, is proposed. The identification of the linear elastic 2D Cosserat constitutive parameters is performed, by using the Hill–Mandel technique, based on the macrohomogeneity condition. The influence of the selection of the UC is analyzed and some critical issues are outlined. Numerical examples for a specific composite with cubic symmetry are shown.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The computational homogenization techniques have proved to be very effective to predict the macroscopic behavior of composite materials. Complex nonlinear mechanisms may be taken into account, related both to constitutive and geometric effects. In this framework, the problem of satisfactorily reproducing the mechanical response of structural elements made from heterogeneous materials is tackled considering two scales: a macroscopic and a microscopic scale. At the macroscopic level, the actual heterogeneous material is replaced by an equivalent homogeneous medium. The homogenized constitutive response is obtained by solving a Boundary Value Problem (BVP) defined at the microscopic scale, where a Representative Volume Element (RVE) is selected. At the RVE level, all the information concerning the texture and mechanical behavior of the constituents are available in detail.
Analyzed textures
Boundary conditions required for the perturbation fields when 2D Cosserat strain components are applied
Depending on the choice of the continuum theory adopted at both macro- and micro-level, different equivalent homogenized models are triggered. Indeed, the classical Cauchy continuum theory can be considered suitable only when the intrinsic length at the micro-scale is very small, compared to the macro-scale structural length [2, 5, 16, 18, 20]. On the contrary, when strong strain and stress gradients at the macro-level occur, or when the microscopic length of the constituents is comparable to the wavelength of variation of the strain and stress mean fields at the macro-level, some intrinsic limits emerge. This is due to the fact that no length scale is accounted for in the Cauchy theory. Hence, the information that the micro-level transfers to the macro-level is insensitive to the dimension of the constituents.
RVE of the two-phase composite material
UCs considered for the composite material
By adopting generalized continua, this limit is overcome and the length scales are naturally accounted for. Many authors have focused on coupling different continuum models at the two scales. In most cases at the microscopic level the classical Cauchy continuum is adopted, especially because nonlinear constitutive relationships are well-established in this framework. At the macro-level, second-gradient [5, 7, 18, 19], couple stress [31, 33] or micropolar Cosserat [2, 13, 14, 16] continua are used. However, among these, only the Cosserat model incorporates an additional strain quantity, measuring the relative rotation, i.e. the difference between macroscopic and microscopic rotation. Hence, on the one hand the Cosserat model is based on an enriched kinematic description with respect to the second-gradient model, as it contains the additional rotation field. On the other hand, it does not contain all the additional higher-order terms, as for example the axial modes. Note that, by disregarding some of the higher order terms defined in the second-gradient model, couple-stress formulation can be derived. With reference to beam models, the difference between the couple-stress and Cosserat models can be considered as equivalent to that between the Euler–Bernoulli and Timoshenko theory, as also observed in [17]. Depending on the specific application field, the most suitable generalized model has to be adopted. In particular, the Cosserat model has turned out to be appropriate in several cases, as for example in brick/block masonry [30], in which the relative rotation has a clear physical meaning.
\(K_{1}\) component on the UC (a): (1) horizontal and (2) vertical perturbation components along the horizontal lines
\(K_{1}\) component on the UC (a): (1) horizontal and (2) vertical perturbation components along the vertical lines
In this work, the focus is on composite materials characterized by periodic texture, i.e. made from the regular arrangement of Unit Cells (UCs). The computational homogenization procedure presented in [1, 13], coupling the Cosserat and Cauchy medium at the macro- and micro-level, respectively, is adopted. This is based on an idea originally proposed by [16], where a polynomial kinematic map was used to link the two levels. The displacement field at the micro-level is represented as the superposition of the kinematic map and an unknown perturbation field, due to the heterogeneous nature of the material. To be noted is that the procedure discussed in [16] has some drawbacks, as also remarked in [17]. Firstly, it fails to satisfy the balance equations in the case of homogenized material. In fact, no conditions requiring the divergence-free stress state in the inner domain are imposed, as on the contrary is assumed in classical homogenization procedures [24, 25]. Furthermore, when the Cosserat macroscopic strain components are applied to the UC, the perturbation fields are no longer periodic [17], differently from the case of Cauchy macroscopic strains. In [1] a revision of the above procedure is presented, proposing some enhancements to overcome the highlighted limits. A modified kinematic map is proposed, which ensures that no perturbation of the displacement fields arises when homogeneous microstructure is considered for the UC, as it is expected. Moreover, to derive the most suitable BCs to be applied to the UC when this is subjected to higher order terms of the polynomial map, the authors investigate on the actual distribution of the perturbation fields in a RVE made of a large number of UCs. The results of these analyses clearly show that non periodic distributions emerge, different depending on the applied terms of the polynomial map. Thus, regarding the proper characterization of the perturbation fields, when the Cosserat macroscopic strains are applied to the UC, some open issues remain. Standing on these observations, the present paper focuses on the more correct and accurate determination of the perturbation displacement fields, with respect to the available proposals. To this end, a new method is established. A three-step homogenization procedure is proposed, on the basis of the micromechanical approach presented in [33], where a technique grounded on the asymptotic approach [8] is used and a second gradient continuum is employed at the macroscopic level. In [33] the perturbation displacement field in the UC is expressed as a function of the components of the macroscopic displacement gradients. In particular, it is decomposed into different contributions related to the first and second gradients of the kinematic map. Such an approach was recently adopted in [6], which focused on the problem of the displacement continuity across the UC boundary, in the case of second order computational homogenization. It was showed that, thanks to the introduction of generalized periodicity conditions, the continuity of this field across the interfaces is guaranteed.
\(K_{1}\) component on the UC(b): (1) horizontal and (2) vertical perturbation component along the horizontal lines
\(K_{1}\) component on the UC (b): (1) horizontal and (2) vertical perturbation components along the vertical lines
Here, the original idea presented in [33] is extended to the case of a 2D Cosserat continuum at the macro-level, expressing the perturbation field in function of the first, second and third gradient of the kinematic map. To verify the effectiveness of the proposed procedure in the considered framework, the distribution of the perturbation fields on a single UC is compared with the results for a RVE, obtained by arranging a large number of UCs.
\(\varTheta \) component on the UC (a): (1) horizontal and (2) vertical perturbation component along the horizontal lines
\(\varTheta \) component on the UC (a): (1) horizontal and (2) vertical perturbation components along the vertical lines
When generalized continua are considered at the macro-level, while the standard Cauchy continuum is retained at the micro-level, a further debated issue is the identification of the effective constitutive parameters. Due to the lack of a direct correspondence between strain and stress components at the two levels, some problems arise. Different approaches have been proposed, each with distinct advantages and drawbacks. Several authors derive the homogenized constitutive components starting from the generalized Hill–Mandel macrohomogeneity condition, regardless of whether they consider a Cosserat [13, 16] or a second-order [12, 18, 19, 32] continuum at the macro-level. The evaluation of the macroscopic stresses is obtained as the weighted average of microscopic stresses over the volume. The microscopic coordinates work as weighting functions, leading in some cases to physically inconsistent results [33]. Furthermore, higher order constitutive components are identified, also when a homogeneous elastic material at the micro-level is considered.
\(\varTheta \) component on the UC(b): (1) horizontal and (2) vertical perturbation component along the horizontal lines
\(\varTheta \) component on the UC(b): (1) horizontal and (2) vertical perturbation components along the vertical lines
To overcome these drawbacks, a different approach, based on the spatial average theorem, to derive the macroscopic balance equations, is proposed in [33] in the case of second order or couple stress continuum at the macro-level. In this way, the higher order constitutive coefficients depend only on the microscopic perturbation, that vanishes in the case of homogeneous material. This technique is, however, applied within the framework of the asymptotic approach. Its extension to the case of continua at the macro- and micro-levels, characterized by a different number of kinematic and static fields, as well as by a different number of governing equations, is not straightforward. Other interesting proposals can be found in the framework of the asymptotic methods [6, 29], directly causing the internal length parameter to vanish, when the material is homogeneous. Analytical derivation of the bending moduli in the case of a homogenization procedure, coupling a couple stress continuum at the macro-level with a Cauchy medium at the micro-scale, is presented in [9], considering a dilute suspension of spherical inclusions embedded in an isotropic elastic matrix.
The generalized Hill–Mandel macrohomogeneity condition is used in this work to identify the linear elastic homogenized coefficients of the Cosserat continuum adopted at the macro-level and to put in evidence the drawbacks of this approach. A simple periodic composite medium is considered, by focusing on the influence of the selection of the UC, [11]. A critical interpretation of the obtained results is provided.
The paper is organized as follows: in Sect. 2, the computational homogenization technique is illustrated and the adopted kinematic map is introduced; in Sect. 3, two different procedures for the determination of the perturbation fields are addressed and compared by means of selected numerical tests. Section 4 deals with the problem of identifying the homogenized elastic constitutive terms. Finally, in Sect. 5 some concluding remarks are reported.
2 Cosserat–Cauchy homogenization
The computational homogenization procedure adopts the Cosserat continuum at the macro-level and the Cauchy medium at the micro-level. According to the classical Cosserat formulation for 2D media, at the typical macroscopic material point \({\mathbf {X}}=\{X_{1},\, X_{2}\}^{T}\), the displacement vector \(\mathbf{U}=\{U_{1},\, U_{2},\,\varPhi \}^{T}\) is defined, where \(U_{1}\) and \(U_{2}\) are the translational degrees of freedom and \(\varPhi \) is the rotational one. The Cosserat strain vector is partitioned into three sub-vectors as follows:
where \(\bar{\mathbf {E}}\) collects the axial and symmetric shear strains:
\(\mathbf{{K}}\) is the vector collecting the curvature components, defined as:
and \(\varTheta \) is the skew-symmetric shear component:
Consistently with the strain driven approach, the macroscopic strain components, evaluated at \({\mathbf {X}}\), are used as input variable for the microscopic level. Indeed, the BVP at the micro-level is stated by defining a kinematic map expressed in function of the vector \({\mathbf {E}}\).
The Cosserat stress, work-conjugated with the strain \(\mathbf{E }\), is defined as:
where:
and \(\varSigma _1\) and \(\varSigma _2\) are the axial stress components, \(\varSigma _{12}^{SYM}\) and Z are the symmetric and skew-symmetric shear stress components, respectively, and \(M_1\) and \(M_2\) are the couple stress components. The balance equations, thus, result as:
where \(\mathbf{F }=\{F_1 \ F_2 \ C \}^T\) is the vector of body forces and couple.
Considering a periodic medium, a repetitive UC, containing all the necessary information regarding the material and geometrical properties of the composite, can be selected for the micromechanical and homogenization analyses. In particular, a rectangular UC is analyzed, whose size is \(a_{1} \times a_{2}\) and its center is located at the macroscopic point \({\mathbf {X}}\), characterized by the displacement field \({\mathbf {u}}=\{u_{1},\, u_{2}\}^{T}\), defined at each point \({\mathbf {x}}=\left\{ x_{1},\, x_{2}\right\} ^{T}\) of the UC domain \(\omega \).
The relation between the macro-level displacement vector \(\mathbf{U}({\mathbf {X}})\) and the micro-level displacement field \({\mathbf {u}}\left( {\mathbf {x}}\right) \), derived by enforcing the minization of a proper defined functional as described in detail in [1, 16], results as
where the symbol \(\langle \cdot \rangle _{\omega }\) indicates the average value of the variable in \(\omega \). These represent the homogenization conditions for the micro-level displacement components. Note that the macroscopic rotation \(\varPhi \) is defined as the average rigid rotation of the UC around its center located at \({\mathbf {X}}\).
The following representation form, typical of the first order homogenization approach, where the Cauchy model is used at both the macro- and micro-level [27], is assumed for the displacement field, solution of the BVP at the typical point \({\mathbf {x}}\) of the UC:
in which the dependence on the macroscopic and microscopic coordinates, \({\mathbf {X}}\) and \({\mathbf {x}}\), is indicated. According to Eq. (9), the displacement is expressed as the superposition of an assigned field \({\mathbf {u}}^{*}\left( {\mathbf {X}},{\mathbf {x}}\right) \), i.e., the kinematic map, depending on the macro-level deformation vector \({\mathbf {E}}\), and a perturbation field \(\widetilde{{\mathbf {u}}}\left( {\mathbf {X}},{\mathbf {x}}\right) \). The strain vector at the microscopic level is derived by applying the kinematic operator defined for the 2D Cauchy problem and, in expanded form, it results as:
where \(\bullet _{,i}\) indicates the partial derivative with respect to \(x_i.\) According to Eq. (9), the strain can be written as:
with evident meaning of the symbols. The stress is determined by the following linear elastic constitutive equation:
where \({\mathbf {c}}\left( {\mathbf {x}}\right) =\left[ c_{ij} \left( {\mathbf {x}}\right) \right] \) is the \(3\times 3\) elastic matrix of the composite constituent. In the following, it is assumed that all the constituents are characterized by isotropic behavior.
A key point of the procedure is the definition of a suitable kinematic map, i.e., the form of the assigned field \({\mathbf {u}}^{*}\left( {\mathbf {X}},{\mathbf {x}}\right) \) as a function of the macroscopic strain variables. The different nature of the continua coupled at the two levels implies that this step is not straightforward. In what follows, the third order polynomial map proposed in [1], is adopted.
The linear terms of the map depend on the macroscopic Cauchy strain vector \(\overline{\mathbf{E }}\), while the quadratic and cubic terms depend on the curvatures and the skew-symmetric shear \(\mathbf{K }\) and \(\varTheta \), respectively. The final form of the kinematic map is built in two steps.
-
the first step concerns the definition of the linear terms, involving the macroscopic Cauchy strain. This is a standard homogenization problem and the related part of the kinematic map is very well-known. Indeed, all the homogenization process at the first order can be performed independently on the higher order problem. Thus, with reference to a 2D orthotropic homogenized medium, the effective elastic constants for the equivalent Cauchy medium can be identified and the Young’s moduli \(e_1\) and \(e_2\) and Poisson ratio \(\nu _{12}\) can be determined.
-
once the first order homogenization problem has been solved, the higher order problem can be approached. To ensure that the kinematic map leads to an equilibrated stress field for the first order homogenized material, the quadratic and cubic terms of the map contain the first order homogenized constants, as shown in [1].
In the following, the final and complete form of the kinematic map is presented containing all the additive terms. In the considered orthotropic case, the kinematic map can be written in compact form as:
where
with
In formulas (15)–(17), \(\lambda _{1}=e_{2}/e_{1}\), \(e_{1}\) and \(e_{2}\) are Young’s moduli of the equivalent homogenized orthotropic material, \(\nu _{12}\) is the Poisson ratio and:
where \(\lambda _{2}=e_{2}/g_{12}\), \(g_{12}\) being the homogenized shear modulus, while \(\rho =a_{2}/a_{1}\) is the ratio between the dimensions of the UC and
As briefly discussed above, the matrices \(\mathbf{A }^1\), \(\mathbf{A }^2\), \(\mathbf{A }^3\), multiplying the macroscopic strain vectors \(\overline{\mathbf{E }}\), \(\mathbf{K }\) and \(\varTheta \) in the adopted polynomial map, contain the effective elastic coefficients of the equivalent Cauchy medium. The possible dependence of the kinematic map on the effective elastic coefficients, as a consequence of the enforcement of the balance equations in the homogenized UC, has been observed also in [9, 17] in the case of couple stress and micromorphic media, respectively. In this way the perturbation field arises only as a consequence of the heterogeneous nature of the medium, while vanishes for the homogenized material. It is worth noting that this represents the relevant advantage of the adopted kinematic map. On the other hand, this could also seem to limit the application of the methodology to describe nonlinear constitutive behavior. Indeed, if nonlinear effects, such as plasticity, damage, viscosity, are all accounted for by introducing an inelastic strain in the overall constitutive relationship, the initial effective elastic matrix does not change during the evolution process of the nonlinear mechanisms [2]. As a consequence, the coefficients in the map also remain the same. Moreover, even the tangent stiffness matrix can be obtained as the sum of the initial elastic one and a part that depends on the derivative of the inelastic strain vector with respect to the macroscopic strain.
The effect of the perturbation parts of the displacement field in determining the average macroscopic strains is taken into account by the quantities \(\alpha _{1}\), \(\alpha _{2}\) and \(\alpha _{3}\). In particular, it is set:
with \(k_{1}\), \(k_{2}\) and \(k_{3}\) the average macroscopic strains due to the perturbation parts of the displacement field, resulting as:
For example, when the value \(\hat{K}_1\) is applied, generally a non zero term \(k_1\) is obtained, corresponding to an actual applied curvature equal to \(K_1=\hat{K}_1+k_1\). Note that the quantities \(k_{1}\), \(k_{2}\) and \(\theta \) are not a priori known, since their values depend on the average of the perturbation fields and its derivatives, as shown in Eq. (21). Therefore, they can be computed only after solving the micromechanical problem on the UC, according to the following procedure. Considering for example the case of \(\hat{K}_1\), first the value of \(\alpha _{1}\) is set equal to 1, assuming \(k_1=0\). After solving the boundary value problem on the UC, the perturbation fields and the quantity \(k_1\) are evaluated by means of Eq. (21). This implies that the UC is subjected to a resulting macroscopic curvature \(K_1=\hat{K}_1+k_1\). As a consequence, \(\hat{K}_1=K_1-k_1=\alpha _1K_1\) and the expression reported in Eq. (13) is recovered. The same procedure is followed for the cases of \(K_2\) and \(\varTheta \). Once determined, the parameters \(\alpha _{1}\), \(\alpha _{2}\) and \(\alpha _{3}\) in (20) are definitely known. The strain field derived from the kinematic map, in compact form, results as:
where
The three submatrices in formula (23) have the following explicit forms:
\({\mathbf {I}}\) being the \(3\times 3\) identity matrix.
3 Characterization of the perturbation field
The vector \(\widetilde{{\mathbf {u}}}\left( {\mathbf {X}},{\mathbf {x}}\right) \) introduced in Eq. (9) is an unknown perturbation field, that accounts for the effects of heterogeneities and vanishes in the trivial case of a homogeneous material, thanks to the specific form adopted for the kinematic map. In the case of the first order homogenization, \(\widetilde{{\mathbf {u}}}\left( {\mathbf {X}},{\mathbf {x}}\right) \) is a periodic fluctuation. Hence, the BVP on the UC can be solved by assigning periodic boundary conditions. When higher order polynomials are included in the kinematic map, there is no reason to assume periodic displacement and strain fluctuation fields and anti-periodic traction vectors at the boundary. The anti-periodicity of the tractions, usually holding in the standard first order homogenization, ensures equilibrium at the cell interfaces. In the framework of higher order computational homogenization, as the periodicity conditions may be lost, the anti-periodicity of the tractions at the interfaces between adjacent UCs do not hold anymore [6, 17, 33].
In this section, two different approaches to characterize the fluctuation field are introduced. The first technique, presented in Sect. 3.1, assumes the decomposition of the perturbation field \(\widetilde{{\mathbf {u}}}\left( {\mathbf {X}},{\mathbf {x}}\right) \) in different contributions, related to the first, second and third order gradient of the kinematic map. The second technique, discussed in Sect. 3.2, is based on the enforcement of proper boundary conditions (BCs) on the UC, as described in [1]. These result from the analysis of the actual perturbation field distribution in the RVE undergoing remote fully displacement BCs. A comparison between the numerical results obtained using the adopted procedures for a paradigmatic example of a two-phase composite material, characterized by cubic symmetry, is proposed in Sect. 3.3.
3.1 Micromechanical description of the heterogeneous medium: a three-step homogenization
The procedure based on the methodology proposed in [33] is extended to the case of a 2D Cosserat medium at the macroscopic scale. Here, the main steps of the proposed procedure are addressed, exploiting the superposition principle. Initially, only the first order terms of the kinematic map, multiplying the vector \(\overline{{\mathbf {E}}}\) in (13), are activated; subsequently, the effects of the quadratic terms related to \({\mathbf {K}}\) are considered and, finally, the third order term associated with \(\varTheta \) is taken into account.
When only the linear terms of the kinematic map are considered, the case of the first order homogenization is recovered. In this instance, considering \({\mathbf {K}}={\mathbf {0}}\) and \(\varTheta =0\), the two terms defining the displacement field \({\mathbf {u}}\left( {\mathbf {X,x}}\right) \) in (9) can be expressed as:
where the perturbation term \(\widetilde{{\mathbf {r}}}^{1}\left( {\mathbf {X,x}}\right) \) is an unknown field. Here, it is assumed that \(\widetilde{{\mathbf {r}}}^{1}\left( {\mathbf {X,x}}\right) \) is evaluated as the product of unknown functions times the components of the first gradient of the kinematic map. In particular, this is written in vectorial form as \(\varvec{\gamma }^{1}=\{u_{1,1}^{*},\, u_{1,2}^{*},\, u_{2,1}^{*},\, u_{2,2}^{*}\}^T\). Since it results that \(u_{1,2}^{*}= u_{2,1}^{*}\), only three components of \(\varvec{\gamma }^{1}\) are independent and the following reduced vector can be considered:
Thus, it is assumed that the perturbation term is given by:
Concerning \(\varvec{\varLambda }^{1}\left( {\mathbf {x}}\right) \), it can be written as:
\(\varvec{\varLambda }_{i}^{1}\left( {\mathbf {x}}\right) \), \(i=1,2,3,\) being evaluated by applying the components \(E_{1}\), \(E_{2}\) and \(\varGamma _{12}\) of the vector \(\overline{{\mathbf {E}}}\), respectively, as described in detail in Sect. 3.1.1.
When the presence of the curvature vector \({\mathbf {K}}\) is also considered, with \(\varTheta =0\), the two terms defining the displacement field \({\mathbf {u}}\left( {\mathbf {X,x}}\right) \) in (9) can be expressed as:
where now \(\widetilde{\mathbf {r}}^{2}\left( {\mathbf {X,x}}\right) \) is the only unknown field. Following the same procedure as for the first term \(\widetilde{{\mathbf {r}}}^{1}\left( {\mathbf {X,x}}\right) \), it is assumed that \(\widetilde{{\mathbf {r}}}^{2}\left( {\mathbf {X,x}}\right) \) is expressed as the product of unknown functions and the components of the first gradient of \(\varvec{\overline{\gamma }}^{1}\left( {\mathbf {X,x}}\right) \), which is arranged in the vector \(\varvec{\gamma }^{2}=\{\varepsilon _{1,1}^{*}, \varepsilon _{1,2}^{*}, \varepsilon _{2,1}^{*}, \varepsilon _{2,2}^{*}, \gamma _{12,1}^{*}, \gamma _{12,2}^{*}\}^T\). As, if \(\varTheta =0\), it results that \(\gamma _{12,1}^{*}=\gamma _{12,2}^{*}=0,\) the only nonvanishing components of \(\varvec{\gamma }^{2}\) are arranged in the following vector:
Then, the unknown field \(\widetilde{\mathbf {r}}^{2}\left( {\mathbf {X,x}}\right) \) is represented in the form:
with the matrix \(\varvec{\varLambda }^{2}\left( {\mathbf {x}}\right) \) defined as:
\(\varvec{\varLambda }_{i}^{2}\left( {\mathbf {x}}\right) \), \(i=1,\ldots ,4,\) being functions evaluated according to the procedure illustrated in Sect. 3.1.2.
Finally, when the component \(\varTheta \) is also taken into account, it results that:
The field \(\widetilde{\mathbf {r}}^{3}\left( {\mathbf {X,x}}\right) \) is written as the product of unknown functions times the components of the first gradient of \(\varvec{\overline{\gamma }}^{2}\left( {\mathbf {X,x}}\right) \), which are arranged in the vector:
As in the previous cases, only the relevant and nonvanishing components of \(\varvec{\gamma }^{3}\) are collected in the reduced vector, resulting as:
Again, the unknown vector \(\widetilde{\mathbf {r}}^{3}\left( {\mathbf {X,x}}\right) \) is expressed as:
with
\(\varvec{\varLambda }_{\mathrm {i}}^{3}\left( {\mathbf {x}}\right) \), \(i=1,\ldots ,3\), being functions evaluated according to the procedure illustrated in Sect. 3.1.3.
Finally, the total fluctuation displacement vector \(\widetilde{{\mathbf {u}}}\left( {\mathbf {X,x}}\right) \) can be expressed as the sum of three fields evaluated in sequence (three-step homogenization), according to formulas (29), (33) and (37):
The typical component (\(i=1,2\)) of the vectors \(\widetilde{\mathbf {r}}^{1}\left( {\mathbf {X,x}}\right) \), \(\widetilde{\mathbf {r}}^{2}\left( {\mathbf {X,x}}\right) \) and \(\widetilde{\mathbf {r}}^{3}\left( {\mathbf {X,x}}\right) \) takes the explicit expression:
where
and \(\varLambda _{i1}^{3}\left( {\mathbf {x}}\right) =\varLambda _{i2}^{3}\left( {\mathbf {x}}\right) =\varLambda _{i3}^{3}\left( {\mathbf {x}}\right) =\varLambda _{i}^{3}\left( {\mathbf {x}}\right) \).
Similarly to [6, 33], it is assumed that the functions in \(\varvec{\varLambda }^{i}\left( {\mathbf {x}}\right) \) (\(i=1,2,3\)) satisfy the periodicity conditions in the UC.
In the next sections, the details of the procedure to obtain \(\varvec{\varLambda }^{i}\left( {\mathbf {x}}\right) \) are addressed and the boundary conditions to be imposed on the UC are derived. For the sake of brevity, as of now, the explicit dependence of the macroscopic strain components and of the perturbation fields on \({\mathbf {X}}\) and \({\mathbf {x}}\), respectively, is omitted if not strictly necessary.
It may be remarked that the perturbation field, given by Eq. (39), is expressed as a linear combination of the macroscopic strain components according to Eqs. (40), (41) and (42). The coefficients of the linear combination depend on the functions in \(\varvec{\varLambda }^{i}\left( {\mathbf {x}}\right) \).
3.1.1 First order case
When at the macroscopic level only the presence of the components \(E_{1}\), \(E_{2}\) and \(\varGamma _{12}\) is considered, the first order computational homogenization is recovered. As known [3, 23], in this case the perturbation field is periodic. Hence, the unknown field \(\widetilde{{\mathbf {u}}}\) is evaluated by imposing periodic boundary conditions on the UC. Taking into account Eqs. (27) and (29), the displacement field components in (9) take the following explicit representation form:
Setting \(E_{1}=1\) and \(E_{2}=\varGamma _{12}=0\) in Eq. (44), by solving the micromechanical problem, the functions \(\varLambda _{11}^{1}\) and \(\varLambda _{21}^{1}\) under the periodicity conditions are determined. Analogously, setting \(E_{2}=1\) and \(E_{1}=\varGamma _{12}=0\), it is possible to evaluate the periodic functions \(\varLambda _{12}^{1}\) and \(\varLambda _{22}^{1}\); finally, setting \(\varGamma _{12}=1\) and \(E_{1}=E_{2}=0\), the periodic functions \(\varLambda _{13}^{1}\) and \(\varLambda _{23}^{1}\) are determined.
3.1.2 Second order case
Aiming at the evaluation of the unknown field \(\widetilde{\mathbf {r}}^{2}\), the displacement components in Eq. (9) are now written taking into account Eqs. (31), (40) and (41), the expression of the operator \({\mathbf {A}}^{2}\) given in (16) and setting \(\overline{{\mathbf {E}}}=\mathbf {0}\):
To evaluate the 8 unknown functions \( \varLambda _{ij}^{2}\) (\(i=1,2;j=1,\ldots ,4\)), assuming that the periodicity conditions hold for them, the two components of the displacement field \(u_1\) and \(u_2\) are represented in the form:
where
-
\(u_1^{(1)}\) and \(u_2^{(1)}\) depend only on the unknown functions \( \varLambda _{14}^{2}\) and \(\varLambda _{24}^{2}\),
-
\(u_1^{(2)}\) and \(u_2^{(2)}\) depend only on the unknown functions \( \varLambda _{12}^{2}\) and \(\varLambda _{22}^{2}\),
-
\(u_1^{(3)}\) and \(u_2^{(3)}\) depend only on the unknown functions \( \varLambda _{11}^{2}\) and \(\varLambda _{21}^{2}\),
-
\(u_1^{(4)}\) and \(u_2^{(4)}\) depend only on the unknown functions \( \varLambda _{13}^{2}\) and \(\varLambda _{23}^{2}\).
In particular, it is set:
-
Case 1
$$\begin{aligned} u_{1}^{(1)}&= \left( \varLambda _{12}^{1} x_{2} + \varLambda _{14}^{2}\right) \alpha _1\nu _{12} \, K_{1} \nonumber \\ u_{2}^{(1)}&= \frac{1}{2}\alpha _{1}\left( x_{1}^{2}+\nu _{12}x_{2}^{2}\right) K_{1} +\left( \varLambda _{22}^{1}x_{2} + \varLambda _{24}^{2}\right) \alpha _1 \nu _{12}\,K_{1} \end{aligned}$$(47)Setting \(K_1=1\) the micromechanical problem is solved and the unknown periodic functions \(\varLambda _{14}^{2}\) and \(\varLambda _{24}^{2}\) are determined.
-
Case 2
$$\begin{aligned} u_{1}^{(2)}&=-\alpha _{1}x_{1}x_{2} ^{2} K_{1}-\left( \varLambda _{11}^{1} x_{2} - \varLambda _{12}^{2}\right) \alpha _1\,K_{1} \nonumber \\ u_{2}^{(2)}&= -\left( \varLambda _{21}^{1} x_{2} - \varLambda _{22}^{2}\right) \alpha _1\,K_{1} \end{aligned}$$(48)Setting \( K_1=1\), the micromechanical problem is solved and, in this case, the unknown periodic functions \( \varLambda _{12}^{2}\) and \(\varLambda _{22}^{2}\) are evaluated.
-
Case 3
$$\begin{aligned} u_{1}^{(3)}&=-\alpha _{2}\frac{1}{2}\left( x_{2}^{2}+ \lambda _{1}\nu _{12}x_{1}^{2}\right) K_{2}- \left( \varLambda _{11}^{1} x_{1}+ \varLambda _{11}^{2}\right) \alpha _2 \lambda _{1}\nu _{12} \, K_{2}\nonumber \\ u_{2}^{(3)}&= -\left( \varLambda _{21}^{1} x_{1} + \varLambda _{21}^{2} \right) \alpha _2 \lambda _{1}\nu _{12} \, K_{2} \end{aligned}$$(49)Setting \( K_2=1\), the micromechanical problem is solved and the unknown periodic functions \( \varLambda _{11}^{2}\) and \(\varLambda _{21}^{2}\) are computed.
-
Case 4
$$\begin{aligned} u_{1}^{(4)}&= \left( \varLambda _{12}^{1} x_{1} + \varLambda _{13}^{2} \right) \alpha _2 \, K_{2} \nonumber \\ u_{2}^{(4)}&= \alpha _{2}x_{1}x_{2} K_{2} +\left( \varLambda _{22}^{1} x_{1} + \varLambda _{23}^{2}\right) \alpha _2 \, K_{2} \end{aligned}$$(50)Setting \(K_2=1\), the micromechanical problem is solved and now the unknown periodic functions \( \varLambda _{13}^{2}\) and \(\varLambda _{23}^{2}\) are determined.
It can be proved that, following the proposed procedure, the displacement fields across two adjacent UCs are continuous.
3.1.3 Third order case
Finally, to compute the unknown field \(\widetilde{\mathbf {r}}^{3}\), the displacement components in (9) are expressed considering Eqs. (35), (40), (41) and (42), under the hypothesis that both \(\overline{{\mathbf {E}}}\) and \({\mathbf {K}}\) vanish, as:
The functions \( \varLambda _{i}^{3}\) (\(i=1,2\)) are evaluated assuming periodicity conditions between corresponding edges of the UC.
3.2 Micromechanical description of the heterogeneous medium: analysis of the perturbation field in the RVE
The characterization of the perturbation field \(\widetilde{{\mathbf {u}}}\) is performed considering a RVE obtained as assemblage of a large number of UCs for a selected two-phase periodic composite material; the RVE is subjected to remote fully displacement BCs. In particular, the Cosserat deformation modes are imposed on the boundary, according to the kinematic map in Eq. (13), and the RVE response is evaluated by the Finite Element (FE) method. Hence, the distribution of the perturbation field arising in the central UC of the RVE is taken as the benchmark. It is assumed as the actual field occurring in the composite, when second and third order polynomial terms of the kinematic map related to the additional Cosserat strain components are assigned. Thus, the problem of the derivation of suitable BCs to impose on a single UC is investigated, in order to reproduce, with a satisfactory level of accuracy, the actual distribution of the perturbation field.
In particular, some selected two-phase composite materials, characterized by material symmetries ranging from cubic to orthotropic are analyzed. In Fig. 1, the UCs corresponding to the four different analyzed textures are shown.
In all the considered cases, similar distributions of the perturbation displacement fields on the UC boundary emerge. Differently from the case of the first order homogenization procedure, where periodic BCs are suitably adopted, in the analyzed cases more complex BCs have to be considered, which are different for the two components of \(\mathbf {\widetilde{u}}\). In Fig. 2 the derived BCs are summarized. In the first row, the applied Cosserat macroscopic deformation components are reported; in the second row the BCs for the component \(\widetilde{u}_{1}\) along the horizontal and vertical edges of the UC are schematically reported, while in the third row those for the displacement component \(\widetilde{u}_{2}\) are shown. The symbol “p” indicates periodic BCs, “s” skew-periodic BCs, while “0” indicates zero perturbation displacement BCs.
3.3 Perturbation displacement fields: comparison between the proposed approaches
The approaches presented above to evaluate the perturbation field \(\widetilde{{\mathbf {u}}}\) on the UC are compared by carrying out some numerical tests. Computations are performed by using classical Lagrangian bi-quadratic 8-node FEs within the FEAP code [28].
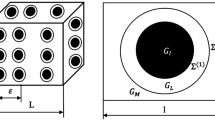
In particular, numerical analyses are developed for a two-phase composite material, characterized by cubic symmetry. The texture is made from a soft matrix with stiff square inclusions, both isotropic, regularly spaced and arranged as shown in Fig. 3, where the RVE is represented. The ratio between Young’s moduli of the inclusions, \(e_{i}\), and of the matrix, \(e_{m}\), is set \(e_{i}/e_{m}=10^{2}\), while the same Poisson ratio \(\nu =0.3\) is used for both the materials. The volume fraction f, defined as the ratio between the area of the inclusions and the total area of the UC, is set equal to 36 %.
In Fig. 3, the dashed lines delimit the central UC represented in Fig. 4a. Of course, the choice of the UC is not unique and different UCs can be selected, as for example that shown in Fig. 4b, [11, 12]. In the following, they will be referred as UC(a) and UC(b).
Micromechanical analyses concerning the macroscopic strain components \(E_1\), \(E_2\) and \(\varGamma _{12}\) are standard and are not presented below. Thus, numerical analyses are carried out only for the components \(K_1\), \(K_2\) and \(\varTheta \).
Fully displacement BCs, evaluated according to the kinematic map in Eq. (13), are imposed at the boundary of the RVE and the corresponding perturbation fields along the edges of the central UC are evaluated. These are compared with those obtained analyzing a single UC and applying the procedures described in Sects. 3.1 and 3.2, denoted in the following by M1 and M2, respectively. Both the UCs represented in Fig. 4 are analyzed.
Since the selected material exhibits cubic symmetry, the expressions of the coefficients s, \(b_{1}\), \(b_{2}\), \(c_{1}\) and \(c_{2}\), defined in Eqs. (18) and (19), become simpler.
In all the reported figures, solid lines correspond to the perturbation displacement fields, evaluated at the boundary of the UC located at the center of the RVE. Dashed lines refer to those evaluated for the single UC, adopting the procedure M1, and dotted lines correspond to the results obtained imposing the BCs deduced from the procedure M2. Moreover, the values of the displacements are normalized with respect to the maximum value in the UC of the correspondent component, obtained from the kinematic map.
Initially, the values of the coefficients \(\alpha _1\), \(\alpha _2\) and \(\alpha _3\) are determined. To this end, the UCs represented in Fig. 4 are analyzed and the integrals in Eq. (21) are evaluated. From computations, it results that the values of \(k_1/K_1\), \(k_2/K_2\) and \(\theta /\varTheta \) are lower than \(10^{-2}\) in this case, so that their effect can be neglected; then, in the following it is assumed \(\alpha _1=\alpha _2=\alpha _3=1\). It is worth noting that these coefficients are generally not negligible. Indeed, their values depend on the specific geometrical and mechanical properties of the UC. Nevertheless, the coefficients \(\alpha _1\), \(\alpha _2\) and \(\alpha _3\) can be computed following the procedure described in Sect. 2. It could be also emphasized that the very low values of the ratios \(k_1/K_1\), \(k_2/K_2\) and \(\theta /\varTheta \) are due to the kinematic map here adopted, that avoids the presence of perturbation displacements when homogeneous media are considered.
First of all, the case where \(K_{1}\ne 0\) is considered, while all the other macroscopic strain components vanish. In this case, the displacements applied at the boundary of the RVE are \(u_{1}^{*} = -K_{1}x_{1}x_{2}, u_{2}^{*} = \dfrac{1}{2}K_{1}(x_{1}^{2}+\nu _{12}x_{2}^{2})\).
In Figs. 5 and 6, the results for the UC(a) are reported. In particular, in Fig. 5 the horizontal and vertical perturbation components are plotted along the TOP and BOTTOM horizontal lines (see Fig. 3). No differences arise between the results for the horizontal component, while it is evident that a better approximation of the vertical component is obtained with M1 compared to M2. Instead, in Fig. 6 the three procedures lead to the same results for both horizontal and vertical components along the vertical lines (LEFT and RIGHT).
Figures 7 and 8 show the horizontal and vertical components of the perturbation fields along horizontal and vertical edges considering the UC(b). Obviously, the central UC in the RVE is selected accordingly. In this case, too, it emerges that the procedure M1 is more effective in capturing the actual response of the composite material. To be noted is that the solution corresponding to the curvature \(K_{2}\) can be obtained by rotating by \(\pi /2\) that evaluated for \(K_{1}\).
Finally, the case \(\varTheta \ne 0\) is considered. Now, the applied BCs on the RVE are computed according to \(u_{1}^{*} = \varTheta s\left[ 3b_{1}x_{1}^{2}x_{2}+c_{1}x_{2}^{3}\right] , u_{2}^{*} = - \varTheta s\left[ 3b_{2}x_{1}x_{2}^{2}+c_{2}x_{1}^{3}\right] \).
In Figs. 9 and 10, the results for the UC(a) are first shown. In this case, the horizontal and vertical perturbation components along the TOP and BOTTOM lines coincide with the vertical and horizontal components along the LEFT and RIGHT lines, respectively. In Figs. 11 and 12, the case of the UC(b) is analyzed. Also considering this macro-strain component, there is an evident improvement in reproducing the displacement field of the RVE, for all the considered components, adopting the procedure M1.
3.4 Characterization of the tractions
As mentioned in Sect. 3, the classical anti-periodicity of the tractions on the UC boundary, holding in the first order homogenization framework, is not verified in relation to the higher order deformation modes. Considering, for example, the case of \(K_1=1\) and all the other macroscopic strain components set equal to zero, it is interesting to show the actual trends of the traction components along the boundaries of the central unit cell extracted from the RVE (Fig. 3), made assembling UC(a) (Fig. 4). This will be assumed as the reference solution.
In Fig. 13a, b the traction components \(t_1\) and \(t_2\) are plotted along the top (\(t_{1/2}^T\)) and bottom (\(t_{1/2}^B\)) edges. It emerges that the \(t_1\) component is skew-periodic, while the \(t_2\) component is periodic.
Traction components along the TOP and BOTTOM edges of the UC(a) in the RVE: a \(t_1\) component; b \(t_2\) component
In Fig. 14a, b the traction components \(t_1\) and \(t_2\) are plotted along the left (\(t_{1/2}^L\)) and right (\(t_{1/2}^R\)) edges. Also in this case it results that the \(t_1\) component is skew-periodic, while the \(t_2\) component is periodic.
Traction components along the LEFT and RIGHT edges of the UC(a) in the RVE: a) \(t_1\) component; b) \(t_2\) component
The reported distributions, satisfying the equilibrium conditions enforced in the adopted FE formulation, show that the classical anti-periodicity conditions do not hold anymore.
It appears also relevant to show the same distributions, obtained by analyzing the single UC and by applying the two procedures M1 and M2, in comparison with the reference solution. In Fig. 15a, b the \(t_1\) and \(t_2 \) components, respectively, are reported along the top edge of UC(a). Similarly, in Fig. 16a, b the \(t_1\) and \(t_2 \) components, respectively, are depicted along the left edge of UC(a). In all the shown cases, a satisfactory agreement with the reference trends emerges, mainly when the more complex procedure M1 is adopted.
Comparison of the traction components along the TOP edge on the UC(a): a \(t_1\) component; b \(t_2\) component. Solid lines: reference solution (UC extracted from the RVE); dashed lines: solution obtained with procedure \(M_1\); dotted lines: solution obtained with procedure \(M_2\)
Comparison of the traction components along the LEFT edge on the UC(a): a \(t_1\) component; b \(t_2\) component. Solid lines: reference solution (UC extracted from the RVE); dashed lines: solution obtained with procedure \(M_1\); dotted lines: solution obtained with procedure \(M_2\)
It can be deduced that, although the UC satisfies the equilibrium condition with zero body forces, the equilibrium between adjacent cells is not ensured. This is a consequence of the adopted approximated BCs. Note that, if the classical periodicity conditions were adopted to evaluate the perturbation field \(\tilde{\mathbf {{u}}}\), the derived tractions on the UC boundary would have been significantly far from the reference solution. Indeed, these are not reported in Figs. 15 and 16, as their values are completely out of range.
4 Identification of the constitutive terms
The identification procedure adopted in this work is based on the generalized Hill–Mandel macrohomogeneity condition. The virtual work evaluated at the macroscopic Cosserat point is set equal to the average virtual work of the heterogeneous Cauchy medium in the UC. Thus, the following expression holds:
where \(\varvec{\varSigma }\) is the Cosserat stress vector evaluated at the macroscopic point, while \(\varvec{\sigma }\) is the Cauchy stress vector at the typical point of the UC.
After solving the BVP on the UC and determining the microscopic strain and stress fields, \(\varvec{\varepsilon }\) and \(\varvec{\sigma }\), the homogenized Cosserat elastic constitutive matrix \({\mathbf {C}}\) can be derived by using Eq. (52). In particular, considering a two-phase composite material with a regular arrangement of the inclusions, characterized by orthotropic texture, the homogenized Cosserat elastic constitutive matrix, expressed in a reference frame aligned with the principal axes of the material, results as:
Regarding the two-phase composite medium examined in Sect. 3.3, the macroscopic Cosserat elasticity matrix \({\mathbf {C}}\) is evaluated considering the two UCs shown in Fig. 4. It is worthwhile noting that the two specific UCs here analyzed are the same as those adopted by [11, 12], where it is remarked that the results of the identification procedure depend on the choice of the UC. In particular, they suggest the criterion of centering the UC in the stiffer phase, to determine the couple-stress constitutive constants. Here, the dependence of the identification results on the centering of the UC is analyzed. Indeed, differently from the Cauchy coefficients, which are proved to be independent on the specific choice of the UC (for a given composite), for the bending and skew-symmetric shear Cosserat coefficients this is not straightforward, at least in the framework of computational homogenization. The constants \(C_{11}\), \(C_{22}\), \(C_{12}\) and \(C_{33}\), appearing in the first \(3\times 3\) submatrix of \({\mathbf {C}}\) and involved in the constitutive relationship between the Cauchy stress and strain components, are evaluated according to the classical homogenization procedure. Here, the attention is focused on the determination of \(C_{44}\), \(C_{55}\) and \(C_{66}\), governing the bending and skew-symmetric shear behavior of the Cosserat equivalent medium.
Aiming at determining the coefficient \(C_{44}\), the macroscopic strain component \(K_{1}=1\) is applied to the UC, with all the other components set equal to zero. Hence, the applied kinematic map, in this case, results as:
For the two selected UCs, \(C_{44}\) is evaluated and reported in Table 1, by using both the above presented procedures M1 and M2. Note that, due to the cubic symmetry of the composite material, the case \(K_{2}=1\) leads to results which are the rotated of the case \(K_{1}=1\), so that it is \(C_{55}=C_{44}\). It emerges that the two adopted methods, M1 and M2, lead to homogenized constitutive parameters that differ by about 8 % for the same UC. Moreover, the obtained results depend on the choice of the UC. Indeed, the values of \(C_{44}\) computed for the two UCs differ by 14 %, when the method M1 is adopted, and about 27 % when the method M2 is employed. The dependence of the identified coefficient \(C_{44}\) on the choice of the UC can be reasonably related to the adopted polynomial kinematic map, as well as to the identification procedure.
To motivate the above results, the expression of the average internal work in Eq. (52), evaluated over the UC, is reported in expanded form as:
in which clearly emerges that the relative position of the two (stiffer and softer) constituents, with respect to the UC center, strongly influences the value of the identified parameter. Indeed, when the stiffer constituent is farer from the center, the value of \(C_{44}\) is higher. This problem is well-known in literature [12, 15, 20] and is related to the definition of the higher-order or couple stresses as the volume average of the product of microscopic stresses and microscopic coordinates over the UC.
Further numerical tests are performed to investigate on the influence of the size of the RVE [17, 21]. Various square RVEs are considered, taking into account assemblages of \(3 \times 3\), \(5 \times 5\), \(7 \times 7\), \(9 \times 9, \ldots , 15 \times 15\) UCs, subjected to the boundary conditions shown in Fig. 2, which correspond to the M2 methodology illustrated in Sect. 3.2. The average internal work is evaluated over the entire RVE domains and rescaled by factor \(L^{2}\) with L the size of the square RVE. This identification procedure is denoted as P1.
In Table 2, the values of \(C_{44}\) computed for the different RVEs are reported. Thanks to the introduction of the factor \(L^{2}\), the dependence of the homogenized coefficient \(C_{44}\) on the size of the RVE is avoided. To the same end, also in [22] a correction to the higher order constitutive coefficients is introduced. As the RVE size increases, the scaled values of \(C_{44}\) for the two UCs in Fig. 4 converge to the same quantity, from above and from below, respectively.
Simple calculations reveal that the converged value of \(C_{44}\) in Table 2 can be obtained following a simple procedure. Let the classical first order homogenization be accomplished and the homogenized moduli for the equivalent Cauchy medium derived. Then, the obtained equivalent homogeneous UC is considered and is subjected to the higher order term of the polynomial kinematic map, corresponding to the curvature \(K_1\). As a result, the value \(C_{44}=18.1\) is obtained, which represents the converged bending elastic coefficient. It can be remarked that in the latter case, since a homogeneous UC is considered, where the perturbation displacement field vanishes, no BVPs have to be solved for the computation of \(C_{44}\). This leads to think that the response of the heterogeneous medium tends to the response of the Cauchy medium subjected to a curvature.
A possible alternative for the evaluation of the elastic coefficient \(C_{44}\), different from the previous one and characterized by the independence on the RVE size is herein proposed and denoted as P2. The main idea consists in distinguishing in the RVE internal work (right hand side of Eq. 52) the contribution of the classical Cauchy strain components from that related to the Cosserat additional deformation modes. When the RVE total internal work is computed by summing the work evaluated in each UC composing it, the contribution associated to the classical Cauchy deformation modes acting on the UC has to be ignored. In other words, this corresponds to subtract from the strain distribution in the UC its average value and then, on the basis of the resulting strains, compute the internal work to evaluate the elastic coefficient \(C_{44}\). In this way only the pure bending effect is taken into account, while the axial Cauchy modes are disregarded. Of course, the same procedure can be applied for the other Cosserat modes to identify \(C_{55}\), when different from \(C_{44}\), and \(C_{66}\).
In Table 2 the values of the elastic coefficient \(C_{44}\) computed adopting the procedure P2 are also reported. The numerical results show that the identified values remain almost the same as the RVE size increases; the very small variation observed for the \(C_{44}\) value is due to the boundary effects.
In Table 3 the values of \(C_{44}\) are reported considering two different contrasts in the elastic properties of the constituents, i.e. \(e_i/e_m=10^3\) and \(e_i/e_m=10\). The same trend as in Table 2 is shown. Even in this case, the procedure P1 leads to identify different values of the elastic coefficient \(C_{44}\) when RVE size is increased, with the value of \(C_{44}\) converging to the one obtained considering the homogenized Cauchy medium; on the contrary, the procedure P2 is able to obtain a value for \(C_{44}\) which is (almost) independent on the RVE size.
When it is set \(\varTheta =1\), while all the other macro-level strain components are equal to zero, the components of the kinematic map are:
Table 4 collects the results in terms of the coefficient \(C_{66}\) for the two selected UCs, evaluating the perturbation displacement fields with M1 and M2 methods. Again, different results are obtained for the two UCs and for the two adopted methods. The average virtual work results as:
In this case, too, it is evident that the position of the two constituents, with respect to the center of the reference system in the UC, influences the value of the average work. In Table 5 the values of \(C_{66}\), for the same RVEs considered in the previous application (\(3 \times 3\), \(5 \times 5\),...,\(15 \times 15\)) are derived using the two proposed procedures, i.e. P1 and P2. Adopting the procedure P1, a convergence value for \(C_{66}\) is reached from above in the case of the UC(a) and from below for the UC(b), as the RVE size increases. Note that in this case the convergence rate is slower than for \(C_{44}\) and, again, the converged results are not influenced by the choice of the UC. Then, computations are also performed adopting the procedure P2; in this case, the identified value of \(C_{66}\) does not (substantially) change for the different RVE sizes, showing the suitability of the proposed approach.
In order to validate the effectiveness of the presented homogenization procedure, a structural 2D application on a rectangular wall made from a composite material is presented. The geometry together with the loading and boundary conditions are reported in Fig. 17, adopting the following dimensionless parameters: \(B/H=1.6\), \(b/H=0.4\), \(e_{i}H/p=250000\), \(e_{i}/e_{m}=100\), \(\nu _{i}=0.3\) and \(\nu _{m}=0.3\). The wall is made from the periodic repetition of \(16 \times 10\) UCs, adopting the UC(a) and (b). In Fig. 17 the arrangement considered by adopting UC(a) is shown on the left, while on the right side that corresponding to the adoption of UC(b) is reported. The numerical simulations are performed considering the response of the heterogeneous materials, compared with the response of the homogenized Cosserat media. The values of the homogenized elastic coefficients \(C_{44}\), \(C_{55}\) and \(C_{66}\), used in the equivalent Cosserat models, are derived by means of the M1 method, with procedure P2, and these are reported in Tables 1 and 4. The profile of the vertical displacements under the vertical load area is firstly derived on the equivalent Cauchy model. Then, this vertical displacement distribution is applied at the top edge of the wall and its response is evaluated by using both the micromechanical and the Cosserat models. Regarding these last, the rotation degrees of freedom at the boundary are not restrained. Due to the symmetry of the problem, only one half of the panel is considered.
Panel under vertical load: geometry and boundary conditions
The structural stiffness is evaluated by dividing the total vertical reaction by the maximum vertical displacement at the midspan of the top edge. In Table 6 the values of the stiffness, obtained considering the different UCs, are shown. The second column shows the results obtained by the micromechanical analysis of the real heterogeneous structure, while the third, fourth and fifth columns contain the stiffness of the equivalent homogenized medium, evaluated by adopting the Cosserat, Cauchy and couple stress model at the macro-level, respectively. It is noteworthy that the position of the inclusions in the heterogeneous medium significantly influences the response, causing a difference of about 7 % in the stiffness values. For both the considered UCs, the homogenized Cosserat models provide the better estimation of the stiffness. As expected, the Cauchy model gives results not influenced by the arrangement of the UCs. The Cosserat based homogenization results in a stiffer or softer medium, depending on the position of the stiff inclusion in the UC. Finally, also the results obtained by using the couple stress model are shown for comparison, resulting stiffer than the Cosserat ones, since the rotational deformation component vanishes in this case. With reference to the UC(a), in Fig. 18, on the left side, the vertical stress along a horizontal alignment placed at the mid-height of the panel is reported, for both the heterogeneous (solid line) and the homogenized (dashed line) models. On the right side, instead, the comparison of the vertical displacements along the same alignment is shown. Analogously, in Fig. 19 the same distributions as in Fig. 18 are shown in the case of UC(b).
UC(a) Left: Vertical stress versus panel abscissa at height H = 5. Solid line: heterogeneous model; Dashed line: Cosserat homogenized model. Right: Vertical stress versus panel abscissa at height H = 5. Solid line: heterogeneous model; Dashed line: Cosserat homogenized model
UC(b) Left: Vertical stress versus panel abscissa at height H=5. Solid line: heterogeneous model; Dashed line: Cosserat homogenized model. Right: Vertical stress versus panel abscissa at height H=5. Solid line: heterogeneous model; Dashed line: Cosserat homogenized model
From the comparison of the vertical stress distributions, it is clear that the effective Cosserat models provide results close to the average of that evaluated with the heterogeneous models. In Fig. 18 the stress distributions show more pronounced peaks with respect to the analogous in Fig. 19 and this is related to the position of the measurement line, that in the former case intersects both the constituents, while in the latter case runs exclusively along the matrix.
5 Conclusions
Focusing on the computational homogenization, where the Cosserat and Cauchy continuum models are assumed at the macro- and micro-level, to study periodic 2D composite materials, some relevant topics were discussed and analyzed. To characterize the perturbation fields in presence of higher order polynomial boundary conditions, a micromechanical three-step computational homogenization was adopted. The results obtained by analyzing a single UC, proper selected for the composite analyzed, are in a very good agreement with the reference solution evaluated on a large RVE made from the same material. The observed little discrepancies are due to the lacking in fully satisfying the kinematic compatibility between the adjacent UCs. Furthermore, the perturbation fields, evaluated by applying on the UC the BCs derived in [1] and reported for comparison, match worst the reference solution, although the results are satisfactory taking into consideration the simplicity of the procedure.
The other issue discussed in the paper concerns the identification of the homogenized linear elastic constitutive parameters. Reference was made to the additional Cosserat components, thus relating \(K_{1}\), \(K_{2}\) and \(\varTheta \) to the work-conjugated stresses, for the studied two-phase composite material. The classical Hill-Mandel procedure was adopted. By analyzing two different UCs, selected for representing the composite texture, it emerged that the constitutive response of the homogenized medium depends on the choice of the cell. In fact, while the elastic Cauchy coefficients are independent on the specific choice of the UC, for the bending and skew-symmetric shear Cosserat coefficients this does not occur, at least in the framework of computational homogenization. This fact is also confirmed by the results obtained from the structural application. The two different UCs used to build the structure lead to slightly different results, which agree with those evaluated with the equivalent Cosserat media. It is also highlighted that considering a RVE made from an assemblage of UCs, the elastic coefficients converge to the same value, apart from the considered UC. This value corresponds to that evaluated by simply considering at the micro-level a homogenized Cauchy medium.
An alternative procedure has been proposed to avoid the dependence of the identified Cosserat elastic coefficients on the RVE size, based on the idea of evaluating in the RVE only the internal work related to the Cosserat deformation modes by eliminating the Cauchy strain contribution. This proposal resulted to be effective in overcoming the mentioned drawback of the classical Hill–Mandel procedure. It is worth noting that, in the framework of the asymptotic techniques applied to the strain gradient models [4, 8, 10, 26, 29], some limits arising when the computational homogenization is performed are naturally overcome. For example, the higher order terms automatically vanish in the case of homogeneous medium. Furthermore, the identified higher order effective elastic coefficients seem not to depend on the selection of the UC. Considering this approach, the theory has been developed in a rigorous and robust mathematical tool, in which hierarchy of equilibrium problems is solved at the different orders, considering proper auxiliary body forces (with zero volume average) and obtaining periodic perturbation functions. Nevertheless, to date the asymptotic technique has been satisfactorily applied to link a higher order Cauchy continuum at the macro-level to a classical first order Cauchy medium at the micro-level. On the other hand, this has not been adopted in the case of the Cosserat–Cauchy homogenization, due to the difficulty of coupling, at the two scales, continua endowed with different number of displacement degrees of freedom. On the contrary, the computational homogenization is well-established and widely adopted in this context, although some open issues still remain.
The proposed paper is a contribution to better clarify some aspects. In particular:
-
1.
the effectiveness of simplified periodicity/skew-periodicity conditions with respect to more complex procedures is shown;
-
2.
some new advancements in the problem of the identification of an equivalent Cosserat continuum starting from a heterogeneous Cauchy model are made;
-
3.
some open issues in the framework of the Cosserat–Cauchy homogenization procedure are remarked.
Hence, it appears relevant to carry on further developments, focusing on the formulation of the link between the macro- and micro-levels, as well as on the improvement of the identification procedure.
References
Addessi D, De Bellis ML, Sacco E (2013) Micromechanical analysis of heterogeneous materials subjected to overall cosserat strains. Mech Res Commun 54:27–34
Addessi D, Sacco E (2012) A multi-scale enriched model for the analysis of masonry panel. Int J Solids Struct 49:865–880
Anthoine A (1995) Derivation of the in-plane elastic characteristics of masonry through homogenization theory. Int J Solids Struct 32(2):137–163
Bacigalupo A (2014) Second-order homogenization of periodic materials based on asymptotic approximation of the strain energy: formulation and validity limits. Meccanica 49(6):1407–1425
Bacigalupo A, Gambarotta L (2010) Second-order computational homogenization of heterogeneous materials with periodic microstructure. ZAMM Z Angew Math Mech 90(10–11):796–811
Bacigalupo A, Gambarotta L (2012) Computational two-scale homogenization of periodic masonry: characteristic lengths and dispersive waves. Comput Method Appl Mech 213–216:16–28
Bacigalupo A, Gambarotta L (2013) Multi-scale strain-localization analysis of a layered strip with debonding interfaces. Int J Solids Struct 50:2061–2077
Bakhvalov N, Panasenko G (1989) Homogenisation: averaging processes in periodic media. Mathematical problems in the mechanics of composite materials. Springer, New York
Bigoni D, Drugan WJ (2007) Analytical derivation of Cosserat moduli via homogenization of heterogeneous elastic materials. J Appl Mech 74:741–753
Boutin C (1996) Microstructural effects in elastic composites. Int J Solids Struct 33(7):1023–1051
Bouyge F, Jasiuk I, Boccara S, Ostoja-Starzewski M (2002) A micromechanically based couple-stress model of an elastic orthotropic two-phase composite. Eur J Mech A Solid 21:465–481
Bouyge F, Jasiuk I, Ostoja-Starzewski M (2001) A micromechanically based couple-stress model of an elastic two-phase composite. Int J Solids Struct 38:1721–1735
De Bellis M, Addessi D (2011) A Cosserat based multi-scale model for masonry structures. Int J Multiscale Comput 9(5):543–563
Feyel F (2003) A multilevel finite element method (fe2) to describe the response of highly non-linear structures using generalized continua. Comput Method Appl Mech 192:3233–3244
Forest S (1998) Mechanics of generalized continua: construction by homogeneization. J. Phys. IV France 8
Forest S, Sab K (1998) Cosserat overall modeling of heterogeneous materials. Mech Res Commun 25:449–454
Forest S, Trinh D (2011) Generalized continua and non-homogeneous boundary conditions in homogenisation methods. ZAMM Z Angew Math Mech 91(2):90–109
Kaczmarczyk L, Pearce C, Bicanic N (2008) Scale transition and enforcement of rve boundary conditions in second-order computational homogenization. Int J Numer Methods Eng 74:506–522
Kouznetsova V, Geers M, Brekelmans W (2004a) Multi-scale second-order computational homogenization of multi-phase materials: a nested finite element solution strategy. Comput Method Appl Mech 193:5525–5550
Kouznetsova VG (2002) Computational homogenization for the multi-scale analysis of multi-phase materials. Ph.D. thesis, Technische Universiteit Eindhoven
Kouznetsova VG, Geers MGD, Brekelmans WAM (2004b) Size of a representative volume element in a second-order computational homogenization framework. Int J Multiscale Comput Eng 2:575–598
Li J (2011) A micromechanics-based strain gradient damage model for fracture prediction of brittle materials part I: homogenization methodology and constitutive relations. Int J Solids Struct 48(24):3336–3345
Miehe C (2002) Strain-driven homogenization of inelastic microstructures andcomposites based on an incremental variational formulation. Int J Numer Methods Eng 55:1285–1322
Sánchez-Palencia E (1980) Non homogeneous media and vibration theory, vol 127 of Lecture Notes in Physics. Springer, Berlin
Sanchez-Palencia E (1987) Boundary layers and edge effects in composites. In: Sánchez-Palencia E, Zaoui A (eds.) Homogenization techniques for composite media. Lecture notes in physics 272. Springer, Berlin, p 121–192
Smyshlyaev VP, Cherednichenko K (2000) On rigorous derivation of strain gradient effects in the overall behaviour of periodic heterogeneous media. J Mech Phys Solids 48:1325–1357
Suquet P (1987) Elements of homogenization for inelastic solid mechanics. In: Sánchez-Palencia E, Zaoui A (eds.) Homogenization Techniques for Composite Media. Lecture Notes in Physics 272. Springer, Berlin, p 193–278
Taylor R (2011) FEAP-A finite element analysis program, Version 8.3. Department of Civil and Environmental Engineering, University of California at Berkeley, California
Tran TH, Monchiet V, Bonnet G (2012) A micromechanics-based approach for the derivation of constitutive elastic coefficients of strain-gradient media. Int J Solids Struct 49:783–792
Trovalusci P, Masiani R (2003) Non-linear micropolar and classical continua for anisotropic discontinuous materials. Int J Solids Struct 40(5):1281–1297
van der Sluis O, Schreurs PJG, Brekelmans WAM, Meijer HEH (2000) Overall behaviour of heterogeneous elastoviscoplastic materials: effect of microstructural modelling. Mech Mater 32:449–462
van der Sluis O, Vosbeek PHJ, Schreurs PJG, Meijer HEH (1999) Homogenization of heterogeneous polymers. Int J Solids Struct 36:3193–3214
Yuan X, Tomita Y, Andou T (2008) A micromechanical approach of nonlocal modeling for media with periodic microstructures. Mech Res Commun 35(1–2):126–133
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Addessi, D., De Bellis, M.L. & Sacco, E. A micromechanical approach for the Cosserat modeling of composites. Meccanica 51, 569–592 (2016). https://doi.org/10.1007/s11012-015-0224-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11012-015-0224-y