1 Introduction

A study of the dynamics of fluid transport by peristaltic motion of the confining walls is important in understanding a variety of biological and engineering phenomena. Specifically, such motion appears in swallowing food through oesophagus, urine transport from kidney to bladder, the transport of spermatozoa, roller and finger pumps, the motion of chyme in the small intestine, the mechanical and neurological aspects of reflex, transport of lymph in the lymphatic vessels and in the vasomotion of small blood vessels such as arterioles, venules and capillaries. Initial studies on peristalsis were carried out for Newtonian fluid. These include the work of Shapiro [1], Shapiro et al. [2], Fung and Yih [3], Jaffrin [4], Brown and Hung [5], Takabatake and Ayukawa [6] and many others. It is pertinent to mention that Shapiro et al. [2] performed the analysis of peristaltic motion in wave frame of reference while Fung and Yih [3] used laboratory frame of reference. The choice of Newtonian fluid in the above mentioned studies restricted their application to urine transport only. This is because most of the fluids occurring in physiology and industry are non-Newtonian in nature and have a great impact on the mathematical and physical nature of the problem. Motivated by this fact, Raju and Devanathan [7] performed a study regarding peristaltic flow of blood using power-law fluid. In continuation [8], they utilized the constitutive equation of a viscoelastic fluid with fading memory in their analysis. Their work motivated several other researcher to work on theoretical analysis of peristaltic motion of different model capable of predicting different non-Newtonian characteristics such as shear thinning or shear thickening [9–12], thixotropy [13], normal stress effect [14], spurt [15, 16], viscoelasticity [17–19] etc.

In all the above-mentioned attempts peristaltic flows have been discussed in two-dimensional channels or axisymmetric tubes. But in reality, the geometry of most physiological conduits and glandular ducts is curved. The effect of curvature seems meaningful in this context. This fact provides a natural motivation to study peristaltic flow in curved channels. It is seen from the available studies that very less attention is focused on the peristaltic flows in curved channels. Sato et al. [20] discussed the two-dimensional peristaltic flow of a viscous fluid in a curved channel in the laboratory frame of reference. They have used long wavelength and low Reynolds number approximations in deriving the flow equations. Ali et al. [21] provided the analysis of two-dimensional peristaltic motion in the wave frame of reference. In another paper, Ali et al. [22] investigated peristaltic motion of a third grade fluid in a curved channel. Some resent studies on peristaltic flows in a curved channel regarding the effects of compliant wall, non-Newtonian rheology, unsteadiness, magnetic field and slip condition can be found in refs. [23–36].

Literature survey indicates that up till now there is not available a single attempt regarding peristaltic motion of an Oldroyd-B fluid in a curved channel under long wavelength assumption. This is perhaps because of discrepancy of Oldroyd-B model in predicting viscoelastic features when peristaltic flow under long wavelength approximation is considered in straight geometries. This fact also motivated us to look whether viscoelastic parameters will retain in the analysis of peristaltic motion of Oldroyd-B fluid in curved channel under long wavelength approximation or not. To our surprise, we found the answer in affirmative and thus detail analysis is performed to investigate the simultaneous effects of viscoelasticity and curvature of the channel on the peristaltic transport.

The presentation of paper is as follows: Sect. 2 presents the formulation of the problem. Rate of volume flow and appropriate boundary conditions are given in Sect. 3. The method of solution is illustrated in Sect. 4. Section 5 consists of a detailed discussion about the results. We end up the paper by giving some concluding remarks in Sect. 6.

2 Description of the problem

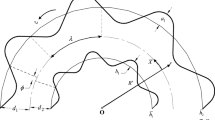
Consider a homogeneous incompressible Oldroyd-B fluid in a curved channel of width 2a. The channel is coiled in a circle of radius R* having its centre at origin O. The schematic diagram of the flow geometry is given in Fig. 1. Let \( \bar{V} \) and \( \bar{U} \) be the velocity components in radial (\( \bar{R} \)) and axial (\( \bar{X} \)) directions, respectively. The fluid is set into motion due to the contraction and expansion of the flexible walls of the channel. The mathematical expressions describing the wall geometry are:

Fig. 1
figure 1

Schematic diagram of the problem

Full size image
$$ H\left( {\bar{X},\bar{t}} \right) = a + b \text{sin}\left[ {\left( {\frac{2\pi }{\lambda }} \right)\left( {\bar{X} - c\bar{t}} \right)} \right] , \quad \quad {\text{Upper}}\, {\text{wall}} $$
(1)
$$ - H\left( {\bar{X},\bar{t}} \right) = - a - b \text{sin}\left[ {\left( {\frac{2\pi }{\lambda }} \right)\left( {\bar{X} - c\bar{t}} \right)} \right] , \quad \quad {\text{Lower}}\, {\text{wall}} $$
(2)

In above expressions c is the speed, λ is the wavelength, b is the amplitude and \( \bar{t} \) is the time.

For the flow under consideration the velocity field is of the following form

$$ \bar{\varvec{V}} = \left[ {\bar{V}\left( {\bar{X},\bar{R},\bar{t}} \right), \bar{U}\left( {\bar{X},\bar{R},\bar{t}} \right), 0 } \right], $$
(3)

and equations that given the present flow are

$$ \nabla .\bar{\varvec{V}} = 0 , $$
(4)
$$ \rho \frac{{d{\bar{\mathbf{V}}}}}{{d\bar{t}}} = \nabla .\bar{\varvec{T}} , $$
(5)

The constitutive equation for an Oldroyd-B fluid is given by

$$ \bar{\varvec{T}} = - p\bar{\varvec{I}} + \varvec{\bar{S}}, $$
(6)

where the extra stress tensor \( \bar{\varvec{S}} \) satisfies [31]

$$ \left( { 1 { + }\lambda_{1} \frac{D}{{D\bar{t}}}} \right)\bar{\varvec{S}} = \mu \left( { 1 { + }\lambda_{2} \frac{D}{{D\bar{t}}}} \right)\bar{\varvec{A}}_{1} . $$
(7)

In the above equation μ is the coefficient of shear viscosity, \( D/D\bar{t} \) is the contravariant convected derivative, λ t (i = 1, 2) are relaxation and retardation times, respectively, \( \bar{A}_{1} \) is the first Rivlin–Ericksen tensor defined by [37, 38]

$$ \bar{\varvec{A}}_{1} = \left( {grad\bar{\varvec{V}}} \right) + \left( { {grad\bar{\varvec{V}}} } \right)^{T} , $$
(8)
$$ \frac{{D\bar{\varvec{S}}}}{{D\bar{t}}} = \frac{{\partial \bar{\varvec{S}}}}{{\partial \bar{t}}} + \left( {\bar{\varvec{V}}.{\varvec{\nabla }}} \right){\bar{\varvec{S}}} - {\bar{\varvec{L}}}{\bar{\varvec{S}}} - \bar{\varvec{S}} {\bar{\varvec{L}}}^{T},\left(\begin{aligned} {\text{for a contravariant tensor}} \hfill \\{\text{of rank 2}} \hfill \\ \end{aligned} \right) $$
(9)

and

$$ \frac{{D\bar{\varvec{b}}}}{{D\bar{t}}} = \frac{{\partial \bar{\varvec{b}}}}{{\partial \bar{t}}} + \left( {\bar{\varvec{V}} .{\mathbf{\nabla }}} \right)\bar{\varvec{b}} - {\bar{\varvec{L}}\bar{\varvec{b}}}.\quad \left( {\text{for a contravriant vector}} \right) $$
(10)

In view of Eq. (6), we can write Eq. (5) as

$$ \rho \frac{{d{\bar{\mathbf{V}}}}}{{d\bar{t}}} = - {\mathbf{\nabla }}\bar{p} + {\mathbf{\nabla }} .\bar{\varvec{S}}. $$
(11)

Now to find the two-dimensional equations we need to eliminate \( \bar{\varvec{S}} \) between Eqs. (11) and (7). To this end, we apply the operator \( \left( {1 + \lambda_{1} \frac{D}{{D\bar{t}}}} \right) \) to the momentum Eq. (11) and get

$$ \rho \left( { 1 { + }\lambda_{1} \frac{D}{{D\bar{t}}}} \right)\frac{{d\bar{\varvec{V}}}}{{d\bar{t}}} = - \left( { 1 { + }\lambda_{1} \frac{D}{{D\bar{t}}}} \right){\mathbf{\nabla }}\bar{p} + \left( { 1 + \lambda_{1} \frac{D}{{D\bar{t}}}} \right){\mathbf{\nabla }} .\bar{\varvec{S}}. $$
(12)

Following Harris [38] we use the commutatively of the operator ∇ and \( D/D\bar{t} \) i.e.

$$ \frac{D}{{D\bar{t}}}\left( {{\mathbf{\nabla }}{\mathbf{.}}} \right) = {\mathbf{\nabla }}.\left( {\frac{D}{{D\bar{t}}}} \right). $$
(13)

Therefore Eq. (12) becomes

$$ \rho \left( { 1 { + }\lambda_{1} \frac{D}{{D\bar{t}}}} \right)\frac{{d\bar{\varvec{V}}}}{{d\bar{t}}} = - {\mathbf{\nabla }}\left( { 1 + \lambda_{1} \frac{D}{{D\bar{t}}}} \right)\bar{p} + {\mathbf{\nabla }} .\left( { 1 + \lambda_{1} \frac{D}{{D\bar{t}}}} \right)\bar{\varvec{S}}, $$

which in view of Eq. (7) takes the form

$$ \rho \left( { 1 { + }\lambda_{1} \frac{D}{{D\bar{t}}}} \right)\frac{{d\bar{\varvec{V}}}}{{d\bar{t}}} = - {\mathbf{\nabla }}\bar{p}^{*} + \left( { 1 { + }\lambda_{2} \frac{D}{{D\bar{t}}}} \right){\mathbf{\nabla }} .\bar{\varvec{A}}_{\varvec{1}} , $$
(14)

where \( \bar{p}^{*} \) is the modified pressure.

For two-dimensional velocity field defined by (3), Eqs. (4) and (14) yield the following equations:

$$ \frac{\partial }{{\partial \overline{R} }}\left\{ {\left( {\overline{R} + R^{*} } \right)\overline{V} } \right\} + R^{*} \frac{{\partial \overline{U} }}{{\partial \overline{X} }} = 0, $$
(15)
$$ \begin{aligned} &- \frac{{\overline{U}^{2} }}{{\overline{R} + R^{*} }} + \overline{V} \frac{{\partial \overline{V} }}{{\partial \overline{R} }} + \frac{{\partial \overline{V} }}{{\partial \overline{t} }} + \frac{{R^{*} \overline{U} }}{{\overline{R} + R^{*} }}\frac{{\partial \overline{V} }}{{\partial \overline{X} }} + \upsilon \left( { - \frac{{R^{*} }}{{\overline{R} + R^{*} }}\frac{{\partial^{2} \overline{U} }}{{\partial \overline{X} \partial \overline{R} }} + \frac{{3R^{*} }}{{\left( {\overline{R} + R^{*} } \right)^{2} }}\frac{{\partial \overline{U} }}{{\partial \overline{X} }} + \frac{{2\overline{V} }}{{\left( {\overline{R} + R^{*} } \right)^{2} }} - \frac{2}{{\overline{R} + R^{*} }}\frac{{\partial \overline{V} }}{{\partial \overline{R} }}} \right. - 2\frac{{\partial^{2} \overline{V} }}{{\partial \overline{R}^{2} }} \hfill \\ &\quad \left. { - \left( {\frac{{R^{*} }}{{\overline{R} + R^{*} }}} \right)^{2} \frac{{\partial^{2} \overline{V} }}{{\partial \overline{X}^{2} }}} \right) + \lambda_{1} \left( { - \frac{{2\overline{U} }}{{\overline{R} + R^{*} }}\frac{{\partial \overline{U} }}{{\partial \overline{t} }} - \frac{{2R^{*} \overline{U}^{2} }}{{\left( {\overline{R} + R^{*} } \right)^{2} }}\frac{{\partial \overline{U} }}{{\partial \overline{X} }} + \frac{{\overline{U}^{2} \overline{V} }}{{\left( {\overline{R} + R^{*} } \right)^{2} }} - \frac{{2\overline{U} \overline{V} }}{{\overline{R} + R^{*} }}\frac{{\partial \overline{U} }}{{\partial \overline{R} }} + \frac{{\overline{U}^{2} }}{{\overline{R} + R^{*} }}\frac{{\partial \overline{V} }}{{\partial \overline{R} }}} \right. + \overline{V}^{2} \frac{{\partial^{2} \overline{V} }}{{\partial \overline{R}^{2} }} + \frac{{\partial^{2} \overline{V} }}{{\partial \overline{t}^{2} }} \hfill \\ &\quad\left. { + 2\overline{V} \frac{{\partial^{2} \overline{V} }}{{\partial \overline{R} \partial \overline{t} }} + \frac{{2R^{*} \overline{U} }}{{\overline{R} + R^{*} }}\overline{V} \frac{{\partial^{2} \overline{V} }}{{\partial \overline{R} \partial \overline{X} }} - \frac{{2R^{*} \overline{U} \overline{V} }}{{\left( {\overline{R} + R^{*} } \right)^{2} }}\frac{{\partial \overline{V} }}{{\partial \overline{X} }} + 2\left( {\frac{{R^{*} }}{{\overline{R} + R^{*} }}} \right)\overline{U} \frac{{\partial^{2} \overline{V} }}{{\partial \overline{X}^{2} }} + \left( {\frac{{R^{*} }}{{\overline{R} + R^{*} }}} \right)^{2} \overline{U}^{2} \frac{{\partial^{2} \overline{V} }}{{\partial \overline{X}^{2} }}} \right) + \lambda_{2} \left( { - \frac{{R^{*} }}{{\overline{R} + R^{*} }}\frac{{\partial^{3} \overline{U} }}{{\partial \overline{X}^{2} \partial \overline{R} }}} \right. \hfill \\ &\quad- \left( {\frac{{R^{*} }}{{\overline{R} + R^{*} }}} \right)^{2} \overline{U} \frac{{\partial^{3} \overline{U} }}{{\partial \overline{X}^{2} \partial \overline{R} }} + \frac{{3R^{*} }}{{\left( {\overline{R} + R^{*} } \right)^{2} }}\frac{{\partial^{2} \overline{U} }}{{\partial \overline{X} \partial \overline{t} }} + \frac{{3R^{*2} \overline{U} }}{{\left( {\overline{R} + R^{*} } \right)^{3} }}\frac{{\partial^{2} \overline{U} }}{{\partial^{2} \overline{X} }} - \frac{{R^{*} \overline{V} }}{{\overline{R} + R^{*} }}\frac{{\partial^{3} \overline{U} }}{{\partial \overline{R}^{2} \partial \overline{X} }} + \frac{{4R^{*} \overline{V} }}{{\left( {\overline{R} + R^{*} } \right)^{2} }}\frac{{\partial^{2} \overline{U} }}{{\partial \overline{X} \partial \overline{R} }} - \frac{{6R^{*} \overline{V} }}{{\left( {\overline{R} + R^{*} } \right)^{3} }}\frac{{\partial \overline{U} }}{{\partial \overline{X} }} \hfill \\ \end{aligned} $$
$$ \begin{aligned} &- \frac{{4\overline{V}^{2} }}{{\left({\overline{R} + R^{*} } \right)^{3} }} + \frac{{R^{*}}}{{\overline{R} + R^{*} }}\frac{{\partial^{2} \overline{U} }}{{\partial \overline{X} \partial \overline{R} }}\frac{{\partial \overline{V} }}{{\partial \overline{R} }} - \frac{{3R^{*} }}{{\left({\overline{R} + R^{*} } \right)^{2} }}\frac{{\partial \overline{U}}}{{\partial \overline{X} }}\frac{{\partial \overline{V}}}{{\partial \overline{R} }} + \frac{{2\overline{V} }}{{\left({\overline{R} + R^{*} } \right)^{2} }}\frac{{\partial \overline{V}}}{{\partial \overline{R} }} + \frac{2}{{\overline{R} + R^{*}}}\left( {\frac{{\partial \overline{V} }}{{\partial \overline{R} }}}\right)^{2} - \frac{{2\overline{V} }}{{\overline{R} + R^{*}}}\frac{{\partial^{2} \overline{V} }}{{\partial \overline{R}^{2} }}+ 2\frac{{\partial \overline{V} }}{{\partial \overline{R}}}\frac{{\partial^{2} \overline{V} }}{{\partial \overline{R}^{2} }}\hfill \\ &\quad- 2\overline{V} \frac{{\partial^{3} \overline{V}}}{{\partial \overline{R}^{3} }} - 2\frac{{\partial^{3} \overline{V}}}{{\partial \overline{R}^{2} \partial \overline{t} }} -\frac{{2R^{*} \overline{U} }}{{\overline{R} + R^{*}}}\frac{{\partial^{3} \overline{V} }}{{\partial \overline{R}^{2}\partial \overline{X} }} - \frac{2}{{\overline{R} + R^{*}}}\frac{{\partial^{2} \overline{V} }}{{\partial \overline{R}\partial \overline{t} }} - \frac{{2R^{*} \overline{U} }}{{\left({\overline{R} + R^{*} } \right)^{2} }}\frac{{\partial^{2}\overline{V} }}{{\partial \overline{R} \partial \overline{X} }} -\left( {\frac{{R^{*} }}{{\overline{R} + R^{*} }}} \right)^{2}\overline{V} \frac{{\partial^{3} \overline{V} }}{{\partial\overline{R} \partial \overline{X}^{2} }} + \frac{2}{{\left({\overline{R} + R^{*} } \right)^{2} }}\frac{{\partial \overline{V}}}{{\partial \overline{t} }} \hfill \\ &\quad+ \frac{{2R^{*}}}{{\left( {\overline{R} + R^{*} } \right)^{2} }}\overline{U}\frac{{\partial \overline{V} }}{{\partial \overline{t} }} +\frac{{R^{*} }}{{\overline{R} + R^{*} }}\frac{{\partial \overline{U}}}{{\partial \overline{R} }}\frac{{\partial \overline{V}}}{{\partial \overline{X} }} + \left( {\frac{{R^{*} }}{{\overline{R}+ R^{*} }}} \right)\frac{{\partial^{2} \overline{U} }}{{\partial\overline{R}^{2} }}\frac{{\partial \overline{V} }}{{\partial\overline{X} }} + 2\left( {\frac{{R^{*} }}{{\overline{R} + R^{*} }}}\right)^{3} \frac{{\partial^{2} \overline{U} }}{{\partial\overline{X}^{2} }}\frac{{\partial \overline{V} }}{{\partial\overline{X} }} + \left( {\frac{{R^{*} }}{{\overline{R} + R^{*} }}}\right)^{2} \frac{{\partial^{2} \overline{V} }}{{\partial\overline{R} \partial \overline{X} }}\frac{{\partial \overline{V}}}{{\partial \overline{X} }} \hfill \\ &\quad+\frac{{3R^{*2} }}{{\left( {\overline{R} + R^{*} } \right)^{3}}}\left( {\frac{{\partial \overline{V} }}{{\partial \overline{X} }}}\right)^{2} + \frac{{2R^{*2} }}{{\left( {\overline{R} + R^{*} }\right)^{3} }}\overline{V} \frac{{\partial^{2} \overline{V}}}{{\partial \overline{X}^{2} }} + \left( {\frac{{R^{*}}}{{\overline{R} + R^{*} }}} \right)^{2} \frac{{\partial\overline{V} }}{{\partial \overline R} }\frac{{\partial^{2}\overline{V} }}{{\partial \overline{X}^{2} }} - \left( {\frac{{R^{*}}}{{\overline{R} + R^{*} }}} \right)^{2} \frac{{\partial^{3}\overline{V} }}{{\partial \overline{t} \partial \overline{X}^{2} }}- \left( {\frac{{R^{*} }}{{\overline{R} + R^{*} }}} \right)^{3}\overline{U} \frac{{\partial^{3} \overline{V} }}{{\partial\overline{X}^{3} }} \\ &\quad= - \frac{1}{\rho}\frac{{\partial \bar{p}^{*} }}{{\partial \overline{R} }}, \hfill\\ \end{aligned} $$
(16)
$$ \begin{aligned} & \frac{{\partial \overline{U} }}{{\partial \bar{t}}} + \frac{{R^{*} \overline{U} }}{{\overline{R} + R^{*} }}\frac{{\partial \overline{U} }}{{\partial \overline{X} }} + \frac{{\overline{U} }}{{\overline{R} + R^{*} }}\overline{V} + \overline{V} \frac{{\partial \overline{U} }}{{\partial \overline{R} }} + \upsilon \left( {\frac{{\overline{U} }}{{\left( {\overline{R} + R^{*} } \right)^{2} }} - \frac{1}{{\overline{R} + R^{*} }}\frac{{\partial \overline{U} }}{{\partial \overline{R} }} - \frac{{\partial^{2} \overline{U} }}{{\partial \overline{R}^{2} }} - 2\left( {\frac{{R^{*} }}{{\overline{R} + R^{*} }}} \right)^{2} \frac{{\partial^{2} \overline{U} }}{{\partial \overline{X}^{2} }} - \frac{{R^{*} }}{{\overline{R} + R^{*} }}\frac{{\partial^{2} \overline{V} }}{{\partial \overline{R} \partial \overline{X} }}} \right. \hfill \\ &\quad\left. { - \frac{{3R^{*} }}{{\left( {\overline{R} + R^{*} } \right)^{2} }}\frac{{\partial \overline{V} }}{{\partial \overline{X} }}} \right) + \lambda_{1} \left( { - \frac{{\overline{U}^{3} }}{{\left( {\overline{R} + R^{*} } \right)^{2} }} + \frac{{\overline{U}^{2} }}{{\overline{R} + R^{*} }}\frac{{\partial \overline{U} }}{{\partial \overline{R} }} + \frac{{\partial^{2} \overline{U} }}{{\partial \overline{t}^{2} }} + 2\left( {\frac{{R^{*} \overline{U} }}{{\overline{R} + R^{*} }}} \right)\frac{{\partial^{2} \overline{U} }}{{\partial \overline{X} \partial \overline{t} }} + \left( {\frac{{R^{*} }}{{\overline{R} + R^{*} }}} \right)^{2} \overline{U}^{2} \frac{{\partial^{2} \overline{U} }}{{\partial \overline{X}^{2} }} + 2\overline{V} \frac{{\partial^{2} \overline{U} }}{{\partial \overline{X} \partial \overline{t} }}} \right. \hfill \\ &\quad\left. { + \frac{{2R^{*} \overline{U} \overline{V} }}{{\overline{R} + R^{*} }}\frac{{\partial^{2} \overline{U} }}{{\partial \overline{R} \partial \overline{X} }} - \frac{{2R^{*} \overline{U} \overline{V} }}{{\left( {\overline{R} + R^{*} } \right)^{2} }}\frac{{\partial \overline{U} }}{{\partial \overline{X} }} - \frac{{2\overline{U} \overline{V}^{2} }}{{\left( {\overline{R} + R^{*} } \right)^{2} }} + \overline{V}^{2} \frac{{\partial^{2} \overline{U} }}{{\partial \overline{R}^{2} }} + \frac{{2\overline{U} \overline{V} }}{{\overline{R} + R^{*} }}\frac{{\partial \overline{V} }}{{\partial \overline{R} }} + \frac{{2\overline{U} }}{{\overline{R} + R^{*} }}\frac{{\partial \overline{V} }}{{\partial \overline{X} }} + \frac{{2R^{*} \overline{U}^{2} }}{{\left( {\overline{R} + R^{*} } \right)^{2} }}\frac{{\partial \overline{V} }}{{\partial \overline{X} }}} \right) \hfill \\ &\quad+ \lambda_{2} \left( { - \frac{{\partial^{3} \overline{U} }}{{\partial \overline{R}^{2} \partial \overline{t} }} - \frac{{R^{*} \overline{U} }}{{\overline{R} + R^{*} }}\frac{{\partial^{3} \overline{U} }}{{\partial \overline{R}^{2} \partial \overline{X} }} - \frac{1}{{\overline{R} + R^{*} }}\frac{{\partial^{2} \overline{U} }}{{\partial \overline{R} \partial \overline{X} }} - \frac{{2R^{*} \overline{U} }}{{\left( {\overline{R} + R^{*} } \right)^{2} }}\frac{{\partial^{2} \overline{U} }}{{\partial \overline{R} \partial \overline{X} }} + \frac{{R^{*} }}{{\overline{R} + R^{*} }}\frac{{\partial \overline{U} }}{{\partial \overline{R} }}\frac{{\partial^{2} \overline{U} }}{{\partial \overline{R} \partial \overline{X} }} + \frac{1}{{\left( {\overline{R} + R^{*} } \right)^{2} }}\frac{{\partial \overline{U} }}{{\partial \overline{t} }}} \right. \hfill \\ &\quad+ \frac{{3R^{*} }}{{\left( {\overline{R} + R^{*} } \right)^{3} }}\overline{U} \frac{{\partial \overline{U} }}{{\partial \overline{X} }} - \frac{{2R^{*} }}{{\left( {\overline{R} + R^{*} } \right)^{2} }}\frac{{\partial \overline{U} }}{{\partial \overline{R} }}\frac{{\partial \overline{U} }}{{\partial \overline{X} }} + \frac{{R^{*} }}{{\overline{R} + R^{*} }}\frac{{\partial^{2} \overline{U} }}{{\partial \overline{R}^{2} }}\frac{{\partial \overline{U} }}{{\partial \overline{X} }} + 2\left( {\frac{{R^{*} }}{{\overline{R} + R^{*} }}} \right)^{3} \frac{{\partial^{2} \overline{U} }}{{\partial \overline{X}^{2} }}\frac{{\partial \overline{U} }}{{\partial \overline{X} }} - 2\left( {\frac{{R^{*} }}{{\overline{R} + R^{*} }}} \right)^{2} \frac{{\partial^{3} \overline{U} }}{{\partial \overline{X}^{2} \partial \overline{t} }} \hfill \\ &\quad- 2\left( {\frac{{R^{*} }}{{\overline{R} + R^{*} }}} \right)^{3} \frac{{\partial^{3} \overline{U} }}{{\partial \overline{X}^{3} }} - \frac{{\overline{U} }}{{\left( {\overline{R} + R^{*} } \right)^{3} }}\overline{V} + \frac{{\overline{V} }}{{\left( {\overline{R} + R^{*} } \right)^{2} }}\frac{{\partial \overline{U} }}{{\partial \overline{R} }} - \overline{V} \frac{{\partial^{3} \overline{U} }}{{\partial \overline{X}^{3} }} - 2\left( {\frac{{R^{*} }}{{\overline{R} + R^{*} }}} \right)^{2} \overline{V} \frac{{\partial^{3} \overline{U} }}{{\partial \overline{R} \partial \overline{X}^{2} }} + \frac{{6R^{*2} \overline{V} }}{{\left( {\overline{R} + R^{*} } \right)^{3} }}\frac{{\partial^{2} \overline{U} }}{{\partial \overline{X}^{2} }} \hfill \\ &\quad- \frac{{2\overline{U} }}{{\left( {\overline{R} + R^{*} } \right)^{2} }}\frac{{\partial \overline{V} }}{{\partial \overline{R} }} + \frac{2}{{\overline{R} + R^{*} }}\frac{{\partial \overline{U} }}{{\partial \overline{R} }}\frac{{\partial \overline{V} }}{{\partial \overline{R} }} - \frac{{2\overline{U} }}{{\overline{R} + R^{*} }}\frac{{\partial^{2} \overline{V} }}{{\partial \overline{R}^{2} }} + 2\frac{{\partial \overline{U} }}{{\partial \overline{R} }}\frac{{\partial^{2} \overline{V} }}{{\partial \overline{R}^{2} }} - \frac{{R^{*} \overline{V} }}{{\overline{R} + R^{*} }}\frac{{\partial^{3} \overline{V} }}{{\partial \overline{R}^{2} \partial \overline{X} }} + \left( {\frac{{R^{*} }}{{\overline{R} + R^{*} }}} \right)^{2} \frac{{\partial \overline{U} }}{{\partial \overline{X} }}\frac{{\partial^{2} \overline{V} }}{{\partial \overline{R} \partial \overline{X} }} \hfill \\ &\quad- \frac{{R^{*} }}{{\left( {\overline{R} + R^{*} } \right)^{2} }}\overline{V} \frac{{\partial^{2} \overline{V} }}{{\partial \overline{R} \partial \overline{X} }} - \frac{{R^{*} }}{{\overline{R} + R^{*} }}\frac{{\partial^{3} \overline{V} }}{{\partial \overline{R} \partial \overline{X}^{2} }} - \left( {\frac{{R^{*} }}{{\overline{R} + R^{*} }}} \right)^{2} \overline{U} \frac{{\partial^{3} \overline{V} }}{{\partial \overline{R} \partial \overline{X}^{2} }} + \frac{{3R^{*2} }}{{\left( {\overline{R} + R^{*} } \right)^{3} }}\frac{{\partial \overline{U} }}{{\partial \overline{X} }}\frac{{\partial \overline{V} }}{{\partial \overline{X} }} + \frac{{9R^{*} }}{{\left( {\overline{R} + R^{*} } \right)^{3} }}\overline{V} \frac{{\partial \overline{V} }}{{\partial \overline{X} }} \hfill \\ &\quad- \frac{{3\overline{R} R^{*2} }}{{\left( {\overline{R} + R^{*} } \right)^{3} }}\frac{{\partial^{2} \overline{V} }}{{\partial \overline{X} \partial \overline{t} }}\left. { - \frac{{3R^{*2} }}{{\left( {\overline{R} + R^{*} } \right)^{3} }}\frac{{\partial^{2} \overline{V} }}{{\partial \overline{X} \partial \overline{t} }} + \left( {\frac{{R^{*} }}{{\overline{R} + R^{*} }}} \right)^{2} \frac{{\partial \overline{U} }}{{\partial \overline{R} }}\frac{{\partial^{2} \overline{V} }}{{\partial \overline{X}^{2} }}} \right) = - \frac{1}{\rho }\frac{{R^{*} }}{{\overline{R} + R^{*} }}\frac{{\partial \bar{p}^{*} }}{{\partial \overline{X} }}, \hfill \\ \end{aligned} $$
(17)

It is pointed out here that Eqs. (16) and (17) do not contain term involving λ 2. Thus using the approach of Harris [38], one would get the same governing equations for Oldroyd-B and Maxwell fluids for peristaltic flow in a curved channel. Note that we have used curvilinear coordinates \( \left( {\bar{R}, \bar{X}} \right) \) with scale factor given by h 1 = 1 and \( h_{2} = \left( {\bar{R} + R^{*} } \right)/R^{*} \) in deriving the above equations.

Employing the transformations given below to switch from laboratory frame to wave frame

$$ \bar{x}= \bar{X} - c\bar{t}, \bar{r} = \bar{R}, \bar{u} = \bar{U} - c, \bar{v} = \bar{V}, $$
(18)

Equations (15)–(17) can be put in the following form

$$ \frac{\partial }{{\partial \overline{r} }}\left\{ {\left( {\bar{r} + R^{*} } \right)\bar{v}} \right\} + R^{*} \frac{{\partial \bar{u}}}{{\partial \bar{x}}} = 0, $$
(19)
$$ \begin{aligned} &- \frac{{\left( {\bar{u} + c} \right)^{2} }}{{\bar{r} + R^{*} }} + \bar{v}\frac{{\partial \bar{v}}}{{\partial \overline{r} }} - c\frac{{\partial \bar{v}}}{{\partial \bar{x}}} + \frac{{R^{*} \left( {\bar{u} + c} \right)}}{{\bar{r} + R^{*} }}\frac{{\partial \bar{v}}}{{\partial \bar{x}}} + \upsilon \left( { - \frac{{R^{*} }}{{\bar{r} + R^{*} }}\frac{{\partial^{2} \bar{u}}}{{\partial \bar{x}\partial \bar{r}}} + \frac{{3R^{*} }}{{\left( {\bar{r} + R^{*} } \right)^{2} }}\frac{{\partial \bar{u}}}{{\partial \bar{x}}} + \frac{{2\bar{v}}}{{\left( {\bar{r} + R^{*} } \right)^{2} }} - \frac{2}{{\bar{r} + R^{*} }}\frac{{\partial \bar{v}}}{{\partial \bar{r}}}} \right. - 2\frac{{\partial^{2} \bar{v}}}{{\partial \bar{r}^{2} }} \hfill \\ &\quad \left. { - \left( {\frac{{R^{*} }}{{\bar{r} + R^{*} }}} \right)^{2} \frac{{\partial^{2} \bar{v}}}{{\partial \bar{x}^{2} }}} \right) + \lambda_{1} \left( {2c\frac{{\left( {\bar{u} + c} \right)}}{{\bar{r} + R^{*} }}\frac{{\partial \bar{u}}}{{\partial \bar{x}}} - 2\frac{{R^{*} \left( {\bar{u} + c} \right)^{2} }}{{\left( {\bar{r} + R^{*} } \right)^{2} }}\frac{{\partial \bar{u}}}{{\partial \bar{x}}} + \frac{{\left( {\bar{u} + c} \right)^{2} }}{{\left( {\bar{r} + R^{*} } \right)^{2} }}\bar{v} - 2\frac{{\left( {\bar{u} + c} \right)\bar{v}}}{{\bar{r} + R^{*} }}\frac{{\partial \bar{u}}}{{\partial \bar{r}}} + \frac{{\left( {\bar{u} + c} \right)^{2} }}{{\bar{r} + R^{*} }}\frac{{\partial \bar{v}}}{{\partial \bar{r}}}} \right. + \bar{v}^{2} \frac{{\partial^{2} \bar{v}}}{{\partial \bar{r}^{2} }} \hfill \\ &\quad\left. { - 2c\bar{v}\frac{{\partial^{2} \bar{v}}}{{\partial \bar{r}\partial \bar{x}}} + \frac{{2R^{*} \bar{v}\left( {\bar{u} + c} \right)}}{{\bar{r} + R^{*} }}\frac{{\partial^{2} \bar{v}}}{{\partial \bar{r}\partial \bar{x}}} - \frac{{2R^{*} \bar{v}\left( {\bar{u} + c} \right)}}{{\left( {\bar{r} + R^{*} } \right)^{2} }}\frac{{\partial \bar{v}}}{{\partial \bar{x}}} + c^{2} \frac{{\partial^{2} \bar{v}}}{{\partial \bar{x}^{2} }} + 2\left( {\frac{{R^{*} }}{{\bar{r} + R^{*} }}} \right)\left( {\bar{u} + c} \right)\frac{{\partial^{2} \bar{v}}}{{\partial \bar{x}^{2} }} + \left( {\frac{{R^{*} }}{{\bar{r} + R^{*} }}} \right)^{2} \left( {\bar{u} + c} \right)^{2} \frac{{\partial^{2} \bar{v}}}{{\partial \bar{x}^{2} }}} \right) \hfill \\ &\quad+ \lambda_{2} \left( { - \frac{{R^{*} }}{{\bar{r} + R^{*} }}\frac{{\partial^{3} \bar{u}}}{{\partial \bar{x}^{2} \partial \overline{r} }}} \right. - \left( {\frac{{R^{*} }}{{\bar{r} + R^{*} }}} \right)^{2} \left( {\bar{u} + c} \right)\frac{{\partial^{3} \bar{u}}}{{\partial \bar{x}^{2} \partial \overline{r} }} - \frac{{3cR^{*} }}{{\left( {\bar{r} + R^{*} } \right)^{2} }}\frac{{\partial^{2} \bar{u}}}{{\partial \bar{x}^{2} }} + \frac{{3R^{*2} \left( {\bar{u} + c} \right)}}{{\left( {\bar{r} + R^{*} } \right)^{3} }}\frac{{\partial^{2} \bar{u}}}{{\partial \bar{x}^{2} }} - \frac{{R^{*} \bar{v}}}{{\bar{r} + R^{*} }}\frac{{\partial^{3} \bar{u}}}{{\partial \bar{r}^{2} \partial \bar{x}}} \hfill \\ &\quad+ \frac{{4R^{*} \bar{v}}}{{\left( {\bar{r} + R^{*} } \right)^{2} }}\frac{{\partial^{2} \bar{u}}}{{\partial \bar{x}\partial \bar{r}}} - \frac{{6R^{*} }}{{\left( {\bar{r} + R^{*} } \right)^{3} }}\bar{v}\frac{{\partial \bar{u}}}{{\partial \bar{x}}} - \frac{4}{{\left( {\bar{r} + R^{*} } \right)^{3} }}\bar{v}^{2} + \frac{{R^{*} }}{{\bar{r} + R^{*} }}\frac{{\partial^{2} \bar{u}}}{{\partial \overline{x} \partial \bar{r}}}\frac{{\partial \bar{v}}}{{\partial \bar{r}}} - \frac{{3R^{*} }}{{\left( {\bar{r} + R^{*} } \right)^{2} }}\frac{{\partial \bar{u}}}{{\partial \bar{x}}}\frac{{\partial \bar{v}}}{{\partial \bar{r}}} + \frac{2}{{\left( {\bar{r} + R^{*} } \right)^{2} }}\bar{v}\frac{{\partial \bar{v}}}{{\partial \bar{r}}} \hfill \\ &\quad+ \frac{2}{{\bar{r} + R^{*} }}\left( {\frac{{\partial \bar{v}}}{{\partial \bar{r}}}} \right)^{2} - \frac{{2\bar{v}}}{{\bar{r} + R^{*} }}\frac{{\partial^{2} \bar{v}}}{{\partial \bar{r}^{2} }} + 2\frac{{\partial \bar{v}}}{{\partial \bar{r}}}\frac{{\partial^{2} \bar{v}}}{{\partial \bar{r}^{2} }} - 2\bar{v}\frac{{\partial^{3} \bar{v}}}{{\partial \bar{r}^{3} }} + 2c\frac{{\partial^{3} \bar{v}}}{{\partial \bar{r}^{2} \partial \overline{x} }} - 2\frac{{R^{*} \left( {\bar{u} + c} \right)}}{{\bar{r} + R^{*} }}\frac{{\partial^{3} \bar{v}}}{{\partial \bar{r}^{2} \partial \bar{x}}} + 2c\frac{1}{{\bar{r} + R^{*} }}\frac{{\partial^{2} \bar{v}}}{{\partial \bar{r}\partial \bar{x}}} \hfill \\ &\quad- 2\frac{{R^{*} \left( {\bar{u} + c} \right)}}{{\left( {\bar{r} + R^{*} } \right)^{2} }}\frac{{\partial^{2} \bar{v}}}{{\partial \bar{r}\partial \bar{x}}} - \left( {\frac{{R^{*} }}{{\bar{r} + R^{*} }}} \right)^{2} \bar{v}\frac{{\partial^{3} \bar{v}}}{{\partial \bar{r}\partial \bar{x}^{2} }} - \frac{2c}{{\left( {\bar{r} + R^{*} } \right)^{2} }}\frac{{\partial \bar{v}}}{{\partial \bar{x}}} - \frac{{2cR^{*} \left( {\bar{u} + c} \right)}}{{\left( {\bar{r} + R^{*} } \right)^{2} }}\frac{{\partial \bar{v}}}{{\partial \bar{x}}} + \frac{{R^{*} }}{{\bar{r} + R^{*} }}\frac{{\partial \bar{u}}}{{\partial \bar{r}}}\frac{{\partial \bar{v}}}{{\partial \bar{x}}} + \left( {\frac{{R^{*} }}{{\bar{r} + R^{*} }}} \right)\frac{{\partial^{2} \bar{u}}}{{\partial \bar{r}^{2} }}\frac{{\partial \bar{v}}}{{\partial \bar{x}}} \hfill \\ &\quad+ 2\left( {\frac{{R^{*} }}{{\bar{r} + R^{*} }}} \right)^{3} \frac{{\partial^{2} \bar{u}}}{{\partial \bar{x}^{2} }}\frac{{\partial \bar{v}}}{{\partial \bar{x}}} + \left( {\frac{{R^{*} }}{{\bar{r} + R^{*} }}} \right)^{2} \frac{{\partial^{2} \bar{v}}}{{\partial \bar{r}\partial \bar{x}}}\frac{{\partial \bar{v}}}{{\partial \bar{x}}} + \frac{{3R^{*2} }}{{\left( {\bar{r} + R^{*} } \right)^{3} }}\left( {\frac{{\partial \bar{v}}}{{\partial \bar{x}}}} \right)^{2} + \frac{{2R^{*2} }}{{\left( {\bar{r} + R^{*} } \right)^{3} }}\bar{v}\frac{{\partial^{2} \bar{v}}}{{\partial \bar{x}^{2} }} + \left( {\frac{{R^{*} }}{{\bar{r} + R^{*} }}} \right)^{2} \frac{{\partial \bar{v}}}{{\partial \bar{r}}}\frac{{\partial^{2} \bar{v}}}{{\partial \bar{x}^{2} }} + \hfill \\ &\quad\left. {c\left( {\frac{{R^{*} }}{{\bar{r} + R^{*} }}} \right)^{2} \frac{{\partial^{3} \bar{v}}}{{\partial \bar{x}^{3} }} - \left( {\frac{{R^{*} }}{{\bar{r} + R^{*} }}} \right)^{3} \left( {\bar{u} + c} \right)\frac{{\partial^{3} \bar{v}}}{{\partial \bar{x}^{3} }}} \right) = - \frac{1}{\rho }\frac{{\partial \bar{p}^{*} }}{{\partial \bar{r}}}, \hfill \\ \end{aligned} $$
(20)
$$ \begin{aligned} & - c\frac{{\partial \bar{u}}}{{\partial \bar{x}}} + \frac{{R^{*} \left( {\bar{u} + c} \right)}}{{\bar{r} + R^{*} }}\frac{{\partial \bar{u}}}{{\partial \bar{x}}} + \frac{{\left( {\bar{u} + c} \right)}}{{\bar{r} + R^{*} }}\bar{v} + \bar{v}\frac{{\partial \bar{u}}}{{\partial \bar{r}}} + \upsilon \left( {\frac{{\left( {\bar{u} + c} \right)}}{{\left( {\bar{r} + R^{*} } \right)^{2} }} - \frac{1}{{\bar{r} + R^{*} }}\frac{{\partial \bar{u}}}{{\partial \bar{r}}} - \frac{{\partial^{2} \bar{u}}}{{\partial \bar{r}^{2} }} - 2\left( {\frac{{R^{*} }}{{\bar{r} + R^{*} }}} \right)^{2} \frac{{\partial^{2} \bar{u}}}{{\partial \bar{x}^{2} }} - \frac{{R^{*} }}{{\bar{r} + R^{*} }}\frac{{\partial^{2} \bar{v}}}{{\partial \bar{r}\partial \bar{x}}}} \right. \hfill \\ &\quad\left. { - \frac{{3R^{*} }}{{\left( {\bar{r} + R^{*} } \right)^{2} }}\frac{{\partial \bar{v}}}{{\partial \bar{x}}}} \right) + \lambda_{1} \left( { - \frac{{\left( {\bar{u} + c} \right)^{3} }}{{\left( {\bar{r} + R^{*} } \right)^{2} }} + \frac{{\left( {\bar{u} + c} \right)^{2} }}{{\bar{r} + R^{*} }}\frac{{\partial \overline{u} }}{{\partial \bar{r}}} + c^{2} \frac{{\partial^{2} \bar{u}}}{{\partial \bar{x}^{2} }} - 2c\left( {\frac{{R^{*} }}{{\bar{r} + R^{*} }}} \right)\left( {\bar{u} + c} \right)\frac{{\partial^{2} \bar{u}}}{{\partial \bar{x}^{2} }} + \left( {\frac{{R^{*} }}{{\bar{r} + R^{*} }}} \right)^{2} \left( {\bar{u} + c} \right)^{2} \frac{{\partial^{2} \bar{u}}}{{\partial \bar{x}^{2} }} - 2c\bar{v}\frac{{\partial^{2} \bar{u}}}{{\partial \bar{x}^{2} }}} \right. \hfill \\ &\quad\left. { + \frac{{2R^{*} \left( {\bar{u} + c} \right)\bar{v}}}{{\bar{r} + R^{*} }}\frac{{\partial^{2} \bar{u}}}{{\partial \bar{r}\partial \bar{x}}} - \frac{{2R^{*} \left( {\bar{u} + c} \right)\bar{v}}}{{\left( {\bar{r} + R^{*} } \right)^{2} }}\frac{{\partial \bar{u}}}{{\partial \bar{x}}} - \frac{{2\left( {\bar{u} + c} \right)\bar{v}^{2} }}{{\left( {\bar{r} + R^{*} } \right)^{2} }} + \bar{v}^{2} \frac{{\partial^{2} \bar{u}}}{{\partial \bar{r}^{2} }} + \frac{{2\left( {\bar{u} + c} \right)\bar{v}}}{{\bar{r} + R^{*} }}\frac{{\partial \bar{v}}}{{\partial \overline{r} }} + \frac{{2\left( {\bar{u} + c} \right)}}{{\bar{r} + R^{*} }}\frac{{\partial \bar{v}}}{{\partial \bar{x}}} + \frac{{2R^{*} \left( {\bar{u} + c} \right)^{2} }}{{\left( {\bar{r} + R^{*} } \right)^{2} }}\frac{{\partial \bar{v}}}{{\partial \bar{x}}}} \right) \hfill \\ &\quad+ \lambda_{2} \left( {\frac{{\partial^{3} \bar{u}}}{{\partial \bar{r}^{3} }} - \frac{{R^{*} \left( {\bar{u} + c} \right)}}{{\bar{r} + R^{*} }}\frac{{\partial^{3} \overline{u} }}{{\partial \bar{r}^{2} \partial \bar{x}}} - \frac{1}{{\bar{r} + R^{*} }}\frac{{\partial^{2} \bar{u}}}{{\partial \bar{r}\partial \bar{x}}} - \frac{{2R^{*} \left( {\bar{u} + c} \right)}}{{\left( {\bar{r} + R^{*} } \right)^{2} }}\frac{{\partial^{2} \bar{u}}}{{\partial \bar{r}\partial \bar{x}}} + \frac{{R^{*} }}{{\bar{r} + R^{*} }}\frac{{\partial \bar{u}}}{{\partial \bar{r}}}\frac{{\partial^{2} \bar{u}}}{{\partial \bar{r}\partial \bar{x}}} - \frac{c}{{\left( {\bar{r} + R^{*} } \right)^{2} }}\frac{{\partial \bar{u}}}{{\partial \bar{x}}}} \right. + \frac{{3R^{*} \left( {\bar{u} + c} \right)}}{{\left( {\bar{r} + R^{*} } \right)^{3} }}\frac{{\partial \bar{u}}}{{\partial \bar{x}}} \hfill \\ &\quad- \frac{{2R^{*} }}{{\left( {\bar{r} + R^{*} } \right)^{2} }}\frac{{\partial \bar{u}}}{{\partial \bar{r}}}\frac{{\partial \bar{u}}}{{\partial \bar{x}}} + \frac{{R^{*} }}{{\bar{r} + R^{*} }}\frac{{\partial^{2} \bar{u}}}{{\partial \bar{r}^{2} }}\frac{{\partial \bar{u}}}{{\partial \bar{x}}} + 2\left( {\frac{{R^{*} }}{{\bar{r} + R^{*} }}} \right)^{3} \frac{{\partial^{2} \bar{u}}}{{\partial \bar{x}^{2} }}\frac{{\partial \bar{u}}}{{\partial \bar{x}}} + 2c\left( {\frac{{R^{*} }}{{\bar{r} + R^{*} }}} \right)^{2} \frac{{\partial^{3} \bar{u}}}{{\partial \bar{x}^{3} }} - 2\left( {\frac{{R^{*} }}{{\bar{r} + R^{*} }}} \right)^{3} \frac{{\partial^{3} \bar{u}}}{{\partial \bar{x}^{3} }} - \frac{{\left( {\bar{u} + c} \right)\bar{v}}}{{\left( {\bar{r} + R^{*} } \right)^{3} }} \hfill \\ &\quad+ \frac{{\bar{v}}}{{\left( {\bar{r} + R^{*} } \right)^{2} }}\frac{{\partial \bar{u}}}{{\partial \bar{r}}} - \bar{v}\frac{{\partial^{3} \bar{u}}}{{\partial \bar{x}^{3} }} - 2\left( {\frac{{R^{*} }}{{\bar{r} + R^{*} }}} \right)^{2} \bar{v} \frac{{\partial^{3} \bar{u}}}{{\partial \bar{r}\partial \bar{x}^{2} }} + \frac{{6R^{*2} \bar{v}}}{{\left( {\bar{r} + R^{*} } \right)^{3} }}\frac{{\partial^{2} \bar{u}}}{{\partial \bar{x}^{2} }} - \frac{{2\left( {\bar{u} + c} \right)}}{{\left( {\bar{r} + R^{*} } \right)^{2} }}\frac{{\partial \bar{v}}}{{\partial \bar{r}}} + \frac{2}{{\bar{r} + R^{*} }}\frac{{\partial \bar{u}}}{{\partial \bar{r}}}\frac{{\partial \bar{v}}}{{\partial \bar{r}}} - \frac{{2\left( {\bar{u} + c} \right)}}{{\bar{r} + R^{*} }}\frac{{\partial^{2} \bar{v}}}{{\partial \bar{r}^{2} }} \hfill \\ &\quad+ 2\frac{{\partial \bar{u}}}{{\partial \bar{r}}}\frac{{\partial^{2} \bar{v}}}{{\partial \bar{r}^{2} }} - \frac{{R^{*} \bar{v}}}{{\bar{r} + R^{*} }}\frac{{\partial^{3} \bar{v}}}{{\partial \bar{r}^{2} \partial \bar{x}}} + \left( {\frac{{R^{*} }}{{\bar{r} + R^{*} }}} \right)^{2} \frac{{\partial \bar{u}}}{{\partial \bar{x}}}\frac{{\partial^{2} \bar{v}}}{{\partial \bar{r}\partial \bar{x}}} - \frac{{R^{*} \bar{v}}}{{\left( {\bar{r} + R^{*} } \right)^{2} }}\frac{{\partial^{2} \bar{v}}}{{\partial \bar{r}\partial \bar{x}}} - \frac{{R^{*} }}{{\bar{r} + R^{*} }}\frac{{\partial^{3} \bar{v}}}{{\partial \bar{r}\partial \bar{x}^{2} }} - \left( {\frac{{R^{*} }}{{\bar{r} + R^{*} }}} \right)^{2} \left( {\bar{u} + c} \right)\frac{{\partial^{3} \bar{v}}}{{\partial \bar{r}\partial \bar{x}^{2} }} \hfill \\ &\quad+ \frac{{3R^{*2} }}{{\left( {\bar{r} + R^{*} } \right)^{3} }}\frac{{\partial \bar{u}}}{{\partial \bar{x}}}\frac{{\partial \bar{v}}}{{\partial \bar{x}}} + \frac{{9R^{*} \bar{v}}}{{\left( {\bar{r} + R^{*} } \right)^{3} }}\frac{{\partial \bar{v}}}{{\partial \bar{x}}}\left. { - \frac{{3cR^{*2} }}{{\left( {\bar{r} + R^{*} } \right)^{3} }}\frac{{\partial^{2} \bar{v}}}{{\partial \bar{x}^{2} }} + \left( {\frac{{R^{*} }}{{\bar{r} + R^{*} }}} \right)^{2} \frac{{\partial \bar{u}}}{{\partial \bar{r}}}\frac{{\partial^{2} \bar{v}}}{{\partial \bar{x}^{2} }}} \right) = - \frac{1}{\rho }\frac{{R^{*} }}{{\bar{r} + R^{*} }}\frac{{\partial \bar{p}^{*} }}{{\partial \bar{x}}}, \hfill \\ \end{aligned} $$
(21)

Defining the following dimensionless variables

$$ x = \frac{2\pi }{\lambda }\bar{x}, \quad \eta = \frac{{\bar{r}}}{a}, \quad u = \frac{{\bar{u}}}{c}, \quad v = \frac{{\bar{v}}}{c}, \text{Re} = \frac{\rho ca}{\pi }, \quad p = \frac{{2\pi a^{2} }}{\lambda \mu c}\bar{p}^{*} ,\quad \delta = \frac{2\pi a}{\lambda },\quad S = \frac{a}{\mu c}\bar{S}, k = \frac{{R^{*} }}{a}, $$
(22)

and the stream function [21]

$$ u = - \frac{\partial \psi }{\partial \eta },\quad v = \delta \frac{k}{k + \eta }\frac{\partial \psi }{\partial x}. $$
(23)

The continuity Eq. (19) is satisfied identically and Eqs. (20) and (21) after using long wavelength and low Reynolds number approximations [11–13, 20–22] reduce to

$$ \frac{\partial p}{\partial \eta } = 0, $$
(24)
$$ - \frac{k}{k + \eta }\left( {1 - \frac{\partial \psi }{\partial \eta }} \right) - \frac{{\partial^{2} \psi }}{{\partial \eta^{2} }} - \left( {k + \eta } \right)\frac{{\partial^{3} \psi }}{{\partial \eta^{3} }} + We\left( {\frac{k}{k + \eta }\left( {1 - \frac{\partial \psi }{\partial \eta }} \right)^{3} + \left( {1 - \frac{\partial \psi }{\partial \eta }} \right)^{2} \frac{{\partial^{2} \psi }}{{\partial \eta^{2} }}} \right) = k\frac{\partial p}{\partial x}, $$
(25)

where \( We = \lambda_{1} c^{2} /\upsilon \) is the Weissenberg number and k is the dimensionless radius of curvature.

Eliminating pressure between Eqs. (24) and (25), we get the following compatibility equation

$$ \frac{\partial }{\partial \eta }\left( { - \frac{k}{k + \eta }\left( {1 - \frac{\partial \psi }{\partial \eta }} \right) - \frac{{\partial^{2} \psi }}{{\partial \eta^{2} }} - \left( {k + \eta } \right)\frac{{\partial^{3} \psi }}{{\partial \eta^{3} }} +We\left( {\frac{k}{k + \eta }\left( {1 - \frac{\partial \psi }{\partial \eta }} \right)^{3} + \left( {1 - \frac{\partial \psi }{\partial \eta }} \right)^{2} \frac{{\partial^{2} \psi }}{{\partial \eta^{2} }}} \right)} \right) = 0. $$
(26)

We mention here that under long wavelength assumption, Eq. (26) corresponds to peristaltic flow of Maxwell fluid due to vanishing of the terms involving retardation constant. But still it is capable of predicting simultaneous effects of viscoelasticity and curvature of the channel. Such an equation cannot be obtained when peristaltic flow is considered in straight channel or tube which is evident by taking limit of Eq. (26) when k → ∞. In that case Eq. (26) reduces to the corresponding equation of peristaltic transport of Newtonian fluid in a straight channel.

3 Volume flow rate and boundary conditions

In laboratory frame, we define

$$ Q = \int\limits_{{ - \bar{H}}}^{{\bar{H}}} {\bar{U}d\bar{R}, } $$
(27)

as volume flow rate.

The above expression in the wave frame becomes

$$ F = \int\limits_{{ - \bar{H}}}^{{\bar{H}}} {\bar{u}d\bar{r},} $$
(28)

where \( \bar{H} \) is a function of \( \bar{x} \) alone. In views of Eqs. (18), (27) and (28) we can write

$$ Q = F + 2c\bar{H}, $$
(29)

Defining the time-averaged flux over a period T at a fixed position \( \bar{X} \) as

$$ \bar{Q} = \frac{\text{1}}{T}\int\limits_{0}^{T} {Qdt,} $$
(30)

and utilizing Eq. (29) into (30), one finds

$$ \bar{Q} = q + 2ac, $$
(31)

In dimensionless variables Eq. (29) reads

$$ \Theta = q + 2, $$
(32)

where \( \Theta = \bar{Q}/ac\, {\text{and}}\, q = F/ac \) are the dimensionless mean flows in laboratory frame and wave frame, respectively.

In terms of stream function Ψ we can write

$$ q = - \int\limits_{ - h}^{h} {\frac{\partial \psi }{\partial \eta }d\eta = - \left( {\varPsi \left( h \right) - \varPsi \left( { - h} \right)} \right),} $$
(33)

Selecting \( \varPsi \left( h \right) = { - q}/2 \), we have\( \varPsi \left( { - h} \right) = q/2 \). Therefore, the appropriate boundary conditions in the wave frame are

$$ \psi = - \frac{q}{2}, \frac{\partial \psi }{\partial \eta } = 1, {\text{at}}\, \eta = h = 1 + \varPhi { \sin }x, $$
(34)
$$ \psi = \frac{q}{2}, \frac{\partial \psi }{\partial \eta } = 1, {\text{at}}\, \eta = - h = - 1 - \varPhi { \sin }x, $$
(35)

where Φ = b/a is the amplitude ratio.

The dimensionless pressure rise over one wavelength is defined by [21, 22]

$$ \varDelta p = \int\limits_{0}^{2\pi } {\frac{dp}{dx}dx.} $$
(36)

4 Method of solution

Due to nonlinear nature of Eq. (26), an exact solution is not possible. Therefore, we opted to go for numerical solution. To this end, we employed built-in routine bvp4c for solving nonlinear ordinary differential equation using computational software Matlab. In the limit when k → ∞ or We = 0, our result reduce to the corresponding results for a Newtonian fluid in a straight channel.

5 Results and discussion

In this section graphical results are displayed for various values of Weissenberg number (We) and dimensionless radius of curvature (k) in order to analyze flow characteristics, pumping and trapping phenomena associated with peristaltic motion.

Figure 2a shows the velocity profile u(η) at cross–sections x = −π/2 (narrow part the channel) for different values of We when Θ = 4 and k = 2. We observe from this figure that for We = 0 and k = 2, velocity profile is not symmetric about η = 0 and maximum in it lies below η = 0. A symmetry about η = 0 is observed for We = 0.25. A further increase in We shifts the maximum in velocity towards the upper wall.

Fig. 2
figure 2

Variation of u(η) for different values of We at cross section x = −π/2 (a, b), x = 0 (c, d) and x = π/2 (e, f) with Φ = 0.4 and k = 2. Left panel correspond to Θ = 4 while right panel are for Θ = 2

Full size image

The velocity profiles for different values of We, by taking Θ = 2 and keeping other parameters same as in Fig. 2a, are shown in Fig. 2b. This figure depicts the same behavior as predicted by Fig. 2a but for very large values of We compared with those chosen in Fig. 2a. Figure 2c illustrates velocity profiles at x = 0 (undisturbed part of the channel) by keeping other parameters same as chosen in Fig. 2a. Again this figure shows similar behavior of velocity profile as observed in Fig. 2a. Figure 2d exhibits asymmetry and shift of maximum in velocity towards the upper wall for values of We greater in comparison with those chosen in Fig. 2c. Similar observations can be drawn from Fig. 2e, f.

The effects of dimensionless radius of curvature (k) on velocity profile of Oldroyd-B fluid are shown through Fig. 3. A striking observation is made from this figure i.e. velocity becomes asymmetric and maximum in it shifts towards the upper wall for small values of k. This observation to contrary to that what is observed for a Newtonian fluid. For a Newtonian fluid, a decrease in k shifts the maximum in velocity towards the lower wall. In general it is concluded from Figs. 2 and 3 are that viscoelastic fluid driven by peristaltic waves in a curved channel behaves in a very different way than that of a Newtonian fluid. Perhaps the role of Weissenberg number here, which characterizes the viscoelastic fluid is to counteract the effects of curvature and make the velocity symmetric even for very small values of k. For large values of We the viscoelastic effects dominate the effect of curvature and shift the maximum in velocity profile towards the upper wall.

Fig. 3
figure 3

Variation of u(η) for different values of k at a cross section x = π/2 with We = 5, Θ = 1.64 with Φ = 0.4

Full size image

The plots of pressure gradient dp/dx over one wave length for various values of We and k are shown in Figs. 4 and 5, respectively. We observe from Fig. 4 that dp/dx increases in the wider part of the channel while it decreases in the narrow part of the channel by increasing We. Opposite trend can be observed by increasing k as evident from Fig. 5.

Fig. 4
figure 4

Variation of dp/dx over one wavelength for differential values of We with k = 2, Φ = 0.4 and \( \Theta \) = 0

Full size image
Fig. 5
figure 5

Variation of dp/dx over one wavelength for differential values of k with We = 5, Φ = 0.4 and Θ = 0

Full size image

Figures 6 and 7 are plotted to see the variation of pressure rise per wavelength (Δp) against dimensionless mean flow rate Θ for various values of We and k, respectively.

Fig. 6
figure 6

Variation of Δp for different values of We with k = 2 and Φ = 0.4

Full size image
Fig. 7
figure 7

Variation of \( \varDelta p \) for differential values of k with We = 5 and Φ = 0.4

Full size image

Following interesting observations can be made from these figures.

  • In pumping region (Δp > 0, Θ > 0) there exists a critical value of flow rate Θ, below which Δp decreases and above which it increases, by increasing We. Thus pressure resistance for a viscoelastic fluid is lesser in magnitude than that for a Newtonian fluid.

  • The situation is different in free pumping (Δp = 0) and co-pumping region (Δp < 0; Θ > 0). Here Δp increases by increasing We.

  • Δp in pumping region increases in going from curved to straight channel below a certain critical value of Θ. Above this critical value a reverse trend is observed. This reverse trend also prevails in free pumping and co-pumping regions.

The streamline patterns for different values of We and k are shown in Figs. 8 and 9. It is observed that the presence of curvature in channel destroys the symmetry of circulating bolus of the fluid. However, as expected the circulating bolus of fluid regain its symmetry for large values of k.

Fig. 8
figure 8

Streamlines for a We = 0, b We = 2, c We = 5 and d We = 8 with k = 2. The other parameters chosen are Θ = 1.5 and Φ = 0.8

Full size image
Fig. 9
figure 9

Streamlines for a k = 2, b k = 3.5, c k = 5 and d k → ∞ with We = 5. The other parameters chosen are Θ = 1.5 and Φ = 0.8

Full size image

The effects of We on streamline patterns are quite interesting. Here, as observed for velocity profile there is competition between We and k. For small values of We the effects of k are dominant and bolus is shifting towards the upper wall. However, an increase in We counteracts the effects of k and as a result bolus regain its symmetry. A further increase in We dominates the effects of k thus making the bolus asymmetric and at the same time shifts it towards the lower wall.

Figure 10 is plotted to see the effects of curvature on lower trapping limit (i.e. maximum value of Θ for which trapping occurs). It is observed that lower trapping limit increases by increasing curvature of the channel.

Fig. 10
figure 10

Streamlines for a k = 2 and b k → ∞ with We = 0.2. The other parameters chosen are Θ = 1 and Φ = 0.8

Full size image

A general observation after examining streamlines plots is that for a symmetric channel mixing phenomenon is strong due symmetric nature of the circulating region. However, for a curved channel due to shift of bolus in lower half of the channel, there is no mixing of fluid in the upper half of the channel.

6 Concluding remarks

A mathematical model is presented to explore the simultaneous effects of curvature of channel and viscoelasticity on peristaltic transport. The problem is governed by fourth order nonlinear ordinary differential equation which is solved numerically using Matlab built-in routine bvp4c. The effects of various emerging parameters on basic features of peristalsis are explained through various plots. The main points of the conducted study can be summarized as follows:

  • An increase in curvature results in asymmetric velocity profiles with maxima lying below η = 0.

  • The effects of Weissenberg number are to counteract the effects of curvature and thus making the velocity profiles symmetric. For large values of We, the viscoelastic effects dominate resulting in asymmetric velocity profiles whose maxima lie above η = 0.

  • Δp decreases by increasing We or k below a certain critical values of Θ. Above this value a reverse trend is observed.

  • The circulating bolus of fluid becomes asymmetric by increasing curvature of channel. However, an increase in We counteract the effects of curvature and helps the bolus to regain its symmetrical shape.

  • For large value of We viscoelastic effects dominate resulting in asymmetry of bolus.

  • The mixing phenomena in a straight channel is stronger than that in a curved channel.