1 Introduction

There is an extensive list of real-life problems where the stochastic nature of the phenomena under investigation can be modeled by the aid of a sum of a random number of random variables. In collective risk theory, for example, letting M denote the number of claims (or losses) in a specific time period and \(X_j\) the amount of the jth claim (or loss), for \(j=1,2,\ldots , M\), the sum \(X_1+X_2+\ldots +X_M\) corresponds to the aggregate amount of claims (or losses) of the insurance portfolio in that period (e.g., Klugman et al. 2019). In epidemiology, if M denotes the number of susceptibles at a specific time (e.g., Brauer 2008), then the number of infected individuals may be expressed as \(X_1+X_2+\ldots +X_M\), where \(X_j\) indicates whether the jth susceptible got infected (\(X_j=1\)) or not (\(X_j=0\)).

In general, let \(X_1,X_2,\ldots\) be a sequence of stochastically independent and identically distributed random variables (r.v.) and M a non-negative integer-valued r.v., independent of the \(X_j\)’s. The random variable

$$\begin{aligned} S_M=\sum _{j=1}^{M}X_j \end{aligned}$$
(1)

(convention: \(S_M=0\) if \(M=0\)) is usually referred to as random sum model. Note also that, in queueing theory, the equilibrium waiting time distribution in the G/G/1 model follows a distribution related to the random sum model (1); moreover, in ruin theory, several quantities (e.g., ruin probabilities, Laplace transform of ruin time, surplus before ruin and, density at ruin) of the celebrated Sparre Andersen risk model (e.g., Asmussen and Albrecher 2010) can be studied by the aid of the tail probability of the random sum model with M having a suitable geometric distribution.

When \(X_j\)’s follow a discrete distribution, (1) is usually referred to as discrete random sum model and its distribution as discrete compound distribution. In the collective risk theory, the discrete sum model can also be applied when the severity distribution, i.e., the distribution of \(X_j\), is defined on \(0,1,\ldots , x_{max}\) with its values representing multiples of some monetary unit. In this case, \(x_{max}\) will stand for the largest possible payment and could be finite or infinite. If M belongs to the well known Panjer class of counting distributions, Panjer (1981), Sundt (1982), and Waldmann (1996) derived very efficient recursive schemes for the probability mass function, cumulative distribution function and tail probabilities of \(S_M\).

However, considering, for example, an insurance company, it is reasonable to assume that besides the losses suffered due to the M claims, it also has an operational cost, say U; hence, its total expenses (operational costs and aggregate claims) will be given by

$$\begin{aligned} S=U+S_M=U+\sum _{j=1}^{M}X_j. \end{aligned}$$
(2)

The main aim of the present article is the study of the extended random sum (2), when U and M belong to the Panjer class, \(X_j\)’s are i.i.d. positive integer-valued random variables and all random variables appearing in (2) are assumed to be independent. A sum of similar nature was discussed in Kalashnikov (1997) (Example 3.4), in terms of the time needed by a pedestrian to cross an one-way road.

Another motivation for looking at the aforementioned model stems from the fact that a number of waiting times distributions for runs defined on a sequence of binary trials can be expressed as extended random sums, and therefore, their exact distribution can be deduced as a special case of the distribution of (2). Note that the notion of run (also referred to as “spells” or “episodes” in social sciences; e.g., Cornwell 2015, Ch. 4) which can be defined as an interrupted sequence of identical events, plays a prominent role in many real-life applications (e.g., Fu and Lou 2003). For example, researchers are typically interested in studying the sequence of status (defective or not) of the inspected items from a production line, the number of consecutive days a worker spent in unemployment, and the number of consecutive insurance claims exceeding a predetermined limit, among others. Similar frameworks may be encountered in a plethora of different disciplines such as quality control, actuarial science, reliability theory, molecular biology, epidemiology, medicine, criminology, and experimental psychology, to mention a few (e.g., Lou 1996; Godbole et al. 1997; Glaz et al. 2001; Balakrishnan and Koutras 2002; Eryilmaz 2008; Glaz et al. 2009; Glaz and Balakrishnan 2012; Balakrishnan et al. 2021).

In the literature, several schemes of counting the number of runs in a (ordered) sequence of events have been employed; among them, the most popular are probably the non-overlapping, at least and overlapping scheme. According to these schemes, once a (pre-specified) number of consecutive identical events, say k, shows up, a run is counted and (a) the enumeration immediately starts from scratch, under the non-overlapping scheme, (b) the enumeration re-starts only after the current run is interrupted by a different type of event, under the at least scheme, whereas (c) we keep counting the occurrence of runs, as far as the same event is still occurring, under the overlapping scheme. For example, in the sequence of binary outcomes 0000111001000, we observe 4, 3 and 6 runs of zeros of length \(k=2\) under the non-overlapping, at least and overlapping scheme, respectively. The corresponding waiting time distributions for the rth appearance of a run of length k, which have been named as negative binomial distributions of order k, is then of special theoretical and applied interest; for example, in the previous binary sequence the waiting times for the appearance of \(r=3\) runs of zeros of length \(k=2\) equals 9, 12 and 4, under the non-overlapping, at least and overlapping scheme, respectively. Needless to say, for \(k=1\), the three waiting time distributions reduce to the well-known negative binomial distribution.

Probability mass functions, probability generating functions or recursive formulas of the three waiting time distributions mentioned above can be found in the literature, assuming, for example, that the sequence of binary trials consist of independent and identically distributed binary trials or Markov dependent trials (e.g., Koutras 1997; Balakrishnan and Koutras 2002, Ch. 4); however, for some of these methods the calculations needed to obtain the exact distribution turn out to be computationally intractable, especially, for large values of k and/or r. The present work also focuses to the derivation of computationally efficient recursive relations for the probability mass function, the cumulative distribution function and the tail probabilities of the negative binomial distributions of order k.

The rest of this paper is organized as follows. In Section 2, we study the relation between the negative binomial distributions of order k and the distribution of the extended discrete random sum. In Section 3, we derive efficient recurrence relations for the probability mass function, cumulative distribution function and survival function of S, along with recursive formulas for its factorial moments. The general results of Section 3 are subsequently used in Section 4 for studying the negative binomial distributions of order k, taking advantage of the relations established in Section 2. Some practical and numerical aspects of the new results are considered in Section 5, in terms of their application to the total expenses (operational costs and aggregate claims) of an insurance company.

2 Random sum representations for the negative binomial distributions of order k

In this section, we illustrate how the waiting times for multiple run occurrences can be represented as properly defined random sums. The approach taken here departs from the techniques used so far, which exploit representations as sums of fixed number of random variables; e.g., Hirano et al. (1991), Koutras (1997) or Balakrishnan and Koutras (2002).

To start with, consider a sequence \(Z_1, Z_2, \ldots\) of i.i.d. binary trials with \(Z_j\)=1 (success) or 0 (failure), for \(j=1,2,\ldots\) and \(P(Z_j=1)=p\in (0,1)\), \(P(Z_j=0)=q=1-p\). Let us also denote by \(T_{r,k}^{(N)}\), \(T_{r,k}^{(A)}\) and \(T_{r,k}^{(O)}\), the waiting time for the rth appearance of a success run of length k, under the the non-overlapping, at least and overlapping scheme, respectively; although the waiting times \(T_{r,k}^{(N)}\), \(T_{r,k}^{(A)}\), \(T_{r,k}^{(O)}\), are also denoted as \(T_{r,k}^{(I)}\), \(T_{r,k}^{(II)}\), \(T_{r,k}^{(III)}\), in the relevant literature (e.g., Balakrishnan and Koutras 2002), here we adopted the first notation as it may help the reader to more easily recall which scheme is being referred to.

Apparently, for \(r=1\), all three variables describe the waiting time for the first occurrence of a success run of length k; hence, \(T_{1,k}^{(N)}=T_{1,k}^{(A)}=T_{1,k}^{(O)}=T_k\) where \(T_k\) is a random variable following the geometric distribution of order k. The notations that will be used in the sequel are:

  • \(f_{r,k}^{(i)}(x)=P(T_{r,k}^{(i)}=x)\), i=N, A, O for the probability mass function of the negative binomial distributions of order k.

  • \(f_{k}(x)=P(T_k=x)\) for the probability mass function of the geometric distribution of order k; moreover, we shall write \(T_k\sim G_k(p)\).

The proof of the main result of this section, Theorem 1, makes use of some useful results, concerning the probability generating functions of the waiting times \(T_{r,k}^{(N)}\), \(T_{r,k}^{(A)}\) and \(T_{r,k}^{(O)}\). Using the formulas provided in Balakrishnan and Koutras (2002) (Ch. 4.2.2), one may easily conclude that the probability generating functions of \(T_{r,k}^{(N)}\), \(T_{r,k}^{(A)}\) and \(T_{r,k}^{(O)}\) take on the forms

$$\begin{aligned} E\left[ u^{T_{r,k}^{(N)}}\right] =\frac{(pu)^{rk}}{Q_k(u)^r}, \end{aligned}$$
(3)
$$\begin{aligned} E\left[ u^{T_{r,k}^{(A)}}\right] =\left[ \frac{qu}{1-pu}\right] ^{r-1}\left[ \frac{(pu)^k}{Q_k(u)}\right] ^r, \end{aligned}$$
(4)
$$\begin{aligned} E\left[ u^{T_{r,k}^{(O)}}\right] =\frac{(pu)^k}{Q_k(u)}\left[ pu+qu\frac{(pu)^k}{Q_k(u)}\right] ^{r-1}, \end{aligned}$$
(5)

where

$$\begin{aligned} Q_k(u)=1-\frac{q[1-(pu)^k]u}{1-pu}. \end{aligned}$$

Considering the special case \(r=1\), for any of (3)–(5), we readily obtain the probability generating function of \(T_k\sim G_k(p)\) as

$$\begin{aligned} E\left[ u^{T_k}\right] =\frac{(pu)^{k}}{Q_k(u)}=P_T(u). \end{aligned}$$
(6)

From (3) and \(k=1\), we may deduce the next well known probability generating function of the negative binomial distribution with parameters r and p, symb. Nb(r, p),

$$\begin{aligned} E\left[ u^{T_{r,1}^{(N)}}\right] =\left( \frac{pu}{1-qu}\right) ^r. \end{aligned}$$
(7)

Obviously, Nb(1, p) leads to the standard geometric distribution with support \(\{0,1,\ldots \}\), to be denoted hereafter by G(p), whereas the shifted geometric distribution with support \(\{1,2,\ldots \}\), will be denoted by \(G_{sh}(p)\).

Moreover, if B follows the typical binomial distribution with parameters r (number of trials) and p (success probability), symb. \(B\sim b(r,p)\), its probability generating function reads

$$\begin{aligned} E\left[ u^{B}\right] =(pu+q)^r. \end{aligned}$$
(8)

Suppose now that Y follows the truncated geometric distribution with support \(1,2,\ldots ,k\), symb. \(Y\sim G_{tr}^{k}(p)\); then, the probability mass function of Y is given by

$$\begin{aligned} f_{Y}(y)=q\frac{p^{y-1}}{1-p^k},~y=1,2,\ldots ,k, \end{aligned}$$
(9)

whereas its probability generating function by

$$\begin{aligned} E\left[ u^{Y}\right] =\frac{qu [1-(pu)^k]}{(1-p^k)(1-pu)}. \end{aligned}$$
(10)

One may easily verify that \(G_{tr}^{k}(p)\) is a conditional geometric distribution, namely, \(Y {\mathop {=}\limits ^{d}} T \vert T \le k\) where \(T\sim G_{sh}(p)\).

We are now ready to state the next theorem, expressing the distributions of the negative binomial distributions of order k, as the distributions of properly defined random sums.

Theorem 1

Suppose that the waiting times \(T_{r,k}^{(N)}\), \(T_{r,k}^{(A)}\) and \(T_{r,k}^{(O)}\) are defined on a sequence of independent and identically distributed binary trials, with success probability p. Then,

$$\begin{aligned} T_{r,k}^{(i)}-c{\mathop {=}\limits ^{d}}U+\sum _{j=1}^{M}X_j \end{aligned}$$
(11)

where

  1. (a)

    for i = N, we have

    $$\begin{aligned} c=kr, U=0, M\sim Nb(r,p^k), \text { and } X_1,X_2,\ldots \sim G_{tr}^{k}(p), \end{aligned}$$
  2. (b)

    for i = A, we have

    $$\begin{aligned} c=r(k+1)-1, U\sim Nb(r-1,q), M\sim Nb(r,p^k), \text { and } X_1,X_2,\ldots \sim G_{tr}^{k}(p), \end{aligned}$$
  3. (c)

    for i = O, we have

    $$\begin{aligned} c=k+r-1, U+k\sim G_{k}(p), M\sim b(r-1,q), \text { and } X_1,X_2,\ldots \sim G_{k}(p), \end{aligned}$$

and all variables involved in the RHS of (11) (i.e., U, M and \(X_1,X_2,\ldots\) \()\) are independent.

Proof

(a) It is well known that, for the random sum \(S_M=X_1+X_2+\ldots +X_M\), we have

$$\begin{aligned} P_{S_M}(u)=P_M(P_X(u)). \end{aligned}$$

Since, \(M\sim Nb(r,p^k)\) we may write, by recalling (7), that

$$\begin{aligned} P_{S_{M}}(u)=P_{M}(P_X(u))=\left[ \frac{p^k}{1-(1-p^k)P_X(u)}\right] ^r. \end{aligned}$$

The probability generating function of \(P_X(u)\), when \(X_i\sim G_{tr}^k(p)\), is given by (10) and after simple algebraic calculations we get

$$\begin{aligned} P_{S_{M}}(u)=\left[ \frac{p^k}{Q_k(u)}\right] ^r=u^{-k r}\frac{(pu)^{rk}}{Q_k(u)^r} \end{aligned}$$
(12)

which, in view of (3), yields

$$\begin{aligned} P_{S_{M}}(u)=u^{-k r}E\left[ u^{T_{r,k}^{(N)}}\right] =E\left[ u^{T_{r,k}^{(N)}-kr}\right] . \end{aligned}$$

This completes the proof.

(b) Combining (4) and (12) we get

$$\begin{aligned} u^{-[r(k+1)-1]}E\left[ u^{T_{r,k}^{(A)}}\right] =\biggl (\frac{1-p}{1-pu}\biggr )^{r-1}P_{S_{M}}(u) \end{aligned}$$

and upon observing that the first term in the RHS can be viewed as the probability generating function of \(U\sim Nb(r-1,q)\) (c.f. (7)) we may write

$$\begin{aligned} T_{r,k}^{(A)}-r(k+1)+1{\mathop {=}\limits ^{d}}U+S_{M}, \end{aligned}$$

and therefore,

$$\begin{aligned} E\left[ u^{T_{r,k}^{(A)}-r(k+1)+1}\right] =E[u^{U}]E[u^{S_M}]. \end{aligned}$$

The result follows immediately by taking into account that U is independent of \(S_M\).

(c) By virtue of (5) we get

$$\begin{aligned} E\left[ u^{T_{r,k}^{(O)}-(k+r-1)}\right] =\frac{p^k}{Q_k(u)} \left[ p+q\frac{(pu)^k}{Q_k(u)}\right] ^{r-1}, \end{aligned}$$

and if \(B\sim b(r-1,q)\) and \(T_k\sim G_k(p)\) we may write the RHS as follows (c.f. (6) and (8))

$$\begin{aligned} E\left[ u^{T_k-k}\right] E[u^{S_B}] \end{aligned}$$

where \(S_{B}=X_1+X_2+\ldots +X_{B}\), with \(X_i\sim G_k(p)\). Making use of the independence of the random variables involved in the above expressions, we conclude that

$$\begin{aligned} T_{r,k}^{(O)}-(k+r-1){\mathop {=}\limits ^{d}}T_k-k+\sum _{j=1}^{B}X_j, \end{aligned}$$

and this completes the proof.

3 Recursive formulas for extended random sums

According to Theorem 1 a shifted version of the three negative binomial distributions of order k admits a random sum representation of the form \(U+\sum _{j=1}^{M}X_j\), where \(X_1, X_2, \ldots\), is a properly defined sequence of independent and identically distributed positive integer-valued random variables, independent of the non-negative integer-valued random variable M.

A common feature in the three representations provided in Theorem 1 is that the random variable M belongs to the Panjer class of counting distributions. Moreover, the random variable U is either degenerate (\(U=0\)) or it belongs to the same class (with different parameters). Before proceeding with the main results of this section, let us recall that a discrete random variable M belongs to the Panjer class of non-negative integer-valued random variables (symb., \(M\in {\mathcal {R}}(a,b,0)\)) if its probability mass function satisfies the recurrence relation

$$\begin{aligned} P(M=m)=\Bigl (a+\frac{b}{m}\Bigr )P(M=m-1), ~m=1,2,\ldots , \end{aligned}$$
(13)

for some constants a and b; e.g., Panjer (1981). For this class of counting distributions, we always have \(a<1\), and the only non-degenerate members of this family are the Poisson, the binomial and the negative binomial distribution. It can be verified that b(r, p) and Nb(r, p) obey the recurrence scheme (13) with \(a=-p(1-p)\), \(b=(r+1)p/(1-p)\) and \(a=p\), \(b=(r-1)p\), respectively.

The next theorem provides efficient recursive schemes for the evaluation of the probability mass function and cumulative distribution function of \(U+S_M\); subsequently, an analogous recursion is given for its tail probabilities.

Theorem 2

Let \(X_1, X_2, \ldots\) be a sequence of independent and identically distributed positive integer-valued random variables, with probability mass function and cumulative distribution function f(x) and F(x), respectively. Let \(S=U+X_1+\ldots +X_M\), where \(M\in {\mathcal {R}}(a,b,0)\), \(U\in {\mathcal {R}}(a_1,b_1,0)\) are independent random variables which are independent of \(X_j\)’s as well. Then, the probability mass function \(f_S(x)=P(S=x)\) and cumulative distribution function \(F_S(x)=P(S\le x)\) of S obey the following recurrence relations:

$$\begin{aligned} (a)\;f_S(x)=\sum _{i=1}^{x}\gamma _i(x)f_S(x-i),~~~~ \end{aligned}$$
(14)
$$\begin{aligned} (b)\;F_S(x)=\sum _{i=1}^{x}(\gamma _i(x)+\delta _i(x))F_S(x-i), \end{aligned}$$
(15)

with initial values \(f_S(0)=F_S(0)=P(U=0)P(M=0)\), and

$$\begin{aligned} \gamma _i(x)=\left( a+\frac{bi}{x}\right)\kern .1500em f(i)+\frac{1}{x}(a_1+b_1)(a_1^{i-1}-c_i),~~ \delta _i(x)=\frac{1}{x}(1-aF(i-1)) \end{aligned}$$

where \(c_1=0\), \(c_i=a\sum _{m=1}^{i-1}f(m)a_1^{i-m-1}, i=2,3,\ldots ~.\)

Proof

(a) Let us denote by \(P_S(u)=E[u^S]\), \(P_{S_M}(u)=E[u^{S_M}]\), \(P(u)=E[u^X]\) the probability generating functions of \(S, S_M\) and \(X_j\)’s, respectively. The conditions set in Theorem 2 imply that U and \(S_M\) are independent random variables, and therefore, the probability generating function of S takes on the form

$$\begin{aligned} P_{S}(u)=P_U(u)P_{S_M}(u) \end{aligned}$$
(16)

and differentiating with respect to u we get

$$\begin{aligned} P_S^{\prime }(u)=\frac{P_U^{\prime }(u)}{P_{U}(u)}P_{S}(u)+P_U(u)P_{S_M}^{\prime }(u). \end{aligned}$$
(17)

Differentiating next the formula \(P_{S_M}(u)=P_M(P(u))\) with respect to u and taking into account that the probability generating function of M, \(P_{M}(u)=E[u^M]\), satisfies the differential equation,

$$\begin{aligned} P_{M}^{\prime }(u)=\frac{a+b}{1-au}P_{M}(u), \end{aligned}$$
(18)

we obtain

$$\begin{aligned} \begin{aligned} P_{S_M}^{\prime }(u)=P^{\prime }(u)P_{M}^{\prime }(P(u))=\frac{(a+b)P^{\prime }(u)}{1-aP(u)}P_{S_M}(u). \end{aligned} \end{aligned}$$

Substituting the last expression into the right-hand side of (17), and reusing (16), and (18), we may write

$$\begin{aligned} P_{S}^{\prime }(u)=\left[ \frac{a_1+b_1}{1-a_1u}+\frac{(a+b)P^{\prime }(u)}{1-aP(u)}\right] P_S(u). \end{aligned}$$
(19)

Let us next multiply both sides of (19) by \(u(1-a P(u))\), to obtain

$$\begin{aligned} u(1-a P(u))P_{S}^{\prime }(u)=(a+b)uP_{S}(u)P^\prime (u)+\frac{a_1+b_1}{1-a_1u}(1-a P(u))uP_{S}(u) , \end{aligned}$$
(20)

and observe that

$$\begin{aligned} \frac{u}{1-a_1u}(1-a P(u))=\sum _{x=1}^{\infty }\left( a_1^{x-1}-a\sum _{m=1}^{x-1}f(m)a_1^{x-m-1}\right) u^x. \end{aligned}$$

Replacing \(P_S(u)\) and P(u) by their series expansions and then picking up the coefficients of \(u^x\), \(x\ge 1\), we obtain that

$$\begin{aligned} f_S(1)=\biggl [(a_1+b_1)+(a+b)f(1)\biggr ]f_S(0), \end{aligned}$$

and for \(x=2,3,\ldots\)

$$\begin{aligned} \begin{aligned} xf_S(x)&=a\sum _{i=1}^{x-1}(x-i)f(i)f_S(x-i)+(a+b)\sum _{i=1}^{x}if(i)f_S(x-i)\\&+(a_1+b_1)\left[ \sum _{i=1}^{x}a_1^{x-i}f_S(x-i)-\sum _{i=2}^{x}c_if_S(x-i)\right] \\&=\sum _{i=1}^{x}(ax+bi)f(i)f_S(x-i)\\&+(a_1+b_1)\left[ \sum _{i=1}^{x}a_1^{i-1}f_S(x-i)-\sum _{i=2}^{x}c_if_S(x-i)\right] . \end{aligned} \end{aligned}$$

Since the last relation reproduces the previous one for \(x=1\), we may state that it holds true for all \(x=1,2,3,\ldots\). The proof is easily completed by extending the last summation in the range \(i=1,2,\ldots ,x\) (by convention \(c_1=0\)) and dividing both sides by x.

(b) Let \({\widehat{P}}_S(u)=\sum _{x=0}^{\infty }F_S(x)u^x\) be the generating function of \(F_S(x), x=0,1,\ldots\) and \(\widehat{P}_{1,S}(u)=\sum _{x=0}^{\infty }F_{1,S}(x)u^x\) the generating function of the auxiliary quantities \(F_{1,S}(x)=\sum _{i=0}^{x}F_S(i)\), for each \(x=0,1,\ldots\). Then, it can be easily verified that

$$\begin{aligned} {\widehat{P}}_{S}(u)=\frac{P_S(u)}{1-u}\quad \text{ and }\quad {\widehat{P}}_{1,S}(u)=\frac{\widehat{P}_S(u)}{1-u}. \end{aligned}$$
(21)

Dividing both sides of (20) by \(1-u\) and taking into account (21), we get the following differential equation for \({\widehat{P}}_{S}(u)\),

$$\begin{aligned} \begin{aligned} u\widehat{P}_{S}^{\prime }(u)=&u\widehat{P}_{1,S}^{\prime }(u)+aP(u)[u\widehat{P}_{S}^{\prime }(u)-u\widehat{P}_{1,S}^{\prime }(u)]\\ +&\frac{a_1+b_1}{1-a_1u}{\widehat{P}}_S(u)-a\frac{a_1+b_1}{1-a_1u}P(u){\widehat{P}}_S(u), \end{aligned} \end{aligned}$$

which yields for \(x\ge 1\),

$$\begin{aligned} \begin{aligned}&xF_S(x)\\&=F_{1,S}(x-1)+a\sum _{i=1}^{x-1}(x-i)f(i)F_S(x-i)-a\sum _{i=1}^{x-1}f(i)F_{1,S}(x-i-1)\\&+(a_1+b_1)\left[ \sum _{i=1}^{x}a_1^{x-1}F_S(x-i)-\sum _{i=2}^{x}c_iF_S(x-i)\right] +(a+b)\sum _{i=1}^{x}if(i)F_S(x-i)\\&=\sum _{i=1}^{x}\left[ (ax+bi)f(i)+(a_1+b_1)(a_1^{i-1}-c_i)\right] F_S(x-i) +F_{1,S}(x-1)\\&-a\sum _{i=1}^{x-1}f(i)F_{1,S}(x-i-1). \end{aligned} \end{aligned}$$
(22)

Observe next that, for \(x=1,2,\ldots\), we have

$$\begin{aligned} \sum _{i=1}^{x-1}f(i)F_{1,S}(x-i-1)=\sum _{i=2}^{x}F(i-1)F_S(x-i), \end{aligned}$$

and since \(F_{1,S}(x-1)=\sum _{i=1}^{x}F_S(x-i)\) and \(F_Y(0)=0\), we may write

$$\begin{aligned} F_{1,S}(x-1)-a\sum _{i=1}^{x-1}f(i)F_{1,S}(x-i-1)=\sum _{i=1}^{x}(1-aF(i-1))F_{S}(x-i). \end{aligned}$$
(23)

Substituting (23) into (22), recursion (15) follows.

Theorem 2 provides simple recurrences for the probability mass function and the cumulative distribution function of the random sum S which make use the parameters \(a,b,a_1,b_1\) of the Panjer families involved in the distributions of U and M, and the probability mass function f(x) of \(X_j\)’s. One can easily establish an analogous recurrence relation for the tail probabilities \(\overline{F}_S(x)=P(S>x)\) of S. This can be accomplished by following a procedure analogous to the one used for proving part (b) of Theorem 2 or by simply replacing \(\overline{F}_S(x)=1-F_S(x)\) in (15) and carrying our some simple algebraic calculations in the resulting equality. Hence, the deduced recurrence takes on the form

$$\begin{aligned} \overline{F}_S(x)=\sum _{i=1}^{x}\left( \gamma _i(x)+\delta _i(x)\right) \overline{F}_S(x-i)+\epsilon (x),~x=1,2\ldots \end{aligned}$$
(24)

where

$$\begin{aligned} \epsilon (x)=\frac{1}{x}(a_1+b_1)\left( \sum _{i=1}^{x}c_i-\frac{1-a_1^x}{1-a_1}\right) -\frac{a+b}{x}\sum _{i=1}^{x}if(i), x\ge 1, \end{aligned}$$

with initial condition \(\overline{F}_S(0)=1-P(U=0)P(M=0)\).

It is of interest to note that, the recurrences of Theorem 2 may be restated in the form

$$\begin{aligned} f_S(x)=\sum _{i=1}^{x}\left( A_i+\frac{B_i}{x}\right) f_S(x-i),F_S(x)=\sum _{i=1}^{x}\left( A_i+\frac{B_i^\prime }{x}\right) F_S(x-i), \end{aligned}$$
(25)

where \(A_i=af(i)\), \(B_i=bi f(i)+(a_1+b_1)(a_1^{i-1}-c_i)\) and \(B_i^{\prime }=B_i+(1-aF(i-1))\). The last expressions have an apparent resemblance to the Panjer recursions, as well as to the recurrences obeyed by the generalization of Panjer’s counting distributions class considered by Sundt (1982).

Manifestly, the recurrences developed in this section will reduce to the recurrences for the classical random sum \(S_M=\sum _{j=1}^{M}X_j\) (see Panjer 1981) if we set \(a_1=b_1=0\) in which case the random variable U becomes degenerate with its mass concentrated at 0.

Closing this section, we provide some hints for the calculation of the moments of \(S=U+S_M\). The mean and the variance of S can be easily obtained by noting that, by virtue of the independence of U and \(S_M\),

$$\begin{aligned} E[S]=E[U]+E[S_M] \text { and } V[S]=V[U]+V[S_M]. \end{aligned}$$

On the other hand, a well known result for the random sum \(S_M=\sum _{j=1}^{M}X_j\) states that

$$\begin{aligned} E[S_M]=E[M]E[X], V[S_M]=E[M]V[X]+V[M]E[X]^2, \end{aligned}$$

and taking into account that \(M\in {\mathcal {R}}(a,b,0)\), and \(U\in {\mathcal {R}}(a_1,b_1,0)\), we have (Panjer 1981)

$$\begin{aligned} E[M]=\frac{a+b}{1-a},~~ E[U]=\frac{a_1+b_1}{1-a_1}, ~V[M]=\frac{a+b}{(1-a)^2}, ~V[U]=\frac{a_1+b_1}{(1-a_1)^2}. \end{aligned}$$

Then, we easily arrive at the following expressions

$$\begin{aligned} \begin{aligned} E[S]&=\frac{a_1+b_1}{1-a_1}+\frac{a+b}{1-a}E[X], \\ V[S]&=\frac{a_1+b_1}{(1-a_1)^2}+\frac{a+b}{1-a}V[X]+\frac{a+b}{(1-a)^2}E[X]^2. \end{aligned} \end{aligned}$$

We provide next a recurrence scheme for the evaluation of the factorial moments of S under the same conditions on M, U and \(X_j\), as in Theorem 2.

Theorem 3

Let

$$\begin{aligned} \begin{aligned}&m_n=E[S(S-1)\cdots (S-n+1)]\\&\mu _n=E[X(X-1)\cdots (X-n+1)] \end{aligned} \end{aligned}$$

for \(n=1,2,\ldots\) be the factorial moments of order \(n \ge 1\) of S and X, respectively (convention: \(m_0=\mu _0=1\)). Then, the following recurrence holds true

$$\begin{aligned} m_n=\frac{1}{1-a}\sum _{i=1}^{n}\left( {\begin{array}{c}n-1\\ i-1\end{array}}\right) \theta _im_{n-i} \end{aligned}$$

where

$$\begin{aligned} \theta _i=\left( \frac{na}{i}+b\right) \mu _i+(i-1)!\frac{a_1+b_1}{a_1}\left( \left( \frac{a_1}{1-a_1}\right) ^{i}-a\sum _{m=1}^{i}\frac{1}{(i-m)!}\left( \frac{a_1}{1-a_1}\right) ^m\mu _{i-m+1}\right) \end{aligned}$$

Proof

Multiplying both sides of (19) by \(1-aP(u)\) we get

$$\begin{aligned} (1-aP(u))P_{S}^{\prime }(u)=\left[ (a+b)P^{\prime }(u)+(1-aP(u))(a_1+b_1)R(u)\right] P_{S}(u)\end{aligned}$$

with \(R(u)=\frac{1}{1-a_1u}\). Application of Leibnitz’s formula for obtaining the derivative of order n in both sides of the above equation, gives

$$\begin{aligned} \begin{aligned} (1-a)P_{S}^{(n+1)}(u)&=a\sum _{i=1}^{n}\left( {\begin{array}{c}n\\ i\end{array}}\right) P^{(i)}(u)P_{S}^{(n+1-i)}(u)\\&+(a+b)\sum _{i=0}^{n}\left( {\begin{array}{c}n\\ i\end{array}}\right) P^{(i+1)}(u)P_{S}^{(n-i)}(u)\\&+\sum _{i=0}^{n}\left( {\begin{array}{c}n\\ i\end{array}}\right) (a_1+b_1)[R^{(i)}(u)-aM^{(i)}(u)]P_{S}^{(n-i)}(u) \end{aligned} \end{aligned}$$
(26)

with \(M(u)=R(u)P(u)\). Now, since

$$\begin{aligned} \sum _{i=1}^{n}\left( {\begin{array}{c}n\\ i\end{array}}\right) P^{(i)}(u)P_{S}^{(n+1-i)}(u) =\sum _{i=0}^{n}\left( {\begin{array}{c}n\\ i\end{array}}\right) \frac{n-i}{i+1}P^{(i+1)}(u)P_{S}^{(n-i)}(u) \end{aligned}$$

relation (26) can equivalently be written as

$$\begin{aligned} \begin{aligned}&(1-a)P_{S}^{(n+1)}(u)\\&=\sum _{i=1}^{n}\left( {\begin{array}{c}n\\ i\end{array}}\right) \biggl \{\Bigl (\frac{n+1}{i+1}a+b\Bigr )P^{(i+1)}(u)+(a_1+b_1)[R^{(i)}(u)-aM^{(i)}(u)]\biggr \}P_{S}^{(n-i)}(u) \end{aligned} \end{aligned}$$

or

$$\begin{aligned} \begin{aligned}&(1-a)P_{S}^{(n)}(u)\\&=\sum _{i=1}^{n}\left( {\begin{array}{c}n-1\\ i-1\end{array}}\right) \biggl \{\Bigl (\frac{n}{i}a+b\Bigr )P^{(i)}(u)(a_1+b_1)[R^{(i-1)}(u)-aM^{(i-1)}(u)]\biggr \}P_{S}^{(n-i)}(u). \end{aligned} \end{aligned}$$

The proof is completed by noting that

$$\begin{aligned} R^{(i)}(u)=\frac{i!a_1^i}{(1-a_1u)^{i+1}} \end{aligned}$$

and

$$\begin{aligned} M^{(i)}(u)=\sum _{m=0}^{i}\left( {\begin{array}{c}i\\ m\end{array}}\right) R^{(m)}(u)P^{(i-m)}(u) =\sum _{m=0}^{i}\left( {\begin{array}{c}i\\ m\end{array}}\right) \frac{m!a_1^{m}}{(1-a_1u)^{m+1}}P^{(i-m)}(u). \end{aligned}$$

4 Recursions for the negative binomial distributions of order k

In this section, we are going to take advantage of the results of Sections 2 and 3 in order to derive recursive formulas for the distributions of \(T_{r,k}^{(N)}\), \(T_{r,k}^{(A)}\) and \(T_{r,k}^{(O)}\). We start with the simplest case where the waiting times \(T_{r,k}^{(N)}\), \(T_{r,k}^{(A)}\) and \(T_{r,k}^{(O)}\) are defined on a sequence \(Z_1, Z_2, \ldots\) of i.i.d. trials (Section 4.1) and apply Theorem 2 to establish recurrences for the probability mass function, cumulative distribution function, tail probabilities and moments in a unified way; it is worth stressing out that some of the results given in this section have also been obtained in the past by exploiting different techniques adjusted to the special nature of each waiting time variable.

Next, in Section 4.2, we derive new results under a more general set up for \(Z_1, Z_2, \ldots\). More specifically, we assume that \(Z_1, Z_2, \ldots\) is a sequence of binary random variables of order k (Aki 1985). This case is also treated in a uniform way by considering first a slight generalization of Theorem 2 and then deriving all the desired results by a direct application of that.

4.1 Independent and identically distributed binary variables

The next proposition provides recurrences for the probability mass function, the cumulative distribution function and the tail probabilities of \(T_{r,k}^{(N)}\), as well as for its factorial moments. In the statements and the proofs that follow we shall be using the next notations

$$\begin{aligned} \begin{aligned}&\xi _i(p) = \sum _{j=1}^{i}j^{i}p^{j-1},\\&\psi _1(x)=\left\{ \begin{array}{ll} \frac{1-xqp^{x-1}-p^x}{q},&{}x\le k+1\\ \frac{1-(1+kq)p^k}{q}+kp^{k-1}(1-p^{x-k}),&{}x\ge k+1, \end{array}\right. \\&\epsilon =\epsilon (x,k,r)=\frac{1}{x-kr},~\eta =\epsilon (x+1,k+1,r) \end{aligned} \end{aligned}$$

and \(\epsilon _i=\epsilon _i(x,k,r)=1+(r-1)i\epsilon\), \(\eta _i=\epsilon _i(x+1,k+1,r)\), \(\alpha _i(p)=p^{i-1}-qp^{i-2}\min \{i-1,k\}\), \(i=1,2,\ldots\). We also set \(\xi _i(p)=1\) and \(\xi _i(p)=0\), for \(i=0\) and \(i\ge k+1\), respectively.

Proposition 4

For the probability mass function, the cumulative distribution function, the tail probabilities and the factorial moments \((m_n^{(N)})\) of \(T_{r,k}^{(N)}\), the following recursions hold true:

$$\begin{aligned} \begin{aligned} (i)\quad&f_{r,k}^{(N)}(x)=\sum _{i=1}^{\min \{x-kr,k\}}\epsilon _iqp^{i-1}f_{r,k}^{(N)}(x-i),x \ge kr+1,\\ (ii)\quad&F_{r,k}^{(N)}(x)=\sum _{i=1}^{x-kr}(\epsilon +q\epsilon _i)p^{i-1}F_{r,k}^{(N)}(x-i), kr+1\le x\le k(r+1),\\&F_{r,k}^{(N)}(x)=\sum _{i=1}^{k}(\epsilon +q\epsilon _i)p^{i-1}F_{r,k}^{(N)}(x-i)+p^k\epsilon \sum _{i=k+1}^{x-kr}F_{r,k}^{(N)}(x-i), \\&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~x\ge k(r+1)+1,\\ (iii)\quad&\overline{F}_{r,k}^{(N)}(x)=\sum _{i=1}^{x-kr}(\epsilon +q\epsilon _i)p^{i-1}\overline{F}_{r,k}^{(N)}(x-i)-r\left[ \frac{\epsilon }{q}-\left( \frac{\epsilon }{q}+1\right) p^{x-kr}\right] ,\\&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~kr+1\le x\le k(r+1),\\&\overline{F}_{r,k}^{(N)}(x)=\sum _{i=1}^{k}(\epsilon +q\epsilon _i)p^{i-1}\overline{F}_{r,k}^{(N)}(x-i)+p^k\epsilon \sum _{i=k+1}^{x-kr}\overline{F}_{r,k}^{(N)}(x-i)\\&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~-r\epsilon \left[ \frac{1}{q}-\left( \frac{1}{q}+k\right) p^{k}\right] , x \ge k(r+1)+1,\\ (iv)\quad&m_{n}^{(N)}=\frac{1}{p^k}\sum _{i=1}^{n}\left( {\begin{array}{c}n-1\\ i-1\end{array}}\right) \left[ \left( \frac{n}{i}+r-1\right) \xi _i(p)+(-1)^{i-1}rk(i-1)!\right. \\&~~~~~~~~~~~~~~~~~~~~~~~~~\left. -rk\sum _{m=1}^{i}(-1)^{m-1}\left( {\begin{array}{c}i-1\\ n-1\end{array}}\right) (m-1)!\xi _{i-m}(p)\right] m_{n-i}^{(N)} \end{aligned} \end{aligned}$$

with initial conditions \(f_{r,k}^{(N)}(kr)=F_{r,k}^{(N)}(kr)=1-\overline{F}_{r,k}^{(N)}(kr)=p^{kr}\).

Proof

(i) According to Theorem 1a, \(T_{r,k}^{(N)}-kr\) has the same distribution with \(S=X_1+X_2+\ldots +X_{M}\), where \(M\in {\mathcal {R}}(a,b,0)\) with \(a=1-p^k\), \(b=(r-1)(1-p^k)\) and \(X_j\sim G_{tr}^{(k)}(p)\). Therefore, S satisfies the conditions of Theorem 2, with \(a_1=b_1=0\), and \(f(x)=\frac{q}{1-p^k}p^{x-1}\), \(x=1,2,\ldots ,k\). A direct application of Theorem 2i yields that the probability mass function of S satisfies the recursion

$$\begin{aligned} f_S(x)=P(S=x)=\left\{ \begin{array}{ll} \sum _{i=1}^{\min \{x,k\}}\Bigl [1+\frac{(r-1)i}{x}\Bigr ]qp^{i-1}f_S(x-i),&{}x=1,2,\ldots \\ p^{kr},&{}x=0. \end{array}\right. \end{aligned}$$

The proof of this part is easily completed on observing that \(f_S(x)=f_{r,k}^{(N)}(x+kr)\), for \(x=0,1,\ldots\).

(ii) The cumulative distribution function of \(X\sim G_{tr}^{(k)}(p)\) is given by (see (9))

$$\begin{aligned} F(x)=\left\{ \begin{array}{ll} 0,&{}x=0\\ \frac{1-p^x}{1-p^k},&{}1\le x\le k-1\\ 1,&{}x\ge k \end{array}\right. \end{aligned}$$
(27)

and the sum \(\sum _{i=1}^{x}\delta _i(x)F_S(x-i)\) appearing in the RHS of (15) takes on the form

$$\begin{aligned} \begin{aligned} \sum _{i=1}^{x}&F_S(x-i)-a\sum _{i=1}^{x}F(x-i)F_S(x-i)\\&= \left\{ \begin{array}{ll} \sum _{i=1}^{x}p^{i-1}F_S(x-i),&{}1\le x\le k\\ \sum _{i=1}^{k}p^{i-1}F_S(x-i)+p^k\sum _{i=k+1}^{x}F_S(x-i),&{}x\ge k+1. \end{array}\right. \end{aligned} \end{aligned}$$
(28)

Hence, (15) reduces to

$$\begin{aligned} F_S(x)= \left\{ \begin{array}{ll} \sum _{i=1}^{\min \{x,k\}}\Bigl [1+\frac{(r-1)i}{x}\Bigr ]p^{i-1}qF_S(x-i)+\frac{1}{x}\sum _{i=1}^{x}p^{i-1}F_S(x-i),&{}1\le x\le k\\ &{}\\ \sum _{i=1}^{\min \{x,k\}}\Bigl [1+\frac{(r-1)i}{x}\Bigr ] p^{i-1}qF_S(x-i)+\frac{1}{x}\sum _{i=1}^{k}p^{i-1}F_S(x-i)&{}\\ +\frac{1}{x}p^k\sum _{i=k+1}^{x}F_S(x-i),&{}x\ge k+1, \end{array}\right. \end{aligned}$$

and the proof is completed by taking into account that \(F_S(x)=F_{r,k}^{(N)}(x+kr)\), for \(x=0,1,\ldots\).

(iii) Comparing (15) and (24), it is clear that \(F_S(x)\) and \(\overline{F}_S(x)\) obey the same recurrence scheme with the exception of the extra term \(\epsilon (x)\) appearing in \(\overline{F}_S(x)\). The proof is easily established by noting that in our case (\(a_1=b_1=0\)) we have \(x\epsilon (x)=(a+b)\sum _{i=1}^{x}if(i)=r\sum _{i=1}^{\min \{x,k\}}i p^{i-1}q\), for \(x=0,1,\ldots\) and use of \(F_S(x)=F_{r,k}^{(N)}(x+kr)\), for \(x=0,1,\ldots\).

(iv) Taking into account the form of \(\xi _i(p)\) and (9), we may write

$$\begin{aligned} \xi _i(p)=(1-p^k)m_i^{(Y)} \end{aligned}$$

where \(m_i^{(Y)}\) denotes the ith factorial moment of the random variable Y. Furthermore, from Theorem 1 we know that \(T_{r,k}^{(i)}-kr{\mathop {=}\limits ^{d}}\sum _{j=1}^{M}X_j\), \(M\sim Nb(r,p^k)\), and \(X_1,X_2,\ldots \sim G_{tr}^{k}(p)\). Then, using Theorem 3 with \(a=1-p^k, b=(r-1)(1-p^k), a_1=b_1=0\) and the above form of \(\xi _i(p)\), the proof is readily completed.

The recursive formula provided above for \(f_{r,k}^{(N)}(x)\) has also been given by Philippou and Georghiou (1989) while a similar recurrence is mentioned by Charalambides (1986). The techniques for deriving these results are entirely different from the one used here: the first authors exploited Fibonacci-type polynomials, the latter made use of truncated Bell polynomials. It is also noteworthy that, for \(f_{r,k}^{(N)}(x)\) there exists also closed formulae involving single and multiple summations with binomial or multinomial coefficients respectively; see Chapter 4 in Balakrishnan and Koutras (2002) for more details. The recursive schemes for \(F_{r,k}^{(N)}(x)\) and \(\overline{F}_{r,k}^{(N)}(x)\) given in part (ii) and (iii) of Proposition 4, to the best of our knowledge, have not appeared in the literature up to now.

The following result may be proved in much the same way as Proposition 4, and therefore, the proof is omitted.

Proposition 5

For the probability mass function, the cumulative distribution function, the tail probabilities and the factorial moments \((m_n^{(A)})\) of \(T_{r,k}^{(A)}\), the following recursions hold true:

$$\begin{aligned} \begin{aligned}(i)\quad &f_{r,k}^{(A)}(x)=q\sum _{i=1}^{\min \{1/\eta ,k\}}\eta _i p^{i-1} f_{r,k}^{(A)}(x-i)+(r-1)\eta p\sum _{i=1}^{1/\eta } \alpha _i(p)f_{r,k}^{(A)}(x-i),\\&~~~~~~~~~~~~~~x\ge (k+1)r;\\(ii)\quad &F_{r,k}^{(A)}(x)= \sum _{i=1}^{1/\eta } \biggl \{ (\eta +\eta _i q)p^{i-1}+p\eta \alpha _i(p)\biggr \}F_{r,k}^{(A)}(x-i),\\&~~~~~~~~~~~~~~(k+1)r\le x\le (k+1)r+k-1;\\&F_{r,k}^{(A)}(x)=\sum _{i=1}^{k} (\eta +\eta _i q)p^{i-1}F_{r,k}^{(A)}(x-i)+(r-1)p \eta \sum _{i=1}^{1/\eta }\alpha _i(p)F_{r,k}^{(A)}(x-i)\\&+p^k \eta \sum _{i=k+1}^{1/\eta }F_{r,k}^{(A)}(x-i),x\ge (k+1)r+k.\\(iii)\quad &\overline{F}_{r,k}^{(A)}(x)= \sum _{i=1}^{1/\eta }\biggl \{(\eta +\eta _i q)p^{i-1}+(r-1)p \eta \alpha _i(p)\biggr \}\overline{F}_{r,k}^{(A)}(x-i)\\&+(r-1)p \eta \Bigl [\psi _1\bigl (1/\eta \bigr )-\frac{1-p^{1/\eta }}{q}\Bigr ]-\frac{\eta r}{q}\Bigl \{1-[1+(q/\eta )]p^{1/\eta } \Bigr \},\\&~~~~~~~~~~~~~~(k+1)r\le x\le (k+1)r+k-1;\\&\overline{F}_{r,k}^{(A)}(x)=\sum _{i=1}^{k}(\eta +\eta _i q)p^{i-1}\overline{F}_{r,k}^{(A)}(x-i)+(r-1)p\eta \sum _{i=1}^{1/\eta }\alpha _i(p)\overline{F}_{r,k}^{(A)}(x-i)\\&+p^k \eta \sum _{i=k+1}^{1/\eta }\alpha _i(p)\overline{F}_{r,k}^{(A)}(x-i)+(r-1)p \eta \Bigl [\psi _1\bigl (1/\eta \bigr )-\frac{1-p^{1/\eta }}{q}\Bigr ]\\&-r \eta [1-(1+kq)p^k],x\ge (k+1)r+k,\\(iv) \quad &m_{n}^{(A)}=\frac{1}{p^k}\sum _{i=1}^{n}\left( {\begin{array}{c}n-1\\ i-1\end{array}}\right) \left\{ \left( \frac{n}{i}+r-1\right) \xi _i(p)\right. \\&\left. +(-1)^{i-1}[r(k+1)-1](i-1)!-[r(k+1)-1]\sum _{m=1}^{i}\left( {\begin{array}{c}i-1\\ m-1\end{array}}\right) \frac{(m-1)!p^{m-1}}{q^m}\xi _{i+1-m}(p)\right. \\&\left. +(r-1)p\left[ \frac{(i-1)!p^i}{q^i}-\sum _{m=1}^{i}(-1)^{m-1}\left( {\begin{array}{c}i-1\\ m-1\end{array}}\right) \frac{(m-1)!p^{m-1}}{q^m}\xi _{i+1-m}(p)\right] \right\} m_{n-i}^{(A)} \end{aligned} \end{aligned}$$

with initial conditions

\(f_{r,k}^{(A)}\bigl ((k+1)r-1\bigr )=F_{r,k}^{(A)}\bigl ((k+1)r-1\bigr )=1-\overline{F}_{r,k}^{(A)}\bigl ((k+1)r-1\bigr )=q^{r-1}p^{kr}\).

As far as we know, no recurrence relations have appeared in the literature for the probability mass function, the cumulative distribution function, the tail probabilities and the factorial moments of \(T_{r,k}^{(A)}\). Muselli (1996) developed the following exact formula for the evaluation of \(f_{r,k}^{(A)}(x)\)

$$\begin{aligned} f_{r,k}^{(A)}(x)=\sum _{j=r}^{\left[ \frac{x+1}{k+1}\right] }(-1)^{j-r}\left( {\begin{array}{c}j-1\\ r-1\end{array}}\right) p^{jk}q^{j-1}\times \left\{ \left( {\begin{array}{c}x-jk-1\\ j-2\end{array}}\right) +q\left( {\begin{array}{c}x-jk-1\\ j-1\end{array}}\right) \right\} . \end{aligned}$$

The results of this section are completed by providing formulae for computing the distribution of the waiting time corresponding to the overlapping scheme. More specifically, in the next Proposition the distribution of \(T_{r,k}^{(O)}\) is expressed in terms of the distribution of \(T_{r,k}^{(N)}\).

Proposition 6

For the probability mass function of \(T_{r,k}^{(O)}\), the following formula hold true, for \(x\ge k+r-1\):

$$\begin{aligned} f_{r,k}^{(O)}(x)=\sum _{i=1}^{r}\left( {\begin{array}{c}r-1\\ i-1\end{array}}\right) q^{i-1}p^{r-i}f_{i,k}^{(N)}(x-r+1). \end{aligned}$$

The same formula remains valid if we replace the probability mass functions f by the cumulative distribution functions F and the tail probabilities \(\overline{F}\).

Proof

Following similar steps with those of proving Theorem 1c, we can see that \(T_{r,k}^{(O)}-(r-1)\) is distributed as \(S=X_1+X_2+\ldots +X_{B+1}\), with \(B\sim b(r-1,q)\) and \(X_i\sim G_k(p)\). Applying the total probability theorem we may write

$$\begin{aligned} f_S(x)=\sum _{i=1}^{r}P(B+1=i)f_{i}^{*}(x),x\ge 0, \end{aligned}$$

where

$$\begin{aligned} P(B+1=i)=\left( {\begin{array}{c}r-1\\ i-1\end{array}}\right) q^{i-1}p^{r-i}, i=1,2,\ldots ,r, \end{aligned}$$

and \(f_{i}^{*}(x)=P(X_1+\ldots +X_i=x)\). Note next that \(X_i\sim G_k(p)\) implies that \(f_{i}^{*}(x)=f_{i,k}^{(N)}(x)\), for \(x=0,1,\ldots\), and thus

$$\begin{aligned} f_S(x)=\sum _{i=1}^{r}P(B+1=i)f_{i,k}^{(N)}(x),x\ge 0. \end{aligned}$$

Formula (i) is readily deduced by taking into account that \(f_S(x)=f_{r,k}^{(O)}(x+r-1)\), for \(x\ge r-1\), and thus \(f_{i,k}^{(N)}(x-r+1)>0\) for \(x\ge ki+r-1\). Arguing in a similar way, we may easily obtain (ii) and (iii).

Ling (1989) proved the formula given in Proposition 6, by carrying out mathematical induction on r. He also established the following recursive scheme which makes use of the probability mass function of \(G_k(p)\)

$$\begin{aligned} f_{r,k}^{(O)}(x)=pf_{r-1,k}^{(O)}(x-1)+q\sum _{j=k+r-2}^{x-k-1}f_{r-1,k}^{(O)}(j)f(x-j-1). \end{aligned}$$
(29)

The computational efficiency of the above recursive schemes (Propositions 4-6), in terms of the time needed for computing the probability mass function (until its 90th percentile), is indicatively considered in Table 1. Specifically, the computational time of the recursive schemes of the negative binomial distributions of order k, as provided by Propositions 4-6 (i.e., the three different counting schemes), is demonstrated and further compared to the recursive schemes deduced by the Markov chain imbedding technique (e.g., Section 4.2.1, in Balakrishnan and Koutras 2002). For the overlapping scheme, we also provide the computational times of (29). As can be seen in Table 1, the suggested recursive schemes have the best computational times, in most of the cases. A notable exception to that is the case of the overlapping counting where for small values of k, the recursive scheme deduced by the Markov chain imbedding technique (MCI) exhibit the smallest computing times.

Table 1 Computational times (in seconds), for the evaluation of the probability mass function (until the 90th percentile) using recursive schemes (MCI: the recursive scheme deduced by the Markov chain imbedding technique)
Full size table

4.2 The case of binary sequence of order k

Let us recall that \(X_0, X_1, \ldots\), with \(X_j\in \{0,1\}\) for all \(j=1,2,\ldots ,\) is said to be a binary sequence of order k (Aki 1985), if there exist a positive integer k and real numbers \(0<p_1,\ldots ,p_k<1\) such that \(P(X_n=1\vert X_0=x_0, X_1=x_1, \ldots , X_{n-1}=x_{n-1})=p_j\), for any n with \(j=n_0-[(n_0-1)/k]k\), and \(n_0\) being the smallest positive integer with \(x_{n-n_0}=0\) ([a] stands for the largest integer not exceeding a; convention: \(P(X_0=0)=1\)). Note that if \(p_j=p\), for all j, then the sequence is i.i.d.

Under this type of dependence, it is known that the probability generating function of \(T_{r,k}^{(N)}\) is given by (Aki 1985)

$$\begin{aligned} E\left[ u^{T_{r,k}^{(N)}}\right] =\left[ \frac{p_1\cdots p_ku^k}{R(u)}\right] ^r=\left[ \frac{\pi _k u^k}{R(u)}\right] ^r, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} \pi _i=&p_1\cdots p_i, i=1,2,\ldots, \\ R(u)=&1-\sum _{i=1}^{k}\pi _{i-1}q_iu^i, \end{aligned} \end{aligned}$$

with \(\pi _0=1\) and \(q_i=1-p_i\). Employing the Markov chain imbedding technique (e.g., Fu 1986; Fu and Koutras 1994; Koutras and Alexandrou 1997; Koutras 1997; Chadjiconstantinidis et al. 2000; Fu and Lou 2003), the next theorem can be proved.

Theorem 7

The probability generating functions of \(T_{r,k}^{(A)}\) and \(T_{r,k}^{(O)}\), defined on a binary sequence of order k, with probabilities \(p_1, p_2, \ldots , p_k\), are given by

$$\begin{aligned} E\left[ u^{T_{r,k}^{(A)}}\right] =\left( \frac{q_ku}{1-p_ku}\right) ^{r-1}\left[ \frac{\pi _ku^k}{R(u)}\right] ^r, \end{aligned}$$
(30)
$$\begin{aligned} E\left[ u^{T_{r,k}^{(O)}}\right] =\frac{\pi _ku^k}{R(u)}\left[ p_ku+q_ku\frac{\pi _k u^k}{R(u)}\right] ^{r-1}. \end{aligned}$$
(31)

Proof

In order to prove (30) and (31) we employ the Markov chain imbedding technique. Roughly speaking, consider a process \(Y_t\) which both keeps track of the current success run length and also of the number of success runs met until time t, under the at least scheme; i.e., \(Y_t=(i,r)\) if and only if the last i outcomes of the sequence are all successes (1) and the previous a failure (0), and r success runs with at least length k have already been met. Then, this process is a Markov chain embeddable variable of binomial type (e.g., Koutras 1997), wherein the only non-zero elements of the \((k+1)\times (k+1)\) transition matrices \(A=[a_{ij}]\) and \(B=[b_{ij}]\), are given by

$$\begin{aligned} \begin{aligned}&a_{i1}=\left\{ \begin{array}{ll} q_i,&{}i=1,2,\ldots ,k\\ q_k,&{}i=k+1 \end{array}\right. ,\\&a_{i,i+1}=p_i,i=1,2,\ldots ,k-1;\;a_{k+1,k+1}=b_{k,k+1}=p_k. \end{aligned} \end{aligned}$$

Let \(\beta _i=\textbf{e}_iB\textbf{1}^{\prime }\), \(i=1,2,\ldots ,k+1\), where \(\textbf{1}^{\prime }\) represents the \((k+1)\times 1\) column vectors with all its entries being 1, and \(\textbf{e}_i\) is the \(1\times (k+1)\) row vector having 1 in the ith position and 0 elsewhere. Then \(\beta _i=0\) for \(i=1,2,\ldots ,k-1,k+1\) and \(\beta _k=p_k\). Thus, if

$$\begin{aligned} H_1(u,w)=\sum _{r=0}^{\infty }E\left[ u^{Z_{r,k}^{(A)}}\right] w^r, \end{aligned}$$

we get by Theorem 3.1 in Koutras (1997) that

$$\begin{aligned} H_1(u,w)=wup_k\textbf{e}_1[I-u(A+wB)]^{-1}\textbf{e}_k^{\prime }, \end{aligned}$$

where I is the identity matrix of order \(k+1\) and \(\textbf{e}_i^{\prime }\) is the transpose vector of \(\textbf{e}_i\); hence it is straightforward to see after some routine calculations that

$$\begin{aligned} H_1(u,w)=\frac{w\pi _k(1-p_ku)u^k}{(1-p_ku)R(u)-w\pi _kq_ku^{k+1}}. \end{aligned}$$

Expanding the latter in a Taylor series around \(w=0\) and considering the coefficient of \(w^r\), we get

$$\begin{aligned} E\left[ u^{T_{r,k}^{(A)}}\right] =\frac{\pi _k(1-p_ku)(\pi _kq_ku^{k+1})^{r-1}u^k}{(1-p_ku)^rR^r(u)}, \end{aligned}$$

and so (30) follows.

In order to prove (31), a similar process is introduced with the \((k+1)\times (k+1)\) transition matrices \(A=[a_{ij}]\) and \(B=[b_{ij}]\) having non-zero elements given by

$$\begin{aligned} a_{i1}=\left\{ \begin{array}{ll} q_i,&{}i=1,2,\ldots ,k\\ q_k,&{}i=k+1 \end{array}\right. a_{i,i+1}=p_i,\;i=1,2,\ldots ,k-1,b_{k,k+1}=b_{k+1,k+1}=p_k; \end{aligned}$$

hence

$$\begin{aligned} \beta _i=\textbf{e}_iB\textbf{1}^{\prime }=\left\{ \begin{array}{ll} 0,&{}i=1,2,\ldots ,k-1\\ p_k,&{}i=k,k+1. \end{array}\right. \; \end{aligned}$$

Therefore, if \(H_2(u,w)=\sum _{r=0}^{\infty }E\left[ u^{Z_{r,k}^{(O)}}\right] w^r\), then again by Theorem 3.1 in Koutras (1997) we have that

$$\begin{aligned} \begin{aligned} H_2(u,w)=&wup_k\textbf{e}_1[I-u(A+wB)]^{-1}(\textbf{e}_k^{\prime }+\textbf{e}_{k+1}^{\prime })\\ =&\frac{w\pi _ku^k}{(1-wp_ku)R(u)-w\pi _kq_ku^{k+1}}=\frac{w\pi _ku^k}{R(u)-w[p_kuR(u)+\pi _kq_ku^{k+1}]}, \end{aligned} \end{aligned}$$

and so expanding the latter into a Taylor series around \(w=0\) and considering the coefficient of \(w^r\), we get

$$\begin{aligned} E\left[ u^{T_{r,k}^{(O)}}\right] =\frac{\pi _ku^k[p_kuR(u)+\pi _kq_ku^{k+1}]^{r-1}}{R^r(u)}, \end{aligned}$$

which proves (31).

To state analogue results to Theorem 1, under the binary sequence of order k, we need the auxiliary i.i.d. positive integer-valued random variables \(Y_1, Y_2, \ldots\) with probability mass function

$$\begin{aligned} f_Y(i)=P(Y=i)=\frac{\pi _{i-1}q_i}{1-\pi _k},i=1,2,\ldots ,k,p_0=1 \end{aligned}$$

and the random variable W following \(Nb(r,\pi _k)\), \(r=1,2,\ldots\) independent of \(Y_j\)’s, having probability mass function

$$\begin{aligned} P(W=n)=\left( {\begin{array}{c}r+n-1\\ n\end{array}}\right) \pi _k^r(1-\pi _k)^{n},n=0,1,\ldots . \end{aligned}$$

Moreover, let \(W_1, W_2, \ldots\) stand for a sequence of independent and identically distributed positive integer-valued random variables, with \(W_j\) following the extended geometric distribution of order k (Aki 1985), i.e., their probability generating function is given by \(E\left[ u^{T_{1,k}^{(N)}}\right]\). We are now ready to state the following theorem, through which the shifted distributions of \(T_{r,k}^{(N)}\), \(T_{r,k}^{(A)}\) and \(T_{r,k}^{(O)}\), defined on the binary sequence of order k, are expressed as properly defined random sums, similar to that of Theorem 1 (the proofs of the results of this section are omitted, because the steps are quite similar to the ones used for the i.i.d. case).

Theorem 8

Suppose that the waiting times \(T_{r,k}^{(N)}\), \(T_{r,k}^{(A)}\) and \(T_{r,k}^{(O)}\) are defined on a binary sequence of order k, with probabilities \(p_1, p_2, \ldots , p_k\). Assume also that all the random variables W, B, and U are independent random variables, being also independent of the previously defined \(Y_j\)’s and \(W_j\)’s. Then, each of the following results hold:

$$\begin{aligned} \begin{aligned} (a)\quad&T_{r,k}^{(N)}-kr{\mathop {=}\limits ^{d}}\sum _{i=1}^{W}Y_i, \text { with } W\sim Nb(r,\pi _k), \\ (b)\quad&T_{r,k}^{(A)}-r(k+1)+1{\mathop {=}\limits ^{d}}U+\sum _{i=1}^{W}Y_i,\text { with } U \sim Nb(r-1,1-p_k), \\ (c)\quad&T_{r,k}^{(O)}-(k+r-1){\mathop {=}\limits ^{d}}U+\sum _{i=1}^{B}W_i, \text { with } U+k \sim W_i, B\sim B(r-1,1-p_k). \end{aligned} \end{aligned}$$

Based on the previous result and Theorem 2, the next corollary results.

Corollary 4.1

For the probability mass function, the cumulative distribution function and the tail probabilities of \(T_{r,k}^{(N)}\), defined on a binary sequence of order k, with probabilities \(p_1, p_2, \ldots , p_k\), the following recursions hold true:

$$\begin{aligned} \begin{aligned}(i)\quad &f_{r,k}^{(N)}(x)= \sum _{i=1}^{\min \{x-kr,k\}}\epsilon _i \pi _{i-1}q_if_{r,k}^{(N)}(x-i),x\ge kr+1,\\(ii)\quad& F_{r,k}^{(N)}(x)=\sum _{i=1}^{x-kr}(\epsilon +\epsilon _iq_i)\pi _{i-1}F_{r,k}^{(N)}(x-i), kr+1\le x\le k(r+1),\\&F_{r,k}^{(N)}(x)=\sum _{i=1}^{k}(\epsilon +\epsilon _iq_i)\pi _{i-1}F_{r,k}^{(N)}(x-i)+\pi _{k} \epsilon \sum _{i=k+1}^{x-kr}F_{r,k}^{(N)}(x-i),x\ge k(r+1)+1,\\(iii)\quad&\overline{F}_{r,k}^{(N)}(x)=\sum _{i=1}^{x-kr}(\epsilon +\epsilon _iq_i)\pi _{i-1}\overline{F}_{r,k}^{(N)}(x-i)-r \epsilon \sum _{i=1}^{x-kr}i\pi _{i-1}q_i, kr+1\le x\le k(r+1),\\&\overline{F}_{r,k}^{(N)}(x)= \sum _{i=1}^{k}(\epsilon +\epsilon _iq_i) \pi _{i-1}\overline{F}_{r,k}^{(N)}(x-i)+ \pi _k \epsilon \sum _{i=k+1}^{x-kr}\overline{F}_{r,k}^{(N)}(x-i)-r \epsilon \sum _{i=1}^{k}i\pi _{i-1}q_i,\\&~~~~~~~~~~~~~~ x\ge k(r+1)+1, \end{aligned} \end{aligned}$$

with \(f_{r,k}^{(N)}(kr)=F_{r,k}^{(N)}(kr)=1-\overline{F}_{r,k}^{(N)}(kr)=\pi _{k}^r.\)

Note that the formulae of Corollary 4.1 are analogues to the ones provided in Proposition 4 (replace \(\eta +q\eta _i\) and \(p^{i-1}\) in Proposition 4, by \(\eta +q_i\eta _i\) and \(\pi _{i-1}\), respectively).

Similarly, due to Theorems 8 and 2, the next results for the distribution of \(T_{r,k}^{(A)}\) can be deduced.

Corollary 4.2

For the probability mass function, the cumulative distribution function and the tail probabilities of \(T_{r,k}^{(A)}\), defined on a binary sequence of order k, with probabilities \(p_1, p_2, \ldots , p_k\), the following recursions hold true:

$$\begin{aligned} \begin{aligned}(i)\quad&f_{r,k}^{(A)}(x)=\sum _{i=1}^{\min \{1/\eta ,k\}}\eta _i\pi _{i-1}q_if_{r,k}^{(A)}(x-i)\\&+(r-1)p_k \eta \sum _{i=1}^{1/\eta }[p_k^{i-1}-d_1(i)]f_{r,k}^{(A)}(x-i), x\ge (k+1)r,\\(ii)\quad&F_{r,k}^{(A)}(x)=\sum _{i=1}^{1/\eta }\biggl \{(\eta _iq_i+\eta )\pi _{i-1}\\&+(r-1)p_k \eta [p_k^{i-1}-d_1(i)]\Bigr \}F_{r,k}^{(A)}(x-i),(k+1)r\le x\le (k+1)r+k-1,\\&F_{r,k}^{(A)}(x)=\sum _{i=1}^{k}(\eta _iq_i+\eta )\pi _{i-1}F_{r,k}^{(A)}(x-i)+(r-1)ip_k \eta \sum _{i=1}^{1/\eta }[p_k^{i-1}-d_1(i)]{F}_{r,k}^{(A)}(x-i)\\&+\pi _k \eta \sum _{i=k+1}^{1/\eta }F_{r,k}^{(A)}(x), x\ge (k+1)r+k,\\(iii)\quad&\overline{F}_{r,k}^{(A)}(x)=\sum _{i=1}^{1/\eta }\biggl \{(\eta _iq_i+\eta )\pi _{i-1}+(r-1)p_k \eta [p_k^{i-1}-d_1(i)]\biggr \}\overline{F}_{r,k}^{(A)}(x-i)\\&+(r-1)p_k \eta \Bigl [c_1\big (1/\eta \bigr )-\frac{1-p_k^{1/\eta }}{q_k}\Bigr ]-r \eta \sum _{i=1}^{1/\eta }i\pi _{i-1}q_i,\\&(k+1)r\le x\le (k+1)r+k-1,\\&\overline{F}_{r,k}^{(A)}(x)=\sum _{i=1}^{k}\biggl \{(\eta _iq_i+\eta )\pi _{i-1}\overline{F}_{r,k}^{(A)}(x-i)\\&+(r-1)p_k \eta \sum _{i=1}^{1/\eta }[p_k^{i-1}-d_1(i)]\biggr \}\overline{F}_{r,k}^{(A)}(x-i)+\pi _k \eta \sum _{i=k+1}^{1/\eta }\overline{F}_{r,k}^{(A)}(x-i)\\&+(r-1)p_k \eta \Bigl [c_1\big (1/\eta \bigr )-\frac{1-p_k^{1/\eta }}{q_k}\Bigr ]-r \eta \sum _{i=1}^{k}i\pi _{i-1}q_i,\;x\ge (k+1)r+k, \end{aligned} \end{aligned}$$

with

$$\begin{aligned} \begin{aligned}&d_1(i)=\sum _{j=1}^{\min \{i-1,k\}}\pi _{j-1}q_jp_k^{i-j-1}, i\ge 2, d_1(1)=0, \\&c_1(x)=\sum _{i=2}^{x}d_1(i),x\ge 2, \end{aligned} \end{aligned}$$

and initial conditions \(f_{r,k}^{(A)}((k+1)r-1)=F_{r,k}^{(A)}((k+1)r-1)=1-\overline{F}_{r,k}^{(A)}((k+1)r-1)=1-q_k^{r-1}\pi _{k}^r\).

The next recursion refers to the waiting time corresponding to the overlapping scheme; please note that in the following relations the corresponding formulas for the waiting time of the non-overlapping scheme, as they provided by Corollary 4.1 are also used.

Corollary 4.3

For the probability mass function defined on a binary sequence of order k, with probabilities \(p_1, p_2, \ldots , p_k\), the following recursions hold true:

$$\begin{aligned} f_{r,k}^{(O)}(x)= \sum _{i=1}^{r}\left( {\begin{array}{c}r-1\\ i-1\end{array}}\right) q_k^{i-1}p_k^{r-i}f_{i,k}^{(N)}(x-r+1),x\ge k+r-1 \end{aligned}$$

The same formula remains valid if we replace the probability mass functions f by the cumulative distribution functions F and the tail probabilities \(\overline{F}\).

5 Application

In this section, we discuss some details on the application of the extended random sum model \(S=S_M+U\), to the study of the total expenses of an insurance company. As already stated in Section 1, under this framework \(S_M=\sum _{j=1}^{M}X_j\) stands for the aggregate claims amount and U may encompass all company operational costs, with U and \(X_j\)’s taking positive integer values.

The questions to be faced by the practitioner when applying the model pertain to the selection of the appropriate distributions for U, M and \(X_j\)’s. In actuarial practice, the number of claims, M, is usually described by a member of the Panjer family R(a, b, 0) (e.g., Klugman et al. 2019), while for \(X_j\)’s it is necessary to engage distributions that can accommodate extreme observations, i.e., large claims that occur with low frequency.

The Pareto distribution is a very popular model for describing extreme phenomena. It was first introduced for the study of economic models dealing with income data. Due to its heavy tail, Pareto distribution has been extensively used as a severity distribution to describe extreme losses (e.g., Guillen et al. 2011), especially for the high-risk types of insurance, e.g., medical malpractice insurance. A more flexible model that contains the Pareto distribution as a special case is offered by the Burr (Type XII) distribution, symb. \(Br_{\theta }(\alpha ,\beta )\), with probability density function

$$\begin{aligned} f_Y(y)=\frac{\alpha \beta y^{\beta -1}}{\theta ^{\beta }(1+(y/\theta )^{\beta })^{\alpha +1}}, ~y>0, \end{aligned}$$
(32)

where \(\alpha , \beta\) and \(\theta\) are positive parameters. Besides, the two parameter Pareto distribution (obtained for \(\beta =1\)), it also includes as special cases the log-logistic, exponential and Weibull distribution (as limiting cases). For more details, the interested reader is referred to Johnson et al. (2005).

In our framework, \(X_j\)’s may be seen as multiples of a monetary unit, while the underlying exact (continuous) severity distribution should posses the heavy-tail property. A reasonable approach to meet these requirements is offered by “discretizing” the \(Br_{\theta }(\alpha ,\beta )\) model. As stated by Klugman et al. (2019), a typical way for constructing a discrete severity distribution from a continuous one is to place the discrete probabilities on multiples of the desired unit of measurement h. If the exact losses Y (continuous random variable) follow (32), the implied discrete distribution of \(X_j\)’s (symb., \(DBr_{\theta }(\alpha ,\beta )\)) will be generated by the formulas

$$\begin{aligned} \begin{aligned} f(0)&=P(Y<h/2)=F_Y(h/2)\\ f(xh)&=P(xh-h/2<Y<xh+h/2)\\&=F_Y(xh+h/2)-F_Y(xh-h/2), x=1,2,\ldots , \end{aligned} \end{aligned}$$
(33)

where

$$F_Y(y)=1-\frac{1}{(1+(y/\theta )^\beta )^{\alpha }}, y>0,$$

is the cumulative distribution function of \(Br_{\theta }(\alpha ,\beta )\).

According to the last formula, the probability placed at xh is obtained by accumulating all the probability of Y one-half span on either sides of xh, i.e., it rounds all amounts to the nearest monetary unit, h. For a detailed study of the Burr and Pareto distribution, including statistical inference and stochastic ordering properties, we refer to, e.g., Panjer (2006), Krishna and Pundir (2009), and Klugman et al. (2019).

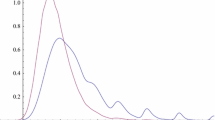
In Fig. 1, we present plots of the \(DBr_{\theta }(\alpha ,\beta )\) for several choices of \(\alpha ,\beta\), and \(\theta\) (using \(h=0.75\)). It is clear that the discretization of the Burr (Type XII) distribution still offers the opportunity to model (discrete) data with heavy tails, while most of the properties of \(Br_{\theta }(\alpha ,\beta )\) seem to carry over nicely to \(DBr_{\theta }(\alpha ,\beta )\) (e.g., unimodality for \(\beta >1\)), especially upon choosing the appropriate values for h.

Let us next move to the distribution of the third component of our model, i.e., the operating cost U. The heavy tail assumption made on \(X_j\)’s is typically not realistic for the operating costs r.v. U; on the contrary, a “smooth” discrete distribution seems to be a fair choice for that variable.

If the distribution of U has a shape similar to the normal distribution, a plausible discrete distribution that may be used for fitting our data is offered by b(m, p) with m sufficiently large to justify the convergence of \((U-mp)/(\sqrt{mp(1-p)})\) to the standard normal distribution. It should be stressed that, if we assume that \(U\sim b(m,p)\) we shall have \(V[U]/E[U]=1-p<1\), therefore this approach makes sense only for the case when the data justify the underdispersion (\(V[U]<E[U]\)) of the fitting distribution. Under this framework the exact distribution of the company total expenses, as expressed by the extended random sum model (2), can be easily calculated by the aid of recurrence (25), with \(B_1=bf(1)+mp/q\) and

$$\begin{aligned} \begin{aligned}&A_i=af(i), i\ge 1\\&B_i=bif(i)+m\left[ (-1)^{i-1}\left( \frac{p}{q}\right) ^i+a\sum _{j=1}^{i-1}(-1)^j\left( \frac{p}{q}\right) ^jf(i-j)\right] , i\ge 2. \end{aligned} \end{aligned}$$

The case of overdispersed data (\(V[U]>E[U]\)) can be treated by the use of the negative binomial distribution Nb(r, p) with \(p=E[U]/V[U]\). In this case, the resulting distribution for the total expenses obeys the recurrence (25) with \(B_1=bf(1)+rp\) and

$$\begin{aligned} \begin{aligned}&A_i=af(i), i\ge 1\\&B_i=bif(i)+r\left[ p^i-a\sum _{j=1}^{i-1}f(i-j)p^j\right] , i\ge 2. \end{aligned} \end{aligned}$$

Finally, if our data imply that \(V[U]\approx E[U]\) the most appropriate discrete distribution for U is the Poisson distribution with parameter \(\lambda =E[U]\approx V[U]\). Taking into account that the Poisson distribution with parameter \(\lambda\) can be viewed as a member of the Panjer family R(a, b, 0) with \(a=0\), \(b=\lambda\) we conclude that the distribution of the total expenses satisfies the recurrence scheme (25) with \(B_1=bf(1)+\lambda\) and

$$\begin{aligned} \begin{aligned}&A_i=af(i), i\ge 1,\\&B_i=bif(i)-a\lambda f(i-1), i\ge 2. \end{aligned} \end{aligned}$$

In Fig. 2, we provide plots for the probability mass function of the total expenses when \(X_j\sim DB_1(1,1)\) (with \(h=1\)), \(M\sim Nb(r,p)\), and U follows a binomial, negative binomial or Poisson distribution. At the left part of this figure, we can see how the distribution of the total expenses is affected, changing the distribution of the number of claims, M; note that U has a similar mean (close to 5), for every case (binomial, negative binomial and Poisson distribution). As it was expected, increasing the parameter value r of the distribution of M, the tails of the total expenses become heaviest. At the right part of Fig. 2, we consider the effect of changing the parameters of the distribution of U; generally, as the mean value of U is increasing, its role to the distribution of the total expenses becomes more significant, resulting also in heaviest tails. Fig. 3 includes the probability mass function of the total expenses when U and M follow a negative binomial distribution and \(X_j\sim DB_\theta (\alpha ,\beta )\) (with \(h=1\)), for several choices of \(\alpha ,\beta\), and \(\theta\); the heavy tail property is also met for appropriate choice of parameter values.

Fig. 1
figure 1

The probability mass function of \(DBr_{\theta }(\alpha ,\beta )\), for several choices of \(\alpha ,\beta\), \(\theta\) and \(h=0.75\)

Full size image
Fig. 2
figure 2

The probability mass function of the extended sum, when \(X_j\)’s follow the \(DBr_{1}(1,1)\) (with \(h=1\)), M follows a negative binomial distribution and U follows a binomial, negative binomial or Poisson distribution

Full size image
Fig. 3
figure 3

The probability mass function of the extended sum, when M, U follow a negative binomial distribution and \(X_j\)’s follow the \(DBr_{\theta }(\alpha ,\beta )\) (with \(h=1\)), for several choices of \(\alpha ,\beta\), and \(\theta\)

Full size image

6 Conclusions

In this work, recursive relations for the probability mass function, cumulative distribution function, tail probabilities and the factorial moments, of an extension of the discrete random sum model was established. The new model and the suggested methodology was exploited for the study of the negative binomial distributions of order k (for the three most popular enumerating schemes, i.e., the non-overlapping, at least and overlapping), offering computationally efficient ways for obtaining their exact distribution functions. A roadmap is also highlighted for applying our results in the study of the total expenses (operational costs and aggregate claims) of an insurance company, providing a new direction to the study of this problem; for doing so, a discretization of the severity distribution is also suggested, which is a plausible way of keeping significant properties of well known heavy tailed continuous random variables.