On Distribution and Average Run Length of a Two-Stage Control Process

Abstract

In this article a method, using finite Markov chains, to obtain the run-length properties of a two-stage control process is presented. The method furnishes the obtaining of the distribution of waiting time to signal that gives additional insight into the design and performance of a control chart when a warning zone is considered to feature a two-stage control process and when a departure from the null assumption can be clearly defined. An example is given for illustration when samples come from a normal population, though not necessary, with an outlined process inspection scheme. A second example is given to demonstrate the extension of our approach to modelling Markov dependent data observations.

1 Introduction

Shewhart shares in his book Shewhart (1931) since 1931 on the importance of distribution theory for the reason that no matter what definition is used for quality, its measurement is a variable. Page (1955) and the Western Electric Company (1956) since the 1950s have been using the idea of incorporating zones in a chart to monitor the conformity of items in a production line based on some measurable characteristic of those items. Croasdale (1974) introduces first in 1974 the idea of setting up a control chart of two parts (double-sampling scheme) to monitor process mean, with a warning zone in the first part but without an out-of-control zone which only is incorporated in the second part of the chart in design. Later, Daudin (1992) and Irianto and Shinozaki (1998) have modified and improved the double-sampling scheme judging by the criterion of average run length (ARL). Since then it continues to receive much attention in research and to be studied extensively, for example, by Wu and Spedding (2000) and Yang and Wu (2017).

When production is being set up naturally in a way that materials have to undergo a series of steps for a product to be made, a sequence of processing steps is needed to produce silicon-based integrated circuit for an example, the production can be modelled as a staged system. Duffuaa et al. (2009) look into a problem when the number of non-conforming items, based on some quality characteristic of the items, in a sample from a lot at the end of the first process is large enough, the whole lot is inspected (100% inspection) before going through the next process. A final quality characteristic is considered as a convolution of the quality characteristic measured from the first process and a separate quality characteristic measured at the end of the second process for items in a sample from a lot, based on the assumption that quality-characteristic measurements of each item from the two processes in series are independent. Pricing a product depend then on the number of non-conforming items in the second sample based on final quality characteristic. In contrast to optimising total profit, the interest of Aslam et al. (2018) is in designing an attribute control chart for production also in the setup of a series of two independent processes. In the first step, a first process alone is considered to be in-control if the number of non-conforming items in a sample from the process is smaller than some threshold and proceed to the second step, the two processes together is declared to be out-of-control otherwise. In the second step, judge then, independent of the first process, the number of non-conforming items in a sample from the other process. The two processes combined is considered to be in-control if the convolution of the number of non-conforming items from the first process and of the number from the second process is smaller than some threshold, the two processes together is to be declared out-of-control otherwise. Li and Liu (2006), on the other hand, study a two-stage production control system in a perspective from that of queue scheduling, the goal therewith is to optimize the work-in-process between the two stages by analyzing the busy period steady-state distribution of a queueing system. The two-stage CCC$_2^{}$ chart introduced by Chan et al. (1997) and later the CCC$_{1 + \gamma }^{}$ chart by Chan et al. (2003) can be used to detect shifts in the fraction of nonconforming item produced by a manufacturing process, in other words, the authors’ primary interest is in the probability of failure for each trial of a Bernoulli process. The decision rules are based on the number of inspected items required to obtain the first or the second failure. They propose that by splitting the overall false-alarm probability (type I error rate) $\alpha \in (0, 1)$ into two parts $(1 - \gamma )\alpha$ and $\gamma \alpha$, $\gamma \in (0, 1)$, determine first a boundary on the number of trials required to observe the first failure, and then a boundary on the number of trials required to observe the second failure in aid of process control.

Our main goal has a twofold aim: to provide analytic formulas for the distribution of time to signal and the average run length for a two-stage control process. The result will cover various quality control charts suitable for the incorporation of a warning zone (or a mechanism to trigger warning signals), such as a chart based on runs and patterns (see Mosteller (1941) for example), an $\bar{X}$-chart, a cumulative sum (CUSUM) chart, an exponentially weighted moving average (EWMA) chart, and finite Markov chain imbeddable quality control processes in general (see Fu et al. (2002), Fu et al. (2003), Koutras et al. (2007), Chang and Wu (2011) and Bersimis et al. (2014) for example). The finite Markov chain imbedding technique has been successfully used as well in the theoretical developments of system reliability modelling (see Fu and Lou (1991), Koutras (1996), Chang and Huang (2010), Eryilmaz (2016), Eryilmaz et al. (2016) and Chang et al. (2018) for example) and their application in financial risk management (see  Koutras et al. (2016) for example). In this manuscript the same technique will be adopted to study the properties of our proposed two-stage statistical process control.

The nomenclature and the results from literatures to be adopted throughout will be brought forth in the next section. The main results for our proposed method are presented in Sect. 3. Detailed examples to illustrate our theoretical results are given in Sect. 4 and are followed by some concluding remarks.

2 Notation and Preliminary Results

Let $\varphi _1^{}$ represent the first-stage quality control process which is homogeneous finite Markov chain imbeddable, and its imbedded homogeneous Markov chain $\{ Y_1(t) \}_{t=0}^n$, defined on state space $\Omega _1$ containing an out-of-control state $\gamma _1^{}$ and a warning state $\theta$, has a transition probability matrix in the form of

$$\begin{aligned} \varvec{M}_1 = \begin{pmatrix} \varvec{N}_1 &{} \varvec{C}_{\theta }^{\prime } &{} \varvec{C}_{\gamma _1^{}}^{\prime } \\ \varvec{O} &{} \begin{array}{c} 1 \\ 0 \end{array} &{} \begin{array}{c} 0 \\ 1 \end{array} \\ \end{pmatrix} \end{aligned}$$

(1)

for all $t = 1, \ldots , n$.

Let $\varphi _2^{}$ represent the second-stage quality control process which is homogeneous finite Markov chain imbeddable, and its imbedded homogeneous Markov chain $\{ Y_2(t) \}_{t=0}^n$, defined on state space $\Omega _2$ containing an out-of-control state $\gamma _2^{}$, has a transition probability matrix in the form of

$$\begin{aligned} \varvec{M}_2 = \begin{pmatrix}\varvec{N}_2 &{} \varvec{C}_{\gamma _2^{}}^{\prime } \\ \varvec{O} &{} 1 \\ \end{pmatrix} \end{aligned}$$

(2)

for all $t = 1, \ldots , n$. It will be seen throughout the manuscript that the symbol $\varvec{O}$ is used to denote a zero matrix or vector of an appropriate size.

Readers may see Fu et al. (2003) for an in-depth discussion of the approach to Markov chain imbedding for the control scheme of Shewhart-type with or without supplementary runs rules, Cusum-type, weighted moving average-type, or a combination of Shewhart-type and a Cusum- or moving average-type under the normality and independence assumptions on the sampled observations from a process.

Definition 1

$(\varphi _1^{}, \varphi _2^{})$ is a two-stage control process if the process follows the proceeding steps:

• (i) Given a warning limit and a control limit (or action line, which more often than not are determined by product designer or are given to meet a product design specification), define an in-control, an out-of-control and a warning zone for the first-stage process. Given another control limit (whether a new random sample drawn to start the second stage is to be combined with the last sample from the first stage or not when a warning signal appears), define an in-control and an out-of control zone for the second-stage process.

• (ii) Begin (first-stage) process control by taking a random sample of size $k_1 > 0$ of items from a production line and obtain sample statistic $Y_1(t)$ for sampling time $t = 1, 2, \ldots$.

• (iii) When $Y_1(t)$ belongs to the in-control zone, return to step (ii) for sampling time $t + 1$; else when $Y_1(t)$ belongs to the out-of-control zone, proceed to step (vi); else, $Y_1(t)$ belongs to the warning zone and based on the sample, one can be irresolute with regard to whether the process is prone to a shift, activate then the second-stage process control.

• (iv) In the second stage, take a sample of size $k_2 > 0$ from the production line and obtain sample statistic $Y_2(t)$ for sampling time $t = 1, 2, \ldots$.

• (v) When $Y_2(t)$ belongs to the in-control zone, return to step (iv) for sampling time $t + 1$; else $Y_2(t)$ belongs to the out-of-control zone, proceed to step (vi).

• (vi) An out-of-control alarm is issued and actions are taken to identify and remove probable causes. Reset t to 0 and return to step (ii).

We assume throughout this article that the control processes $\varphi _1^{}$ and $\varphi _2^{}$ are finite Markov chain imbeddable, their transition probability matrices are $\varvec{M}_1$ of the form in (1) and $\varvec{M}_2$ of the form in (2), respectively.

Definition 2

Define the following waiting-time random variables

$$\begin{aligned} W_{\gamma _1^{}}&= \inf _{1 \le n}^{} \{ n:\; Y_1(n) = \gamma _1^{} \}, \end{aligned}$$

(3)

$$\begin{aligned} W_{\theta }&= \inf _{1 \le n}^{} \{ n:\; Y_1(n) = \theta \}, \end{aligned}$$

(4)

$$\begin{aligned} W_{\gamma _2^{}}&= \inf _{1 \le n}^{} \{ n:\; Y_2(n) = \gamma _2^{} \}, \end{aligned}$$

(5)

and let W be the waiting time of a two-stage control process $(\varphi _1^{}, \varphi _2^{})$ being in an out-of-control state (either $\gamma _1^{}$ in the first stage or $\gamma _2^{}$ in the second stage), that is,

$$\begin{aligned} W = \min (W_{\gamma _1^{}}, W_{\theta } + W_{\gamma _2^{}}) \end{aligned}$$

which is a random variable.

By applying Theorem 2 of Fu et al. (2016), we have the distributions of waiting-time random variables $W_{\gamma _1^{}}$, $W_{\theta }$ and $W_{\gamma _2^{}}$, and in the long term the mean time to the first occurrence of $\gamma _1^{}$, $\theta$ and $\gamma _2^{}$ being $E[W_{\gamma _1^{}}]$, $E[W_{\theta }]$ and $E[W_{\gamma _2^{}}]$, respectively. Proofs are omitted here.

Theorem 1

Given $\varphi _1^{}$ and $\varphi _2^{}$, and $\varvec{M}_1$ and $\varvec{M}_2$, it follows from (3)–(5) in Definition 2that

• (i)
  $$\begin{aligned} P(W_{\gamma _1^{}} = n) = \varvec{\xi }_0^{} \varvec{N}_1^{n - 1} \varvec{C}_{\gamma_1^{}}^{\prime } \qquad \qquad \mathrm{for} \;n=1,2,\dots \end{aligned}$$

  and

  $$\begin{aligned} E[W_{\gamma_1^{}}] = \varvec{\xi }_0^{} (\varvec{I} - \varvec{N}_1)_{}^{-2} \varvec{C}_{\gamma _1^{}}^{\prime }, \end{aligned}$$
• (ii)
  $$\begin{aligned} P(W_{\theta } = n) = \varvec{\xi }_0^{} \varvec{N}_1^{n - 1} \varvec{C}_{\theta }^{\prime } \qquad \qquad \mathrm{for} \;n=1,2,\dots \end{aligned}$$

  and

  $$\begin{aligned} E[W_{\theta }] = \varvec{\xi }_0^{} (\varvec{I} - \varvec{N}_1)_{}^{-2} \varvec{C}_{\theta }^{\prime}, \end{aligned}$$
• (iii)
  $$\begin{aligned} P(W_{\gamma _2^{}} = n) = \varvec{\eta }_0^{} \varvec{N}_2^{n - 1} \varvec{C}_{\gamma _2^{}}^{\prime } \qquad \qquad \mathrm{for} \;n=1,2,\dots \end{aligned}$$

  and

  $$\begin{aligned} E[W_{\gamma _2^{}}] = \varvec{\eta }_0^{} (\varvec{I} - \varvec{N}_2)_{}^{-2} \varvec{C}_{\gamma _2^{}}^{\prime }, \end{aligned}$$

where $\varvec{N}_1$, $\varvec{C}_{\gamma _1^{}}$ and $\varvec{C}_{\theta }^{}$ are given in (1), $\varvec{N}_2$ and $\varvec{C}_{\gamma _2^{}}$ are given in (2), and row vectors $\varvec{\xi }_0^{}$ and $\varvec{\eta }_0^{}$, each with non-negative elements that sum to one, are initial probability distributions for $\varphi _1^{}$ and $\varphi _2^{}$, respectively.

3 Distribution and ARL of Two-Stage Control Process

The distribution of W, or is called the run length for a chart, which is the number of different time points at which some process characteristic is measured and plotted on a (control) chart until (and including) the first appearance of an out-of-control alarm, can be obtained by the following theorem.

Theorem 2

Given $\varphi _1^{}$ and $\varphi _2^{}$, we have

• (i) for $n = 1$,

  $$\begin{aligned} P(W = n) = P(W = W_{\gamma _1^{}} = n) = \varvec{\xi }_0^{} \varvec{C}_{\gamma _1^{}}^{\prime }, \end{aligned}$$

• (ii) and for $n \ge 2$,

  $$\begin{aligned} P(W = n) = \varvec{\xi }_0^{} \varvec{N}_1^{n - 1} \varvec{C}_{\gamma _1^{}}^{\prime } + \sum _{i=1}^{n - 1} (\varvec{\xi }_0^{} \varvec{N}_1^{i - 1} \varvec{C}_{\theta }^{\prime })(\varvec{\eta }_0^{} \varvec{N}_2^{n - i - 1} \varvec{C}_{\gamma _2^{}}^{\prime }), \end{aligned}$$

where $\varvec{\xi }_0^{}$ and $\varvec{\eta }_0^{}$ are initial distributions with respect to $\varphi _1^{}$ and $\varphi _2^{}$, and $\varvec{N}_1$, $\varvec{C}_{\gamma _1^{}}^{}$ and $\varvec{C}_{\theta }^{}$ are defined in (1), $\varvec{N}_2$ and $\varvec{C}_{\gamma _2^{}}^{}$ are defined in (2).

Proof

It follows from the definitions of waiting times $W_{\gamma _1^{}}$, $W_{\theta }$, $W_{\gamma _2^{}}$ and W that a two-stage control process gives an out-of-control alarm at n if either $\{W = W_{\gamma _1^{}} = n\}$ or $\{W = W_{\theta } + W_{\gamma _2^{}} = n\}$ occurs. Note that

$$\begin{aligned} \{W = W_{\theta } + W_{\gamma _2^{}} = n\} = \bigcup _{n_1^{} = 1}^{n - 1} \{ W_{\theta } = n_1^{},\; W_{\gamma _2^{}} = n_2^{},\; n_1^{} + n_2^{} = n \}, \end{aligned}$$

and those $n - 1$ events are mutually exclusive. Hence,

$$\begin{aligned} P(W = n)&= P(W = W_{\gamma _1^{}} = n) + P(W = W_{\theta } + W_{\gamma _2^{}} = n) \\ \nonumber&= P(W = W_{\gamma _1^{}} = n) + \sum _{n_1^{} = 1}^{n - 1} P(W_{\theta } = n_1^{},\; W_{\gamma _2^{}} = n - n_1^{}). \end{aligned}$$

Since $W_{\theta }$ and $W_{\gamma _2^{}}$ are stochastically independent, it follows from Theorem 1 that

$$\begin{aligned} \sum _{n_1^{} = 1}^{n - 1} P(W_{\theta } = n_1^{},\; W_{\gamma _2^{}} = n - n_1^{})&= \sum _{n_1^{} = 1}^{n - 1} P(W_{\theta } = n_1^{}) P(W_{\gamma _2^{}} = n - n_1^{}) \\ \nonumber&= \sum _{n_1^{} = 1}^{n - 1} (\varvec{\xi }_0^{} \varvec{N}_1^{n_1^{} - 1} \varvec{C}_{\theta }^{\prime }) (\varvec{\eta }_0^{} \varvec{N}_2^{n - n_1^{} - 1} \varvec{C}_{\gamma _2^{}}^{\prime }) \end{aligned}$$

This completes the proof.

The average run length, E[W], of a two-stage control process $(\varphi _1^{}, \varphi _2^{})$ is a result of the following theorem.

Theorem 3

Given a two-stage control process $(\varphi _1^{}, \varphi _2^{})$, we have

$$\begin{aligned} E[W] = \varvec{\xi }_0^{} (\varvec{I} - \varvec{N}_1)_{}^{-2} \varvec{C}_{\gamma _1^{}}^{\prime } + \kappa _1^{} \varvec{\xi }_0^{} (\varvec{I} - \varvec{N}_1)_{}^{-2} \varvec{C}_{\theta }^{\prime } + \kappa _2^{} \varvec{\eta }_0^{} (\varvec{I} - \varvec{N}_2)_{}^{-1} \varvec{1}_{}^{\prime }, \end{aligned}$$

(6)

where

$$\begin{aligned} \kappa _1^{} = \sum _{i = 1}^{\infty } \varvec{\eta }_0^{} \varvec{N}_2^i \varvec{C}_{\gamma _2^{}}^{\prime } = 1, \qquad \kappa _2^{} = \sum _{i = 1}^{\infty } \varvec{\xi }_0^{} \varvec{N}_1^i \varvec{C}_{\theta }^{\prime } < 1, \qquad \nonumber \varvec{1} = (1\; 1\; \ldots \; 1). \end{aligned}$$

Equation (6) can then be reduced to

$$\begin{aligned} E[W] = \varvec{\xi }_0^{} (\varvec{I} - \varvec{N}_1)_{}^{-1} \varvec{1}_{}^{\prime } + \kappa _2^{} \varvec{\eta }_0^{} (\varvec{I} - \varvec{N}_2)_{}^{-1} \varvec{1}_{}^{\prime }. \end{aligned}$$

(7)

Proof

Note that

$$\begin{aligned} P(W = n) = P(W = W_{\gamma _1^{}} = n) + P(W = W_{\theta } + W_{\gamma _2^{}} = n) \end{aligned}$$

for $n = 1, 2, \ldots$, and it follows that

$$\begin{aligned} E[W] = \sum _{n = 1}^{\infty } nP(W = W_{\gamma _1^{}} = n) + \sum _{n = 1}^{\infty } nP(W = W_{\theta } + W_{\gamma _2^{}} = n). \end{aligned}$$

It is trivial that $P(W_{\theta } + W_{\gamma _2^{}} = n) = 0$ when $n = 1$, it further follows that

$$\begin{aligned} E[W]&= \sum _{n = 1}^{\infty } nP(W = W_{\gamma _1^{}} = n) + \sum _{n = 2}^{\infty }\sum _{n_1^{} = 1}^{n - 1} nP(W_{\theta } = n_1^{},\; W_{\gamma _2^{}} = n - n_1^{}) \nonumber \\&= \sum _{n = 1}^{\infty } nP(W_{\gamma _1^{}} = n) + \sum _{n = 2}^{\infty }\sum _{n_1^{} = 1}^{n - 1} (n_1^{} + n_2^{})P(W_{\theta } = n_1^{},\; W_{\gamma _2^{}} = n_2^{}), \end{aligned}$$

(8)

where $n_1^{} + n_2^{} = n$. The variables $W_{\theta }$ and $W_{\gamma _2^{}}$ are stochastically independent, hence, Eq. (8) can be written as

$$\begin{aligned} E[W]&= \sum _{n = 1}^{\infty } nP(W_{\gamma _1^{}} = n) + \sum _{n_2^{} = 1}^{\infty } P(W_{\gamma _2^{}} = n_2^{}) \sum _{n_1^{} = 1}^{\infty } n_1^{} P(W_{\theta } = n_1^{}) \nonumber \\&\quad + \sum _{n_1^{} = 1}^{\infty } P(W_{\theta } = n_1^{}) \sum _{n_2^{} = 1}^{\infty } n_2^{} P(W_{\gamma _2^{}} = n_2^{}). \end{aligned}$$

(9)

The result in (6) follows from (9) and Theorem 1, and Eq. (7) follows from $\kappa _1^{} \equiv 1$ and $\varvec{C}_{\gamma _1^{}}^{\prime } + \varvec{C}_{\theta }^{\prime } = (\varvec{I} - \varvec{N}_1) \varvec{1}_{}^{\prime }$. This completes the proof.

In a similar argument, we can obtain the moment generating function of W to be

$$\begin{aligned} M_W^{}(s) = E[e_{}^{sW}]&= \sum _{n = 1}^{\infty } e_{}^{ns} P(W = n) \\ \nonumber&= \sum _{n = 1}^{\infty } e_{}^{ns} \left[ P(W = W_{\gamma _1^{}} = n) + P(W = W_{\theta } + W_{\gamma _2^{}} = n) \right] \\ \nonumber&= \sum _{n = 1}^{\infty } e_{}^{ns} P(W_{\gamma _1^{}} = n) + \sum _{n = 2}^{\infty } e_{}^{(n_1^{}s + n_2^{}s)} P(W_{\theta } = n_1^{}, W_{\gamma _2^{}} = n_2^{}) \\ \nonumber&= \sum _{n = 1}^{\infty } e_{}^{ns} P(W_{\gamma _1^{}} = n) + \Bigg [ \sum _{n_1^{} = 1}^{\infty } e_{}^{n_1^{}s} P(W_{\theta } = n_1^{}) \Bigg ] \Bigg [ \sum _{n_2^{} = 1}^{\infty } e_{}^{n_2^{}s} P(W_{\gamma _2^{}} = n_2^{}) \Bigg ] \end{aligned}$$

for some $|s| < \delta$, and $\delta > 0$.

Hence, from Theorem 1, the form of the moment generating function of W can be written as

$$\begin{aligned} M_W^{}(s)&= \sum _{n = 1}^{\infty } e_{}^{ns} \varvec{\xi }_0^{} \varvec{N}_1^{n - 1} \varvec{C}_{\gamma _1^{}}^{\prime } + \sum _{n_1^{} = 1}^{\infty } e_{}^{n_1^{}s} \varvec{\xi }_0^{} \varvec{N}_1^{n_1^{} - 1} \varvec{C}_{\theta }^{\prime } \sum _{n_2^{} = 1}^{\infty } e_{}^{n_2^{}s} \varvec{\eta }_0^{} \varvec{N}_2^{n_2^{} - 1} \varvec{C}_{\gamma _2^{}}^{\prime } \\ \nonumber&= \varvec{\xi }_0^{} (\varvec{I} - e_{}^s\varvec{N}_1)_{}^{-1} \varvec{C}_{\gamma _1^{}}^{\prime } + \left[ \varvec{\xi }_0^{} (\varvec{I} - e_{}^s\varvec{N}_1)_{}^{-1} \varvec{C}_{\theta }^{\prime } \right] \sum _{n_2^{} = 1}^{\infty } e_{}^{n_2^{}s} \varvec{\eta }_0^{} \varvec{N}_2^{n_2^{} - 1} (\varvec{I} - \varvec{N}_2)\varvec{1}_{}^{\prime } \\ \nonumber&= \varvec{\xi }_0^{} (\varvec{I} - e_{}^s\varvec{N}_1)_{}^{-1} \varvec{C}_{\gamma _1^{}}^{\prime } + \left[ \varvec{\xi }_0^{} (\varvec{I} - e_{}^s\varvec{N}_1)_{}^{-1} \varvec{C}_{\theta }^{\prime } \right] \left[ \varvec{\eta }_0^{} (\varvec{I} - e_{}^s\varvec{N}_2)_{}^{-1} (\varvec{I} - \varvec{N}_2)\varvec{1}_{}^{\prime } \right] . \end{aligned}$$

It can easily be verified that

$$\begin{aligned} E[W] = \frac{d}{ds} M_W^{}(s) \Bigr \vert _{s=0}^{} = \varvec{\xi }_0^{} (\varvec{I} - \varvec{N}_1)_{}^{-2} \varvec{C}_{\gamma _1^{}}^{\prime } + \varvec{\xi }_0^{} (\varvec{I} - \varvec{N}_1)_{}^{-2} \varvec{C}_{\theta }^{\prime } + \kappa _2^{} \varvec{\eta }_0^{} (\varvec{I} - \varvec{N}_2)_{}^{-1} \varvec{1}_{}^{\prime }, \end{aligned}$$

and the same expression is also found in Theorem 3.

We will denote in the rest of this article, by conventions, E[W] by $ARL_0$ under the assumption that parameters specifying the quality of an output are of their desired values, and by $ARL_1$ under the alternative when there is a departure away from such assumption. Two simple examples will later be provided for readers to easily understand the mechanism and the main spirit of a two-stage control procedure of general type, some technical remarks regarding the two-stage procedure deserve special consideration.

Remark 1

In contrast to how a warning line is typically added in a single-stage control scheme for the purpose of signaling for action to seek out and eradicate cause of trouble when a cluster of points on the chart is considered to be peculiar, e.g., supplementary rules in Fu et al. (2003) are used to set off out-of-control signals that tend to make charts more sensitive (and therefore increasing the rate of false alarm), supplementary rules in Shewhart-type control chart in our examples are used merely to set off warnings when sample points on a chart remain within control limits. As a matter of fact, a warning line (or a set of warning lines) is not a necessity in this two-stage control process for defining a warning state in Markov chain imbedding. The warning state is a general notion for a set of decision rules being used as a mechanism to switch to the second stage of process control which may have more stringent rules than those of the first for signaling trouble. Instead of an out-of-control alarm being issued when suspicious, a warning signal gives a hint for the possibility of the process being charted may be off its course, but definitive evidence is not in presence to call for action.

Remark 2

The conditions for (1) and (2) are rather mild. They are satisfied with most finite Markov chain imbeddable quality control processes. The conditions are given to make the proof simple and tractable for our results. The conditions can be extended in several directions and the results will hold.

Remark 3

A multitude of charts that can be studied using a two-stage control procedure is more inclusive than what can be considered using the method in Fu et al. (2003). Despite that in special scenarios a two-stage control chart may be studied using the method in Fu et al. (2003), computations based on the two-stage approach will definitely gain efficiency due to the use of much smaller matrices when the state space of a Markov chain being analyzed using their method is large, and especially when it is associated with a transition matrix largely of zeros. In these special scenarios, the set of states corresponding to the second-stage process as a whole is closed to the set of states corresponding to the first-stage process according to Feller (1968) by his Definition in Section 4 of Chapter XV. In other words, states in the set corresponding to the first-stage process can not be reached from any state of the set corresponding to the second-stage process, and some or all states corresponding to the second-stage process may be reached from the set of warning states that needs to be defined for the first-stage process. However, the initial state of the second-stage process may or may not necessarily be dependent upon the warning states.

Remark 4

The results shown above can be extended to the case when the first-stage control process $Y_1(t)$ has m warning states, and associated with them are m options for the second-stage control process as $Y_{2j}^{}(t)$, $j = 1, \dots , m$. The distribution of W of the process is then, for $n = 1, 2, \ldots$,

$$\begin{aligned} P(W = n) = \varvec{\xi }_0^{} \varvec{N}_1^{n - 1} \varvec{C}_{\gamma _1^{}}^{\prime } + \sum _{j=1}^m \sum _{i=2}^{n - 1} (\varvec{\xi }_0^{} \varvec{N}_1^{i - 1} \varvec{C}_{\theta _j^{}}^{\prime })(\varvec{\eta }_0^{} \varvec{N}_{2j}^{n - i - 1} \varvec{C}_{\gamma _{2j}^{}}^{\prime }), \end{aligned}$$

and the formula to obtain ARL is now

$$\begin{aligned} E[W]&= \varvec{\xi }_0^{} (\varvec{I} - \varvec{N}_1)_{}^{-2} \varvec{C}_{\gamma _1^{}}^{\prime } + \sum _{j=1}^m \kappa _{1j}^{} \varvec{\xi }_0^{} (\varvec{I} - \varvec{N}_1)_{}^{-2} \varvec{C}_{\theta _j^{}}^{\prime } + \sum _{j=1}^m \kappa _{2j}^{} \varvec{\eta }_0^{} (\varvec{I} - \varvec{N}_{2j}^{})_{}^{-1} \varvec{1}_{}^{\prime }, \end{aligned}$$

where

$$\begin{aligned} \kappa _{1j}^{} = \sum _{i=1}^{\infty } \varvec{\eta }_0^{} \varvec{N}_{2j}^{i - 1} \varvec{C}_{\gamma _{2j}^{}}^{\prime } = 1 \qquad \qquad \mathrm{for} \ j = 1, \ldots , m, \end{aligned}$$

and

$$\begin{aligned} \kappa _{2j}^{} = \sum _{i=1}^{\infty } \varvec{\xi }_0^{} \varvec{N}_1^{i - 1} \varvec{C}_{\theta _j^{}}^{\prime } < 1 \qquad \qquad \mathrm{for} \ j = 1, \ldots , m. \end{aligned}$$

Remark 5

For the practical use of our two-stage process control procedure, an idea similar to that of Chan et al. (2003) can be incorporated into decision rules to allow automatic determination, from a statistical point of view, when an alarm may be considered as a signal for “process being out-of-control” from a “false alarm”.

In practice of setting up an upper control limit to detect upward shift or a lower control limit to detect downward shift of some process characteristic, or whether it be given both upper and lower control limits in a setup to detect a shift in either direction, early appearance of an out-of-control alarm gives ground for alleged irregularity of the process. Since waiting time is here a discrete random variable, let

$$\begin{aligned} n_{\alpha }^{} \equiv \max \{ n: P(W \le n) \le \alpha \} \end{aligned}$$

(10)

be the critical value for waiting time corresponding to nominal type I error rate $0< \alpha < 1$, or simply the $100\alpha$th percentile of waiting-time distribution. If the first occurrence of an out-of-control alarm appears at or before the $n_{\alpha }^{}$th trial in either the first or the second stage, there is considerable evidence for that investigation and corrective action may be required. Otherwise, when the first occurrence of an out-of-control alarm appears after the $n_{\alpha }^{}$th trial in either the first or the second stage, it may be interpreted as a false alarm and the process is regarded as in control, reset n to 0 and the next inspection will correspond to $n = 1$ of the first stage of the process control.

Furthermore, the quantity in (10) can be regarded as a decision rule in a hypothesis test where the null hypothesis states that the process being examined is under control. In a typical situation, one may reject the null hypothesis if the first appearance of out-of-control alarm is observed from a sample at or before the $n_{\alpha }^{}$th time point since the initial of the monitoring process or since a reset of the process. The probability $P(W \le n_{\alpha }^{} \mid$ H$_\mathrm{o}^{})$ is then the true type I error rate. On the other hand, the performance of a test in various degrees of departure of the truth away from the null hypothesis can be assessed by looking at type II error rate, i.e., $P(W > n_{\alpha }^{} \mid$ H$_\mathrm{a}^{})$.

4 Example and Numerical Study

Example 1

Please refer to Fig. 1 for an example of a chart for two-stage control process only for the purpose of demonstration. Let us suppose that each observation of some quality characteristic is $X(t) \sim$ N($\mu = 0$, $\sigma _{}^2 = 1$), $t = 1, 2, \ldots$. In the first stage, consider the three zones $A = [x_1^{}, \infty )$, $B = [y_1^{}, x_1^{})$, and $C = (-\infty , y_1^{})$, one has $p_{\scriptscriptstyle A}^{} = P(X(t) \in A)$, $p_{\scriptscriptstyle B}^{} = P(X(t) \in B)$, and $p_{\scriptscriptstyle C}^{} = P(X(t) \in C)$ for each t:

• (i) an out-of-control alarm is issued when an observation appears in zone A;

• (ii) a warning signal is issued when two consecutive observations appear in zone B, then the second-stage control process is initiated;

• (iii) or first-stage control process continues otherwise.

Fig. 1

Example chart for two-stage control process

With understanding, the imbedded Markov chain $\{ Y_1(t) \}$ induced by the sequence $\{ X(t) \}$ defined on the state space $\Omega _1 = \{\phi _1^{}, B, C, \theta , \gamma _1^{}\}$ has the transition matrix

$$\begin{aligned} \varvec{M}_1 = \begin{array}{l} \phi _1^{} \\ C \\ B \\ \theta \\ \gamma _1^{} \end{array} \left( \begin{array}{ccccc} 0 &{} p_{\scriptscriptstyle C}^{} &{} p_{\scriptscriptstyle B}^{} &{} 0 &{} p_{\scriptscriptstyle A}^{} \\ 0 &{} p_{\scriptscriptstyle C}^{} &{} p_{\scriptscriptstyle B}^{} &{} 0 &{} p_{\scriptscriptstyle A}^{} \\ 0 &{} p_{\scriptscriptstyle C}^{} &{} 0 &{} p_{\scriptscriptstyle B}^{} &{} p_{\scriptscriptstyle A}^{} \\ 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ \end{array} \right) = \left( \begin{array}{ccc} \varvec{N}_1 &{} \varvec{C}_{\theta }^{\prime } &{} \varvec{C}_{\gamma _1^{}}^{\prime } \\ \varvec{O} &{} \begin{array}{c} 1 \\ 0 \end{array} &{} \begin{array}{c} 0 \\ 1 \end{array} \\ \end{array} \right) \qquad \mathrm{for \ all} \ t = 1, 2, \ldots , \end{aligned}$$

where $\phi _1^{}$ stands for the initial (dummy) state (not out-of-control) in which the process is represented prior to the first observation of the first stage, $\gamma _1^{}$ the state in which the process is considered as out-of-control, and $\theta$ the state in which a warning is to be given.

In the second stage, if initiated, let us consider zone $D = [x_2^{}, \infty )$ with $p_{\scriptscriptstyle D}^{} = P(X(t) \in D)$ and zone $E = (-\infty , x_2^{})$ with $p_{\scriptscriptstyle E}^{} = P(X(t) \in E)$ for each t:

• (i) an out-of-control alarm is issued when an observation appears in zone D;

• (ii) or second-stage control process continues otherwise.

The imbedded Markov chain $\{ Y_2(t) \}$ here induced by the sequence $\{ X(t) \}$ in the second stage defined on the state space $\Omega _2 = \{ \phi _2^{}, E, \gamma _2^{} \}$ has the transition matrix

$$\begin{aligned} \varvec{M}_2 = \begin{array}{l} \phi _2^{} \\ E \\ \gamma _2^{} \end{array} \left( \begin{array}{ccc} 0 &{} p_{\scriptscriptstyle E}^{} &{} p_{\scriptscriptstyle D}^{} \\ 0 &{} p_{\scriptscriptstyle E}^{} &{} p_{\scriptscriptstyle D}^{} \\ 0 &{} 0 &{} 1 \\ \end{array} \right) = \left( \begin{array}{cc} \varvec{N}_2 &{} \varvec{C}_{\gamma _2^{}}^{\prime } \\ \varvec{O} &{} 1 \\ \end{array} \right) \qquad \qquad \mathrm{for \ all} \ t = 1, 2, \ldots , \end{aligned}$$

where $\phi _2^{}$ stands for the initial (dummy) state (not out-of-control) in which the process is represented prior to the first observation of the second stage, and $\gamma _2^{}$ the state in which the process is considered as out-of-control.

By setting $y_1^{} = 1.8807936$ and $x_1^{} = 3.5400838$, variable X(t) belongs to the zones C and B with probabilities $p_{\scriptscriptstyle C}^{} = 0.97$ and $p_{\scriptscriptstyle B}^{} = 0.0298$, respectively. Note that $p_{\scriptscriptstyle A}^{} + p_{\scriptscriptstyle B}^{} + p_{\scriptscriptstyle C}^{} = 1$, so that $p_{\scriptscriptstyle A}^{} = 0.0002$. By setting $x_2^{} = 1.8807936$, X(t) belongs to zone E with probability $p_{\scriptscriptstyle E}^{} = 0.97$, so then $p_{\scriptscriptstyle D}^{} = 0.03$. Let $\varvec{\xi }_0 = (1\; 0\; 0\; 0\; 0)$ and $\varvec{\eta }_0 = (1\; 0\; 0)$, the waiting-time distribution of the out-of-control alarm is tabulated in Table 1. In Table 2 are the ARLs with various choices of ($p_{\scriptscriptstyle A}^{}$, $p_{\scriptscriptstyle B}^{}$, $p_{\scriptscriptstyle C}^{}$, $p_{\scriptscriptstyle D}^{}$, $p_{\scriptscriptstyle E}^{}$) which can be used to suggest control limits given that a process is in control. Probability values with four decimal places are handpicked except those for $p_{\scriptscriptstyle D}^{}$ and $p_{\scriptscriptstyle E}^{}$ given sets of control limits in (A4), (A5) and (A6), where with chosen ($p_{\scriptscriptstyle A}^{}$, $p_{\scriptscriptstyle B}^{}$, $p_{\scriptscriptstyle C}^{}$), that are searched particularly to achieve the ARL of 370.37037.

Table 1 Waiting-time distribution

Table 2 Two-stage control process and its ARL

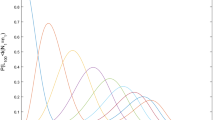
For each specified $\alpha$ the $100\alpha$th percentile of the waiting-time distribution of out-of-control signal for each control reference of (A1) to (A6) is placed in Table 3. In Fig. 2 are the cumulative waiting-time distributions, $P(W \le n)$ for $n = 1, \ldots , 5000$, of the out-of-control alarm for references (A1) to (A4) in Table 2. The distributions for references (A5), (A6) and (A7) almost mimic that for (A4).

Table 3 $100\alpha$th percentile of the waiting-time distribution of out-of-control signal

Fig. 2

Cumulative waiting-time distribution of out-of-control alarm

The ARLs for the case when only the second stage is used as a single-stage control process with various values for the control limit are displayed in Table 4. It is well known that in such case, the formula to obtain the average run length of the control process simply is

$$\begin{aligned} ARL = \eta _0^{} (\varvec{I} - \varvec{N}_2)_{}^{-1} \varvec{1}_{}^{\prime }. \end{aligned}$$

(11)

In comparing the ARLs in Table 4 to those in Table 2, if we compare reference (B1) to (A1), the ARL is lengthened when a portion solely of the out-of-control zone in the single-stage design is transformed into a warning zone to form the first stage of a two-stage control process while the second stage is kept the same to that of (B1). Comparing (B1) to (A2), the ARL is not affected when a portion solely of the in-control zone in the single-stage design is transformed into a warning zone to form the first stage while the second stage is kept the same to that of (B1). However, if a second stage is augmented with a tighter in-control zone as (B2) is compared to (A1), the ARL can be shortened.

Table 4 Single-stage control process and its ARL

The behaviour of ARL requires to be studied numerically when portions from each of the out-of-control zone and the in-control zone are combined to form a new warning zone in the first stage of a two-stage control process, and when this is practised however, the ARL can be controlled by the choice of the warning zone and by how the out-of-control zone is set up in the second stage as (B3) is compared to (A3) and (A4). It is not surprising that various choices of warning limit in the first stage, and control limits in the first and the second stages, may yield the same ARL as seen in (B3) compared to that in (A4), (A5) and (A6). It seems that a slightly wider in-control zone set up in the first stage can go with a much tighter in-control zone set up in the second stage to maintain the same ARL to that of a single-stage control process.

Supposedly, the N($\mu = 0$, $\sigma _{}^2 = 1$) normality assumption for X(t) is hypothesized under the null for an in-control process. By choosing $y_1^{} = 1.6448536$, $x_1^{} = 2.78215045$, and $x_2^{} = 2.78215045$, therefore ($p_{\scriptscriptstyle A}^{}$, $p_{\scriptscriptstyle B}^{}$, $p_{\scriptscriptstyle C}^{}$, $p_{\scriptscriptstyle D}^{}$, $p_{\scriptscriptstyle E}^{}$) = (0.0027, 0.0473, 0.95, 0.0027, 0.9973), the in-control ARL for such two-stage control process is 370.37037 and $\max \{ n$: $P(W \le n \mid$ H$_\mathrm{o}^{}) \le \alpha \} = 18$ for the nominal $\alpha = 0.05$. We take a look then at the behaviour of out-of-control process ARL and the waiting-time distribution of an alarm when there is a shift away in mean under the alternative. In other words, obtain for the same warning and control limits the ARL when there is a small positive shift in mean to d for each of $d = 0.01$, $d = 0.025$ and $d = 0.05$, and for each of a larger shift of $d = 0.1$, $d = 0.25$ and $d = 0.5$. Results are organised in Table 5. The cumulative waiting-time distributions of out-of-control signal are displayed in order from right to left and by line width as seen in Fig. 3. Furthermore, we plot in Fig. 4 with the vertical axis being $\beta = P(W > 18 \mid$ H$_\mathrm{a}^{}$: $\mu = d)$ and the horizontal axis being d for d starting from 0.005 to 2.5 with intervals of 0.005. A graph of any relation between $\beta$ and d here is usually called an operating-characteristic curve. We wish to point out that the outcome of ARL calculation depends on how accurate the probability of a sample statistic to fall in each of the regions A to E, thus the values used to construct the two transition matrices $\varvec{M}_1$ and $\varvec{M}_2$, is estimated. Estimation of these transition probabilities is well dependent on the, either parametric or empirical, estimation of the sampling distribution of the statistic being monitored for a given set of control and warning limits. For example, if X(t) of an in-control process was to have a Student’s t-distribution with five degrees of freedom, the setting of $y_1^{} = 2.0150484$, $x_1^{} = 4.686915$ and $x_2^{} = 4.686915$ would yield the same values for ($p_{\scriptscriptstyle A}^{}$, $p_{\scriptscriptstyle B}^{}$, $p_{\scriptscriptstyle C}^{}$, $p_{\scriptscriptstyle D}^{}$, $p_{\scriptscriptstyle E}^{}$) as before; if X(t) was to have a chi-square distribution with six degrees of freedom, the setting of $y_1^{} = 12.591587$, $x_1^{} = 20.0619$ and $x_2^{} = 20.0619$ would yield the same values for the set of transition probabilities, and therefore an in-control ARL of 370.37037 and the same waiting-time distribution of false alarm, as those of the N($\mu = 0$, $\sigma _{}^2 = 1$) setup in the above.

Table 5 ARL of two-stage control process when there is a shift in mean to N($\mu = d$, $\sigma _{}^2 = 1$)

Fig. 3

Cumulative waiting-time distribution of out-of-control alarm when there is a shift in mean

Fig. 4

Type II error rate when there is a shift in mean

Finally, we demonstrate numerically one advantage of a two-stage process control with a flexibility to adjust control limits at each stage and possibly having an out-of-control signal sooner when there is a shift away in process mean. With normality assumption N($\mu = 0$, $\sigma _{}^2 = 1$) about X(t) while the process is in control, ARLs are calculated and displayed in Table 6 for a small shift of $\mu + d$ for $d = 0.01$, $d = 0.025$ and $d = 0.05$, and for a larger shift of $d = 0.1$, $d = 0.25$ and $d = 0.5$, had a single-stage process control been chosen. We then choose reference (A6) in Table 2 for a two-stage process control example and recalculate the ARLs for the same shifts in mean, numerical results are organised in Table 7. In comparing the results in both tables, it can be seen that when the concern is in the upper tail region of a distribution above some target of a process, the two-stage control process provides an out-of-control alarm marginally faster for all our studied processes with a positive shift away from the target.

Table 6 ARL of single-stage control process with an upper control limit of 2.78215045 when there is a shift in mean to N($\mu = d$, $\sigma _{}^2 = 1$)

Table 7 ARL of two-stage control process when there is a shift in mean to N($\mu = d$, $\sigma _{}^2 = 1$)

Example 2

This example is created to show the possibility of extending our method in the case when some kind of dependency structure exists among time-homogeneous data observations. With this in mind, let us reconsider Example 1, in addition, suppose that the process $X(t = 1), X(t = 2), \ldots , X(t = n)$ is first-order Markov dependent. Given constant $c_0^{}$ and suppose marginally $X(t) \sim f(x) = (\sqrt{2\pi })_{}^{-1} \exp \{ -(x - c_0^{})_{}^2 / 2 \}$ for all $t = 1, \ldots , n$, $-\infty< x < \infty$, and the conditional distribution function of $X(t + 1) = y$ given $X(t) = x$ is $f(y \mid x) = (\sqrt{2\pi })_{}^{-1} \exp \{ -(y - x)_{}^2 / 2 \}$ for $t = 1, \ldots , n$, $-\infty< y < \infty$. The joint density of $X(t = 1) = z_1^{}, X(t = 2) = z_2^{}, \ldots , X(t = n) = z_n^{}$ will then be $f(z_1^{}, z_2^{}, \ldots , z_n^{}) = f(z_1^{}) f(z_2^{} \mid z_1^{}) f(z_3^{} \mid z_2^{}) \cdots f(z_n^{} \mid z_{n - 1}^{})$.

Having the same control rules as those in Example 1, the imbedded Markov chain $\{ Y(t)$, $\Omega _t$, $t = 0, 1, 2, \ldots \}$ on the state space $\Omega _t = \{ \phi , C, B, \theta , E, \gamma _1^{}, \gamma _2^{} \}$ for the process $\{ X(t)$, $t = 0, 1, 2, \ldots \}$, where for any t while in the first stage, $Y(t) = C$ when an observation appears in ($-\infty , y_1^{}$) at t, $Y(t) = \theta$ when both observations at $t - 1$ and t appear in [$y_1^{}, x_1^{}$), or $Y(t) = B$ when an observation appears in [$y_1^{}, x_1^{}$) just at t, otherwise, $Y(t) = \gamma _1^{}$ when an observation appears in [$x_1^{}, \infty$). On the other hand, for any t while in the second stage, $Y(t) = E$ when an observation appears in ($-\infty , x_2^{}$) at t, or $Y(t) = \gamma _2^{}$ when an observation appears in [$x_2^{}, \infty$). Y(t) has the transition matrix

$$\begin{aligned} \varvec{M}_t = \begin{array}{l} \phi \\ C \\ B \\ \theta \\ E \\ \gamma _1^{} \\ \gamma _2^{} \end{array} \left( \begin{array}{ccccccc} 0 &{} p_{\scriptscriptstyle C}^{} &{} p_{\scriptscriptstyle B}^{} &{} 0 &{} 0 &{} p_{\scriptscriptstyle A}^{} &{} 0 \\ 0 &{} p_{\scriptscriptstyle CC}^{} &{} p_{\scriptscriptstyle CB}^{} &{} 0 &{} 0 &{} p_{\scriptscriptstyle CA} &{} 0 \\ 0 &{} p_{\scriptscriptstyle BC}^{} &{} 0 &{} p_{\scriptscriptstyle BB}^{} &{} 0 &{} p_{\scriptscriptstyle BA}^{} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} p_{\scriptscriptstyle BE}^{} &{} 0 &{} p_{\scriptscriptstyle BD}^{} \\ 0 &{} 0 &{} 0 &{} 0 &{} p_{\scriptscriptstyle EE}^{} &{} 0 &{} p_{\scriptscriptstyle ED}^{} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ \end{array} \right) = \left( \begin{array}{cc} \varvec{N} &{} \varvec{C} \\ \varvec{O} &{} \varvec{I} \end{array} \right) \qquad \mathrm{for} \ t = 1, 2, \ldots , n \end{aligned}$$

which is independent of t, where $\phi$ stands for the (dummy) state (not out-of-control) which the process is in at the initial time $t = 0$ prior to the first observation of the first stage, $\gamma _1^{}$ is used to denote the state of the process when it is considered to be out-of-control in the first stage, and $\gamma _2^{}$ in the second stage, and

$$\begin{aligned} p_{\scriptscriptstyle A}^{}&= \int _{x_1^{}}^{\infty } \frac{1}{\sqrt{2\pi }}\, e_{}^{-(x - c_0^{})_{}^2 / 2} dx,\quad p_{\scriptscriptstyle B}^{} = \int _{y_1^{}}^{x_1^{}} \frac{1}{\sqrt{2\pi }}\, e_{}^{-(x - c_0^{})_{}^2 / 2} dx,\quad p_{\scriptscriptstyle C}^{} = \int _{-\infty }^{y_1^{}} \frac{1}{\sqrt{2\pi }}\, e_{}^{-(x - c_0^{})_{}^2 / 2} dx, \end{aligned}$$

$$\begin{aligned} p_{\scriptscriptstyle BA}^{}&= P(X(t + 1) \in A \mid X(t) \in B) = \frac{ \int _{y_1^{}}^{x_1^{}} \left( \int _{x_1^{}}^{\infty } \frac{1}{\sqrt{2\pi }}\, e_{}^{-(y - x)_{}^2 / 2} dy \right) \frac{1}{\sqrt{2\pi }}\, e_{}^{-(x - c_0^{})_{}^2 / 2} dx }{ \int _{y_1^{}}^{x_1^{}} \frac{1}{\sqrt{2\pi }}\, e_{}^{-(x - c_0^{})_{}^2 / 2} dx }, \\ p_{\scriptscriptstyle BB}^{}&= \frac{ \frac{1}{2\pi } \int _{y_1^{}}^{x_1^{}} \left( \int _{y_1^{}}^{x_1^{}} e_{}^{-(y - x)_{}^2 / 2} dy \right) e_{}^{-(x - c_0^{})_{}^2 / 2} dx }{ \int _{y_1^{}}^{x_1^{}} \frac{1}{\sqrt{2\pi }}\, e_{}^{-(x - c_0^{})_{}^2 / 2} dx },\quad p_{\scriptscriptstyle BC}^{} = \frac{ \frac{1}{2\pi } \int _{y_1^{}}^{x_1^{}} \left( \int _{-\infty }^{y_1^{}} e_{}^{-(y - x)_{}^2 / 2} dy \right) e_{}^{-(x - c_0^{})_{}^2 / 2} dx }{ \int _{y_1^{}}^{x_1^{}} \frac{1}{\sqrt{2\pi }}\, e_{}^{-(x - c_0^{})_{}^2 / 2} dx }, \end{aligned}$$

$$\begin{aligned} p_{\scriptscriptstyle CA}^{}&= \frac{ \frac{1}{2\pi } \int _{-\infty }^{y_1^{}} \left( \int _{x_1^{}}^{\infty } e_{}^{-(y - x)_{}^2 / 2} dy \right) e_{}^{-(x - c_0^{})_{}^2 / 2} dx }{ \int _{-\infty }^{y_1^{}} \frac{1}{\sqrt{2\pi }}\, e_{}^{-(x - c_0^{})_{}^2 / 2} dx },\quad p_{\scriptscriptstyle CB}^{} = \frac{ \frac{1}{2\pi } \int _{-\infty }^{y_1^{}} \left( \int _{y_1^{}}^{x_1^{}} e_{}^{-(y - x)_{}^2 / 2} dy \right) e_{}^{-(x - c_0^{})_{}^2 / 2} dx }{ \int _{-\infty }^{y_1^{}} \frac{1}{\sqrt{2\pi }}\, e_{}^{-(x - c_0^{})_{}^2 / 2} dx }, \\ p_{\scriptscriptstyle CC}^{}&= \frac{ \frac{1}{2\pi } \int _{-\infty }^{y_1^{}} \left( \int _{-\infty }^{y_1^{}} e_{}^{-(y - x)_{}^2 / 2} dy \right) e_{}^{-(x - c_0^{})_{}^2 / 2} dx }{ \int _{-\infty }^{y_1^{}} \frac{1}{\sqrt{2\pi }}\, e_{}^{-(x - c_0^{})_{}^2 / 2} dx }, \end{aligned}$$

$$\begin{aligned} p_{\scriptscriptstyle BD}^{}&= \frac{ \frac{1}{2\pi } \int _{y_1^{}}^{x_1^{}} \left( \int _{x_2^{}}^{\infty } e_{}^{-(y - x)_{}^2 / 2} dy \right) e_{}^{-(x - c_0^{})_{}^2 / 2} dx }{ \int _{y_1^{}}^{x_1^{}} \frac{1}{\sqrt{2\pi }}\, e_{}^{-(x - c_0^{})_{}^2 / 2} dx },\quad p_{\scriptscriptstyle BE}^{} = \frac{ \frac{1}{2\pi } \int _{y_1^{}}^{x_1^{}} \left( \int _{-\infty }^{x_2^{}} e_{}^{-(y - x)_{}^2 / 2} dy \right) e_{}^{-(x - c_0^{})_{}^2 / 2} dx }{ \int _{y_1^{}}^{x_1^{}} \frac{1}{\sqrt{2\pi }}\, e_{}^{-(x - c_0^{})_{}^2 / 2} dx }, \end{aligned}$$

$$\begin{aligned} p_{\scriptscriptstyle ED}^{}&= \frac{ \frac{1}{2\pi } \int _{-\infty }^{x_2^{}} \left( \int _{x_2^{}}^{\infty } e_{}^{-(y - x)_{}^2 / 2} dy \right) e_{}^{-(x - c_0^{})_{}^2 / 2} dx }{ \int _{-\infty }^{x_2^{}} \frac{1}{\sqrt{2\pi }}\, e_{}^{-(x - c_0^{})_{}^2 / 2} dx },\quad p_{\scriptscriptstyle EE}^{} = \frac{ \frac{1}{2\pi } \int _{-\infty }^{x_2^{}} \left( \int _{-\infty }^{x_2^{}} e_{}^{-(y - x)_{}^2 / 2} dy \right) e_{}^{-(x - c_0^{})_{}^2 / 2} dx }{ \int _{-\infty }^{x_2^{}} \frac{1}{\sqrt{2\pi }}\, e_{}^{-(x - c_0^{})_{}^2 / 2} dx }. \end{aligned}$$

Given $y_1^{}$, $x_1^{}$ and $x_2^{}$, the probabilities $p_{\scriptscriptstyle A}^{}$, $p_{\scriptscriptstyle B}^{}$, $p_{\scriptscriptstyle C}^{}$, $p_{\scriptscriptstyle BA}^{}, \ldots , p_{\scriptscriptstyle EE}^{}$ can be obtained by numerical integration. Hence, the distribution of W of the two-stage control process in this case simply is

$$\begin{aligned} P(W = n) = (1\; 0\; 0\; 0\; 0\; 0\; 0) \varvec{N}_{}^{n - 1} (\varvec{I} - \varvec{N}) \varvec{1}^{\prime }. \end{aligned}$$

(12)

For the purpose of illustration and to simplify our computation, for $t = 1, 2, \ldots$ under the null assumption, suppose marginally $X(t) \sim$ N(0, 1), and conditionally, $X(t + 1) \mid X(t) = x \sim$ N(0, 1) for all $x \in (-\infty , y_1^{})$ and $X(t + 1) \mid X(t) = x \sim$ N($y_1^{}, 1$) for all $x \in [y_1^{}, x_1^{}$) when in the first stage. Suppose conditionally $X(t + 1) \mid X(t) = x \sim$ N(0, 1) for all $x \in (-\infty , x_2^{})$ when in the second stage.

By choosing $y_1^{} = 1.6448536$, $x_1^{} = 2.78215045$, and $x_2^{} = 2.78215045$, therefore ($p_{\scriptscriptstyle A}^{}$, $p_{\scriptscriptstyle B}^{}$, $p_{\scriptscriptstyle C}^{}$, $p_{\scriptscriptstyle D}^{}$, $p_{\scriptscriptstyle E}^{}$) = (0.0027, 0.0473, 0.95, 0.0027, 0.9973). The transition matrix of our imbedded Markov chain to obtain the distribution of time to an out-of-control alarm in this case is

$$\begin{aligned} \varvec{M}_t = \begin{array}{l} \phi \\ C \\ B \\ \theta \\ E \\ \gamma _1^{} \\ \gamma _2^{} \end{array} \left( \begin{array}{ccccccc} 0 &{} 0.95 &{} 0.0473 &{} 0 &{} 0 &{} 0.0027 &{} 0 \\ 0 &{} 0.95 &{} 0.0473 &{} 0 &{} 0 &{} 0.0027 &{} 0 \\ 0 &{} 0.5 &{} 0 &{} 0.3723 &{} 0 &{} 0.1277 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0.8723 &{} 0 &{} 0.1277 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0.9973 &{} 0 &{} 0.0027 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ \end{array} \right) \qquad \mathrm{for} \ t = 1, 2, \ldots , n. \end{aligned}$$

The in-control $ARL_0$ for such two-stage control process can be calculated to be 256.3 using (11) with $\varvec{N}$ in place of $\varvec{N}_2$, and it can easily be obtained that $\max \{ n$: $P(W \le n \mid$ H$_\mathrm{o}^{}) \le \alpha \} = 5$ for the nominal type I error rate of $\alpha = 0.05$.

When independence is to be assumed about the data generated from the process $X(t = 1)$, $X(t = 2)$, $\ldots , X(t = n)$, the transition matrix of Y(t), for $t = 1, \ldots , n$, will become

$$\begin{aligned} \varvec{M}_t = \begin{array}{l} \phi \\ C \\ B \\ \theta \\ E \\ \gamma _1^{} \\ \gamma _2^{} \end{array} \left( \begin{array}{ccccccc} 0 &{} p_{\scriptscriptstyle C}^{} &{} p_{\scriptscriptstyle B}^{} &{} 0 &{} 0 &{} p_{\scriptscriptstyle A}^{} &{} 0 \\ 0 &{} p_{\scriptscriptstyle C}^{} &{} p_{\scriptscriptstyle B}^{} &{} 0 &{} 0 &{} p_{\scriptscriptstyle A} &{} 0 \\ 0 &{} p_{\scriptscriptstyle C}^{} &{} 0 &{} p_{\scriptscriptstyle B}^{} &{} 0 &{} p_{\scriptscriptstyle A}^{} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} p_{\scriptscriptstyle E}^{} &{} 0 &{} p_{\scriptscriptstyle D}^{} \\ 0 &{} 0 &{} 0 &{} 0 &{} p_{\scriptscriptstyle E}^{} &{} 0 &{} p_{\scriptscriptstyle D}^{} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ \end{array} \right) = \left( \begin{array}{cc} \varvec{N} &{} \varvec{C} \\ \varvec{O} &{} \varvec{I} \end{array} \right) \qquad \mathrm{for} \ t = 1, 2, \ldots , n, \end{aligned}$$

and formula (12) can still be used for computation for the distribution of W of the two-stage control process, and therefore obtain the in-control $ARL_0$ to be 370.37037 and $\max \{ n$: $P(W \le n \mid$ H$_\mathrm{o}^{}) \le \alpha \} = 18$ at the nominal type I error rate of $\alpha = 0.05$, which are the same to what we have seen earlier in Example 1.

5 Concluding Remarks

As an alternative to single-stage control scheme, we present a method to evaluate the performance of implementing a mechanism to advise process inspector of the potential risk in the first stage of a two-stage control process. The aim in this work is to not merely compare a specific two-stage control chart to a previously known single-stage type of chart (e.g., Shewhart chart), but to demonstrate the computational feasibility in designing a Markov chain imbeddable two-stage process control. Our method relies on a Markov chain approach in aid to obtain an analytical expression for each of the various statistical properties, such as the average run length and the distribution of time to signal, of a chart. Obtaining the waiting-time distribution of false alarm allows one to determine for inference the actual type I error rate when process is on-target. The quantiles of the distribution of time to false alarm then allows one to further obtain the probability of failing to reject the false in-control null assumption about the process when there is a shift away from the null. With a clear-cut process inspection scheme, the method of analysis can be extended in a straightforward manner even when the first or the second stage, or both, of a two-stage control process is to be monitored using a plot of Shewhart-type, Cusum-type, or a weighted moving average type without or with supplementary runs rules in the sense of Champ and Woodall (1987), or with more complicated rules in the sense of  Fu et al. (2003). One may also consider the processes studied by Chang and Wu (2011) when data points, on a plot of Shewhart-type, Cusum-type and/or EWMA-type without or with certain feature, are autoregressive in nature in the first or the second stage, or in both.

We have taken into account the possibility and flexibility of monitoring under the on-target assumption in different aspects of the same process in two stages. The approach is quite general and it requires simply the probability of a process characteristic being monitored to fall into each of finitely partitioned zones to construct a transition matrix for the imbedded Markov chain. The distribution of warning state(s) of the first stage acting as a mechanism to initiate the second stage of the control process is also necessary, in addition to carefully determined probability for each possible initial state of the imbedded Markov chain of the second stage. Another advantage of this approach is that it allows one to consider a partition of the warning zone in a way that each of the multiple rules being used to give out a warning signal when observations appear in one or multiple of the subzones may lead to a different second-stage process control corresponding to that particular rule. Apart from the possibility to consider multiple warning rules, the condition met by a process for it to be considered out-of-control can also be defined by more than one runs-rule as an extension to such rather straightforward example.

When a single-stage chart is supplemented with rules as additional ways to signal (out-of-control), there may be a general theory which allows one to investigate the probability of a false alarm set off by each rule when instead the same set of rules is used as a way to give warnings (not an out-of-control signal) in the first stage and to start off the second stage of a two-stage control process which eventually suggests the overall process to be in control. With some diligence in this line of work one may bring answers to such question to light that could be of interest to some readers. Furthermore, we anticipate that the method presented here can be applied easily to the case shall action lines and warning states are to be set in a chart to signal about possible shift of a process away in the above or below from a target. When additionally a cost model is available as a function of the state space of imbedded Markov chains, economic feasibility of a chart design can also be studied.