Updating Mining Resources with Uncertain Data

Abstract

In mining operations, the time delay between grade estimations and decision-making based on those estimations can be substantial. This may lead to the scheduling of stopes mining that is based on information which is seriously out of date and, consequently, results in a substantial mined resources and reserves bias. To mitigate this gap between the grade estimation of an orebody and its exploitation, this paper proposes a method to quickly update resources and reserves that are integrated into the concept of real-time mining. The current standard for grade data collection in underground mines relies on a conventional chemical lab analysis of sparse drill hole or chip/face samples. The proposed methodology for the continuous and swift updating of mine resources and reserves requires a constant and rapid stream of measurements at the stopes. Consequently, this work proposes using portable X-ray fluorescence (XRF) devices to carry out the fast and abundant monitoring of ore grades. However, these fast data are highly uncertain; hence, the objective of this proposed method is to use the total data measurements and integrate their uncertainty into the resources modeling. The first step in the proposed methodology consists of creating a joint distribution function between “uncertain” XRF and the corresponding “hard” measurements based on empirical historical data. Then, the uncertainty of the XRF measurements is derived from these joint distributions through the conditional distribution of the real values applied to the known XRF measurement. The second step involves updating the reserves by integrating these uncertain XRF data, which are quantified by conditional distributions, into the grade characterization models. To achieve this, a stochastic simulation with point distributions is applied. An actual case study of a copper sulfide deposit illustrates the proposed methodology.

1 Introduction

Autonomous operations, integrated within digital innovation, are among the mining industry’s most important medium-term targets (Fisher and Schnittger 2012; Matysek and Fisher 2016; Sganzerla et al. 2016). However, before reaching that technological stage, the industry must take the intermediate steps of engaging in the real-time monitoring and management of mining operations. These are the two most important factors of the real-time mining concept (Osterholt and Benndorf 2015). Most modern mining operations incorporate real-time geographical position monitoring of some mining equipment—jumbos, trucks, conveyors, etc.—since Wi-Fi systems are commonplace in underground mines. The main problem with the implementation of real-time monitoring and management in mining is down to resource and reserve estimation. The updating of resources and reserves has been the subject of some studies, particularly by simulating residuals (Vargas-Guzmán and Dimitrakopoulos 2002; Jewbali and Dimitrakopoulos 2011) and, more recently, with an adaptation of the ensemble Kalman filter approach to mining processes (Wambeke and Benndorf 2017). Nevertheless, in such situations, the problem of prompt updating (real-time updating) remains. In fact, in most mining routines, the delay between sampling at the stopes location, grade estimations, and decisions about mining stopes during production can be lengthy (in many cases, months). In some cases, this can result in the use of seriously outdated information and, consequently, a substantial bias in mined reserves. The main reason for this operational gap is the intrinsic spatial heterogeneity of mineral resources, which makes any prediction about resources and reserves an exercise that is prone to uncertainty and risk (Dimitrakopoulos et al. 2002; Journel and Kyriakidis 2004).

This study discusses how to bring the monitoring and updating of resources as close as possible to the concept of real-time mining. This entails a framework that changes from the paradigm of a discontinuous and extended monitoring and control process to one that is more continuous and “real time”, with the subsequent management of resource uncertainty. This study proposes using portable X-ray fluorescence (XRF) (Kalnicky and Singhvi 2001) as a tool for monitoring face samples in underground stopes. XRF samples are fast, albeit uncertain, measurements depending on the small-scale heterogeneity of different ore types. The basic rationale of the methodology is to take those fast, but imprecise, measurements (soft data) into account when assessing reserves and the respective uncertainty.

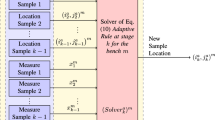
There are three basic steps in the proposed fast resource monitoring and updating process:

• 1. The first step consists of building a reference database for a joint distribution function between the fast/uncertain data and the “hard” data, such as the face sample data obtained in the lab. This joint distribution can be obtained by pairing copper grades measured by XRF and by the laboratory analysis of face samples at the same location. To this end, there must be a monitoring campaign to obtain historical XRF and face data, sampled simultaneously at the same locations. Biplots of these duplets of sample measurements could allow an estimation of bivariate distributions between these two types of samples. If they demonstrate different bivariate behaviors, then these distributions can be estimated for each ore type.

• 2. The next two phases refer to the uncertainty assessment of fast monitoring and the integration of uncertainty into reserve updating. For new XRF measurements, local conditional XRF distributions based on the historical and stationary bivariate distributions (step 1) are estimated at each sample location. These conditional distributions represent a new measurement of XRF data uncertainty. This is detailed in Sect. 2.2.

• 3. Grade resources are characterized by stochastic simulation with point distributions (Horta and Soares 2010; Soares et al. 2017) based on the previously estimated local conditional distributions on the new XRF locations.

2 Fast Data Collection at Mining Stopes in an Underground Mine

2.1 Historical XRF and Face Sample Data at the Same Location

The proposed methodology is illustrated in a copper sulfide deposit (Zambujal orebody) case study. The deposit is composed of two main ore types: massive and stockwork. The most heterogeneous ore type—stockwork—was chosen to illustrate the methodology for resource evaluation with uncertain data. Available data for this study are copper grades from drill core samples and from stopes face samples.

The first step in the proposed methodology involves creating a data set of historic copper grade XRF measurements and face sample measurements at the same locations as a way of estimating the stationary bivariate distribution function for each ore type. At each stope, a maximum of nine XRF and face samples were taken at the same location. The face samples were analyzed following a conventional procedure in the chemical lab. The sampling layout of the stockwork ore type (Fig. 1), adopted by the mine routine, allows us to achieve representative samples of the Cu-rich chalcopyrite veins that are dispersed throughout the volcanic rock.

Fig. 1

Face sample collection layout at: a massive ore type, b stockwork ore type

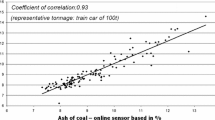
The scatter plot of 145 XRF/face sample measurements pairs is shown in Fig. 2. Although there is a high correlation (more than 95%) between the two measurements, there is a noticeable dispersion of portable XRF measurements, particularly on high face sample grades. This is due to the nature of grade dispersion in stockwork, where high-grade values are frequently caused by thin veins of chalcopyrite. Hence, a small displacement in the location of XRF and face samples can lead to substantial differences in measured values. For example, see the increase of the conditional variance of XRF values above the 5% threshold. Marginal histograms are represented in Fig. 3 and the main statistics in Table 1.

Fig. 2

X-ray fluorescence (XRF)/face sample scatter plot

Fig. 3

Histograms: a lab measurements, b XRF measurements

Table 1 Mean, variance, quartiles 25 to 75, minimum, and maximum for both measurement types

2.2 XRF Data Uncertainty Assessment

Given the scarcity of data in this test (Fig. 2), especially at high values (Cu > 5%), a bivariate probability density function (PDF) was estimated. This is achieved by using a simulated annealing optimization algorithm, GSLIB’s SCATSMTH (Deutsch and Journel 1992), based on the experimental scatter plot shown in Fig. 2. The resulting estimated PDF is represented in Fig. 4.

Fig. 4

XRF/face samples bivariate probability density function (PDF)

Here, it is worth making two points. The first is that different bivariate distributions can be derived for each ore type and different orebody localities, depending on the local conditional variability of both types of sample measurements. The second is that the amount of data used to derive this bivariate distribution is strictly dependent on the local variability of both types of data (e.g., a massive and much less heterogeneous ore type in terms of the spatial distribution of copper, which is not touched upon in this study, needs much less data). The idea is to produce a reliable and spatially representative estimate of the bivariate distribution between hard and uncertain samples.

Consider the XRF measured grades as $z_{s} (x)$ and the equivalent grade values obtained with the conventional chemical analysis in the laboratory as $z(x)$. The estimated bivariate distribution function $F(Z(x), Z_{s} (x))$ is assumed to be stationary and representative of the area in which this study was conducted. This means that, in a future fast-sampling campaign, given new XRF measurements at the spatial location $x_{0}$, $z_{S} (x_{0} )$, from the bivariate distribution $f(Z(x), Z_{s} (x))$ an estimate for the equivalent point conditional distribution of $z(x_{0} )$ can be made, given the known XRF value $z_{S} (x_{0} )$, $f(Z(x_{0} )\left| { Z_{s} (x_{0} ) = z_{S} (x_{0} )} \right.)$ (see the example in Fig. 5). Hence, the new set of sampling values (XRF values), taken from new stopes, have an uncertainty that is equivalent to the conditional density distributions calculated from the bivariate density function (examples in Fig. 6 of some point distributions).

Fig. 5

Local point distributions provided by the fast XRF sampling (example of a fast measurement of Cu = 8.3% provides the conditional distribution shown on the right-hand side)

Fig. 6

Examples of local point distributions $f(Z(x) |Z_{s} (x))$

3 Resource Characterization with Uncertainty Data: Stochastic Simulation with Point Distributions

In the next methodological step, the grade models are assessed using uncertainty data that are characterized by the conditional distributions obtained as described in Sect. 2, after new XRF measurements.

When the available experimental information is uncertain, like XRF data, the integration of this uncertainty into stochastic models to characterize the spatial dispersion of the grades is the challenge this paper seeks to address. This challenge has been approached in several works, both by estimated local cumulative distribution functions (CDFs) with indicator cokriging with soft data (Journel 1986; Zhu and Journel 1993) and by estimated local CDFs for stochastic simulation, with indicator formalism (Alabert 1987). The main limitations of these methods are essentially related to the properties of the indicator formalism to characterize continuous variables and the cumbersome task of indicator covariance model estimation in particular (Goovaerts 1997).

In this paper, direct sequential simulation (DSS) with point distributions is applied to integrate the uncertainty of data derived from the fast acquisition XRF data measurements (Soares et al. 2017). The DSS with point distributions can be summarized in two major steps:

• 1. The generation of a spatially correlated data set. Before simulating the entire grid of nodes, a set of experimental data values at the XRF measurement locations are drawn from the corresponding local point conditional distributions $f({\text{Z}}({\text{x}}_{0} ) | {\text{Z}}_{\text{s}} ({\text{x}}_{0} ) = z({\text{x}}_{0} ))$. The generation of this spatially correlated data set is obtained by the following sequence: (i) first, the local mean and variance at the randomly selected XRF data location $x_{0}$ are estimated by simple kriging (Journel and Huijbregts 1978), conditioned to the eventual existing neighborhood “hard” data (borehole or face sample data) and the previously simulated XRF data, $z^{*} (x_{0} )_{SK}$ and $\sigma^{*} (x_{0} )_{SK}$; then, (ii) a data value $z(x_{0} )$ is drawn from the point distribution $f(Z(x_{0} )|Z_{s} (x_{0} ))$, focused on the estimated local mean and variance identified with the simple kriging estimate and variance, $z^{*} (x_{0} )_{SK}$ and $\sigma^{*} (x_{0} )_{SK}$ (previous step), following the outline of DSS (Soares 2001). The resulting simulated experimental data values $z(x_{\alpha } ), \alpha = 1, N$ reproduce both the local CDFs and the spatial continuity, as revealed by the spatial covariance. Return to step 1(i) following a random path until all point distributions have been simulated.

• 2. The second major step is the simulation of the entire grid of nodes. Once the correlated data set is generated, the grid of nodes is simulated using the traditional DSS approach. Return to step 1 to generate another data set and subsequent simulated grid nodes.

The spatial uncertainty of grades, assessed with the set of simulated realizations, reproduces the uncertainty of XRF data through to the local dispersion of conditional point distributions.

4 Selected Study Area

Only core and XRF data are used in the examples given in Sect. 5, which illustrates the situation of a future fast-sampling routine in which only these two types of data are available. Both the XRF and core data set locations are presented in Fig. 7, which shows the overlap of both data clouds. The higher density of the XRF data, in red, becomes self-evident and it is easy to recognize that there are parts of the orebody in which only core data are available (Fig. 7, blue dots). Hence, the study was conducted in an area in which both XRF and core data measurements coexist (Fig. 7). Histograms for face samples and drill hole sets are shown in Fig. 8. Experimental semi-variograms are calculated using core data (Fig. 9). The semi-variogram model is a combination of two spherical structures with a nugget effect of 25% of the sill.

Fig. 7

Selected area in which both XRF and core data measurements coexist. XRF samples are plotted in red and core samples are plotted in blue

Fig. 8

Histogram of: a XRF and b core sample data

Fig. 9

Fitted semi-variogram: a main direction, b first minor, and c second minor

5 Results of Stochastic Simulation with XRF Uncertain Data Measurements

A reference case is created to evaluate the results of the proposed methodology. Given the available data, here this reference case is considered the closest image to reality, and, so, it was created with the largest quantity of available information. A set of 32 simulations ran with both core sample and face sample data, which is presented in detail in Sect. 5.1.

Three test scenarios were run to evaluate the performance of the proposed methodology, from which two were compared with a reference case. The three tests, carried out at the same location to validate the proposed methodology, were as follows:

• 1. In the first test, the grades simulation was performed using the proposed methodology based only on XRF point distribution data. In this case, the simulations are not conditioned to core sample data. This test is intended to mimic those situations in the mine routine in which only XRF data, obtained in a real-time framework, is available. These results are presented in Sect. 5.2.

• 2. In the second test, the Cu grades are characterized with just “hard”/core sample data. To achieve this, we deploy classical DSS using only core sample data (“hard” data). Therefore, since its results are obtained without any real-time data (XRF), it relies solely on the same data used in standard mine routines. These results are presented in Sect. 5.3.

• 3. The last test intends to mimic situations in which the Cu grades are simulated with the proposed methodology using both core sample data and the uncertain XRF measurements (point distributions). These results are presented in Sect. 5.4.

Section 5.5 compares the results of Sects. 5.3 and 5.4 with the reality assumed in Sect. 5.1.

5.1 Reference Case

The reference case is obtained by running a stochastic simulation with all the hard data available and the core and face sample data. The local mean of the 32 realizations (E-type estimator) was calculated for the entire area. Two small areas, A and B, were chosen to illustrate the performance of the proposed method (Fig. 10). At its center, area A contains a face sample with a low value (0.97%, magnified representation in Fig. 10b). Area B is a cross-section centered on a face sample with a high value (32.91%, magnified representation in Fig. 10d).

Fig. 10

Reference model: a cross-section, from which small area A was taken; b magnified version of area A; c cross-section, from which small area B was taken; d magnified version of area B

Figure 11 shows two views of areas A and B with the XRF samples (red) and core samples (blue) used in the exercises outlined in Sect. 5.2 below.

Fig. 11

Two views of areas A and B with the XRF samples (red) and core samples (blue)

5.2 Simulation of Grades with Point Distributions Data Only

The first test consisted of the stochastic sequential simulation with point distributions; the proposed method, by using exclusively uncertain data, the real-time XRF data. The purpose of this exercise is simply to confirm that the simulation of point distributions honors the uncertainty of the high and low sample values as revealed by the global bivariate distribution function. The mean of 32 realizations (E-type estimator) is shown in the same small cross-sections of the reference case, in areas A and B (Fig. 12a, b, respectively). Figure 12c, d represents the variance of the simulated ensemble for areas A and B, respectively. These show lower local variance at area A, which is associated with a lower mean than is found at area B, which has a higher local mean.

Fig. 12

Simulation with the point distributions: a E-type estimator of area A; b E-type estimator of area B; c variance of the realizations in area A; d variance of the realizations in area B. The color scale is the same for all maps; e the color map used

It is worth noting that the lower uncertainty associated with expected low values and the higher uncertainty corresponding to high sample values, which is revealed in the bivariate distribution shown in Fig. 4, is reproduced in the simulated maps of areas A and B. This means that, when fast samples have high uncertainty, this is considered in the simulated realizations. On the other hand, when fast sample values have low uncertainty, this is reflected in the local lower variance of the simulated model.

5.3 Simulation of Cu Grades with “Hard”/Core Data

The second exercise consists of running DSS using just core sample data (hard data). Figure 13a, b shows the local mean of 32 simulations for areas A and B, respectively. As the existing hard data close to areas A and B are homogeneous, this implies smoother patterns of Cu grades in both situations. Figure 13c, d shows the variance for the same areas A and B. The images of variances with only hard data are smoother and have a similar value range in areas A and B.

Fig. 13

Simulation with core data: a E-type estimator of area A; b E-type estimator of area B; c variance of the realizations in area A; d variance of the realizations in area B; e the color map used

5.4 Simulation of Cu Grades by Integrating Both Drill Hole Data and Uncertain XRF Measurements (Point Distributions)

The third and final exercise applies the proposed methodology using both core sample data (hard data) and the uncertain XRF measurements (point distributions). Figure 14a, b shows the local mean of 32 simulations using the proposed methodology in areas A and B, respectively. Figure 14c, d represents the variances of simulated realizations in areas A and B, respectively.

Fig. 14

Simulation of Cu grades by using both the core data and the uncertain XRF measurements: a E-type estimator of area A; b E-type estimator of area B; c variance of the realizations in area A; d variance of the realizations in area B; e the color map used

The final models of the mean and variance of simulated realizations (Fig. 14) mostly show the influence of the uncertain data. It is important to emphasize that (i) the higher density and quantity of data provides more information for conditioning the simulation, which is reflected in the final E-type models. This is also emphasized in the quantitative comparison with the reference case of Fig. 10 (Sect. 5.5). Also, (ii) the local variance maps show the influence of XRF data with low uncertainty (area A) or high uncertainty (area B).

5.5 Comparison with the Reference Case

To compare the E-type estimators from the last two exercises—simulation only with hard data and the proposed simulation with hard data and point distributions from XRF data—the difference between them and the E-type of the reference model is calculated.

Figure 15 shows the differences between the reference case of area A (Fig. 10b) and the E-type estimators resulting from the simulation with hard data (Fig. 15a). The differences between the area A reference case and the E-type resulting from the proposed method with hard and uncertain data are shown in Fig. 15b.

Fig. 15

Differences between the reference case of area A and: a the E-type estimator resulting from the simulation with hard data; b the E-type resulting from the proposed method with hard and uncertain data

The same exercise is presented in Fig. 16 for area B. It shows the differences between the area B reference case (Fig. 10d) and the E-type estimator resulting from the simulation with hard data (Fig. 16a). The differences between the reference case and the E-type resulting from the proposed method with hard and uncertain data are shown in Fig. 16b.

Fig. 16

Differences between the reference case of area B and: a the E-type estimator resulting from the simulation with hard data; b the E-type resulting from the proposed method with hard and uncertain data

It is worth noting the following: (i) when the uncertainty of XRF data is low (area A), the deviations to the reference case are negligible; (ii) even when the uncertainty of XRF data is high, the deviation to the reference case shows that it is better to use the uncertain data; (iii) considering the reference case being the closest scenario to reality, this exercise clearly displays the advantages of the proposed method in accounting for fast and uncertain data.

6 Final Remarks

Two important issues about the real-time mining concept are addressed in this paper: the fast monitoring of grades, in this case, at the face of stopes of production fronts, and the integration of the uncertainty of fast measurements for updating resources by using DSS with uncertain data.

The results of the proposed methodology are very promising for monitoring grades with fast (uncertain) measurements and for the simulation method, which can integrate the uncertain data. It is also worth noting that the case study was conducted with the most heterogeneous ore type at the Neves-Corvo mine, a cupriferous stockwork ore type.

One of the main conclusions of this study is that it is worth accounting for the fast uncertain measurements if the data uncertainty is included in the reserves evaluation model. In this case, a better resources model is obtained when uncertain grade measurements are considered than is obtained when they are discarded.

Also, the uncertainty of fast measurements, as quantified by the point distribution probability, is derived from the bivariate distributions (historical data) between XRF and face samples. These bivariate distributions must be considered stationary and representative of the area from which the XRF data are taken. This means that they must be estimated for each ore type and periodically validated and updated with new face samples and lab measurements.