1 Introduction

Earth surface systems (ESS) develop and change over time. Theories of geomorphic, soil, hydrologic, and ecosystem evolution call for either (or both) increasing or decreasing complexity as they develop. Thus, key questions across the Earth and environmental sciences involve the extent to which ESS become more or less varied and complex as they evolve. Here the concern is with complexity with respect to the evolutionary or successional pattern or pathway itself, rather than complexity of the individual elements. Thus, the concern is with the properties of, for instance, a phylogenetic tree rather than complexity of the taxa represented, or of the network of state transitions in geomorphic evolution or vegetation change rather than properties of the landforms or vegetation communities involved. The question is thus not whether, for example, ecosystems or soils become more complex over time, but whether the network of transitions among system states becomes more or less complex. This is addressed by applying algebraic graph theory methods to some archetype (representative idealized) patterns of ESS development to assess structural complexity, network irregularity, and historical contingency properties.

This paper extends previous work exploring complexity of temporal trends in ESS represented as graphs or networks. Earlier papers sought to measure the degree of historical contingency in ESS (Phillips 2013a) and to quantify the robustness of chronosequences (Phillips 2015). In the first instance, the networks were based on the idea of inheritance between temporal episodes—for example, given a set of relationships among geomorphic factors in a river, those that determine or influence the same factor in a subsequent developmental episode (Phillips 2013a). In the second, chronosequences were used to define system states (stages or phases of the sequence) and possible transitions among them based on observed or inferred changes among states. The path stability (degree to which developmental trajectories are sensitive to disturbance) of the derived networks was determined (Phillips 2015). This paper expands on the previous work by considering the actual network of changes over time and how complexity might changes as systems continue to evolve.

Beyond the general scientific urge to quantify and the temptation to measure something because it can be measured, there are compelling reasons to assess the complexity of evolutionary sequences. Most obviously, if the complexity of such sequences is known or can be computed, questions of the evolution of complexity can be addressed once the (or an) appropriate sequential model has been identified. For several decades it has been widely recognized that simple progress-to-equilibrium models are incomplete and not always applicable (Scheidegger 1983; DeAngelis and Waterhouse 1987; Montgomery 1989; Phillips 1992), but the understanding of state transitions in ESS is still rudimentary in many cases (Huttl et al. 2014). Further, as ESS evolve they “compute intrinsically and store information” (Still et al. 2010). Information and complexity are closely related in a statistical sense, but methods for estimating stored information in historical data are currently restricted mainly to relatively long time series of integer or ratio-level numerical data (Still et al. 2010). As entropy (and thus information) is directly related to graph spectral properties described below (Geller et al. 2012), the approach developed here could be useful in assessing the information stored in an evolutionary sequence.

The questions addressed here are particularly relevant for the study of responses to climate change and direct human impacts. For example, in a review of ecological state-and-transition models, Twidwell et al. (2013) found an overemphasis on historical climax plant communities and an assumption that these are optimal and that changes indicate degradation (at least within the U.S. Department of Agriculture, which has the world’s largest database of STMs). Twidwell et al. (2013) also identified an overemphasis on certain drivers (e.g., grazing) and a failure to consider climate change. Svenning and Sandel (2013) analyzed disequilibrium vegetation dynamics under future climate change and noted that predictive studies have focused on equilibrium endpoints with little consideration of historical trajectories. These reviews suggest the need for a better appreciation of varying developmental pathways and their complexity.

In contrast to approaches that implicitly or explicitly assume convergent development, emerging studies on the role of initial conditions in ESS development assume more homogeneous conditions in early stages, with increasing heterogeneity over time. In their review of the role of initial development processes as key factors in landscape development, Raab et al. (2012) identified a common pattern of less complexity initially, with increasing complexity over time due to sensitivity to initial conditions and amplification of variations. Biber et al. (2013) study of interrelationships among substrate, topography, and vegetation in early stages of ESS development also assumed increasing complexity. Raab et al. (2012) also noted the importance of historical information for understanding the contemporary state of an environmental system.

The problem of measuring complexity in evolutionary sequences is also relevant to historical reconstruction. Due to the incompleteness of the stratigraphic record, stratigraphy has been referred to as a set of frozen accidents (Miall 2015) with more gap than record (Ager 1973). The same applies to paleoenvironmental data more generally. Spatial records may also contain significant gaps, as in, for example, nugget effects in spatial data. Miall and Miall (2001) and Bailey (1998) have highlighted some of the problems and issues associated with applying particular conceptual models of sedimentary sequences, and argued for consideration of more complex possibilities. Analysis of historical sequences as networks adds to our understanding of their phenomenology and instrumentality. The ability to assess their complexity may aid in choosing appropriate frameworks for filling gaps (if, e.g., the goal is to choose the least complex of competing models) or assessing the informational implications of such decisions.

In general, complexity is the state or quality of being complex, and complex means consisting of many different and connected parts. Complexity implies complications, intricacies, and difficulties. Scientific definitions are not inconsistent with these ideas, but are more specific and nuanced. In many cases complexity in ESS is understood in the context of contemporary complexity science, implying coupled dynamics over a broad range of scales and/or showing emergent or self-organized behavior. A 2007 volume, Complexity in Geomorphology (Murray and Fonstad 2007), for example, is firmly in this category, as is Phillips (1998) study of complexity in pedology, and a number of works on ecological complexity (Burkett et al. 2005).

However, consistent but broader perspectives also exist, such as the aims and scope of the journal Ecological Complexity (http://www.journals.elsevier.com/ecological-complexity/), for instance, along with Richards (2002) discussion of complexity in physical geography. Cadenasso et al. (2006) presented a view of ecosystem complexity specifically designed to incorporate both nonlinear dynamical systems and complexity science aspects, and the broader, more general ecological complexity evident to field scientists. They identify the critical dimensions of complexity as heterogeneity, connectivity, and history. Heterogeneity incorporates structural complexity, spatial variability and heterogeneity, and connectivity reflects the interconnectedness of system components. History relates to historical contingency; the extent to which relationships extend beyond direct, contemporary links, involving phenomena such as lag, memory, and legacy effects. Cadenasso et al. (2006) also recognize the related issue of complicatedness; how large a system is and how many components it contains. In this paper graph complexity, network (ir)regularity, and inferential synchronization are assessed. While the measures do not map precisely onto Cadenasso et al.’s criteria, they do reflect, respectively, structural complexity, network heterogeneity, and historical contingency. Connectivity influences all three measures.

2 Background: Evolutionary Pathways in Earth Surface Systems

Beyond the obvious coexistence and overlap among landforms, soils, and ecosystems, theoretical frameworks in geomorphology, pedology, and ecology have themselves coevolved, both historically (Osterkamp and Hupp 1996) and recently (Thoms et al. 2007; Butler and Sawyer 2012). Thus all three perspectives are briefly reviewed here.

2.1 Geomorphology

Phillips (2014) analyzed geomorphic development involving decreasing or increasing variability in terms of convergent vs. divergent development. Convergence involves decreased amplitude of variations, increased spatial isotropy, and decreasing complexity. For instance, convergent landform development includes topographic evolution involving decreasing relief, and weathering that leads to smoothing of rough, irregular rock surfaces. Divergence results in increased average amplitudes of variations, amplification of initial differences, and increasing spatial complexity. Relief-increasing topographic evolution and erosional dissection of initially more uniform surfaces are examples. Steady-state, with no net convergence or divergence, may also occur in some geomorphic systems. Phillips (2014) argued that both convergent and divergent modes are common in real landscapes and showed that switches between convergent and divergent trends often occur due to a common structure in geomorphic systems which leads to dynamically unstable interactions and divergence in earlier stages of development. Later, as thresholds are approached, the systems become dynamically stable and switch to convergent modes.

Debates on divergent vs. convergent evolution have existed nearly as long as geomorphology itself. This is best illustrated by the classic nineteenth and twentieth century debates on the increase or decrease of relief during topographic evolution (Thorn 1988; Goudie 2011), though this and similar problems have rarely been expressed explicitly in terms of convergence and divergence. Exceptions include Scheidegger (1983), Johnson and Watson-Stegner (1987), Johnson et al. (1987), Twidale (1991), Phillips (1995), Phillips (2002), Gournellos (1997), and Gunnell and Louchet (2000). From the 1990s, studies of deterministic chaos, dynamical instability, and other forms of nonlinear complexity in geomorphic systems showed that divergent development occurs frequently in a variety of geomorphic phenomena, and at a range of spatial and temporal scales (Elverfeldt 2012).

Dynamic equilibrium-based theories of landscape evolution, that emerged in the early twentieth century, gained prominence in the 1960s, and arguably remain dominant today (Gregory and Lewin 2014) postulate convergent development. Even before the advent of nonlinear approaches, however, classic theories of (Davis 1899, 1902; Penck 1924) allowed for either divergent or convergent development of topography. These depend on the stage in a cycle of erosion (Davis) or the relative rates of uplift vs. denudation (Penck).

On more restricted spatial and temporal scales understandings of geomorphic development have also been expanded from linear sequences or simple cycles to more varied patterns of landform and landscape change. This is best illustrated by the supplementation of linear stream channel evolution models with constructs allowing for multiple pathways (Phillips 2013b; Van Dyke 2013, 2016).

2.2 Pedology

Traditionally, conceptual models of pedogenesis focused on convergent pathways, such as development of climax soils, where, for example, properties inherited from parent material become less prominent and those associated with the regional climate more important (Dokuchaev 1883; Marbut 1923; Jenny 1941). Broad-scale climate–soil correlations and soil–landscape relationships support this notion, but at more local scales divergent evolution has been increasingly recognized.

At the landscape scale, some chronosequence studies indicate divergent pedogenesis, where soil variability and diversity increases over time (Phillips 1993, 2001a; Barrett and Schaetzl 1993; Barrett 2001; Saldana and Ibanez 2004). Other studies at this scale show divergent pedogenesis associated with dynamical instabilities in topographic/soil coevolution, vertical translocation processes, and persistence of pedological impacts of disturbances (Ibanez et al. 1994; Schaetzl et al. 2006; Toomanian et al. 2006; Samonil et al. 2014, 2015; Valtera et al. 2015). Some pedon-scale studies also show dynamically unstable trends toward increasing variability (Phillips 2000, 2001b; Montagne et al. 2013) that imply non-convergent development at broader scales.

Both convergent and divergent pathways of pedogenesis are common, at different spatial scales, times or stages of soil landscape evolution, or contingent on specific factors such as thickness of the weathering mantle (Johnson et al. 1987; Gracheva et al. 2001; Temme 2015).

2.3 Ecology

Foundational theories of ecological succession from the late nineteenth century and early twentieth century are based on a monotonic linear progression toward a stable climax community (Cowles 1899; Clements 1916). Later, conceptual frameworks allowing for more complex and variable successional patterns were introduced (Gersmehl 1976; Cattelino et al. 1979; Westoby et al. 1989). State-and-transition models, while motivated by and often associated with alternative stable state concepts, are a general tool for describing and predicting ecological state changes that can accommodate virtually any pathway (Briske et al. 2005; Bestelmeyer et al. 2009; Phillips 2011). Recent reviews and syntheses of succession theories are given by Mori (2011) and Pulsford (2014). These make it clear that successional trends or ecological change more generally may be linear (or cyclical, when disturbance resets the system), convergent, divergent, or characterized by various possible transitions among system states.

Different patterns may also be evident at different scales within the same system. For example, in an old-growth forest (Woods 2007) found convergence in some habitats, but not across habitats, with successional dynamics structured at the habitat-patch scale.

Scale dependence and both convergent and divergent paths within the same system were also found by Dini-Andreote et al. (2015), who used a chronosequence to study the balance of stochastic and deterministic processes in microbial succession. They identified several pathways that involve different roles of homogeneous vs. heterogeneous selection pressure, and thus either convergent or divergent paths.

In evolutionary ecology, a key issue involves niche differentiation vs. niche convergence. Classic niche theory, based on the former, predicts competing species will evolve to use different resources and interact less. Many examples of niche differentiation exist; a recent one that specifically links partitioning to soils and geological controls is Kohout et al. (2015) study of mycorhyzzal communities. Niche-convergence ideas, by contrast, predict that species evolve to use similar resources and increase their interactions. Aarsen (1983) proposed an evolutionary theory of coexistence, particularly applicable to plants, involving not only natural selection for niche differentiation, but also selection for competitive combining ability. The latter involves reciprocal selective effects in which approximately equal competitive advantages are maintained. Empirical examples of niche convergence include Ackerly (2004) reconstructions of leaf evolution in California chaparral vegetation and Elias et al. (2008) studies of mutualistic interactions in butterflies. Niche convergence is also linked to neutral theories of community assembly (Hubbell 2006).

However, the issue is not a simple matter of niche differentiation and (or versus) niche convergence. Miller et al. (2014) followed the evolution of four species of Protozoa during succession and found that during evolution in multispecies systems weak competitors evolved to be stronger, while strong competitors evolved to become weaker. This does not conform to expectations of either niche partitioning or convergence, implying a need to rethink the roles of competition and evolution in structuring communities.

Additionally, there is niche construction, whereby organisms modify the abiotic environment to create or expand niches for themselves and/or other organisms (Odling-Smee et al. 2003; Matthews et al. 2014). The interactions among niche partitioning, convergence, and construction, evolution, and ecosystem functions for plants are discussed by Thorpe et al. (2011). In particular, they highlight potential effects of histories of coexistence within a region.

Niche construction, differentiation, and convergence have fundamentally different implications with respect to evolutionary trajectories and complexity. Construction indicates the possible expansion of state space, while differentiation and convergence, respectively, imply increasing or decreasing niche complexity within a existing state space.

3 Assessing Complexity in ESS Evolution

From the overview above it is clear that evolution of ESS may follow linear, cyclical, convergent, divergent, or other pathways. Linear trends or convergence toward a stable climax or steady-state imply simplification and reduced richness (defined as the number of, e.g., soil series, vegetation communities, landform types, etc.) over time. Divergence signifies increasing richness and diversification.

However, other patterns of change over time are less clear with respect to changes in richness over time. Further, richness is only one aspect of complexity. Others include evenness (relative abundance of types or system states), the network of possible transitions among states, and the degree of historical contingency. Richness/evenness, network of possible transitions, and contingency correspond to the heterogeneity, connectivity, and historical aspects of complexity identified by Cadenasso et al. (2006). A theoretical framework for assessing complexity of evolutionary sequences or patterns represented as networks is outlined below.

4 Theory

A chronosequence, successional pattern, or other historical sequence can be treated as a network. Each node in the network represents a system state, such as a landform type, vegetation community, soil type, or developmental stage. The network nodes are connected by historical patterns of transition among states, which may be established by observation, historical reconstruction, theory, or experiments. A network may include transformations back to a previously existing state, and can be represented as a directed graph, where states that occur more than once are represented as a single node (Fig. 1).

Fig. 1
figure 1

Evolutionary sequence (pedogenetic pathways) of soil landscapes in the coastal plain of North Carolina, USA, shown as a directed graph. (Derived from Phillips 2015)

Full size image

The graph has an \(N \times N \) adjacency matrix A, where n is the number of system states or graph nodes. The elements of A are zero if the state on the vertical axis (rows) cannot or does not transition to the corresponding state on the horizontal axis (columns), and 1 otherwise, with zeros on the diagonal. These transitions are represented by edges (links) in the graph. This is an unweighted, unsigned directed graph. Weighted graphs may have entries other than 0, 1 to represent varying probabilities of transitions. Directed graphs of this type may have entries of \(-1\), 0, 1 depending on whether existence of the row state inhibits, has no effect on, or promotes transition to the column state. Phillips (2015) presented a method for analyzing the path stability or robustness of chronosequences represented by a signed digraph. Here the unsigned form is used for maximum generality.

The adjacency matrix has N eigenvalues \(\lambda \), such that \(\lambda _{1} \ge \lambda _{2} \ge \cdots \lambda _{\mathrm{N}}\). The largest eigenvalue \(\lambda _{1}\) is the graph spectral radius and is widely used in algebraic graph theory as a measure of the complexity of graphs and networks (Biggs 1994). In general, spectral radius remains constant or increases with network size (N) and increases with the number of edges or links m. The spectral radius is sensitive to the number of cycles within a graph (paths that start and end at the same node) and has thus been used to measure the complexity of food webs, for example (Fath and Haines 2001). For networks of contemporaneously interacting agents, \(\lambda _{1}\) is related to the presence or absence of coherence in those interactions (Restrepo et al. 2006).

Spectral radius is related to the maximum in- and out-degrees of the graph nodes (the number of links ending and starting, respectively, at a node). Kwapisz (1996) showed that the upper bound for the spectral radius of a directed graph is the geometric mean of the maximum in-degree (\({d}^{-}_{\mathrm{max}})\) and maximum out-degree (\({d}^{+}_{\mathrm{max}})\)

$$\begin{aligned} \lambda _{1} \le \left[ {( {{d}^{-}_{\mathrm{max}} })( {{d}^+_\mathrm{max}} )} \right] ^{0.5} \end{aligned}$$
(1)

Graph regularity is the extent to which graph nodes vary in their degree (number of in- and out-links); in a regular graph the degrees of all nodes or vertices are equal. Graph regularity is important in this context because it indicates the extent to which a subgraph is representative of the larger graph structure. Because the evolutionary patterns of ESS are sometimes imperfectly known (or incomplete, for systems still developing), this relates to whether an incomplete observed evolutionary network may be representative. Elphick and Wocjan (2014) developed a spectral measure of graph irregularity

$$\begin{aligned} \beta =\lambda _1 /d, \end{aligned}$$
(2)

where d is the mean vertex degree. A graph with \(\beta = 1\) has the highest degree of subgraph representativeness of the entire graph. \(\beta>\) 1 reflects increasing degree of a small number of nodes, with other nodes remaining much less connected. \(\beta < 1\) indicates that node connectedness varies across the network.

The spectral radius and irregularity index provide quite different information, despite the dependence of \(\beta \) on \(\lambda _{1}\). For example, a fully connected graph (any state can transition to any other) has the highest possible spectral radius for a given N, but a \(\beta \) value of 1, as it is a regular graph. Thus, while a fully connected is the most complex structure for a graph of a given size, any subgraph is representative of the overall structure.

4.1 Historical Contingency

A key element of complexity is historical contingency (Cadenasso et al. 2006; Phillips 2013a). Historical contingency can be assessed based on algebraic connectivity. Algebraic connectivity of graph \(G(\mu (G))\) is a measure a graph synchronization: the extent to which nodes or elements of a network act or change simultaneously, or in a predictable sequence. Convergence properties of a network are also dependent on algebraic connectivity. Literal synchronization is not relevant to historical or evolutionary graphs, but Phillips (2013a) generalized graph synchronization to the notion of inferential synchronization—the extent to which observations or inferences at one point in the network can be applied to components elsewhere in the graph (synchronization terminology is retained because of its wide use in the graph and network theory literature). In a graph representing temporal stages of development, a high degree of inferential synchronization would indicate a low degree of historical contingency, as one part of the graph (i.e., a subgraph) would be representative of network dynamics in another portion of the graph.

Fiedler (1973) showed that the second smallest eigenvalue of the Laplacian matrix \((\lambda (L)_{N-1} )\) of an undirected graph is related to convergence and synchronization properties, and coined the term algebraic connectivity. The Laplacian of the adjacency matrix is obtained by

$$\begin{aligned} {\varvec{L=D-A}}, \end{aligned}$$
(3)

where \({\varvec{D}}\) is the degree matrix, with the degree of each node on the diagonal and zeros otherwise.

The second smallest Laplacian eigenvalue of directed graphs has also been used to indicate synchronization and convergence (Merris 1994; Lafferriere et al. 2004). Wu 2005 extended Fiedler’s algebraic connectivity to directed graphs, acknowledging that this generalization can be direct; that is, defining algebraic connectivity for directed graphs as \(\lambda (L)_{N-1.}\) However, Wu (2005) and Molitierno (2006) developed alternative algebraic connectivity measures for directed graphs that are related, but not equal, to the second smallest Laplacian eigenvalue. Here \(\lambda ( L)_{N-1}\) is used directly to indicate algebraic connectivity.

5 Evolutionary Archetypes

Based on Eqs. (1) and (2), the maximum spectral radius and irregularity index can be calculated for some archetypal graph structures that represent evolutionary sequences in ESS, along with the algebraic connectivity and the rate at which N, m increase with length of the historical sequence. These archetypes include linear, cyclical, convergent, divergent, and bifurcating tree structures.

Linear sequences are represented by classic monotonic, monoclimax succession models. A pioneer community succeeds to one or more intermediate serial stages, culminating in the climax community. Some fluvial channel evolution models also have this form (Van Dyke 2013), as well as pedogenesis towards a climax soil at the pedon scale. A Davisian cycle from original uplift to peneplain, before renewal by new uplift (Davis 1899, 1902) is also a linear or chain-type graph.

Cycle graphs are linear sequences, plus a return to the starting point. In addition to the cycle of erosion, ecological succession with disturbances that can reset the sequence can be treated as cycles. The sequence stratigraphy conceptual model for interpreting sedimentary sequences is also cyclical (Miall and Miall 2001). Alternative stable state models, most of which involve two stable states, are essentially cycles of \(N =2.\)

In a convergent graph, multiple initial states converge (in the simplest form, in one step) to a single attractor state. This could correspond, for example, to a transition where a major disturbance such as a massive deposition event or volcanic eruption transforms a variety of existing topographic or landform states to a single state.

Divergent graphs involve transitions to multiple possible states from a single starting point (in the simplest case), or from a small number to a larger number of states. Dynamical instability and chaos, and models based thereon, indicate divergent sequences for landscape, landform, and soil evolution. Biological evolution by speciation is also divergent, as is niche differentiation. Patch-gap dynamics in ecology (Forman 1995) also imply divergent evolution.

Divergent patterns may involve simple radiation (transition from a single starting point to multiple alternative states in a single step), or sequential stages of bifurcation, which produces a dendritic or tree graph. Some models of chaotic dynamics are based on patterns of successive bifurcations (May 1973; Hui and Li 2003), and phylogenetic trees in evolutionary biology illustrate this structure. A reverse bifurcation (convergence of nodes two at a time) is also a possible structure for a convergent evolutionary graph. For clarity, the one-step many-to-one or one-to-many state transitions will be referred to as simple convergent or divergent patterns to distinguish them from tree-type graphs. The fully connected evolutionary graph exists where history (or theory) indicates that a direct transition between any two known states is possible (where such transitions are also equally probable, this would also constitute a random transition pattern). This is useful not only as a reference structure, but some ecological state-and-transition models are also fully connected (Twidwell et al. 2013).

5.1 Complicatedness

If the developmental sequence of an ESS is characterized by q events, episodes, transitions, or phases (\(q=1,2,3,\ldots \)) we can determine changes in complicatedness (N, m), which influence spectral radius and structural complexity \((\lambda _1)\), irregularity \(({\upbeta })\), and historical contingency and inferential synchronization \((\mu (G))\) over time (i.e., as q increases).

Linear and cycle type patterns become more complicated in direct proportion to the length of the sequence, while bifurcating and other branching patterns increase their nodes and links at an exponential rate (Table 1). Simple convergence and divergence are special cases here, as complicatedness clearly decreases or increases over time, respectively, and the number of nodes is unrelated to q. For \(q>{1}\), the simple structures become n-furcating patterns.

Table 1 Number of nodes (N) and links (m) in relation to the number of events or stages (q) in an evolutionary sequence for archetypal graph structures
Full size table

For the fully connected case, if we assume that new states are created by or during the historical transitions, and considering only actual (as opposed to potential or hypothetical) transitions, then \(q \ge N^{2}- N\) to produce a given N.

5.2 Structural complexity

Table 2 shows the maximum spectral radius for the archetypal graph structures described above. The last row generalizes the bifurcating pattern to sequences with n potential forks at each step (n-furcations). Fully connected and simple divergent and convergent graph types are sensitive to the number of system states, though the former is more strongly so, with linear dependence vs. increasing as the square root of N. The bifurcating pattern is more complex than the linear or cyclical, but in all cases the spectral radius is insensitive to the length of the sequence. Note that just as the simple convergent and divergent graphs have identical spectral radii for a given N, so also would convergent patterns with the same topology have the same \({\varvec{\lambda }}_1\) as the divergent forking types.

Structural complexity of the historical sequence, as indicated by the spectral radius, is constant with increasing q for all the archetypical patterns except fully connected, for which \(\lambda _1 \) increases linearly with N, and the simple converging/diverging patterns, where \(\lambda _1\) increases as the square root of N. Complexity increases with the number of possible splits at each historical transition.

Table 2 Maximum spectral radius for archetypal graph structures
Full size table

5.3 Graph Irregularity

The irregularity indices are shown in Table 3. The fully connected graph is regular, and \(\beta \) = 1. In simple divergent or convergent graphs \(\beta \) increases as \( N^{0.5}\), while the linear graph asymptotically approaches 0.5 as N increases, the constant value for a cycle of any length.

Table 3 Maximum irregularity index for archetypal graph structures
Full size table

For n-furcating trends, N increases as a power function of the number of steps in the sequence n(b)

$$\begin{aligned} N=( {n^{n( b)-1}-1})/( {n-1}). \end{aligned}$$
(4)

Mean degree is then

$$\begin{aligned} d=[ {n+( {n+1})}]/N. \end{aligned}$$
(5)

Thus, for a bifurcating sequence \(\beta \) falls quickly below 1 as n(b) increases, asymptotically approaching a value of \(0.4713333{\ldots }(=1.414/3)\).

The irregularity index is constant for cycle and fully connected graphs of all sizes (0.5, 1.0, respectively). \(\upbeta \) decreases with size and number of steps in splitting graph types, converging toward \(n^{0.5}/( {n+1}) \quad . \)The simple convergent and divergent sequences increase as \(N^{0.5}.\)

5.4 Historical contingency

Inferential synchronization is directly, and historical contingency inversely, related to \(\mu (G)\) (Phillips 2013a). Lower algebraic connectivity indicates a high degree of historical contingency and path dependence. All forms are equal in this regard except for the cycle, where \(\mu (G)\) decreases as a function of N, and the fully connected, which increases with N. Though the cycle algebraic connectivity declines with m, it is > 1, which it asymptotically approaches. Thus fully connected graphs have the lowest degree of historical contingency, and linear, convergent, divergent, and forking graph types have maximum historical contingency. Cycles are intermediate, but closer to the latter, with \(\mu ( G)<1.5\,\text{ for }\,N>6.\)

6 Graph Maturation

The sequences represented by evolutionary graphs develop over time. Referring to the appearance of each state or form as a historical transition, with a one-state starting point and a single transition only one form is possible, an \(A \rightarrow B\) linear graph. With two transitions an \(N =3\) linear graph is possible, or an \(N =2\) cycle. With further transitions, many more possible graph structures emerge. An evolutionary graph may be called mature when enough transitions have occurred for the graph structure to become evident. For example, an ecological state-and-transition model for rangelands could be considered mature when all plausible ecological states relevant to the management context have been identified. Or, a phylogenetic tree could be considered mature when enough nodes and branches have been identified to define its overall branching structure.

Starting with a linear sequence, several possibilities emerge, alone or in combinations or sequences: (1) indefinite continuation of the linear sequence; (2) progression of the linear sequence to a persistent attractor or sink state; (3) divergent branching; (4) transition from a linear sequence to a cycle; and (5) graph articulation by returning to previously existing states (other than the cyclical return to an initial state). With a multiple-state starting point, or following development of multiple states, convergent branching is also possible.

What are the complexity implications of these trends? As a linear sequence gets longer it becomes more complicated, but its low structural complexity does not change; nor does the algebraic connectivity. The irregularity index decreases toward 0.5. If the sequence repeats (becomes a cycle) the spectral radius remains the same, and the irregularity index is constant at 0.5. The algebraic connectivity decreases relative to a linear sequence of the same N. The cycle is slightly more complicated than the linear trend of the same N, but once established this does not change.

Development of forks or divergences in a sequence increases complicatedness, structural complexity, and irregularity and decreases algebraic connectivity (thus increasing historical contingency). These changes compared to linear sequences or cycles are fairly intuitively obvious with respect to increases in N, m and structural complexity (Table 4). Historical contingency increases slightly relative to a cycle and is the same as for a linear sequence. The decrease in \(\beta \) indicates a decline in the extent to which a subset of the graph (e.g., an incomplete observation of the evolutionary sequence) is representative of the overall pattern.

Graph maturation may occur as every relevant state has occurred and multiple transitions between them are observed. The addition of one or more transitions to previously existing states other than a return to the initial state increases \(\lambda _{1}\) and decreases \(\beta \) relative to a cycle. Though N does not increase in this scenario, m does, and thus the sequence becomes more complicated. Algebraic connectivity increases. If new transitions continue to add new links (progressing toward mesh structures and full connectivity), this further increases \(\lambda _{1}\) and pushes the irregularity index toward unity. Algebraic connectivity increases, and thus historical contingency declines.

Diverging graphs and those more highly connected than linear sequences and cycles are more complex than the latter. However, they differ from each other with respect to different aspects of complexity. More highly connected structures have greater structural complexity, as indicated by the spectral radius. However, they also have greater algebraic connectivity, indicating a lower degree of historical contingency. Once the network has matured, observations, analyses, and models are more representative of long-term behavior than for graphs with lower \(\mu (G)\) and thus lower inferential synchronization. Further, the forking structures have irregularity indices farther from 1, indicating higher irregularity and less ability to infer graph behavior from subgraphs.

An important general point is that although the maximum possible spectral radius increases with N, the actual complexity indicated by \(\lambda _{1}\) does not necessarily, depending on the connection patterns. Thus, while addition of new nodes may increase the complicatedness of a network, other aspects of complexity may increase, decrease, or remain unchanged.

7 Examples

There are few examples of network or graph-based analyses of evolutionary, developmental, successional or chronosequences in geosciences (Heckmann et al. 2015; Phillips et al. 2015), However, network-based methods have been applied to identification of key transitions, historical contingency, and memory in time series and historical data in climatology, paleoclimatology, and seismology (Marwan et al. 2009; Donges et al. 2011; Donner and Donges 2012; Telesca and Lovallo 2012; Radebach 2013). Phillips (2015) analyzed the network of possible pedological transitions revealed in a soil chronosequence via graph theory, but did not analyze the temporal network of transitions. Two empirical examples are given below.

Fig. 2
figure 2

Forest succession in the North Carolina coastal plain. a The traditional successional model (linear sequence), with the dotted line indicating possible resetting of the sequence by large disturbances (cycle). b Successional pathways where frequent or occasional fires occur

Full size image
Table 4 Algebraic connectivity for archetype graph structures
Full size table

7.1 Coastal Plain Forest Succession

In the southeastern US coastal plain, the general successional pathway on abandoned cropland or other situations where pre-existing forest has been removed from upland sites, and where fire is excluded, begins with a variety of pioneers and early successional species. Pines (Pinus spp.) eventually become dominant, forming a canopy. The pines are shade-intolerant, so as the canopy develops hardwoods become established, and a mixed pine/hardwood forest is the next seral stage. Hardwoods eventually become dominant, and the climax community is a variant of the southern mixed hardwood forest. Forest succession in this region is reviewed by Ware et al. (1993) and Batista and Platt (1977).

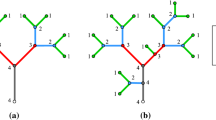
The historical role of disturbance by recurrent fire has been a subject of some debate, but sources above agree that without fire the successional pattern is represented by the linear sequence in Fig. 2a, which could also be construed as a cycle if one allows for the possibility of rare large fires, tropical cyclone or tornado events, or logging to return vegetation to the pioneer stage. Allowing for more frequent fires, however, leads to the graph of Fig. 2b, where fire favors pines, with the specific transitions depending on fire severity and pre-fire vegetation (4).

Table 5 Properties of graphs represented in a linear succession without, and successional cycle with, the dashed link and b state transitions with fire effects
Full size table

Complexity indicators are shown in Table 5. Including fire effects increases the structural complexity, and reduces the historical contingency, as vegetation depends more on the time since the most recent fire than stage along a monotonic pathway. The irregularity index > 1 represents the increasing concentration of edges in the lower part of Fig. 2b, especially the mixed hardwood climax.

7.2 Alluvial Channels

The classical channel evolution model (CEM) for incised alluvial channels is a linear sequence of six stages (or could be construed as an \(N =5\) cycle, as the 6\(\mathrm{th}\) stage is similar to the initial state). Phillips (2013b) developed a flow-channel fitness model that, when interpreted as a state-and-transition model (STM), can be represented as in Fig. 3, with \(N = 5, m = 12\).

Fig. 3
figure 3

State-and-transition model for alluvial channel changes. Underfit and overfit refer, respectively, to channels that are too large or small relative to a reference discharge (Phillips 2013b)

Full size image
Fig. 4
figure 4

Complexity indicators for linear CEM, CEM treated as a cycle, and STM in Fig. 3. Spectral radius values are, respectively, 1.000, 1.000, and 2.562; irregularity indices are 0.599, 0.500, and 1.067; and algebraic connectivity is 1.000, 1.000, and 3.000

Full size image

The contrast in \(\lambda _{1},\beta , \mathrm{and} \mu (G)\) can be seen in Fig. 4. The increase in spectral radius reflects the greatly increased structural complexity, and the threefold increase in algebraic connectivity indicates the reduced historical contingency. This is consistent with the idea that channel change responds to changes in sediment supply and transport capacity rather than simply either developing toward or maintaining a steady-state equilibrium condition. The irregularity index indicates that a subgraph of the STM is more representative of the system than a subset of the CEM.

If an alluvial channel may also be either bed or suspended load dominated under different scenarios, and thus aggradation and degradation potentially dominated by either width or depth adjustments, then Fig. 3 can be taken as a STM with \(N=7\) and \(m = 32\) (Phillips 2013b). In this case \(\lambda _{1}= 4.702; \beta =0.514\); and \(\mu (G)\)= 6. Thus complexity and inferential synchronization increase substantially, while the irregularity index declines, reflecting the increasing relative density of links associated with the aggradation and degradation states.

8 Discussion

As mentioned in the introduction, Twidwell et al. (2013) found that ecological state-and-transition models overemphasize historical climax communities and certain drivers of change. With respect to vegetation response to climate change, Svenning and Sandel (2013) also noted an overemphasis on equilibrium endpoints, and under-appreciation of historical trajectories. In both cases rectifying those shortcomings will almost certainly result in increasing articulation of transition networks, which the results here show will lead to increases in structural complexity and regularity, and decreases in historical contingency.

Recent studies on the role of initial conditions in ESS development assume more homogeneous conditions in early stages, with increasing heterogeneity over time (Raab et al. 2012; Biber et al. 2013). Structural complexity for any form of divergence is greater than for a linear or cycle trend, as is graph irregularity. Historical contingency remains high, as algebraic connectivity in simple or forking divergent graphs is the same as in linear graphs, and less than that of cycles.

With respect to stratigraphic or paleoenvironmental sequences, a fundamental relationship exists between complexity and interpretation. Bailey (1998), for example, proposed an alternative approach to stratigraphic analysis based not on sequence stratigraphy (a cyclic model), but on complex, potentially chaotic behaviors. Thus, observed gaps in or deviations from the expected sequence are not (without independent evidence) assumed to be due to gaps in the record, but are accepted as representing transitions as they actually occurred. This inevitably converts (the graph representation of) the sequence from a simple cycle to a more complex network.

With respect to divergent vs. convergent evolution in geomorphology, the analyses here show that diverging vs. converging patterns of the same size (N, m) and topology have no differences with respect to complexity. In this case complexity change is dependent on directionality of the directed graph, so that converging patterns result in reduced richness and fewer potential outcomes, and diverging patterns the opposite. The convergent–divergent mode switching found by Phillips (2014) would tend to increase ESS system complicatedness and structural complexity, decrease irregularity, and increase algebraic connectivity. Similar outcomes with respect to evolutionary network complexity occur as linear or cyclical sequence models are expanded and elaborated to more strongly connected state-and-transition type models. Compare, for example, the linear fluvial biogeomorphic succession model of Corenblit et al. (2009) with the state transitions identified by Rountree et al. (2000), or the classic linear channel evolution models compared to more recent multi-path CEMs (Van Dyke 2013, 2016).

Debates regarding evolutionary pathways of soil formation have also highlighted convergent and (or versus) divergent evolution, so implications are similar to those for geomorphology of this regard. Still to be resolved, however, are the scale-contingent differences in divergence or divergence in pedogenesis often encountered, and how they may affect overall complexity. Similar issues arise in ecology and geomorphology, though they have not been as widely discussed as in pedology. For niche convergence vs. partitioning, the implications are as discussed for divergent vs. convergent trends above. Where niche construction occurs, however, it would in general tend to increase spectral radius and algebraic connectivity, with changes in irregularity dependent on the relative changes in \(\lambda _{1}\) and d.

In ecology, binary alternative stable state models are often linked to ideas from complexity science. However, in graph terms these are essentially N = 2 cycles and thus are no more complex than linear or cyclical succession models. Where there are >2 alternative states, however, as in many ecological STMs, the graph structural complexity increases accordingly.

Graph maturation requires that an evolutionary sequence has been completed, or continued long enough for its structural pattern to fully emerge, and that observations of state changes are sufficient to reflect the pattern. For immature graphs—those that are still developing or incompletely observed—complicatedness and structural complexity cannot decrease, though they may remain constant. Trends that develop splits or forks will increase in overall complexity and a decrease in the irregularity index, while the algebraic connectivity remains unchanged. Trends that result in denser interconnections among graph nodes with generally increase complexity and algebraic connectivity.

9 Conclusions

Evolutionary trends and historical trajectories in ESS can be considered as a network of transitions between system states, stages, or conditions. By representing these networks as directed graphs, techniques from algebraic graph theory can be used to quantify several aspects of complexity. These were applied to several archetypal structures of ESS historical trajectories: linear sequences, cycles, simple convergent and divergent, and splitting or forking (bifurcating or n-furcating).

The spectral radius of the graph adjacency matrix is a measure of graph structural complexity, and is highest for fully connected graphs, lowest for linear sequential and cyclic graphs, and intermediate for various divergent and convergent patterns. The irregularity index \(\beta \) (equal to the ratio of spectral radius to mean degree) represents the extent to which a subgraph of the network (perhaps representing censored or incomplete observation of the evolutionary sequence) is representative of the full graph. Fully connected graphs have \(\beta \) = 1, indicating maximum regularity. Lower values, such as those found in linear and cycle patterns, are associated with low spectral radii, while higher values, such as those found in divergent and convergent patterns, are linked to a single or few highly connected nodes with other poorly connected nodes. Algebraic connectivity (\(\mu (G)\)) indicates graph inferential synchronization and is inversely related to historical contingency. The highest values and lowest historical contingency are associated with fully connected and strongly connected mesh graphs, whereas splitting or forking structures and linear sequences all have \(\mu (G)\) = 1, with cycles slightly higher.

ESS evolve, and so do their directed graphs. Starting with a linear sequence, divergent branching, cycles, and graph articulation by transitions back to previously existing states can occur. None of these trends reduces complicatedness or structural stability, which can only remain constant or increase. Algebraic connectivity may increase, thus decreasing historical contingency.

Improving some of the perceived shortcomings in ecological succession and state transition models, as well as conceptual models of change in geomorphic systems, generally involves further elaborating possible state changes (graph links), thus likely pushing our understanding of those systems toward more structurally complex but less historically contingent constructs. These are illustrated by two applications, to forest succession and alluvial channel change.

Many issues related to evolution of geomorphic, pedologic, and ecological systems involve the relative prevalence of convergent and (or versus) divergent trends. Diverging vs. converging graphs of the same size and topology have no differences with respect to complexity. In this case complexity change is dependent on directionality of the directed graph, so that converging patterns result in reduced richness and fewer potential outcomes, and diverging patterns the opposite. Convergent-divergent mode switching, however, would generally increase ESS complexity, decrease irregularity, and increase algebraic connectivity.