In the contemporary science, much attention is given to the development of the method aimed at the evaluation of the concentration of hydrogen in metals; in particular, in the process zone, where the material is deformed under stresses exceeding the yield strength. In [1–16], the influence of the stress-strain state on the distribution of hydrogen in the process zone was investigated in various specific cases.

Formulation of the Problem and Its Solution

The distribution of the concentration of hydrogen near the crack tip was found on the basis of the solution of the Fick equation, which takes into account the influence of the gradient of mechanical stresses on the diffusion of hydrogen in the process zone [12]:

$$ \frac{\partial C}{\partial t}=\overrightarrow{\nabla}\left(D\overrightarrow{\nabla}C\right)-\overrightarrow{\nabla}\left(\frac{D{V}_{\mathrm{H}}C}{RT}\overrightarrow{\nabla}{\upsigma}_h\right), $$
(1)

where C = C(x, y, t) is the hydrogen concentration, \( \overrightarrow{\nabla}=\left(\partial /\partial x,\partial /\partial y\right) \) is the Hamiltonian operator, D is the diffusion coefficient, R is the universal gas constant, T is absolute temperature, V H is the partial molar volume of hydrogen in the metal, σ h is the hydrostatic component of the stress tensor in the metal, and t is time.

The Fick equation (1) is solved in a two-dimensional domain S (Fig. 1). In this case, it is assumed that the hydrogen distribution in the domain S is uniform and equal to C 0. Hence, we use the following initial conditions for the distribution of hydrogen:

$$ {\left.C\left(x,y,t\right)\right|}_{t=0}={C}_0. $$
(2)
Fig. 1
figure 1

Schematic diagram of the plate (a) and its partition into finite elements (b): 2l 0 is the initial crack size, Δl = l − l 0 is the process zone of the material, and p are tensile forces.

Full size image

It was also assumed that the flow of hydrogen on the boundary of the domain S is equal to zero.

After simple transformations, Eq. (1) can be rewritten in the form of the following finite-element equation [17]:

$$ \left[M\right]\left[\frac{\partial C}{\partial t}\right]+\left[K\right]\left[C\right]=0, $$
(3)

where [C] is the hydrogen concentration at the nodes and [M] and [K] are, respectively, the global matrices of the concentration capacity and diffusion. The elements of these matrices have the form

$$ \begin{array}{l}\kern6em {m}_{ij}^{\left(\mathrm{e}\right)}={\displaystyle \underset{S^{\left(\mathrm{e}\right)}}{\iint }{N}_i\left(x,y\right){N}_j\left(x,y\right)}dx\kern0.5em dy,\hfill \\ {}{k}_{ij}^{\left(\mathrm{e}\right)}=D{\displaystyle \underset{S^{\left(\mathrm{e}\right)}}{\iint}\left(\frac{\partial {N}_i}{\partial x}\frac{\partial {N}_j}{\partial x}+\frac{\partial {N}_i}{\partial y}\frac{\partial {N}_j}{\partial y}\right)} dxdy,\hfill \\ {}\kern4em -\frac{D{V}_{\mathrm{H}}}{RT}{\displaystyle \underset{S^{\left(\mathrm{e}\right)}}{\iint }{N}_j{\displaystyle \sum_{m=1}^4{\upsigma}_{hm}}\left(\frac{\partial {N}_i}{\partial x}\frac{\partial {N}_m}{\partial x}+\frac{\partial {N}_i}{\partial y}\frac{\partial {N}_m}{\partial y}\right)}dx\kern0.5em dy,\hfill \end{array} $$
(4)

where S (e) is the area of an element, i = 1, 2, …, n, j = 1, 2, …, n; σ hm are hydrostatic stresses at the nodes of the element, and N i are shape functions.

The hydrostatic stresses were found [17] as a result of the solution the following equation:

$$ \left[{K}_{ep}\right]\kern0.5em \left[d\updelta \right]=\left[dP\right], $$
(5)

where

$$ \left[{K}_{ep}\right]={\displaystyle \underset{S^{\left(\mathrm{e}\right)}}{\iint }{\left[\mathrm{B}\right]}^{\mathrm{T}}\left[{D}_{ep}\right]\kern0.5em \left[B\right]dS}, $$

[B] is the matrix of differentiation of displacements, D ep is the matrix that establishes the relationship between the increments of stresses and strains in the elastoplastic domain, [dP] is the increment of the vector of displacements, and [dP] is the increment of the vector of force loading.

Equation (5) was used to find hydrostatic stresses with simultaneous guaranteeing the validity of the von-Mises yield conditions [18]

$$ \sqrt{3}\overline{\upsigma}-{\upsigma}_T-k{\overline{\upvarepsilon}}_p^m=0, $$
(6)

where \( \overline{\upsigma}=\sqrt{\frac{1}{2}\left({s}_{xx}^2+{s}_{yy}^2\right)+{\upsigma}_{xy}^2} \), \( {\overline{\upvarepsilon}}_p=\sqrt{\frac{1}{3}\left(2{\upvarepsilon}_{px}^2+2{\upvarepsilon}_{py}^2+2{\upvarepsilon}_{pz}^2+{\upvarepsilon}_{pxy}^2\right)} \), s xx , s yy , and s zz are deviatoric stresses, ε px , ε py , ε pz , and ε pxy are the components of plastic strains, and the values of k and m are found from the data used for the construction of the stress–strain diagram.

Hydrogen Concentration in the Process Zone of a Hydrogenated Stretched Plate

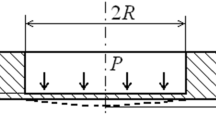
By using the algorithm of calculations described above, we determine the redistribution of the hydrogen concentration in a rectangular thin plate (120 × 150 mm) with a thickness h = 1.9 mm weakened by a central blunt crack with an initial length 2l 0 = 25 mm. The plate was stretched by uniformly distributed forces P (Fig. 1а). For the correct description of the behavior of hydrostatic stresses and the redistribution of hydrogen concentration, we split a one-fourth part of the plate in the vicinity of the crack tip into 3159 finite quadrangular linear elements by using 3330 nodal points. Note that the sizes of elements in the vicinity of the tip of a blunt crack are smaller than its radius of curvature (Fig. 1b) chosen by taking into account the technical possibilities available in the course of experiments. To find hydrostatic stresses, we use the experimentally plotted true stress–strain diagrams.

We computed the distribution of hydrogen in a plate of 65G steel for which the quantities appearing in equations (3) and (5) are as follows: D = 10− 10 m2/sec, R = 8.31 J/(mole ⋅ K), V H = 1.96 cm3/mole, T = 295°K, E = 198 ⋅ 103 MPa, σy = 525 МPа, σu = 980 МPа, S i = 1350 МPа, and the radius of the crack tip ρ = 0.05 mm. The numerical results are shown in Fig. 2, where we use the following notation: ξ = x/2δ p , where x is the distance from the crack tip, C 0 is the initial hydrogen concentration in the plate,

$$ \begin{array}{lll}{\updelta}_p(p)=-\frac{8{\upsigma}_0{l}_0}{\uppi E} \ln \left( \cos \frac{\uppi p}{2{\upsigma}_0}\right)\hfill & \left[11\right],\hfill & {\upsigma}_0\approx \left({\upsigma}_{\mathrm{y}}+{S}_i\right)/2,\hfill \end{array} $$

and C H = C H(x, 0, t) is the hydrogen concentration near the crack tip. In this case, the values of δ p (p) are equal to δ p (116) = 2.9 ⋅ 10− 3 mm, δ p (174) = 6.5 ⋅ 10− 3 mm, and δ p (278) = 1.7 ⋅ 10− 2 mm.

Fig. 2
figure 2

Distributions of hydrogen concentration in the process zone (a–c) under loading of a plate made of 65G steel by tensile stresses p = 116 MPa (a), 174 MPa (b), and 278 MPa (c) at different times: (1) 30 min; (2) 120; (3) 360; (4) 720 min. The distribution of hydrogen near the crack tip at a distance ξ < 5 is presented in (d–f) on the enlarged scale.

Full size image

In all plots, under different loads at the point ξ = 40 corresponding to x = 80δ p , we observe a kink in the lines that describe the distribution of hydrogen concentration. This can be explained by the fact that this point correspond to end of the region of plastically deformed metal whose length can be found by using the formula [11]

$$ {l}_p\left({\updelta}_p\right)=\frac{\uppi E}{8{\upsigma}_0}{\updelta}_p(p). $$

For 65G steel, the length of the plastic zone on the continuation of the crack is l p (δ p ) ≈ (80 − 85)δ p .

Moreover, the finite-element modeling enables us to obtain a series of other interesting results. In particular, we plotted the distributions of strains ε y (Figs. 3a, b) and hydrostatic stresses (Figs. 3c, d) in the process zone depending on the radius of the crack tip under the action of various tensile forces.

Fig. 3
figure 3

Distributions of plastic strains (a, b) and hydrostatic stresses (c, d) near the crack tip for 65G steel, ρ = 0.05 mm (a, c) and 0.1 mm (b, d), under different tensile forces: (1) p = 278 MPa; (2) 174 MPa; (3) 116 MPa (the lines correspond to the numerical results, and the dots correspond to the experimental data).

Full size image

Similar calculations were also performed for 20 steel and 40Kh steels. In Fig. 4а, we show results of evaluation of hydrostatic stresses for the indicated steels under the following stresses: 220 МРа for 20 steel, 275 МРа for 40Kh steel, and 300 МРа for 65G steel. In Fig. 4а, we also present the results of evaluation of the distribution of hydrostatic pressures near the crack tip for 20 steel obtained by the experimental method of digital speckle correlation under the ultimate force.

Fig. 4
figure 4

Distributions of hydrostatic stresses in the process zone for the investigated materials under loading (a) and after unloading (b): (1) 20 steel, (2) 65G steel, (3) 40Kh steel (the lines and dots correspond to the numerical and experimental data, respectively).

Full size image

For this purpose, we loaded a hydrogenated specimen of 20 steel weakened by a fatigue crack. In the process zone, by the method of digital correlation of images [19] and the corresponding program of calculations, for each level of loading (200, 400, 600 kg, etc.), we determined the field of elastoplastic displacements in front of the crack tip. Choosing the gauge lengths a x and a y (0.5, 1.0, 2.0, and 3.0 mm), we found the distributions of strains along the Ox- and Oy-axes at the same points, in particular, for the limiting equilibrium state.

The strains in the direction of the Ox- and Oy-axes at an any point of the region of observation ε xi and ε yi were determined as the ratio of the increment of displacements at this point Δa xi and Δa yi along the corresponding axis to the nominal length a i (ε i  = Δa i /a i ) under the action of forces.

We assume that the mechanical properties of the material in the region of observations are homogeneous. This is why the stress–strain diagrams are invariant at each point of the region.

The stresses σ xi and σ yi in the process zone are determined from the true tensile stress–strain diagram of the specimen without stress concentrators (Fig. 5а) according to the corresponding values of strains ε xi and ε yi obtained at the same points by the method of speckle correlation.

Fig. 5
figure 5

Stress–strain diagrams (a) of hydrogenated materials [(1) 65G steel; (2) 40Kh steel, and (3) 20 steel] and the schematic diagram (b) of the determination of stresses σ xi and σ yi (i = 1, …, n).

Full size image

The procedure of determination of the stresses σ xi and σ yi in the zone of observations is shown in the scheme presented in (Fig. 5b).

The hydrostatic stress σ hi at each point of the process zone is given by the following formula [11]: σ hi  = (σ 1i  + σ 2i  + σ 3i )/3, where σ ji (j = 1,2,3) are principal stresses. In view of the fact that the invariant of the stressed state

$$ {I}_1^{\upsigma}=\left({\upsigma}_x+{\upsigma}_y+{\upsigma}_z\right)=\left({\upsigma}_1+{\upsigma}_2+{\upsigma}_3\right) $$

is independent of the coordinate system, we determined the hydrostatic stresses on the continuation of the crack line from the formula σ hi  = (σ xi  + σ yi  + σ zi )/3 and studied their redistribution in the process zone for 20 steel under loading (see Fig. 4а) and after complete unloading (see Fig. 4b).

It is easy to see that the experimental results satisfactorily correlate with the numerical data. This enables us to conclude that the finite-element method is a fairly efficient tool in modeling these complex processes.

As follows from Fig. 4, in both cases, the hydrostatic stresses are maximal at a certain distance from the crack tip. These stresses depend on the yield strength of the material, i.e., the higher the yield strength (40Kh steel), the higher the level of hydrostatic stresses (800 МPа) formed in the process zone.

In Fig. 6, we show the distribution of the relative hydrogen concentration in the process zone in the case of tension of the plate and after its complete unloading. For 20 steel, we compared the levels of hydrogen concentration in the process zone with the experimental data obtained at the Paton Institute of Electric Welding of the Ukrainian National Academy of Sciences by the mass spectrometry method after complete unloading. Note that the numerical results are in satisfactory agreement with the experimental data.

Fig. 6
figure 6

Distributions of the relative hydrogen concentration in the process zone for different materials under loading (a) and after unloading (b): (1) 20 steel; (2) 65G steel; (3) 40Kh steel (the lines correspond to the numerical results and the dots correspond to the experimental data).

Full size image

Comparing the plots presented in Figs. 4а and 6а and in Figs. 4b and 6b, we establish the correspondence between the distribution of the hydrogen concentration and the distribution of hydrostatic stresses near the crack tip. As in the case of σ h , the maximum hydrogen concentration is attained at a certain distance from the crack tip. Note that the amount of hydrogen in the process zone increases with hydrostatic stresses.

In the unloaded specimen, the concentration of residual hydrogen near the crack tip (Fig. 6b) is 1.5–3 times lower than at the time of attainment the limiting equilibrium state in this zone (Fig. 6а). This is explained by the compressive stresses formed after unloading in the process zone (see Fig. 4b) and should be taken into account in the process of operation and in the course technical diagnostics of structural elements after their scheduled shutdowns.

Analyzing the numerical results obtained for 20 steel, 65G steel, and 40Kh steel (Figs. 4 and 6), we can conclude that the hydrogen concentration in the process zone strongly depends on the level of hydrostatic stresses in this zone which, in turn, depends on the mechanical properties of the material.

By using the values of C H max presented above (Fig. 6), we plotted the dependence of the maximum relative hydrogen concentration in the process zone on σy/σu (the squares in Fig. 7). This dependence is practically linear and well described by the formula

$$ {C}_{\mathrm{H}\kern0.5em \max}\approx {C}_0\left(0.5+1.4\frac{\upsigma_{\mathrm{y}}}{\upsigma_{\mathrm{u}}}\right) $$

(the line in Fig. 7) for the range of values 0.4 < σy/σu < 1. For the additional verification, we used the data of calculations obtained for three more types of steels (22K, 16GNM, and Kh70) with different values of σy and σu. In the plot, these results are marked by the circles (Table 1).

Fig. 7
figure 7

Dependence of the maximum relative hydrogen concentration on the mechanical properties of the material.

Full size image
Table 1 Mechanical Properties of the Investigated Steels and the Corresponding Maximum Hydrogen Concentration in the Process Zone
Full size table

Thus, by using the dependence presented in (Fig. 7), we can approximately evaluate the maximum hydrogen concentration in the process zone formed in the loaded materials for steels with different values of σy.

Conclusions

We theoretically determined and experimentally confirmed the distributions of hydrostatic stresses and the concentration of hydrogen on the continuation of the crack line in a uniformly stretched plate (Fig. 1) and after complete unloading of the specimens by using the true stress–strain diagrams of the hydrogenated metal. We plotted the dependences of hydrogen concentration near the crack tip on the mechanical characteristics of the material, which can be used for the evaluation of hydrogen concentration in the hydrogenated metal with given yield strength.