Hydrogen embrittlement (HE) of metals has been the long-standing problem of physicochemical mechanics of materials [1–4]. The process of hydrogen-assisted fracture (HAF) of metals consists of several stages [4–6], one of which is hydrogen transport from the harsh environment towards certain locations within metal where hydrogen assisted damage takes place. Diverse studies [5–8] argued that hydrogen transport inside metals could proceed by two different mechanisms: via the movement by dislocations during continuing plastic straining and via the lattice diffusion affected by stress-strain state in the material. It has been repeatedly substantiated [5, 8– 10] that hydrogen diffusion in metal can be the dominating mode of hydrogen supply to prospective microstructural fracture sites under a broad range of circumstances. Then, evaluation of the stress-and-strain assisted hydrogen diffusion is of great interest for rationalization of HE manifestations and gaining the HAF predictive capability, e.g., via assessment of the local critical hydrogen concentrations in the fracture sites on the basis of dedicated experimentation, and afterwards, their use to predict the HAF susceptibility of structural parts under diverse loading-environmental conditions in service, as it has been suggested elsewhere, see, e.g., [11–15]. These tasks require efficient procedures for the solution of specific boundary-value problems of the stress-strain assisted diffusion.

Concerning this, in the general case nonlinear and nonsteady-state, coupled problem of mechanics and mass transfer, various analysis procedures have been developed including one- and two-dimensional (1D and 2D) linearized and nonlinear formulations for different cases of solid geometry and loading [11–13,15–20]. Obviously, the multi-dimensional approach is usually more realistic when irregularities of geometries and of associated stress-strain states in solids, e.g., when cracks and notches are present, can make diffusion trajectories to be not straight lines suitable for 1D treatment, but substantially curved paths. Concerning the sustained loading or 1D situations, required diffusion simulations can be performed numerically using fairly modest computer facilities with home-made [13,15–20] or commercial (e.g., ABAQUS) software codes. However, when nonsteadystate loading cases (monotonic or cyclic) are dealt with, the accounting for transient stress-strain fields, which produce the time dependence of the coefficients of the equation of stress-strain assisted diffusion, makes calculations extremely laborious and difficult to accomplish. Only very few attempts [19,20] have been advanced towards involving the transient loading effects on hydrogen diffusion in 2D. Although spatially multi-dimensional considerations of hydrogen diffusion are obviously more adequate for notched and cracked geometries, computing of transient solutions may be prohibitively expensive. Moreover, geometry variations of the deformable body under finite deformations that can occur, e.g., near notches and cracks, may cause severe aggravation, as far as this implies simulation of diffusion in variable domains with changeable diffusion distances between material points. Then, someway linearized or reduced-dimension simplified analyses can be the only feasible ways to resolve the stress-strain assisted diffusion.

Cylindrical bars with circumferential V- and U-notches, where different triaxial stress-strain states can be generated, are frequently used in experiments of both inert-environment fracture and HE of metals [9, 14, 15, 21– 23]. Working their results out, e.g., to assess the critical local conditions for HAF events to occur [13–15], requires efficient means to find out transient hydrogen concentration distributions in such specimens.

This paper is aimed at examining the suitability of simplified treatments of hydrogen transport associated with HAF in certain notched geometries under rising load by means of comparison between various 1D and 2D analyses. The aim of the paper is to assess if the simpler solutions, which may be generated within looser, but easier to perform, modeling approaches, can provide acceptable results along the diffusion depth towards prospective rupture sites beneath the notch root, so that sophisticated simulations, which are quite more expensive, might be eluded. Within this framework, the study is limited to the case of the stress-only assisted diffusion considering that the involvement of strain must not interfere substantially in the matter of suitability of the examined analysis procedures for the purpose. Particularly, the study deals with U-notched specimens of prestressing steel wires used in previous experiments [21,23], which are taken here as the reference cases for simulations. Corresponding comprehensive 2D modeling of transient stress-strain assisted hydrogen diffusion was discussed elsewhere [24].

Theoretical Background [5,8,11–13,16–18,25]

HAF is considered to be the result of synergistic action of the stress-strain state and the amount of hydrogen, which is supplied from the environment to potential fracture loci in metal. Correspondingly, the local fracture event takes place in a certain locus identified by its position vector \( \vec{x} \) when the concentration C of hydrogen accumulated there over time t reaches the critical level C cr dependent on the stress-strain state:

$$ C\left( {\vec{x},t} \right) = {C_{\text{cr}}}\left( {\underline{\underline \sigma } \left( {\vec{x},t} \right),{{\underline{\underline \varepsilon } }_p}\left( {\vec{x},t} \right)} \right), $$
(1)

where \( \underline{\underline \sigma } \) and \( {\underline{\underline \varepsilon }_p} \) are, respectively, the stress and plastic strain tensors generated by applied loading. Touching between the concentration distribution surface and the criterial one, C \( \left( {\vec{x},t} \right) \) and C cr \( \left( {\vec{x},t} \right) \) renders the location \( {\vec{x}_{\text{cr}}} \) and time t cr of an elementary HAF event [11,12].

As regards hydrogen diffusion, phenomenological consideration attending the stress effect on hydrogen behavior in metals yields the equation of stress-assisted diffusion under isothermal conditions as follows [5,8,16,17,25]:

$$ \frac{{\partial C}}{{\partial t}} = \nabla \left( {D\nabla C - DC\frac{{{V_H}}}{{RT}}\nabla \sigma } \right), $$
(2)

where D is the diffusion coefficient, V H is the partial molal volume of hydrogen in metal, R is the universal gas constant, T is the absolute temperature, and σ=σ\( \left( {\vec{x},t} \right) \) is the hydrostatic stress. The instantaneous concentration distribution C eq \( \left( {\vec{x},t} \right) \) corresponding to equilibrium between hydrogen in the stressed metal and in surrounding hydrogenating environment, which has fixed thermodynamic activity of hydrogen, provides the upper bound of hydrogenation from environment in a solid at some instantaneous stress field σ\( \left( {\vec{x},t} \right) \) under monotonic loading. Taking into account that the diffusion driving force and flux are nil at equilibrium, it can be easily shown [5,8,25] that

$$ {C_{\text{eq}}}\left( {\vec{x},t} \right) = {C_0}\exp \left( {\frac{{{V_H}}}{{RT}}\sigma \left( {\vec{x},t} \right)} \right), $$
(3)

where the equilibrium concentration in the stress-strain free metal C 0 under given conditions of hydrogenating environment represents the environmental thermodynamic activity of hydrogen.

Under the presumption of hydrogenating environments with not too low thermodynamic activity of hydrogen, the surface step of hydrogen entry into material can be considered fast enough [5,6,8,16], so that the boundary condition of hydrogen diffusion in metal may be set down keeping on the metal surface r that contacts with the environment, i.e., for \( \vec{x} \) ∈ Γ the equilibrium hydrogen concentration according to expression (3).

Analysis Cases

An extensive experimental program, which was performed by the same research team [21,23,26,27] for the same-type as-received pearlitic steel (C 0.80%, Mn 0.69%, Si 0.23%, P 0.12%, S 0.009%, Al 0.004, Cr 0.265%, V 0.060) with the use of various circumferentially U-notched specimens, was taken as the reference for simulations.

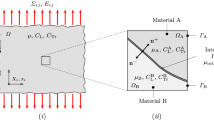
On this way, two different bar geometries used in these experiments were analyzed (Fig. 1). They are characterized by the notch root radius ρ and depth a in relation to the specimen diameter d . Having the same depth a/d = 0.1 , the notch A has a small root radius, ρ/d = 0.03 , and the notch C has a large one, ρ/d = 0.4 . Modeling was performed for the notched specimens of the diameter d = 12 mm and the gauge half-length l = 12.5 mm.

Fig. 1
figure 1

Scheme of the notched specimen and the nomenclature of analyzed notch geometries: (I) notch A; (II) notch C.

Full size image

These notched bars were made from the steel wire with the yield stress and ultimate tensile strength 720 and 1270 MPa, respectively. More data about the steel, including its stress-strain diagram used to evaluate the stress-strain states in the specimens, are given elsewhere [23,26,27].

In accordance with the reference HAF experiments [21], which were constant-extension-rate traction (CERT) of specimens under identical conditions of cathodic hydrogenation, the formulations of combined boundary-value problems of solid mechanics and diffusion governed by Eq. (2) were accomplished by posing corresponding boundary conditions:

  1. (i)

    the mechanical one of axial displacement with the prescribed constant rate \( \dot{u} \) applied at z = ±l ;

  2. (ii)

    the environmental one given by the equilibrium concentration C eq on the metal-environment interface Γ according to equality (3), i.e., C(Γ, t) = C eq(Γ, t).

Considering environmental hydrogenation the initial condition for diffusion was taken nil, C(\( \dot{u} \) ∉ Γ, t=0)=0. Due to the symmetry with respect to the notch net-sections, corresponding axisymmetric boundary-value problems were finally stated for the specimen halves, i.e., for 2D-domains in cylindrical coordinates r and z , which are shadowed in Fig. 1, with obvious boundary conditions of nil axial displacement and hydrogen flux on the plane of the notch symmetry.

Hydrogen effect on material in considered tests [21] was characterized in terms of the time to hydrogen assisted fracture t HAF depending on the displacement rate \( \dot{u} \) applied at the extremes of the specimen gauge length. Under the reasonable supposition that the mechanical behavior of the steel in an inert environment under explored range of rather slow loadings is rate-time insensitive, combination of the results on hydrogen-assisted [21] and unassisted [26] fracture is presented in Fig. 2a after transforming the original data on the fracture displacement u f under arbitrary loading rate in inert environment into corresponding times to hydrogen-unaffected fracture t f =u f /\( \dot{u} \) under definite values of \( \dot{u} \) during testing. These t f values set the natural upper bounds for the hydrogen diffusion time in the forthcoming simulations, so that further computations will be limited to the intervals 0 ≤ t ≤ t f , corresponding to respective analysis cases.

Fig. 2
figure 2

Experimental manifestations of HAF in notched specimens A (filled points) and C (open points) in CERT under cathodic hydrogenation at various traction rates \( \dot{u} \) [16,23]: (a) relative time to fracture in hydrogen environment; (b) extension of the hydrogen-assisted micro-damage zone, the TTS, beneath the notch root.

Full size image

On the other hand, as it has been well documented, HAF in pearlitic steels proceeds via microstructural damage mechanism that causes characteristic fractography called tearing topography surface (TTS) [9,21,28,29]. Figure 2b displays the data [21] about the TTS extension beneath the notch root, x TTS, under different loading conditions. This delimits the regions of potential locations of hydrogen damage loci in specimens in the analysis cases under consideration, being 0 < x cr : x TTS. In effect, x TTS defines the hydrogen diffusion depths x ≤ x TTS within which the reliable evaluation of hydrogen concentration is of interest from the point of view of interpretation of HAF phenomena.

This way, combination of the experimental data [21,26] provides assigning realistic loading conditions, i.e., the values of traction rate \( \dot{u} \), together with diffusion times and depths of interest concerning simulations of hydrogen accumulation in notched specimens in the course of CERT under hydrogenating environment. In particular, calculations were performed for CERT under isothermal conditions (T = 300 K) for applied extension rates \( \dot{u} \) = 0.001 and 0.1 mm/min. The values of relevant parameters of the metal-hydrogen system were taken according to the available data for steels [3,4]: V H =2∙10 -6 m3/mole and D =6.6 .10 -11 m2 /sec .

Modeling Procedures

The subject of interest, i.e., the stress-assisted hydrogen diffusion in elastoplastic notched bars, is the coupled problem of mechanics and mass transfer. To be consistent with the reference experiments [21,26], where substantial inelastic deformations of specimens used to occur, revelation of the stresses and deformations requires adequate elastoplastic analysis. As far as elastoplastic stress-strain behavior of steels is known to manifest usually indiscernible sensibility to hydrogen up to the point of fracture (unless extraordinarily severe hydrogenation would per se produce irreversible damages in metal), the requested simulations can be performed in two sequential stages: solution of the elastoplastic boundary-value problem of hydrogen unaffected mechanics of solids at the first one, which provides the input for subsequent calculations at the next stage of the stress-assisted diffusion in deformed solids according to the adopted statement of the initial boundary-value problem of diffusion.

The solid mechanics solutions were accomplished with the use of a general purpose nonlinear finite element (FE) code, and the stress-and-deformation data for the chosen analysis cases were generated as described in detail elsewhere [23,26,27]. In short, material constitutive model of the rate-time independent elastoplasticity with the von Mises yield surface, associated flow rule and isotropic hardening was used, where the steel stress-strain master curve was taken according to the test data [27]. Solutions were performed applying monotonically rising displacement u = \( \dot{u} \) t at the specimen gauge-length end z = l till attainment of the value of fracture displacement u f in an inert environment according to the experiments [26]. Because in the reference tests [21,26] remarkable deformations, which altered real material distances, used to occur before HAF, the deforming geometry update was considered among the analysis options. This way, to explore the consequences of finite geometry changes for the generated stresses and hydrogen diffusion in notched bars, the elastoplastic solutions were generated both in the large- and infinitesimal-strain formulations. In the first one, corresponding extension of the incremental plasticity equations of Prandtl–Reuss in terms of the Jaumann rate of Cauchy stress, additive decomposition of strain rates and the updated Lagrangian method were used, and the FE equations were solved in usual incremental manner performing at each step a recuperation of stress via return mapping to the yield surface and an update of deformed geometry. The minutiae of mechanical analysis (FE mesh designs, solution routine, etc.) are described elsewhere [23,26,27].

Afterwards, taking the former results (stresses and deformation displacements) as the input, computations of the transient stress-assisted diffusion were performed using the FE procedure and computer code developed by the authors and described in full detail elsewhere [13,16–18,24,30].

The “as is” or “strong” formulation of axisymmetric (i.e., 2D in the coordinates r and z , Fig. 1) coupled transient initial boundary-value problem of doubly-nonlinear mechanics (finite-deformation elastoplasticity) and of stress assisted diffusion in the deforming (updated) geometry will be denoted henceforward as the 2D**-formulation. This is to reflect the 2D dimensionality and double geometry update, which is made at both mechanical and diffusion stages of calculations. This approach, although being fairly comprehensive, requires update of the shapes and of all the matrices (of mass, conductivities, etc.) for all FEs along the whole loading-and diffusion history. This is hardly feasible for transient loading-and-diffusion as far as the amount of computations rises steeply along long-lasting FE-solution route because all FE data must be reiteratively updated at every time-integration step.

To loosen this restraint, a series of less comprehensive (“weaker”), but progressively less expensive from the computational point of view, formulations were considered. Reductions of the grade of accounting for the geometrical nonlinearity (finite deformations) in the coupled axisymmetric problem, as well as of the dimensionality of the treatment of diffusion (but not of the mechanics) from 2D to 1D by means of focusing on the diffusion along the depth x towards prospective rupture sites beneath the notch roots, were explored to dismount the problem complexity.

As regards the treatment of coupled axisymmetric 2D problem, cutbacks in the matter of the deforming solid geometry update were twofold giving rise to the weaker model approaches 2D* and 2D.

In the 2D* one, transient finite deformations were considered solely at the mechanical stage of the solution, where comprehensive data about stresses and deformations were generated following the “strong” (doublynonlinear) formulation. But the stress-assisted diffusion was treated there in a weaker 2D formulation, which consisted in mapping of the more realistic doubly-nonlinear mechanical solution onto material points in the undeformed solid configuration and subsequent solution of the diffusion problem in the fixed domain neglecting eventual transient geometry changes, but still using thoroughly defined stress fields.

In the next 2D one, accounting for finite deformations was ruled out at all, i.e., the analysis was confined to infinitesimal-strain elastoplasticity, which is potentially less realistic, accompanied by diffusion computations in undeformed solid configurations. These simplifications eased substantially the simulations of diffusion due to avoidance of numerous re-calculations of certain FE matrices (of mass and stress-unaffected part of conductivity) along with the update of deformed element shapes, as well as owing to reduction of the amount of calculations to obtain other varying matrices (of stress-affected conductivity) along the transient loading routes.

The next step of simplifications consisted in carrying out 1D simulations of the stress-assisted diffusion along solely the depth x = r -a in the plane of the notch symmetry (Fig. 1), where HAF events really take place, that is, disregarding the ∂/∂z members of the ∇-operator in Eq. (2). Notwithstanding, the appropriate 2D axisymmetric mechanical solutions were used there as the inputs for stress state and deformed geometry along the coordinate x , wherever pertinent. To this end, a series of 1D approaches were examined.

The most comprehensive among them was the 1D** formulation where the data from doubly-nonlinear axisymmetric mechanical solution were employed in calculations of diffusion accomplished with the update of the deformed element shapes, i.e., along the true diffusion distance x in the deformed configuration. This was followed by the 1D* one, where diffusion was calculated along the undeformed diffusion distance X , i.e., without updating the element sizes, but the realistic stress-state in material points was acquired there from the finite-deformation 2D mechanical solution. Finally, element deformations were disregarded at all in the approach 1D, where the infinitesimal-strain mechanical analysis data were accounted for. As a matter of fact, computer resources available for the present work were insufficient to accomplish the 2D** simulations. Nevertheless, comparisons of the results generated along with the other analysis procedures made it possible to apprehend the consequences of proceeding in accordance with whichever modeling course.

Simulation Results

The approximate analysis procedures set down in the previous section were explored in order to clarify the ranges of their suitability for analysis of HAF in notched bars. To adjust the presentation of mechanical solutions to the considered real CERT cases (Fig. 2) according to the purposes of this study, the profiles of hydrostatic stress against the depth in the net-section of the notch, which were calculated for various values of applied displacement u, are displayed in Fig. 3 as corresponding to certain instants of the relative time under constant extension rate, i.e., taking t /t f  = u/u f . These time instants in Fig. 3 were chosen to fit roughly the top and bottom times of fracture under HE, t HAF , which occurred in the reference HAF experiments [21] performed under different loading rates, Fig. 2a, i.e., t HAF /t f  = 0.45 and 0.8 for the A notch, and 0.35 and 0.8 for the C notch in the range of the extension rates \( \dot{u} \) of interest, i.e., from 0.001 to 0.1 mm/min. The gray horizontal bars on these plots, Fig. 3, show the depth intervals 0 ≤ x ≤ x TTS where HAF loci can be situated in respective analysis cases according to the reference experimental results [21] presented in Fig. 2b.

Fig. 3
figure 3

Hydrostatic stress distributions along the depth beyond the notch root in the net sections of the notches A (to the left) and C (to the right) at indicated instants of time during CERT: solid and broken lines (filled quads and circles) display, respectively, large-strain solutions in terms of the deformed diffusion depth x and undeformed one X , and dash-dot lines (open circles) represent the small-strain analysis results. Horizontal gray bars show approximately the extensions x TTS of the hydrogen affected TTS fractography, which were obtained in HAF experiments [21] that terminated at corresponding values of fracture time t HAF/t f (see Fig. 2).

Full size image

Hydrogen concentration distributions in the notch net sections in material points identified with their undeformed depths X beyond the notch tip, which were calculated following the modeling procedures under exploration, are shown in Fig. 4. The data corresponding to the traction rate \( \dot{u} \) = 0.001 mm/min are there given for diffusion times that match roughly the half and the whole time to fracture t HAF in the reference HAF experiments [21] (Fig. 2)a, i.e., for t HAF /t f  = 0.23 and 0.45 for the A notch, and 0.18 and 0.35 for the C notch, which attain several hours in absolute terms. The results for \( \dot{u} \) = 0.1 mm/min are given for the times nearly twice as long as respective experienced times t HAF relative to t f (but being these rather short now – of the order of few minutes – in absolute terms) merely to show that at these fairly long times different solution procedures scarcely develop differences. Again, the gray horizontal bars in Fig. 4 show approximately the depth intervals 0 ≤ x ≤ x TTS according to Fig. 2b for HAF site locations in the simulated experiments [21].

Fig. 4
figure 4

Hydrogen concentration distributions in the net sections of notches A (to the left) and C (to the right) under indicated loading rates during CERT, which were obtained for specified diffusion times according to different analysis procedures: 2D (dash-dot line with open squares), 1D** (solid line with filled squares), 1D* (broken line with filled circles) and 1D (dotted line with open squares). Horizontal gray bars show approximately the sizes x TTS of HAF zones observed at given traction rates \( \dot{u} \) in experiments [21] (see Fig. 2).

Full size image

Figures 5 and 6 shows the evolutions of hydrogen concentration in certain material points X of the specimen net sections during CERT. To indicate the domains of interest where the acceptability of generated solutions for interpretation of HAF is concerned, but now as regards the suitable modeling time-spans 0 ≤ t ≤ t HAF , the gray horizontal bars show there approximately these intervals for the respective analysis cases according to the reference tests data [21] presented in Fig. 2a. In addition, these bars are placed on the particular plots that display concentration evolutions at the depths X approximately corresponding to the experimentally observed [21] extensions of hydrogen affected zone x TTS on fracture surfaces given in Fig. 2b.

Fig. 5
figure 5

Evolutions of hydrogen concentration expressed in physical and relative times (the scales, respectively, at the top and bottom of the plots) in notch A samples in the indicated material points X of the notch net section under loading rates of 0.1 (to the left) and 0.001 mm/min (to the right) according to different analysis procedures: 2D (dash-dot line with open squares), 1D** (solid line with filled squares), 1D* (broken line with filled circles) and 1D (dotted line with open circles). On the plots for X values, which correspond roughly to the HAF zone sizes in respective experiments, X ≈ x TTS , gray bars mark approximately the experienced time scales of HAF, t HAF (see Fig. 2).

Full size image
Fig. 6
figure 6

Evolutions of hydrogen concentration expressed in physical and relative times (the scales, respectively, at the top and bottom of the plots) in notch C samples in the indicated material points X of the notch net section under loading rates of 0.1 (to the left) and 0.001 mm/min (to the right) according to different analysis procedures: 2D (dash-dot line with open squares), 1D** (solid line with filled squares), 1D* (broken line with filled circles) and 1D (dotted line with open circles). Gray bars have here the same significance as in Fig. 5.

Full size image

Discussion

As has been mentioned, the tried analysis procedures suppose progressive loss of plausibility of weaker approaches in comparison with 2D** modeling, being this latter one the most comprehensive, but inoperative for computational expenses. Concerning the explored model approaches, the following sources of concentration deviations between them can be pointed out:

  • the first factor, which emerges from Fig. 3, is the degree of fidelity of the mechanical phase of analysis regarding the accounting for finite deformations that may alter the stress-strain fields at elevated levels of loading, which, in turn, must have repercussions for the stress-strain assisted hydrogen diffusion;

  • the next one emanating from the mechanics and detectable in Fig. 3, too, is due to finite deformations that can alter diffusion distances towards prospective fracture sites beyond the notch root more or less substantially according to the deformation magnitudes and their in-depth expansions, which both depend on the instantaneous load levels;

  • now, the last consists in reduction of the diffusion problem dimensionality from 2D to 1D, which, according to the handbook 1D and 2D solutions of more trivial stress-unaffected transport problems [31,32], must be expected, roughly, to influence inappreciably the result at both rather short and fairly long diffusion times t , when these solutions approach the equilibrium concentration C eq being the same for all 1D and 2D formulations irrespectively of the dimensionality, as well as to manifest negligible discrepancies for all times provided the diffusion distances from the hydrogen entry surface are small comparing with its curvature radii, x < < ( ρ and (d/2 -a)), where the solution for plane entry surface C = C eqerfc (x/(\( 2\sqrt {{Dt}} \))) could be the solution asymptote.

Then, the accuracies of the modeling procedures under trial must depend on the time t and diffusion depth x , and also on the attainable load level, which under fixed loading rates \( \dot{u} \) corresponds to definite time under loading (and hydrogenation). Since the destination of such diffusion simulations is the interpretation of HE in specified notched bars, the space-time area of interest in further analysis of solutions is limited to the extension of the domain of possible HAF events, which is bounded spatially by the size x TTS of the hydrogen affected fracture zone (Fig. 2b), i.e., corresponds to x ≤ x TTS, and limited to the diffusion times up to the respective times to fracture t HAF , i.e., to t ≤ t HAF .

As regards the first two factors, which concern the issue of deforming geometry update at any of the two simulation phases, i.e., the analyses of mechanics and diffusion, their effects must be rather minor, and on occasion negligible, within the area of interest {x ≤ x TTS, t ≤ t HAF < t f }, as it can be presumed from the closeness of the mechanical analysis results shown in Fig. 3. This is confirmed in Figs. 4–6 where the formulations 1D, 1D* and 1D** render the grades of concentration deviations similar to those manifested in Fig. 3 by respective stress-deformation solutions over this domain of interest. Within the relevant space-time areas, the faint differences when passing from the formulation 1D to 1D* or 1D** is due to fairly minor shortening of the deformed distances between material points and decrease of the stress concentration in the A notch root vicinity when finite-deformations are taken into account. This is attributable to the updating of the deformed specimen geometry and corresponding notch blunting as a consequence, which results in the decrease of hydrostatic stress concentration (Figs. 3a and 3c), as well as of the concentration of hydrogen at longer diffusion times (cf., e.g., Figs. 4c and 5c). Then, disregard of the transient alteration of the solid geometry (i.e., of the diffusion distances) at the phase of diffusion calculations performed with the stress input from the doubly-nonlinear mechanical analysis, i.e., switching from 1D** to 1D* formulation, can scarcely deteriorate the result, as it is seen in Figs. 4–6. On the other hand, the 1D* procedure is much less expensive computationally than the 1D** one, as far as there is no need to update all FE matrices at every step along the time integration routine [16–18,30]. In due course, the 1D* formulation (deformed geometry update at the sole mechanical phase of simulations) can bring minor improvement with respect to the 1D one (no geometry update at all) for the whole range of simulated HAF cases. These deductions about the consequences of geometry updating seem to be extensible on the assessment of the suitability of 2D modeling approaches 2D vs. 2D* or 2D**.

In contrast, the factor of dimensionality of the diffusion boundary-value problem formulation can produce substantial divergence of the solutions C(x,t) in the domains of interest, as it occurs for the notch A (see, in particular, Fig. 5f), whereas for the notch C the differences remain there rather minor, as it can be seen when comparing the results of the otherwise identical approaches 1D and 2D in Figs. 4–6, where the domains of interest are marked approximately by gray bars.

To address this issue, it is worth pointing out the commonplaces of the behavior of the solutions of transport problems [31,32], that the non-1D solutions in the regions with curved surfaces, which bring forth the divergent flux trajectories, are usually overestimated by respective 1D approximate formulations that assume parallelstraight-line diffusion paths. However, it follows that both 1D and multi-D approaches are asymptotically equivalent near the entry surface at short times converging one to another as \( x\sqrt {{Dt}} /{\rho^2} = \xi \sqrt {\tau } \to 0 \), where dimensionless variables ξ = x/ρ and τ = Dt/ρ2 are introduced to afford more generality to these considerations in accordance with usual similitude criteria of the transport problems. On the other hand, the solutions C(x,t) for stress-assisted diffusion under monotonic loading, which could be obtained following whichever of analyzed modeling strategies, all have the exact common supremum determined by the instantaneous equilibrium hydrogen distribution C(x,t) according to expression (3), which can be approached as \( \xi \sqrt {\tau } \)→0 with greater or less lag depending on the loading rate and diffusion depth. At any rate, this makes impossible unlimited divergence of the solutions rendered by different modeling approaches, but the discrepancies are always restrained: the smaller the diffusion depths or longer the times, the lower the discrepancies, although they can be significant at some intermediate times τ and larger depths ξ.

In particular, in the case of notch C, the diffusion distances of interest x ≤ x TTS (Fig. 2b) remain small in relative terms, i.e., they hardly ever exceed 0.15ρ, so that at all times t, up to several hours, the discrepancy between 1D and 2D analyses at these depths remains rather minor, see Fig. 4b, d, f and Fig. 6. In contrast, for the notch A, the relative diffusion depth of interest x/ρ can be as large as approximately 0.8 (cf. Fig. 2b), so that at such distances the excess of the 1D results over the 2D ones can be expected to remain unimportant only at rather short diffusion times, Figs. 4a, c, e and 5, or at quite long ones so that the equilibrium concentration (3) can be approached if this is the case in particular occurrence of HAF.

Considering the impact of the model dimensionality on the simulation adequacy for the purpose of the present HAF cases work-outs, the region of the acceptable relative error of the 1D formulation in comparison with the 2D formulation may be estimated from the data presented in Figs. 5 and 6 as {0 ≤ ξ ≤ 0.2, 0 ≤ \( \xi \sqrt {\tau } \) ≤ 0.6}. This one is substantially narrower than the area of interest for the notch A case, which is {0 ≤ ξ ≤ 0.8, 0 ≤ \( \xi \sqrt {\tau } \) ≤ 1.9}, and covers this region for the C notch being {0 ≤ ξ ≤ 0.15, 0 ≤ \( \xi \sqrt {\tau } \) ≤ 0.05}. Nevertheless, as regards the simulation of HAF for the notch A, certain analysis cases can yet fit the region of suitability of 1D simulation, such as the one of faster extension rate \( \dot{u} \) = 0.1 mm/min, Figs. 4e and 5a, b, where the space-time span for HAF is limited to ξ ≤ x TTS/ρ ≈ 0.17 with τ ≤ Dt HAF/ρ2 ≈ 0.09, and thus \( \xi \sqrt {\tau } \) ≤ 0.05.

This way, 1D modeling can over estimate appreciably the concentration and, correspondingly, the rate of hydrogenation of notched samples in comparison with 2D description, unless the space-time spans for HAF were confined to the limits established approximately in the previous paragraph. These limits of suitability of the 1D vs. the 2D approaches may be loosened having the positions x cr of HAF nuclei and times t cr to HAF initiation defined more accurately than merely an extension of TTS, x TTS, and the overall time to fracture, t HAF , which both include the stage of hydrogen-assisted subcritical crack growth after HAF initiation, so that they overreach the desired variables more or less significantly. Anyway, it follows that the choice concerning suitability of 1D or 2D modeling is case- and purpose-dependent. For faster loading rates, where HAF usually occurs at shorter times and higher loading levels, the optimal choice is expected to be the 1D or 1D* formulation depending on which one fits adequately the mechanical situation, as far as neither has computational advantages at the phase of diffusion simulations, whereas the 1D** procedure may be beneficial for the concentration solution accuracy at fairly large deformations in the spatial domain of HAF occurrence near the notch root. For slow loading rates, the degree of adequacy provided by 1D descriptions may be insufficient, and the errors are higher when larger diffusion distances in relative terms with respect to the notch radii are involved. Only 2D procedures become then suitable. Among them, similarly to in the case of 1D ones, it is advisable to choose between 2D or 2D* vs. 2D** analyses accordingly to the level of stress-strain and deformations differences between them within the HAF zone.

Moreover, if the purpose of concentration solution C(x,t) was to ascertain the HAF criterion (1) through evaluation of the critical concentration C cr using this diffusion solution together with the experimentally assessed HAF site and time, x cr and t cr , the use of 1D modeling of hydrogenation could render substantial overestimation of C cr . If so, the usage of this critical concentration to evaluate afterwards the structural lives at HE under other geometry-and-loading circumstances would lead to their overestimation, too, i.e., to excessively optimistic assessment of the risk of HAF in structures. On the other hand, if the critical concentration in the criterion (1) were established with certainty by any other means, the use of 1D diffusion solutions, which overestimate the rate of hydrogenation near notches, would render conservative evaluations of the notched member lives in service under HE.

Conclusions

Concerning the analysis of hydrogen diffusion as a key element towards elucidation of the hydrogen embrittlement (HE) phenomena near notches under monotonic loading, multi-dimensional modeling with updating of the deformed geometry, although providing the most comprehensive simulation of transient stress-strain assisted diffusion, turns out to be prohibitively expensive from the computational viewpoint. This inconvenience can be lessened to a greater or less degree by the way of diffusion modeling optimization using simplified analysis strategies, but by the cost of possible accuracy deterioration, which depends on the diffusion times and distances involved in hydrogen-assisted fracture (HAF) under particular circumstances of the solid geometry and loading.

A series of formulations of the problem of stress-assisted hydrogen diffusion, which involved different grades of accounting for the mechanical nonlinearity (finite- or infinitesimal-strain elastoplasticity) near notches and one- or two-dimensional modeling of diffusion, were explored to clarify their suitability for the analysis of HAF in notched samples. It turned out that the 2D formulation of the diffusion problem without continuous geometry update along with the transient loading, but taking the stress input from the doubly-nonlinear mechanics simulation, must remain suitable for the majority of situations. However, its still rather elevated computational expenses may prompt to resort to more opportune modeling approaches.

To this end, various 1D formulations of the diffusion boundary-value problem can be reasonable ways of diffusion solution optimization. The analysis procedure, which employs the stress-strain data from the full-scale doubly-nonlinear mechanical solution for the notched member as the input for the diffusion calculations, but disregarding continuous update of the deforming diffusion distances, appears to be an optimal choice among 1D formulations. Although 1D approximations always overvalue metal hydrogenation near notches more or less substantially in comparison with 2D ones, corresponding 1D and 2D solutions are asymptotically equivalent at short diffusion times or small distances from the hydrogen entry surface at the notch tip. For this reason, for different geometry-and-loading cases, respective time-space domains do exist where 1D analysis procedures turn out to be fairly suitable to carry out calculations of metal hydrogenation for the purposes of HAF analysis. The estimates of these time-space regions for round U-notched bars are obtained in the paper on the basis of calculations performed following various 1D and 2D modeling procedures.

Anyway, it is pointed out that the choice of the right procedure for the stress-strain assisted diffusion simulations in notched members is case- and purpose-dependent.