Numerical characterization of a piezoelectric composite with hollow metal fillers including new figures of merit, pore shape effects, and distinct piezoceramic types

Abstract

This paper focuses on the numerical analysis of the properties of porous piezoelectric composites with metal-doped pore surfaces and assesses their effectiveness as piezoelectric sensors and actuators. Two types of porous piezoelectric composite systems are considered: the ordinary porous system and the system with metalized pore surfaces (SMPS). The pore surfaces of the SMPS were anticipated to be entirely coated by a very thin metal layer. To determine the effective moduli, homogenization problems were solved numerically using the finite element analysis of the representative cells using the ANSYS APDL package. The homogenization problems were solved considering piezoceramics substrates with different anisotropy of piezomoduli and representative cells with cubic and spherical pores. Several figures of merit, including novel figures of merit intended towards actuator applications, have been researched to evaluate the performance of the SMPS. The results of computational experiments demonstrated that pore shape has less impact on the effective elastic and dielectric characteristics but has a greater effect on the values of the piezomoduli. For various piezoceramic materials in the composite matrix, effective piezomoduli are also subject to the greatest influence, particularly transverse and shear piezomoduli. Abnormal behavior of the transverse piezomodulus and an increase in dielectric permittivities were observed as the porosity fraction was enhanced. The transverse actuation effect of the SMPS rises dramatically with increasing porosity. In this regard, it was concluded that piezoelectric transducers built from the SMPS may be efficiently employed in various actuators based on the transverse piezoelectric effect and transverse vibration modes.

1 Introduction

For many decades, piezoelectric materials have been used in helpful technologies such as medical ultrasound scanners, pressure sensors, aerospace industries, smart material systems, microelectromechanical systems (MEMS), and structural health monitoring (SHM). To improve the efficiency of transducers for various applications, non-classical media with electromechanical coupling can be used. For example, in recent years, researchers have actively studied new types of electromechanical devices based on electrostrictive, flexoelectric, photostrictive, and magnetostrictive actuators (Huang et al. 2016; Dai et al. 2021; Singh et al. 2021). In contrast to conventional piezoceramics, the mechanical strain gradient and the electric polarization, or the mechanical response and the electric field gradient, are linearly coupled in flexoelectric materials. For topological optimization of piezoelectric/flexoelectric materials, a computational design approach including isogeometric analysis (IGA), the multiphase vector level set (LS), and pointwise density-mapping techniques was developed in Ghasemi et al. (2018, 2020a). Ghasemi et al. proposed a MATLAB realization of a three-dimensional isogeometric flexoelectricity formulation with a truncated pyramid configuration (Ghasemi et al. 2020b). The flexoelectric materials’ unique electromechanical coupling mechanism enables electrically sensing strain gradient information in mechanical structures, which is considered as a sensitive indicator of the structural health condition.

Another approach is to use piezoelectric multilayer structures (Jha and Ray 2019; Ray 2021) and heterogeneous piezoceramic materials. Among diverse piezoelectric composites, porous piezoceramic materials find numerous effective practical applications (Kuscer et al. 2020; Levassort et al. 2007; Mercadelli et al. 2010; Ringgaard et al. 2015; Rybyanets et al. 2019), especially in hydroacoustic transducers and medical ultrasound devices, since they have low acoustic impedance, high hydrostatic strain and voltage coefficients, wide bandwidth, and low Q factor. Due to its high piezoelectric sensitivity, porous piezoceramics has recently become a promising material for energy storage devices (Bowen et al. 2016; Nasedkin et al. 2021b; Roscow et al. 2017, 2015; Safaei et al. 2019; Sezer and Koç 2021; Zhang et al. 2017). However, the relative effective elastic stiffness moduli and relative permittivities of porous piezoceramics rapidly decrease with increasing porosity. Absolute values of the effective piezomoduli $e^{\mathrm{eff}}_{i\alpha }$ decrease, while other relative piezomoduli associated with hydrostatic coefficients may increase, almost do not depend or slightly drop with the porosity growth (Iyer and Venkatesh 2010, 2011, 2014; Martínez-Ayuso et al. 2017; Nasedkin and Nassar 2021a; Nguyen et al. 2016). Degradation of stiffness moduli is, apparently, the most critical factor for the durability and reliability of devices with active elements made of porous piezoelectric ceramics.

Functional and electromechanical characteristics of piezoceramics with metallic inclusions differ dramatically from those of porous piezoelectric ceramics. The addition of metallic inclusions to the piezoceramic matrix can enhance the composite’s strength characteristics. Unfortunately, due to the greater electric field created inside the piezoelectric matrix, the incorporation of metallic inclusions into the piezocomposites increases the dielectric permittivity characteristics, electrical capacitance, and dielectric losses. Therefore, such piezocomposites are used as active materials in dielectric capacitors and energy storage devices (Du et al. 2016; Nan et al. 2010). The relative stiffness moduli and dielectric constants of piezoceramics with metal inclusions increase with increasing the metal volume fraction. These changes have different effects on equivalent piezomoduli. Thus, the absolute value of the relative piezomodulus $e^{\mathrm{eff}}_{31}$ decreases with increasing porosity, but the piezomoduli $e^{\mathrm{eff}}_{33}$ and $e^{\mathrm{eff}}_{15}$ increase with increasing porosity. Meanwhile, all other relative effective piezomoduli ($d^{\mathrm{eff}}_{i \alpha }$, $h^{\mathrm{eff}}_{i \alpha }$, and $g^{\mathrm{eff}}_{i \alpha }$) decrease with increasing porosity, and more significantly in comparison with conventional porous piezoceramics, see Bottero and Idiart (2016), Nasedkin et al. (2021a), Nasedkin and Nassar (2021a).

In Rybyanets and Naumenko (2013), Rybyanets et al. (2018), Rybyanets et al. developed a novel approach for fabricating the porous piezoelectric composites by transporting nanoparticles of a metal or a metal oxide in the ceramic matrices. As a result of this technology, it is possible to obtain porous piezoceramics, in which metal particles are deposited at the pore boundary. This piezocomposite is a hybrid of traditional porous piezoceramics and piezoceramics with metallic inclusions. The properties of porous piezoelectric ceramics with pore surface metallization were studied in Nasedkin and Nassar (2021a), Nasedkin and Nassar (2021b), Nasedkin and Nassar (2021c), Nasedkin and Nassar (2021d), Nasedkin et al. (2020) and Nasedkin and Nassar (2020).

Thus, in Nasedkin and Nassar (2021a) and Nasedkin et al. (2020), a comparative analysis of four types of piezocomposites with extreme properties of inclusions was carried out. Namely, the cases of ordinary porous piezoceramics, porous piezoceramics with conductive pore boundaries, porous piezoceramics with absolutely rigid pore boundaries, and porous piezoceramics with conductive and rigid pore boundaries were considered. Homogenization problems were solved in a cube-shaped cell with a spherical pore in Nasedkin and Nassar (2021a), and in a cubic lattice with a random arrangement of cubic pores in Nasedkin and Nassar (2021a) and Nasedkin et al. (2020).

In Nasedkin and Nassar (2021d) for a unit cell in the form of a cube with a spherical pore, metallization was taken into account by adding an elastic layer with conducting properties to the pore boundary. The influence of the metal layer thickness was analyzed up to the complete filling of the pore with the metal. In Nasedkin and Nassar (2020) for a similar unit cell with only conducting properties of the pore surface, the influence of the polarization field inhomogeneity of the piezoceramic matrix is analyzed, and the model considered in Nasedkin and Nassar (2021b) is a combination of models from Nasedkin and Nassar (2021d) and Nasedkin and Nassar (2020). Finally, in Nasedkin and Nassar (2021c), an elementary cell of a porous piezoelectric composite in the form of a cube with a cubic pore at partially conducting pore faces was considered.

Furthermore, hard and soft piezoceramic substrates (PZT-4 or PZT-5H) were employed as a piezoceramic matrix in these studies; however, the impacts of pore shape on the effective properties of a porous piezoelectric composite with conductive pore boundaries were not studied. We also analyzed the quality factors that characterize the exceptional properties of individual piezomoduli that occur in the considered piezocomposites.

Here, we explored two distinct porous piezocomposites. The first composite under study is the Ordinary Porous System (OPS), which doesn’t contain the metal layer on the pore surface. The second system, the porous piezocomposite with metalized pore boundaries, is of vital significance to us. For simplicity, we called this metalized porous piezocomposite the System with a Metalized Pore Surface (SMPS).

We investigated the effect of pore geometry and piezoceramic matrix type on the equivalent moduli of the OPS and SMPS. To evaluate the performance of piezocomposites in a variety of engineering applications, we reviewed several known figures of merit (FOMs) and developed new FOMs to assess the performance of both composite systems.

2 The boundary-value piezoelectric problem for heterogeneous medium

To simulate a piezoelectric composite in the volume $\varOmega$, we used the linear theory of piezoelectricity with standard constitutive equations relating mechanical stresses ${\mathbf{T}}$ and electric induction ${\mathbf{D}}$ with strains ${\mathbf{S}}$ and with electric field ${\mathbf{E}}$ (Berlincourt et al. 1964; Yang 2005)

$$\begin{aligned} {\mathbf{T}}={\mathbf{c}}^E \cdot {\mathbf{S}}-{\mathbf{e}}^* \cdot {\mathbf{E}}, \quad {\mathbf{D}}={\mathbf{e}} \cdot {\mathbf{S}}+{{\varvec{\varepsilon }}}^S \cdot {\mathbf{E}}. \end{aligned}$$

(1)

The elastic strains ${\mathbf{S}}$ and the electric field intensity vector ${\mathbf{E}}$ can be obtained from the mechanical displacement ${\mathbf{u}}= {\mathbf{u}}({\mathbf{x}})$ and the electric potential $\varphi = \varphi ({\mathbf{x}})$, respectively, using the following relationships

$$\begin{aligned}&{\mathbf{S}}={\mathbf{L}}(\nabla )\cdot {\mathbf{u}}, \quad {\mathbf{E}}=-\nabla \varphi , \end{aligned}$$

(2)

$$\begin{aligned}&{\mathbf{L}}^*(\nabla )=\left[ \begin{array}{cccccc} \partial _1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{} \quad \partial _3 &{}\quad \partial _2 \\ 0 &{}\quad \partial _2 &{}\quad 0 &{}\quad \partial _3 &{}\quad 0 &{}\quad \partial _1 \\ 0 &{}\quad 0 &{}\quad \partial _3 &{}\quad \partial _2 &{}\quad \partial _1 &{}\quad 0 \\ \end{array} \right] , \quad \nabla =\left\{ \begin{array}{c} \partial _1\\ \partial _2\\ \partial _3\\ \end{array} \right\} . \end{aligned}$$

(3)

The static piezoelectric homogenization problem includes the equilibrium equations neglecting the body forces and the quasi-electrostatic equation without the free electric charges

$$\begin{aligned} {\mathbf{L}}^*(\nabla )\cdot {\mathbf{T}}=0,\quad \nabla \cdot {\mathbf{D}}=0. \end{aligned}$$

(4)

The external boundary conditions applied here on the boundary $\varGamma = \partial \varOmega$ have the following standard form for the effective moduli method (Berger et al. 2006; Nasedkin and Nassar 2021a; Nasedkin and Shevtsova 2011; Nasedkin et al. 2020; Singh et al. 2021)

$$\begin{aligned} {\mathbf{u}}={\mathbf{L}}^*({\mathbf{x}})\cdot {\mathbf{S}}_0,\quad \varphi =-{\mathbf{x}}\cdot {\mathbf{E}}_0,\quad {\mathbf{x}}\in \varGamma . \end{aligned}$$

(5)

In (1)–(5), ${\mathbf{T}}= \{T_{1}$, $T_{2}$, $T_{3}$, $T_{4}$, $T_{5}$, $T_{6}$}= {$\sigma _{11}$, $\sigma _{22}$, $\sigma _{33}$, $\sigma _{23}$, $\sigma _{13}$, $\sigma _{12}$} is the array of mechanical stress components $\sigma _{ij}$; ${\mathbf{S}} = \{S_{1}$, $S_{2}$, $S_{3}$, $S_{4}$, $S_{5}$, $S_{6}$}= {$S_{11}$, $S_{22}$, $S_{33}$, $2S_{23}$, $2S_{13}$, $2S_{12}$} is the array of the strain components $S_{ij}$; ${\mathbf{D}}$ is the vector of electric induction or the electric charge displacement vector; ${\mathbf{c}}^E$ is the $6\times 6$ matrix of short-circuit elastic stiffness moduli $c^E_{\alpha \beta }$; e is the $3\times 6$ matrix of the piezoelectric moduli (stress coefficients) $e_{i \beta }$; ${\varvec{\varepsilon }}^S$ is the $3\times 3$ matrix of the dielectric permittivity moduli $\varepsilon ^S_{ij}$ at fixed mechanical strain; ${\mathbf{L}}(\nabla )$ and $\nabla$ are differential matrix and vector operators, respectively; ${\mathbf{L}}({\mathbf{x}})$ is the matrix of the same structure as (3), when the argument $\nabla$ is replaced by ${\mathbf{x}}$; ${\mathbf{x}} = \{x, y, z\} = \{x_1, x_2, x_3\}$ is the vector of spatial coordinates; ${\mathbf{S}}_0$ and ${\mathbf{E}}_0$ are the six-dimensional and three-dimensional arrays with some constant values; $(\ldots )^*$ denotes the matrix transpose operation; and $(\ldots )\cdot (\ldots )$ is the scalar product operation of matrices or vectors; $\alpha , \beta =1, 2, \ldots , 6$; $i, j=1, 2, 3$.

The representative volume $\varOmega$ of the piezocomposites understudy can be generally defined as follows: $\varOmega =\varOmega ^m \cup \varOmega ^c$, where $\varOmega ^m$ is the volume filled with the basic piezoelectric material, and $\varOmega ^c$ is the volume of the compound pore. The compound pore $\varOmega ^c$ for the SMPS consists of a vacuum pore $\varOmega ^p$ with a very thin metal layer $\varOmega ^e$ on its surface, i.e., $\varOmega ^c=\varOmega ^e \cup \varOmega ^p$. The OPS doesn’t contain the metal layer on the pore surface, i.e., $\varOmega ^c= \varOmega ^p$, and $\varOmega =\varOmega ^m \cup \varOmega ^p$.

We modeled the pore as a piezoelectric material with negligible material moduli. In the metal layer, we defined another piezoelectric material with negligible elastic stiffnesses, negligible piezomoduli, and very high dielectric constants. This approach of modeling pores and conductive inclusions was previously justified in Nasedkin and Nassar (2021a), Nasedkin and Nassar (2021d) and Nasedkin et al. (2020). As a result, it is convenient for solving homogenization problems for both the OPS and the SMPS. On the interfaces between any two neighboring phases, e.g., I and II, we considered the standard full contact conditions

$$\begin{aligned}&{\mathbf{u}}^I={\mathbf{u}}^{II}, \quad {\mathbf{L}}^*(\mathbf{n})\cdot {\mathbf{T}}^I={\mathbf{L}}^*(\mathbf{n})\cdot {\mathbf{T}}^{II},\quad {\mathbf{x}}\in \varGamma ^i, \end{aligned}$$

(6)

$$\begin{aligned}&\varphi ^I=\varphi ^{II},\quad \mathbf{n}\cdot {\mathbf{D}}^I=\mathbf{n}\cdot {\mathbf{D}}^{II},\quad {\mathbf{x}}\in \varGamma ^i, \end{aligned}$$

(7)

where I and II may be the piezoceramic matrix ($\varOmega ^m$) and the conductive layer ($\varOmega ^e$), or the conductive layer ($\varOmega ^e$) and the vacuum pore ($\varOmega ^p$), respectively; $\varGamma ^i = \varGamma ^e$ or $\varGamma ^p$, $\varGamma ^e$ and $\varGamma ^p$ are the boundaries of the volumes $\varOmega ^e$ and $\varOmega ^p$, respectively; $\mathbf{n}$ is the unit normal vector to the corresponding surface.

It is worth noting that for the OPS the problem (1)–(7) in $\varOmega$ is equivalent to the problem (1)–(5) in $\varOmega ^m$ with the following conditions on the interface boundary

$$\begin{aligned} {\mathbf{L}}^*(\mathbf{n})\cdot {\mathbf{T}}=0,\quad \mathbf{n}\cdot {\mathbf{D}}=0,\quad {\mathbf{x}}\in \varGamma ^p, \end{aligned}$$

because such equations are essentially satisfied when a fictitious piezoelectric material with marginal small moduli fills the pore.

For the SMPS, if the very thin metal layer completely covers the pore boundary, the problem (1)–(7) in $\varOmega$ is equivalent to the problem (1)–(5) in $\varOmega ^m$ with the conditions on the interface boundary of the form

$$\begin{aligned} {\mathbf{L}}^*(\mathbf{n})\cdot {\mathbf{T}}=0,\quad \varphi =\varPhi ^c,\quad \int _{\varGamma ^c}{} \mathbf{n}\cdot {\mathbf{D}}d\varGamma =0,\quad {\mathbf{x}}\in \varGamma ^c, \end{aligned}$$

where $\varPhi ^c$ is an unknown constant electric voltage on $\varGamma ^c$.

Further, from the solutions of the problems (1)–(7), we obtained the effective moduli associated with the constitutive equations (1). These effective piezomoduli were used later to calculate the other effective moduli associated with the following constitutive equations

$$\begin{aligned}&{\mathbf{S}}={\mathbf{s}}^E \cdot {\mathbf{T}}+{\mathbf{d}}^* \cdot {\mathbf{E}},\ \quad {\mathbf{D}}={\mathbf{d}}\cdot {\mathbf{T}}+{\varvec{\varepsilon }}^T\cdot {\mathbf{E}}, \end{aligned}$$

(8)

$$\begin{aligned}&{\mathbf{T}}={\mathbf{c}}^D \cdot {\mathbf{S}}-{\mathbf{h}}^* \cdot {\mathbf{D}},\quad {\mathbf{E}}=-{\mathbf{h}}\cdot {\mathbf{S}}+{\varvec{\beta }}^S\cdot {\mathbf{D}}, \end{aligned}$$

(9)

$$\begin{aligned}&{\mathbf{S}}={\mathbf{s}}^D \cdot {\mathbf{T}}+{\mathbf{g}}^* \cdot {\mathbf{D}},\quad {\mathbf{E}}=-{\mathbf{g}}\cdot {\mathbf{T}}+{\varvec{\beta }}^T\cdot {\mathbf{D}}, \end{aligned}$$

(10)

where

$$\begin{aligned}&{\mathbf{s}}^E=({\mathbf{c}}^E)^{-1}, \quad {\mathbf{d}}={\mathbf{e}}\cdot {\mathbf{s}}^E, \quad {\varvec{\varepsilon }}^T={\varvec{\varepsilon }}^S+{\mathbf{d}}\cdot {\mathbf{e}}^*,. \end{aligned}$$

(11)

$$\begin{aligned}&{\mathbf{c}}^D={\mathbf{c}}^E+{\mathbf{e}}^* \cdot {\mathbf{h}},\quad {\mathbf{h}}={\varvec{\beta }}^S \cdot {\mathbf{e}}, \quad {\varvec{\beta }}^S=({\varvec{\varepsilon }}^S)^{-1}, \end{aligned}$$

(12)

$$\begin{aligned}&{\mathbf{s}}^D={\mathbf{s}}^E-{\mathbf{d}}^* \cdot {\mathbf{g}}= ({\mathbf{c}}^D)^{-1},\quad {\mathbf{g}}={\mathbf{h}}\cdot {\mathbf{s}}^D ={\varvec{\beta }}^T\cdot {\mathbf{d}},\nonumber \\&\quad {\varvec{\beta }}^T=({\varvec{\varepsilon }}^T)^{-1}. \end{aligned}$$

(13)

Here, ${\mathbf{s}}^E$ and ${\mathbf{s}}^D$ are the $6\times 6$ matrices of elastic compliance moduli under constant electric field (short circuit) and constant electric charge density (open circuit), respectively; ${\mathbf{c}}^D$ is the $6\times 6$ matrix of elastic stiffness moduli under constant electric charge density; ${\mathbf{d}}$, ${\mathbf{h}}$, ${\mathbf{g}}$ are the $3\times 6$ matrices of the piezoelectric moduli (charge coefficients, strain coefficients, voltage coefficients, respectively); ${\varvec{\varepsilon }}^T$ is the $3\times 3$ matrix of the dielectric permittivity moduli under constant mechanical stress; ${\varvec{\beta }}^S$ and ${\varvec{\beta }}^T$ are the $3\times 3$ matrices of dielectric impermeability moduli under constant mechanical strain and mechanical stress, respectively.

Regarding the piezomoduli, we utilized the most common designations corresponding to the second equations (1), (8)–(10) according to the direct piezoelectric effect under a mechanical influence. For example, the piezoelectric charge coefficient $d_{j\beta }$ is so named because when the mechanical stress $T_{\beta }$ is applied, according to the second equation (8), it determines the produced electrical induction $D_j$, i.e., electric charge. If we focus on the first equations (1), (8)–(10) for the inverse piezoelectric effect under the electrical influence, then the piezoelectric constants can be called differently. Thus, the piezoelectric coefficient $d_{j\beta }$ can be considered the piezoelectric strain coefficient, since with an applied electric field $E_j$ it determines developed mechanical strain $S_{\beta }$.

Although the constitutive relations (1), (8)–(10) are analogous, in some cases, distinct constitutive equations and material moduli (11)–(13) may be more convenient. Some of the effective material coefficients (11)–(13) are utilized in the next section to calculate the figure of merits (FOMs).

3 Figures of merit (FOMs)

Various performance metrics or FOMs have been developed to determine the effectiveness of piezoelectric materials and piezoelectric devices. These indicators can be considered material characteristics oriented to specific intended applications. For stationary or low-frequency operation modes of piezoelectric devices, the quality indicators usually contain only material moduli. For transient dynamics and high-frequency applications, these indicators may also include damping parameters (Priya 2010; Song et al. 2020) and resonance characteristics. In this section, we consider FOMs defined only through material moduli. These indicators can help us determine the performance of new porous piezoceramic composites with metalized pore boundaries in different quasistatic practical applications.

We assume that the piezoelectric material belongs to the 6mm anisotropy class, i.e., to the same class as piezoelectric ceramics.

3.1 Electromechanical coupling coefficients

Electromechanical coupling coefficients are some of the earliest and well known FOMs (Berlincourt et al. 1964; Bowen et al. 2016; Kenji and Giniewicz 2003; Yang 2005). They have several definitions, which often yield the same value. We only investigated the electromechanical coupling coefficients for canonical piezoelectric transducers, where some of the mechanical and electric field components on the right-hand sides of the corresponding constitutive equations are nonzero.

For example, consider the most used constitutive equations (8). Using these equations, the energy per unit volume or the energy density $U = ({\mathbf{T}} \cdot {\mathbf{S}} + {\mathbf{D}} \cdot {\mathbf{E}})/2$ can be represented in the form $U = U_e + 2U_m + U_d$, where $U_e = ({\mathbf{T}}^* \cdot {\mathbf{s}}^E \cdot {\mathbf{T}})/2$ is the mechanical energy density, $U_d = ({\mathbf{E}}^* \cdot {\varvec{\varepsilon }}^T\cdot {\mathbf{E}})/2$ is the electrical energy density, $U_m = ({\mathbf{E}}^* \cdot {\mathbf{d}} \cdot {\mathbf{T}})/2$ is the mixed energy density. Then, the following formula can be used for the electromechanical coupling coefficients

$$\begin{aligned} k^2=\frac{U_m^2}{U_e U_d}. \end{aligned}$$

(14)

If in piezoelectric transducer such a state is realized when among the mechanical stresses only one component $T_{\beta }$ is nonzero, and among the components of the electric field vector, only one component $E_j$ is also nonzero, then from (14) we obtain

$$\begin{aligned} k_{j\beta }^2=\frac{d_{j\beta }^2}{\varepsilon _{jj}^T s_{\beta \beta }^E}. \end{aligned}$$

(15)

Similarly, from (9), (14), when $U_e = ({\mathbf{S}}^* \cdot {\mathbf{c}}^D \cdot {\mathbf{S}})/2$, $U_d = ({\mathbf{D}}^* \cdot {\varvec{\beta }}^S\cdot {\mathbf{D}})/2$, $U_m = -({\mathbf{D}}^* \cdot {\mathbf{h}} \cdot {\mathbf{S}})/2$, for the electromechanical state with nonzero components $S_{\beta }$ and $D_j$, we obtain other electromechanical coupling coefficients

$$\begin{aligned} {\tilde{k}}_{j\beta }^2=\frac{h_{j\beta }^2}{\beta _{jj}^S c_{\beta \beta }^D}. \end{aligned}$$

(16)

In Eq. (16), ${\tilde{k}}_{15} = k_{15}$, and the coefficients ${\tilde{k}}_{33}$ and ${\tilde{k}}_{15}$ for piezoceramics are often denoted as follows Berlincourt et al. (1964): ${\tilde{k}}_{33} = k_t$, ${\tilde{k}}_{31}= {k}^{\prime \prime \prime }_{31}$.

It should be noted that in the constitutive relations (8) and (9), extensive quantities ${\mathbf{T}}$ and ${\mathbf{E}}$ are located on one side of the equal sign, and intensive quantities ${\mathbf{S}}$ and ${\mathbf{D}}$ are located on the other. Meanwhile, in the constitutive equations (1) and (10), extensive and intensive quantities are located both on the left and on the right, and in such cases, the electromechanical coupling coefficients must be determined by the formula

$$\begin{aligned} \frac{k^2}{1-k^2}=\frac{U_m^2}{U_e U_d}, \end{aligned}$$

(17)

where $U=(U_e- U_m) + (U_m+ U_d)$.

Here, for Eq. (10), $U_e = ({\mathbf{T}}^* \cdot {\mathbf{s}}^D \cdot {\mathbf{T}})/2$, $U_d = ({\mathbf{D}}^* \cdot {\varvec{\beta }}^T\cdot {\mathbf{D}})/2$, $U_m = ({\mathbf{D}}^* \cdot {\mathbf{g}} \cdot {\mathbf{T}})/2$, and for nonzero fields $T_{\beta }$ and $D_j$ with Eqs. (13) and (17) we obtain the same coefficients as in (15)

$$\begin{aligned} k_{j\beta }^2=\frac{g_{j\beta }^2}{\left( \beta _{jj}^T s_{\beta \beta }^D + g_{j\beta }^2\right) } = \frac{g_{j\beta }^2}{\beta _{jj}^T s_{\beta \beta }^E} = \frac{d_{j\beta }^2}{\varepsilon _{jj}^T s_{\beta \beta }^E}. \end{aligned}$$

Similarly, for Eq. (1), $U_e = ({\mathbf{S}}^* \cdot {\mathbf{c}}^E \cdot {\mathbf{S}})/2$, $U_d = ({\mathbf{E}}^* \cdot {\varvec{\varepsilon }}^S\cdot {\mathbf{E}})/2$, $U_m = -({\mathbf{E}}^* \cdot {\mathbf{e}} \cdot {\mathbf{S}})/2$, and for nonzero fields $S_{\beta }$ and $E_j$, with Eqs. (12) and (17) we have the electromechanical coupling coefficients coinciding with (16)

$$\begin{aligned} {\tilde{k}}_{j\beta }^2=\frac{e_{j\beta }^2}{\left( \varepsilon _{jj}^S c_{\beta \beta }^E + e_{j\beta }^2\right) } = \frac{e_{j\beta }^2}{\varepsilon _{jj}^S c_{\beta \beta }^D} =\frac{h_{j\beta }^2}{\beta _{jj}^S c_{\beta \beta }^D}. \end{aligned}$$

The downsides of the definitions (14), (17) are that they are dependent on energies, which in turn rely on constitutive relations. For these reasons, more general energetic definitions of electromechanical coupling coefficients are preferable.

So, from the sensing applications point of view, the electromechanical coupling coefficient $k^2$ describes the conversion efficiency from the mechanical energy entering in the piezoelectric material $(U^{\mathrm{ mech}}_{\mathrm{ input}})$ to the electrical energy stored inside the material $(U^{\mathrm{ elec}}_\mathrm{ stored})$. From the viewpoint of actuator applications, the electromechanical coupling coefficient measures the conversion efficiency from the electrical energy entering in the piezoelectric material $(U^{\mathrm{ elec}}_{\mathrm{ input}})$ to the stored mechanical energy $(U^{\mathrm{ mech}}_{\mathrm{ stored}})$. As shown in many works, e.g. Deutz et al. (2018), Roscow et al. (2015) and Roscow et al. (2019), for canonical cases, these values turn out to be equal and coincide with (15), (16)

$$\begin{aligned} k^2=\frac{U^{\mathrm{ elec}}_{\mathrm{ stored}}}{U^{\mathrm{ mech}}_\mathrm{ input}}=\frac{U^{\mathrm{ mech}}_{\mathrm{ stored}}}{U^{\mathrm{ elec}}_\mathrm{ input}}. \end{aligned}$$

(18)

To calculate the energies in (18), an idealized cycle of changes in the elastic or electrical state can be considered by analyzing a part of mechanical energy that can be converted into electrical energy or, conversely, a portion of electrical energy that can be converted into mechanical energy. Namely, by calculating the energy in the piezoelectric transducer under mechanical stress with short-circuited electrodes $U_E$ and the energy with open electrodes $U_D$, or by calculating the energy with an active electric field of the free transducer $U_T$ and the energy of the clamped transducer $U_S$, one can determine the coupling coefficient by the formulas

$$\begin{aligned} k^2=\frac{U_E-U_D}{U_E}, \quad k^2=\frac{U_T-U_S}{U_T}. \end{aligned}$$

These formulas change depending on active external influences. So, under strain effects or with applied electric charges (currents), we have

$$\begin{aligned} k^2=\frac{U_D-U_E}{U_D}, \quad k^2=\frac{U_S-U_T}{U_S}, \end{aligned}$$

here, the electromechanical coupling factor is also identical in both cases.

Therefore, upon applying mechanical stress $T_\beta$ on the piezoelectric material, the stored electrical energy equals the product of the entering mechanical energy $(U^{\mathrm{ mech}}_\mathrm{ input})$ and the coupling coefficient $k^2={d^2}/({\varepsilon ^T s^E})$; so, the compliance effect is canceled out. As a consequence, the coupling coefficient is an insignificant FOM for determining the material efficiency in energy harvesting and sensing applications, as stated in Deutz et al. (2018) and Priya (2007). Although many works (Iyer and Venkatesh 2010, 2011) demonstrated that introducing porosity to the piezoelectric materials enhances their performance in the sensing applications, we found that the coupling coefficient of the OPS decreases with the porosity growth. This confirms that the coupling factor doesn’t assess the material’s functioning accurately.

3.2 Transduction coefficients (TC = dg)

According to Islam and Priya (2006), the fundamental factor for evaluating the piezoelectric material as an energy harvester is the transduction coefficient, which equals the product of the piezoelectric charge and voltage moduli $d\, g$ or $d^2/\varepsilon ^T$. However, the transduction coefficient deduced in Deutz et al. (2018), Islam and Priya (2006) and Roscow et al. (2019) assesses the material efficiency in sensing and energy harvesting applications. For sensor applications, the stored electrical energy per unit volume can be related to the sensor transduction coefficient when applying mechanical stress $T_\beta$ for open circuit voltage as follows

$$\begin{aligned} U^{\mathrm{ elec}}_{\mathrm{ stored}}=\frac{1}{2} C V^2/(2At)=\frac{1}{2}\varepsilon _{jj}^T E^2_j=\frac{1}{2}\left( d_{j\beta }^2/ \varepsilon _{jj}^T\right) T^2_{\beta }. \end{aligned}$$

Here, the piezoelectric material is treated as a capacitor plate, $C = \varepsilon _{jj}^T\cdot A/t$ is the capacitance, $V = -E_j t$ is the piezoelectric voltage developed between the electrodes, $E_j = -T_\beta d_{j\beta } \varepsilon _{jj}^T$, A is the cross-sectional area, and t is the thickness of the plate.

This ensures that the stored electric energy due to applied stress is independent of the material compliance; consequently, the transduction coefficient evaluates the sensing effect of the material better than the coupling coefficient $k^2$. The transduction coefficient for sensor applications can be expressed by the formula

$$\begin{aligned} (TC_{j\beta })_S=\frac{d_{j\beta }^2}{\varepsilon _{jj}^T} \end{aligned}$$

(19)

In the same way, we derived the transduction coefficient $(TC_{j\beta })_A$, which assesses the material’s actuating effect. When an electric field $E_j$ is applied on the free piezoelectric transducer, the stored mechanical energy be Eq. (18) equals the product of the entering electric energy $\left( U^\mathrm{ elec}_{\mathrm{ input}}= \varepsilon ^T_{jj} E_j^2/2 \right)$ and the coupling coefficient $k^2_{j\beta }=d_{j\beta }^2 /(\varepsilon ^T_{jj} s^E_{\beta \beta })$; so, the dielectric permittivity effect is canceled out. So, considering the method presented in Islam and Priya (2006), the stored mechanical energy under upon applying an electric field can be related to the actuator transduction coefficient $(TC_{j\beta })_A$ as follows

$$\begin{aligned} U^{\mathrm{ mech}}_{\mathrm{ stored}}=k^2_{j\beta } U^{\mathrm{ elec}}_\mathrm{ input}=\frac{1}{2}\, \left( d_{j\beta }^2/s_{\beta \beta }^E\right) E_j^2. \end{aligned}$$

So, the transduction coefficient for actuating effect can be expressed by the formula

$$\begin{aligned} (TC_{j\beta })_A=\frac{d_{j\beta }^2}{s_{\beta \beta }^E}. \end{aligned}$$

(20)

Thus, the sensor (energy harvesting) transduction coefficient $(TC_{j \beta })_S$ assesses the material’s ability to convert the entering mechanical energy to a stored electric energy; whereas, the actuator transduction coefficient $(TC_{j \beta })_A$ evaluates the material’s ability to transform the entering electrical energy to a stored mechanical energy.

3.3 Energy transmission coefficients $\lambda _{max}$

When using the piezoelectric transducer as an actuator, the actual work performed depends on the mechanical load. The energy production constitutes a fraction of the energy retained from the piezoelectric effect. If the piezoelectric actuator is free from mechanical stresses or clamped, the total output power appears to be zero. In Kenji and Giniewicz (2003), the maximum energy transmission coefficient was determined as follows:

• for actuator applications $\lambda _{\mathrm{1\, max}}=[U^{\mathrm{ mech}}_{\mathrm output}/U^\mathrm{ elec}_{\mathrm input}]_{\mathrm{max}}$,

• for sensing (energy harvesting) applications $\lambda _{\mathrm{1\, max}}=[U^{\mathrm{ elec}}_{\mathrm output}/U^\mathrm{ mech}_{\mathrm input}]_{\mathrm{max}}$.

In both cases $\lambda _{\mathrm{1\, max}}$ can be obtained using the following relationship

$$\begin{aligned} \lambda _\mathrm{1\, max}=\left[ \frac{1}{k}-\root \of {\frac{1}{k^2}-1}\right] ^2=\left[ \frac{1}{k}+\root \of {\frac{1}{k^2}-1}\right] ^{-2}. \end{aligned}$$

(21)

However, Deutz et al. (2018) reported that the maximum transmission coefficient, obtained in Kenji and Giniewicz (2003), is satisfied when the strain resulting from the external mechanical stress is equal to the strain generated due to the applied electric field. In this situation, the actual output power tends to zero. As a consequence, they concluded that the maximum transmission coefficient can’t estimate the material efficiency. Instead of the maximum transmission coefficient, they introduced the transmission coefficient for maximum output energy, as indicated in the following relationship

$$\begin{aligned} \lambda _{\mathrm{2\, max}}=\frac{k^2}{4-2 k^2}. \end{aligned}$$

(22)

To derive this relationship, they applied an electric field E on the piezoelectric transducer, which is primarily subjected to a compressive mechanical load, and estimated the resultant output mechanical energy due to interaction between the externally applied mechanical stress and the converse piezoelectric effect. After that, they obtained the maximum output mechanical energy as follows

$$\begin{aligned} \vert U^{\mathrm{mech}}_{\mathrm{output \, max}} \vert =\frac{d^2}{8s}\, |{\mathbf{E}}|^2, \end{aligned}$$

where d is the piezoelectric charge coefficient, s is the corresponding elastic compliance modulus.

This concept implies that the maximum output mechanical energy occurs when the strain produced by the external mechanical load is half the strain induced due to the applied electric field. Also, this relationship of the maximum output mechanical energy confirms the actuator transduction coefficient $(TC_{j\beta })_A$ presented in (20). However, the second concept appears to be more effective physically, both concepts $\lambda _{\mathrm{1\, max}}$ and $\lambda _{\mathrm{2\, max}}$ are approximately identical when $k^2<0.5$ (Deutz et al. 2018), as seen in Fig. 1. In this work $k^2<0.5$ for all studied cases, so $\lambda _{\mathrm{1\, max}} \cong \lambda _{\mathrm{2\, max}}=\lambda _{\mathrm{max}}$.

Fig. 1

The maximum transmission coefficient $\lambda _{\mathrm{1\, max}}$ and the transmission coefficient for maximum output energy $\lambda _{\mathrm{2\, max}}$ versus the coupling coefficient $k^2$

As stated in Deutz et al. (2018) and Roscow et al. (2019), the transmission coefficient is used to estimate the portion of the stored energy, which is eventually transformed into productive work. This fraction defines the coupling between the stored energy and the maximum output energy according to the formulas

$$\begin{aligned} U_{\mathrm{output \, max}}=\frac{\lambda _{\mathrm{max}}}{k^2}\, U_\mathrm{stored}=\frac{1}{4-2 k^2} \, U_{\mathrm{stored}}. \end{aligned}$$

3.4 Energy harvesting FOMs

Knowing that the stored energy mainly depends on the transduction coefficients $(TC_{j \beta })_S$ and $(TC_{j \beta })_A$ for sensor and actuator applications, respectively; we derived the energy harvesting figures of merit $(FOM_{j \beta })_S$ and $(FOM_{j \beta })_A$ for evaluating the efficiency of piezoelectric transducers in sensor and actuator applications, respectively, as follows

$$\begin{aligned}&(FOM_{j \beta })_S= \frac{\lambda _{j \beta \, \mathrm{max}}}{k_{j \beta }^2}\, (TC_{j \beta })_S, \end{aligned}$$

(23)

$$\begin{aligned}&(FOM_{j \beta })_A= \frac{\lambda _{j \beta \, \mathrm{max}}}{k_{j \beta }^2}\, (TC_{j \beta })_A, \end{aligned}$$

(24)

where the coefficient $\lambda _{j \beta \, \mathrm{max}}$ is determined by (21) or (22) for $k = k_{j \beta }$.

3.5 Hydrostatic figure of merit $HFOM=d_h g_h$

The hydrostatic FOM (HFOM) measures the piezoelectric transducer’s efficiency for use in hydrophone devices. Higher values of the HFOM mean a better device’s ability to distinguish the acoustic signal from the ambient noise. The HFOM can be calculated using the following equation (Iyer and Venkatesh 2014; Yang et al. 2010; Zhang et al. 2018)

$$\begin{aligned} HFOM=d_h \, g_h, \end{aligned}$$

(25)

where $d_h=d_{33}+2d_{31}$, and $g_h=d_h/\varepsilon _{33}^T$.

4 Finite element models and simulation methodology

For conducting analysis, we have developed a set of special programs in the APDL language that implement algorithms for solving homogenization problems in the ANSYS finite element package.

4.1 Representative volumes and material properties

The first objective of this work is to compare the effective material properties of a unit cell with a cubic pore and a unit cell with a spherical pore for the OPS and the SMPS. The second objective was to study the effect of the material of the piezoceramic matrix on effective moduli. In this regard, calculations for two types of unit cells were carried out for three different piezoceramic materials, namely, modified PbTiO$_3$ (I) (Bowen et al. 2016; Ikegami et al. 1971), TBKS (Bowen et al. 2016), and PZT-5H (Kunkel et al. 1990). These materials were chosen for their varying longitudinal to transverse piezomoduli ratios. For the materials PbTiO$_3$, TBKS, and PZT-5H, the ratio $e_{33}/e_{31}=16.73, \, -11.34$, and $-3.58$, respectively. The material properties of the piezoelectric materials under consideration were listed in Table 1. Here, $\varepsilon _0=8.85 \cdot 10^{-12}$ (F/m) is the vacuum dielectric permittivity. For the vacuum pore $\varOmega ^p$, we defined the values $(c_{\alpha \beta }^E)_p=\kappa c_{\alpha \beta }^E$, $(e_{i\alpha })_p=\kappa e_{i\alpha }$, $(\varepsilon _{ii}^S)_p=\varepsilon _0,$ for elastic moduli, piezomoduli, and dielectric permittivities, respectively, where $\kappa =10^{-10}$. For the metalized pore surface $\varOmega ^e$, we defined the material properties as follows: $(c_{\alpha \beta }^E)_e=\kappa c_{\alpha \beta }^E$, $(e_{i\alpha })_e=\kappa e_{i\alpha }$, $(\varepsilon _{ii}^S)_p=\chi \varepsilon _0$, where $\chi =10^{12}$.

Table 1 The material properties of the considered piezoelectric materials ($c_{\alpha \beta }^E$ in GPa, $e_{i\beta }$ in C/m$^2$)

We solved the homogenization problems (1)–(7) for two geometric configurations of the representative unit cell element $\varOmega$. In both cases, the volume $\varOmega$ is a cube with edge length L and contains a pore at its center. A simple porosity model is employed in this work to investigate the influence of pore shape on the effective moduli of the considered composites. The findings obtained using this simple periodic representative volume were verified using a random representative volume in Nasedkin and Nassar (2021a), and there was good agreement, particularly when porosity was less than 40%.

In the first geometric model, the compound pore $\varOmega ^c$ was modeled by a sphere with radius $R=L \root 3 \of {3\,\upsilon _p/{4\pi }}$, where $\upsilon _p = |\varOmega ^c|/|\varOmega |$ denotes the porosity volume fraction. The pore outer radius R satisfies the inequality $R<L/2$ the percentage of porosity $p=100\upsilon _p$ in this model is limited, $p<52 \%$. For SMPS, inside the volume of a composite pore $\varOmega ^c$ we modeled the metalized pore surface $\varOmega ^e$ by a spherical layer with radii $R-h$ and R.

For the second case of the unit cell, we constituted a cubic pore with edge length B, where $B=L \ \root 3 \of {\upsilon _p}$. Here, the metalized pore surface was modeled by a cubic layer with the edges $B-h$ and B. It’s worth noting that the centers of both representative volumes are the global origin.

The layer thickness in both cases was assumed to be $h=R/10$. This value was chosen for the convenience of constructing a high-quality finite element mesh, since the layer thickness does not affect the results when modeling a conductive coating of a pore with a piezoelectric medium with very high dielectric permittivities and with negligible stiffness moduli and piezomoduli, as detailed in Nasedkin and Nassar (2021a), Nasedkin and Nassar (2021d) and Nasedkin et al. (2020).

The 10-node tetrahedral elements SOLID227 with the option of piezoelectric analysis were applied to create the finite element mesh. In these elements, each node has three translational degrees of freedom (DOFs) ($u_x$, $u_y$, and $u_z$) and one DOF for the electric voltage ($\varphi$); so, the total number of DOFs is four times the total number of nodes utilized in the finite element model. We used a free mesh with the ability to control the maximum edge length of the elements ($l_{el}$). Table 2 presents a convergence test of certain relative effective properties with respect to $l_{el}$. (The technique for determining these effective moduli and the notation for the relative moduli will be presented below.) The effective moduli presented in Table 2 show monotonic convergence as max allowable element edge length $l_{el}$ decreases. For such simple grids, the findings for both investigated composites were obtained with acceptable relative accuracy utilizing various piezoceramic matrices by restricting the element’s maximum edge to L/8 when the porosity is less than 40% and L/10 for greater porosity volume fractions. The maximum error is 1.1% is related to the relative piezomodulus $r(e_{33})$.

Table 2 Convergence test of the effective properties in terms of the maximum allowable edge length ($l_{el}$) of the finite elements

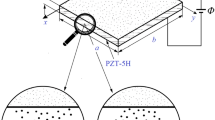
Examples of the employed finite element meshes for the SMPS are shown in Fig. 2. Here, piezoelectric elements SOLID227 with different material properties are depicted in various colors. The light blue elements represent the volume occupied with the main piezoelectric material ($\varOmega ^m$), the red elements represent the metalized pore surface ($\varOmega ^e$), and the light gray elements represent the volume occupied with the vacuum ($\varOmega ^p$).

Fig. 2

Finite element mesh for the back half of unit cell at porosity $p=20$% for the SMPS with a spherical pore and a cubic pore in (a) and (b), respectively, and a unit cell with a spherical pore with named boundaries in (c)

4.2 Computation of the effective moduli

We solved the boundary-value homogenization problems (1)–(7) using the finite element method to obtain the effective moduli of the OPS and the SMPS. These problems were solved under certain non-zero influences ${\mathbf{S}}_0$ and ${\mathbf{E}}_0$ in the external boundary conditions (5) according to the method of effective moduli (Hori and Nemat-Nasser 1998; Martínez-Ayuso et al. 2017; Nasedkin and Shevtsova 2011; Nasedkin et al. 2020). Because the SMPS is a piezocomposite with insufficiently explored material properties, we defined a complete set of its effective moduli , i.e., 81 material constants. We considered an asymmetric elastic stiffness matrix (36 elastic moduli $c_{\alpha \beta }^{E\, \mathrm{eff}}$), different values for the direct and the converse piezoelectric effects (36 piezomoduli $e_{i \beta }^{d\, \mathrm{eff}}$ and $e_{i \beta }^{c\, \mathrm{eff}}$), and nine permittivity constants $\varepsilon _{ij}^{S\, \mathrm{eff}}$.

Using the concept of the effective moduli method, we solved the homogenization problems (1)–(7) nine times. Each time, the problem was solved under one non-zero component of the boundary-conditions array of ${\mathbf{S}}_0$ and ${\mathbf{E}}_0$, defined in (5). These boundary conditions were discussed in more detail in Nasedkin and Nassar (2021a), Nasedkin and Shevtsova (2011) and Nasedkin et al. (2020). Then, we used the following formula to calculate the average value of the stress and electric induction components obtained from the boundary-value problem’s solutions

$$\begin{aligned} \langle \cdots \rangle =\frac{1}{|\varOmega |} \int _\varOmega (\cdots ) \,d\varOmega . \end{aligned}$$

(26)

Using the average values of the solutions’ components, we obtained the effective moduli of the piezocomposites under study. First, we solved the problem (1)–(7) six times ($\beta = 1, 2, \ldots , 6$) for the following values in the boundary conditions (5)

$$\begin{aligned} S_{0\zeta }=S_0 \delta _{\zeta \beta }, \quad {\mathbf{E}}_{0}=0, \end{aligned}$$

(27)

where $\zeta = 1, 2, \ldots , 6$; $S_0$ is a non-zero constant value.

The prescribed non-zero displacements $u_i$ for the homogenization boundary value problems (1)–(7), (27) with $\beta = 1, 2, \ldots , 6$ on the boundaries $B_1, B_2, \ldots , B_6$, according to Fig. 2c, are presented in Table 3. Here, the electric potential $\varphi$ and the unstated $u_j$ values for each boundary are equal to zero.

Table 3 The prescribed non-zero displacements (${{\tilde{u}}}_i = u_i/S_0$) at the nodes located on the boundaries ($B_1$ to $B_6$) for the problems with $\beta = 1, 2, \dots , 6$ in Eq. (27)

Finding the averaged components of stresses and electric induction using (26), according to Nasedkin and Nassar (2021a), Nasedkin and Shevtsova (2011), Nasedkin et al. (2020), and Nasedkin and Nassar (2020), we obtained for each problem (1)–(7), (27) with fixed $\beta \in \{1, 2, \ldots , 6\}$ the column of matrices of effective stiffnesses and piezomoduli for direct piezoelectric effect

$$\begin{aligned} c_{\alpha \beta }^{E\, \mathrm{eff}}=\langle T_{\alpha } \rangle / \gamma _0, \quad e_{i\beta }^{d\, \mathrm{eff}}=\langle D_k \rangle /\gamma _0, \end{aligned}$$

(28)

where $\alpha = 1, 2, \ldots , 6$; $i=1, 2 , 3$; $\gamma _0=S_0$ for $\beta =1, 2 , 3$; $\gamma _0=2S_0$ for $\beta =4, 5 , 6$.

After that, we solved the problems (1)–(7) three times ($k=1, 2 , 3$) considering the non-zero external electric field influences

$$\begin{aligned} {\mathbf{S}}_{0}=0, \quad E_{0j}=E_0\delta _{jk}, \end{aligned}$$

(29)

where $j=1, 2 , 3$, $E_0$ is the constant non-zero value.

Table 4 shows the applied values of the electric potential ($\varphi$) for the homogenization boundary value problems (1)–(7), (29) with $k=1, 2, 3$. The displacements ($u_i$) are set to zero on all outer surfaces in this case.

Table 4 The prescribed electric potential (${\tilde{\varphi }} = \varphi /E_0$) at the nodes located on the boundaries ($B_1$ to $B_6$) for the problems with $k=1, 2, 3$ according to Eq. (29)

By recalculating the averaged components of stresses and electric induction, we determined for each problem (1)–(7), (29) with fixed $k \in \{1, 2, 3\}$ the piezomoduli from converse piezoelectric effect and the column of the matrix of the dielectric permittivity moduli

$$\begin{aligned} e_{k \alpha }^{c\, \mathrm{eff}}=-\langle T_\alpha \rangle /E_0, \quad \varepsilon _{ik}^{S\, \mathrm{eff}}=\langle D_i \rangle /E_0, \end{aligned}$$

(30)

where $\alpha = 1, 2, \ldots , 6; i=1, 2, 3$.

Thus, to determine the complete set of effective moduli, three homogenization boundary value problems involving extending the representative volume along with one of the coordinate axes, three shear problems, and three problems involving a given electric potential varying along one of the coordinate axes need to be solved. Given non-zero functions of displacements or potential in all problems change linearly and provide constant deformations and electric fields for a homogeneous medium. These boundary conditions at the vertices of a cubic representative volume coincide with the conditions accepted for asymptotic homogenization problems or homogenization problems in cells with periodic boundary conditions (Berger et al. 2006; Martínez-Ayuso et al. 2017).

Note that, as was proved in Nasedkin et al. (2020), the matrices of effective elastic stiffnesses and permittivities should be symmetric, and the effective piezoelectric moduli for the direct piezoelectric effect and for the converse piezoelectric effect should be equal

$$\begin{aligned} c_{\alpha \beta }^{E\, \mathrm{eff}}= c_{\beta \alpha }^{E\, \mathrm{eff}}, \quad \varepsilon _{ik}^{S\, \mathrm{eff}}= \varepsilon _{ki}^{S\, \mathrm{eff}}, \quad e_{k \alpha }^{d\, \mathrm{eff}}=e_{k \alpha }^{c\, \mathrm{eff}} = e_{k \alpha }^{\mathrm{eff}}. \end{aligned}$$

(31)

Equalities (31) for the moduli (28), (30) were also obtained up to an error in computations from our numerical calculations. In addition, for piezocomposites with a piezoceramic matrix, the effective medium remained mainly a material of the 6mm class of anisotropy. Therefore, only ten effective moduli ($c^{E\, \mathrm{eff}}_{11}$, $c^{E\, \mathrm{eff}}_{12}$, $c^{E\, \mathrm{eff}}_{13}$, $c^{E\, \mathrm{eff}}_{33}$, $c^{E\, \mathrm{eff}}_{44}$, $e^{\mathrm{eff}}_{31}$, $e^{\mathrm{eff}}_{33}$, $e^{\mathrm{eff}}_{33}$, $\varepsilon ^{S\, \mathrm{eff}}_{11}$, $\varepsilon ^{S\, \mathrm{eff}}_{33}$) are of interest for analysis.

5 Results and discussions

5.1 Effects of the pore shape on fundamental material properties

In the first part of this discussion, we analyzed the effects of the pore shape on the relative effective moduli for the three considered piezoceramics. The relative effective moduli are the effective moduli of the piezocomposites understudy related to analogous moduli of the considered dense piezoelectric material, i.e., $r(e_{33})=e_{33}^{\mathrm{eff}}/e_{33}$, etc. We supposed that axes $x_1$, $x_2$, and $x_3$ refer to axes x, y, and z, respectively, and that the axis $x_3$ is the direction of initial polarization. In Figs. 3 and 4, we used the letter ‘S’ and the circle line marker to express the spherical pore shape; also, we used the letter ‘C’ and the square line marker to express the cubic pore shape. The blue lines are related to the spherical-shaped pore, whereas the red lines are related to the cubic-shaped pore. The solid lines depict the OPS, while the dashed lines depict the SMPS.

Fig. 3

The relative piezomoduli $r(e_{31})$, $r(e_{33})$, and $r(e_{15})$ versus porosity volume fraction $\upsilon _p$, for the OPS and the SMPS considering the following piezoelectric materials: PbTiO$_3$ in (a–c); TBKS in (d–f); and PZT-5H in (g–i)

Figure 3 describes the variations of the relative piezomoduli $r(e_{31} )$, $r(e_{33})$, and $r(e_{15})$ versus porosity for three different piezoceramic materials: PbTiO$_3$, TBKS, and PZT-5H. The relative piezoelectric coefficients $r(e_{33})$ and $r(e_{15})$ of both systems decrease with the rise in porosity. For the SMPS, Fig. 3 shows that the transverse effective relative piezomodulus $e_{31}^{\mathrm{eff}}$ and the shearing effective relative piezomodulus $e_{15}^{\mathrm{eff}}$ depend on the pore geometry more significantly than the longitudinal effective piezomodulus $e_{33}^{\mathrm{eff}}$. Also, effective coefficients for the SMPS depend on the pore’s geometric shape more than the corresponding effective properties for the OPS.

On contrary to the piezomoduli $r(e_{33})$ and $r(e_{15})$, the relative transverse piezoelectric modulus $r(e_{31})$ of the SMPS produced from TBKS or PZT-5H increases with the porosity growth, as seen in Fig. 3d, g. Through rising porosity, the relative transverse piezoelectric coefficient $r(e_{31})$ of the SMPS made from the modified piezoceramic material PbTiO$_3$ reduces to the extent that it becomes negative, as shown in Fig. 3a.

The relative effective piezomodulus $r(e_{31})$ of the SMPS with the matrix from the piezoceramics PbTiO$_3$ behaves differently from the similar modulus if piezoceramics TBKS and PZT-5H were considered. One can explain the reason behind this action as follows. The effective piezomodulus $e_{31}^{\mathrm{eff}}$ of the PbTiO$_3$ for the SMPS decreases, as do effective TBKS and PZT-5H SMPS’ transverse piezomoduli, with the porosity rise. The dense piezoceramics TBKS and PZT-5H have negative transverse piezomoduli $e_{31}$; while the dense piezoceramics PbTiO$_3$ has a positive value of the transverse piezomodulus. The relative transverse piezomodulus $r(e_{31})$ is calculated using the relationship $r(e_{31})=e_{31}^\mathrm{eff}/e_{31}$. As a result, for the SMPS considering TBKS or PZT-5H, the transverse piezomodulus $r(e_{31})$ grows with values greater than one when the porosity increases, as seen in Fig. 3d, g. However, due to the positive coefficient $e_{31}$ of dense piezoceramics PbTiO$_3$, the relative piezomodulus $r(e_{31})$ of the SMPS using PbTiO$_3$ significantly decreases with the porosity boost. For the SMPS made from PbTiO$_3$, the effective piezoelectric coefficient $e_{31}^{\mathrm{eff}}$ decreases until reaching zero (at porosity volume fraction $\upsilon _p=0.27$ for spherical porous system, $\upsilon _p=0.18$ for cubic porous system) and then takes negative values with the increase of porosity. When applying an external E-field $E_{03}$ on the SMPS with spherical pore made from PbTiO$_3$, the system expands in the transverse direction if porosity volume fraction $\upsilon _p<0.27$; however, the system shrinks in the transverse direction if $\upsilon _p>0.27$, as seen in Fig. 3a. This is a major change in this material’s crystal symmetry.

Note also that the transverse modulus $e_{31}$ of dense piezoceramics PbTiO$_3$ not only has a positive sign but also its value is much less than the absolute values in comparison with similar piezoelectric moduli of piezoceramics TBKS and PZT-5H. Therefore, the relative piezomodulus $r(e_{31})$ behavior versus porosity for PbTiO$_3$ differs significantly from those of TBKS and PZT-5H.

Fig. 4

The relative elastic moduli $r(c_{33})$, $r(c_{13})$, and the relative dielectric permittivity modulus $r(\varepsilon _{33}^S)$ versus porosity $\upsilon _p$, for the OPS and the SMPS considering the following piezoelectric materials: PbTiO$_3$ in (a–c); TBKS in (d–f); and PZT-5H in (g–i)

Figure 4 presents the variations of the relative elastic stiffness moduli $r(c_{33})$, $r(c_{13})$, and the relative dielectric permittivity modulus $r(\varepsilon _{33}^S)$ depending on the porosity volume fraction $\upsilon _p$. It is obvious that the growth of porosity reduces all elastic stiffness moduli. We observed that the effective elastic moduli $c_{13}^{\mathrm{eff}}$, $c_{12}^\mathrm{eff}$, and $c_{44}^{\mathrm{eff}}$ depend on the pore geometry more than the effective elastic moduli $c_{11}^{\mathrm{eff}}$ and $c_{33}^\mathrm{eff}$.

The relative dielectric modulus $r(\varepsilon _{11}^S)$ varies with porosity increase similarly to the dielectric modulus $r(\varepsilon _{33}^S)$. Unlike the OPS, the SMPS’ effective dielectric permittivities monotonically boost with the increase in porosity.

5.2 Clarification of unusual behavior of dielectric permittivity moduli and transverse piezomodulus for the SMPS

Fig. 5

E-field vector plot (a), electric flux density D-vector plot (c), and stress x-component contour plot (e) for the OPS; and E-field vector plot (b), electric flux density D-vector plot (d), and stress x-component contour plot (f) for the SMPS, at porosity $\upsilon _p= 0.35$ in the back half of the unit cell without the vacuum pore volume $\varOmega ^p$

In the next part of the discussion, we are more interested in material PZT-5H because it is common in practical application; and we also considered the spherical porous system since it is closer to reality. Figure 5 shows the system states that are used to determine the effective dielectric permittivity modulus $\varepsilon _{33}^{S\, \mathrm{eff}}$ and the effective piezomodulus $e_{31}^{\mathrm{eff}}$ based on the solution of the homogenization problem (1)–(7), (29), (30) for $k = 3$, i.e. under nonzero boundary conditions for the electric potential with $E_{03} = E_0$, here $E_0=1$. Figure 5a, b show the E-field vector plot for the OPS and the SMPS, respectively; Fig. 5c, d present the electric flux density D-vector plot for the OPS and the SMPS, respectively; while Fig. 5e, f introduce the nodal solution of the stress x-component ($\sigma _{11}$) for the OPS and the SMPS, respectively.

The exceptional dependence of the relative dielectric modulus $r(\varepsilon _{33}^{\mathrm{S\, eff}})$ of the SMPS on the porosity can be explained as follows. According to the equations (30), the effective dielectric permittivity $\varepsilon _{33}^\mathrm{S\, eff}=\langle D_3 \rangle /\langle E_3 \rangle =(\langle D_3 \rangle ^m+ \langle D_3 \rangle ^e+ \langle D_3 \rangle ^p)/E_0$, where $\langle D_3 \rangle ^m = (1/|\varOmega |) \int _\varOmega D^m_3 \,d\varOmega$, etc. Even if there is an electric field influence on the pore volume, the resulting electric induction in this volume ($\langle D_3 \rangle ^p$) is negligible due to the negligible dielectric permittivity of the vacuum. So, the effective dielectric permittivity of the SMPS becomes $\varepsilon _{33}^\mathrm{S\, eff}=(\langle D_3 \rangle ^m+ \langle D_3 \rangle ^e)/E_0$. Knowing that $E_0$ is a nonzero constant value, the dielectric permittivity modulus $\varepsilon _{33}^{\mathrm{S\, eff}}$ directly depends on the sum $(\langle D_3 \rangle ^m+ \langle D_3 \rangle ^e)$. The metalized pore surface (layer $\varOmega ^e$) in the SMPS can be considered as a conductor placed in a uniform electric field. The electric charges in the conductor move freely and generate an electric field inside the conductor opposing the original electric field. So, the influence of the applied electric field is restricted in the volume filled with the piezoelectric material $\varOmega ^m$, as seen in Fig. 5b. So, the resulting integral value of the electric induction $\langle D_3 \rangle ^m$ in the SMPS is higher than the analogous value in the OPS, as shown in Fig. 5c, d. Figure 5d shows a strong electric induction produced in the metal layer $\langle D_3 \rangle ^e$ due to the increased local E-field at the interface between the piezoelectric material and the conductor. The phenomenon of enhanced permittivity owing to the presence of a conductor within a dielectric material was explored in Roscow et al. (2017) and Du et al. (2016). As a result, the effective permittivity modulus $\varepsilon _{33}^\mathrm{S\, eff}$ of the SMPS increase with porosity growth.

In contrast to the SMPS, Fig. 5a indicates that a portion of the electric field’s influence is lost inside the pore for the OPS, i.e., $\langle E_3 \rangle ^m\, <\, E_0$. The integral value of the electric flux density generated in the pore is negligible because of the minimal dielectric permittivity of the vacuum. So, the effective permittivity modulus $\varepsilon _{33}^{\mathrm{S\, eff}}$ for the OPS decreases with the porosity rise.

The piezomodulus $e_{31}^{\mathrm{eff}}$ can be calculated from (30) as follows: $e_{31}^{\mathrm{eff}}=-\langle \sigma _{11} \rangle$ $/ \langle E_3 \rangle = -\langle \sigma _{11} \rangle ^m\, /\, E_0$. Noting that the resulted stresses in the volume $\varOmega ^e \cup \varOmega ^p$, upon applying an E-field $E_{03}=E_0$ on the external boundary of $\varOmega$, are negligible due to the negligible piezomoduli of the related materials. From Fig. 5b, f, we can observe that the maximum absolute value of the stress component $\sigma _{11}$ and the E-field vectors occur in the same regions. From the comparison between Fig. 5e, f, we can see that the pore for the SMPS tends to be elongated in the z-direction; however, Fig. 5 shows only the non-deformable unit cell configuration. So, we can conclude that the E-field vectors in the SMPS are irregular in direction, and their influence is restricted in the volume $\varOmega ^m$ as in Fig. 5b, due to the presence of the metalized pore surface. This increased the integral values of the stress components $\sigma _{11}$ and $\sigma _{22}$, as seen in Fig. 5, (f) for $\sigma _{11}$; but decreased the integral value of the stress component $\sigma _{33}$. As a result, the effective value of the SMPS’ transverse piezomodulus $e_{31}^{\mathrm{eff}}$ boosts with the porosity growth, unlike the analogous modulus of the OPS, as in Fig. 3g.

5.3 Evaluating the performance of the systems under study in various applications

In this subsection, we used the FOMs (15), (19), (20), (23)–(25) derived from section 3 to evaluate the efficiency of the OPS and the SMPS in various engineering applications. In Fig. 6, we plotted all FOMs of the OPS and the SMPS, relatively to the corresponding values of the pure PZT-5H material, to illustrate the advantages and disadvantages that both systems achieve.

Fig. 6

The coupling coefficients $k^2$ (a), the sensor transduction coefficients (b), the actuator transduction coefficient (c), energy harvesting/sensing FOMs (d), actuation FOMs (e), and hydrostatic FOM (f) versus porosity $\upsilon _p$, for the OPS and the SMPS

Figure 6 displays the different relative FOMs under consideration as functions of porosity volume fraction $v_p$. The FOMs of the OPS and the SMPS are shown using continuous lines and dashed lines, respectively. The transverse, longitudinal, and shearing operating modes were plotted for each FOM using blue, red, and green curves, respectively.

Figure 6a demonstrates that the relative longitudinal and shearing coupling coefficients of the SMPS decrease faster than the same coefficients of the OPS when the porosity increases. When the porosity is less than 47%, the transverse coupling coefficient of the SMPS is higher than that of the OPS.

The sensing transduction coefficient $(TC_{j\beta })_S$ is plotted in Fig. 6b for different cases under study. Figure 6b indicates that the OPS exhibits greater longitudinal and shearing sensing transduction coefficients than the SMPS. However, the SMPS exhibits greater transverse transduction when porosity p is less than 47%.

The actuator transduction coefficient $(TC_{j\beta })_A$ is shown in Fig. 6c. For all operating modes, the SMPS exhibits higher actuation transduction coefficient values than the OPS. The SMPS transverse actuator transduction coefficient increases monotonically with the porosity growth due to the great values of the transverse piezomodulus $d_{31}^{\, \mathrm eff}$.

The sensor and actuator’s energy harvesting FOM are presented in Fig. 6d, e, respectively. They are like the sensing and actuation transduction coefficients shown in Fig. 6b, c, respectively. The OPS exhibits better performance than the SMPS in longitudinal and shearing sensor applications due to the great values of $(FOM_{33})_S$ and $(FOM_{15})_S$; however, the SMPS exhibits greater efficiency than the OPS in the transverse sensor, at porosity $p< 0.47$, and all operating modes of actuator applications.

Figure 6f presents the hydrostatic FOM (HFOM) for both composites. From this figure, we can infer that the OPS produces better performance in hydrophone applications when porosity is less than 38% while the SMPS exhibits greater HFOM for higher porosity fraction.

Fig. 7

The sensor tansduction coefficient $(TC_{31})_S$, actuator tansduction coefficient $(TC_{31})_A$, and the hydrostatic FOM (HFOM) versus porosity for the SMPS designed based on the piezoelectric substrates PbTiO$_3$ and TBKS in (a, b), respectively

Due to the improved performance of the SMPS, particularly the transverse actuator operating mode, as shown in Fig. 6c, e, we investigated certain FOMs of the SMPS created based on the piezoelectric substrates PbTiO3 and TBKS. Figure 7 presents the sensor transduction coefficient $(TC_{31})_S$, actuator transduction coefficient $(TC_{31})_A$, and the hydrostatic FOM (HFOM) as functions of porosity for the SMPS produced with the piezoelectric matrices PbTiO$_3$ and TBKS, respectively in (a) and (b). Unlike the HFOM of the SMPS created with PZT-5H, the HFOM of the SMPS developed with the piezoelectric substrates PbTiO$_3$ and TBKS is less than the analogous coefficient of the analogous pure piezoelectric material. The transverse sensor transduction coefficient of the SMPS created with PbTiO$_3$ and TBKS is almost independent of porosity when porosity volume fraction is lower than 45% and decreases for higher porosity fractions. The most notable finding is that the transverse actuator transduction coefficient $(TC_{31})_A$ rises with increasing porosity for all investigated systems.

6 Conclusions

This paper studied two different porous piezoelectric composites. The first composite is an ordinary porous system (OPS), which is a two-phase piezocomposite with 3-0 connectivity consisting of a piezoelectric material and a pore inside it. The second composite is a system with a metalized pore surface (SMPS), which is a three-phase piezocomposite with 3-0-0 connectivity. The SMPS’s construction is similar to the OPS but contains a metal layer on the pore surface. This layer of metal was designed in Rybyanets and Naumenko (2013) and Rybyanets et al. (2018) to enhance the electromechanical and functional properties of the OPS.

To find the effective moduli, we solved the boundary value piezoelectric problems with specific essential boundary conditions. In these problems, the pores were filled with a hypothetical piezoelectric material with negligible moduli. We also used piezoelectric material with very high dielectric permittivity and negligible piezoelectric and stiffness moduli to model the metal layer. This approach used was substantiated earlier (Nasedkin and Nassar 2021a; Nasedkin et al. 2020; Nasedkin and Nassar 2020) based on Hill’s principle, which states that the potential energies of the composite and the equivalent homogeneous medium under the same external influences are equal.

We explored the influence of the pore shape on the effective properties of both systems. We used a cubic pore and a spherical pore in this study. We constructed these piezocomposites using three distinct piezoceramics, i.e., PbTiO$_3$, TBKS, and PZT-5H. Because both systems exhibit different effective moduli, we reviewed typical piezoelectric transducers’ figures of merit (FOMs) to assess the performance of these systems in various engineering applications. Most of the previously studied FOMs assess the efficiency of piezoelectric transducers in sensing/energy harvesting applications. Here, we introduced new figures of merit ($(TC_{j\beta })_A$ and $(FOM_{j\beta })_A$), which measure the piezoelectric transducer’s efficiency in actuator applications.

The primary findings of this study can be summarized as follows.

• 1. The transverse and shearing elastic stiffnesses and piezoelectric moduli of both systems are more dependent on the pore shape than the longitudinal elastic moduli, piezomoduli, and dielectric permittivities; however, the dependence of the effective moduli on the pore shape is not significant. So, even though the spherical pore is closer to reality, we can study more complicated representative volumes with a random distribution of pores using the cubic pores.

• 2. Introducing porosity to the piezoelectric material enhances its performance in longitudinal and shearing sensor applications. Also, the transverse sensing effect of the OPS is improved in the case of large porosity. However, the actuation effect of the OPS decreases with the porosity increase for all modes of operation.

• 3. The metal layer in the SMPS restricts the influence of the externally applied E-field in the volume filled with the piezoelectric material and produces a very strong electric induction inside it, which increases the transverse piezomodulus and the dielectric permittivity moduli of the SMPS with the porosity rise.

• 4. The SMPS transverse actuating effect increases significantly with increasing porosity. Also, the transverse sensing effect of the SMPS is higher than the analogous effect of the OPS for a wide range of porosity values.

• 5. In hydrophone applications, the OPS outperforms the corresponding pure piezoelectric materials in all examined piezoelectric matrices; however, the SMPS outperforms the analogous pure piezoelectric materials for significant percentages of porosity only when made using the piezoceramic matrix PZT-5H.

• 6. The piezoelectric transducers made from the SMPS can be used efficiently in contracting actuators, tube actuators, and bending actuators, which can be utilized effectively in active vibration control systems.

Further studies of this research may consider more complicated representative volumes, partially metalized pore surfaces, and experimental validations.