One-step semi-implicit integration of general finite-strain plasticity models

Abstract

Using the Kröner–Lee elastic and plastic decomposition of the deformation gradient, a differential-algebraic system is obtained (in the so-called semi-explicit form). The system is composed by a smooth nonlinear differential equation and a non-smooth algebraic equation. The development of an efficient one-step constitutive integrator is the goal of this work. The integration procedure makes use of an explicit Runge–Kutta method for the differential equation and a smooth replacement of the algebraic equation. The resulting scalar equation is solved by the Newton–Raphson method to obtain the plastic multiplier. We make use of the elastic Mandel stress construction, which is power-consistent with the plastic strain rate. Iso-error maps are presented for a combination of Neo-Hookean material using the Hill yield criterion and a associative flow law. A variation of the pressurized plate is presented. The exact Jacobian for the constitutive system is presented and the steps for use within a structural finite element formulation are described .

1 Introduction

This work deals with finite strain elasto-plasticity. Finite strain plasticity, see, e.g. Nemat-Nasser (2004), including any relevant hardening, damage and strain-rate effects, is a key ingredient in a realistic simulation. The comprehensive discussion by Wriggers (2008) shows the effects commonly included in the simulations and the numerical consequences of the Kröner–Lee decomposition (Kröner 1960; Lee and Liu 1967; Lee 1969). In the earliest numerical developments, the multiplicative decomposition was applied to specific hyperelastic laws and yield functions, see Simo and Ortiz (1985), Simo (1988), Moran et al. (1990), Lubliner (1990), Simo (1992) and Areias and Matouš, (2008). Currently, most papers and implementations make use of more general spatial-configuration approach to finite strain plasticity, which has been summarized in Wriggers (2008). However, some limits to the elastic and/or plastic laws still exist in recent works, such as the restriction to isotropic hyperelastic laws (the case of Vladimirov et al. 2010 and Areias et al. 2012) or the use of a Kirchhoff/Saint-Venant elastic law, which is the case of Schröder et al. (2002). In certain cases, coaxiality is assumed in the integrator, see also Eidel and Gruttmann (2003), resulting in a single scalar equation.

In terms of finite element technology, it is worth mentioning that mixed and enhanced finite elements do not always provide the required deformation gradient to feed the constitutive integrator and this has been the subject of discussion for a considerable time (Betsch and Stein 1999). Although some work exists on the combination of classical multiplicative plasticity with assumed strain elements, a more direct approach is to make use of the work by Eidel and Gruttmann (2003). A purely material configuration is here adopted and therefore, besides the constitutive history variables, only the Green–Lagrange strain ${\boldsymbol{E}}$ or the right Cauchy–Green tensor ${\boldsymbol{C}}$ are required as sources to the finite strain plasticity integrator.

This results in a differential-algebraic system (cf. Hairer et al. 1989), with the flow law being a smooth differential equation for the plastic deformation gradient ${\boldsymbol{F}}_{p}$ (which is the differential variable) and a non-smooth algebraic equation corresponding to the loading/unloading Kuhn–Tucker conditions. The algebraic variable is the plastic multiplier (or alternatively the time). In our case, smoothing of the algebraic equation is performed, as in Areias et al. (2012), a topic which is further discussed by Scalet and Auricchio (2018). The following sections of this work discuss the equations, implementation and error assessment of the proposed algorithm.

2 Constitutive updating using the elastic Mandel stress tensor

Hyperelastic laws can directly incorporated in assumed-strain large deformation element formulations. Inelastic laws often entail technicalities with respect to the presence of the assumed deformation gradient (Betsch and Stein 1999) which led to the use of the Mandel stress tensor approach in the material setting. A comprehensive description of the arguments involved is provided by Eidel and Gruttmann (2003). Note that there is a compromise: the Mandel stress (Mandel 1973), instead of the Cauchy stress, is present in the yield function.

We make use of the Kröner–Lee decomposition (Kröner 1960; Lee and Liu 1967; Lee 1969), which is a multiplicative decomposition of the deformation gradient ${\boldsymbol{F}}$, in which a stress-free (“relaxed”) intermediate configuration is assumed (see also Lubliner 1990 and Menzel 2006):

$$\begin{aligned} {\boldsymbol{F}}={\boldsymbol{F}}_{e}{\boldsymbol{F}}_{p} \end{aligned}$$

(1)

This is now relatively standard (Simo and Ortiz 1985), with ${\boldsymbol{F}}_{e}$ providing the elastic part of the deformation and ${\boldsymbol{F}}_{p}$ being the plastic part of the deformation. That is, local unloading is obtained by imposing ${\boldsymbol{F}}_{e}={\boldsymbol{I}}$, see Lubliner (1990), defining the so-called intermediate (or unloaded) configuration.

From (1), the velocity gradient is determined by its definition and then partitioned ${\boldsymbol{L}}=\dot{{\boldsymbol{F}}}{\boldsymbol{F}}^{-1}={\boldsymbol{L}}_{e}+{\boldsymbol{F}}_{e}{\boldsymbol{L}}_{p}{\boldsymbol{F}}_{e}^{-1}$ with ${\boldsymbol{L}}_{e}=\dot{{\boldsymbol{F}}}_{e}{\boldsymbol{F}}_{e}^{-1}$ and ${\boldsymbol{L}}_{p}=\dot{{\boldsymbol{F}}}_{p}{\boldsymbol{F}}_{p}^{-1}$. Here, ${\boldsymbol{L}}_{p}$ is defined in the unloaded configuration. Since the second Piola-Kirchhoff stress is a function of the elastic part of ${\boldsymbol{F}}$ by means of ${\boldsymbol{C}}_{e}={\boldsymbol{F}}_{e}^{T}{\boldsymbol{F}}_{e}$ (cf. Gurtin 1981), the second Piola-Kirchhoff stress at the intermediate configuration is given by a function ${\boldsymbol{S}}_{e}\left( {\boldsymbol{C}}_{e}\right)$ (this form was proved thermodynamically by Mandel 1974), from which energy consistency results in the following form for the second Piola-Kirchhoff stress

$$\begin{aligned} {\boldsymbol{S}}={\boldsymbol{F}}_{p}^{-1}{\boldsymbol{S}}_{e}\left( {\boldsymbol{C}}_{e}\right) {\boldsymbol{F}}_{p}^{-T} \end{aligned}$$

(2)

The flow law follows standard arguments (Eidel and Gruttmann 2003; Menzel 2006), assuming that the initial plastic deformation gradient corresponds to the identity, $\left[ {\boldsymbol{F}}_{p}\right] _{0}={\boldsymbol{I}}$. Following standard derivations on plasticity, a yield function $\phi$ is introduced, as well as a plastic multiplier ${\dot{\gamma }}$. We summarize the constitutive system as:

$$\begin{aligned}&{\boldsymbol{S}} ={\boldsymbol{F}}_{p}^{-1}{\boldsymbol{S}}_{e}\left( {\boldsymbol{C}}_{e}\right) {\boldsymbol{F}}_{p}^{-T} \end{aligned}$$

(3)

$$\begin{aligned}&\dot{{\boldsymbol{F}}}_{p} ={\dot{\gamma }}{\boldsymbol{N}}\left( {\boldsymbol{T}}_{e}\right) {\boldsymbol{F}}_{p}\end{aligned}$$

(4)

$$\begin{aligned}&\left[ {\boldsymbol{F}}_{p}\right] _{0} ={\boldsymbol{I}}\end{aligned}$$

(5)

$$\begin{aligned}&\prec \phi \left( {\boldsymbol{T}}_{e}\right) +{\dot{\gamma }}\succ -{\dot{\gamma }}=0 \end{aligned}$$

(6)

with $\prec \bullet \succ =\frac{\bullet +\left| \bullet \right| }{2}$ being the unit ramp function. In (4), the elastic Mandel stress (Mandel 1973) ${\boldsymbol{T}}_{e}$ is defined as:

$$\begin{aligned} {\boldsymbol{T}}_{e}={\boldsymbol{C}}_{e}{\boldsymbol{S}}_{e}\left( {\boldsymbol{C}}_{e}\right) \end{aligned}$$

(7)

Assuming associativeness of the flow law, we have the flow vector ${\boldsymbol{N}}\left( {\boldsymbol{T}}_{e}\right)$ determined from the derivative of $\phi \left( {\boldsymbol{T}}_{e}\right)$:

$$\begin{aligned} {\varvec{{\boldsymbol{N}}}}({\boldsymbol{T}}_{e})={\mathrm {d}\phi \left( {\boldsymbol{T}}_{e}\right) }/ {\mathrm {d}{\boldsymbol{T}}_{e}} \end{aligned}$$

(8)

The Mandel stress tensor is, in terms of plastic dissipation power, conjugated to ${\boldsymbol{L}}_{p}$, which implies that the flow law (4) is power-consistent. To increase the conciseness of the constitutive equations, we use the replacement ${\boldsymbol{Q}}_{p}={\boldsymbol{F}}_{p}^{-1}$ and remove ${\boldsymbol{C}}_{e}$ and ${\boldsymbol{T}}_{e}$ from the list of constitutive unknowns, resulting in the more convenient system:

$$\begin{aligned}&{\boldsymbol{S}} ={\boldsymbol{Q}}_{p}{\boldsymbol{S}}_{e}\left( {\boldsymbol{Q}}_{p}^{T}{\boldsymbol{C}}{\boldsymbol{Q}}_{p}\right) {\boldsymbol{Q}}_{p}^{T} \end{aligned}$$

(9)

$$\begin{aligned}&\dot{{\boldsymbol{Q}}}_{p} =-{\dot{\gamma }}{\boldsymbol{Q}}_{p}{\boldsymbol{N}}\left[ {\boldsymbol{Q}}_{p}^{T} {\boldsymbol{C}}{\boldsymbol{Q}}_{p}{\boldsymbol{S}}_{e}\left( {\boldsymbol{Q}}_{p}^{T}{\boldsymbol{C}}{\boldsymbol{Q}}_{p}\right) \right] \end{aligned}$$

(10)

$$\begin{aligned}&\left[ {\boldsymbol{Q}}_{p}\right] _{0} ={\boldsymbol{I}}\end{aligned}$$

(11)

$$\begin{aligned}&\prec \phi \left[ {\boldsymbol{Q}}_{p}^{T}{\boldsymbol{C}}{\boldsymbol{Q}}_{p}{\boldsymbol{S}}_{e} \left( {\boldsymbol{Q}}_{p}^{T}{\boldsymbol{C}}{\boldsymbol{Q}}_{p}\right) \right] +{\dot{\gamma }}\succ -{\dot{\gamma }}=0 \end{aligned}$$

(12)

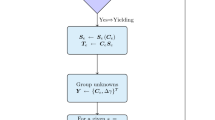
In Eqs. (10–12), ${\boldsymbol{Q}}_{p}$ and ${\dot{\gamma }}$ are the constitutive unknowns. System (10, 12) is a differential-algebraic system (DAE) with (9) being calculated after its solution. For the rate-independent case, the system is autonomous and we can re-write the DAE system in semi-explicit nonlinear autonomous form:

$$\begin{aligned}&\dot{{\boldsymbol{Q}}}_{p} =\Psi \left( {\dot{\gamma }},{\boldsymbol{C}},{\boldsymbol{Q}}_{p}\right) \end{aligned}$$

(13)

$$\begin{aligned}&\Phi ({\dot{\gamma }},{\boldsymbol{C}},{\boldsymbol{Q}}_{p}) =0 \end{aligned}$$

(14)

This is a index-1 DAE, considering ${\dot{\gamma }}$ as the algebraic variable. We note that since in (14), ${\partial \Phi (\dot{\gamma ,{\boldsymbol{C}},{\boldsymbol{Q}}_{p})}}/{\partial {\dot{\gamma }}}$ is non-invertible in general, we cannot use a standard fully explicit Runge–Kutta (RK) method for this system, see also Hairer et al. (1989). Since we have an autonomous system, we consider ${\dot{\gamma }}$ as an unknown parameter and solve the system in a semi-implicit form. It turns out that, since $\Psi$ is homogeneous of degree one with respect to ${\dot{\gamma }}$, this will play a specific role in numerical integration. With that in mind, we introduce the following nomenclature:

$$\begin{aligned}&\dot{{\boldsymbol{Q}}}_{p} ={\dot{\gamma }}\Psi _{\star }\left( {\boldsymbol{C}},{\boldsymbol{Q}}_{p}\right) \Rightarrow \end{aligned}$$

(15)

$$\begin{aligned}&{\mathrm {d}{\boldsymbol{Q}}_{p}}/{\mathrm {d}\gamma } =\Psi _{\star }({\boldsymbol{C}},{\boldsymbol{Q}}_{p})\quad \text {for} \ {{\dot{\gamma }}\ne 0} \end{aligned}$$

(16)

It is straightforward to write (10–12) as a non-smooth differential system, and therefore standard ODE integration analysis is applicable.

3 Integration

A description of the semi-implicit time-integration algorithm for system (13–14) now follows. Traditionally, when one-step methods are selected to integrate DAE, fully-implicit RK methods are employed (Petzold August 1986). In alternative, extrapolation methods such as the one described by Deuflhard, Hairer and Zugck can be used (Deuflhard et al. 1987). For our specific system, we can still apply an explicit RK method for the differential variable. We use superscripts n and $n+1$ to identify two consecutive time-steps and use $\Delta t$ as the time-step size. The number of stages (s) and the corresponding Runge–Kutta coefficients $a_{pq}$, $b_{p}$ and $c_{p}$ with $p,q=1,\ldots ,s$ define the explicit Runge–Kutta procedure, see Hairer et al. (2008). Applying the explicit RK integration with s stages for $\dot{{\boldsymbol{Q}}}_{p}$ and the backward-Euler method for the plastic multiplier ${\dot{\gamma }}$ results in:

$$\begin{aligned} {\boldsymbol{Q}}_{p}^{n+1}&={\boldsymbol{Q}}_{p}^{n}+{\dot{\gamma }}^{n+1}\Delta t\sum _{p=1}^{s}b_{p}\Psi _{\star }\nonumber \\&\quad \times \left[ c_{p}\Delta {\boldsymbol{C}}+{\boldsymbol{C}}^{n}, {\boldsymbol{Q}}_{p}^{n}+{\dot{\gamma }}^{n+1}\Delta t\sum _{q=1}^{p-1}a_{pq}\varvec{\kappa }_{q}\right] \end{aligned}$$

(17)

$$\begin{aligned} \gamma ^{n+1}&=\gamma ^{n}+\underbrace{{\dot{\gamma }}\Delta t}_{\Delta \gamma } \end{aligned}$$

(18)

where $\Delta {\boldsymbol{C}}={\boldsymbol{C}}^{n+1}-{\boldsymbol{C}}^{n}$. Note that in (18), a simple backward-Euler integration is performed, since $\Delta \gamma$ is determined implicitly. We now introduce the notation $\varvec{\kappa }_{p}$ to simplify Eq. (17):

$$\begin{aligned} \varvec{\kappa }_{p}=\Psi _{\star }\left[ c_{p}\Delta {\boldsymbol{C}} +{\boldsymbol{C}}^{n},{\boldsymbol{Q}}_{p}^{n}+{\dot{\gamma }}^{n+1}\Delta t\sum _{q=1}^{p-1}a_{pq}\varvec{\kappa }_{q}\right] \end{aligned}$$

(19)

By defining the product $\phi _{\star }=\Delta t\phi$, and making use of the argument $\Delta \gamma ,$ ${\varvec{\kappa }}_{p}\equiv {\varvec{\kappa }}_{p}\left( \Delta \gamma \right)$, the constitutive system reads:

$$\begin{aligned}&{\boldsymbol{Q}}_{p}^{n+1}={\boldsymbol{Q}}_{p}^{n}+\Delta \gamma \sum _{p=1}^{s}b_{p} \varvec{\kappa }_{p}\left( \Delta \gamma \right) \end{aligned}$$

(20)

$$\begin{aligned}&\prec \phi _{\star }\left\{ \left( {\boldsymbol{Q}}_{p}^{n+1}\right) ^{T}\cdot {\boldsymbol{C}}^{n+1}\cdot {\boldsymbol{Q}}_{p}^{n+1}\cdot {\boldsymbol{S}}_{e}\right. \nonumber \\&\left. \quad \times \left[ \left( {\boldsymbol{Q}}_{p}^{n+1}\right) ^{T}\cdot {\boldsymbol{C}}^{n+1}\cdot {\boldsymbol{Q}}_{p}^{n+1} \right] \right\} +\Delta \gamma \succ -\Delta \gamma =0 \end{aligned}$$

(21)

$$\begin{aligned}&{\boldsymbol{Q}}_{p}^{0} ={\boldsymbol{I}} \end{aligned}$$

(22)

In (20–21) we have used the function ${\varvec{\kappa }}_{p}\left( \Delta \gamma \right) =\Psi _{\star }\left[ c_{p}\Delta {\boldsymbol{C}}+{\boldsymbol{C}}^{n},{\boldsymbol{Q}}_{p}^{n}+\Delta {\boldsymbol{Q}}_{p}^{n}\left( \Delta \gamma \right) \right]$ with $\Delta {\boldsymbol{Q}}_{p}^{n}\left( \Delta \gamma \right) =\Delta \gamma \sum _{q=1}^{p-1}a_{pq} \varvec{\kappa }_{q}\left( \Delta \gamma \right)$. We note that $\Psi _{\star }({\boldsymbol{C}},{\boldsymbol{Q}})$ is the following function of ${\boldsymbol{C}}$ and ${\boldsymbol{Q}}$:

$$\begin{aligned} \Psi _{\star }({\boldsymbol{C}},{\boldsymbol{Q}})=-{\boldsymbol{Q}}\cdot {\boldsymbol{N}}\left[ {\boldsymbol{Q}}^{T}\cdot {\boldsymbol{C}} \cdot {\boldsymbol{Q}}\cdot {\varvec{{\hat{S}}}}_{e}\left( {\boldsymbol{Q}}^{T}\cdot {\boldsymbol{C}}\cdot {\boldsymbol{Q}} \right) \right] \end{aligned}$$

(23)

The second Piola-Kirchhoff stress at step $n+1$ is given by its definition at ${\boldsymbol{C}}_{e}=\left( {\boldsymbol{Q}}_{p}^{n+1}\right) ^{T}\cdot {\boldsymbol{C}}^{n+1}\cdot {\boldsymbol{Q}}_{p}^{n+1}$:

$$\begin{aligned} {\boldsymbol{S}}^{n+1}={\boldsymbol{Q}}_{p}^{n+1}\cdot \hat{{\boldsymbol{S}}}_{e} \left[ \left( {\boldsymbol{Q}}_{p}^{n+1}\right) ^{T}\cdot {\boldsymbol{C}}^{n+1}\cdot {\boldsymbol{Q}}_{p}^{n+1} \right] \cdot \left( {\boldsymbol{Q}}_{p}^{n+1}\right) ^{T} \end{aligned}$$

(24)

With the Eqs. (20–21), the following observations are in order:

• 1. The right-hand-side of Eq. (20) is a polynomial of degree s of $\Delta \gamma$.

• 2. Introducing $\hat{{\boldsymbol{Q}}}_{p}(\Delta \gamma )={\boldsymbol{Q}}_{p}^{n}+\Delta \gamma \sum _{p=1}^{s}b_{p}\varvec{\kappa }_{p}\left( \Delta \gamma \right)$ and $\hat{{\boldsymbol{C}}}_{e}(\Delta \gamma ,{\boldsymbol{C}}^{n+1})=\hat{{\boldsymbol{Q}}}_{p}^{T} (\Delta \gamma )\cdot {\boldsymbol{C}}^{n+1}\cdot \hat{{\boldsymbol{Q}}}_{p}(\Delta \gamma )$ the resulting non-smooth Eq. (21), can be solved for $\Delta \gamma$, with the argument of $\phi _{\star }$ being $\hat{{\boldsymbol{C}}}_{e}(\Delta \gamma ,{\boldsymbol{C}}^{n+1})\cdot \hat{{\boldsymbol{S}}}_{e} \left[ \hat{{\boldsymbol{C}}}_{e}\left( \Delta \gamma ,{\boldsymbol{C}}^{n+1}\right) \right]$.

• 3. If $\Delta \gamma =0$ and $\phi _{\star }(0)<0$ then obviously ${\boldsymbol{Q}}_{p}^{n+1}={\boldsymbol{Q}}_{p}^{n}$ and (21) is not required.

Focusing on the constitutive unknown, $\Delta \gamma$, the residual corresponding to (21) is written as:

$$\begin{aligned} r\left( \Delta \gamma ,{\boldsymbol{C}}\right) =\prec \phi _{\star }\left\{ \hat{{\boldsymbol{C}}}_{e}(\Delta \gamma ,{\boldsymbol{C}})\cdot \hat{{\boldsymbol{S}}}_{e} \left[ \hat{{\boldsymbol{C}}}_{e}\left( \Delta \gamma ,{\boldsymbol{C}}\right) \right] \right\} +\Delta \gamma \succ -\Delta \gamma \end{aligned}$$

(25)

An implementation of the RK integration (20) has to be performed. We adopt $s=1$, $s=2$ and $s=4$-stage RK integration with one of the following tableaus (forward-Euler, midpoint and RK4), see Hairer et al. (2008):

$$\begin{aligned} {\boldsymbol{a}}_{1}&=[\star ] \end{aligned}$$

(26)

$$\begin{aligned} {{\boldsymbol{b}}}_{1}&=\{1\}\end{aligned}$$

(27)

$$\begin{aligned} {\boldsymbol{C}}_{1}&=0 \end{aligned}$$

(28)

$$\begin{aligned} {{\boldsymbol{a}}}_{2}&=\left[ \begin{array}{c} \star \\ \frac{1}{2} \end{array}\right] \end{aligned}$$

(29)

$$\begin{aligned} {{\boldsymbol{b}}}_{2}&=\{0,1\}\end{aligned}$$

(30)

$$\begin{aligned} {\varvec{c_{2}}}&=\{0,{1}/{2}\}\end{aligned}$$

(31)

$$\begin{aligned} {{\boldsymbol{a}}}_{4}&=\left[ \begin{array}{ccc} \star &{}\quad \star &{} \star \\ {1}/{2} &{}\quad 0 &{}\quad 0\\ 0 &{}\quad {1}/{2} &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 1 \end{array}\right] \end{aligned}$$

(32)

$$\begin{aligned} {{\boldsymbol{b}}}_{4}&=\{{1}/{6},{1}/{3},{1}/{3}, {1}/{6}\}\end{aligned}$$

(33)

$$\begin{aligned} {\boldsymbol{C}}_{4}&=\{0,{1}/{2},{1}/{2},1\} \end{aligned}$$

(34)

For unit consistency, the yield function $\phi _{\star }$ is nondimensionalized. When applying the Newton–Raphson method to solve (25), we accumulate iterative corrections, which are identified here by $\delta \Delta \gamma _{i_{t}}$ as $\Delta \gamma =\sum _{i_{t}=1}^{n_{iter}}\delta \Delta \gamma _{i_{t}}$ with $i_{t}=1,\ldots ,n_{iter}$ being the iteration counter with $n_{iter}$ being the number of Newton–Raphson iterations, are given by (omitting the arguments):

$$\begin{aligned}&\left( -{\partial r}/{\partial \Delta \gamma }\right) \delta \Delta \gamma _{i_{t}}=r\quad \Leftrightarrow \end{aligned}$$

(35)

$$\begin{aligned}&\left\{ 1-\prec \phi _{\star }+\Delta \gamma \succ _{\beta }'\left[ 1+\phi _{\star }': \left( \hat{{\boldsymbol{C}}}_{e}'\cdot {\boldsymbol{S}}_{e}+\frac{1}{2}{\boldsymbol{C}}_{e} \mathscr {\cdot C}_{e}:\hat{{\boldsymbol{C}}}_{e}'\right) \right] \right\} \delta \Delta \gamma _{i_{t}} =\prec \phi _{\star }+\Delta \gamma \succ _{\beta } -\Delta \gamma \end{aligned}$$

(36)

In (36) we identify the following terms:

$$\begin{aligned}&{\mathscr {C}}_{e} =2\left. \frac{\mathrm {d}\hat{{\boldsymbol{S}}}_{e} \left( {\boldsymbol{C}}_{e}\right) }{\mathrm {d}{\boldsymbol{C}}_{e}}\right| _{{\boldsymbol{C}}_{e}=\hat{{\boldsymbol{C}}}_{e} (\Delta \gamma ,{\boldsymbol{C}}^{n+1})}\end{aligned}$$

(37)

$$\begin{aligned}&\prec x\succ =\lim _{\beta \rightarrow 0}\prec x\succ _{\beta }\end{aligned}$$

(38)

$$\begin{aligned}&\prec x\succ _{\beta }' ={\mathrm {d}\prec x\succ _{\beta }}/{x} \end{aligned}$$

(39)

$$\begin{aligned}&\phi '_{\star } ={\mathrm {d}\phi _{\star }}/{\mathrm {d}{\boldsymbol{T}}_{e}} \end{aligned}$$

(40)

$$\begin{aligned}&\hat{{\boldsymbol{C}}}_{e}' ={\partial \hat{{\boldsymbol{C}}}_{e}(\Delta \gamma ,{\boldsymbol{C}}^{n+1})}/{\partial \Delta \gamma } \end{aligned}$$

(41)

where $\prec x\succ _{\beta }$ is a smooth replacement for the unit ramp function, with $\beta$ being a smoothing parameter. This smooth replacement for the ramp function is defined as (see Chen and Mangasarian 1995, 1996):

$$\begin{aligned} \prec x\succ _{\beta }={\left\{ \begin{array}{ll} x+\alpha ^{-1}\log \left[ 1+\exp \left( -\alpha x\right) \right] & x\ge 0\\ x+\alpha ^{-1}\left\{ -\alpha x+\log \left[ 1+\exp \left( \alpha x\right) \right] \right\} & x<0 \end{array}\right. } \end{aligned}$$

(42)

with $\alpha ={\log 2}/{\beta }$ and $\beta$ is the residual at the origin, see Fig. 1. This is in fact a differentiable replacement for the ramp function satisfying $\prec x\succ =\lim _{\beta \rightarrow 0}\prec x\succ _{\beta }$, $x\in {\mathbb {R}}$.

Fig. 1

Graph of $\left\langle x\right\rangle _{\beta }$ for $\beta =0.1$

After convergence is obtained in (35), we calculate the derivative ${\mathrm {d}\Delta \gamma }/{\mathrm {d}{\boldsymbol{C}}}$, which is required for the sensitivity of the solution:

$$\begin{aligned} \frac{\mathrm {d}\Delta \gamma }{\mathrm {d}{\boldsymbol{C}}^{n+1}}=-\left( \frac{\partial r}{\partial \Delta \gamma }\right) ^{-1}\left( \frac{\partial r}{\partial {\boldsymbol{C}}^{n+1}}\right) \end{aligned}$$

(43)

Omitting arguments, we have

$$\begin{aligned}&\frac{\partial r}{\partial {\boldsymbol{C}}^{n+1}}=\left( \prec \phi _{\star }+\Delta \gamma \succ _{\beta }'\right) \phi _{\star }':\nonumber \\&\quad \left( \hat{{\boldsymbol{C}}}_{e}^{\circ }\odot {\boldsymbol{S}}_{e} +\frac{1}{2}{\boldsymbol{C}}_{e}\cdot {\mathscr {C}}_{e}:\hat{{\boldsymbol{C}}}_{e}^{\circ }\right) \end{aligned}$$

(44)

with:

$$\begin{aligned}&\hat{{\boldsymbol{C}}}_{e}^{\circ } ={\partial \hat{{\boldsymbol{C}}}_{e} (\Delta \gamma ,{\boldsymbol{C}}^{n+1})}/{\partial {\boldsymbol{C}}^{n+1}} \end{aligned}$$

(45)

$$\begin{aligned}&\left[ \hat{{\boldsymbol{C}}}_{e}^{\circ }\odot {\boldsymbol{S}}_{e}\right] _{ijkl} =\left[ \hat{{\boldsymbol{C}}}_{e}^{\circ }\right] _{imkl}\left[ {\boldsymbol{S}}_{e}\right] _{mj} \end{aligned}$$

(46)

We can therefore calculate the total derivative of ${\boldsymbol{C}}_{e}$ with respect to ${\boldsymbol{C}}^{n+1}$ as:

$$\begin{aligned} \hat{{\boldsymbol{C}}}_{e}^{\circledast }(\Delta \gamma ,{\boldsymbol{C}}^{n+1}) =\hat{{\boldsymbol{C}}}_{e}'(\Delta \gamma ,{\boldsymbol{C}}^{n+1})\cdot \frac{\mathrm {d}\Delta \gamma }{\mathrm {d}{\boldsymbol{C}}^{n+1}}+\hat{{\boldsymbol{C}}}_{e}^{\circ }(\Delta \gamma ,{\boldsymbol{C}}^{n+1}) \end{aligned}$$

(47)

These quantities are now introduced in the stress sensitivity, as:

$$\begin{aligned} {\mathscr {C}}&=2\frac{\mathrm {d}{\boldsymbol{S}}}{\mathrm {d}{\boldsymbol{C}}^{n+1}}\nonumber \\&=2\left\{ \left[ \hat{{\boldsymbol{Q}}}_{p}'\cdot \frac{\mathrm {d}\Delta \gamma }{\mathrm {d}{\boldsymbol{C}}^{n+1}} \right] \odot \left[ {\boldsymbol{S}}_{e}\cdot \left( {\boldsymbol{Q}}_{p}^{n+1}\right) ^{T}\right] \right. \nonumber \\&\left. \quad +{\boldsymbol{Q}}_{p}^{n+1}\cdot {\boldsymbol{S}}_{e}\cdot \left[ \hat{{\boldsymbol{Q}}}_{p}'\cdot \frac{\mathrm {d}\Delta \gamma }{\mathrm {d}{\boldsymbol{C}}^{n+1}}\right] ^{T}\right\} \nonumber \\&\quad +\left[ {\boldsymbol{Q}}_{p}^{n+1}\cdot {\mathscr {C}}_{e}:\hat{{\boldsymbol{C}}}_{e}^{\circledast } \left( \Delta \gamma ,{\boldsymbol{C}}^{n+1}\right) \right] \odot \left( {\boldsymbol{Q}}_{p}^{n+1}\right) ^{T} \end{aligned}$$

(48)

where $\hat{{\boldsymbol{Q}}}_{p}'={\mathrm {d}\hat{{\boldsymbol{Q}}}_{p}(\Delta \gamma )}/{\mathrm {d}\Delta \gamma }$. It is now required to specify the derivatives involved in (36):

$$\begin{aligned}&\left[ \hat{{\boldsymbol{C}}}_{e}'\right] _{ij} =\left( \hat{{\boldsymbol{Q}}}_{p}'\right) ^{T} \cdot {\boldsymbol{C}}^{n+1}\cdot {\boldsymbol{Q}}_{p}^{n+1}+\left( {\boldsymbol{Q}}_{p}^{n+1}\right) ^{T}{\boldsymbol{C}}^{n+1} \hat{{\boldsymbol{Q}}}_{p}' \end{aligned}$$

(49)

$$\begin{aligned}&\left[ \hat{{\boldsymbol{C}}}_{e}^{\circ }\right] _{ijkl} =\left[ {\boldsymbol{Q}}_{p}^{n+1}\right] _{ki}\left[ {\boldsymbol{Q}}_{p}^{n+1}\right] _{lj} \end{aligned}$$

(50)

The implementation of this algorithm is performed with Mathematica and AceGen (Wolfram Research Inc 2007; Korelc 2002). We therefore have the procedure described in Table 1.

Table 1 Finite strain constitutive solution with semi-implicit RK integration

In terms of stability of the RK integration, we can still use the known results from the literature for the linear case The linear case is obtained by fixing the flow vector ${\boldsymbol{N}}$. Using the linearized case, we have a vector form of ${\varvec{{\boldsymbol{Q}}}}_{v}$ and the derivative ${\mathrm {d}{\boldsymbol{Q}}_{v}}/{\mathrm {d}\gamma }$ as¹:

$$\begin{aligned} {\mathrm {d}{\boldsymbol{Q}}_{v}}/{\mathrm {d}\gamma }={{\boldsymbol{B}}}{\boldsymbol{Q}}_{v} \end{aligned}$$

(51)

where ${{\boldsymbol{B}}}$ depends on the flow-vector components $N_{ij}$:

$$\begin{aligned} {{{{\boldsymbol{B}}}=-}}\left[ \begin{array}{ccccccccc} N_{11} &{}\quad N_{21} &{}\quad N_{31} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad N_{12} &{}\quad N_{22} &{}\quad N_{32} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad N_{13} &{}\quad N_{23} &{}\quad N_{33}\\ N_{12} &{}\quad N_{22} &{}\quad N_{32} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ N_{13} &{}\quad N_{23} &{}\quad N_{33} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad N_{13} &{}\quad N_{23} &{}\quad N_{33} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad N_{11} &{}\quad N_{21} &{}\quad N_{31} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad N_{11} &{}\quad N_{21} &{}\quad N_{31}\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad N_{12} &{}\quad N_{22} &{}\quad N_{32} \end{array}\right] \end{aligned}$$

(52)

The linearized stability condition for the RK methods is a function of the eigenvalues of ${\boldsymbol{B}}$ (see, e.g. Hairer et al. 2010), we obtain a condition for $z=\Delta \gamma \lambda$ with $\lambda \in {\mathbb {C}}$ being an eigenvalue of B. For the RK4 method, we have the A-stability condition

$$\begin{aligned} R=\underset{z}{{\sup }}\left| 1+z+z^{2}/2+z^{3}/6+z^{4}/24\right| <1 \end{aligned}$$

for $\text {Re}[z]<0$ which we assess here. We set $R=0$ if $\mathrm {Re}[z]\ge 0$.

4 Equilibrium and finite-element implementation

The use of relative strain measures is convenient in finite elements. Hence, a description is herein presented on how to use the constitutive algorithm with these elements. We make use of three configurations, $\Omega _{0}$, $\Omega _{b}$ and $\Omega _{c}$. Configuration $\Omega _{0}$ is undeformed, $\Omega _{b}$ is the reference configuration and $\Omega _{a}$ is the equilibrium configuration. To these three configurations we associate three frames 0,  b and a, respectively. We use the letter ${\boldsymbol{R}}$ to represent a frame, with each basis vector being a column of ${\boldsymbol{R}}$. A generic tensor ${\boldsymbol{T}}$ is written, in frame c for reference configuration $\Omega _{b}$ and equilibrium configuration $\Omega _{a}$ as ${{{\boldsymbol{T}}_{ab}^{c}}}$. Whenever it is obvious, we omit the superscript c. After introducing the relative deformation gradient between configurations $\Omega _{b}$ and $\Omega _{a}$ as ${\boldsymbol{F}}_{ab}$ we have:

$$\begin{aligned} {\boldsymbol{F}}_{ab}={\boldsymbol{F}}_{a0}{\boldsymbol{F}}_{b0}^{-1} \end{aligned}$$

(53)

The Green–Lagrange strain between configurations $\Omega _{a}$ and $\Omega _{b}$ is obviously ${\boldsymbol{E}}_{ab}={1}/{2}\left( {\boldsymbol{F}}_{ab}^{T}{\boldsymbol{F}}_{ab}-{\boldsymbol{I}}\right)$ and therefore we can write ${\boldsymbol{E}}_{a0}={\boldsymbol{E}}$ as:

$$\begin{aligned} {\boldsymbol{E}}_{a0}={\boldsymbol{E}}_{b0}+{\boldsymbol{F}}_{b0}^{T}{\boldsymbol{E}}_{ab}{\boldsymbol{F}}_{b0} \end{aligned}$$

(54)

Change of frame of a given second-order tensor ${\boldsymbol{T}}$ is obtained in general as: ${\boldsymbol{T}}^{a}={\boldsymbol{R}}_{a}{\boldsymbol{T}}^{0}{\boldsymbol{R}}_{a}^{T}$. Polar decomposition of the deformation gradient ${\boldsymbol{F}}_{a0}$ is obtained from the rotation and stretch ${\boldsymbol{U}}_{a0}$ (using the previous notation):

$$\begin{aligned} {\boldsymbol{F}}_{a0}^{a}={\boldsymbol{R}}_{a0}^{a}{\boldsymbol{U}}_{a0}^{a} \end{aligned}$$

(55)

where ${\boldsymbol{R}}_{a0}^{a}={\boldsymbol{R}}_{0}^{T}{\boldsymbol{R}}_{b}$. Having defined the relative Green–Lagrange strain ${\boldsymbol{E}}_{ab}$, which is the traditional Green–Lagrange strain assuming that the initial configuration is $\Omega _{b}$, we now use the power conjugacy between the Green–Lagrange strain rate ($\dot{{\boldsymbol{E}}}$) and the second Piola-Kirchhoff stress (${\boldsymbol{S}}\equiv {\boldsymbol{S}}_{a0}$) to obtain:

$$\begin{aligned} \int _{\Omega _{0}}{\boldsymbol{S}}:\dot{{\boldsymbol{E}}}_{a0}\mathrm {d}\Omega _{0} =\int _{\Omega _{b}}{\boldsymbol{S}}_{ab}:\dot{{\boldsymbol{E}}}_{ab}\mathrm {d}\Omega _{b} \end{aligned}$$

(56)

In addition, in (56), $\dot{{\boldsymbol{E}}}_{ab}={1}/{2}\left( \dot{{\boldsymbol{F}}}_{ab}^{T}{\boldsymbol{F}}_{ab}^{-1} +{\boldsymbol{F}}_{ab}^{-T}\dot{{\boldsymbol{F}}}_{ab}\right)$. From (56) we obtain the following relation:

$$\begin{aligned} {\boldsymbol{S}}_{ab}=\frac{1}{J_{b0}}{\boldsymbol{F}}_{b0}{\boldsymbol{S}}{\boldsymbol{F}}_{b0}^{T} \end{aligned}$$

(57)

where ${\boldsymbol{J}}_{b0}=\det {\boldsymbol{F}}_{b0}$. Generalizing, we have:

$$\begin{aligned} {\boldsymbol{S}}_{ac}=\frac{1}{J_{cb}}{\boldsymbol{F}}_{cb}{\boldsymbol{S}}_{ab}{\boldsymbol{F}}_{cb}^{T} \end{aligned}$$

(58)

In terms of Newton–Raphson iteration, we require the first variation of (56), the tangent modulus (48) is employed to read:

$$\begin{aligned}&\left( \int _{\Omega _{0}}{\boldsymbol{S}}:\delta \dot{{\boldsymbol{E}}}_{a0}\mathrm {d}\Omega _{0} +\int _{\Omega _{0}}\delta {\boldsymbol{E}}_{a0}:{\mathscr {C}}:\dot{{\boldsymbol{E}}}_{a0} \mathrm {d}\Omega _{0}\right) \nonumber \\&\quad ={\boldsymbol{F}}_{\text {ext}}\cdot \dot{{\boldsymbol{u}}} -\int _{\Omega _{0}}{\boldsymbol{S}}:\dot{{\boldsymbol{E}}}_{a0}\mathrm {d}\Omega _{0} \end{aligned}$$

(59)

where ${\boldsymbol{F}}_{\text {ext }}$ is the external load vector and $\dot{{\boldsymbol{u}}}$ is the nodal velocity vector. In our case, pressure is applied in Sect. 6.

5 Prototype model and results

For the hyperelastic law, we use the compressible Neo-Hookean with properties $\mu$ and $\lambda$ (analogous to Lamé parameters in the Hookean case), see Bonet and Wood (2008) for further details:

$$\begin{aligned} {\hat{{\varvec{S}}}}_{e}({\boldsymbol{C}}_{e})=\mu ({\boldsymbol{I}}-{\boldsymbol{C}}_{e}^{-1}) +\lambda \log \left[ \sqrt{\det \left( {\boldsymbol{C}}_{e}\right) }\right] {\boldsymbol{C}}_{e}^{-1} \end{aligned}$$

(60)

corresponding to the following strain energy density:

$$\begin{aligned}&\varPsi ({\boldsymbol{C}}_{e})=\frac{\mu }{2}\left[ \mathrm {tr}\left( {\boldsymbol{C}}_{e}\right) -3\right] -\mu \log \sqrt{\det \left( {\boldsymbol{C}}_{e}\right) }\nonumber \\&\quad +\,\frac{\lambda }{2} \left[ \log \sqrt{\det \left( {\boldsymbol{C}}_{e}\right) }\right] ^{2} \end{aligned}$$

(61)

The nondimensional yield function is given by:

$$\begin{aligned} \phi _{\star }\left( {\boldsymbol{T}}_{e}\right) =\frac{\sigma _{\text {eq}} \left( {\boldsymbol{T}}_{e}\right) }{\sigma _{y}}-1 \end{aligned}$$

(62)

with, as a prototype equivalent stress, a specific Hill-criterion is adopted (the subscript e of ${\boldsymbol{T}}_{e}$ is omitted for conciseness):

$$\begin{aligned}&\sigma _{\text {eq}}^{2}({\boldsymbol{T}}_{e})=\frac{1}{4}\left[ 4T_{11}^{2} +6\left( T_{12}^{2}+T_{21}^{2}\right) +\frac{27}{2}\left( T_{13}^{2} +T_{31}^{2}\right) -9T_{11}T_{22}+9T_{22}^{2}\right. \nonumber \\&\quad \left. +\,6\left( T_{23}^{2} +T_{32}^{2}\right) +T_{11}T_{33}-9T_{22}T_{33}+4T_{33}^{2}\right] \end{aligned}$$

(63)

From which, ${\boldsymbol{N}}\left( {\boldsymbol{T}}_{e}\right) ={\mathrm {d}\phi _{\star } \left( {\boldsymbol{T}}_{e}\right) }/{\mathrm {d}{\boldsymbol{T}}_{e}}$ is determined as:

$$\begin{aligned} {\boldsymbol{N}}\left( {\boldsymbol{T}}_{e}\right) =\frac{1}{\sigma _{y}\sigma _{\text {eq}} \left( {\boldsymbol{T}}_{e}\right) }\left[ \begin{array}{ccc} \frac{8T_{11}-9T_{22}+T_{33}}{8} &{}\quad \frac{3}{2}T_{12} &{} \quad \frac{27}{8}T_{13}\\ \frac{3}{2}T_{21} &{}\quad \frac{18T_{22}-9T_{11}-9T_{33}}{8} &{}\quad \frac{3}{2}T_{23}\\ \frac{27}{8}T_{31} &{}\quad \frac{3}{2}T_{32} &{}\quad \frac{8T_{33}-9T_{22}+T_{11}}{8} \end{array}\right] \end{aligned}$$

(64)

Using the smoothed replacement $\prec {\hat{\phi }}_{\star }\left( {\varvec{C,{\boldsymbol{I}}}}\right) \succ _{\beta }$ with the properties shown in Table 2, the effect of $\beta$ is observable, cf. Fig. 2. In this figure, we easily identify the yield function in the strain space (we adopt the definition ${\boldsymbol{E}}={1}/{2}\left( {\boldsymbol{C}}-{\boldsymbol{I}}\right)$). Smaller $\beta$ results in a sharper representation of the yield function. In terms of strain energy density, Fig. 3 shows the results with $s=4$. It is worth noting that a full one-step integration is required for each pixel in the figure, with the corresponding calculation of ${\boldsymbol{C}}_{e}$. The yield function curbs the growth of $\varPsi$ with ${\boldsymbol{E}}$. The effect of $\beta$ is clear, with a sharper contour being obtained with smaller $\beta$. Iso-error maps for the stress are built with the standard procedure (Simo et al. 2000), but starting from ${\boldsymbol{C}}={\boldsymbol{I}}$. Figure 4 presents the three cases $s=1,2$ and 4 with $\beta =1\times 10^{-3}$, $\beta =1\times 10^{-2}$ and $\beta =1\times 10^{-1}$. The smoothing parameter has a clear effect on the shape of the maps and also the stress error. Larger values of $\beta$ result in larger integration errors. We note that smaller values than $1\times 10^{-3}$ do not produce visible differences with respect to that value. Since $\phi ^{\star }$ is normalized, we note that this value can be adopted in all simulations.

In addition, the effect of s is clear from the forward-Euler to the midpoint rule, with more than double the error obtained when using the forward-Euler method. However, between $s=2$ and $s=4$, some advantage is observed. Higher order methods also show improved Newton–Raphson behavior, related to the accuracy of the flow vector ${\boldsymbol{N}}$ at the solution. In terms of stability function R, we show the results for $s=4$ and $\beta =1\times 10^{-3}$ in Fig. 5. It can be observed that it complies with the condition $R<1$ for positive real parts of the eigenvalues. Of course, in the elastic region, we have $R=1$.

Table 2 Properties for the contour plot of $\prec {\hat{\phi }}_{\star }({\boldsymbol{C}},{\boldsymbol{I}})\succ$ as a function of $E_{11}$ and $E_{22}$

Fig. 2

Representation of $\prec {\hat{\phi }}_{\star }\left( {\boldsymbol{C}},{\boldsymbol{I}}\right) \succ _{\beta }$ for $\beta =1\times 10^{-3}$, $\beta =1\times 10^{-1}$ and $\beta =1$. Range is $E_{11}\in [-0.35,+0.35]$ and $E_{22}\in [-0.35,+0.35]$. $\beta$ is the regularization parameter for the yield function

Fig. 3

Strain energy density logarithm, $\log \varPsi$ in the elasto-plastic case for $\beta =0$, $\beta =1\times 10^{-3}$ and $\beta =1\times 10^{-1}$. Range is $E_{11}\in [-0.35,+0.35]$ and $E_{22}\in [-0.35,+0.35]$. $\beta$ is the regularization parameter for the yield function

Fig. 4

Iso-error maps for $E_{11}\in [-0.6,+0.6]$ and $E_{22}\in [-0.6,+0.6]$. $\beta$ is the regularization parameter for the yield function

Fig. 5

R values for $s=4$, $E_{11}\in [-0.35,+0.35]$ and $E_{22}\in [-0.35,+0.35]$ (outside these bounds R decreases) and $\beta =0.001$. $R=1$ identifies the yield surface

6 Application to an anisotropic elasto-plastic plate under pressure

We consider the problem of a plate under deformation-dependent pressure, see Fig. 6. This is an adaptation of the problem proposed by Buchter et al. (1994) but with anisotropic laws. Relevant properties are shown in Fig. 6 along with the effective strain contour plot $\varepsilon _{p}$. We adopt a rotation $\alpha =\pi /6$ around the z-axis for the Hill criterion, with the same yield function previously introduced 63.

Fig. 6

Square plate under deformation-dependent pressure. Deformed configuration and plot of effective plastic strain $\varepsilon _{p}$ (Hill yield criterion and compressible Neo-Hookean hyperelastic model)

For the compressible Neo-Hookean combined with the Hill yield criterion, Fig. 7 shows the results. We determine the pressure from the central displacement by an additional global equation (see, e.g. Areias et al. 2009 where this procedure was introduced). Very large step sizes are possible and the effect of the order of the RK method is observable. In terms of the effect of $\beta$, we note that $\beta <1\times 10^{-3}$, since the yield function is normalized, are indistinguishable in terms of results. Figure 8 shows the effect of $\beta$ for $\Delta u_{z}=10$ and $s=1$. We can observe lower values of pressure but also a shallower drop for higher values of displacement.

Fig. 7

Square plate under pressure. Effect of step size and order of the RK integrator for the compressible Neo-Hookean/Hill criterion combination. $\beta =1\times 10^{-3}$

Fig. 8

Square plate under pressure. Effect of parameter $\beta$ for the compressible Neo-Hookean/Hill criterion combination. $s=1$

7 Conclusions

We proposed a one-step semi-implicit algorithm to solve the finite-strain elasto-plastic DAE. It makes use of a fourth-order Runge–Kutta method for the differential part of the system and a Newton–Raphson root finder for the algebraic term. Since it is not, in general, possible to transform the constitutive system into a ODE, we replace the integrated differential equation (for ${\mathrm {d}{\boldsymbol{F}}_{p}^{-1}}/{\mathrm {d}t}$) in a smoothed version of the originally non-smooth algebraic equation.

The effects of (1) order of integration s and (2) smoothing parameter $\beta$ are studied for a Neo-Hookean model coupled with the classical Hill yield criterion with both elastic and plastic finite strains. Iso-error maps are presented, allowing the following conclusions:

• 1. Effect of the smoothing parameter $\beta$ is significant, with larger values imposing resulting in a diffuse elasto-plastic interface. This has been verified in the yield function and the strain energy density contour plots. Since $\phi _{\star }$ is normalized, values of $\beta$ less than $1\times 10^{-3}$ produce indistinguishable results.

• 2. Effect of order s is also important, with a pronounced difference between $s=1$ (forward Euler) and $s=2$ (Runge–Kutta midpoint). Iso-error maps show a much higher error with the forward-Euler method. However, between $s=2$ and $s=4$, iso-error maps show some difference but it is not pronounced. The maximum value of the error still shows the benefit of higher order.

• 3. A-stability is verified for the integration of the flow law and $s=4$.

Extensions both in terms of integration algorithms and also more intricate constitutive laws are not difficult to envisage, and one-step extrapolation integrators can replace the classical Runge–Kutta in this work.