Prediction of the dynamic equivalent stiffness for a rubber bushing using the finite element method and empirical modeling

Abstract

A hybrid method using an approximation that is based on the finite element analysis and empirical modeling is proposed to analyze the dynamic characteristics of a rubber bushing. The hyperelastic–viscoplastic model and an overlay method are used to obtain the hysteresis of the rubber bushing in the finite element analysis. A spring, fractional derivatives, and frictional components are used in the empirical model to obtain the dynamic stiffness in wide ranges of the excitation frequencies and amplitudes. The parameters of the proposed empirical model are determined using the hysteresis curves that were obtained from the finite element analysis. The dynamic stiffness of the rubber bushing in the wide ranges of the frequencies and amplitudes was predicted using the proposed hybrid method and was validated using lower arm bushing experiments. The proposed hybrid method can predict the dynamic stiffness of a rubber bushing without the performance of iterative experiments and the incurrence of a high computational cost, making it applicable to analyses of full-size vehicles with numerous rubber bushings under various vibrational loading conditions.

1 Introduction

Rubber bushings are used for several industrial components to transfer motion from one part to another. In automotive suspension systems, rubber bushings play the role of an isolator by reducing the external loadings and transmitted vibrations. Although the rubber bushing is a prevalent component in automobiles, it is still challenging to predict the actual behavior of the rubber bushing due to its dynamic characteristics.

The dynamic characteristics of a rubber bushing are dependent on several factors such as the amplitude, frequency, temperature and so on. The dynamic stiffness of the rubber material is decreased with the increasing of the excitation amplitude. Furthermore, the associated amplitude effect is more evident regarding filled rubber compared with natural rubber, and this is due to the disintegration of the filler-matrix structures that is called the Fletcher-Gent effect (1954) or the Payne effect (1971). Medalia (1978) investigated the amplitude-dependent behavior of elastomeric material by studying the couplings between the materials and the dynamic strain. Dean et al. (1984) studied the variation of the dynamic stiffness of carbon-black filled rubber in terms of the frequency, strain amplitude, and temperature, reporting on the observed inseparable relationships between these measures. Coveney et al. (1995) applied the standard triboelastic solid model (STS) to characterize the amplitude dependence of a heavily filled rubber isolator.

The dynamic stiffness of rubber is increased with the increasing of the frequencies because of the viscoelastic effect that is generated from the delayed reorganization of the polymer chain. This viscoelastic response was initially characterized by the Maxwell model and the Kelvin–Voight model (Findley, Davis 1989); however, the correlations of each model with the creep and the stress relaxation, respectively, are poor. Through a combining of the Maxwell model and the Kelvin–Voight model, the standard linear solid model (SLS) was proposed to overcome these drawbacks (Banks et al. 2011). Kaliske and Rohert (1997) proposed a three-dimensional visocoelastic model based on the Maxwell–Wiechert model. Govindjee and Simo (1992) suggested a viscoelastic-damage model containing the Mullin’s effect (1969), which is the softening phenomenon in filled rubber. Wineman et al. (1998) researched the Popkin-Rogers nonlinear viscoelastic formulations (1968) using the force–displacement approach. Lu (2006) proposed a modified fractional derivative model that was initially adopted by Bagley and Torvik (1983) to predict complex modulus of elastomeric material under high frequencies.

Although linear viscoelastic models can be used to predict the actual behavior of rubber bushings in a small strain state, they are limited by heavily filled rubber and large strain states. To avoid these drawbacks, the coupled model with amplitude and frequency effects was investigated. Berg (1998) proposed a one-dimensional empirical model that is a combination of the spring, dashpot, and Coulomb-friction components that represent the amplitude and frequency dependent behaviors. Sjöberg and Kari (2002) proposed a modified empirical model by using fractional derivative. García Tárrago et al. (2007a, b, c) suggested a dynamic-stiffness model that involves the geometric information of the rubber bushing for which a modified-stiffness term that was suggested by Horton et al. is utilized (2000a, b).

Under a large deformation, the dynamic stiffness shows an increasing tendency unlike a small-deformation case. To describe this effect, Dzierzek (2000) suggested a nonlinear elastic component that accurately provided the dynamic stiffness of the rubber bushing in a wide amplitudinal range. Lijun et al. (2010) proposed a novel model using a nonlinear elastic part and a reduced viscoelastic term. Puel et al. (2013) investigated the implementation of a rate-dependent triboelastic (RT) model for which they adopted a smoothing process. Luo et al. (2013) researched the effect of the preload on the rubber absorber in rail-fastening systems, and they suggested a technique to obtain the dynamic stiffness. Those empirical models are convenient as they can depict the amplitude and frequency effects on the dynamic stiffness by using model parameters that have been obtained from several experiments. In this process, however, the empirical-model parameters are geometry-dependent, and iterative experiments are required to identify the parameters when the geometry changes.

In addition to the empirical bushing models, constitutive modeling has also been studied. The constitutive models can be implemented regardless of the geometry of the bushing because they are geometry-independent. These models are already predefined in the finite element (FE) codes. A hyperelastic–viscoplastic model for which an overlay method that additively superposes the hyperelastic, viscoelastic, and elastoplastic elements was investigated to represent the amplitude and frequency dependencies (Olsson 2007; Gracia et al. 2010). Moreover, Oscar and Centeno (2009) investigated the hyperelastic–viscoelastic bushing model and used full-vehicle transient-crash simulations for its validation. Khajehsaeid et al. (2013) proposed an explicit time-discrete formulations for hyperelastic–viscoelasitc model which was validated with experimental results under axial–torsional coupled modes of elastomeric bushing. Kaya et al. (2016) suggested an approach for the acquisition of the target stiffness of a vehicular rubber bushing using hyperelastic and shape-optimized modeling. Also, Cao et al. (2016) investigated the effects of the rubber bushing on the bearing dynamics using the explicit finite element method (EFEM) and the dynamic bearing model (DBM). Even though constitutive models effectively predict the dynamic stiffness, they require a large computational time to calculate the stiffness value for each corresponding amplitude and frequency.

In this study, to supplement the drawbacks of previous methods, a new approach for which the FE method is combined with the empirical model to predict the bushing dynamic stiffness is proposed. The relevant procedure is shown in Fig. 1. First, a geometric model of a rubber bushing is built using an FE code. A hyperelastic–viscoplastic model that was defined using the overlay method is used to predict the hysteresis curves of the rubber bushing. These hysteresis curves were used to determine the empirical-model parameters for the prediction of the dynamic stiffness of the rubber bushing in wide ranges of frequencies and amplitudes. FE simulations are advantageous because a hysteresis curve can be obtained regardless of the bushing geometry that is used since the FE model is established by the geometry-independent material properties of rubber. However, FE-simulation constructions of the rubber-bushing dynamic stiffness within a wide range of excitation frequencies and amplitudes incur very high computational costs. To reduce this central-processing-unit (CPU) time, a modified empirical model is proposed to complement the FE analysis. The FE simulations of only a few loading cases need to be performed to define the empirical model. Subsequently, the established empirical model predicts the dynamic stiffness of the filled rubber bushing in wide ranges of the excitation frequencies and amplitudes. The proposed hybrid method makes it possible to predict the dynamic stiffness of the rubber bushing without the need for iterative experiments and the incurrence of an expensive computational cost.

Fig. 1

Schematic of a hybrid method combining the finite element analysis and empirical modeling

2 Experiments

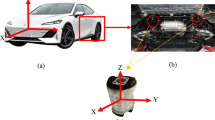
Rubber bushings serves as connectors and shock absorbers in the automotive suspension system illustrated in Fig. 2. Four bushings are ensuring assembly between a metallic sub frame and two lower control arms. Two kinds of bushings are used depending on the most solicited direction of loading such as cylindrical A-bushing (this study) and G-bushing with complex geometry. As denoted previously, the rubber bushings are essential to absorb shocks and vibrations due to irregular ground surfaces, incline of the suspension system and motor induced vibrations. It is important to predict the mechanical properties of the rubber bushing such as dynamic stiffness because it is an indicator of the ability of the part to withstand high levels of shock and vibrations during its lifetime.

Fig. 2

Schematic of an automobile suspension system and the rubber bushing which connects the sub frame to the lower control arms

To characterize the mechanical behavior of the rubber bushing, radial-loading tests were conducted. The specimen that was used in the experiments is a cylindrical lower arm bushing composed of carbon-black filled rubber, and the rubber material is between the inner and outer steel sleeves. The sample and its dimensions are shown in Fig. 3a. The experiments were conducted by following the ASTM D5992-96 standard (1996). The specimen was mounted on an Instron 8801 (Instron, USA.) servo-hydraulic testing machine. The maximum axial-force capacity of the testing-machine actuator is 100 kN, while its load-cell accuracy is 0.005%. A holding jig was used to fix the specimen and to impose the radial-loading condition, as shown in Fig. 3b. Therefore, the outer-bushing sleeve is fixed, and a displacement is imposed onto the inner sleeve as a sine-wave signal with a frequency range of 0.1–20 Hz and an amplitude range of 0.2–2.4 mm. The reaction force was extracted and recorded from these experiments. It was reliable to record reaction forces by using one directional load cell on test machine because a holding jig was used to ensure a fixed radial boundary conditions of rubber bushing. So, the hysteresis curves were obtained by representing displacement (input) against reaction force (output). Moreover, to eliminate the Mullin’s effect of the rubber material, 20 cycles of the sample were initially loaded. By limiting the number of test cycles, a constant temperature was maintained, and this first prevented the heating and then the softening of the specimen.

Fig. 3

a Shape and geometry of the cylindrical rubber bushing and the b Experimental setup

Figure 4 shows the hysteresis loop that was obtained from the radial-loading tests. Note that the measuring noise was not considerable even for small amplitudes. For instance, for an amplitude of 0.2 mm, the total force recorded is almost 300 N. It was large enough compared to measured noise fluctuation of 10 N. In the region of the small amplitude (0.6 mm), under the quasistatic condition, the shape of the hysteresis loop is eliptical, as shown in Fig. 4a. However, under the large amplitude (2.4 mm), the bent hysteresis loop is due to the dominance of compressive stress in the rubber, as shown in Fig. 4a. In this case, the equivalent stiffness shows an increasing tendency. Contrarily, although it is under the large amplitude, this phenomenon does not appear under the axial-loading conditions because shear stress is the main occurrence in the material. Similarly, this amplitude-dependent behavior is also observed under the dynamic condition (10-Hz excitation), as shown in Fig. 4b. In this case, the hysteresis-curve bandwidth is wider than the quasistatic result, and the stiffness magnitude was increased; this behavior is due to the increasing of the viscoelastic-damping force as the excitation frequency was increased.

Fig. 4

Hysteresis curve: a Under a Quasi-static Test (0.1 Hz) and b Under a Dynamic Test (10 Hz)

3 Numerical modeling

3.1 Finite element modeling

Generally, in rheological models, the stress tensor of a rubber bushing is additively decomposed into elastic $\sigma^{e}$, viscoelastic $\sigma^{v}$, and elastoplastic $\sigma^{ep}$ parts, and it is defined by the following equation:

$$ \sigma = \sigma^{e} + \sigma^{v} + \sigma^{ep} $$

(1)

The rate-dependent response is represented by the viscoelastic component. Conversely, the amplitude-dependent response is considered using the elastoplastic component. In the FE modeling, the summation of these effects is performed using the overlay method. For the overlay model, the hyperelastic, viscoelastic, and elastoplastic elements were combined to obtain an equivalent element, as shown in Fig. 5. These elements must share the same nodes to preserve the same displacement field. The commercial FEM package Abaqus (ABAQUS, Inc., USA) offers the possibility to overlap elements with different properties for the attainment of an equivalent behavior.

Fig. 5

Schematic of an overlay method

3.1.1 Hyperelastic model

The hyperelastic effect is mainly considered using the strain-energy density function, which is defined by the uniaxial, biaxial, and shear tests. Among the commonly used hyperelastic models, the Ogden model, which is directly described in terms of the principal stretch ratio, is adopted for the forthcoming analysis and is presented by the following equation:

$$ U = \mathop \sum \limits_{i = 1}^{N} \frac{{2\delta_{i} }}{{\alpha_{i}^{2} }}\left( {\bar{\lambda }_{1}^{{\alpha_{i} }} + \bar{\lambda }_{2}^{{\alpha_{i} }} + \bar{\lambda }_{3}^{{\alpha_{i} }} - 3} \right) + \mathop \sum \limits_{i = 1}^{N} \frac{1}{{D_{i} }}\left( {J - 1} \right)^{2i} $$

(2)

where $\bar{\lambda }_{n}$ denotes the principal stretches, $J$ is the volume ratio, $\delta_{i}$ denotes Ogden model constant, the constants $\delta_{i}$ and $\alpha_{i}$ are obtained by a fitting with the stress–strain curve of the material, and $D_{i}$ denotes the compressibility. In the case of incompressible material, Eq. (2) can be reduced to the following equation:

$$ U = \mathop \sum \limits_{i = 1}^{N} \frac{{2\delta_{i} }}{{\alpha_{i}^{2} }}\left( {\bar{\lambda }_{1}^{{\alpha_{i} }} + \bar{\lambda }_{2}^{{\alpha_{i} }} + \bar{\lambda }_{3}^{{\alpha_{i} }} - 3} \right) $$

(3)

3.1.2 Viscoelastic model

To consider time dependent effect, a viscoelastic model is needed. The rate-dependent behavior is modeled by the Prony series based on the stress-relaxation properties. The Prony series allows for a decrease of the shear modulus. The equation of the Prony series is as follows:

$$ G\left( t \right) = G_{0} \left[ {1 - \mathop \sum \limits_{i = 1}^{N} g_{i} e^{{\left( {\frac{ - t}{{\tau_{i} }}} \right)}} } \right] $$

(4)

where $G\left( t \right)$ and $G_{0}$ represent the shear modulus and the initial shear modulus, respectively, and the terms $g_{i}$ and $\tau_{i}$ denote the dimensionless shear-relaxation modulus and the relaxation time, respectively.

3.1.3 Elastoplastic model

It is already been demonstrated that the dynamic stiffness of rubber-bushing materials exhibit a strong dependence on the displacement amplitude. This observed plastic effect is known as the Payne effect (1971). Since this effect is particularly observed for the present rubber material, it became necessary to add a simple von-Mises plasticity model comprising the Young’s-modulus parameter $E$ and the yield stress $\sigma_{y}$ to the constitutive modeling.

3.2 Empirical model

The objective of this section is to find the expression of the radial dynamic stiffness $\hat{k}_{dyn}$. Even though the dynamic stiffness can be directly determined using the hysteresis curve of the finite element results, an efficient approach is needed to predict the dynamic stiffness in wide amplitudinal and frequency ranges. The FE analysis is one of the available information-attainment solutions here. Nevertheless, an iterative finite element analysis requires considerable computational abilities and time. To supplement this problem, empirical modeling is needed because it permits a reduction of the calculation quantity, which requires several amplitude- and frequency-independent experiments. The rubber bushing is modeled with the spring, fractional derivatives, and frictional parts, as shown in Fig. 6.

Fig. 6

Proposed empirical rubber-bushing model

First, the radial-equivalent strain is given as follows to establish the stress–strain modeling (Garcia Tárrago et al. 2007a):

$$ \varepsilon \left( t \right) = x\left( t \right)\sqrt {\frac{{a^{2} + b^{2} }}{{\left[ {b^{4} - a^{4} } \right]\ln \left( {\frac{a}{b}} \right) - \left[ {a^{2} - b^{2} } \right]^{2} }}} $$

(5)

where $x\left( t \right)$ is the radial displacement and the harmonic excitation is $x\left( t \right) = x_{o} \sin \left( {\omega_{0} t} \right)$. The terms $x_{o}$ and $\omega_{0}$ denote the excitation amplitude and frequency, respectively. Also, $a$ is the inner radius of the rubber bushing and $b$ is the radius of the outer rubber part, as shown in Fig. 3a.

Under the radial-loading condition with the large deformation, the dynamic stiffness showed an increasing tendency with the increasing of the excitation amplitude, and this tendency is the opposite of the small-amplitude tendency. This phenomenon appeared due to the increasing of the compressive stress between the metal sleeves and the rubber. To consider the radial-direction characteristics under a large amplitude, a nonlinear elastic component was proposed by Dzierzek (2000). In this model, the nonlinear elastic part is presented by a spring. The equation for the combining of the nonlinear elastic stress with the equivalent stiffness is as follows:

$$ \sigma_{e} \left( t \right) = k_{t} \beta \frac{{2d_{t} }}{\pi }\tan \frac{\pi \varepsilon }{{2d_{t} }} $$

(6)

where $k_{t}$ denotes the elastic stiffness and is obtained using the quasistatic results; the terms $d_{t}$ and $\beta$ are the nonlinear weighted parameter and the proportional constant, respectively; and $k_{t}$ is a function of the displacement amplitude. The $k_{t}$ is expressed as follows:

$$ k_{t} = p_{1} x^{2} + p_{2} x + p_{3} $$

(7)

where the coefficients $p_{1} , \;p_{2}$, and $p_{3}$ can be determined using the hysteresis curve that was obtained from the finite element analysis.

Moreover, a frictional component must be considered to represent the frictional damping. The frictional stress depending on the equivalent strain can be expressed by the following equation (Dzierzek 2000):

$$ \sigma_{f} \left( t \right) = \left[ {c_{1} \left( {k_{t} \beta \frac{{2d_{t} }}{\pi }\tan \frac{\pi \varepsilon }{{2d_{t} }} - k_{t} \beta \varepsilon } \right)^{{c_{2} }} + c_{3} } \right]\frac{{\dot{\varepsilon }}}{{\sqrt {\left| {\dot{\varepsilon }^{2} - \varepsilon \ddot{\varepsilon }} \right|} }} $$

(8)

where $c_{1}$ and $c_{2}$ are dimensionless frictional constants, and $c_{3}$ represents a static frictional-stress coefficient. This complex form permits the representation of nonlinear frictional damping under a highly nonlinear hysteresis curve.

The frequency-dependent characteristics of the rubber bushing were modeled using a fractional derivative. The fractional derivative was defined using the Riemann–Liouville integral (Oldham, Spanier 1974). It can be used to accurately predict the dynamic stiffness of a rubber bushing in a wide range of frequencies (Sjöberg, Kari 2002). The fractional model is represented as a discrete time and weighted form, as follows:

$$ \sigma_{v} = mD^{\alpha } \varepsilon \approx m\frac{{\Delta t^{ - \alpha } }}{{\varGamma \left( { - \alpha } \right)}}\mathop \sum \limits_{j = 0}^{n - 1} \frac{{\varGamma \left( {j - \alpha } \right)}}{{\varGamma \left( {j + 1} \right)}}\varepsilon_{n - j} , 0 < \alpha < 1 $$

(9)

where $m$ denotes a proportional constant and $\alpha$ represents a time-derivative order. To satisfy the equation of the fractional derivative, the $\alpha$ value must be between 0 and 1. The term $\Delta t$ is the discrete time and $\varepsilon_{n}$ is the strain at the time $t_{n} = n\Delta t$. The Gamma function is denoted by $\varGamma$ and is given by the following equation:

$$ \varGamma \left( \varphi \right) = \mathop \int \limits_{0}^{\infty } x^{\varphi - 1} e^{ - x} dx, \varphi > 0 $$

(10)

The behavior of the rubber is described by the summation of each stress component, as follows:

$$ \sigma_{\text{total}} \left( t \right) = \sigma_{e} + \sigma_{v} + \sigma_{f} $$

(11)

Furthermore, to define the dynamic modulus, the time domains of the stress and the strain need to be converted into a frequency domain through an application of the Fourier transform, as follows:

$$ \hat{\mu }\left( {\omega_{0} } \right) = \frac{{\hat{\sigma }_{\text{total}} \left( {\omega_{0} } \right)}}{{2\hat{\varepsilon }\left( {\omega_{0} } \right)}} $$

(12)

where $\hat{\sigma }_{total}$ and $\hat{\varepsilon }$ denotes frequency domains of total stress and strain respectively. $\hat{\mu }\left( {\omega_{0} } \right)$ denotes the dynamic modulus in the frequency domain.

It is well known that the dynamic stiffness can be expressed as the ratio of the radial load imposed to the bushing, $W$, and the resulting displacement, $d$. Horton et al. (2000a) showed that the displacement $d$ can be calculated by the superposition of the displacements of two special loading conditions, $d_{A}$ and $d_{B}$. By assuming the rubber as homogeneous, isotropic and incompressible and applying the linear theory of elasticity, they established a relationship between the displacements and strains, and thus, they deduced the expression of $d$ as a function of the dynamic modulus $\hat{\mu }$ as follows:

$$ d = \frac{W}{{\hat{k}_{\text{red}} L\hat{\mu }}} = \frac{W}{{10\pi L\hat{\mu }}}\left( {\frac{7}{2}\ln \left( {\frac{a}{b}} \right) - \frac{3}{2}\left[ {\frac{{b^{2} - a^{2} }}{{b^{2} + a^{2} }}} \right] + D} \right) $$

(13)

where $\hat{k}_{red}$ is the non-dimensional representation of the reduced radial stiffness term of cylindrical bushing. Consequently, the radial dynamic stiffness $\hat{k}_{dyn}$ is described by combining a reduced radial-equivalent stiffness term and the dynamic modulus as follows:

$$ \hat{k}_{\text{dyn}} \left( {\omega_{0} } \right) = \frac{W}{d} = \left( {\frac{10\pi }{{\frac{7}{2}\ln \left( {\frac{a}{b}} \right) - \frac{3}{2}\left[ {\frac{{b^{2} - a^{2} }}{{b^{2} + a^{2} }}} \right] + D}}} \right)L\hat{\mu } = \hat{k}_{\text{red}} L\hat{\mu } $$

(14)

where a, b and $L$ are the dimensions of the cylindrical bushing, as shown in Fig. 3a. $D$ is expressed by the application of the modified Bessel function that satisfies the geometric-boundary condition in the radial direction, as follows:

$$ D = \frac{{ - \alpha a\left( {3b^{2} + a^{2} } \right)\left[ {I_{1} \left( {\alpha a} \right)K_{0} \left( {\alpha b} \right) + I_{0} \left( {\alpha b} \right)K_{1} \left( {\alpha a} \right)} \right]}}{{\alpha^{2} ba\left( {b^{2} + a^{2} } \right)\left[ {I_{1} \left( {\alpha b} \right)K_{1} \left( {\alpha a} \right) + I_{1} \left( {\alpha a} \right)K_{1} \left( {\alpha b} \right)} \right]}} + \frac{{4\left( {b^{2} + a^{2} } \right) - \alpha b\left( {b^{2} + 3a^{2} } \right)\left[ {I_{1} \left( {\alpha b} \right)K_{0} \left( {\alpha a} \right) + I_{0} \left( {\alpha a} \right)K_{1} \left( {\alpha b} \right)} \right]}}{{\alpha^{2} ba\left( {b^{2} + a^{2} } \right)\left[ {I_{1} \left( {\alpha b} \right)K_{1} \left( {\alpha a} \right) + I_{1} \left( {\alpha a} \right)K_{1} \left( {\alpha b} \right)} \right]}} $$

(15)

where $\alpha^{2} = 60/L^{2}$, $I_{n}$, and $K_{n}$ represent the modified Bessel-function terms.

4 Results and discussions

4.1 Finite element implementation

The model parameters of the hyperelastic–viscoplastic model were determined using the experiment data. The parameters of the Ogden hyperelastic model were fitted using the uniaxial, biaxial, and shear data of the rubber material. The parameters of the Prony series were obtained using the shear–stress relaxation data that were obtained from different strain levels and show the rate-dependent effect. The FE code of Abaqus makes it possible to evaluate the material behavior and fit the correct material parameters based on the injected experimental uniaxial-, biaxial-, and shear–stress–strain curves and the experimental-relaxation data. The parameters of the elastoplastic model were determined by fitting the hysteresis loops from the experiment results of the rubber and the FE results by reducing the gap between the experimental and numerical force responses. Note that improvements of the identification procedure could be made by introducing automation of the procedure together with a robust identification algorithm. For instance, shape function method of moving least square fitting is a promising alternative as it permits to perform the identification procedure accurately and to make the response easily reconstructable through regularization, refer to Liu et al. (2014) and Li et al. (2016) for complete details. Time Domain Galerkin Method is greatly of interest as it permits, by replacing the weighting function with the shape function in the residual quantity, to improve the accuracy of the identification as demonstrated by Liu et al. (2016).

The geometry of the FE analysis was modeled based on the rubber-bushing specimen. A boundary condition of the FE model is also the same as the experimental conditions that are the fixed condition on the outer sleeve and the applied displacement on the central point of the inner rubber-bushing sleeve. The type of mesh is hexahedral and the element number is 4927, as shown in Fig. 7a. Also, the deformed bushing shape is presented by a combination of the extension and compression modes, as shown in Fig. 7b. Then, a comparison of the hysteresis curves of the FE analysis and the experiments of the rubber was performed for the parameter identification of the elastoplastic model, as shown in Fig. 8. Initially, the parameters of the elastoplastic model were obtained by a fitting of the hysteresis-loop bandwith between the FE analysis and the experiments using the least-square regression method, as shown in Fig. 8a. Subsequently, the parameters were optimized under various amplitudes, as shown in Fig. 8b. In the hysteresis curve from the finite element analysis, the curve bandwidth takes into account the damping force and is represented by the viscoelastic and elastoplastic components. Also, the hysteresis-loop incline indicates a decreased stiffness that is due to the amplitudinal effect, and its behavior is represented by the elastoplastic component. The identified parameters of the hyperelasic–viscoplastic model are shown in Table 1.

Fig. 7

a Geometry of the finite element model and the b deformed shape under radial loading

Fig. 8

Parametric identification of an elastoplastic model, a initial determination of the parameters, and b parametric optimization under various amplitudes

Table 1 Material parameters for the hyperelastic–viscoelastic model

4.2 Parameter identification of the empirical model

The material parameters of the empirical model were determined using the FE results. In this process, a general algorithm for curve fit was the least square regression model already predefined in Matlab toolbox. In addition, the polynomial and sinusoidal cost function were used to minimize the error vector between the input and observed output data. Therefore, all of the parametes, $p_{1}$, $p_{2}$, $p_{3}$, $\beta$, $k_{t}$, $d_{t}$, $c_{1}$, $c_{2}$, $c_{3}$, $m$ and $\alpha$, were identified by the least square regression algorithm. First, the parameters of the elastic and frictional elements were determined using the quasistatic responses that are amplitude-dependent and frequency-independent results. In the elastic part of the numerical model, the subvariables $p_{1}$, $p_{2}$, and $p_{3}$ are determined using the initial stiffness as shown in Fig. 9. Since $\beta$ and $k_{t}$ was formulated using Eq. (6) and the quadratic form of Eq. (7), respectively, involving $p_{1}$, $p_{2}$, and $p_{3}$, they are then deduced simultaneously from these equations. The initial stiffness was identified using the quasistatic simulations at a frequency of 0.1 Hz, for which the amplitudes were varied from 0.2–2.4 mm, as shown in Fig. 9a. In this case, $k_{t}$ denotes only the decreasing stiffness tendencies as the amplitude was increased. To represent the increasing tendencies that are due to the occurrence of the compressive stress under the large amplitude, the nonlinearity of the hysteresis curve needs to be considered; accordingly, the parameter $d_{t}$, which represents the nonlinearity weight, was adopted. This parameter was determined by fitting nonlinearity of curve under the maximum-displacement amplitude of 2.4 mm and at 0.1 Hz results, as shown in Fig. 9b.

Fig. 9

Parametric identification of the nonlinear elastic component. a Determination of $\varvec{k}_{\varvec{t}}$ and $\varvec{\beta}$, and b Determination of $\varvec{d}_{\varvec{t}}$

Second, the parameters of the frictional component, which represent the amplitudinal dependence, were also identified using the quasi-static results under the excitation frequency of 0.1 Hz. The term $c_{3}$, which represents the general hysteresis-loop bandwidth, was calibrated by a fitting with the bandwidth of the hysteresis curve under the minimum excitation displacement, as shown in Fig. 10a. Also, $c_{1}$ and $c_{2}$ were obtained by a fitting with the hysteresis curve under the maximum displacement, as shown in Fig. 10b. The edge shapes of the hysteresis loops of Fig. 10a, b are different. The edge of the hysteresis loop of the FE model is sharper than that of the hysteresis loop of the empirical model; this can be explained by the contribution of the term $\dot{\varepsilon }/\sqrt {\left| {\dot{\varepsilon }^{2} - \varepsilon \ddot{\varepsilon }} \right|}$ of Eq. (8) that acts on the effect of the frictional part. This term produced the frictional part depending on the deformation-speed profile and resulted in the round shape at the edge of the hysteresis loop.

Fig. 10

Parametric identification of the frictional component. a Determination of $\varvec{c}_{3}$ and b determination of $\varvec{c}_{1}$ and $\varvec{c}_{2}$

Finally, the parameters of the fractional derivative were obtained using the dynamic results. The terms $m$ and $\alpha$ were determined by fitting the dynamic stiffness with the changing frequencies at the minimum excitation amplitude of 0.2 mm, as shown in Fig. 11. In this case, the tendencies of the stiffness increase are due to the viscoelastic effect in the rubber materials. The parameters of the proposed empirical model are summarized in Table 2.

Fig. 11

Parametric identification of the fractional-derivative components for $\varvec{m}$ and $\varvec{\alpha}$

Table 2 Parameters of the proposed empirical model

4.3 Amplitude- and frequency-dependent dynamic stiffness

To establish the proposed empirical model, the model parameters were determined based on the finite element results. In this section, to validate the proposed approach, the results of the experiments that were performed on the lower control arm bushings are compared with the results of the proposed hybrid method. The experiments were conducted under the radial-loading condition, as shown in Fig. 3b. The three specimens of the lower control arm cylindrical bushing that were used are shown in Fig. 3a. The loading conditions in terms of the excitation amplitudes and frequencies are the same as those of the experimental section. To determine the deviation of the measurements, the standard deviation and average values are presented together with the numerical results in Figs. 12 and 13.

Fig. 12

Comparison of the dynamic stiffness according to the amplitude under the frequencies of: a 1 Hz, b 5 Hz, c 10 Hz, and d 15 Hz

Fig. 13

Comparison of the dynamic stiffness according to the frequency under the amplitudes of: a 0.7 mm, b 1.4 mm, and c 2.4 mm

Typically, under a small deformation, the dynamic stiffness of a rubber isolator is decreased with the growth of the amplitude due to the disintegration of the filler-matrix structure that is called the Fletcher-Gent or Payne effect, as mentioned previously. However, under a large deformation in the radial direction, the dynamic stiffness shows an increasing tendency with the increasing of the amplitude because of the generated compressive stress between the rubber material and the metal sleeves. The amplitude-dependent behaviors under different frequencies are presented in Fig. 12. Within the small amplitudinal range, the dynamic stiffness was decreased rapidly with the increasing of the amplitude due to the development of the damage of the filler-matrix structure. Contrarily, within the large amplitudinal range, the dynamic stiffness was increased after 1.8 mm with the increasing of the amplitude due to the dominance of the compressive stress rather than the shear stress. In this case, the hysteresis loop showed a bent shape, as shown in Fig. 4. Also, the dynamic stiffness was increased with the increasing of the frequency. The dynamic stiffness under 15 Hz, as shown in Fig. 12d, is larger than those under 1, 5, and 10 Hz.

To investigate the frequency effects, the dynamic stiffness according to the frequencies are presented in Fig. 13. The initial dynamic stiffness was increased sharply with the frequency up to 5 Hz due to the abrupt occurrence of a delayed reorganization time in the polymer structure. However, the dynamic stiffness was increased linearly after 5 Hz, and this is because the long polymer chains of the rubber that were deformed by the loading conditions were not immediately rearranged into the original state. A comparison of the Fig. 13a, b, and c shows that the frequency effects are similar under the small-amplitude (0.7 mm) and large-amplitude (2.4 mm) excitations.

Based on the previously described study, the amplitude- and frequency-dependent dynamic stiffness of the carbon-black filled rubber bushing is presented in Fig. 14. The amplitudinal dynamic stiffness was decreased under the small amplitude, but it tended to increase under the large amplitude. Also, the frequency dynamic stiffness tended to increase readily under the 5-Hz frequency, and then it was increased linearly. These tendencies are commonly observed in terms of the radial-loading conditions of carbon-black filled rubber bushings, and they are well described by the proposed method. It is therefore possible to predict a wide dynamic-stiffness range in consideration of both the amplitudinal and frequency effects of the carbon-black filled rubber bushing by utilizing the proposed hybrid method.

Fig. 14

Dynamic stiffness of filled rubber within wide amplitudinal and frequency ranges

5 Conclusion

In this study, a hybrid method is proposed using the FE analysis and empirical modeling to obtain the dynamic stiffness of a carbon-black filled rubber bushing within wide ranges of excitation frequencies and amplitudes. In the FE analysis, an overlay method for which the hyperelastic, viscoelastic, and elastoplastic elements are combined was used to obtain the hysteresis curve, which was used for the parametric identification of the empirical model. In the empirical model, the nonlinear elastic, viscoelastic, and frictional components are proposed to explain the frequency- and amplitude-dependent behaviors of the filled rubber bushing. The parameters of the frictional component and the nonlinear elastic component were determined using a quasistatic FE analysis. The two parameters of the viscoelastic component were determined using the hysteresis stiffness with the minimum amplitude under different excitation frequencies. The proposed model was validated in a comparison of rubber-isolator experiments that were conducted in the radial direction and under ranges of the excitation amplitudes from 0.2–2.4 mm and the excitation frequencies from 0.1–20 Hz. The dynamic stiffness of the rubber bushing was increased as the frequency was increased; however, it was decreased as the amplitude was increased within a small amplitudinal range, whereas it was increased as the amplitude was increased within a large amplitudinal range. The amplitudinal and frequency dependence of the dynamic stiffness of the filled rubber bushing are clearly evident. The dynamic stiffness that was predicted using the empirical model correlated well with the experiment results. The proposed hybrid method can be used to predict the dynamic stiffness of filled rubber bushings without the need to conduct iterative experiments and the incurrence of a high computational cost. Approximately, using the finite element method only, the equivalent dynamic stiffness of rubber bushing has to be defined by performing simulations in the range of 0.2–2.4 mm amplitudes and 1–20 Hz frequencies. Therefore, for each increment of 0.1 mm of amplitude and 1 Hz of frequency, a table size of 12 × 20 (240 simulations) has to be entirely defined knowing that each simulation usually takes 20–30 min. However, if the empirical model is combined to this approach, the dynamic stiffness table data can be filled from less than 15 cases of simulations. Therefore, the hybrid method is applicable to analyses of full vehicles with numerous bushings under various vibrational loadings.