On congruence extension properties for ordered algebras

Abstract

We introduce four extension properties (CEP, QEP, SCEP and SQEP) for ordered algebras, similar to the congruence extension property (CEP) and the strong congruence extension property of usual (unordered) algebras. All four properties turn out to have a description in terms of commutative squares or pullback diagrams. We then use these categorical descriptions to prove an ordered analogue of the well-known relation TP = AP + CEP, namely that a variety of ordered algebras has the ordered transferability property if and only if it has the ordered amalgamation property and QEP.

1 Preliminaries

As usual in universal algebra, a type is a (possibly empty) set $\Omega$ of operation symbols which is a disjoint union of sets $\Omega _{k}$, $k\in \mathbb {N}\cup \{0\}$.

Definition 1.1

(Cf. [1]) Let $\Omega$ be a type. An ordered $\Omega$-algebra (or simply ordered algebra) is a triple $\mathcal {A}=(A,\Omega _A,\le _{A})$ comprising a poset $(A,\le _{A})$ and a set $\Omega _{A}$ of monotone operations on $A$, where $\omega _{A}\in \Omega _{A}$ has arity $k$ if $\omega \in \Omega _{k}$ and where the monotonicity of $\omega _{A}$ means that

$$\begin{aligned} a_{1}\le _{A}a_{1}^{\prime }\wedge \ldots \wedge a_{k}\le _{A}a_{k}^{\prime }\Longrightarrow \omega _{A}(a_{1},\ldots ,a_{k})\le _{A}\omega _{A}(a_{1}^{\prime },\ldots ,a_{k}^{\prime }) \end{aligned}$$

for all $a_{1},\ldots ,a_{k},a_{1}^{\prime },\ldots ,a_{k}^{\prime }\in A$.

An ordered algebra $\mathcal {B}=(B,\Omega _{B},\le _{B})$ is called a subalgebra of $\mathcal {A}=(A,\Omega _{A},\le _{A})$ if

• (i) $B\subseteq A$,

• (ii) for every $k$ and for every $\omega \in \Omega _{k}$, $\omega _{B}=\omega _{A}\left| _{B^{k}}\right.$,

• (iii) $\le _{B}\;\;=\;\;\le _{A}\cap ~(B\times B)$.

The order and operations on the direct product of ordered algebras are defined componentwise.

A homomorphism $f$: $\mathcal {A}\longrightarrow \mathcal {B}$ of ordered algebras is a monotone operation-preserving map from an ordered $\Omega$-algebra $\mathcal {A}$ to an ordered $\Omega$-algebra $\mathcal {B}$. We call a homomorphism $f$ an order-embedding if additionally

$$\begin{aligned} f(a)\le _{B}f(a^{\prime })\Longrightarrow a\le _{A}a^{\prime } \end{aligned}$$

for all $a,a^{\prime }\in A$. Note that every order-embedding is necessarily injective.

An inequality of type $\Omega$ is a sequence of symbols $t\le t^{\prime }$ with $t$ and $t^{\prime }$ being $\Omega$-terms. We say that $\mathcal {A}$ satisfies inequality $t\le t^{\prime }$ if $t_{\mathcal {A}}\le t_{ \mathcal {A}}^{\prime }$, where $t_{\mathcal {A}},t_{\mathcal {A}}^{\prime }$: $\mathcal {A}^{n}\longrightarrow \mathcal {A}$ are the term functions induced on $\mathcal {A}$ by $t$ and $t^{\prime }$, and $t_{\mathcal {A}}\le t_{\mathcal {A} }^{\prime }$ is defined pointwise. A class $\mathcal {K}$ of ordered $\Omega$-algebras is called a variety if it consists precisely of all the algebras satisfying some set of inequalities; we refer to [1] for further details. Every variety of ordered algebras and their homomorphisms forms a category. Because the pointwise order is compatible with the composition of homomorphisms, considering the set of homomorphisms from $\mathcal {A}$ to $\mathcal {B}$ (for each pair of algebras $\mathcal {A}$ and $\mathcal {B}$) as a poset with respect to the pointwise order one may in fact regard these categories as $\mathsf {Pos}$-categories (categories enriched over the category $\mathsf { Pos}$ of posets and monotone mappings). We recall from [8] that monomorphisms in the categories of ordered algebras are precisely injective homomorphisms.

Given a quasiorder $\theta$ on a poset $(A,\le )$ and $a,a^{\prime }\in A$, we write

$$\begin{aligned} a\underset{\theta }{\le }a^{\prime } \Longleftrightarrow (\exists n\in \mathbb {N} )(\exists a_{1},\ldots ,a_{n}\in A)(a\le a_{1}\,\theta \, a_{2}\le a_{3}\,\theta \, \ldots \,\theta \, a_{n}\le a^{\prime }). \end{aligned}$$

An order-congruence on an ordered algebra $\mathcal {A}= (A,\Omega _A,\le _{A})$ is a congruence $\theta$ of the algebra $(A,\Omega _A)$ such that the following condition (cf. [3]) is satisfied:

$$\begin{aligned} (\forall a,a^{\prime }\in A)\left( a\underset{\theta }{\le }a^{\prime } \underset{\theta }{\le }a\Longrightarrow a\,\theta \, a^{\prime }\right) . \end{aligned}$$

We call a quasiorder $\sigma$ on an ordered algebra $\mathcal {A}$ a compatible quasiorder if it is compatible with operations and extends the order of $\mathcal {A}$. In [1] such relations are called admissible preorders. Both order-congruences and compatible quasiorders play an important role in the theory of ordered algebras. Let us denote the sets of all order-congruences and compatible quasiorders of $\mathcal {A}$ by $\mathsf {Con}(\mathcal {A})$ and $\mathsf {Cqu}(\mathcal {A})$, respectively.

For every subset $H\subseteq A\times A$ there exists the smallest order-congruence $\Theta$ on $\mathcal {A}$ containing $H$, which is the intersection of all order-congruences containing $H$. This $\Theta$ is called the order-congruence generated by $H$. We will need the following result about $\Theta$.

Lemma 1.2

Let $\mathcal {A}$ be an ordered algebra, $H\subseteq A\times A$ and $\Theta$ be the order-congruence on $\mathcal {A}$ generated by $H$. Then for any $c,c^{\prime }\in A$, $c\underset{\Theta }{\le } c^{\prime }$ if and only if $c\le c^{\prime }$ or there exist unary polynomial functions $p_{1},\ldots ,p_{n}$ on $\mathcal {A}$ and pairs $(a_{1},a_{1}^{\prime }),\ldots ,$ $(a_{n},a_{n}^{\prime })\in H\cup H^{-1}$ such that

There are two natural ways of forming quotients of ordered algebras. If $\theta$ is an order-congruence on an ordered algebra $\mathcal {A}=(A,\Omega _{A},\le _{A})$ then one can define an order relation $\preceq$ on the quotient set $A/\theta$ by

$$\begin{aligned}{}[a]\preceq [a^{\prime }]\Longleftrightarrow a\underset{\theta }{\le }a^{\prime }, \end{aligned}$$

$a,a^{\prime }\in A$. With the usual definitions of operations we obtain an ordered $\Omega$-algebra $\mathcal {A}/\theta :=\left( A/\theta ,\Omega _{A/\theta },\preceq \right)$. As in [8], we call such an algebra the regular quotient algebra of $\mathcal {A}$ by an order-congruence $\theta$. Such quotients were introduced in [3].

On the other hand, if $\sigma$ is a compatible quasiorder on $\mathcal {A}$ then $\theta =\sigma \cap \sigma ^{-1}$ is an order-congruence, and one can define an order relation $\sqsubseteq$ on the quotient set $A/\theta$ by

$$\begin{aligned}{}[a]\sqsubseteq [a^{\prime }]\Longleftrightarrow a\sigma a^{\prime }, \end{aligned}$$

$a,a^{\prime }\in A$. Again, with the usual operations we obtain an ordered algebra $\mathcal {A}/\sigma :=\left( A/(\sigma \cap \sigma ^{-1}),\Omega _{A/(\sigma \cap \sigma ^{-1})},\sqsubseteq \right)$; let us call it the quotient algebra of $\mathcal {A}$ by a compatible quasiorder $\sigma$. Such quotients have appeared in [1] and [4]. We note that every variety is closed both under quotient algebras and regular quotient algebras.

If $\sigma$ is a compatible quasiorder then we may consider both the regular quotient algebra $\mathcal {A}/(\sigma \cap \sigma ^{-1})$ and the (non-regular) quotient algebra $\mathcal {A}/\sigma$. They have the same elements and operations, but the order may be different: $\preceq$ is contained in $\sqsubseteq$.

Given a homomorphism $f$: $\mathcal {A}\longrightarrow \mathcal {B}$ of ordered algebras, the directed kernel $\overrightarrow{\ker }f$ of $f$, defined as

$$\begin{aligned} \overrightarrow{\ker }f=\left\{ (a,a^{\prime })\in \mathcal {A\times A}\mid f(a)\le f(a^{\prime })\right\} \end{aligned}$$

(see [4]) is clearly a compatible quasiorder on $\mathcal {A}$. Hence

$$\begin{aligned} \ker f=(\overrightarrow{\ker }f)\cap (\overrightarrow{\ker }f)^{-1} \end{aligned}$$

is an order-congruence on $\mathcal {A}$. So we have the quotient algebras

$$\begin{aligned} \mathcal {A}/\ker f=\left( A/\ker f,\Omega _{A/\ker f},\preceq \right) ,\;\;\;\;\;\; \mathcal {A}/\overrightarrow{\ker }f=\left( A/\ker f,\Omega _{A/\ker f},\sqsubseteq \right) , \end{aligned}$$

with order relations

$$\begin{aligned}{}[a]\preceq [a^{\prime }]\Longleftrightarrow & {} a\underset{\ker f}{\le }a^{\prime }, \\ {[a]}\sqsubseteq [a^{\prime }]\Longleftrightarrow & {} f(a)\le f(a^{\prime })\Longleftrightarrow (a,a^{\prime })\in \overrightarrow{\ker }f. \end{aligned}$$

A homomorphism $g$: $\mathcal {A}\longrightarrow \mathcal {B}$ of ordered algebras is called a Q-homomorphism (cf. [4]) if, for all $b,b^{\prime }\in B$, $b\le _{B}b^{\prime }$ implies that there exist $a,a^{\prime }\in A$ such that

$$\begin{aligned} b=g(a),\;a\underset{\ker g}{\le }a^{\prime },\;g(a^{\prime })=b^{\prime }. \end{aligned}$$

A morphism in a category of ordered algebras is called a regular epimorphism if it is the coequalizer of some pair of morphisms. It was shown in [8] that surjective epimorphisms of ordered algebras are not necessarily regular. We, however, have the following remark as an immediate consequence of Corollary 28 and Theorem 32 of [8].

Remark 1.3

Every regular epimorphism in a category of ordered algebras is surjective.

Theorem 1.4

([8]) Regular epimorphisms in a variety of ordered algebras are precisely Q-homomorphisms.

Theorem 1.5

([8]) For any homomorphism $f$: $\mathcal {A}\longrightarrow \mathcal {B}$ of ordered algebras the diagram

commutes, where the mappings $\pi$ and $\iota$, defined by

$$\begin{aligned} \pi (a):= & {} [a], \\ \iota ([a]):= & {} f(a), \end{aligned}$$

are homomorphisms of ordered algebras. Moreover,

• (1) $\pi$ is a Q-homomorphism;

• (2) $1_{A/\ker f}$ is injective;

• (3) $\iota$ is an order-embedding;

• (4) $1_{A/\ker f}\circ \pi$ is surjective;

• (5) $\iota \circ 1_{A/\ker f}$ is injective.

We will also need the following result, the proof of which is routine.

Theorem 1.6

For any homomorphism $f$: $\mathcal {A}\longrightarrow \mathcal {B}$ and a surjective homomorphism $g$: $\mathcal {A} \longrightarrow \mathcal {C}$ of ordered algebras with $\overrightarrow{\ker }\, g \subseteq \overrightarrow{\ker }f$, the mapping $h$: $\mathcal {C}\longrightarrow \mathcal {B}$, given by $h(c)=f(a)$, where $c=g(a)$, is the unique homomorphism of ordered algebras such that $h\circ g=f$. Moreover,

• (1) $h$ is injective if and only if $\ker f = \ker g$;

• (2) $h$ is an order-embedding if and only if $\overrightarrow{\ker }f = \overrightarrow{\ker }\, g$;

• (3) $h$ is surjective if and only if $f$ is surjective.

2 Congruence and quasiorder extension properties

Congruence extension properties have been investigated in the context of various algebras (see [7] and the references contained therein). The aim of this section is to introduce congruence and quasiorder extension properties for ordered algebras. We shall see that the latter imply the former, but the converse is not necessarily true.

Definition 2.1

We say that an ordered algebra $\mathcal {A}$ has the congruence extension property (CEP) if every order-congruence $\theta$ on any subalgebra $\mathcal {B}$ of $\mathcal {A}$ is the restriction of some order-congruence $\Theta$ on $\mathcal {A}$, i.e. $\Theta \cap (B\times B)=\theta$.

Definition 2.2

We say that an ordered algebra $\mathcal {A}$ has the quasiorder extension property (QEP) if every compatible quasiorder $\sigma$ on any subalgebra $\mathcal {B}$ of $\mathcal {A}$ is the restriction of some compatible quasiorder $\Sigma$ on $\mathcal {A}$, i.e. $\Sigma \cap (B\times B)=\sigma$.

Proposition 2.3

If an ordered algebra has QEP then it has CEP.

Proof

Let $\mathcal {A}$ be an ordered algebra having QEP. Let $\mathcal {B}$ be a subalgebra of $\mathcal {A}$ and $\theta \in \mathsf {Con}(\mathcal {B})$. Then $\underset{\theta }{\le }$ $\in \mathsf {Cqu}(\mathcal {B})$. By QEP there exists $\Sigma \in \mathsf {Cqu}(\mathcal {A})$ such that $\Sigma \cap (B\times B) = \; \underset{ \theta }{ \le }$. Now $\Theta :=\Sigma \cap \Sigma ^{-1}\in \mathsf {Con}(\mathcal {A})$. To complete the proof we need to show that $\Theta \cap (B\times B)=\theta$. To this end, first take $(b,b^{\prime })\in \Theta$ with $b,b^{\prime }\in B$. Then $b \,\Sigma \, b' \,\Sigma \, b$ and hence $b\underset{\theta }{\le }b^{\prime } \underset{\theta }{\le }b$. Since $\theta$ is an order-congruence, we have $b\,\theta \, b^{\prime }$. Now, let $b\,\theta \, b^{\prime }$, where $b,b^{\prime }\in B$. Then, because $\theta$ is symmetric, we also have $b^{\prime }\,\theta \, b$. Now $b\underset{\theta }{\le }b^{\prime }$ and $b^{\prime }\underset{\theta }{\le }b$ imply $b\,\Sigma \, b'$ and $b'\,\Sigma \, b$. Hence $b\,\Theta \, b^{\prime }$, as needed. $\square$

The following example shows that there exist ordered algebras which have CEP but not QEP.

Example 2.4

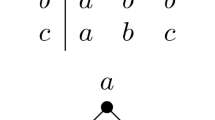
Let $S$ be the pomonoid given by the following Cayley table and Hasse diagram (cf. Example 2 of [2]):

(This $S$ is obtained from a left zero semigroup $\{a,b\}$ by adjoining the external identities $e$ and $1$, one after the other.)

We first show that $S$ has CEP. The proper subpomonoids of $S$ are $U_{1}=\{b,e,1\}$, $U_{2}=\{a,e,1\}$, $U_{3}=\{a,b,1\}$, $U_{4}=\{a,1\}$, $U_{5}=\{e,1\}$, $U_{6}=\{b,1\}$ and $U_{7}=\{1\}$.

Because the smallest and the largest order-congruences (denoted respectively by $\Delta$ and $\nabla$) on any of these subpomonoids are respectively the restrictions of the smallest and the largest order-congruences of $S$, there is nothing to prove for these order-congruences. We therefore leave out $U_{4}$, $U_{5}$ and $U_{6}$ which only admit $\Delta$ and $\nabla$. We can also omit $U_{7}$ which has only one order-congruence $\Delta =\nabla$.

Besides $\Delta$ and $\nabla$, the order-congruences on $U_{1}$, represented by their congruence classes, are:

$$\begin{aligned} \theta _{11}= & {} \{\{b,e\},\{1\}\}, \\ \theta _{12}= & {} \{\{1,e\},\{b\}\}. \end{aligned}$$

Those of $U_{2}$ (which is algebraically isomorphic to $U_{1}$) are:

$$\begin{aligned} \theta _{21}= & {} \{\{a,e\},\{1\}\}, \\ \theta _{22}= & {} \{\{e,1\},\{a\}\}. \end{aligned}$$

And that of $U_{3}$ is:

$$\begin{aligned} \theta _{31}=\{\{a,b\},\{1\}\}. \end{aligned}$$

We next consider the following order-congruences on $S$:

$$\begin{aligned} \Theta _{1}= & {} \{\{a,b,e\},\{1\}\}, \\ \Theta _{2}= & {} \{\{e,1\},\{b\},\{a\}\}. \end{aligned}$$

Now one can easily check that $\theta _{11}=\Theta _{1}\cap (U_{1}\times U_{1})$, $\theta _{12}=\Theta _{2}\cap (U_{1}\times U_{1})$, $\theta _{21}=\Theta _{1}\cap (U_{2}\times U_{2})$, $\theta _{22}=\Theta _{2}\cap (U_{2}\times U_{2})$ and $\theta _{31}=\Theta _{1}\cap (U_{3}\times U_{3})$. Thus $S$ has CEP.

To show that $S$ does not have QEP we consider the compatible quasiorder

$$\begin{aligned} \theta _{11}=\{(b,e),(e,b),(b,b),(e,e),(1,1)\} \end{aligned}$$

on $U_{1}$. (Note that an order-congruence that contains the order is a compatible quasiorder.) Now any compatible quasiorder $\Sigma$ on $S$ extending $\theta _{11}$ must contain $(a,b)=(ea,ba)$. Moreover, since $\Sigma$ extends the order of $S$, it should also contain the pair $(1,a)$. But then, using transitivity, we have $(1,b)\in \Sigma$ from $(1,a),(a,b)\in \Sigma$. Thus $\Sigma \cap (U_{1}\times U_{1})\not =\theta _{11}$ because $(1,b)\not \in \theta _{11}$ and QEP fails for $S$.

There also exist ordered algebras which do not have CEP.

Example 2.5

There exist semigroups which do not have the congruence extension property, see for instance Example 1.2 in [5]. Consider such a semigroup $S$ with discrete order. Then its congruences and order-congruences coincide and it does not have the order-congruence extension property.

It turns out that if an algebra has only nullary or unary operations then it always has QEP.

Theorem 2.6

Let $\Omega =\Omega _{0}\cup \Omega _{1}$. Then every ordered $\Omega$-algebra has QEP (and hence CEP).

Proof

Let $\mathcal {B}$ be a subalgebra of an ordered algebra $\mathcal {A} =(A,\Omega _{A},\le )$, where $\Omega =\Omega _{0}\cup \Omega _{1}$. Let $\sigma \in \mathsf {Cqu}(\mathcal {B})$. Define a relation $\Sigma$ on $A$ by

$$\begin{aligned} \Sigma :=\{(a,a^{\prime })\in A^{2}\mid a\le a^{\prime }\;\text{ or }\; a\le b\,\sigma \, b^{\prime }\le a^{\prime }\quad \text{ for } \text{ some }\;b,b^{\prime }\in B\}. \end{aligned}$$

Clearly $\Sigma$ is reflexive and extends $\le$. If $(a,a')\in \Sigma$, that is, $a\le a'$ or $a\le b\,\sigma \, b'\le a'$ for some $b,b^{\prime }\in B$, and $\omega \in \Omega _1$, then $\omega (a)\le \omega (a')$ or $\omega (a)\le \omega (b)\,\sigma \, \omega (b')\le \omega (a')$ with $\omega (b),\omega (b')\in B$. Hence $\Sigma$ is compatible (note that this argument works because $\Omega =\Omega _{0}\cup \Omega _{1}$). To prove transitivity, suppose that $a\,\Sigma \, a^{\prime }$ and $a^{\prime }\,\Sigma \, a^{\prime \prime }$. If $a\le b_{1}\,\sigma \, b_{2}\le a^{\prime }\le b_{3}\,\sigma \, b_{4}\le a^{\prime \prime }$ then by transitivity of $\le$ we have $b_{2}\le b_{3}$. This implies $b_{2}\,\sigma \, b_{3}$, and $b_{1}\,\sigma \, b_{2}\,\sigma \, b_{3}\,\sigma \, b_{4}$ implies $b_{1}\,\sigma \, b_{4}$. Hence $a\le b_{1}\,\sigma \, b_{4}\le a^{\prime \prime }$ and $(a,a^{\prime \prime })\in \Sigma$. The other three cases can be checked in a similar fashion. So $\Sigma \in \mathsf {Cqu}(\mathcal {A})$.

Finally we show that $\Sigma \cap (B\times B)=\sigma$. Obviously, $\sigma \subseteq \Sigma \cap (B\times B)$. For the converse, assume that $(b,b^{\prime })\in \Sigma \cap (B\times B)$. Then $b\le b^{\prime }$ or $b\le b_{1}\,\sigma \, b_{2}\le b^{\prime }$ for some $b_{1},b_{2}\in B$. In the first case $b\,\sigma \, b^{\prime }$ because $\sigma$ extends the order of $B$. In the second case $b\,\sigma \, b_{1}\,\sigma \, b_{2}\,\sigma \, b^{\prime }$ for the same reason and the transitivity of $\sigma$ yields $b\,\sigma \, b^{\prime }$. $\square$

Corollary 2.7

Every poset has QEP.

Corollary 2.8

If $S$ is a posemigroup or a pomonoid then every $S$-poset has QEP.

3 CEP, QEP and diagrams

In this section we describe CEP and QEP in the language of commutative diagrams. For analogous results in the unordered context the reader is referred to [7]. We begin with a couple of short lemmas.

Lemma 3.1

Let $f$: $\mathcal {A}\longrightarrow \mathcal {B}$ be an order-embedding between ordered $\Omega$-algebras and $\sigma \in \mathsf {Cqu}( \mathcal {A})$. Then

$$\begin{aligned} \sigma ^{\prime }=\{(f(a_{1}),f(a_{2}))\mid (a_{1},a_{2})\in \sigma \}\in \mathsf {Cqu}(f(\mathcal {A})). \end{aligned}$$

Proof

Clearly $\sigma ^{\prime }$ is reflexive and compatible with operations. Transitivity of $\sigma ^{\prime }$ follows from injectivity of $f$. Let us show that $\le _{f(A)}$ $\subseteq \sigma ^{\prime }$. Indeed, if $f(a_{1})\le f(a_{2})$ in $f(\mathcal {A})$ then $f(a_{1})\le f(a_{2})$ in $\mathcal {B}$ and hence $a_{1}\le a_{2}$ in $\mathcal {A}$. Now $(a_{1},a_{2})\in \sigma$, giving $(f(a_{1}),f(a_{2}))\in \sigma ^{\prime }$, as needed. $\square$

The following lemma can be proved similarly.

Lemma 3.2

Let $f$: $\mathcal {A}\longrightarrow \mathcal {B}$ be an order-embedding between ordered $\Omega$-algebras and $\theta \in \mathsf { Con}(\mathcal {A})$. Then

$$\begin{aligned} \theta ^{\prime }=\{(f(a_{1}),f(a_{2}))\mid (a_{1},a_{2})\in \theta \}\in \mathsf {Con}(f(\mathcal {A})). \end{aligned}$$

Theorem 3.3

An algebra $\mathcal {A}$ in a variety $\mathcal {V}$ of ordered $\Omega$-algebras has CEP if and only if each diagram

where $f$ is an order-embedding and $g$ is a regular epimorphism, can be completed to a commutative square

in $\mathcal {V}$, where $f^{\prime }$ is an injective homomorphism. In this case, $g'$ is a regular epimorphism.

Proof

Necessity Let $\mathcal {A}$ have CEP. Consider an order-embedding $f$: $\mathcal {B}\longrightarrow \mathcal {A}$ and a regular epimorphism $g$: $\mathcal {B}\longrightarrow \mathcal {C}$. Let $\theta :=\ker g\in \mathsf {Con}(\mathcal {B})$. Then by Lemma 3.2 we have,

$$\begin{aligned} \theta ^{\prime }:=\{(f(b_{1}),f(b_{2}))\mid (b_{1},b_{2})\in \theta \}\in \mathsf {Con}(f(\mathcal {B})). \end{aligned}$$

Using CEP of $\mathcal {A}$ we obtain $\Theta \in \mathsf {Con}(\mathcal {A})$ such that

$$\begin{aligned} \Theta \cap (f(B)\times f(B))=\theta ^{\prime }. \end{aligned}$$

(3.1)

Consider the diagram

(3.2)

where the natural surjection $\Theta ^\natural$ is a regular epimorphism by Theorem 1.5(1) and Theorem 1.4. Let us prove that $\overrightarrow{\ker }\, g \subseteq \overrightarrow{\ker }(\Theta ^\natural f)$. Suppose that $(x,x')\in \overrightarrow{\ker }\,g$, i.e. $g(x) \le g(x')$. Because $g$ is a Q-homomorphism, there exist $b,b^{\prime }\in B$ such that $g(x)=g(b)$, $g(x') =g(b')$ and $b\underset{\ker g}{\le }b'$. And since $\ker g=\theta$, we can write a sequence

$$\begin{aligned} x \,\theta \, b\le b_{1}\,\theta \,b_{2}\le b_{3}\,\theta \,\ldots \,\theta \,b_{n}\le b' \,\theta \, x' \end{aligned}$$

for some $b_{1},\ldots ,b_{n}\in B$. Applying $f$ to this sequence one obtains

$$\begin{aligned} f(x)\,\theta '\, f(b)\le f(b_{1})\,\theta '\,f(b_{2})\le f(b_{3})\,\theta ^{\prime }\,\ldots \,\theta ^{\prime }\,f(b_{n})\le f(b^{\prime }) \,\theta '\, f(x'). \end{aligned}$$

Condition (3.1) implies that $f(x)\underset{\Theta }{\le }f(x')$, that is, $[f(x)]\le [f(x')]$ in $\mathcal {A}/\Theta$ and $(x,x')\in \overrightarrow{\ker }(\Theta ^\natural f)$.

Now from Theorem 1.6 it follows that there exists a unique homomorphism $f'$: $\mathcal {C}\longrightarrow \mathcal {A}/\Theta$ such that $f'g = \Theta ^\natural f$. To prove that $f'$ is injective, we have to check that $\ker (\Theta ^\natural f) = \ker g = \theta$. Since $\overrightarrow{\ker }\, g \subseteq \overrightarrow{\ker }(\Theta ^\natural f)$, we also have $\theta \subseteq \ker (\Theta ^\natural f)$. For the converse we suppose that $[f(b_{1})]=[f(b_{2})]$ in $\mathcal {A}/\Theta$, $b_1,b_2\in B$, i.e. $(f(b_{1}),f(b_{2}))\in \Theta$. By (3.1), $(f(b_{1}),f(b_{2}))\in \theta ^{\prime }$. Hence there exist $b_{3},b_{4}\in B$ such that $(b_{3},b_{4})\in \theta$ and $(f(b_{1}),f(b_{2}))=(f(b_{3}),f(b_{4}))$. Since $f$ is injective, we have $b_{1}=b_{3}$ and $b_{2}=b_{4}$. Thus also $(b_1,b_2)\in \theta$, and we have shown that $\ker (\Theta ^\natural f) \subseteq \theta$.

Sufficiency Let $\mathcal {B}$ be a subalgebra of $\mathcal {A}$, let $\theta \in \mathsf {Con}(\mathcal {B})$ and let $f$: $B\longrightarrow A$ be the inclusion mapping (which is, of course, an order-embedding). Consider the diagram

where the natural surjection $\theta ^{\natural }$ is a regular epimorphism by Theorem 1.5(1) and Theorem 1.4. By assumption there exists a commutative diagram

where $f^{\prime }$ is an injective homomorphism. Take $\Theta :=\ker g^{\prime }\in \mathsf {Con}(\mathcal {A})$. We prove that $\Theta \cap (B\times B)=\theta$.

Suppose first that $(a_1,a_2)\in \Theta \cap (B\times B)$. Then $a_1,a_2\in B$ and $g^{\prime }(a_1)= g^{\prime }(a_2)$. Now

$$\begin{aligned} g^{\prime }(a_i)=g^{\prime }(f(a_i)) = (g^{\prime }f)(a_i) = (f'\theta ^\natural )(a_i) = f^{\prime }([a_i]) \end{aligned}$$

for $i=1,2$. Hence $f^{\prime }([a_1]) = g^{\prime }(a_1) = g^{\prime }(a_2) = f^{\prime }([a_2])$. Since $f^{\prime }$ is injective, we conclude that $[a_1]= [a_2]$ in $\mathcal {B}/\theta$. This means that $(a_1,a_2)\in \theta$. Conversely, let $(b_{1},b_{2})\in \theta$. Then $[b_{1}]=[b_{2}]$ in $\mathcal {B}/\theta$. Hence

$$\begin{aligned} (g^{\prime }f)(b_{1})=(f' \theta ^\natural )(b_{1})=f'([b_{1}])=f'([b_{2}])= (f' \theta ^\natural )(b_{2})=(g'f)(b_{2}), \end{aligned}$$

which implies that $(b_{1},b_{2})=(f(b_{1}),f(b_{2}))\in \ker g^{\prime }=\Theta$. $\square$

Our next result characterizes QEP in terms of commutative diagrams.

Theorem 3.4

An algebra $\mathcal {A}$ in a variety $\mathcal {V}$ of ordered $\Omega$-algebras has QEP if and only if each diagram

where $f$ is an order-embedding and $g$ is a surjective homomorphism, can be completed to a commutative square

in $\mathcal {V}$, where $f^{\prime }$ is an order-embedding. In this case, $g'$ is a surjective homomorphism.

Proof

Necessity Let $\mathcal {A}$ have QEP.  Consider an order-embedding $f$:  $\mathcal {B}\longrightarrow \mathcal {A}$ and a surjective homomorphism $g$: $\mathcal {B}\longrightarrow \mathcal {C}$. Let $\sigma :=\overrightarrow{\ker }\,g\in \mathsf {Cqu}(\mathcal {B})$. By Lemma  3.1,

$$\begin{aligned} \sigma ^{\prime }:=\{(f(b_{1}),f(b_{2}))\mid (b_{1},b_{2})\in \sigma \}\in \mathsf {Cqu}(f(\mathcal {B})). \end{aligned}$$

Using QEP of $\mathcal {A}$ we obtain $\Sigma \in \mathsf {Cqu}(\mathcal {A})$ such that

$$\begin{aligned} \Sigma \cap (f(B)\times f(B))=\sigma ^{\prime }. \end{aligned}$$

(3.3)

Consider the diagram

(3.4)

Suppose that $(b_{1},b_{2})\in \overrightarrow{\ker }\,g=\sigma$. Then $(f(b_{1}),f(b_{2}))\in \sigma ^{\prime }\subseteq \Sigma$. Consequently, $[f(b_{1})]\le [f(b_{2})]$ in the quotient algebra $\mathcal {A}/\Sigma$ and $(b_1,b_2)\in \overrightarrow{\ker }(\Sigma ^\natural f)$. Thus we have established the inclusion $\overrightarrow{\ker }\, g \subseteq \overrightarrow{\ker }(\Sigma ^\natural f)$.

Now, by Theorem 1.6, there is a uniqe homomorphism $f^{\prime }:\mathcal {C}\longrightarrow \mathcal {A}/\Sigma$ of ordered algebras, which makes the diagram (3.4) commute.

To prove that $f^{\prime }$ is an order-embedding it remains to check that $\overrightarrow{\ker }(\Sigma ^\natural f)\subseteq \overrightarrow{\ker }\, g$. Suppose that $(b_1,b_2)\in \overrightarrow{\ker }(\Sigma ^\natural f)$. Then $[f(b_{1})]\le [f(b_{2})]$ in $\mathcal {A}/\Sigma$, i.e. $(f(b_{1}),f(b_{2}))\in \Sigma$. By (3.3), $(f(b_{1}),f(b_{2}))\in \sigma ^{\prime }$. Hence there exist $b_{3},b_{4}\in B$ such that $(b_{3},b_{4})\in \sigma =\overrightarrow{\ker }\,g$ and $(f(b_{1}),f(b_{2}))=(f(b_{3}),f(b_{4}))$. Since $f$ is injective, we have $b_{1}=b_{3}$ and $b_{2}=b_{4}$, and hence $(b_1,b_2)\in \overrightarrow{\ker }\,g$.

Sufficiency Let $\mathcal {B}$ be a subalgebra of $\mathcal {A}$, let $\sigma \in \mathsf {Cqu}(\mathcal {B})$ and let $f$: $B\longrightarrow A$ be the inclusion mapping. Consider the diagram

By assumption there exists a commutative diagram

where $f^{\prime }$ is an order-embedding. Take $\Sigma :=\overrightarrow{\ker }\, g^{\prime }\in \mathsf {Cqu}(\mathcal {A})$. We prove that $\Sigma \cap (B\times B)=\sigma$.

Suppose that $(a_{1},a_{2})\in \Sigma \cap (B\times B)$. Then $a_{1},a_{2}\in B$ with $g^{\prime }(a_{1})\le g^{\prime }(a_{2})$. Now

$$\begin{aligned} g'(a_{i})=g^{\prime }(f(a_{i}))=(g'f)(a_{i})=(f'\sigma ^\natural )(a_{i}) =f'([a_{i}]) \end{aligned}$$

for $i=1,2$. Hence $f^{\prime }([a_{1}])=g^{\prime }(a_{1})\le g^{\prime }(a_{2})=f^{\prime }([a_{2}])$. Since $f^{\prime }$ is an order-embedding, we conclude that $[a_{1}]\le [a_{2}]$ in $\mathcal {B}/\sigma$. This means that $(a_{1},a_{2})\in \sigma$.

Conversely, let $(b_{1},b_{2})\in \sigma$. Then $[b_{1}]\le [b_{2}]$ in $\mathcal {B}/\sigma$. Hence

$$\begin{aligned} (g^{\prime }f)(b_{1})=(f' \sigma ^\natural )(b_{1})=f'([b_{1}])\le f'([b_{2}])=(f'\sigma ^\natural )(b_{2})=(g^{\prime }f)(b_{2}), \end{aligned}$$

which implies that $(b_{1},b_{2})=(f(b_{1}),f(b_{2}))\in \overrightarrow{ \ker }g^{\prime }=\Sigma$. $\square$

4 Strong extension properites

An unordered algebra $\mathcal {A}$ is said to have the strong congruence extension property, see for instance [6], if any congruence $\theta$ on any subalgebra $\mathcal {B}$ of $\mathcal {A}$ can be extended to a congruence $\Theta$ on $\mathcal {A}$ such that each $\Theta$-class is either contained in $B$ or disjoint from $B$; i.e. $\Theta \cap (B\times A)=\theta$. In this section we define similar properties for ordered algebras.

Definition 4.1

We say that an ordered algebra $\mathcal {A}$ has the strong congruence extension property (SCEP) if any order congruence $\theta$ on any subalgebra $\mathcal {B}$ of $\mathcal {A}$ can be extended to an order congruence $\Theta$ on $\mathcal {A}$ in such a way that $\Theta \cap (B\times A)=\theta$.

From the definitions it is clear that SCEP implies CEP. It turns out that SCEP can also be described in terms of diagrams.

Theorem 4.2

An algebra $\mathcal {A}$ in a variety $\mathcal {V}$ of ordered $\Omega$-algebras has SCEP if and only if each diagram

where $f$ is an order-embedding and $g$ is a regular epimorphism, can be completed to a pullback diagram

in $\mathcal {V}$, where $f^{\prime }$ is an injective homomorphism. In this case, $g'$ is a regular epimorphism.

Proof

Necessity Let $\mathcal {A}$ have SCEP. Consider an order-embedding $f{:}$ $\mathcal {B}\longrightarrow \mathcal {A}$ and a regular epimorphism $g$: $\mathcal {B}\longrightarrow \mathcal {C}$. Let $\theta :=\ker g\in \mathsf {Con}(\mathcal {B})$. By Lemma 3.2, we have:

$$\begin{aligned} \theta ^{\prime }:=\{(f(b_{1}),f(b_{2}))\mid (b_{1},b_{2})\in \theta \}\in \mathsf {Con}(f(\mathcal {B})). \end{aligned}$$

Using SCEP of $\mathcal {A}$ we obtain $\Theta \in \mathsf {Con}(\mathcal {A})$ such that

$$\begin{aligned} \Theta \cap (f(B)\times A)=\theta ^{\prime }. \end{aligned}$$

Consider the diagram

(4.1)

Again, by Theorem 1.6, the mapping $f^{\prime }$: $\mathcal {C}\longrightarrow \mathcal {A}/\Theta$, given by

$$\begin{aligned} f^{\prime }(c):=[f(b)]\in A/\Theta , \end{aligned}$$

where $g(b)=c$, is a homomorphism of ordered algebras, which makes the square (4.1) commute. As in the proof of Theorem 3.3, we see that $f'$ is injective.

We prove that (4.1) is a pullback square. For this, consider a diagram

(4.2)

in which the outer square also commutes. Let us first show that

$$\begin{aligned} (\forall x\in B^{\prime })(\exists !b_{x}\in B)(l(x)=g(b_{x})\wedge k(x)=f(b_{x})). \end{aligned}$$

If $x\in B^{\prime }$, then, by the surjectivity of $g$ (see Remark 1.3), there exists $b\in B$ such that $l(x)=g(b)$. We may therefore calculate

$$\begin{aligned} {}[f(b)]=f^{\prime }(g(b))= f'(l(x))=(f^{\prime }l)(x)=[k(x)] \end{aligned}$$

in $\mathcal {A}/\Theta$. In particular $(f(b),k(x))\in \Theta \cap (f(B)\times A)=\theta ^{\prime }$. This means that $(f(b),k(x))=(f(b_{1}),f(b_{2}))$ for some $(b_{1},b_{2})\in \theta$. So we have $f(b)=f(b_{1})$, $k(x)=f(b_{2})$ and $g(b_{1})=g(b_{2})$. Now, because $f$ is injective, one has $b=b_{1}$, and hence $l(x)=g(b)=g(b_{1})=g(b_{2})$. So $b_{2}$ is the required element. It is unique by the injectivity of $f$.

We next define a mapping $h$: $\mathcal {B}^{\prime }\longrightarrow \mathcal {B}$ by

$$\begin{aligned} h(x):=b_{x}. \end{aligned}$$

This $h$ makes both triangles in (4.2) commutative and it is unique as such because $f$ is an order-embedding. If $x\le x^{\prime }$ in $\mathcal {B}^{\prime }$ then $f(h(x))=k(x)\le k(x^{\prime })=f(h(x^{\prime }))$. Since $f$ is an order-embedding, we have $h(x)\le h(x^{\prime })$ in $\mathcal {B}$. So $h$ is monotone.

To show that $h$ is a homomorphism, take an $n$-ary operation $\omega$ and elements $x_{1},\ldots ,x_{n}\in \mathcal {B}^{\prime }$. Then

$$\begin{aligned} f(h(\omega (x_{1},\ldots ,x_{n})))= & {} k(\omega (x_{1},\ldots ,x_{n})) \\= & {} \omega (k(x_{1}),\ldots ,k(x_{n})) \\= & {} \omega (f(h(x_{1})),\ldots ,f(h(x_{n}))) \\= & {} f(\omega (h(x_{1}),\ldots ,h(x_{n}))). \end{aligned}$$

Since $f$ is injective, we have $h(\omega (x_{1},\ldots ,x_{n}))=\omega (h(x_{1}),\ldots ,h(x_{n}))$, as needed.

Sufficiency Let $\mathcal {B}$ be a subalgebra of $\mathcal {A}$, let $\theta \in \mathsf {Con}(\mathcal {B})$ and let $f:B\longrightarrow A$ be the inclusion mapping. Consider the diagram

By assumption there exists a pullback diagram

where $f^{\prime }$ is an injective homomorphism. Take $\Theta :=\ker g^{\prime }\in \mathsf {Con}(\mathcal {A})$. We prove that $\Theta \cap (B\times A)=\theta$.

Suppose that $(b,a)\in \Theta$ where $b\in B$ and $a\in A$. Then

$$\begin{aligned} g^{\prime }(a)=g^{\prime }(b)=(g^{\prime }f)(b)=(f'\theta ^\natural )(b)=f^{\prime }([b]), \end{aligned}$$

which means that the pair $(a,[b])$ belongs to the subalgebra $\mathcal {K} =\{(x,[y])\mid g^{\prime }(x)=f^{\prime }([y])\}$ of $\mathcal {A}\times \mathcal {B}/\theta$. Clearly the outer square in the diagram

where $p_{1}$ and $p_{2}$ are the projections, commutes. Hence there is a unique morphism $h$: $\mathcal {K}\longrightarrow \mathcal {B}$ such that the triangles commute. Since $(a,[b])\in \mathcal {K}$, we have

$$\begin{aligned} a=p_{1}(a,[b])=(fh)(a,[b])=h(a,[b]), \end{aligned}$$

whence, in particular, $a\in B$. This implies $f^{\prime }([b])=g^{\prime }(a)=(f' \theta ^\natural )(a)=f^{\prime }([a])$. Using injectivity of $f^{\prime }$ we obtain $(b,a)\in \theta$. This proves the inclusion $\Theta \cap (B\times A)\subseteq \theta$.

For the converse, if $(b,b^{\prime })\in \theta$ then $g^{\prime }(b) = (f'\theta ^\natural )(b) = (f' \theta ^\natural )(b^{\prime }) = g^{\prime }(b^{\prime })$, i.e. $(b,b^{\prime })\in \Theta$. This completes the proof. $\square$

Definition 4.3

We say that an ordered algebra $\mathcal {A}$ has the strong quasiorder extension property (SQEP) if for any compatible quasiorder $\sigma$ on any subalgebra $\mathcal {B}$ of $\mathcal {A}$ there exists a compatible quasiorder $\Sigma$ on $\mathcal {A}$ such that

• (1) $\Sigma \cap (B\times B)=\sigma$,

• (2) $\Sigma \cap \Sigma ^{-1} \cap (B\times A) = \sigma \cap \sigma ^{-1}$.

Lemma 4.4

If an ordered algebra has SQEP then it has SCEP and QEP.

Proof

Clearly, SQEP implies QEP. Suppose that an ordered algebra $\mathcal {A}$ has SQEP and $\theta$ is an order-congruence on its subalgebra $\mathcal {B}$. Then $\underset{\theta }{\le }\,\in \mathsf {Cqu}(\mathcal {B})$. Using SQEP one can find $\Sigma \in \mathsf {Cqu}(\mathcal {A})$ such that $\Sigma \cap (B\times B)=\; \underset{\theta }{\le }$ and $\Sigma \cap \Sigma ^{-1} \cap (B\times A) = \; \underset{\theta }{\le } \cap \left( \underset{\theta }{\le }\right) ^{-1} = \theta$. Putting $\Theta := \Sigma \cap \Sigma ^{-1} \in \mathsf {Con}(\mathcal {A})$ we have $\Theta \cap (B\times A) = \theta$. Thus $\mathcal {A}$ has SCEP. $\square$

Theorem 4.5

An algebra $\mathcal {A}$ in a variety $\mathcal {V}$ of ordered $\Omega$-algebras has SQEP if and only if each diagram

where $f$ is an order-embedding and $g$ is a surjective homomorphism, can be completed to a pullback diagram

in $\mathcal {V}$, where $f^{\prime }$ is an order-embedding. In this case, $g'$ is a surjective homomorphism.

Proof

Necessity Let $\mathcal {A}$ have SQEP. Consider an order-embedding $f$: $\mathcal {B}\longrightarrow \mathcal {A}$ and a surjective homomorphism $g$: $\mathcal {B}\longrightarrow \mathcal {C}$. Let $\sigma :=\overrightarrow{\ker }g\in \mathsf {Cqu}(\mathcal {B})$. By Lemma 3.1, we have:

$$\begin{aligned} \sigma ':= \{ (f(b_1),f(b_2))\mid (b_1,b_2)\in \sigma \}\in \mathsf {Cqu}(f(\mathcal {B})). \end{aligned}$$

Using SQEP of $\mathcal {A}$ we obtain $\Sigma \in \mathsf {Cqu}(\mathcal {A})$ such that

$$\begin{aligned} \Sigma \cap (f(B)\times f(B))=\sigma ' \;\;\; \text{ and } \;\;\; \Sigma \cap \Sigma ^{-1} \cap (f(B)\times A) = \sigma ' \cap (\sigma ')^{-1}. \end{aligned}$$

Consider the diagram

(4.3)

Once more, Theorem 1.6 implies that the mapping $f': C\longrightarrow A/(\Sigma \cap \Sigma ^{-1})$, given by

$$\begin{aligned} f^{\prime }(c):=[f(b)], \end{aligned}$$

where $b\in B$ is such that $g(b) = c$, is a homomorphism of ordered algebras which makes the square (4.3) commute. As in the proof of Theorem 3.4 we see that $f'$ is an order-embedding.

We prove that (4.3) is a pullback square. For this, consider a diagram

(4.4)

in which the outer square also commutes. Let us first show that

$$\begin{aligned} (\forall x\in B^{\prime })(\exists !b_{x}\in B)(l(x)=g(b_{x})\wedge k(x)=f(b_{x})). \end{aligned}$$

If $x\in B^{\prime }$, then, by the surjectivity of $g$, there exists $b\in B$ such that $l(x)=g(b)$. We may therefore calculate

$$\begin{aligned} {}[f(b)]=f'(g(b)) = f'(l(x)) =(f'l)(x)=[k(x)] \end{aligned}$$

in $\mathcal {A}/\Sigma$, which means that $(f(b),k(x)) \in \Sigma \cap \Sigma ^{-1}$. Now

$$\begin{aligned} (f(b),k(x))\in \Sigma \cap \Sigma ^{-1} \cap (f(B)\times A)=\sigma ' \cap (\sigma ')^{-1} \end{aligned}$$

implies that $(f(b),k(x))=(f(b_{1}),f(b_{2}))$ for some $(b_{1},b_{2})\in \sigma \cap \sigma ^{-1} = \ker g$. So we have $f(b)=f(b_{1})$, $k(x)=f(b_{2})$ and $g(b_{1}) = g(b_{2})$. Because $f$ is injective, one has $b=b_{1}$, and hence $l(x)=g(b)=g(b_{1})= g(b_{2})$. So $b_{2}$ is the required element. It is unique by the injectivity of $f$.

Next, we define a mapping $h$: $\mathcal {B}^{\prime }\longrightarrow \mathcal {B}$ by

$$\begin{aligned} h(x):=b_{x}. \end{aligned}$$

This $h$ makes both the triangles in (4.4) commutative and it is unique as such because $f$ is an order-embedding (hence a monomorphism). The proof that $h$ is a monotone homomorphism is exactly the same as in the proof of Theorem 4.2.

Sufficiency Let $\mathcal {B}$ be a subalgebra of $\mathcal {A}$, let $\sigma \in \mathsf {Cqu}(\mathcal {B})$, let $f$: $B\longrightarrow A$ be the inclusion mapping, and let $\sigma ^\natural$: $\mathcal {B}\longrightarrow \mathcal {B}/\sigma$ be the natural surjection. By assumption there exists a pullback diagram

where $f^{\prime }$ is an order-embedding. Take $\Sigma :=\overrightarrow{\ker }g'\in \mathsf {Cqu}(\mathcal {A})$. In the proof of Theorem 3.4 we saw that $\Sigma \cap (B\times B)=\sigma$. We prove that $\Sigma \cap \Sigma ^{-1} \cap (B\times A) = \sigma \cap \sigma ^{-1}$, which is equivalent to the equality $\ker g' \cap (B\times A) = \sigma \cap \sigma ^{-1}$.

Suppose that $(b,a)\in \ker g'$ where $b\in B$ and $a\in A$. Then

$$\begin{aligned} g^{\prime }(a)=g^{\prime }(b)=(g^{\prime }f)(b)=(f'\sigma ^\natural )(b)=f^{\prime }([b]), \end{aligned}$$

which means that the pair $(a,[b])$ belongs to the subalgebra $\mathcal {K} =\{(x,[y])\mid g^{\prime }(x)=f^{\prime }([y])\}$ of $\mathcal {A}\times \mathcal {B}/\sigma$. Clearly the outer square in the diagram

where $p_{1}$ and $p_{2}$ are the projections, commutes. Hence there is a unique morphism $h:\mathcal {K}\longrightarrow \mathcal {B}$ such that the triangles commute. Since $(a,[b])\in \mathcal {K}$, we have

$$\begin{aligned} a=p_{1}(a,[b])=(fh)(a,[b])=h(a,[b]), \end{aligned}$$

whence, in particular, $a\in B$. This implies $f^{\prime }([b])=g^{\prime }(a)=(f' \sigma ^\natural )(a)=f^{\prime }([a])$. Using injectivity of $f'$ we obtain $[b]=[a]$, which yields $(b,a)\in \sigma \cap \sigma ^{-1}$. This proves the inclusion $\ker g' \cap (B\times A) \subseteq \sigma \cap \sigma ^{-1}$.

For the converse, if $(b,b^{\prime })\in \sigma \cap \sigma ^{-1}$ then $g'(b) = (f' \sigma ^\natural )(b) = f'([b]) = f'([b']) = (f' \sigma ^\natural )(b') = g'(b')$, i.e. $(b,b')\in \ker g' = \Sigma \cap \Sigma ^{-1}$. This completes the proof. $\square$

We point out one rather strong consequence of SCEP and SQEP.

Proposition 4.6

If an ordered algebra $\mathcal {A}$ has SQEP or SCEP then all its subalgebras are convex.

Proof

Since SQEP implies SCEP, it suffices to consider only $\mathcal {A}$ having SCEP. Let $\mathcal {B}$ be any subalgebra of $\mathcal {A}$. Then $\theta :=B\times B$ is an order-congruence on $\mathcal {B}$. Using SCEP we can find an order-congruence $\Theta$ on $\mathcal {A}$ such that $\Theta \cap (B\times A) = \theta$. It is easy to see that the last equality is equivalent to the fact that $[b]_\Theta = [b]_\theta$ for every $b\in B$. Hence $[b]_\Theta = [b]_\theta = B$ for every $b\in B$. Since every equivalence class of an order-congruence is a convex subset, $B$ is also convex in $A$. $\square$

The following examples show that QEP and CEP do not imply SQEP or SCEP.

Example 4.7

Let $\mathbf {I}=(I,\le )$ be a chain of any cardinality and consider the posemigroup $\mathcal {I}=(I,\min ,\le )$. Observe that any quasiorder $\sigma$ that contains $\le$ is a compatible quasiorder of $\mathcal {I}$. Indeed, since multiplication is commutative we only need to check the implication

$$\begin{aligned} (\forall i,j,k\in I)[(i,j)\in \sigma \Longrightarrow (\min (i,k),\min (j,k))\in \sigma ]. \end{aligned}$$

Because $\mathbf {I}$ is totally ordered, we have three cases: $k>\max (i,j)$, $k<\min (i,j)$ and $\min (i,j)\le k \le \max (i,j)$. The first case reduces to the tautology $(i,j)\in \sigma \Rightarrow (i,j)\in \sigma$, and the second case to the reflexivity for $k$. Consider the third case. If $i\le k\le j$ then $(\min (i,k),\min (j,k)) = (i,k)\in \sigma$ because $\sigma$ contains the order. If $j\le k\le i$ and $(i,j)\in \sigma$ then $(\min (i,k),\min (j,k)) = (k,j)\in \sigma$ because $(k,i)\in \sigma$ and $\sigma$ is transitive.

Therefore $\mathsf {Cqu}(\mathcal {I})=\mathsf {Cqu}(\mathbf {I})$. Since any subposet of $\mathbf {I}$ is a subposemigroup of $\mathcal {I}$, QEP for $\mathcal {I}$ coincides with QEP for $\mathbf {I}$ and, since $\mathbf {I}$ has QEP due to Theorem 2.6, $\mathcal {I}$ has both QEP and CEP.

On the other hand, no chain with at least three elements has either SQEP or SCEP. To see this, consider the three-element chain $\mathbf {2}=\{0<1<2\}$ with a non-convex subalgebra $B=\{0<2\}$, and apply Proposition 4.6.

Example 4.8

The reasoning from Example 4.7 can be duplicated for any partially ordered left (or right) zero semigroup $\mathcal {S}=(S,\cdot ,\le )$. The relevant implication in this case is

$$\begin{aligned} (\forall s,t,u\in S)[(s,t)\in \sigma \Longrightarrow (su,tu)\in \sigma \wedge (us,ut)\in \sigma ]. \end{aligned}$$

Since $(su,tu)=(s,t)\in \sigma$ and $(us,ut)=(u,u)\in \sigma$ (or vice versa in the case of a right zero semigroup), this holds for any quasiorder $\sigma$ of $(S,\le )$. Furthermore, all subsets of $S$ are still subalgebras in this case.

5 Connections with amalgamation and transferability

Using the arrows $\hookrightarrow$ and $\twoheadrightarrow$ respectively to denote order-embeddings and surjective homomorphisms, we can represent QEP by the diagram:

Analogously we can define the amalgamation and transferability properties, abbreviated AP and TP (cf. [7]), with the help of the following diagrams:

Proposition 5.1

(Cf. [7], Prop. 1.6) The following assertions hold in any class $\mathcal {K}$ of ordered algebras.

• (1) If $\mathcal {K}$ is closed under quotients then QEP and AP imply TP.

• (2) TP implies QEP.

• (3) If $\mathcal {K}$ has binary products then TP implies AP.

Proof

(1) Let $\mathcal {K}$ have QEP and AP. Consider an order-embedding $f: \mathcal {B}\longrightarrow \mathcal {A}$ and a morphism $g:\mathcal {B} \longrightarrow \mathcal {C}$. By Theorem 1.5 we have the following diagram, in which $(\ker g)^{\natural }$ is surjective and $\iota$ is an order-embedding:

(5.1)

Then using QEP and AP, respectively, we obtain the upper and lower commutative squares. It is straightforward to see that the outer square also commutes.

(2) This is immediate.

(3) Assume that $\mathcal {K}$ has TP and consider two order-embeddings $f$: $\mathcal {B}\longrightarrow \mathcal {A}$ and $g$: $\mathcal {B}\longrightarrow \mathcal {C}$. Using TP (‘horizontally’ and ‘vertically’) we get commutative squares

Next, considering the morphisms $g^{\prime }$: $\mathcal {A\longrightarrow \mathcal {D}}$, $g^{\prime \prime }$: $\mathcal {A\longrightarrow \mathcal {E}}$, there exists, by the universal property of the product $\mathcal {D}\times \mathcal {E}$, a unique morphism $m$: $\mathcal {A\longrightarrow D}\times \mathcal {E}$ such that $p_{1} m=g^{\prime }$, $p_{2} m=g^{\prime \prime }$; where $p_{1}$ and $p_{2}$ are the projections of $\mathcal {D} \times \mathcal {E}$. By a similar token there exists a unique morphism $n$: $\mathcal {C\longrightarrow D}\times \mathcal {E}$ such that $p_{1} n=f^{\prime }$, $p_{2} n=f^{\prime \prime }$. One can now easily observe that

$$\begin{aligned} p_{2}ng=f^{\prime \prime }g=g^{\prime \prime }f=p_{2}mf \;\;\text { and }\;\; p_{1}ng=f^{\prime }g=g^{\prime }f=p_{1}mf. \end{aligned}$$

This gives $ng=mf$, whence the square

commutes. Finally, if $m(a_{1})\le m(a_{2})$ for $a_{1},a_{2}\in A$ then $(p_{1}m)(a_{1})\le (p_{1}m)(a_{2})$, that is, $g'(a_{1})\le g'(a_{2})$. And since $g'$ is an order-embedding, we conclude that $a_{1}\le a_{2}$. Thus we have shown that $m$ is an order-embedding. In a similar manner one can show that $n$ is an order-embedding. $\square$

Since every variety is closed under quotients and products, we have the following result.

Corollary 5.2

A variety $\mathcal {V}$ of ordered $\Omega$-algebras has TP iff it has QEP and AP.

Next, we consider certain classes of ordered algebras that have AP and TP.

Let $\mathcal {K}$ be a class of ordered $\Omega$-algebras where $\Omega = \Omega _0 \cup \Omega _1$. Take two algebras $\mathcal {A}$ and $\mathcal {C}$ in $\mathcal {K}$. Define a partial order on the set

$$\begin{aligned} A\sqcup C=(\{1\}\times A)\cup (\{2\}\times C) \end{aligned}$$

by

$$\begin{aligned} (i,x)\le (j,y)\Longleftrightarrow i=j\text { \quad and \quad } x\le y\text { in } A\text { or }C\text { (depending on }k). \end{aligned}$$

For each $\omega \in \Omega _{1}$ put

$$\begin{aligned} \omega _{\mathcal {A}\sqcup \mathcal {C}}(1,a):= & {} (1,\omega _{\mathcal {A}}(a)), \\ \omega _{\mathcal {A}\sqcup \mathcal {C}}(2,c):= & {} (2,\omega _{\mathcal {C}}(c)) \end{aligned}$$

and for each $\omega \in \Omega _0$ put

$$\begin{aligned} \omega _{\mathcal {A}\sqcup \mathcal {C}} : = (1,\omega _\mathcal {A}). \end{aligned}$$

These operations are clearly monotone, so $\mathcal {A}\sqcup \mathcal {C}$ is an ordered $\Omega$-algebra. Next, consider the following relation on $A\sqcup C$:

$$\begin{aligned} H=\{\left( (1,\omega _{\mathcal {A}}),(2,\omega _{\mathcal {C}}\right) )\mid \omega \in \Omega _{0}\}. \end{aligned}$$

(5.2)

Let $\theta$ be the order-congruence on $\mathcal {A}\sqcup \mathcal {C}$ generated by $H$. Denote the regular quotient algebra $(\mathcal {A}\sqcup \mathcal {C})/\theta$ by $\mathcal {A}*\mathcal {C}$. We note that

$$\begin{aligned} \omega _{\mathcal {A}*\mathcal {C}}= [(1,\omega _{\mathcal {A}})]= [(2,\omega _{\mathcal {C}})] \end{aligned}$$

for every $\omega \in \Omega _{0}$.

The following lemma is easy to prove.

Lemma 5.3

If $\Omega = \Omega _0 \cup \Omega _1$ then the algebra $\mathcal {A}*\mathcal {C}$ is the coproduct of ordered algebras $\mathcal {A}$ and $\mathcal {C}$ in the category of all ordered $\Omega$-algebras.

Proposition 5.4

Let $\Omega = \Omega _0 \cup \Omega _1$. Then every class $\mathcal {K}$ of ordered $\Omega$-algebras, which is closed under finite coproducts and regular epimorphic images, has AP.

Proof

Consider order-embeddings $f$: $\mathcal {B}\longrightarrow \mathcal {A}$ and $g$: $\mathcal {B}\longrightarrow \mathcal {C}$ in $\mathcal {K}$. As above, we construct the $\Omega$-algebras $\mathcal {A}\sqcup \mathcal {C}$ and $\mathcal {A}*\mathcal {C} = (\mathcal {A}\sqcup \mathcal {C})/\theta$. By assumption and Lemma 5.3, $\mathcal {A}*\mathcal {C}$ belongs to $\mathcal {K}$.

Now let $\Theta$ be the order-congruence on $\mathcal {A}\sqcup \mathcal {C}$ generated by the set

$$\begin{aligned} K=\{\left( (1,f(b)),(2,g(b))\right) \mid b\in B\} \end{aligned}$$

and form the quotient algebra $\mathcal {D}:=(\mathcal {A}\sqcup \mathcal {C})/\Theta$. We note that $H\subseteq K$ (see (5.2)) and hence $\theta \subseteq \Theta$. Define a mapping $h: (\mathcal {A}\sqcup \mathcal {C})/\theta \longrightarrow (\mathcal {A}\sqcup \mathcal {C})/\Theta$ by

$$\begin{aligned} h\left( [x]_\theta \right) := [x]_\Theta . \end{aligned}$$

This mapping is clearly a surjective homomorphism of $\Omega$-algebras. Let us prove that $h$ is a regular epimorphism. Suppose, for this purpose, that $[x]_\Theta \le [x']_\Theta$ in $(\mathcal {A}\sqcup \mathcal {C})/\Theta$. Then $x\underset{\Theta }{\le } x'$, that is,

$$\begin{aligned} x\le x_1 \,\Theta \, x_2 \le x_3 \,\Theta \, \ldots \,\Theta \, x_n \le x' \end{aligned}$$

for some $x_1,\ldots ,x_n\in A\sqcup C$. But then we may write

$$\begin{aligned}{}[x]_\theta \le [x_1]_\theta (\ker h) [x_2]_\theta \le [x_3]_\theta (\ker h) \ldots (\ker h) [x_n]_\theta \le [x']_\theta , \end{aligned}$$

or shortly $[x]_\theta \underset{\ker h}{\le } [x']_\theta$. We have shown that $h$ is a Q-homomorphism and hence it is a regular epimorphism in the variety of all ordered $\Omega$-algebras by Theorem 1.4. Therefore also $(\mathcal {A}\sqcup \mathcal {C})/\Theta$ belongs to the class $\mathcal {K}$.

We define mappings $f^{\prime }$: $C\longrightarrow (A\sqcup C)/\Theta$ and $g^{\prime }$: $A \longrightarrow (A\sqcup C)/\Theta$ by

$$\begin{aligned} f^{\prime }(c):= & {} [(2,c)], \\ g^{\prime }(a):= & {} [(1,a)]. \end{aligned}$$

Clearly these mappings are monotone, make the diagram

commutative and preserve the operations. So $f^{\prime }$ and $g^{\prime }$ are homomorphisms of $\Omega$-algebras.

To complete the proof, we show that $f^{\prime }$ is an order-embedding (for $g^{\prime }$ the proof is analogous). Suppose that we have $c,c^{\prime }\in C$ and $f^{\prime }(c)\le f^{\prime }(c^{\prime })$, i.e. $(2,c)\underset{\Theta }{\le }(2,c^{\prime })$. Using Lemma 1.2, either $(2,c)\le (2,c')$, in which case $c\le c'$, or we have a sequence

where $p_1(x),\ldots ,p_{n}(x)$ are unary $\Omega$-polynomials that depend on $x$ and $(x_{1},y_{1}),\ldots$, $(x_{n},y_{n})\in H\cup H^{-1}$. Now $p_1^{A\sqcup C}(x_{1})\in \{2\}\times C$ by the definition of order and $x_{1}\in \{2\}\times C$ because of the definition of unary operations. Hence $x_{1}=(2,g(b_{1}))$ and $y_{1}=(1,f(b_{1}))$ for some $b_{1}\in B$. Thus we can write

$$\begin{aligned} p_{1}^{A\sqcup C}(x_{1})=p_{1}^{A\sqcup C}(2,g(b_{1}))=(2,p_{1}^{C}(g(b_{1}))). \end{aligned}$$

Now the inequality $(2,c)\le (2,p_{1}^{C}(g(b_{1})))$ implies $c\le p_{1}^{C}(g(b_{1}))$.

Next, because $p_{2}^{A\sqcup C}(x_{2})\in \{1\}\times A$, there exists $b_{2}\in B$ such that $x_{2}=(1,f(b_{2}))$ and $y_{2}=(2,g(b_{2}))$. And again we may write:

$$\begin{aligned} \left( 1,p_{1}^{A}(f(b_{1}))\right) =p_{1}^{A\sqcup C}(y_{1})\le p_{2}^{A\sqcup C}(x_{2})=\left( 1,p_{2}^{A}(f(b_{2}))\right) . \end{aligned}$$

So

$$\begin{aligned} f(p_{1}^{B}(b_{1}))=p_{1}^{A}(f(b_{1}))\le p_{2}^{A}(f(b_{2}))=f(p_{2}^{B}(b_{2})). \end{aligned}$$

But then $p_{1}^{B}(b_{1})\le p_{2}^{B}(b_{2})$, because $f$ is an order-embedding. We have therefore obtained

$$\begin{aligned} c\le p_{1}^{C}(g(b_{1}))=g(p_{1}^{B}(b_{1}))\le g(p_{2}^{B}(b_{2}))=p_{2}^{C}(g(b_{2})), \end{aligned}$$

where $p_{2}^{A\sqcup C}(y_{2})=\left( 2,p_{2}^{C}(g(b_{2}))\right)$. Continuing in this manner we get that $c\le p_n^C(g(b_n))$, where $p_{n}^{A\sqcup C}(y_{n})=\left( 2,p_{n}^{C}(g(b_{n}))\right)$ and $b_n\in B$. Hence $c\le p_{n}^{C}(g(b_{n})) \le c^{\prime }$. $\square$

From Theorem 2.6, Proposition 5.4 and Proposition  5.1 we arrive at the following result.

Corollary 5.5

Let $\Omega = \Omega _0\cup \Omega _1$. Then every variety of ordered $\Omega$-algebras, which is closed under finite coproducts, has TP.

Example 5.6

Let $S$ be a pomonoid. Then $\Omega =\Omega _1$ and clearly the class of all right $S$-posets has TP by Corollary 5.5. Also, the class of all finitely generated right $S$-posets has TP by Theorem 2.6, Proposition 5.4 and Proposition 5.1.