Gorenstein theory for n-th differential modules

Abstract

In this paper the definition of $n$-th differential modules is introduced. It is shown that an $n$-th differential module $(M,\delta _{M},n)$ is Gorenstein projective (resp. injective) if and only if $M$ is Gorenstein projective (resp. injective). It is established that the relations between Gorenstein homological dimensions of an $n$-th differential module and the ones of its underlying module.

1 Introduction

The concept of a differential module was introduced by Cartan and Eilenberg (see [3]), which is a module equipped with a square-zero endomorphism. It is found that differential modules have closely related to commutative algebras, algebraic topology and differential geometry. Many people are interested in differential modules in rencent years. Levin defines a special type of reduction in a free left module over a ring of difference-differential operators. He applies the idea of the Gr$\ddot{\mathrm{o}}$bner basis to determine the Hilbert function of a finitely generated difference-differential module equipped with the natural double filtration (see [11]). Zhou and Winklerb [18] introduce a series of algorithms to construct Gr$\ddot{\mathrm{o}}$bner bases for a class of difference-differential modules. Wu in [16] generalizes the Beke–Schlesinger algorithm that factors differential modules. The authors in [1] establish lower bounds on the class—a substitute for the length of a free complex, and on the rank of a differential module in terms of invariants of its homology.

Enochs and Jenda introduced the notion of Gorenstein projective modules over an arbitrary ring, which is a generalization of finitely generated modules of G-dimension zero over a two-sided noetherian ring. However, not much is known about concrete construction and computation of Gorenstein projective modules in general. Cheng and Zhu in [4] generalized some results of Gorenstein projective objects in the category of $R$-modules and its chain complex category Ch($R$). In the paper [17], Zhang introduced compatible bimodules, described the Gorenstein-projective modules over an upper triangular matrix algebra $\varLambda =\left( \begin{array}{cc} A &{} M \\ 0 &{} B \\ \end{array} \right)$ , where $M$ is a compatible $A$–$B$-bimodule. Moreover, the author proved that if $\varLambda$ is Gorenstein, then $M$ is compatible. Ringel and Zhang in [14] proved that some deep results for the category of perfect differential modules of a path algebra. They also gave the relations between its stable category and the orbit category. Wei in [15] verified that a differential module is Gorenstein projective (resp. injective) if and only if its underlying module is Gorenstein projective (resp. injective). In this paper we introduce the definition of $n$-th differential modules. It is noted that $2$-th differential modules are just the usual differential modules. For an associative ring $R$ with an identity, we prove that an $n$-th differential module $(M,\delta _{M},n)$ is Gorenstein projective (resp. injective) if and only if $M$ is projective (resp. injective). Moreover, we also describe the relations between Gorenstein homological dimensions of an $n$-th differential module and the ones of its underlying module.

The paper is organized as follows. In Sect. 2, we give some notations and some definitions. In Sect. 3, we study the Gorenstein projective and Gorenstein injective theory for $n$-th differential modules.

2 Preliminaries

Throughout this paper, the ring $R$ is always assumed to be an associative ring with an identity, $R$-modules are left modules. The notation $(~)^{T}$ denotes the transpose of vectors or matrices.

Firstly, we give some definition and basic results in this section.

Definition 2.1

Let $M$ be an $R$-module, and $\delta :M\longrightarrow M$ be an endomorphism of $M$. If $\delta ^{n}=0,$ then we call $(M,\delta ,n)$ an $n$-th differential module.

If $n=2,$ then $(M,\delta , n)$ is a usual differential module. So, we always assume that $n\ge 2.$

Definition 2.2

Let $(M,\delta _{M},n), (N,\delta _{N},n)$ be two $n$-th differential modules, $f$ be the homomorphism of $R$-modules from $M$ to $N.$ If $f\delta _{M}=\delta _{N}f,$ we call $f$ the homomorphism of $n$-th differential modules.

Let $X$ be an $R$-module. It is easy to check that $(X^{\oplus n}, \alpha , n)$ is an $n$-th differential module, where $\alpha$ is the endomorphism of $X^{\oplus n}$ induced by the matrix

$$\begin{aligned} A=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 &{}\cdots &{}\cdots &{} 0 \\ 1 &{} 0 &{} 0 &{}\cdots &{}\cdots &{} 0 \\ 0 &{} 1 &{} 0 &{}\cdots &{}\cdots &{}0\\ &{} &{} \ddots &{}\ddots &{}&{} \\ &{} &{} &{}\ddots &{}\ddots &{} \\ 0 &{} 0 &{} 0 &{}\cdots &{} 1 &{} 0 \\ \end{array} \right) _{n\times n.} \end{aligned}$$

Such $n$-th differential modules are called contractible $n$-th differential modules. The notation $\text{ Hom }_{R}((*), C)$ (or $\hbox {Hom}_{R}(I, (*)$) means that the functor $\text{ Hom }_{R}(-, C)$ (or $\hbox {Hom}_{R}(I, -)$ is applied to a complex $(*)$.

Definition 2.3

Let $\mathcal {F}$ be a family of $R$-modules. A proper $\mathcal {F}$-resolution of an $R$-module $M$ is an exact sequence

$$\begin{aligned} \cdots \rightarrow C_{2}\xrightarrow {}C_{1}\xrightarrow {} C_{0}\xrightarrow {}M \xrightarrow {} 0 \end{aligned}$$

(2.1)

where $C_{i}\in \mathcal {F}$ for all $i\ge 0$, and $\text{ Hom }_{R}$ ($C$, (2.1)) is exact for any $C\in \mathcal {F}$.

A proper $\mathcal {F}$-coresolution of an $R$-module $N$ is an exact sequence

$$\begin{aligned} 0 \xrightarrow {}N \xrightarrow {}C_{0}\xrightarrow {}C_{1}\xrightarrow {}C_{2}\rightarrow \cdots \end{aligned}$$

(2.2)

where $C_{i}\in \mathcal {F}$ for all $i\ge 0$, and $\text{ Hom }_{R}$ ((2.2), $C$) is exact for any $C\in \mathcal {F}$.

Definition 2.4

An $R$-module $M$ is called Gorenstein projective if there exists an exact sequence of projective $R$-modules

$$\begin{aligned} \cdots \xrightarrow {}P_{2}\xrightarrow {}P_{1}\xrightarrow {}P_{0}\xrightarrow {}P_{-1}\xrightarrow {}P_{-2}\xrightarrow {}\cdots \end{aligned}$$

(2.3)

such that $M\simeq \text{ Im }(P_{1}\rightarrow P_{0})$ and $\hbox {Hom}_{R}$ ((2.3), $P$) is exact for any projective module $P$.

An $R$-module $N$ is called Gorenstein injective if there exists an exact sequence of injective $R$-modules

$$\begin{aligned} \cdots \xrightarrow {}I_{2}\xrightarrow {}I_{1}\xrightarrow {}I_{0}\xrightarrow {}I_{-1}\xrightarrow {}I_{-2}\xrightarrow {}\cdots \end{aligned}$$

(2.4)

such that $N\simeq \text{ Im }(I_{0}\rightarrow I_{-1})$ and $\hbox {Hom}_{R}$ ($I$, (2.4)) is exact for any injective module $I$.

In the following we denote the category of $R$-modules by $R$-mod, the category of $n$-th differential modules by $\text{ Diff }(R, n)$-mod. It is noted that $\text{ Diff }(R, n)$-mod has enough projective (resp. injective) objects, this result will be given in Proposition 3.5.

3 Gorenstein projective (resp. injective) theory

In this section we describe the main results for the Gorenstein projective (resp. injective) $n$-th differential modules.

Some lemmas are given firstly in the following.

Lemma 3.1

Let $(M,\delta ,n)$ be an $n$-th differential module and $X\in R$-mod.

• (i) Let $f\in \hbox {Hom}_{R}(M,X^{\oplus n}).$ Then $f\in \hbox {Hom}_{\mathrm{Diff}(R, n)}((M,\delta ,n),(X^{\oplus n},\alpha ,n))$ if and only if there exists $g\in \hbox {Hom}_{R}(M,X)$ such that $f=(g,g\delta ,g\delta ^{2},\ldots ,g\delta ^{n-1}).$

• (ii) Let $f\in \hbox {Hom}_{R}(X^{\oplus n},M).$ Then $f\in \hbox {Hom}_{\mathrm{Diff}(R, n)}((X^{\oplus n},\alpha ,n),(M,\delta ,n))$ if and only if there exists $g\in \text{ Hom }_{R}(X,M)$ such that $f=(\delta ^{n-1}g,\delta ^{n-2}g,\ldots ,\delta g,g)^{T}.$

Proof

• (i) $(\Rightarrow )$ Let $f(m)=(p_{1}(m),\ldots ,p_{n}(m))\in X^{\oplus n}$ for $m\in M.$ Since $f$ is the homomorphism of $n$-th differential modules, so $\alpha f=f\delta .$ We calculate

  $$\begin{aligned} \alpha f(m)= & {} (p_{1}(m),p_{2}(m),\ldots ,p_{n}(m))A\\= & {} (p_{2}(m),p_{3}(m),\ldots ,p_{n}(m),0).\\ f\delta (m)= & {} (p_{1}\delta (m),p_{2}\delta (m),\ldots ,p_{n}\delta (m)). \end{aligned}$$

Hence, we have the following equations

$$\begin{aligned} \left\{ \begin{array}{l} p_{1}\delta (m)=p_{2}(m) \\ p_{2}\delta (m)=p_{3}(m)\\ \quad \cdots \quad \cdots \\ p_{n-1}\delta (m)=p_{n}(m)\\ p_{n}\delta (m)=0. \end{array} \right. \end{aligned}$$

Set $g=p_{1}.$ Then we have $f=(g,g\delta ,g\delta ^{2},\ldots ,g\delta ^{n-1})$.

$(\Leftarrow )$ Let $f=(g,g\delta ,g\delta ^{2},\ldots , g\delta ^{n-1})$. By calculating, we have

$$\begin{aligned} f\delta (m)= & {} (g\delta (m),\ldots ,g\delta ^{n-1}(m),g\delta ^{n}(m))\\= & {} (g\delta (m),g\delta ^{2}(m),\ldots ,g\delta ^{n-1}(m),0).\\ \alpha f(m)= & {} (g(m),g\delta (m),\ldots ,g\delta ^{n-1}(m))A\\= & {} (g\delta (m),g\delta ^{2}(m),\ldots ,g\delta ^{n-1}(m),0). \end{aligned}$$

So we obtain $f\delta =\alpha f.$ Hence, $f$ is a homomorphism of $n$-th differential modules.

• (ii) $(\Rightarrow )$ Let $f$ be a homomorphism from $n$-th differential module $(X^{\oplus n}, \alpha , n)$ to $n$-th differential module $(M, \delta , n).$ Set $f=(p_{1}, p_{2},\ldots , p_{n} )^{T}.$ Then

$$\begin{aligned} \delta f(x_{1},x_{2},\ldots ,x_{n})= & {} \delta (p_{1}(x_{1})+p_{2}(x_{2})+\cdots +p_{n}(x_{n}))\\= & {} \delta p_{1}(x_{1})+\delta p_{2}(x_{2})+\cdots +\delta p_{n}(x_{n}).\\ f\alpha (x_{1},x_{2},\ldots ,x_{n})= & {} f((x_{1},x_{2},\ldots ,x_{n})A)\\= & {} f(x_{2},x_{3},\ldots ,x_{n},0)\\= & {} p_{1}(x_{2})+p_{2}(x_{3})+\cdots +p_{n-1}(x_{n}). \end{aligned}$$

So we get the following equations

$$\begin{aligned} \left\{ \begin{array}{l} \delta p_{n}=p_{n-1} \\ \delta p_{n-1}=p_{n-2}\\ \quad \cdots \quad \cdots \\ \delta p_{2}=p_{1}\\ \delta p_{1}=0. \end{array} \right. \end{aligned}$$

Set $g= p_{n}.$ Then we can obtain $f=(\delta ^{n-1}g,\delta ^{n-2}g,\ldots ,\delta g,g)^{T}$.

$(\Leftarrow )$ Let $f=(\delta ^{n-1}g,\delta ^{n-2}g,\ldots ,\delta g,g)^{T}$. We have

$$\begin{aligned} f\alpha (x_{1},x_{2},\ldots ,x_{n})= & {} f(x_{2},x_{3}.\cdots ,x_{n},0)\\= & {} \delta ^{n-1}g(x_{2})+\delta ^{n-2}g(x_{3})+\cdots +\delta g(x_{n}).\\ \delta f(x_{1},x_{2},\ldots ,x_{n})= & {} \delta (\delta ^{n-1}g(x_{1})+\delta ^{n-2}g(x_{2})+\cdots +\delta g(x_{n-1})+g(x_{n}))\\= & {} \delta ^{n}g(x_{1})+\delta ^{n-1}g(x_{2})+\cdots +\delta ^{2} g(x_{n-1})+\delta g(x_{n})\\= & {} 0+\delta ^{n-1}g(x_{2})+\delta ^{n-2}g(x_{3})+\cdots +\delta g(x_{n}). \end{aligned}$$

So $f\alpha =\delta f$. That is, $f$ is a homomorphism of $n$-th differential modules.

The proof is finished $\square$

Lemma 3.2

Let $f:(M,\delta _{M},n)\longrightarrow (N,\delta _{N},n)$ be a homomorphism of $n$-th differential modules and $X$ be an $R$-module.

• (i) $\hbox {Hom}_{R}(f,X)$ is an epimorphism if and only if $\hbox {Hom}_{\text{ Diff }(R, n)}(f,(X^{\oplus n},\alpha ,n))$ is an epimorphism.

• (ii) $\hbox {Hom}_{R}(X,f)$ is an epimorphism if and only if $\hbox {Hom}_{\text{ Diff }(R, n)}((X^{\oplus n},\alpha ,n),f)$ is an epimorphism.

Proof

(i) $\mathbf{(\Rightarrow )}$ Assume that $\text{ Hom }_{R}(f,X)$ is an epimorphism. Let $\varphi$ be a homomorphism from $(M,\delta _{M},n)$ to $(X^{\oplus n},\alpha ,n)$. By Lemma 3.1, we know that there exists $g\in$ $\hbox {Hom}_{R}(M,X)$ such that $\varphi =(g,g\delta _{M},g\delta _{M}^{2},\ldots ,g\delta _{M}^{n-1}).$ Since $\text{ Hom }_{R}(f,X)$ is an epimorphism, there is $h\in \text{ Hom }_{R}(N, X)$ such that $g=hf.$ Set $\psi =(h,h\delta _{N},\ldots ,h\delta _{N}^{n-1}).$ It is easy to know that $\psi$ is a homomorphism of $n$-th differential modules by Lemma 3.1. We also get

$$\begin{aligned} (g,g\delta _{M},\ldots ,g\delta _{M}^{n-1})= & {} (hf,hf\delta _{M},\ldots ,hf\delta _{M}^{n-1})\\= & {} (h,h\delta _{N},\ldots ,h\delta _{N}^{n-1})f \end{aligned}$$

in view of $f\delta _{M}=\delta _{N}f.$ Hence, $\hbox {Hom}_{\text{ Diff }(R, n)}(f,(X^{\oplus n},\alpha ,n))$ is an epimorphism.

$(\Leftarrow )$ Assume $\hbox {Hom}_{\text{ Diff }(R, n)}(f,(X^{\oplus n},\alpha ,n))$ is an epimorphism. Let $g:M\rightarrow X$ be a homomorphism of $R$-modules. By Lemma 3.1, there exists $\varphi =(g,g\delta _{M},g\delta _{M}^{2},\ldots ,g\delta _{M}^{n-1})\in \text{ Hom }_{\text{ Diff }(R, n)}((M,\delta _{M},n),(X^{\oplus n},\alpha , n)).$ Since $\hbox {Hom}_{\text{ Diff }(R, n)}(f,(X^{\oplus n},\alpha ,n))$ is an epimorphism, there exists $\psi :(N,\delta _{N},n)\rightarrow (X^{\oplus n},\alpha ,n)$ such that $\psi f=\varphi .$ By Lemma 3.1, we know that there exists an $R$-modules homomorphism $h:N\rightarrow X$ such that $\psi =(h,h\delta _{N},h\delta _{N}^{2},\ldots ,h\delta _{N}^{n-1})$. Hence,

$$\begin{aligned} (g,g\delta _{M},\ldots ,g\delta _{M}^{n-1})= & {} (h,h\delta _{N},\ldots ,h\delta _{N}^{n-1})f\\= & {} (hf,h\delta _{N}f,\ldots ,h\delta _{N}^{n-1}f)\\= & {} (hf,hf\delta _{M},\ldots ,hf\delta _{M}^{n-1}). \end{aligned}$$

It follows that $hf=g$ and $\hbox {Hom}_{R}(f,X)$ is an epimorphism.

(ii) The proof is similar to (i).

The proof is finished. $\square$

We denote the sequences of $R$-modules and the sequences of $n$-th differential modules by the same notations if there is no confusion.

Proposition 3.3

Let

$$\begin{aligned} 0\rightarrow (M,\delta _{M},n)\rightarrow (N,\delta _{N},n)\rightarrow (L,\delta _{L},n)\rightarrow 0 \end{aligned}$$

(3.1)

be an exact sequence of $n$-th differential modules, and $X$ be an $R$-module. Then the following statements hold.

• (i) $\hbox {Hom}_{\text{ Diff }(R, n)}$ ((3.1), $(X^{\oplus n},\alpha ,n))$ is exact if and only if $\hbox {Hom}_{R}$ ((3.1), $X$) is exact;

• (ii) $\hbox {Hom}_{\text{ Diff }(R, n)}((X^{\oplus n},\alpha ,n)$ , (3.1)) is exact if and only if $\hbox {Hom}_{R}$ ($X$, (3.1)) is exact.

Proof

It is easy to see by the left exactness of Hom functors and Lemma 3.2.

The proof is finished. $\square$

By Proposition 3.3, we get that a contractible $n$-th differential module $(X^{\oplus n},\alpha ,n)$ is projective (resp. injective) object in $\text{ Diff }(R, n)$-mod if and only if $X$ is projective (resp. injective) as an $R$-module.

Lemma 3.4

Let $(M,\delta _{M},n)$ be an $n$-th differential module, and $\mathcal {F}$ be a family of $R$-modules which is closed under direct sums. Let

$$\begin{aligned} 0\rightarrow L\xrightarrow {\lambda }C\xrightarrow {\pi } M\rightarrow 0 \end{aligned}$$

(3.2)

be an exact sequence of $R$-modules, where $C\in \mathcal {F}.$ If

(3.3)

is exact for any $C'\in \mathcal {F}$, then there exists an exact sequence of $n$-th differential modules

$$\begin{aligned} 0\rightarrow (C^{\oplus n-1}\oplus L,\delta _{C^{\oplus n-1}\oplus L},n)\xrightarrow {S}(C^{\oplus n},\alpha ,n)\xrightarrow {T}(M, \delta _{M}, n)\rightarrow 0, \end{aligned}$$

(3.4)

where $T=(\delta ^{n-1}\pi ,\ldots ,\delta ^{2}\pi ,\delta \pi , \pi )^{T},$

$$\begin{aligned} S= & {} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} -1 &{} h &{} 0 &{}\cdots &{}0 \\ 0&{} -1 &{} h &{}\cdots &{}0 \\ \vdots &{} &{}\ddots &{} \ddots &{} \vdots \\ &{} &{}&{} -1 &{} h \\ 0 &{} &{}\cdots &{} 0 &{} \lambda \\ \end{array} \right) _{n\times n,}\\&\left\{ \begin{array}{l} \delta _{C^{\oplus n-1}\oplus L}(x_{1})=x_{2}-h(x_{1}) \\ \delta _{C^{\oplus n-1}\oplus L}(x_{2})=x_{3}-h^{2}(x_{1})\\ \quad \cdots \quad \cdots \\ \delta _{C^{\oplus n-1}\oplus L}(x_{n-2})=x_{n-1}-h^{n-2}(x_{1})\\ \delta _{C^{\oplus n-1}\oplus L}(x_{n-1})=-h^{n-1}(x_{1})-\lambda (y)\\ \delta _{C^{\oplus n-1}\oplus L}(y)=\lambda ^{-1}(h^{n}(x_{1})+h\lambda (y)) \end{array} \right. \end{aligned}$$

for any $(x_{1},\ldots ,x_{n-1},y)\in C^{\oplus n-1}\oplus L$ and $h\in \text{ End }_{R} C$ such that

• (i) $\hbox {Hom}_{\text{ Diff }(R, n)}((C'^{\oplus n},\alpha ,n)$, (3.4)) is exact for any $C'\in \mathcal {F};$

• (ii) $\hbox {Hom}_{R}$ ((3.2), $X$) is exact if and only if $\hbox {Hom}_{\text{ Diff }(R, n)}$ ((3.4), $(X^{\oplus n},\alpha ,n))$ is exact for any $R$-module $X$.

Proof

Since $\hbox {Hom}_{R}$ ($C'$, (3.2)) is exact for any $C'\in \mathcal {F},$ we have $\hbox {Hom}_{R}$ ($C$, (3.2)) is exact. So $\text{ Hom }(C,\pi )$ is an epimorphism. Hence, there exists $h\in \text{ End }_{R}C$ such that $\pi h=\delta \pi .$ We claim that the following diagram commutes

(3.5)

where

$$\begin{aligned} \varsigma =(0,\ldots ,0,1),\qquad \omega =\left( \begin{array}{c} h^{n-1} \\ \vdots \\ h \\ \lambda \\ \end{array} \right) ,\qquad \eta =\left( \begin{array}{c} 1 \\ \vdots \\ 1 \\ 0 \\ \end{array} \right) . \end{aligned}$$

It is obvious that left square is commutative. In fact, the right square is also commutative. Indeed, let $(x_{1},x_{2},\ldots ,x_{n-1},y)\in C^{\oplus n-1}\oplus L$. We calculate

$$\begin{aligned}&T\eta (x_{1},x_{2},\ldots ,x_{n-1},y) =T(x_{1},x_{2},\ldots ,x_{n-1},0)\\&\quad =\delta ^{n-1}\pi (x_{1})+\delta ^{n-2}\pi (x_{2})+\cdots +\delta \pi (x_{n-1}). \pi \omega (x_{1},x_{2},\ldots ,x_{n-1},y)\\&\quad =\pi (h^{n-1}(x_{1})+h^{n-2}(x_{2})+\cdots +h(x_{n-1})+\lambda (y))\\&\quad =\pi h^{n-1}(x_{1})+\pi h^{n-2}(x_{2})+\cdots +\pi h(x_{n-1})+0\\&\quad =\delta ^{n-1}\pi (x_{1})+\delta ^{n-2}\pi (x_{2})+\cdots +\delta \pi (x_{n-1}). \end{aligned}$$

Hence, the diagram (3.5) is commutative. Let $(x_{1},x_{2},\ldots ,x_{n-1},y)\in C^{\oplus n-1}\oplus L.$ Then

$$\begin{aligned}&S(x_{1},x_{2},\ldots ,x_{n-1},y)\\&=(-x_{1},h(x_{1})-x_{2},h(x_{2})-x_{3},\ldots ,h(x_{n-2})-x_{n-1},h(x_{n-1})+\lambda (y)). \end{aligned}$$

If $S(x_{1},x_{2},\ldots ,x_{n-1},y)=0$, we get $x_{1}=\cdots =x_{n-1}=y=0$ because $\lambda$ is injective. Hence, $S$ is injective. Let $m\in M.$ Then there exists $x'_{n}\in C$ such that $\pi (x'_{n})=m.$ Obviously, $(0,\ldots , 0, x'_{n})\in C^{\oplus n}$ and $T(0,\ldots , 0, x'_{n})=m.$ Hence, $T$ is surjective. We calculate

$$\begin{aligned}&TS(x_{1},x_{2},\ldots ,x_{n-1},y)\\&\quad =T(-x_{1},h(x_{1})-x_{2},h(x_{2})-x_{3},\ldots ,h(x_{n-2})-x_{n-1},h(x_{n-1})+\lambda (y))\\&\quad =-\delta ^{n-1}\pi (x_{1})+\delta ^{n-2}\pi h(x_{1})-\delta ^{n-2}\pi (x_{2})+ \cdots +\delta \pi h(x_{n-2})-\delta \pi (x_{n-1})\\&\qquad +\, \pi h(x_{n-1})+0=0. \end{aligned}$$

Hence, $\hbox {Im}S \subseteq \text{ Ker } T.$ Let $(z_{1},\ldots ,z_{n})\in C^{\oplus n}$ and $T(z_{1},\ldots ,z_{n})=0.$ Then we can get

$$\begin{aligned} 0= & {} T(z_{1},\ldots ,z_{n})\\= & {} \delta ^{n-1}\pi (z_{1})+\delta ^{n-2}\pi (z_{2})+\cdots +\delta \pi (z_{n-1})+\pi (z_{n})\\= & {} \pi h^{n-1}(z_{1})+\pi h^{n-2}(z_{2})+\cdots +\pi h(z_{n-1})+\pi (z_{n})\\= & {} \pi ( h^{n-1}(z_{1})+ h^{n-2}(z_{2})+\cdots + h (z_{n-1})+z_{n}). \end{aligned}$$

Hence, $h^{n-1}(z_{1})+ h^{n-2}(z_{2})+\cdots + h (z_{n-1})+z_{n}\in \text{ Ker } \pi =\text{ Im } \lambda .$ So there exists $y\in L$ such that

$$\begin{aligned} \lambda (y)=h^{n-1}(z_{1})+ h^{n-2}(z_{2})+\cdots + h (z_{n-1})+z_{n}. \end{aligned}$$

Set

$$\begin{aligned} \left\{ \begin{array}{l} x_{1}=-z_{1} \\ x_{2}=-(h(z_{1})+z_{2})\\ x_{3}=-(h^{2}(z_{1})+h(z_{2})+z_{3})\\ \quad \cdots \quad \cdots \\ x_{n-1}=-(h^{n-2}(z_{1})+h^{n-3}(z_{2})+\cdots +h(z_{n-2})+z_{n-1}). \end{array} \right. \end{aligned}$$

It is easy to check $S(x_{1},x_{2},\ldots ,x_{n-1},-y)=(z_{1},\ldots ,z_{n}).$ Hence, $\text{ Ker } T\subseteq \text{ Im } S.$ So

$$\begin{aligned} 0\rightarrow C^{\oplus n-1}\oplus L\xrightarrow {S}C^{\oplus n}\xrightarrow {T}M\rightarrow 0, \end{aligned}$$

(3.6)

is exact. For any $(x_{1},x_{2},\ldots ,x_{n})\in C^{\oplus n},$ we calculate

$$\begin{aligned} T\alpha (x_{1},x_{2},\ldots ,x_{n})= & {} T(x_{1},x_{2},\ldots ,x_{n})A\\= & {} T(x_{2},x_{3},\ldots ,x_{n},0)\\= & {} \delta ^{n-1}\pi (x_{2})+\delta ^{n-2}\pi (x_{3})+\cdots +\delta \pi (x_{n}).\\ \delta T(x_{1},x_{2},\ldots ,x_{n})= & {} \delta (\delta ^{n-1}\pi (x_{1})+\delta ^{n-2}\pi (x_{2})+\cdots +\delta \pi (x_{n-1})+\pi (x_{n}))\\= & {} \delta ^{n-1}\pi (x_{2})+\delta ^{n-2}\pi (x_{3})+\cdots +\delta \pi (x_{n}). \end{aligned}$$

That is, $T\in \text{ Hom }_{\text{ Diff }(R, n)}((C^{\oplus n},\alpha ,n),(M,\delta _{M}, n)).$ Similarly, it is easy to check that $S\in \text{ Hom }_{\text{ Diff }(R, n)}((C^{\oplus n-1}\oplus L,\delta _{C^{\oplus n-1}\oplus L},n),(C^{\oplus n},\alpha ,n)).$ Therefore, the sequence (3.4) is an exact sequence.

• (i) Let $C'\in \mathcal {F}.$ Then $\text{ Hom }_{R}(C',\pi )$ is an epimorphism. We consider the following sequence

  

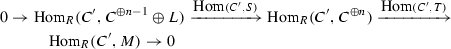  (3.7)

For any $\varphi \in \text{ Hom }_{R}(C',M),$ there exists $g\in \text{ Hom }_{R}(C',C)$ such that $\pi g=\varphi .$ Set $\psi =(0,\ldots ,0,g).$ Then $\psi T =\pi g=\varphi .$ Hence, $\text{ Hom }_{R}(C',T)$ is surjective and $\text{ Hom }_{R}$ ($C'$, (3.6)) is exact. By Proposition 3.3, we get $\text{ Hom }_{\text{ Diff }(R, n)}((C',\alpha ,n)$ , (3.4)) is exact.

• (ii) $(\Rightarrow )$ Let $X\in R$-mod. Assume that $\text{ Hom }_{R}$ ((3.2), $X$) is exact. By Proposition 3.3, it is enough to prove that

is exact. Since Hom functors are left exact, it suffices to prove that $\text{ Hom }_{R}(S, X)$ is an epimorphism . Let $\varphi =( p_{1}, \cdots , p_{n-1}, q)^{T}:C^{\oplus n-1}\oplus L\rightarrow X.$ Then there exists $\theta :C\rightarrow X$ such that $\theta \lambda =q.$ Set

$$\begin{aligned} \psi =\left( \begin{array}{c} \nu _{1} \\ \nu _{2} \\ \vdots \\ \nu _{n-1} \\ \theta \\ \end{array} \right) , \quad \hbox {where}\, \left\{ \begin{array}{l} \nu _{1}=\theta h^{n-1}-p_{n-1}h^{n-2}-\cdots -p_{2}h-p_{1}, \\ \vdots \\ \nu _{n-3}=\theta h^{3}-p_{n-1}h^{2}-p_{n-2}h-p_{n-3},\\ \nu _{n-2}=\theta h^{2}-p_{n-1}h-p_{n-2},\\ \nu _{n-1}=\theta h-p_{n-1},\\ \nu _{n}=\theta . \end{array} \right. \end{aligned}$$

It is easy to check $\varphi =S \psi .$ Hence, $\text{ Hom }_{R}(S, X)$ is an epimorphism. By Proposition 3.3, we get that $\text{ Hom }_{\text{ Diff }(R, n)}$ ((3.4), $(X^{\oplus n},\alpha ,n))$ is exact.

$(\Leftarrow )$ Suppose that $\text{ Hom }_{\text{ Diff }(R, n)}$ ((3.4), $(X^{\oplus n},\alpha ,n))$ is exact. By Proposition  3.3, we know that

$$\begin{aligned} 0\rightarrow \text{ Hom }_{R}(M,X)\rightarrow \text{ Hom }_{R}(C^{\oplus n},X)\rightarrow \text{ Hom }_{R}(C^{\oplus n-1}\oplus L, X)\rightarrow 0 \end{aligned}$$

is exact. It is enough to show $\text{ Hom }_{R}(\lambda ,X)$ is an epimorphism if we want to show

is an exact sequence. Let $\varphi \in \text{ Hom }_{R}(L,X).$ Then $(0, 0,\ldots , 0,\varphi )^{T}\in \text{ Hom }_{R}(C^{\oplus n-1}\oplus L,X).$

So there exists an $R$-modules homomorphism $(p_{1}, p_{2}, \cdots , p_{n-1}, p_{n})^{T}:C^{\oplus n}\rightarrow X$

such that $S(p_{1}, p_{2},\ldots ,p_{n-1}, p_{n})^{T}=(0,0, \cdots ,0 , \varphi )^{T}.$ Hence, $p_{n}\lambda =\varphi .$ That is, $\text{ Hom }_{R}(\lambda ,X)$ is an epimorphism. The proof is finished. $\square$

Obviously, $Diff (R,n)\hbox {-}\mathrm{mod}\simeq R[t]/\langle {t^{n}}\rangle$-mod. So we have

Proposition 3.5

$\text{ Diff }(R, n)$-mod is an abelian category with enough projective objects.

Proof

Here we prove in another way. It is easy to check that $\text{ Diff }(R, n)$-mod is an abelian category. Secondly, thank to Lemma 3.2, the $n$-th differential module $(X^{\oplus n},\alpha ,n)$ is a projective object in $\text{ Diff }(R, n)$-mod if $X$ is projective as an $R$-module. If $\mathcal {F}$ is taken to be the subcategory consisting of projective $R$-modules in Lemma 3.4, for any $(M,\delta _{M}, n),$ there exists $C\in \mathcal {F}$ such that (3.2) is exact. It follows that (3.4) is exact. This means that $\text{ Diff }(R, n)$-mod has enough projective objects. $\square$

Lemma 3.6

Let $(M,\delta _{M}, n)$ be an $n$-th differential module and $\mathcal {F}$ be a family of $R$-modules which is closed under direct sums. Assume that

$$\begin{aligned} 0 \rightarrow M\xrightarrow {\lambda }C\xrightarrow {\pi } L\rightarrow 0 \end{aligned}$$

(3.8)

is an exact sequence of $R$-modules, where $C\in \mathcal {F}$. And assume that ${\text{ Hom }_{R}}$ ((3.8), $C'$) is exact for any $C'\in \mathcal {F}.$ Then there exists an exact sequence of $n$-th differential modules

$$\begin{aligned} 0 \rightarrow (M,\delta _{M},n)\xrightarrow {\widetilde{S}}(C^{\oplus n},\alpha ,n)\xrightarrow {\widetilde{T}} (L\oplus C^{\oplus n-1},\delta _{L\oplus C^{\oplus n-1}},n)\rightarrow 0 \end{aligned}$$

(3.9)

where

$$\begin{aligned} \widetilde{S}=(\lambda ,\lambda \delta ,\lambda \delta ^{2},\ldots ,\lambda \delta ^{n-1}), \ \ \ \widetilde{T}=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} h &{} &{} &{} &{} &{} \\ -1 &{} \ddots &{} &{} &{} &{} \\ &{} \ddots &{} \ddots &{} &{} &{} \\ &{} &{}\ddots &{}\ddots &{} &{} \\ &{} &{} &{} \ddots &{} h &{} 0 \\ &{} &{} &{} &{} -1 &{} \pi \\ \end{array} \right) , \end{aligned}$$

$h\in \text{ End }_{R}C$ such that

• (i) $\text{ Hom }_{\text{ Diff }(R, n)}$ ((3.9), $(C'^{\oplus n},\alpha ,n))$ is exact for any $C'\in \mathcal {F}$.

• (ii) $\hbox {Hom}_{R}$ ($X$, (3.8)) is exact if and only if $\text{ Hom }_{\text{ Diff }(R, n)}((X^{\oplus n},\alpha ,n)$, (3.9)) is exact for any $X\in R$-mod.

Proof

The proof is similar to Lemma 3.4. $\square$

By Lemma 3.6, it is easy to see that $\text{ Diff }(R, n)$-mod has enough injective objects.

In the following we denote by $\mathcal {F}^{\delta }$ the family of $n$-th differential modules $(C^{\oplus n},\alpha ,n)$ with $C\in \mathcal {F}.$

Lemma 3.7

Let $(M,\delta _{M},n)\in \text{ Diff }(R, n)$-mod and $\mathcal {F}$ be a family of $R$-modules which is closed under direct sums.

$$\begin{aligned} \cdots \rightarrow C_{2}\xrightarrow {c_{2}}C_{1}\xrightarrow {c_{1}} C_{0}\xrightarrow {c_{0}}M \xrightarrow {} 0 \end{aligned}$$

(3.10)

is a proper $\mathcal {F}$-resolution of the $R$-module $M.$ Denote $M_{i}=\text{ Im }c_{i}$ for $i\ge 0.$ Then there exists a proper $\mathcal {F}^{\delta }$-resolution of the $n$-th differential module $(M,\delta _{M},n)$

$$\begin{aligned} \cdots \rightarrow (Q_{2}^{\oplus n},\alpha ,n)\xrightarrow {q_{2}}(Q_{1}^{\oplus n},\alpha ,n)\xrightarrow {q_{1}} (Q_{0}^{\oplus n},\alpha ,n)\xrightarrow {q_{0}}(M,\delta _{M},n) \xrightarrow {} 0 \end{aligned}$$

(3.11)

such that

• (i) $Q_{i}\simeq \bigoplus \limits _{k=0}^{i}C_{k},\ \ \text{ Ker } q_{i}\simeq Q_{i}\oplus M_{i+1}$ for all $i\ge 0$.

• (ii) $\text{ Hom }_{R}$ ((3.10), $X$) is exact if and only if $\text{ Hom }_{\text{ Diff }(R, n)}$ ((3.11), $(X^{\oplus n},\alpha ,n))$ is exact for any $R$-module $X$.

Proof

We can get $M_{0}=\text{ Im }c_{0}=M$ by the exactness of the sequence (3.10). On the other hand, we have following commutative diagram

(3.12)

where $\lambda _{i}$ are embeddings, $\pi _{i}=c_{i}$ and $\lambda _{i-1}\pi _{i}=c_{i}.$ Obviously,

(3.13)

are exact. Let $C\in \mathcal {F}.$ It is easy to get that

(3.14)

are exact. In particular, we have the following exact sequence

(3.15)

By Lemma 3.4, there exists an exact sequence of $n$-th differential modules

$$\begin{aligned} 0\rightarrow (C_{0}^{\oplus n-1}\oplus M_{1},\delta _{C_{0}^{\oplus n-1}\oplus M_{1}},n)\rightarrow (C_{0}^{\oplus n},\alpha ,n)\rightarrow (M,\delta _{M},n) \rightarrow {} 0 \end{aligned}$$

(3.16)

such that $\text{ Hom }_{\text{ Diff }(R, n)}((C^{\oplus n},\alpha ,n)$, (3.16)) is exact for any $(C^{\oplus n},\alpha ,n)\in \mathcal {F}^{\delta }$. Moreover, $\text{ Hom }_{R}$ ((3.13), $X$) is exact if and only if $\text{ Hom }_{\text{ Diff }(R, n)}$ ((3.16), $(X^{\oplus n},\alpha ,n))$ is exact for any $X\in R$-mod. It is easy to see that the sequence

(3.17)

is exact. Let $C\in \mathcal {F},\ \varphi =\left( \begin{array}{c} P_{1} \\ P_{2} \\ \end{array} \right) \in \text{ Hom }_{R}(C,\ C_{0}\oplus M_{1}).$ There exists $g: C\rightarrow C_{1}$ such that $g\pi _{1}=p_{2}$ by the epimorphism of $\text{ Hom }_{R}(C,\pi _{1})$. Set $\psi =\left( \begin{array}{c} p_{1} \\ g\\ \end{array} \right) .$ Obviously, $\psi \left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} \pi _{1} \\ \end{array} \right) =\varphi .$ Hence, we get the exact sequence

$$\begin{aligned} 0\rightarrow \text{ Hom }(C,M_{2})\rightarrow \text{ Hom }(C,C_{0}\oplus C_{1})\rightarrow \text{ Hom }(C,C_{0}\oplus M_{1}) \rightarrow 0. \end{aligned}$$

(3.18)

Repeating the same process for (3.16) as (3.15), we can obtain the exact sequence

$$\begin{aligned} 0\rightarrow ((C_{0}\oplus C_{1})^{\oplus n-1}\oplus M_{2},\delta ,n)\rightarrow ((C_{0}\oplus C_{1})^{\oplus n},\alpha ,n)\rightarrow (C_{0}\oplus M_{1},\delta ,n) \rightarrow 0. \end{aligned}$$

Take this process successively, we get the exact sequence of $n$-th differential modules

$$\begin{aligned}&0\rightarrow ((C_{0}\oplus \cdots \oplus C_{i})^{\oplus n-1}\oplus M_{i+1},\delta ,n)\rightarrow ((C_{0}\oplus \cdots \oplus C_{i})^{\oplus n},\alpha ,n)\\&\quad \rightarrow (C_{0}\oplus \cdots \oplus C_{i-1}\oplus M_{i},\delta ,n) \rightarrow 0. \end{aligned}$$

Set $Q_{i}=C_{0}\oplus \cdots \oplus C_{i},$ then the above exact sequence becomes

$$\begin{aligned} 0\rightarrow (Q_{i}^{\oplus n-1}\oplus M_{i+1},\delta ,n)\rightarrow ( Q_{i}^{\oplus n},\alpha ,n)\rightarrow (Q_{i-1}\oplus M_{i},\delta ,n) \rightarrow 0 \end{aligned}$$

(3.19)

and satisfies $\text{ Hom }_{\text{ Diff }(R, n)}((C^{n},\alpha ,n)$, (3.19)) is exact for any $C\in \mathcal {F},$ $\text{ Hom }_{R}$ ((3.10), $X$) is exact if and only if $\text{ Hom }_{\text{ Diff }(R, n)}$ ((3.19), $(X^{\oplus n},\alpha ,n))$ is exact for any $X\in \mathcal {F}$. Since $(Q_{i-1}\oplus M_{i},\delta ,n)\hookrightarrow (Q_{i-1}^{\oplus n-1}\oplus M_{i},\delta ,n),$ we get

$$\begin{aligned} \cdots \rightarrow (Q_{i+1}^{\oplus n},\alpha ,n)\rightarrow (Q_{i}^{\oplus n},\alpha ,n)\rightarrow (Q_{i-1}^{\oplus n},\alpha ,n) \rightarrow \cdots \rightarrow (M,\delta ,n) \rightarrow 0 \end{aligned}$$

is exact. This completes the proof. $\square$

Lemma 3.8

Let $(M,\delta _{M},n)\in \text{ Diff }(R, n)$-mod and $\mathcal {F}$ be a family of $R$-modules which is closed under direct sums.

(3.20)

is a proper $\mathcal {F}$-coresolution of the $R$-module $M.$ Denote $M_{i}=\text{ Im }c_{i}$ for $i\ge 0.$ Then there exists a proper $\mathcal {F}^{\delta }$-coresolution of the $n$-th differential module $(M,\delta _{M},n)$

(3.21)

such that

• (i) $Q_{i}\simeq \bigoplus \limits _{k=o}^{i}C_{k},\ \text{ Coker } q_{i}\simeq Q_{i}\oplus M_{i+1}$ for all $i\ge 0$.

• (ii) $\text{ Hom }_{R}$ ($X$, (3.20)) is exact if and only if $\text{ Hom }_{\text{ Diff }(R, n)}((X^{\oplus n},\alpha ,n)$, (3.21)) is exact for any $R$-module $X$.

Proof

The proof is similar to Lemma 3.7. $\square$

Theorem 3.9

Let $(M,\delta _{M},n)\in \text{ Diff }(R, n)$-mod, $X\in R$-mod. Then the following conclusions hold

• (i) $\text{ Ext }_{\text{ Diff }(R, n)}^{i}((M,\delta _{M},n),(X^{\oplus n},\alpha ,n))=0$ $\Longleftrightarrow \text{ Ext }_{R}^{i}(M,X)=0$ for all $i\ge 1$.

• (ii) $\text{ Ext }_{\text{ Diff }(R, n)}^{i}((X^{\oplus n},\alpha ,n),(M,\delta _{M},n))=0$ $\Longleftrightarrow \text{ Ext }_{R}^{i}(X,M)=0$ for all $i\ge 1$.

Proof

Let

(3.22)

be a projective resolution of $R$-module $M$. By Lemma 3.7, there exists a projective resolution of $n$-th differential module $(M,\delta _{M},n)$

(3.23)

such that $\hbox {Hom}_{R}$ ((3.22), $X$) is exact if and only if $\hbox {Hom}_{\text{ Diff }(R, n)}$ ((3.23), $(X^{\oplus n},\alpha ,n))$ is exact. Hence, we can get

$$\begin{aligned}&\mathrm{Ext}_{\mathrm{Diff}(R, n)}^{i}((M,\delta _{M},n),(X^{\oplus n},\alpha ,n))=0\\&\Longleftrightarrow \text{ Hom }_{\text{ Diff }(R, n)}((3.23),(X^{\oplus n},\alpha ,n))\ \text{ is } \text{ exact }\\&\Longleftrightarrow {\text{ Hom }_{R}}((3.22),X)\ \text{ is } \text{ exact }\\&\Longleftrightarrow \text{ Ext }_{R}^{i}(M,X)=0, \end{aligned}$$

where $i\ge 1.$ We finish the proof of statement (i). (ii) is similar to prove. The proof is finished. $\square$

Next we will give the first main theorem of this paper.

Theorem 3.10

Let $(M,\delta _{M},n)$ be an $n$-th differential module. Then we have the following results

• (i) $(M,\delta _{M},n)$ is Gorenstein projective if and only if $M$ is Gorenstein projective as an $R$-module.

• (ii) $(M,\delta _{M},n)$ is Gorenstein injective if and only if $M$ is Gorenstein injective as an $R$-module.

Proof

We first prove the statement (i).

$(\Rightarrow )$ Assume that $(M,\delta _{M},n)$ is a Gorenstein projective $n$-th differential module. Then there exists an exact sequence of projective $n$-th differential modules

(3.24)

such that $(M,\delta _{M},n)\simeq \text{ Im }((P_{0},\delta _{0},n)\rightarrow (P_{-1},\delta _{-1},n))$ and $\hbox {Hom}_{\text{ Diff }(R, n)}$ ((3.24), $(P^{\oplus n},\alpha ,n))$ is exact for any projective $n$-th differential module $(P^{\oplus n},\alpha ,n)$. By Proposition 3.3, we get $\hbox {Hom}_{R}$ ((3.24), $P$) is exact for projective $R$-module $P.$ Hence, $M$ is Gorenstein projective by the definition.

$(\Leftarrow )$ Assume that $M$ is Gorensten projective. We can get an exact sequence of projective modules

$$\begin{aligned} \cdots \xrightarrow {}P_{2}\xrightarrow {}P_{1}\xrightarrow {}P_{0}\xrightarrow {}P_{-1}\xrightarrow {}P_{-2}\xrightarrow {}\cdots \end{aligned}$$

(3.25)

such that $M\simeq \text{ Im }(P_{0}\rightarrow P_{-1})$ and $\hbox {Hom}_{R}$ ((3.25), $P$) is exact for any projective $R$-module $P.$ Hence, we get the following two exact sequences

$$\begin{aligned}&\cdots \xrightarrow {}P_{2}\xrightarrow {}P_{1}\xrightarrow {}P_{0}\xrightarrow {}M\xrightarrow {}0\end{aligned}$$

(3.26)

$$\begin{aligned}&0\xrightarrow {}M\xrightarrow {}P_{-1}\xrightarrow {}P_{-2} \xrightarrow {}P_{-3}\xrightarrow {}\cdots \end{aligned}$$

(3.27)

and $\hbox {Hom}_{R}$ ((3.26), $P$), $\text{ Hom }$ ((3.27), $P$) are exact for any projective $R$-module $P.$ By Lemma 3.7 and Lemma  3.8, we can get the following exact sequences

$$\begin{aligned}&\cdots \xrightarrow {}(Q_{2}^{\oplus n},\alpha ,n)\xrightarrow {}(Q_{1}^{\oplus n},\alpha ,n)\xrightarrow {}(Q_{0}^{\oplus n},\alpha ,n)\xrightarrow {}(M,\delta _{M},n)\xrightarrow {}0\end{aligned}$$

(3.28)

$$\begin{aligned}&0\xrightarrow {}(M,\delta _{M},n)\xrightarrow {}(Q_{-1}^{\oplus n},\alpha ,n)\xrightarrow {}(Q_{-2}^{\oplus n},\alpha ,n) \xrightarrow {}(Q_{-3}^{\oplus n},\alpha ,n)\xrightarrow {}\cdots \end{aligned}$$

(3.29)

where $Q_{i}$ are projective, $\hbox {Hom}_{\mathrm{Diff}(R, n)}$ ((3.28), $(P^{\oplus n},\alpha , n))$ and $\text{ Hom }_{\mathrm{Diff}(R, n)}$ ((3.28), $(P^{\oplus n},\alpha ,n))$ are exact for any projective $n$-th differential module $(P^{\oplus n},\alpha ,n).$ By the exact sequences (3.28) and (3.29), we get an exact sequence of projective $n$-th differential modules

$$\begin{aligned}&\cdots \xrightarrow {}(Q_{2}^{\oplus n},\alpha ,n)\xrightarrow {}(Q_{1}^{\oplus n},\alpha ,n)\xrightarrow {}(Q_{0}^{\oplus n},\alpha ,n)\xrightarrow {}(Q_{-1}^{\oplus n},\alpha ,n)\nonumber \\&\qquad \quad \xrightarrow {}(Q_{-2}^{\oplus n},\alpha ,n) \xrightarrow {}\cdots \end{aligned}$$

(3.30)

such that $(M,\delta _{M},n)\simeq \text{ Im }((Q_{0}^{\oplus n},\alpha ,n)\!\rightarrow \!(Q_{-1}^{\oplus n},\alpha ,n))$ and $\text{ Hom }_{\mathrm{Diff}(R, n)}$ ((3.30), $(P^{\oplus n},\alpha ,n))$ is exact for any projective $n$-th differential module $(P^{\oplus n},\alpha ,n).$ Hence, $(M,\delta _{M},n)$ is a Gorenstein projective $n$-th differential module.

The statement (ii) is similar to prove. This finishes the proof of the theorem. $\square$

Let $M$ be an $R$-module. The Gorenstein projective dimension of $M$, denoted by $\mathrm {Gpd}M$, is defined to be the minimal integer $n$ such that there is an exact sequence $0\rightarrow P_n\rightarrow \cdots \rightarrow P_0\rightarrow M\rightarrow 0$ with all $P_i$’s Gorenstein projective, or $\infty$ if no such exact sequence exists. The Gorenstein injective dimension of $M$, denoted by $\mathrm {Gid}M$, is defined dually. Moreover, the supresum of Gorenstein projective dimensions of all $R$-modules coincides with the supresum of Gorenstein injective dimensions of all $R$-modules, which is called the Gorenstein global dimension of $R$ and is denoted by $\mathrm {Ggd}R$ [2].

We have the following result for these Gorenstein homological dimensions.

Theorem 3.11

Let $(M,\delta _{M},n)$ be an $n$-th differential module, and $p\in \mathbb {Z}^{+}.$

• (i) $\text{ Gpd }\ (M,\delta _{M},n)\le p\Longleftrightarrow \text{ Gpd }\ M\le p.$

• (ii) $\text{ Gid }\ (M,\delta _{M},n)\le p\Longleftrightarrow \text{ Gid }\ M\le p.$

• (iii) $\text{ Ggd }\ \text{ Diff }(R, n)\le p\Longleftrightarrow \text{ Ggd }\ R\le p.$

Proof

We first prove the statement (i).

$(\Rightarrow )$ Assume that $\text{ Gpd }\ (M,\delta _{M},n)\le p$. There exists an exact sequence of $n$-th differential modules

$$\begin{aligned}&\cdots \xrightarrow {}(M_{n},\delta _{M_{n}},n)\xrightarrow {}(P_{n-1}^{\oplus n},\alpha ,n)\xrightarrow {}\cdots \xrightarrow {}(P_{0}^{\oplus n},\alpha ,n)\nonumber \\&\qquad \quad \xrightarrow {}(M,\delta _{M},n)\xrightarrow {}0 \end{aligned}$$

(3.31)

where $(P_{i}^{\oplus n},\alpha ,n)$ are projective $n$-th differential modules, $(M,{\delta _{M}}_{n},n)$ is a Gorenstein projective $n$-th differential module. It is easy to get the following exact sequence of $R$-modules

$$\begin{aligned} 0\xrightarrow {}M_{n}\xrightarrow {}P_{n-1}^{\oplus n}\xrightarrow {}\cdots \xrightarrow {}P_{1}^{\oplus n}\xrightarrow {}P_{0}^{\oplus n}\xrightarrow {}M\xrightarrow {}0 \end{aligned}$$

(3.32)

By Theorem 3.9, we can get $M_{n}$ is Gorenstein projective. Hence, $\text{ Gpd }\ M\le p.$

$(\Leftarrow )$ Assume that $\text{ Gpd }\ M\le p.$ Then there exists an exact sequence

$$\begin{aligned} 0\xrightarrow {}P_{n}\xrightarrow {}P_{n-1}\xrightarrow {}\cdots \xrightarrow {}P_{1}\xrightarrow {}P_{0}\xrightarrow {}M\xrightarrow {}0 \end{aligned}$$

(3.33)

where $P_{n}$ is Gorenstein projective, $P_{n-1},\ldots ,P_{0}$ are projective. By Lemma 3.7, there exists the following exact sequence of $n$-th differential modules

$$\begin{aligned}&0\xrightarrow {}(N_{n},\delta _{N},n)\xrightarrow {}(Q_{n-1}^{\oplus n},\alpha ,n)\xrightarrow {}\cdots \xrightarrow {}(Q_{1}^{\oplus n},\alpha ,n)\xrightarrow {}(Q_{0}^{\oplus n},\alpha ,n)\nonumber \\&\qquad \xrightarrow {}(M,\delta _{M},n)\xrightarrow {}0 \end{aligned}$$

(3.34)

where $Q_{i}$ are projective, and $N_{n}$ is Gorenstein projective. So we can get that $(N_{n},\delta _{N},n)$ is a Gorenstein projective $n$-th differential module. Hence, $\text{ Gpd }\ (M,\delta _{M},n)\le p.$ This finishes (i).

The statement (ii) can be proved in a way similar to (i).

The statement (iii) can be gotten from the definition of Gorenstein global dimension.

This finishes the proof. $\square$