Order-Dual Relational Semantics for Non-distributive Propositional Logics: A General Framework

Abstract

The contribution of this paper lies with providing a systematically specified and intuitive interpretation pattern and delineating a class of relational structures (frames) and models providing a natural interpretation of logical operators on an underlying propositional calculus of Positive Lattice Logic (the logic of bounded lattices) and subsequently proving a generic completeness theorem for the related class of logics, sometimes collectively referred to as (non-distributive) Generalized Galois Logics (GGL’s).

1 Introduction

1.1 Motivation

This article is model-theoretically driven. It’s point of departure is the realization that the relational semantics for non-distributive propositional logics is typically ad hoc and messy and, despite the sometimes ingenuous solutions offered [4, 10, 11, 17, 23, 45], it is perhaps fair to say that it remains non-intuitive and its suitability for intended applications (such as temporal, or dynamic extensions of non-distributive propositional logic) is dubious.

The main contribution of this paper, building on the existing literature, lies with providing a systematically specified and intuitive interpretation pattern and delineating a class of relational structures (frames) and models providing a natural interpretation of logical operators on an underlying propositional calculus of Positive Lattice Logic (PLL, the logic of bounded lattices) and subsequently proving a generic completeness theorem for the related class of logics, sometimes collectively referred to as (non-distributive) Generalized Galois Logics (GGL’s).

GGL’s, introduced by Dunn [15] initially as the logics of distributive lattice expansions (i.e. distributive lattices with additional operators with well-defined monotonicity and distribution, or co-distribution properties) have come to also include the logics of bounded lattice expansions [4, 26, 28–30, 32]. While the algebraic semantics for such systems is well-understood [19–21, 37–39], the relational semantics proposed over the last decade or so for the case where distribution of conjunctions over disjunctions and conversely is not assumed appears to typically lack the necessary intuitive support, witness [8, 23, 45], which is nevertheless precisely the distinctive feature and value of relational semantics, at least when modal and, more specifically, temporal, or dynamic operators are involved. This has been pointed out in [10, 11], where some progress towards a more intuitive and natural semantics has been made.

Order-dual semantics for non-distributive systems [32], an idea rooted [26] in every lattice representation theorem, uses both a satisfaction $\Vdash$ and a co-satisfaction (dual satisfaction, or refutation) relation, designated by the notation $\Vdash ^{\partial }$ in this article. In the standard approach for a classical and even distributive setting, $\Vdash ^{\partial }$ is understood as set complement ($x\Vdash ^{\partial }\varphi ~\text {iff}~x \notin [{\kern -2.3pt}[{\varphi }]{\kern -2.3pt}]$ ) and it therefore coincides with $\nVdash$. In the case of Orthologic, it can be easily seen from the results presented in this article (see also [31]) that dual satisfaction, $x\Vdash ^{\partial }\varphi$, is the same as $x\Vdash \neg \varphi$ and use of $\Vdash ^{\partial }$ becomes thereby redundant. This is no longer the case for systems without an orthonegation operator, but perhaps with weaker forms of negation, and both truth [[φ]] and refutation ((φ) ) sets need to be considered, related by a Galois connection (Sections 1.2 and 2.2). There are a number of logical operators of interest whose intuitive meaning is specifiable in such a semantic setting, including familiar classical operators (necessity, possibility), but also additional ones such as falsifiability, irrefutability, weak forms of implication etc.

In this article, a large class of logical operators is identified (Section 2), specified in terms of generic and intuitive satisfaction and co-satisfaction (refutation) patterns, a natural axiomatization of the corresponding minimal logical systems is proposed (Section 3) and completeness by a traditional canonicity argument is proven (Section 4).

1.2 Preliminaries on Frames and Models

By a Bidirectional K-Algebra (a K _b -algebra) $\mathcal {B}=(B,0,1,\wedge ,\vee ,-,\Box ,\blacklozenge )$ we mean a Boolean algebra with a pair of residuated normal modal operators, i.e. such that for all b ∈ B, $b\leq \Box \blacklozenge b$ and $\blacklozenge \Box b \leq b$ (and $\Box 1=1,\;\blacklozenge 0=0$, by normality).

Lemma 1.1

Given a frame $\mathfrak {F}=(X,R)$ , let λ,ρ be the Galois connection generated by R, after [5], by Eq. 1 , let also $\blacksquare ,\lozenge ,\Box ,\blacklozenge$ be the Jónsson-Tarski image operators [33] generated by the complement $\overline {R}$ of R by Eqs. 2 and 3

$$\begin{array}{@{}rcl@{}} \lambda U & \!\,=\, \{x\;|\; URx\}\,=\,\{x\;|\;\forall u\;(u\in U\;\!\!\!\Longrightarrow\!\!\;uRx)\} & \rho V \;\!\,=\, \{y\;|\; yRV\}\,=\,\{y\;|\;\forall v\;(v\in V\;\!\!\!\Longrightarrow\!\!\!\;yRv)\} \end{array} $$

(1)

$$\begin{array}{@{}rcl@{}} \Box U \!\!&=\!\;\{x\;|\;\forall y\;(x\overline{R} y\;\!\!\Longrightarrow\!\!\!\; y\in U)\} &\blacklozenge U\;\!\,=\, \{x\;|\;\exists y\;(y\overline{R} x\;\text{ and }\;y\in U)\} \end{array} $$

(2)

$$\begin{array}{@{}rcl@{}} \blacksquare U \!\!&=\!\;\{x\;|\;\forall y\;(y\overline{R} x\;\!\!\Longrightarrow\!\!\!\; y\in U)\} & \lozenge U\;\!\,=\,\{x\;|\;\exists y\;(x\overline{R} y\;\text{ and }\;y\in U)\} \end{array} $$

(3)

and let Γ = λρ and Δ = ρλ be the resulting closure operators on the powerset of X. Then

• 1. $(\mathcal {P}(X),\varnothing ,X,\bigcap ,\bigcup ,-,\Box ,\blacklozenge )$ is a complete, concrete and atomic K _b -algebra

• 2. $\lambda \rho ={\Gamma }=\blacksquare \lozenge$ and $\rho \lambda ={\Delta }=\Box \blacklozenge$

• 3. $\blacklozenge \rho A=-A=\overline {\lambda }\lozenge A$ and $\lozenge \lambda D=-D=\overline {\rho }\blacklozenge D$ , for all Γ-stable sets A = ΓA and Δ-stable sets D = ΔD

Proof

• 1) is straighforward, from definitions. For 2), it follows by simple calculation that

  $$\begin{array}{@{}rcl@{}} \lambda\rho U &=& \{x\;|\;(\rho U)Rx\}\qquad = \{x\;|\;\forall y\;(y\in\rho U\Longrightarrow yRx)\}\\ &=& \{x\;|\;\forall y\;(y\overline{R} x \Longrightarrow y\not\in\rho U)\} \\ &=& \{x\;|\;\forall y\;(y\overline{R} x\Longrightarrow \exists z\;(z\in U~\text{ and }~ y\overline{R} z) )\} \> \\ &=& \blacksquare\lozenge U \end{array} $$

Similarly, $\rho \lambda U = \Box \blacklozenge U$. For 3), by simple calculation we obtain $\blacklozenge \rho A=\blacklozenge \Box (-A)=-\blacksquare \lozenge A=-A$ and similarly for a Δ-stable set D. □

Let $\mathcal {G}_{\lambda }(X)$ be the complete lattice of Γ-stable subsets of X and $\mathcal {G}_{\rho }(X)$ the family of Δ-stable subsets. As usual, for a partial order (W, ≤ ), (W, ≤ )^op = (W, ≥ ) stands for the opposite of (W, ≤ ) (order reversed). $\varnothing _{\lambda }$ designates the bottom element of $\mathcal {G}_{\lambda }(X)$, i.e. $\varnothing _{\lambda }=\bigcap \mathcal {G}_{\lambda }(X)$, and similarly for $\varnothing _{\rho }$.

Definition 1.2 (Lattice Frames)

Frames (X, R), with R ⊆ X×X, will be referred to as lattice frames. Their family of propositions is the family $\mathcal {G}_{\lambda }(X)$ of Γ-stable sets, while $\mathcal {G}_{\rho }(X)$ is the family of co-propositions.

We may think of the Galois connection as a pair of quasi-negation operators, mapping a proposition A to a co-proposition ρ A and, conversely, a co-proposition B to a proposition λ B (such that A = λ(ρ A) and B = ρ(λ B)).

To each lattice frame we associate (a) a K _b -algebra structure (bidirectional modal structure), with modal operators generated as the image operators of $\overline {R}$, the complement of R, as well as (b) a dual Galois structure, with the families $\mathcal {G}_{\lambda }(X),\;\mathcal {G}_{\rho }(X)$ of Γ and Δ stable sets, respectively. Letting $\overline {\mathcal {G}_{\lambda }(X)}=\{-A\;|\; A\in \mathcal {G}_{\lambda }(X)\},\; \overline {\mathcal {G}_{\rho }(X)}=\{-B\;|\; B\in \mathcal {G}_{\rho }(X)\}$, the following commutative (given Lemma 1.1) diagram depicts the interaction between the two structures, i.e. the way that modal and Galois maps operate on stable sets.

General lattice frames are structures $\mathfrak {g}=(X,R,\mathfrak {P}_{\lambda })$, with $\mathfrak {P}_{\lambda }$ a sublattice of $\mathcal {G}_{\lambda }(X)$ and we let $\mathfrak {P}_{\rho }=\{\rho A\;|\; A\in \mathfrak {P}_{\lambda }\}$ (which is a sublattice of $\mathcal {G}_{\rho }(X)$). General frames, as the reader recalls, were first introduced by Thomason [46], see e.g. [6] for more details. General frames combine the advantages of algebraic semantics with those of relational, Kripke-style semantics, and we shall prefer to phrase our semantics in general frame terms, where all operators in the dual algebra of the frame are generated by relations that are part of the frame specification.

Notational Conventions

Throughout this article we make the following notational conventions:

• we use a, b, c, d, e for lattice elements and x, y, z, u, v, w for lattice filters

• x _a = a ↑ designates the principal filter generated by the lattice element a

• Γ, Δ are used to designate closure operators, typically on subsets of some set X and we simplify notation by writing Γx for the more accurate Γ({x}), for x ∈ X, and similarly for Δ

• we overload the use of ≤ whose primary use is for the lattice order and write

  • x ≤ y for filter inclusion

  • x ≤ U, where x ∈ X, U ⊆ X as an abbreviation for ∀u ∈ U x ≤ u. Similarly for U ≤ x

  • similarly, we let a ≤ x, for a lattice element a and a filter x, designate the fact that a is a lower bound of the elements in x (i.e. ∀b ∈ x a ≤ b). Note that a ≤ x iff x ≤ x _a (the filter x is contained in the principal filter generated by a)

• [[ ]] and (() ) are used as the representation and dual representation maps, respectively and they are also used for the interpretation and co-interpretation function, simplifying [[[φ]]] to [[φ]], where [φ] is the equivalence class of φ, and similarly for (() ).

2 Distribution Types, Relations and Operators

2.1 Jónsson-Tarski and Generalized Image Operators

The reader will recall that n-ary additive operators (and similarly for multiplicative ones ) on a Boolean algebra are represented in Jónsson-Tarski’s well known representation theorem [33] as image operators of canonical (n + 1)-ary relations on the set $\mathcal {U}$ of ultrafilters of the Boolean algebra defined as shown in Eq. 4

(4)

while the induced image operators are defined on subsets $U_{i}\subseteq \mathcal {U}$ by Eq. 5

(5)

The canonical frame for a Boolean logic whose Lindenbaum-Tarski algebra has the additive operators f _i , i ∈ I is then the frame $\mathfrak {F}=(\mathcal {U}, (R_{i})_{i\in I})$ and the canonical interpretation, assigning to each sentence φ the set of ultrafilters containing its equivalence class (under provability) satisfies the natural semantic clause in Eq. 6, where is an n-ary additive operator and is the corresponding canonical relation R _i and similarly for n-ary multiplicative operators , interpreted with the satisfaction clause (7).

(6)

(7)

For unary modal operators clauses (6, 7) specialize to the familiar satisfaction conditions

(8)

admitting a number of variant intuitive interpretations as alethic, dynamic, doxastic, epistemic, or temporal modalities.

In extending from the Boolean to the merely distributive case, the set $\mathcal {U}$ of ultrafilters is replaced by the set $\mathcal {P}$ of prime filters and otherwise the canonical relations R _i and the corresponding image operators F _i are defined again by Eqs. 4 and 5. The prime filter canonical frame construction, as the reader knows, is identical to the ultrafilter canonical frame construction if the underlying distributive lattice is a Boolean algebra. A number of contributions have appeared in print for the merely distributive case, including Intuitionistic [3, 7, 24, 40, 43] or Relevant Modal Logic [42], as well as semantic treatments of distributive systems with negative modal operators (negation, modally interpreted) [12–14, 16, 48].

Extending to the case of a mere bounded lattice it is possible to provide a representation theorem that reduces to that of distributive lattices when the original lattice happens to be a distributive one [22, 27, 47]. Though the representation of lattice operators on a bounded lattice may be proven in these cases to reduce to the Jónsson-Tarski image operators for appropriate accessibility relations when the bounded lattice happens to be distributive [22, 23], this fails completely when the lattice is non-distributive (e.g. an ortholattice, or an orthomodular lattice) and the resulting relational semantics in [9, 17, 23] appears to have difficulties in providing intuitive relational semantics for intended applications such as temporal, or dynamic extensions of non-distributive propositional logic. For an application motivated approach, it is then preferable to make use of a bounded lattice representation theorem as in [28] that allows for the representation of additional operators as Jónsson-Tarski image operators, thus providing full support to intuitive relational semantics for intended applications (temporal, or dynamic extensions of non-distributive propositional logic). The cost of this approach, it should be clarified, is that it does not reduce to the classical Stone [44] or Priestley [41] representation of distributive lattices when the represented bounded lattice happens to be distributive.

In a recent report [32] based on [28], we have indeed shown that PLL can be extended with n-ary diamonds and m-ary boxes interpreted precisely as in the classical case by the conditions (6, 7), allowing even for a temporal interpretation of modalities in a non-distributive setting as we elaborated in [30]. To construct a canonical model, the lattice representation theorem of [28], reviewed here as Theorem 4.1, is extended, replacing ultrafilters $\mathcal {U}$, or prime filters $\mathcal {P}$ with the set of lattice filters $\mathcal {F}$, a tradition initiated by Goldblatt [25] in his semantic analysis of Orthologic.

With both a satisfaction $\Vdash$ and a co-satisfaction (refutation) relation $\Vdash ^{\partial }$ present, a number of logical operators of interest can be semantically specified. For a first example, consider a falsifiability operator ⋊, which in a distributive logic without classical negation is interpreted in models over frames (X, R ^∗) by the clause $x\Vdash \rtimes \varphi$ iff ∃y (x R ^∗ y and $y\nVdash \varphi )$. It appears to be impossible to prove completeness with this semantic approach in a non-distributive setting and thus an alternative must be sought. One possible way around this problem has been explored in both [9], using polarities (X, Y, R, R _∗) as well as in our own [32], using single-sorted frames (X, R, R _∗) and where in both cases R is used to generate a Galois connection. In each of [9, 32], falsifiability has been interpreted dually as impossibility, by the expected clause $x\Vdash ^{\partial }\rtimes \varphi$ iff $\forall y\;(xR_{*} y\;\longrightarrow \;y\nVdash ^{\partial }\varphi )$ and then the clause for $x\Vdash \rtimes \varphi$ can be derived using the Galois connection and setting $x\Vdash \rtimes \varphi$ iff x ∈ λ((⋊φ) ) iff $\forall y\;(y\Vdash ^{\partial }\rtimes \varphi \;\Longrightarrow \;yRx)$. But perhaps this is not the best possible solution. Indeed, note that in the clause for falsifiability in a distributive setting, $y\nVdash \varphi$ is the same as y∉[[φ]], which in our non-distributive setting is equivalent to $y\in \blacklozenge \,(\!\!\!(\varphi )\!\!\!)$ (Section 1.2).

Intuitively, assuming we had an appropriate accessibility relation R ^∗, the standard clause could be re-written as

$$\begin{array}{@{}rcl@{}} \begin{array}{lll} x\Vdash\rtimes\varphi &\quad \mathrm{ iff } &\;\; \exists y\;(xR^{*} y~\text{ and }~\exists v\;(v\overline{R} y~\text{ and }~v \Vdash^{\varphi}))\\ & \quad\mathrm{ iff } & \;\;\exists v\exists y\;(xR^{*}y~ \text{ and }~ v\overline{R} y~ \text{ and } ~ v\Vdash^{\partial} \varphi)\\ &\quad \mathrm{ iff } & \;\;\exists v\;(xR_{*} v~\text{and}~v\Vdash^{\partial}\varphi) \end{array} \end{array} $$

where we set x R _∗ v iff ∃y (x R ^∗ y and $v\overline {R} y)$ and where $\overline {R}$ is the complement of R.

It then appears that clause (9) is the natural semantic clause for falsifiability in a non-distributive setting, which raises the question whether a completeness theorem for a logic with falsifiability, interpreted by Eq. 9, can be proven.

$$ x\Vdash\rtimes\varphi\;~\mathrm{ iff }\;~\exists y\;(xR_{*} y~\text{ and }~ y\Vdash^{\partial}\varphi) $$

(9)

For another example, a natural notion of irrefutability can be captured by an operator with the semantics below (intuitively, x sees φ as irrefutable iff no $R_{\boxminus }$-successor of x refutes it)

$$ x\Vdash\boxminus\varphi\;\,\mathrm{ iff }\;\,\forall y\;(xR_{\boxminus} y\;\Longrightarrow\; y\nVdash^{\partial}\varphi) $$

(10)

That this is indeed an intuitive notion of irrefutability follows from the fact that, in the setting we have presented in Section 1.2, $-(\!\!\!({\varphi })\!\!\!)=\lozenge [{\kern -2.3pt}[{\varphi }]{\kern -2.3pt}]$ and, therefore, the above clause is equivalent to the following one.

$$ x\Vdash\boxminus\varphi\;\,\mathrm{ iff }\,\;\forall y\;(xR_{\boxminus} y\;\Longrightarrow\; \exists z\;(y\overline{R} z\;\text{ and }\; z\Vdash\varphi)) $$

The question that arises is whether there might be a general semantic pattern, similar to the interpretation pattern for n-ary modalities [6] based on the Jónsson-Tarski representation [33]. This could then form the backbone of Kripke-style semantics [34–36] the role of which in the progress of research in modal logic has been instrumental, replacing the obscurity of existing semantic approaches at the time by an intuitive semantic account. In Fitting’s words [18] “After a rocky start in the first half of the twentieth century, modal logic hit its stride in the second half. [...] Possible-world semantics provided a technical device with intuitive appeal, and almost overnight the subject became something people felt they understood, rightly or wrongly”. It appears, to this author at least, that the situation with the semantics of modal extensions of PLL and, more generally, of lattice-based substructural logics is currently similar to the pre-Kripkean era of modal logic semantics on a classical propositional basis.

In the sequel we build up to a proposal of such a systematic treatment for a large class of logical operators on PLL, semantically specified.

Definition 2.1 (Distribution Types)

A distribution type is an element δ of the set {1, ∂}^{n + 1}, for some n≥0, typically to be written as δ = (i ₁,…, i _n ;i _{n + 1}) and where i _{n + 1} ∈ {1, ∂} will be referred to as the output type of δ. A similarity type τ is a collection of distribution types, τ = {δ ₁,…, δ _k }. We refer to types δ of the form (1,…,1;1) as additive types and to types δ ^′ of the form (∂,…, ∂; ∂) as multiplicative types.

To each distribution type δ = (i ₁,…, i _n ;i _{n + 1}) we associate a pair of relations $R_{\delta },R_{\delta }^{\partial }\subseteq X^{n+1}$ from which generalized image operators are defined (see Definition 2.3).

Remark 2.2 (Notational Convention)

When δ = (i ₁,…, i _n ;1) is of output type 1, we designate the relations by , rather than $R_{\delta },R_{\delta }^{\partial }$. Similarly, if δ = (i ₁,…, i _n ;∂) is of output type ∂, we use the notation R _⊖, $R_{\ominus }^{\partial }$ for $R_{\delta },R_{\delta }^{\partial }$. In other words, R _δ is either, or R _⊖, depending on the output type of δ, and similarly for $R_{\delta }^{\partial }$. The relations (and similarly for $R_{\ominus }, R_{\ominus }^{\partial }$ are used to define a pair of order-dual operators(⊖, ⊖^∂, respectively) and we think of a relation $R_{\delta }^{\partial }$ as the ‘dual’ of the relation R _δ . In the canonical frame construction of Section 4 the two relations $R_{\delta },R_{\delta }^{\partial }$ are literally order-dual (see Eqs. 23 and 24).

Definition 2.3 (Generalized Image Operators)

Let δ = (i ₁,…, i _n ;i _{n + 1}) be a distribution type and $R_{\delta },R_{\delta }^{\partial }\subseteq X^{n+1} (n+1)$-ary relations on a set X. Then Eqs. 11 and 12

(11)

(12)

define the generalized image operators generated by the relations, when δ = (i ₁,…, i _n ;1) is of output type 1, while Eqs. 13 and 14

$$\begin{array}{@{}rcl@{}} \ominus(U_{1},\ldots,U_{n}) \!\!\!&=&\!\!\! \left\{x\;\!|\!\; \forall u_{1},\ldots,u_{n}\;\left( \bigwedge\limits_{j=1{\cdots} n}^{i_{j}=1}(u_{j}\in U_{j})\wedge \bigwedge\limits_{r=1{\cdots} n}^{i_{r}=\partial}(u_{r}\!\in\!\rho U_{r}) \;\!\!\Longrightarrow\!\!\; xR_{\ominus} u_{1}{\cdots} u_{n}\right)\right\} \end{array} $$

(13)

$$\begin{array}{@{}rcl@{}} \ominus^{\partial}(U_{1},\ldots,U_{n}) \!\!\!&=&\!\!\! \left\{x\;\!|\!\; \exists u_{1},\ldots,u_{n}\;\left( xR_{\ominus}^{\partial} u_{1}{\cdots} u_{n}\wedge \bigwedge\limits_{j=1{\cdots} n}^{i_{j}=1}(u_{j}\in \lambda U_{j})\wedge \bigwedge\limits_{r=1{\cdots} n}^{i_{r}=\partial}(u_{r}\!\in\! U_{r})\right)\right\} \end{array} $$

(14)

define them when δ = (i ₁,…, i _n ;∂) is of output type ∂.

The definition of the image operator in Eq. 11 is a generalization of the Jónsson-Tarski additive image operators in a mere distributive setting (lacking a complementation operator), resulting by the addition of the extra conditions that u _r ∈ ρ U _r , whenever i _r = ∂, a case that is captured in a Boolean context by composition with classical negation. For an intuitive reading, the reader may wish to think of U _r as the interpretation of some sentence φ, in which case ρ U _r is its co-interpretation and therefore u _r ∈ ρ U _r is intended to designate the semantic fact $u_{r}\Vdash ^{\partial }\varphi$, which in a distributive setting is identical to $u_{r}\nVdash \varphi$.

In [30, 32] we have shown how to model the necessity operator (unary, or n-ary) in a non-distributive context while adhering to the classical relational interpretation (7). Equation 13 defines the order-dual of a generalized ‘diamond’ operator, defined with Eq. 11. Interestingly enough, this is not a necessity operator, but rather a generalized irrefutability operator, when specialized to a distribution type of the form δ = (∂,…, ∂; ∂). The reader may wish to take a look at this point at the last example in 2.1, with Eqs. 19 and 20 comparing necessity and irrefutability side-by-side. The reader is reminded that in a distributive context and with semantics based on prime filters $\Vdash ^{\partial }$ coincides with $\nVdash$ and hence $x\Vdash ^{\partial }\varphi$ is the same as $x\Vdash \varphi$ in the distributive case and, thereby, necessity and irrefutability coincide. But this is not necessarily the case in a non-distributive setting, at least in the approach taken in this article. In other words, truth and refutation sets are related in the standard approach to the semantics of distributive logics by ((φ) ) = −[[φ]] whereas, as discussed in Section 1.2, in the non-distributive case ((φ) ) = ρ([[φ]]) and [[φ]] = λ((φ) ) (see also Definition 2.8 of lattice frames and models). Therefore, in the absence of both an orthonegation operator and of distributivity, it appears that more subtle notions can be semantically captured, such as a distinction between necessity and irrefutability.

Definition 2.4 (τ -Frames)

Let τ = 〈δ ₁,…, δ _k 〉 be a similarity type and recall the notational convention made in Remark 2.2. A τ-frame$\mathfrak {F}_{\tau }=(X,R,(R_{\delta },R_{\delta }^{\partial })_{\delta \in \tau })$ is a lattice frame (X, R) together with a pair of relations $R_{\delta },R_{\delta }^{\partial }\subseteq X^{n+1}$, for each δ ∈ τ, where n + 1 = ℓ(δ) is the length of δ = (i ₁,…, i _n ;i _{n + 1}). For each δ _∨ = (i ₁,…, i _n ;1)∈τ of output type 1, and where is its corresponding relation pair we let be the generalized image operators generated by , respectively, defined by Eqs. 11 and 12. Similarly, for each δ _∧ = (i ₁,…, i _n ;∂)∈τ of output type ∂ and where $(R_{\ominus },R_{\ominus }^{\partial })$ is its corresponding relation pair we let ⊖,⊖^∂ be the generalized image operators generated by $R_{\ominus },R_{\ominus }^{\partial }$, respectively, defined by Eqs. 13 and 14. The following requirements are placed on the operators of the frame.

• 1. $\mathcal {G}_{\lambda }(X)$ is closed under the operators , while $\mathcal {G}_{\rho }(X)$ is closed under the operators .

• 2. the operators and the operators ⊖, ⊖^∂ are order-dual, i.e. they are interdefinable by means of the Galois connection generated by the binary relation R of the frame. More specifically, for any sets $A_{1},\ldots ,A_{n}\in \mathcal {G}_{\lambda }(X)$ and any $D_{1},\ldots ,D_{n}\in \mathcal {G}_{\rho }(X)$ the following two (equivalent) conditions hold: , . Similarly, the following two (equivalent) conditions hold: ⊖(A ₁,…, A _n ) = λ(⊖^∂(ρ A ₁,…, ρ A _n )) and ⊖^∂(D ₁,…, D _n ) = ρ(⊖(λ D ₁,…, λ D _n )).

A general τ-frame$\mathfrak {g}_{\tau }=(X,R,(R_{\delta },R_{\delta }^{\partial })_{\delta \in \tau },\mathfrak {P}_{\lambda })$ is a frame with a distinguished sublattice $\mathfrak {P}_{\lambda }\subseteq \mathcal {G}_{\lambda }(X)$ such that restrict to operators of the respective distribution type on $\mathfrak {P}_{\lambda }$ and similarly for , and $\mathfrak {P}_{\rho }$.

Definition 2.4 includes the case of main focus in this article, where in each argument place operators either distribute, or co-distribute over either joins, or meets, always returning the same type of operator, i.e. either uniformly a join, or uniformly a meet. But it also includes the case of quasi-normal operators that may fail to distribute over either joins or meets in some argument place, being merely monotone or antitone at that place. An example of such an operator was studied in [32] and it is an operational notion of implication, semantically weakened to the requirement that φ− ◇ψ holds at some state iff after any successful confirmation of φ, the conclusion ψ becomes verifiable in the resulting state.

Remark 2.5

(τ-Frames and Ordinary Kripke Frames) Kripke frames are instances of τ-frames. Indeed, since every subset of a Kripke frame is a proposition, it must be that the closure operator induced by the frame relation is the identity operator. This is achieved simply by considering the relation x R y iff x ≠ y. The reader can easily verify that each of λ, ρ is the set-complement operator so that any subset U ⊆ X is Γ-stable, simply because ΓU = λ ρ U = −−U = U.

For a distribution type δ and its associated relation pair $R_{\delta },R_{\delta }^{\partial }$ it follows from the above definition of the dual operators and ⊖, ⊖^∂, given that in the case of Kripke frames the Galois connection involved is defined by set-complementation, that (and similarly for ⊖^∂) is the classical dual of , since the condition in Definition 2.4 reduces to . Given this identity and the definitions of (and similarly for ⊖, ⊖^∂) we obtain after some obvious logical manipulation that

We may then simply take , given also the fact that it is desirable in the classical setting to interpret dual operators by the same accessibility relation.

In the next definition the intended meaning of distribution types is clarified and it is what the reader has no doubt anticipated.

Definition 2.6 (Normal Operators)

Following [33], an n-ary monotone operator $\mathfrak {f}:\mathcal {L}^{n}\longrightarrow \mathcal {L}$ will be called additive if it distributes over joins of $\mathcal {L}$ in each argument place. More generally, if $\mathcal {L}_{1},\ldots ,\mathcal {L}_{n}, \mathcal {L}$ are bounded lattices, then a monotone function $\mathfrak {f}:\mathcal {L}_{1}\times \cdots \times \mathcal {L}_{n}\longrightarrow \mathcal {L}$ is additive, if for each i, $\mathfrak {f}$ distributes over binary joins of $\mathcal {L}_{i}$, i.e. $\mathfrak {f}(a_{1},\ldots ,a_{i-1},b\vee d,a_{i+1},\ldots ,a_{n})=\mathfrak {f}(a_{1},\ldots ,a_{i-1},b,a_{i+1},\ldots ,a_{n})\vee \mathfrak {f}(a_{1},\ldots ,a_{i-1},d,a_{i+1},\ldots ,a_{n})$.

As a matter of notation, we write $\mathcal {L}^{1}$ for $\mathcal {L}$ and $\mathcal {L}^{\partial }$ for its opposite lattice (where order is reversed, usually designated as $\mathcal {L}^{op}$). Similarly, ≤ ^∂ designates the opposite order.

An n-ary operator $\mathfrak {f}$ on a lattice $\mathcal {L}$ is normal [28] if it is an additive function $\mathfrak {f}:\mathcal {L}^{i_{1}}\times \cdots \times \mathcal {L}^{i_{n}}\longrightarrow \mathcal {L}^{i_{n+1}}$, where each i _j , for j = 1,…, n, n + 1, is in the set {1, ∂}, i.e. $\mathcal {L}^{i_{j}}$ is either $\mathcal {L}$, or $\mathcal {L}^{\partial }$. For a normal operator $\mathfrak {f}$ on $\mathcal {L}$, its distribution type is the (n + 1)-tuple $\delta (\mathfrak {f})=(i_{1},\ldots ,i_{n};i_{n+1})$.

An n-ary operator that may fail the additivity condition in some (though not in all) argument place will be referred to as a partial normal, or quasi-normal operator and its type will be designated by a sequence $\mu =\mu (\mathfrak {f})=(i_{1},\ldots ,\underline {i_{j}},\ldots ,i_{n};i_{n+1})$ indicating the position(s) where additivity fails by an underbar.

Each of the operators , is an operator in the K _b -algebra associated to the underlying lattice frame of a τ-frame.

Lemma 2.7

• 1. In the generalized image operators have the monotonicity properties corresponding to their respective type δ

• 2. If δ is of output type 1, then for each j = 1,…,n such that i _j = 1, the operator 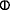distributes over arbitrary unions of sets. In particular then, if δ = (1,…,1;1) is an additive type, then is a completely additive operator in K _b (X,R)

• 3. If δ is of output type ∂, then for each j = 1,…,n such that i _j = 1, the operator ⊖ co-distributes over arbitrary unions of sets, turning them to intersections.

• 4. If δ is of output type 1, then for each j = 1,…,n such that i _j = ∂, the inclusion holds, where only the argument at the j-th place is displayed

• 5. If δ is of output type ∂, then for each j = 1,…,n such that i _j = ∂, the inclusion $\ominus (\ldots ,\bigcap _{k}W_{j_{k}},\ldots )\subseteq \bigcap _{k}\ominus (\ldots ,W_{j_{k}},\ldots )$ holds.

Proof

For 1), we need to show that are monotone/antitone at the j-th position, accordingly as i _j = i _{n + 1}, or i _j ≠i _{n + 1}. In the sequel we let U _{< j} abbreviate the sequence U ₁,…, U _j−1 and similarly for U _>j and U _{j + 1},…, U _n .

For , with δ of output type i _{n + 1} = 1, assume that i _j = 1 = i _{n + 1} and that U ⊆ V. To show that , let . By definition, there exist u ₁,…, u _n such that, , for each s ∈ {1,…, n} such that i _s = 1, and u _r ∈ ρ U _r , for each r ∈ {1,…, n} such that i _r = ∂. In particular, u _j ∈ U ⊆ V. Then it follows from the definition that . Hence is monotone at the j-th position in this case. If i _j = ∂ ≠ 1 = i _{n + 1} and , let again u ₁,…, u _n be such that , for each s ∈ {1,…, n} such that i _s = 1, and u _r ∈ ρ U _r , for each r ∈ {1,…, n} such that i _r = ∂. Then in particular, u _j ∈ ρ V and since U ⊆ V, by assumption, it follows that u _j ∈ ρ V ⊆ ρ U. Hence and therefore is antitone at the j-th position in that case.

For ⊖, with δ of output type ∂, assume that i _j = 1≠i _{n + 1} and that U ⊆ V. To show that ⊖(U _{< j} , V, U _>j )⊆⊖(U _{< j} , U, U _>j ), let x ∈ ⊖(U _{< j} , V, U _>j ). To show that x ∈ ⊖(U _{< j} , U, U _>j ) let u ₁,…, u _n be any points such that u _s ∈ U _s , for each s ∈ {1,…, n} such that i _s = 1, and u _r ∈ ρ U _r , for each r ∈ {1,…, n} such that i _r = ∂. In particular, u _j ∈ U ⊆ V and then since we assume that x ∈ ⊖(U _{< j} , V, U _>j ) it follows from the definition of the operator that x R _⊖ u ₁⋯u _n . Hence we may conclude that x ∈ ⊖(U _{< j} , U, U _>j ). Next suppose that i _j = ∂ = i _{n + 1} and assume that x ∈ ⊖(U _{< j} , U, U _>j ). Given any u ₁,…, u _n such that u _s ∈ U _s , for each s ∈ {1,…, n} such that i _s = 1, and u _r ∈ ρ U _r , for each r ∈ {1,…, n} such that i _r = ∂ and where in particular u _j ∈ ρ V, it follows that u _j ∈ ρ U and since x ∈ ⊖(U _{< j} , U, U _>j ), by assumption, the definition implies that x R _⊖ u ₁⋯u _n . Therefore, x ∈ ⊖(U _{< j} , V, U _>j ).

For 2), one direction follows from the monotonicity properties of part 1), verified by the above arguments. It remains to show that , when i _j = 1).

Assuming , let u ₁,…, u _n be such that , for each s ∈ {1,…, n} such that i _s = 1, and u _r ∈ ρ U _r , for each r ∈ {1,…, n} such that i _r = ∂. In particular, $u_{j}\in \bigcup _{k}W_{k}$, hence u _j ∈ W _k , for some k, from which it follows that and thereby .

For 3), one direction is a consequence of the monotonicity properties and we only need to verify that $\bigcap _{k}\ominus (U_{<j},W_{k},U_{>j})\subseteq \ominus (U_{<j},\bigcup _{k}W_{k},U_{>j})$.

Assuming x ∈ ⊖(U _{< j} , W _k , U _>j ), for all k, let u ₁,…, u _n be any points such that $\bigwedge _{i_{s}=1}u_{s}\in U_{s}$ and $\bigwedge _{i_{r}=\partial }u_{r}\in \rho U_{r}$. In particular, under the assumption that i _j = 1 and given that $U_{j}=\bigcup _{k}W_{k}$, there is some k such that u _j ∈ W _k . Since x ∈ ⊖(U _{< j} , W _k , U _>j ), for all k, it follows that x R _⊖ u ₁⋯u _n . Therefore $x\in \ominus (U_{<j},\bigcup _{k}W_{k},U_{>j})$.

4) and 5) follow by the monotonicity properties of , verified in part 1). □

2.2 Interpretation Patterns and Models

The language of PLL is generated by the schema L∋φ: = p (p ∈ P)|⊤|⊥|φ∧φ|φ∨φ, where P is a countable, non-empty set of propositional variables and we use ∨ to designate disjunction. Axioms and rules are stated below in the form of a symmetric consequence system (a single sentence on each side of the turnstile).

Definition 2.8 (Lattice Models)

Given a Lattice Frame $\mathfrak {F}=(X,R)$, where R ⊆ X×X, a Lattice Model $\mathfrak {M}=(\mathfrak {F},V)$ is a frame together with an admissible valuation V = (V ₁, V ₂) consisting of a pair of valuations $V_{1}:P\longrightarrow \mathcal {G}_{\lambda }(X)$ and $V_{2}:P\longrightarrow \mathcal {G}_{\rho }(X)$ such that V ₁(p) = λ V ₂(p) and V ₂(p) = ρ V ₁(p).

An interpretation [[ ]] and co-interpretation (or refutation) (() ) is a pair of functions extending V ₁, V ₂, respectively, to all sentences of the language and subject to the conditions in Table 1, together with the constraint that for all φ, [[φ]] = λ((φ) ) and ((φ) ) = ρ[[φ]]], i.e. all triangles in the diagram in Table 1 commute (where $\mathcal {L}$ is the Lindenbaum-Tarski algebra of PLL).

Table 1 Interpretation and dual interpretation

A model on a general lattice frame $\mathfrak {g}$ is a pair $\mathfrak {M}=(\mathfrak {g},V)$ where V is an admissible valuation as previously detailed, but with the additional requirement that for every propositional variable p, $\;V_{1}(p)\in \mathfrak {P}_{\lambda }$ and then also $V_{2}(p)\in \mathfrak {P}_{\rho }$. The satisfaction $\Vdash$ and co-satisfaction $\Vdash ^{\partial }$ relations are defined by $x\Vdash \varphi$ iff x ∈ [[φ]] and $x\Vdash ^{\partial }\varphi$ iff x ∈ ((φ) ).

A sentence φ is (dually) satisfied in a model $\mathfrak {M}=(\mathfrak {F},V)=((X,R),V)$ if there is a world x ∈ X such that $x\Vdash \varphi$ (respectively, $y\Vdash ^{\partial }\varphi$, for some y ∈ X). It is (dually) valid in $\mathfrak {M}$ iff it is satisfied (respectively, dually satisfied) at all worlds x ∈ X (respectively, at all y ∈ X). Similarly for a model $\mathfrak {M}=(\mathfrak {g},V)$ on a general frame $\mathfrak {g}$.

A sequent φ ⊩ ψ is valid in a model $\mathfrak {M}$ iff for every world x of $\mathfrak {M}$, if $x\Vdash \varphi$, then $x\Vdash \psi$. Equivalently, the sequent is valid in the model $\mathfrak {M}$ iff for every world y, if $y\Vdash ^{\partial }\psi$, then $y\Vdash ^{\!\!\partial }\!\!\varphi$. The sequent is valid in a frame $\mathfrak {f}$ if it is valid in every model $\mathfrak {M}$ based on the frame $\mathfrak {f}$. Similarly for a model $\mathfrak {M}=(\mathfrak {g},V)$ on a general frame $\mathfrak {g}$. Finally, we say that the sequent is valid in a class $\mathbb {F}$ of (general) frames iff it holds in every frame in $\mathbb {F}$.

Given the interpretation and co-interpretation functions and the conditions in Table 1, the satisfaction $\Vdash$ and dual satisfaction (co-satisfaction, refutation) $\Vdash ^{\partial }$ relations from worlds to sentences are defined as in Table 2, so that $[{\kern -2.3pt}[{\varphi }]{\kern -2.3pt}] =\{x\in X\;|\; x\Vdash \varphi \}$ and $(\!\!\!(\varphi )\!\!\!)=\{x\in X\;|\; x\Vdash ^{\partial }\varphi \}$.

Table 2 Satisfaction and dual satisfaction relations

Soundness of PLL is straightforward to prove and the interested reader need only observe that for any sentence φ its interpretation [[φ]] is a Γ-stable set, while its co-interpretation ((φ) ) is Δ-stable.

Definition 2.9 (Propositional τ -Languages)

The propositional language of τ-frames is the extension PLL _τ of the language of PLL with an n-ary operator ○^δ for each δ ∈ τ. Explicitly, sentences are generated by the grammar φ: = p (p ∈ P) | ⊤ | ⊥ | φ∧φ | φ∨φ | ○^δ (φ,…, φ) (δ ∈ τ).

We next specify a natural and uniform interpretation pattern for τ-languages, interpreted over τ-frames.

Definition 2.10

A model $\mathfrak {M}=(\mathfrak {g},V)$ on a general τ-frame $\mathfrak {g}$ is a lattice model (on the underlying general lattice frame) in the sense of Definition 2.8 where the satisfaction and co-satisfaction relations are subject to the following additional conditions, where we make the convention to write for ○^δ when δ = (i ₁,…, i _n ;1) is of output type 1 and we write ⊖^δ, respectively, when δ = (i ₁,…, i _n ;∂) is of output type ∂.

(15)

(16)

$$ \begin{array}{lll} x\!\Vdash\! \ominus^{\delta}(\varphi_{1},\ldots,\varphi_{n}) \!\!\!&~\mathrm{ iff }~&\!\! \forall u_{1},\ldots,u_{n}\;(\bigwedge\limits_{j\,=\,1\cdots n}^{i_{j}\,=\,1}(u_{j}\!\Vdash\!\varphi_{j})\!\wedge\! \bigwedge\limits_{r\,=\,1{\cdots} n}^{i_{r}\,=\,\partial}(u_{r}\Vdash^{\partial}\varphi_{r}) \;\!\!\Longrightarrow\!\!\; xR_{\ominus} u_{1}{\cdots} u_{n}) \end{array} $$

(17)

$$ \begin{array}{lll} x\Vdash^{\partial} \ominus^{\delta}(\varphi_{1},\ldots,\varphi_{n}) &~\mathrm{ iff }~& \exists u_{1},\ldots,u_{n}\;(xR_{\ominus}^{\partial} u_{1}{\cdots} u_{n}\wedge \bigwedge\limits_{j=1\cdots n}^{i_{j}=1}(u_{j}\Vdash\varphi_{j})\\ &&\quad\quad\quad\quad\quad\quad \wedge \bigwedge\limits_{r=1\cdots n}^{i_{r}=\partial}(u_{r}\Vdash^{\partial}\varphi_{r}))\\ \end{array} $$

(18)

Satisfaction and validity are defined as in lattice models (Definition 2.8).

Example 2.1

We present some cases of interest for the operators:

• If δ = (1; 1), then Eq. 15 specializes to the clause

  

  so that is a unary diamond operator $\lozenge$. Similarly, is an n-ary diamond operator with the familiar satisfaction clause, since the satisfaction clause in the above definition reduces to the clause in Eq. 6. In particular, the distribution type δ = (1,1;1) corresponds to the binary diamond operator known as the fusion operator in substructural and relevance logics.

• If δ = (∂; 1), then is the falsifiability operator we discussed in motivating the present section. Indeed, the satisfaction clause (15) provided above becomes

  

  In words, φ is falsifiable at x iff it is refuted at some successor state u of x.

• If δ = (1;∂), then ⊖^1;∂ is an impossibility operator, i.e. a modally interpreted negation operator ∼ whose semantics in a distributive setting (using an accessibility relation R ^∗, see e.g. [14]) is provided by the clause $x\Vdash \sim \varphi$ iff $\forall u\;(xR^{*} u\;\Longrightarrow \; u\nVdash \varphi )$.

  That this is indeed the case for δ = (1;∂) can be seen from the respective clause (17) instantiated below, where $\overline {R}_{\ominus ^{1;\partial }}$ is the complement of $R_{\ominus ^{1;\partial }}$

  $$x\Vdash \ominus^{1;\partial}\varphi\,\;\mathrm{ iff }\,\;\forall u\;(u\Vdash\varphi\;\Longrightarrow\;xR_{\ominus^{1;\partial}}u) ~\,\mathrm{ iff }~\,\forall u~(x\overline{R}_{\ominus^{1;\partial}}u\;\Longrightarrow\;u\not\Vdash\varphi) $$

• If δ = (∂; ∂) then the respective clause (17) reads as follows

  $$x\Vdash\ominus^{\partial;\partial}\varphi\;~\mathrm{ iff }\;~\forall u\;(u\Vdash\varphi\;\Longrightarrow\;xR_{\ominus^{\partial;\partial}}u) \;~\mathrm{ iff }\;~ \forall u\;(x\overline{R}_{\ominus^{\partial;\partial}}u\;\Longrightarrow\;u\nVdash^{\partial}\varphi) $$

  which is precisely the irrefutability operator we also discussed in motivating the present section.

• If δ = (1, ∂; ∂), then ⊖^{1, ∂; ∂} = −◇ is an implication operator, with satisfaction clause instantiating (17),

  $$\begin{array}{@{}rcl@{}} x\Vdash\varphi -\!\diamond\psi~\;\mathrm{ iff }\; ~\forall u,&& \!\!\!\!v\;(u\Vdash\varphi\text{ and }v\Vdash^{\partial}\psi\;\Longrightarrow x R_{-\!\diamond}uv)\;~\mathrm{ iff }\;~ \\\forall u, &&\!\!\!\!v\;(x\overline{R}_{-\!\diamond}uv \text{ and } u\Vdash\varphi\;\Longrightarrow v\nVdash^{\partial}\psi) \end{array} $$

  which we treated in [32] and as noted there it resembles the clause for Relevant implication [1, 2], except for replacing satisfaction of the conclusion at v by its non-refutation. Co-satisfaction is specified by the following clause, instantiating (9)

  $$x\Vdash^{\partial}\varphi {-\!\diamond}\psi\;~\mathrm{ iff }\;~ \exists u,v\;(xR_{-\!\diamond}uv\text{ and }u\Vdash\varphi, \text{ but }v\Vdash^{\partial}\psi) $$

  which is the natural analogue of a clause for negated implication.

• For δ = (∂,1;∂), the operator ⊖^δ = ⊖^∂,1;∂ is a reverse implication ◇–, as the reader can easily see by instantiating the corresponding satisfaction clause (17).

• The case δ = (∂, ∂; ∂) corresponds to a binary non co-refutability operator, with semantic clause (instantiating (17) and after contraposition and writing ⊘ for ⊖^{∂, ∂; ∂})

  $$\begin{array}{@{}rcl@{}} x\Vdash\varphi\oslash\psi~\,\mathrm{ iff }~\,\forall u,&&\!\!\! v\;(x\overline{R}_{\oslash}uv\;\Longrightarrow\;(u\nVdash^{\partial}\varphi\text{ or }v\nVdash^{\partial}\psi))~ \,\mathrm{ iff }~\,\\\forall u, && \!\!\!v\;(x\overline{R}_{\oslash}uv\text{ and }u\Vdash^{\partial}\varphi\;\Longrightarrow\;v\nVdash^{\partial}\psi) \end{array} $$

  It is interesting to note that the order-dual of an n-ary diamond, of distribution type δ = (1,…,1;1), is the n-ary non co-refutability operator and the difference with n-ary box is shown in their respective satisfaction clauses, listed side-by-side in Eqs. 19 and 20, where we write $\boxtimes$ for ⊖^{∂⋯∂; ∂}.

  

  (19)
  $$\begin{array}{@{}rcl@{}} x\Vdash\boxtimes(\varphi_{1},\ldots,\varphi_{n}) & \quad\mathrm{ iff } \quad& \forall u_{1}{\cdots} u_{n}\;(xR_{\boxtimes} u_{1}{\cdots} u_{n}\;\Longrightarrow\; \bigvee\limits_{r=1{\cdots} n}(u_{r}\nVdash^{\partial}\varphi_{r}))\\ \end{array} $$

  (20)

3 Logics of Bounded Lattice Expansions

Let $\mathcal {L}=(L,\wedge ,\vee ,0,1)$ be a bounded lattice and PLL designate Positive Lattice Logic (the propositional logic of bounded lattices).

Definition 3.1

A lattice expansion is a structure $\mathcal {L}=(L,\wedge ,\vee ,0,1,(\mathfrak {f}_{i})_{i\in k})$ where k>0 is a natural number and for each i ∈ k, $\;\mathfrak {f}_{i}$ is a normal operator on $\mathcal {L}$ of some specified arity $\alpha (\mathfrak {f}_{i})\in \mathbb {N}^{+}$ and distribution type δ(i). The similarity type of $\mathcal {L}$ is the k-tuple $\tau (\mathcal {L})=\langle \delta (0),\ldots ,\delta (k-1)\rangle$. Where τ is a similarity type, $\mathbb {L}_{\tau }$ is the class of lattice expansions of similarity type τ.

Bounded modal lattices implicative lattices (L,∧,∨,0,1, →), ortholattices (L, ∧, ∨, 0, 1, ¬) and residuated lattices (L,∧,∨,0,1,←,∘,→) are examples of normal bounded lattice expansions. The similarity type of residuated lattices is the type τ = 〈(∂,1;∂), (1, 1; 1), (1, ∂; ∂)〉 and analogously for the other cases.

Definition 3.2

For a given similarity type τ, the minimal inequational theory of $\mathbb {L}_{\tau }$ is the theory $\mathcal {E}_{0}(\tau )$ in the first-order language with equality $\mathcal {L}(\leq )$ of partial orders whose axioms are the following:

• Equality and partial order axioms

• Bounded lattice axioms

• For each n-ary normal operator $\mathfrak {f}:\mathcal {L}^{i_{1}}\times \cdots \times \mathcal { L}^{i_{n}}\longrightarrow \mathcal {L}^{i_{n+1}}$ of distribution type δ

  • Monotonicity rules: $\frac {a\leq ^{i_{j}}b}{\mathfrak {f}(\ldots ,a,\ldots )\leq ^{i_{n+1}}\mathfrak {f}(\ldots ,b,\ldots )}$, for each j = 1,…, n and where ≤ ¹ = ≤ and ≤ ^∂ = ≥

  • Distribution axioms: $\mathfrak {f}(\ldots ,a\vee ^{i_{j}}b,\ldots )=\mathfrak {f}(\ldots ,a,\ldots )\vee ^{i_{n+1}}\mathfrak {f}(\ldots ,b,\ldots )$, where ∨¹ = ∨ and ∨^∂ = ∧.

An inequational theory $\mathcal {E}(\tau )$ for $\mathbb {L}_{\tau }$ is any superset of $\mathcal {E}_{0}(\tau )$ in the first-order language $\mathcal {L}(\leq )$ of partial orders.

For example, the normal modal theory $\mathcal {E}(\langle \ldots ,(1;1),(\partial ;\partial )\ldots \rangle )$ will include the normality axioms and for the unary normal possibility and necessity operators.

Definition 3.3

For a given similarity type τ, the propositional language L(τ) for $\mathbb {L}_{\tau }$ is the τ-language of Definition 2.9, generated by the grammar: φ: = p (p ∈ P)|⊤|⊥|φ∧φ|φ∨φ|○^δ (φ,…, φ) (for each δ ∈ τ), where P is a countable, nonempty set of propositional variables. The minimal propositional logic Λ₀(τ) (or PLL _τ ) is the extension of PLL, axiomatized by the axioms and rules below

with, in addition,

• a monotonicity rule R _i for each i ∈ k: $\frac {\varphi _{1}\vdash ^{i_{1}}\psi _{1} \,\, {\cdots } \,\, \varphi _{\alpha (i)}\vdash ^{i_{\alpha (i)}}\psi _{\alpha (i)}}{\bigcirc ^{\delta }(\varphi ^{\prime }_{1},\ldots ,\varphi ^{\prime }_{\alpha (i)}) \vdash ^{i_{\alpha (i)+1}} \bigcirc ^{\delta }\!(\psi ^{\prime }_{1},\ldots ,\psi ^{\prime }_{\alpha (i)})}$, where α(i) is the arity of ○^δ, for each j = 1,…, α(i), $\;\varphi _{j}\vdash ^{i_{j}}\psi _{j}$ stands for φ _j ⊩ψ _j if i _j = 1 and it stands for ψ _j ⊩φ _j if i _j = ∂ and similarly for the conclusion of the rule, while $\varphi ^{\prime }_{j}=\varphi _{j}$ and $\psi ^{\prime }_{j}=\psi _{j}$ if i _j = 1 and $\varphi ^{\prime }_{j}=\psi _{j}$ and $\psi ^{\prime }_{j}=\varphi _{j}$ if i _j = ∂

• distribution axioms ${D_{i}^{j}}$ for each i ∈ k and each j = 1,…, α(i):

  $$\begin{array}{@{}rcl@{}} &&\bigcirc^{\delta}\!(\varphi_{1},\ldots,\zeta{\vee}^{i_{j}}\xi,\ldots,\varphi_{\alpha(i)}) \vdash^{\alpha(i)+1} \bigcirc^{\delta}\!(\varphi_{1},\ldots,\zeta,\ldots,\varphi_{\alpha(i)}) {\vee}^{\alpha(i)+1}\\ &&\bigcirc^{\delta}\!(\varphi_{1},\ldots,\xi,\ldots,\varphi_{\alpha(i)}) \end{array} $$

  where the same convention as above applies to the superscripted turstile and the superscripted ∨^r is ∨ if the superscript r = 1 and it is ∧ if the superscript r = ∂.

Notation is perhaps awkward, but the idea is really simple, as an example or two will show. Indeed, consider first the case of implication →, of distribution type (1, ∂; ∂). The monotonicity rule, literally transcribed, is the rule $\frac {\varphi \vdash ^{1}\varphi ^{\prime } \quad \psi \vdash ^{\partial }\psi ^{\prime }}{\varphi \rightarrow \psi \vdash ^{\partial }\varphi ^{\prime }\rightarrow \psi ^{\prime }}$ which, given the above notational conventions, is exactly the familiar rule $\frac {\varphi \vdash \varphi ^{\prime } \quad \psi ^{\prime }\vdash \psi }{\varphi ^{\prime }\rightarrow \psi ^{\prime }\vdash \varphi \rightarrow \psi }$ and similarly for co-distribution over joins in the first and distribution over meets in the second position. For an n-ary diamond operator, whose distribution type is (1,…,1;1), all superscripted turnstiles in the monotonicity rule are plain turnstiles. The same is true of the distribution rule, where in addition ∨¹ = ∨. For an n-ary box operator , whose type is (∂,…, ∂; ∂), after following through with the notational convention the monotonicity rule becomes . For the distribution axiom, note first that ∨^∂ = ∧ and given also the notational convention on the superscripted turnstile the axiom becomes the familiar one , where we only displayed the sentence at the j-place (any j = 1,…, n).

Given the way we defined the minimal logic Λ₀(τ) as a symmetric consequence system, with axioms and rules being a direct syntactic copy of the axioms and rules of the minimal inequational theory $\mathcal {E}_{0}(\tau )$, the following is no surprise.

Theorem 3.4

The Lindenbaum-Tarski algebra of the logic Λ ₀ (τ) is an algebra in the class $\mathbb {L}_{\tau }$.

As a consequence, we derive an algebraic soundness and completeness result for the minimal logic Λ₀(τ).

Corollary 3.5 (Algebraic Soundness and Completeness)

Λ ₀ (τ) is sound and complete in the class $\mathbb {L}_{\tau }$ of bounded lattice expansions by normal operators, for each similarity type τ.

τ-languages are interpreted (Definition 2.10) over τ-frames (Definition 2.4). Soundness of PLL _τ in the class of general frames of Definition 2.4, for any similarity type τ, is immediate, by the way we defined frames. Completeness of PLL _τ is proven in the next section.

4 A Canonical Frame Construction

In Section 2 we presented a natural and intuitive relational semantics for the logics of bounded lattice expansions discussed in Section 3. The models we presented build on the idea of order-dual semantics we introduced in [32], an idea that is inherent in every lattice representation theorem [26] and which makes use of both a satisfaction and a co-satisfaction relation. The complex algebras $\mathfrak {g}_{\tau }^{+}$ of the frames of Section 2 are bounded lattice expansions with a natural family of operators of well-determined distribution types and which are generated by relations in the frame and include the usual logical operators familiar from the study of specific logical systems. The logic of bounded lattice expansions is then the logic of the relational semantic structures specified in Section 2. Soundness of the logic in the class of frames specified rests on the proof of Lemma 2.7 for the monotonicity axioms and it is otherwise immediate by the fact that we require of frames that the restrictions of the operators in the family $\mathfrak {P}_{\lambda }$ satisfy the desired distribution properties axiomatized by corresponding distribution axioms in the minimal logic Λ₀(τ). Completeness can be perhaps shown in many ways and we present our own canonical construction in this section, based on and extending [28].

4.1 Canonical Lattice Frame

Quoting from [32] we list the following representation result, based on previous work [28] by this author. For more proof details the reader is referred to [28, 32].

Theorem 4.1 (Modal Lattice Representation)

For every bounded lattice (L, 0, 1, ∧, ∨) there is a concrete, complete and atomic K _b -algebra K _b (X,R) generated by a frame (X, R), such that if $\mathcal {G}_{\lambda }(X), \mathcal {G}_{\rho }(X)$ are its associated lattices of Γ and Δ stable sets and $\overline {\mathcal {G}_{\lambda }(X)}=\{-A\;|\; A\in \mathcal {G}_{\lambda }(X)\}, \overline {\mathcal {G}_{\rho }(X)}=\{-B\;|\; B\in \mathcal {G}_{\rho }(X)\}$ then

• 1. there is a lattice embedding $[{\kern -2.3pt}[\;]{\kern -2.3pt}]: L\longrightarrow \mathcal {G}_{\lambda }(X)$ and a lattice dual embedding $(\!\!\!(\;)\!\!\!): L\longrightarrow \mathcal {G}_{\rho }(X)^{op}$ such that [[a]]=λ((a) ) and ((a) )=ρ([[a]]) and therefore $[{\kern -2.3pt}[{a}]{\kern -2.3pt}]={\Gamma }([{\kern -2.3pt}[{a}]{\kern -2.3pt}])=\blacksquare \lozenge ([{\kern -2.3pt}[{a}]{\kern -2.3pt}])$ is Γ-stable and $(\!\!\!({a})\!\!\!)={\Delta }(\!\!\!({a})\!\!\!)=\square \blacklozenge \,(\!\!\!({a})\!\!\!)$ is Δ-stable

• 2. the composition $\lozenge [\!\![a]\!\!]=-(\!\!\!(a)\!\!\!)$ is an embedding of L into $\overline {\mathcal {G}_{\rho }(X)}$ , while the composition $\blacklozenge (\!\!\!({a})\!\!\!)=-[{\kern -2.3pt}[{a}]{\kern -2.3pt}]$ is a co-embedding of L into $\overline {\mathcal {G}_{\lambda }(X)}$.

Proof

The proof of the first claim is implicit in the results of this author’s [28] where a lattice is represented in its partially-ordered space of filters (X, ≤ ), generalizing Goldblatt’s representation of ortholattices [25] in their filter space. Indeed, letting be the Dedekind-McNeille Galois connection generated by the partial order relation of filter inclusion and $\mathcal {G}_{\lambda }(X)$ the family of Γ-stable subsets of X, $A={\Gamma } A=\lambda \rho A=\blacksquare \lozenge A$ (where $\blacksquare ,\lozenge$ are generated by $\nleq$), by the results of [28] stable sets A = ΓA are generated as upper closures of singletons, A = Γx, and a lattice element a is represented as the set [[a]] = Γx _a = {x | x _a ≤x}={x | a ∈ x} of filters containing it, where x _a = a ↑ is the principal filter generated by a and a ∈ x iff x _a ≤ x iff x ∈ Γx _a .

It is also dually represented as the set ((a) ) = {x | x ≤ x _a }={x | a ≤ x}. Meets are represented as stable set intersections, [[a∧b]] = [[a]]∩[[b]], while joins are represented as closures of unions [[a∨b]] = Γ([[a]]∪[[b]]) = λ(ρ([[a]])∩ρ([[b]])) and dually represented as intersections. By Lemma 1.1 we then have $[{\kern -2.3pt}[{a\vee b}]{\kern -2.3pt}] = \blacksquare (\lozenge [{\kern -2.3pt}[{a}]{\kern -2.3pt}]\cup \lozenge {[{\kern -2.3pt}[{b}]{\kern -2.3pt}]})=[{\kern -2.3pt}[{a}]{\kern -2.3pt}]{\vee } [{\kern -2.3pt}[{b}]{\kern -2.3pt}]$ , while for any a we have $[{\kern -2.3pt}[{a}]{\kern -2.3pt}]={\Gamma } x_{a}=\lambda \rho (\{x_{a}\})=\blacksquare \lozenge (\{x_{a}\})$. The image of the representation map is identified in [28] as the set of stable-compact-open subsets of X, where X is topologized by the subbasis $\mathcal {S}=\{[{\kern -2.3pt}[{a}]{\kern -2.3pt}]\;|\; a\in L\}\cup \{X\setminus [{\kern -2.3pt}[{a}]{\kern -2.3pt}]\;|\; a\in L\}$. By [28] ((a∨b) ) = ((a) ) ∩ ((b) ) and $(\!\!\!(a\wedge b)\!\!\!)={\Delta }(\,(\!\!\!(a)\!\!\!)\,\cup \, (\!\!\!(b)\!\!\!)\,)=\rho (\lambda \,(\!\!\!(a)\!\!\!)\cap \lambda (\!\!\!(b)\!\!\!)\,)=\square (\blacklozenge \,(\!\!\!(a)\!\!\!)\cup \blacklozenge (\!(b)\!))$. □

The following result is then immediate and we merely list it below (for details, the reader is referred to [28]).

Theorem 4.2

PLL is sound and complete in the class of (general) lattice frames.

4.2 Normal Operators and Canonical Relations

Let $\mathcal {L}=(L,\wedge ,\vee ,0,1,\mathfrak {f})$ be a bounded lattice expansion with a normal n-ary operator $\mathfrak {f}$ of some distribution type $\delta (\mathfrak {f})=(i_{1},\ldots ,i_{n};i_{n+1})$, let $\mathbb {L}_{\tau }$ be the class of algebras for the similarity type τ = 〈δ〉 and let Λ₀(τ) be the corresponding minimal propositional logic for this similarity type. To prove that the logic is complete in the respective class of τ-frames we define a filter operator $\mathfrak {f}^{\sharp }$ and (n + 1)-ary relations $R^{\mathfrak {f}}, \;R^{\mathfrak {f},\partial }$ by distinguishing, for technical reasons, the two cases corresponding to the output type (1, or ∂). A lattice operator $\mathfrak {f}$ of distribution type δ _∨ = (i ₁,…, i _n ;1) is consistently denoted in this paper by the generic symbol , while for an operator with distribution type δ _∧ = (i ₁,…, i _n ;∂) we consistently use the symbol ⊖. Hence we define the filter operator $\mathfrak {f}^{\sharp }$ for the two distinct cases and ⊖^♯ by Eqs. 21 and 22 and the corresponding relations, the same for each of the cases , by Eqs. 23 and 24. The definitions we provide below are essentially the same as those in our [28], except for the presentation, which is now simpler.

(21)

$$\begin{array}{@{}rcl@{}} \ominus^{\sharp}(x_{1},\ldots,x_{n})\;\;\;\;&=&\;\;\; \bigvee\left\{\mathfrak{f}(a_{1},\ldots,a_{n})\!\uparrow\;|\;\bigwedge^{i_{j}=1}_{j=1{\cdots} n}(a_{j}\leq x_{j}) \wedge\bigwedge^{i_{j}=\partial}_{j=1{\cdots} n}(a_{j}\in x_{j})\right\}, (i_{n+1}=\partial)\;\;\;\; \;\;\;\;\; \end{array} $$

(22)

$$\begin{array}{@{}rcl@{}} xR^{\mathfrak{f}}x_{1}{\cdots} x_{n}\;\;&\mathrm{ iff }&\;\; \mathfrak{f}^{\sharp}(x_{1},\ldots,x_{n})\leq x\;\;\;\;\;\; \end{array} $$

(23)

$$\begin{array}{@{}rcl@{}} xR^{\mathfrak{f},\partial}x_{1}{\cdots} x_{n}\;\;&\mathrm{ iff }&\;\; x\leq \mathfrak{f}^{\sharp}(x_{1},\ldots,x_{n})\;\;\;\;\;\; \end{array} $$

(24)

For a lattice element a ∈ L, let [[a]] = {x | a ∈ x} and ((a) ) = {x | a ≤ x}, as in Theorem 4.1.

Lemma 4.3

Let $\mathfrak {f}$ be an n-ary normal lattice operator of any distribution type δ = (i ₁ ,…,i _n ; i _n+1 ). Then

• 1. $\mathfrak {f},\mathfrak {f}^{\sharp }$ have the same monotonicity type. In other words, if for all j=1,…,n, if x _j ≤u _j whenever i _j =1 and u _j ≤x _j whenever i _j = ∂, then $\mathfrak {f}^{\sharp }(x_{1},\ldots ,x_{n})\leq ^{i_{n+1}}\mathfrak {f}^{\sharp }(u_{1},\ldots ,u_{n})$ , where $\leq ^{i_{n+1}}$ is ≤ if i _n+1 =1 and it is ≥ if i _{n + 1} = ∂

• 2. $\mathfrak {f}^{\sharp }(x_{e_{1}},\ldots ,x_{e_{n}})=\mathfrak {f}(e_{1},\ldots ,e_{n})\!\uparrow$ , for any lattice elements e ₁ ,…,e _n

• 3. For any lattice elements a ₁ ,…,a _n , $[{\kern -2.3pt}[{\mathfrak {f}(a_{1},\ldots ,a_{n})}]{\kern -2.3pt}]=R^{\mathfrak {f}}x_{a_{1}}{\cdots } x_{a_{n}}$ and $(\!\!\!(\,{\mathfrak {f}(a_{1},\ldots ,a_{n})}\,)\!\!\!)=R^{\mathfrak {f},\partial }x_{a_{1}}{\cdots } x_{a_{n}}$

• 4. For any lattice elements a ₁ ,…,a _n and filters u ₁ ,…,u _n , if a _j ∈ u _j , whenever i _j = 1 and a _j ≤ u _j , whenever i _j = ∂, then $\mathfrak {f}^{\sharp }(x_{a_{1}},\ldots ,x_{a_{n}})\leq ^{i_{n+1}}\mathfrak {f}^{\sharp }(u_{1},\ldots ,u_{n})$ . Equivalently, under these assumptions, 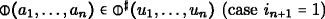and ⊖(a₁ ,…,a _n ) ≤ ⊖ ^♯ (u ₁ ,…,u _n ) (case i _n+1 = ∂). In yet other words, and ⊖^♯ (u ₁ ,…,u _n )∈((f(a ₁ ,…,a _n ) ) ), under the same assumptions.

Proof

For 1), let u ≤ v and separate the cases. Assume first i _{n + 1} = 1 = i _j , i.e. $\mathfrak {f}$ is monotone at the j-th position. Then for any element e, if e ≤ v, then e ≤ u and this implies that the defining set S _v for $\mathfrak {f}^{\sharp }(\overline {x},v,\overline {y})$ is contained in the corresponding defining set S _u for $\mathfrak {f}^{\sharp }(\overline {x},u,\overline {y})$. Hence $\mathfrak {f}^{\sharp }(\overline {x},u,\overline {y})=\bigwedge S_{u}\leq \bigwedge S_{v}=\mathfrak {f}^{\sharp }(\overline {x},v,\overline {y})$ and so $\mathfrak {f}$ is also monotone at the j-th position.

Assume now i _{n + 1} = 1≠∂ = i _j , i.e. $\mathfrak {f}$ is antitone at the j-th position. Then for any element e, if e ∈ u, then e ∈ v and therefore S _u ⊆S _v , from which we obtain $\mathfrak {f}^{\sharp }(\overline {x},v,\overline {y})=\bigwedge S_{v}\leq \bigwedge S_{u}=\mathfrak {f}^{\sharp }(\overline {x},u,\overline {y})$ and so $\mathfrak {f}^{\sharp }$ is also antitone at the j-th position.

If i _{n + 1} = ∂, separate again the two cases i _j = 1, i _j = ∂ as above. Since now $\mathfrak {f}^{\sharp }$ is defined by taking a join, the desired conclusion easily follows, by the same considerations as above.

For 2), assume first that i _{n + 1} = 1. Let a ₁,…, a _n be lattice elements such that if i _j = 1, then $a_{j}\leq x_{e_{j}}$ and if i _j = ∂, then $a_{j}\in x_{e_{j}}$. In the first case, a _j ≤e _j and because $\mathfrak {f}$ is monotone in the j-th position, by the case assumption i _{n + 1} = 1, it follows that $\mathfrak {f}({\cdots } a_{j}\cdots )\leq \mathfrak {f}({\cdots } e_{j}\cdots )$. In the second case, e _j ≤a _j and because $\mathfrak {f}$ is antitone in the j-th position it follows again that $\mathfrak {f}({\cdots } a_{j}\cdots )\leq \mathfrak {f}({\cdots } e_{j}\cdots )$ . Hence $\mathfrak {f}(a_{1},{\ldots } a_{n})\leq \mathfrak {f}(e_{1},{\ldots } e_{n})$, i.e $\mathfrak {f}(e_{1},{\ldots } e_{n})\!\uparrow \leq \mathfrak {f}(a_{1},{\ldots } a_{n})\!\uparrow$. When i _{n + 1} = 1, then clearly $\mathfrak {f}(e_{1},{\ldots } e_{n})\!\uparrow$ is the meet (intersection) of the principal filters in the definition of $\mathfrak {f}^{\sharp }$ in Eq. 21, since it is both a member of the set whose meet is taken in the definition and below all elements in that set. If i _{n + 1} = ∂, then $\mathfrak {f}$ is antitone at the j-th position when i _j = 1 and monotone when i _j = ∂ hence the previous inequalities are reversed and $\mathfrak {f}(e_{1},{\ldots } e_{n})\!\uparrow$ is now the largest element in the set described in the definition of $\mathfrak {f}^{\sharp }$.

For 3), $[{\kern -2.3pt}[{\mathfrak {f}(a_{1},\ldots ,a_{n})}]{\kern -2.3pt}]=\{x\;|\; \mathfrak {f}(a_{1},\ldots ,a_{n})\in x\}=\{x\;|\; \mathfrak {f}(a_{1},\ldots ,a_{n})\!\uparrow \leq x\}=\{x\;|\; \mathfrak {f}^{\sharp }(x_{a_{1}},\ldots ,x_{a_{n}})\leq x\}=R^{\mathfrak {f}}x_{a_{1}}{\cdots } x_{a_{n}}$, by definition and using the first case of the Lemma, and similarly for $(\!\!\!(\,\mathfrak {f}(a_{1},\ldots ,a_{n}))\!\!\!)$.

4) is a direct consequence of the first claim. □

4.3 Completeness Proof

The canonical general frame is the structure $\mathfrak {g}_{\tau }^{c}=(X,\leq , (R^{\delta },R^{\delta ,\partial })_{\delta \in \tau },\mathfrak {P}_{\lambda })$ where $X=\mathcal {F}$ is the set of all filters of the Lindenbaum-Tarski algebra of the logic (including the improper filter), ≤ is filter inclusion, $\mathfrak {P}_{\lambda }$ is the set of stable sets generated as upper closures of principal filters and for each distribution type δ ∈ τ, R ^δ, R ^{δ, ∂} are defined as in Eqs. 23 and 24 using the filter operators $\mathfrak {f}^{\sharp }$ defined in Eqs. 21 and 22 and where $\mathfrak {f}$ is the operator of distribution type δ.

Lemma 4.4 (Canonical Frame Lemma)

The canonical frame satisfies all frame conditions of Definition 2.4.

Proof

We prove the Lemma with a series of Claim proofs.

Claim 4.5

The defined operators preserve stable sets and restrict to operators on $\mathfrak {P}_{\lambda },\mathfrak {P}_{\rho }$, respectively.

For the proof, we distinguish cases according to the output type.

Case with

By Eq. 21, the definition of the filter operator is

and the corresponding set operators are defined by Eqs. 11 and 12, repeated below, where the canonical relations are defined by and .

We first show that the operator preserves Γ-stable sets. Letting A _i = Γx _i , for i = 1,…, n, we have

Conversely, if then by choosing u _j = x _j for each j = 1,…, n it follows by the defining condition for membership in , which is now trivially satisfied by the choice of the u _j that .

Hence and therefore restricts to an operator on $\mathcal {G}_{\lambda }(X)$. That also restricts to an operator on $\mathfrak {P}_{\lambda }$ is seen by the following simple calculation, given also Lemma 4.3.

Given that Γx _a = [[a]], the above is proof that and hence the representation map is a homomorphism.

We next show that the operator preserves Δ-stable sets. Indeed, let $D_{i}={\Delta } x_{i}\in \mathcal {G}_{\rho }(X)$, for i = 1,…, n. Then we have the following computation.

where the converse direction follows by the monotonicity properties of , verified in Lemma 4.3.

In particular, if $x_{j}=x_{a_{j}}$, the following computation shows that restricts to an operator on $\mathfrak {P}_{\rho }$ and that the representation map is a homomorphism.

Hence .

Case , with Then the definition of the filter operator is

$$\ominus^{\sharp}(x_{1},\ldots,x_{n})\;=\; \bigvee\left\{f(a_{1},\ldots,a_{n})\!\uparrow\;|\;\bigwedge^{i_{j}=1}_{j=1{\cdots} n}(a_{j}\leq x_{j})\wedge\bigwedge^{i_{j}=\partial}_{j=1{\cdots} n}(a_{j}\in x_{j})\right\} $$

The corresponding set operators ⊖,⊖^∂ are defined by Eqs. 13 and 14, Definition 2.4, repeated below,

$$\begin{array}{@{}rcl@{}} \ominus(U_{1},\ldots,U_{n}) \!\!&=&\!\!\! \left\{x\;|\; \forall u_{1},\ldots,u_{n}\left( \bigwedge\limits_{j\,=\,1{\cdots} n}^{i_{j}\,=\,1}(u_{j}\in U_{j})\!\wedge\! \bigwedge\limits_{r\,=\,1{\cdots} n}^{i_{r}\!=\partial}(u_{r}\in\rho U_{r}) \;\!\!\Longrightarrow\!\!\; xR^{\ominus} u_{1}{\cdots} u_{n}\right)\right\}\\ \ominus^{\partial}(U_{1},\ldots,U_{n}) \!\!&=&\!\!\! \left\{x\;|\; \exists u_{1},\ldots,u_{n}\left( xR_{\ominus}^{\partial} u_{1}{\cdots} u_{n}\!\wedge\! \bigwedge\limits_{j=1{\cdots} n}^{i_{j}=1}(u_{j}\in \lambda U_{j})\!\wedge\! \bigwedge\limits_{r=1{\cdots} n}^{i_{r}=\partial}(u_{r}\in U_{r})\right)\right\} \end{array} $$

while the canonical relations are defined by x R ^⊖ u ₁⋯u _n iff ⊖^♯(u ₁,…, u _n ) ≤ x and x R ^{⊖, ∂} u ₁⋯u _n iff x ≤ ⊖^♯(u ₁,…, u _n ).

If A _i = Γx _i , for i = 1,…, n, are in $\mathcal {G}_{\lambda }(X)$, then the following computation shows that ⊖ restricts to an operator on $\mathcal {G}_{\lambda }(X)$.

$$\begin{array}{@{}rcl@{}} \begin{array}{ll} x\!\in\! \ominus({\Gamma} x_{1},\ldots,{\Gamma} x_{n}) & \text{iff}~~\forall u_{1},\ldots,u_{n}\;\left( \bigwedge_{j\,=\,1{\cdots} n}^{i_{j}\,=\,1}(u_{j}\in {\Gamma} x_{j})\!\wedge\! \bigwedge_{r=1{\cdots} n}^{i_{r}=\partial}(u_{r}\!\in\!\rho {\Gamma} x_{r})\;\!\!\Longrightarrow\!\!\;x R^{\ominus} u_{1}{\cdots} u_{n}\right)\\ & \text{iff}~~\forall u_{1},\ldots,u_{n}\;\left( \bigwedge_{j\,=\,1{\cdots} n}^{i_{j}\,=\,1}(x_{j}\!\leq\! u_{j})\!\wedge\! \bigwedge_{r\,=\,1{\cdots} n}^{i_{r}\!=\partial}(u_{r}\leq x_{r})\;\!\!\Longrightarrow\!\!\;\ominus^{\sharp}(u_{1},\ldots, u_{n})\!\leq\! x\right)\\ & \text{iff}~~\ominus^{\sharp}(x_{1},\ldots, x_{n})\!\leq\! x \end{array} \end{array} $$

where again the converse direction follows by the monotonicity properties of ⊖^♯, verified in Lemma 4.3. Therefore, $\ominus ({\Gamma } x_{1},\ldots ,{\Gamma } x_{n})={\Gamma }(\ominus ^{\sharp }(x_{1}\cdots x_{n}))\in \mathcal {G}_{\lambda }(X)$.

In particular, if $x_{j}=x_{a_{j}}=a_{j}\!\uparrow$, then the following calculation demonstrates that ⊖ restricts to an operator on $\mathfrak {P}_{\lambda }$ (the lattice of upper closures of principal filters).

$$\begin{array}{@{}rcl@{}} \begin{array}{ll} x\in \ominus({\Gamma} x_{a_{1}},\ldots,{\Gamma} x_{a_{n}}) &\quad\mathrm{ iff} \; \ominus^{\sharp}(x_{a_{1}},\ldots, x_{a_{n}})\leq x\\ &\quad \mathrm{ iff } \;\ominus(a_{1},\ldots,a_{n})\!\uparrow\;\leq x\\ &\quad \mathrm{ iff } \;\;x\in {\Gamma}(\ominus(a_{1},\ldots,a_{n})\!\uparrow) \end{array} \end{array} $$

Hence $\ominus ({\Gamma } x_{a_{1}},\ldots ,{\Gamma } x_{a_{n}})={\Gamma }(\ominus (a_{1},\ldots ,a_{n})\!\uparrow )$. In particular, the above calculation shows that the representation function is a homomorphism, since we have in fact demonstrated that ⊖([[a ₁]],…,[[a _n ]])=[[⊖(a ₁,…, a _n )]].

To see, next, that ⊖^∂ preserves Δ-stable sets, let $D_{i}={\Delta } x_{i}\in \mathcal {G}_{\rho }(X)$, for i = 1,…, n.

$$\begin{array}{@{}rcl@{}} \begin{array}{ll} x\in\ominus^{\partial}({\Delta} x_{1},\ldots,{\Delta} x_{n}) \Longrightarrow \quad \exists u_{1},\ldots,u_{n}\;(x\leq\ominus^{\sharp}(u_{1},\ldots,u_{n})\\ {\kern15.5pc}\wedge\bigwedge_{j=1{\cdots} n}^{i_{j}=1}(u_{j}\in\lambda{\Delta} x_{j})\\ {\kern16.5pc}\wedge \bigwedge_{r=1{\cdots} n}^{i_{r}=\partial}(u_{r}\in{\Delta} x_{r}))\\ {\kern8.3pc}\Longrightarrow \quad \exists u_{1},\ldots,u_{n}\;(x\leq\ominus^{\sharp}(u_{1},\ldots,u_{n})\\ {\kern15.5pc}\wedge\bigwedge_{j=1{\cdots} n}^{i_{j}=1}(x_{j}\leq u_{j})\\ {\kern16.5pc}\wedge \bigwedge_{r=1{\cdots} n}^{i_{r}=\partial}(u_{r}\leq x_{r}))\\ {\kern8.3pc}\Longrightarrow \quad \exists u_{1},\ldots,u_{n}\;(x\leq\ominus^{\sharp}(u_{1},\ldots,u_{n})\\ {\kern15.5pc}\leq \ominus^{\sharp}(x_{1},\ldots,x_{n}))\\ {\kern8.3pc}\Longrightarrow \quad x\leq \ominus^{\sharp}(x_{1},\ldots,x_{n}))\\ {\kern8.3pc}\Longrightarrow \quad x\in{\Delta}(\ominus^{\sharp}(x_{1},\ldots,x_{n})) \end{array} \end{array} $$

Conversely, if x ∈ Δ(⊖^♯(x ₁,…, x _n )), i.e. x ≤ ⊖^♯(x ₁,…, x _n )), then choosing u _j = x _j the defining property for membership of x in the set ⊖^∂(Δx ₁,…,Δx _n ) is trivially satisfied. Hence, $\ominus ^{\partial }({\Delta } x_{1},\ldots ,{\Delta } x_{n})={\Delta }(\ominus ^{\sharp }(x_{1},\ldots ,x_{n}))\in \mathcal {G}_{\rho }(X)$.

In particular, if $x_{j}=x_{a_{j}}$ are principal filters, then we obtain by the above argument, given also Lemma 4.3, that $\ominus ^{\partial }({\Delta } x_{a_{1}},\ldots ,{\Delta } x_{a_{n}})={\Delta }(\ominus (a_{1},\ldots ,a_{n})\!\uparrow )$ and this shows that ⊖^∂ restricts to an operator on $\mathfrak {P}_{\rho }$, as well as that the representation is a homomorphism, since the above conclusion can be rewritten as ((⊖(a ₁,…, a _n ) ) )=⊖^∂(((a ₁) ),…,((a _n ) ) ).

This completes the proof of Claim 4.5.

Claim 4.6

If $A_{1}={\Gamma } x_{1},\ldots ,A_{n}={\Gamma } x_{n}\in \mathcal {G}_{\lambda }(X)$ and $D_{1}={\Delta } y_{1},\ldots ,D_{n}={\Delta } y_{n}\in \mathcal {G}_{\rho }(X)$, then all of the following hold:

For the proof of the claim note that

where we used Claim 4.5. The other cases are similar.

By the proofs of Claims 4.5 and 4.6 we have shown that the canonical frame satisfies the frame conditions of Definition 2.4.

Claim 4.7

The distribution conditions of Definition 2.4 hold in the canonical general frame.

For the proof of the case of an operator , let i _j = 1 for some j = 1,…, n, let x, z ₁,…, z _n be filters such that , i.e. , let also A = Γx _a , B = Γx _b and $D_{r}={\Gamma } x_{a_{r}}$, for r ≠ j, be members of $\mathfrak {P}_{\lambda }$. Assume, furthermore, that z _j ∈ A∨B, while for r ≠ j z _r ∈ D _r .

Notice that Γx _a ∨Γx _b = Γ(x _a ∩x _b )=Γx _a∨b . Furthermore,

The proof of the case of an operator ⊖ is by essentially the same argument, using the proof of Claim 4.5 as we did above.

This completes the proof of Claim 4.7 and of Lemma 4.4. □

Lemma 4.8 (Canonical Interpretation Lemma)

The canonical interpretation [[ ]] and co-interpretation (() ), defined by [[φ]]={x∈X|[φ]∈x} and ((φ) )={x∈X|[φ]≤x}, where [φ] is the equivalence class (under provability) of φ, satisfy the model conditions of Definition 2.10.

Proof

The claim is true by definition for the case of propositional variables and the case of lattice operators has been handled in the proof of Theorem 4.1. For the case of an operator $\mathfrak {f}$ of distribution type δ, we separate the cases according to the output type of δ.

When the output type is 1, we designate $\mathfrak {f}$ by , as we have been consistently doing throughout this article. Let in the Lindenbaum-Tarski algebra of the logic.

Claim 4.9

iff there exist filters u ₁,…, u _n such that (a) , (b) a _j ∈ u _j whenever i _j = 1 and (c) a _j ≤u _j whenever i _j = ∂.

For the proof of the claim, first let u ₁,…, u _n be filters such that and a _j ∈ u _j whenever i _j = 1, while a _j ≤u _j whenever i _j = ∂. By Lemma 4.3 the last two assumptions imply that . By the same Lemma 4.3, hence the hypothesis implies that . In addition, by definition of and hypothesis we have and thereby .

Conversely, assume and choose $u_{i}=x_{a_{i}}$, for i = 1,…, n. For a principal filter x _e it is the case that both e ∈ x _e and e ≤ x _e . Hence it holds that a _j ∈ u _j whenever i _j = 1 and a _i ≤u _j whenever i _j = ∂. It remains to verify that which, by definition, is the same as . Given that $u_{j}=x_{a_{j}}$, given also that by Lemma 4.3 this is equivalent to , which is precisely the case assumption and this completes the proof of the claim. □

Consider now the case where the output type of δ is ∂. Then we designate $\mathfrak {f}$ by ⊖ and let [⊖(φ ₁,…, φ _n )]=⊖(a ₁,…, a _n ) in the Lindenbaum-Tarski algebra of the logic.

Claim 4.10

⊖(a ₁,…, a _n ) ∈ x iff for any filters u ₁,…, u _n if both (i) a _j ∈ u _j whenever i _j = 1 and (ii) a _j ≤u _j whenever i _j = ∂, then x R _⊖ u ₁⋯u _n , i.e. ⊖^♯(u ₁,…, u _n ) ≤ x.

For the proof, assume first ⊖(a ₁,…, a _n ) ∈ x, let u ₁,…, u _n be any filters and suppose conditions (i) and (ii) hold. By Lemma 4.3 the conditions imply that $\ominus ^{\sharp }(u_{1},\ldots ,u_{n})\leq \ominus ^{\sharp }(x_{a_{1}},\ldots ,x_{a_{n}})$, where the latter is identical to (⊖(a ₁,…, a _n )) ↑. Therefore, ⊖(a ₁,…, a _n ) ≤ ⊖^♯(u ₁,…, u _n ), i.e. ⊖(a ₁,…, a _n ) is below every element of the filter ⊖^♯(u ₁,…, u _n ). Since by assumption ⊖(a ₁,…, a _n ) ∈ x and x is a filter it follows that every element of ⊖^♯(u ₁,…, u _n ) is in x. In other words, ⊖^♯(u ₁,…, u _n ) ≤ x.

Conversely, assume that for any filters u ₁,…, u _n if conditions (i) and (ii) hold, then ⊖^♯(u ₁,…, u _n ) ≤ x and choose $u_{j}=x_{a_{j}}$ for j = 1,…, n. Trivially (i) and (ii) hold for principal filters regardless of the side condition and therefore $\ominus ^{\sharp }(x_{a_{1}},\ldots ,x_{a_{n}})\leq x$, but $\ominus ^{\sharp }(x_{a_{1}},\ldots ,x_{a_{n}})=(\ominus (a_{1},\ldots ,a_{n}))\!\uparrow$, this shows that ⊖(a ₁,…, a _n ) ∈ x and hence the proof of the claim is complete.

For the co-interpretation, we again separate the cases according to the output type of δ and we consider first the case where it is 1.

Claim 4.11

iff for any filters u ₁,…, u _n if (1) a _j ∈ u _j whenever i _j = 1 and (2) a _j ≤u _j whenever i _j = ∂, then , i.e. .

To prove the left to right direction, assume , let u ₁,…, u _n be any filters and assume that conditions (1) and (2) hold. Condition (1) is equivalent to $x_{a_{j}}\leq u_{j}$, when i _j = 1, while condition (2) is equivalent to $u_{j}\leq x_{a_{j}}$ when i _j = ∂. The values of i _j indicate monotonicity and antitonicity at the respective places according to whether i _j = i _{n + 1} = 1 or not. By Lemma 4.3, case 1, . The hypothesis , given Lemma 4.3, is equivalent to and we then get the desired conclusion, .

For the converse, choosing in particular $u_{j}=x_{a_{j}}$ for each j = 1,…, n we obtain . But the latter is the principal filter , by Lemma 4.3 and thereby we obtain .

Finally, we consider the case where the output type of δ is ∂.

Claim 4.12

⊖(a ₁,…, a _n ) ≤ x iff there exist filters u ₁,…, u _n such that x ≤ ⊖^♯(u ₁,…, u _n ) and (a) a _j ∈ u _j whenever i _j = 1, while (b) a _j ≤u _j when i _j = ∂.

From right to left, if filters u ₁,…, u _n exist with the properties described in the claim, then by the monotonicity properties of ⊖^♯ (Lemma 4.3) we obtain $\ominus ^{\sharp }(u_{1},\ldots ,u_{n})\leq \ominus ^{\sharp }(x_{a_{1}},\ldots ,x_{a_{n}})$ from which it follows that ⊖(a ₁,…, a _n ) ≤ x, using Lemma 4.3.

For the left to right direction, assume and consider $u_{j}=x_{a_{j}}$. Then trivially a _j ∈ u _j whenever i _j = 1, while a _j ≤u _j when i _j = ∂ (simply because e ∈ x _e and e ≤ x _e , for any principal filter x _e ). Furthermore, the hypothesis is equivalent to $x\leq \ominus ^{\sharp }(x_{a_{1}},\ldots ,x_{a_{n}})=\ominus ^{\sharp }(u_{1},\ldots ,u_{n})$ by choice of the u _j .

This completes both the proof of the claim and the proof of the canonical interpretation Lemma.

We may then conclude with a completeness result.

Theorem 4.13 (Completeness)

Let τ = 〈δ ₁ ,…,δ _k 〉 be a similarity type and Λ ₀ (τ) the corresponding minimal propositional logic for this type, in the sense of Definition 3.3. Then Λ ₀ (τ) is sound and complete in the class of general frames of Definition 2.4.

5 Conclusions

In this article we presented a natural, intuitive and uniform relational semantics for the logics of bounded lattice expansions. We fixed a class of semantic structures with operators generated by relations by generic patterns, in the spirit of the Jónsson-Tarski [33] representation theorem, though more general, and including the cases of familiar operators such as implication, possibility, fusion, negation as falsifiability etc.

The models we presented build on the idea of order-dual semantics we introduced in [32], an idea that is inherent in every lattice representation theorem [26] and which makes use of both a satisfaction and a co-satisfaction (refutation) relation. The complex algebras $\mathfrak {g}_{\tau }^{+}$ of the frames of Section 2 are bounded lattice expansions with a natural family of operators of well-determined distribution types and which are generated by relations in the frame and include as special cases the usual logical operators familiar from the study of specific logical systems. The logic of bounded lattice expansions is then the logic of the relational semantic structures specified in Section 2, for which we proved a generic completeness theorem, by a traditional canonicity argument, in Section 4.

Comparing to existing approaches, our semantic structures and interpretation patterns are simple and intuitive, despite the absence of distribution, and it then appears that our approach and results may facilitate the study of logical systems on a non distributive propositional basis, such as modal, or substructural systems, sometimes collectively referred to as (non-distributive) Generalized Galois Logics (GGLs) [4]. Though we have explicitly only treated operators that are normal in the sense of having a well specified distribution type, the observant reader will have noticed that the same approach applies to quasi-normal operators that may fail distribution in some argument place and this may prove useful in studying logics over a non-distributive propositional basis where the additional operators are not normal in the usual modal logic sense.