1 Introduction

While randomized studies are the gold standard for estimating treatment effectiveness, there are numerous occasions when they are not feasible. Moreover, there are numerous times when meaningful information is available from observational studies regarding the potential effectiveness of a particular treatment on an outcome. Unfortunately, with rare diseases or outcomes, observational and clinical studies aimed at identifying effective treatments to reduce the risk of disease or death often require long term follow-up of participants in order to observe a sufficient number of events to precisely estimate the treatment effect. In such studies, observing the outcome of interest during follow-up may be difficult and high rates of censoring may be observed which often leads to reduced power when applying straightforward statistical methods developed for time-to-event data.

In light of these challenges, alternative methods have been proposed to take advantage of auxiliary information that may potentially improve efficiency when estimating marginal survival and improve power when testing for a treatment effect in a randomized study (Cook and Lawless 2001). For example, when the available auxiliary information consists of a single discrete variable, fully nonparametric approaches (Rotnitzky and Robins 2005; Murray and Tsiatis 1996) that incorporate this variable when estimating marginal survival have been shown to produce more efficient estimates when compared to the Kaplan–Meier estimator (Kaplan and Meier 1958). When the auxiliary information includes continuous variables and/or multiple variables, semi parametric and parametric approaches such as regression adjustment are often considered. However, while these methods can be used to improve efficiency, they often rely on correct model specification. For example, the Cox proportional hazards model (Cox 1972) incorporating baseline covariates is often used to obtain an estimate of marginal survival and test for a treatment effect but the validity and performance of this approach also depends on the correct specification of the Cox model (Lagakos 1988; Lagakos and Schoenfeld 1984; Lin and Wei 1989).

A promising alternative to regression adjustment methods that has gained much recent attention is augmentation approaches which generally involve an augmentation term that is a function of the auxiliary information (Lu and Tsiatis 2008; Garcia et al. 2011; Tian et al. 2012; Zhang 2015; Zhang et al. 2008; Parast et al. 2014). For example, Lu and Tsiatis (2008) proposed an augmentation procedure to improve the efficiency of estimating the log hazard ratio from the Cox model, and demonstrated substantial gains in power when compared to the standard log-rank test. Garcia et al. (2011) used a similar covariate augmentation approach to improve efficiency when using a more general class of survival models and Zhang (2015) developed augmented versions of the Nelson–Aalen and Kaplan–Meier estimators.

When auxiliary information consists of information collected over time such as repeated measurements after baseline or the occurrence of an intermediate event, incorporating this information to improve efficiency becomes more difficult due to the semi-competing risks nature of the data (Fine et al. 2001). That is, when the primary outcome is a terminal event such as death and the intermediate event is a non-terminal event such as hospitalization or cancer recurrence, the occurrence of the terminal event would censor the non-terminal event but not vice versa. Therefore, if an individual dies before the intermediate event occurs or before the repeated measurements are obtained, this auxiliary information is not available for that individual. Recently, Parast et al. (2014) proposed a landmark estimation procedure that uses a landmarking approach to overcome these semi-competing risk issues. Specifically, this procedure incorporates intermediate event information observed up to a landmark time, \(t_0\), for those who have survived and are still under observation at \(t_0\), in the estimation of marginal survival and a treatment effect. In addition, a smoothing component of the landmark estimation procedure ensures the consistency of survival estimates and thus these estimates do not require one to correctly specify a model relating the intermediate event to the primary outcome. Parast et al. (2014) demonstrated that significant gains in efficiency can be obtained. Other previously proposed methods to improve efficiency by using intermediate information include a kernel estimation approach (Gray 1994), a three-state model approach (Finkelstein and Schoenfeld 1994), an augmented score and augmented likelihood approach (Fleming et al. 1994), a multiple imputation approach (Faucett et al. 2002), a nonparametric approach (Murray and Tsiatis 1996, 2001), and a targeted shrinkage regression approach (Li et al. 2011).

While the methods described above allow for increased efficiency and power through the use of auxiliary information, they are generally not valid in observational study settings. That is, these methods require the assumption that the potential outcomes for each individual under treatment and control are independent of treatment group assignment, an assumption that holds in a randomized clinical trial setting but is very unlikely to hold in an observational setting. When this assumption is violated, methods that do not account for this “selection” bias can result in biased estimates of survival and treatment effectiveness.

There are a number of statistical methods available that attempt to account for potential selection bias including regression adjustment, matching methods, and inverse probability of treatment (IPT) weighting (or propensity score weighting). The goal of such methods is to estimate survival and treatment effects appropriately adjusting for the fact that individuals in one treatment group may differ from those in another group on factors other than treatment alone. In the case of IPT weighting, an average treatment effect in the population can be estimated by re-weighting individuals based on their probability of treatment such that the treatment groups are, in essence, balanced on all observed factors other than treatment (Hernán et al. 2000; Rosenbaum and Rubin 1983b, 1984). Xie and Liu (2005) proposed an IPT weighted Kaplan–Meier estimate of survival and a corresponding test statistic to test for a difference in survival distributions and showed that consistent estimates that account for selection bias can be obtained. Other methods based on weighting and stratification include Nieto and Coresh (1996) and Amato (1988) where the general approach is to stratify individuals by the observed confounders, estimate survival in each strata, and appropriately combine the resulting survival estimates. Alternatively, survival estimates can be adjusted for observed confounders and compared using a specified regression model such as the Cox model, but as in the case where one aims to gain efficiency by using a Cox model, when the model is not correctly specified the resulting estimates may not be valid (Thomsen et al. 1991; Therneau 2000; Chen and Tsiatis 2001). A number of doubly robust estimators that combine IPT weights (IPTW) and a model for survival, often a Cox regression model, have been proposed and lead to consistent estimates when either the model used to obtain the IPTW or the regression model is correct (Zhang and Schaubel 2012a, b; Bai et al. 2013).

While these previously developed time-to-event methods provide valuable tools for inference in an observational setting, methods that can improve efficiency through the use of auxiliary information that includes intermediate event information and are valid in an observational setting are still lacking. In this paper we develop the landmark estimation procedure of Parast et al. (2014) for use in an observational setting such that one can obtain consistent estimates of survival and a treatment effect with improved efficiency by taking advantage of baseline and intermediate event auxiliary information. We compare our proposed estimates to those obtained using the Kaplan–Meier estimator, the original landmark estimation procedure (which one would expect to be biased as selection bias is not accounted for), and the IPT weighted Kaplan–Meier estimator (which we expect to be unbiased but less efficient since auxiliary information is not incorporated). We illustrate the resulting reduction in bias and gains in efficiency through a simulation study and apply our procedure to an AIDS dataset to examine the effect of previous antiretroviral therapy on survival.

2 Estimation of survival in an observational study

2.1 Notation and potential outcomes framework

For the \(i\hbox {th}\) subject, let \(T_{{\scriptscriptstyle {\mathbb {L}}}i}\) denote the time of the primary event of interest, \(\mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}i}}\) denote the vector of intermediate event times, \(\mathbf{Z}_{i}\) denote the vector of baseline (pretreatment) covariates, and \(C_i\) denote the censoring time assumed independent of \((T_{{\scriptscriptstyle {\mathbb {L}}}i},\mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}i}},\mathbf{Z}_i)\). Due to censoring, \(T_{{\scriptscriptstyle {\mathbb {L}}}i}\) and \(\mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}i}}\) are only potentially observed. Instead, we observe \(X_{{\scriptscriptstyle {\mathbb {L}}}i}= \min (T_{{\scriptscriptstyle {\mathbb {L}}}i}, C_{i}), \mathbf {X_{{\scriptscriptstyle {\mathbb {S}}}i}}= \min (\mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}i}}, C_{i})\) and \(\delta _{{\scriptscriptstyle {\mathbb {L}}}i}= I(T_{{\scriptscriptstyle {\mathbb {L}}}i}\le C_{i}), \mathbf {\delta _{{\scriptscriptstyle {\mathbb {S}}}i}}= I(\mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}i}}\le C_{i})\). When \(T_{{\scriptscriptstyle {\mathbb {L}}}i}\) is a terminal event, such as death, this would represent a semi-competing risks setting where \(\mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}i}}\) is additionally subject to informative censoring by \(T_{{\scriptscriptstyle {\mathbb {L}}}i}\), while \(T_{{\scriptscriptstyle {\mathbb {L}}}i}\) is only subject to administrative censoring and cannot be censored by \(\mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}i}}\). Let \(t_0\) denote some landmark time prior to t, such as a 1-year check up time following disease diagnosis. Our goal is to estimate \(S(t) = P(T_{{\scriptscriptstyle {\mathbb {L}}}i}>t)\) appropriately using baseline covariate information and intermediate event information collected up to \(t_0\), where t is a clinically relevant pre-specified time point such that \(P(X_{{\scriptscriptstyle {\mathbb {L}}}i}> t \mid T_{{\scriptscriptstyle {\mathbb {L}}}i}\ge t_0) \in (0, 1)\) and \(P(T_{{\scriptscriptstyle {\mathbb {L}}}i}\le t_0, T_{{\scriptscriptstyle {\mathbb {S}}}i}\le t_0) \in (0, 1)\).

In order to rigorously define the survival and treatment effect quantities we aim to estimate, we consider a potential outcomes framework. Assume there are two treatments, Treatment 1 and Treatment 0 and let \(G_i = 1\) or 0 denote the treatment received by individual i. Each individual has two potential outcomes: \(T_{{\scriptscriptstyle {\mathbb {L}}}1i}\), which is the time of the long term event after receiving treatment 1, and \(T_{{\scriptscriptstyle {\mathbb {L}}}0i}\), which is the time of the long term event after receiving treatment 0. However, in reality we only observe one of these outcomes for each patient \(T_{{\scriptscriptstyle {\mathbb {L}}}i}= T_{{\scriptscriptstyle {\mathbb {L}}}1i}I(G_i = 1) + T_{{\scriptscriptstyle {\mathbb {L}}}0i}I(G_i=0)\). Due to censoring, we define \(X_{{\scriptscriptstyle {\mathbb {L}}}1i}= \min (T_{{\scriptscriptstyle {\mathbb {L}}}1i}, C_{i}), \mathbf {X_{{\scriptscriptstyle {\mathbb {S}}}1i}}= \min (\mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}1i}}, C_{i})\) and \(\delta _{{\scriptscriptstyle {\mathbb {L}}}1i}= I(T_{{\scriptscriptstyle {\mathbb {L}}}1i}\le C_{i}), \delta _{{\scriptscriptstyle {\mathbb {S}}}1i}= I(\mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}1i}}\le C_{i})\) or \(X_{{\scriptscriptstyle {\mathbb {L}}}0i}= \min (T_{{\scriptscriptstyle {\mathbb {L}}}0i}, C_{i}), \mathbf {X_{{\scriptscriptstyle {\mathbb {S}}}0i}}= \min (\mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}0i}}, C_{i})\) and \(\delta _{{\scriptscriptstyle {\mathbb {L}}}0i}= I(T_{{\scriptscriptstyle {\mathbb {L}}}0i}\le C_{i}), \delta _{{\scriptscriptstyle {\mathbb {S}}}0i}= I(\mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}0i}}\le C_{i})\). In essence, there are two levels of missing data in this framework. First, since individuals are assigned to only one treatment, only \(T_{{\scriptscriptstyle {\mathbb {L}}}1i},\mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}1i}}\) or \(T_{{\scriptscriptstyle {\mathbb {L}}}0i}, \mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}0i}}\) are potentially observable. Second, we are additionally not able to observe \(T_{{\scriptscriptstyle {\mathbb {L}}}1i}, \mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}1i}}\) for all individuals with \(G_i = 1\) (and similarly \(T_{{\scriptscriptstyle {\mathbb {L}}}0i}, \mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}0i}}\) for all individuals with \(G_i = 0\)) due to censoring.

2.2 Estimation of survival using the Kaplan–Meier estimator

We aim to estimate survival at time t within each treatment group, \(S_1(t) = P(T_{{\scriptscriptstyle {\mathbb {L}}}1}> t)\) and \(S_0(t) = P(T_{{\scriptscriptstyle {\mathbb {L}}}0}> t)\). To make our assumptions explicit we define:

Assumption A.1

\((T_{{\scriptscriptstyle {\mathbb {L}}}1i}, \mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}1i}}, T_{{\scriptscriptstyle {\mathbb {L}}}0i}, \mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}1i}}, \mathbf{Z}_i) \perp C_i \mid G_i\)

Assumption A.2

\((T_{{\scriptscriptstyle {\mathbb {L}}}1i}, T_{{\scriptscriptstyle {\mathbb {L}}}0i}, \mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}1i}}, \mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}0i}}) \perp G_i \mid \mathbf{Z}_i\)

Assumption A.1 assumes independent censoring and Assumption A.2 is often referred to as the assumption of no unmeasured confounders (Rosenbaum and Rubin 1983b) or the assumption of strong ignorability (Robins et al. 2000). Without loss of generality, we first focus on estimation of \(S_1(t)\). In a randomized clinical trial (RCT) setting, instead of Assumption A.2, one could make the much stronger assumption that \((T_{{\scriptscriptstyle {\mathbb {L}}}1i}, T_{{\scriptscriptstyle {\mathbb {L}}}0i}, \mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}1i}}, \mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}0i}}) \perp G_i\) which would hold due to random treatment assignment. In such a randomized setting, a common nonparametric approach to estimate survival is the Kaplan–Meier (KM) estimate (Kaplan and Meier 1958),

$$\begin{aligned} \widehat{S}_{ \text{ KM }, j}(t) = \left\{ \begin{array}{ll} 1 &{}\quad \text{ if } t<t_{1j}\\ \prod \nolimits _{t_{kj} \le t} \left[ 1-\frac{d_{kj}}{y_{kj}}\right] &{}\quad \text{ if } t\ge t_{1j} \end{array} \right. \end{aligned}$$
(1)

where \(t_{1j},\ldots ,t_{Dj}\) are the distinct observed long term event times in treatment group j, \(d_{kj}\) is the number of events at time \(t_{kj}\) in treatment group j, and \(y_{kj}\) is the number of patients at risk at \(t_{kj}\) in treatment group j.

However, in an observation study where treatment is not randomized, one cannot assume that

\((T_{{\scriptscriptstyle {\mathbb {L}}}1i}, T_{{\scriptscriptstyle {\mathbb {L}}}0i}, \mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}1i}}, \mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}0i}}) \perp G_i\). Indeed, individual characteristics that may be associated with treatment may also be associated with the potential outcome. For example, if the exposure of interest was diabetes and the long term outcome was death, individual characteristics such as age, body mass index, gender and diet may be associated with both the likelihood of having diabetes and survival. Analyses which ignore selection bias (i.e. that the distribution of confounders differ in the two treatment groups) can result in biased estimates of treatment effectiveness, particularly if treatment selection is related to treatment effectiveness or the primary long term event of interest. However, it may be possible to identify such individual characteristics and appropriately adjust methods originally developed for an RCT setting accordingly. Specifically, if \(\mathbf{Z}_i\) contains all individual characteristics that may be associated with both treatment and the outcome, then among individuals with the same \(\mathbf{Z}_i\), treatment group and the potential outcomes would be independent (Assumption A.2). Therefore, methods that appropriately account for the differential distribution of \(\mathbf{Z}_i\) within treatment groups will lead to valid estimation of the quantities of interest (Rosenbaum and Rubin 1983b).

Methods that take advantage of this assumption to estimate survival and treatment effects in the presence of selection bias include regression adjustment and IPT weighting. IPT weighting involves appropriately weighting estimates or estimating equations by the inverse of the probability of treatment or the propensity score, \(W_j(\mathbf{Z}_i) = P(G_i=j \mid \mathbf{Z}_i)\), the probability of being in treatment group j given individual characteristics. It has been shown that when Assumption A.2 holds and \(W_j(\mathbf{Z}_i)\) is known or can be consistently estimated, \({T_{{\scriptscriptstyle {\mathbb {L}}}1i}, \mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}1i}}, T_{{\scriptscriptstyle {\mathbb {L}}}0i}, \mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}1i}}} \perp G_i \mid W_j(\mathbf{Z}_i)\)(Rosenbaum and Rubin 1983b, 1984; Hernán et al. 2000). That is, among individuals with the same propensity score, treatment and the potential outcomes are independent. A particular example of an IPT weighted estimator in our setting is the IPT weighted Kaplan–Meier (IPTW KM) estimator (Xie and Liu 2005) of \(S_{j}(t)\):

$$\begin{aligned} \widehat{S}_{\tiny IPTW, j}(t) = \left\{ \begin{array}{ll} 1 &{}\quad \text{ if } \,t<t_{1j}\\ \prod \nolimits _{t_{kj} \le t} \left[ 1 -\frac{d_{kj}^w}{y_{kj}^w}\right] &{}\quad \text{ if } \, t\ge t_{1j} \end{array} \right. \end{aligned}$$

where \(d_{kj}^w = \sum _{i: X_{{\scriptscriptstyle {\mathbb {L}}}i}= t_{kj}, \delta _{{\scriptscriptstyle {\mathbb {L}}}i}= 1} {\widehat{W}_j(\mathbf{Z}_i)}^{-1} \delta _{{\scriptscriptstyle {\mathbb {L}}}i}I(G_i = j)\) and \(y_{kj}^w = \sum _{i: X_{{\scriptscriptstyle {\mathbb {L}}}i}{ \ge } t_{kj}} {\widehat{W}_j(\mathbf{Z}_i)}^{-1} I(G_i = j)\), \(W_j(\mathbf{Z}_i) = {P(G_{i} = j \mid \mathbf{Z}_i)}\), and \(\widehat{W}_j(\mathbf{Z}_i)\) is the estimated propensity score.

2.3 Landmark estimation of survival in an observational study

In this section we aim to develop the landmark estimation procedure of Parast et al. (2014) in the potential outcomes framework such that bias resulting from selection bias would be eliminated and estimates obtained would provide improved efficiency compared to the IPTW KM estimate by incorporating baseline and intermediate event information. As in Parast et al. (2014), we note that for \(t>t_0\), \(S_1(t)= P(T_{{\scriptscriptstyle {\mathbb {L}}}1i}> t)\) can be expressed as \(S_1(t\mid t_0) S_1(t_0)\), where

$$\begin{aligned} S_1(t\mid t_0) = P(T_{{\scriptscriptstyle {\mathbb {L}}}1i}> t \mid T_{{\scriptscriptstyle {\mathbb {L}}}1i}> t_0) \quad \text{ and }\quad S_1(t_0) = P(T_{{\scriptscriptstyle {\mathbb {L}}}1i}> t_0). \end{aligned}$$

In essence, we aim to incorporate intermediate event information in estimation of \(S_1(t\mid t_0)\) to improve the efficiency of the overall estimate of S(t), but we desire an approach that (a) does not require that we correctly specify the relationship between the intermediate event and the primary outcome since any specified model is unlikely to hold in practice and (b) accounts for selection bias. Throughout, we assume that \(t_0\) is pre-selected and fixed, however we discuss the selection of \(t_0\) further in the Discussion. We first focus on obtaining a consistent estimate of \(S_1(t \mid t_0)\) and note that,

$$\begin{aligned} S_1(t|t_0) = P(T_{{\scriptscriptstyle {\mathbb {L}}}1}>t \mid T_{{\scriptscriptstyle {\mathbb {L}}}1}> t_0) = E\{P(T_{{\scriptscriptstyle {\mathbb {L}}}1}>t \mid T_{{\scriptscriptstyle {\mathbb {L}}}1}> t_0,{\mathbf {H}}_{1})\} = E\{S_1(t|t_0, {\mathbf {H}}_{1})\} \end{aligned}$$
(2)

where \(S_1(t|t_0, {\mathbf {H}}_{1}) = P(T_{{\scriptscriptstyle {\mathbb {L}}}1}>t \mid T_{{\scriptscriptstyle {\mathbb {L}}}1}> t_0,{\mathbf {H}}_{1})\) and \({\mathbf {H}}_{1}= \{\mathbf{Z}, I(\mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}1}}\le t_0), \min (\mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}1}}, t_0) \}.\) That is, \({\mathbf {H}}_{1}\) contains all information that is potentially observable up to the landmark time, \(t_0\), for an individual who has survived to \(t_0\) and could include information on multiple intermediate events and/or covariates with repeated measurements before \(t_0\), if such data were available. Note that \({\mathbf {H}}_{1}\) is only observable for those with \(G_i = 1\) and \(X_{{\scriptscriptstyle {\mathbb {L}}}1i}> t_0\). If one were able to obtain a consistent estimate of \(S_1(t \mid t_0, {\mathbf {H}}_{1})\), denoted by \(\widehat{S}_1(t|t_0, {\mathbf {H}}_{1})\), then one could estimate \(S_1(t \mid t_0)\) by

$$\begin{aligned} \widehat{S}_{1}(t|t_0) = \frac{n^{-1} \sum _{i =1}^n \widehat{W}_1(\mathbf{Z}_i)^{-1} \widehat{S}_1(t|t_0, {\mathbf {H}}_{1i}) I(G_i=1)I(X_{{\scriptscriptstyle {\mathbb {L}}}1i}> t_0)}{n^{-1} \sum _{i =1}^n \widehat{W}_1(\mathbf{Z}_i)^{-1} I(G_i=1)I(X_{{\scriptscriptstyle {\mathbb {L}}}1i}> t_0) }. \end{aligned}$$
(3)

We will now show that we may obtain such a consistent estimate, \(\widehat{S}_1(t|t_0, {\mathbf {H}}_{1})\), of \(S_1(t \mid t_0, {\mathbf {H}}_{1}) \) by developing the two-stage procedure in Parast et al. (2014) for use in a setting where selection bias is a concern using IPTW. We first reduce the dimension of \({\mathbf {H}}_{1}\) by approximating \(S_1(t \mid t_0, {\mathbf {H}}_{1})\) with a working semiparametric model, the landmark proportional hazards model (Van Houwelingen and Putter 2012)

$$\begin{aligned} S_1(t \mid t_0,{\mathbf {H}}_{1}) = \exp \left\{ -\varLambda ^{t_0}_0(t)\exp (\varvec{\beta }_1 ^{\mathsf{\scriptscriptstyle {T}}}{\mathbf {H}}_{1}) \right\} , \quad t>t_0 \end{aligned}$$
(4)

where \(\varLambda ^{t_0}_0(\cdot )\) is the unspecified baseline cumulative hazard function for \(T_{{\scriptscriptstyle {\mathbb {L}}}1i}\) among \(\varOmega _{t_0,1} = \{X_{{\scriptscriptstyle {\mathbb {L}}}1i}> t_0, G_i=1\} \) and \(\varvec{\beta }_1\) is an unknown vector of coefficients. Let \(\widehat{\varvec{\beta }}_1\) be the maximizer of the IPT weighted log partial likelihood function,

$$\begin{aligned}&\widehat{\ell }_{t_0}(\varvec{\beta }_1) = \sum _{i \in \varOmega _{t_0,1}} \delta _{{\scriptscriptstyle {\mathbb {L}}}1i}W_1(\mathbf{Z}_i)^{-1}\nonumber \\&\quad \times \left[ \varvec{\beta }_1 ^{\mathsf{\scriptscriptstyle {T}}}{\mathbf {H}}_{1i}- \log \left\{ \sum _{j \in \varOmega _{t_0,1}} W(\mathbf{Z}_j)^{-1} e^{\varvec{\beta }_1 ^{\mathsf{\scriptscriptstyle {T}}}{\mathbf {H}}_{1j}}I(X_{{\scriptscriptstyle {\mathbb {L}}}1j}> X_{{\scriptscriptstyle {\mathbb {L}}}1i},) \right\} \right] . \end{aligned}$$
(5)

In an effort to obtain a final estimate that is robust to model misspecification, we avoid the assumption that this landmark proportional hazards model is correctly specified by focusing only on the resulting risk score \(\widehat{U}_{1i} \equiv \widehat{\varvec{\beta }}_1 ^{\mathsf{\scriptscriptstyle {T}}}{\mathbf {H}}_{1i}\). That is, instead of aiming to obtain an estimate of \(S_1(t\mid t_0, {\mathbf {H}}_{1})= P(T_{{\scriptscriptstyle {\mathbb {L}}}1}>t \mid T_{{\scriptscriptstyle {\mathbb {L}}}1}> t_0,{\mathbf {H}}_{1})\) in (2) and (3), we now change our focus to obtaining an estimate of \(S_{1}(t \mid t_0, U_1) = P(T_{{\scriptscriptstyle {\mathbb {L}}}1}> t \mid T_{{\scriptscriptstyle {\mathbb {L}}}1}>t_0, U_{1})\) where \(U_{1} = \varvec{\beta }_{10}^{\mathsf{\scriptscriptstyle {T}}}{\mathbf {H}}_{1}\) and \(\varvec{\beta }_{10}\) is the limit of \(\widehat{\varvec{\beta }}_1\). Note that the derivation supporting (2) and (3) would still hold when \(S_1(t\mid t_0, {\mathbf {H}}_{1})\) and \(\widehat{S}_1(t\mid t_0, {\mathbf {H}}_{1})\) are replaced by \(S_{1}(t \mid t_0, U_1)\) and \(\widehat{S}_{1}(t \mid t_0, \widehat{U}_1)\), a consistent estimate of \(S_{1}(t \mid t_0, U_1)\), respectively. In this first stage, the working model is essentially used as a tool to reduce the dimension of \({\mathbf {H}}\) by constructing \(\widehat{U}\).

In the second stage, we derive \(\widehat{S}_1(t|t_0, \widehat{U}_1)\), such that an estimate of \(S_1(t\mid t_0)\) can then be obtained as (3) with \( \widehat{S}_1(t\mid t_0, {\mathbf {H}}_{1})\) replaced by \(\widehat{S}_{1}(t \mid t_0, \widehat{U}_1)\). We propose to use an IPT weighted nonparametric conditional Nelson–Aalen estimator (Beran 1981) based on subjects in \(\varOmega _{t_0,1}\) to obtain an estimate of \(S_1(t \mid t_0, U_1)\). Specifically for any given t and u, the synthetic data \(\{(X_{{\scriptscriptstyle {\mathbb {L}}}1i}, \delta _{{\scriptscriptstyle {\mathbb {L}}}1i}, \widehat{U}_{1i}), i \in \varOmega _{t_0,1}\}\) is used to calculate the IPT weighted local constant estimator for the conditional hazard \(\varLambda _1(t \mid t_0,u) = -\log S_1(t\mid t_0,u)\) as

$$\begin{aligned} \widehat{\varLambda }_1(t|t_0,u) = \int _{t_0}^{t} \frac{\sum _{i \in \varOmega _{t_0,1}} \widehat{W}_1(\mathbf{Z}_i)^{-1} K_h(\widehat{U}_{1i} - u) d N_i(z)}{\sum _{i \in \varOmega _{t_0,1}} \widehat{W}_1(\mathbf{Z}_i)^{-1} K_h(\widehat{U}_{1i} - u) Y_{i}(z)} \end{aligned}$$

where \(Y_{i}(t) = I(T_{{\scriptscriptstyle {\mathbb {L}}}1i}\ge t)\), \(N_i(t) = I(T_{{\scriptscriptstyle {\mathbb {L}}}1i}\le t) \delta _{{\scriptscriptstyle {\mathbb {L}}}1i}, K(\cdot )\) is a smooth symmetric density function, \(K_h(x) = K(x/h)/h,\) and \(h=O(n^{-v})\) is a bandwidth with \(1/2 > v > 1/4\). The resulting estimate for \(S_1(t\mid t_0,U_1)\) is \(\widehat{S}_1(t\mid t_0,\widehat{U}_1) = \exp \{ -\widehat{\varLambda }_1(t \mid t_0,\widehat{U}_1) \}\). Finally, \(S_1(t \mid t_0)\) is estimated as (3) with \(\widehat{S}_1(t|t_0, {\mathbf {H}}_{1i})\) replaced by \( \widehat{S}_1(t\mid t_0,\widehat{U}_{1i}) = \exp \{-\widehat{\varLambda }_1(t|t_0, {\widehat{U}_{1i}}) \}\).

Now that we have proposed an estimation procedure for \(S_1(t|t_0)\), an estimate for \(S_1(t_0)\) follows similarly from this same two-stage procedure replacing \({\mathbf {H}}\) with \(\mathbf{Z}\) and \(\varOmega _{t_0,1}\) with \(\varOmega = \{G_i = 1\}\). Specifically, we can obtain an estimate for \(S_1(t_0)\) as

$$\begin{aligned} \widehat{S}_1(t_0) = \frac{\frac{1}{n_1}\sum \widehat{W}_1(\mathbf{Z}_i)^{-1} \widehat{S}_1(t_0 | \mathbf{Z}_i) I(G_i=1)}{\frac{1}{n_1}\sum \widehat{W}_1(\mathbf{Z}_i)^{-1} I(G_i=1)} \end{aligned}$$
(6)

where \( \widehat{S}_1(t_0 | \mathbf{Z}_i)\) is a consistent estimate of \(P(T_{{\scriptscriptstyle {\mathbb {L}}}1}>t_0 | \mathbf{Z}_i)\). To obtain \( \widehat{S}_1(t_0 | \mathbf{Z}_i)\), we use the two stage estimation procedure to obtain a risk score \(\widehat{U}^*_{1i}\) in the first stage and smooth over \(\widehat{U}^*_{1i}\) to obtain \(\widehat{\varLambda }_1(t_0 \mid \widehat{U}^*)\) such that \( \widehat{S}_{1}(t_0\mid \widehat{U}^*_{1i}) = \exp \{ -\widehat{\varLambda }_1(t_0 \mid {\widehat{U}_{1i}^*}) \}\) is a consistent estimator of \(S_1(t_0 \mid U_1^*) = P(T_{{\scriptscriptstyle {\mathbb {L}}}1i}>t_0 | U_{1}^*)\) where \(U_{1}^* = \varvec{\beta }_{10}^{* \mathsf{\scriptscriptstyle {T}}} \mathbf{Z}_i\) and \(\varvec{\beta }_{10}^*\) is the limit of \(\widehat{\varvec{\beta }}_1^*\), the maximizer of the weighted Cox partial likelihood corresponding to the working model,

$$\begin{aligned} S_1(t_0|\mathbf{Z}_1) = \exp \{ -\varLambda _0(t)\exp (\varvec{\beta }_{1}^{*^{\mathsf{\scriptscriptstyle {T}}}} \mathbf{Z}_1) \}, \end{aligned}$$
(7)

which uses only \(\mathbf{Z}\) where \(\varLambda _0(\cdot )\) is the unspecified baseline cumulative hazard function for \(T_{{\scriptscriptstyle {\mathbb {L}}}1i}\), calculated in stage 1.

An estimate for the primary quantity of interest \(S_1(t)\) in an observational study incorporating intermediate event and covariate information collected up to \(t_0\) follows as \(\widehat{S}_{ \text{ LM }, 1} (t) \equiv \widehat{S}_1(t\mid t_0) \widehat{S}_1(t_0)\) where \(\text{ LM }\) indicates that a landmark time, \(t_0\), has been used to decompose the estimate into two components. The estimate for \(S_0(t)\) follows similarly and is denoted as \(\widehat{S}_{ \text{ LM },0} (t)\). The consistency of \(S_j(t)\) follows from the consistency of \(\widehat{S}_j(t \mid t_0)\) and \(\widehat{S}_j( t_0)\) . The consistency of \(\widehat{S}_j(t \mid t_0)\) for \(S_j(t \mid t_0)\) and \(\widehat{S}_j( t_0)\) for \(S_j( t_0)\) is ensured by Assumption A.1 and Assumption A.2, the assumption that the propensity scores \(\widehat{W}_j(\mathbf{Z}_i)\) are consistent estimates for \(W_j(\mathbf{Z}_i)\), the consistency of \(\widehat{\varvec{\beta }}_j\) and \(\widehat{\varvec{\beta }}_j^*\) for some constants \(\varvec{\beta }_{j0}\) and \(\varvec{\beta }_{j0}^*\), respectively, even under misspecification of (4) and (7) (Lin 2000; Lin and Wei 1989; Pan and Schaubel 2008), and the uniform consistency of \( \widehat{S}_j(t\mid t_0,\widehat{U}_{j})\) and \( \widehat{S}_j(t_0,Z)\) which can be shown using similar arguments as in Cai et al. (2010), Du and Akritas (2002), and Parast et al. (2014) under mild regularity conditions. We discuss the assumption concerning the consistency of \(\widehat{W}_j(\mathbf{Z}_i)\) further in the Discussion.

It is worth noting that a similar two-stage approach could be used to gain efficiency even if one only has baseline covariates and no intermediate event information. That is, an estimate of S(t) incorporating only baseline covariate information, \(\mathbf{Z}\), can be obtained as in (6) with \(t_0\) replaced by t. With this approach, no landmarking is used and only a single working model specifying the relationship between \(T_{{\scriptscriptstyle {\mathbb {L}}}j}\) and \(\mathbf{Z}\) for \(j=0,1\) is needed. In our numerical studies, we calculate this estimate to shed light on how much of our observed efficiency gain is due to intermediate event information versus \(\mathbf{Z}\) information alone.

3 Estimation of the treatment effect in an observational study

We aim to estimate the average treatment effect (ATE) in terms of a difference in survival at time t. That is, the treatment effect is defined as the risk difference, \(\Delta (t) = S_1(t) - S_0(t)\). Using landmark estimation in an observational setting, we may obtain \(\widehat{\Delta } _{ \text{ LM }}(t) = \widehat{S}_{ \text{ LM },1} (t) - \widehat{S}_{ \text{ LM },0} (t)\) since \(\widehat{S}_{ \text{ LM },j} (t)\) is a consistent estimate of \(S_j(t)\). The standard error of \(\widehat{\Delta } _{ \text{ LM }}(t)\) can be estimated as \(\widehat{\sigma }(\widehat{\Delta } _{ \text{ LM }}(t))\) using a perturbation-resampling procedure as described in Sect. 4. A normal confidence interval (CI) for \(\Delta (t)\) may be constructed accordingly. To test the null hypothesis of \(H_0: \Delta (t) = 0\), a Wald-type test may be performed based on \(\widehat{Z} _{ \text{ LM }}(t) = \widehat{\Delta } _{ \text{ LM }}(t) / \widehat{\sigma }(\widehat{\Delta } _{ \text{ LM }}(t))\). To examine bias and efficiency in estimation of a treatment effect, we compare this testing procedure to a test based on (1) the KM estimate in an RCT setting, \(\widehat{\Delta }_{ \text{ KM }}(t) = \widehat{S}_{ \text{ KM },1}(t) - \widehat{S}_{ \text{ KM },0}(t)\), 2) the landmark estimation procedure for an RCT setting \(\widehat{\Delta }^{ \text{ RCT }}_{ \text{ LM }}(t) = \widehat{S}^{ \text{ RCT }}_{ \text{ LM },1}(t) - \widehat{S}^{ \text{ RCT }}_{ \text{ LM },0}(t)\), and 3) the IPTW KM estimate \(\widehat{\Delta }_{ \text{ IPTW }}(t) = \widehat{S}_{ \text{ IPTW },1}(t) - \widehat{S}_{ \text{ IPTW },0}(t)\), where \(\widehat{S}^{ \text{ RCT }}_{ \text{ LM },j}(t)\) is the estimate of survival for treatment group j obtained using the landmark estimation procedure for an RCT setting.

4 Variance estimation using perturbation-resampling

To obtain variance estimates, we use a perturbation-resampling method (Park and Wei 2003; Cai et al. 2005; Tian et al. 2007). Specifically, let \(\{{\mathbf {V}}^{(b)}=(V_1^{(b)}, \ldots ,V_n^{(b)})^{\mathsf{\scriptscriptstyle {T}}}, b=1,\ldots ,B\}\) be \(n\times B\) independent copies of a positive random variable U from a known distribution with unit mean and unit variance such as an Exp(1) distribution. To estimate the variance of our proposed procedure, for \(j=0,1\), let

where

$$\begin{aligned} \widehat{\varLambda }^{(b)}_j \left( t|t_0, {\widehat{U}^{(b)}_{ji}}\right) = \int _{t_0}^{t} \frac{\sum _{i \in \varOmega _{t_0,j}} V_i^{(b)} \left[ \widehat{W}_j(\mathbf{Z}_i)^{(b)}\right] ^{-1} K_h\left( \widehat{U}^{(b)}_{ji} - u\right) d N_i(z)}{\sum _{i \in \varOmega _{t_0,j}} V_i^{(b)} \left[ \widehat{W}_j(\mathbf{Z}_i)^{(b)}\right] ^{-1} K_h\left( \widehat{U}^{(b)}_{ji} - u\right) Y_{i}(z)}, \end{aligned}$$

\( \widehat{U}^{(b)}_{ji} = \widehat{\beta }^{(b)}_j {\mathbf {H}}_{ji}\) and \(\widehat{\beta }^{(b)}_j\) is the solution to (5) but with additional weights \(V_i^{(b)}\) and \({\widehat{W}_j(\mathbf{Z}_i)}^{(b)} = {\widehat{P}^{(b)}(G_{i} = j \mid \mathbf{Z}_i)}\) where \(\widehat{P}^{(b)}(G_{i} = j \mid \mathbf{Z}_i)\) is obtained using weights \(V_i^{(b)}\). For example, if \(\widehat{W}_j(\mathbf{Z}_i)\) is estimated using logistic regression,the perturbed version is estimated using weighted logistic regression with weights \(V_i^{(b)}\). Similarly, \(\widehat{S}_j^{ (b) }(t_0)\) can be obtained by replacing \({\mathbf {H}}_i = \mathbf{Z}_i\) throughout and using all patients \(\{G_i = j\}\). We now let \(\widehat{S}_{ \text{ LM },j}^{ (b) }(t) \equiv \widehat{S}_j^{(b)}(t\mid t_0) \widehat{S}_j^{ (b) }(t_0)\) and estimate the variance of \(\widehat{S}_{ \text{ LM },j} (t) \) as the empirical variance of \(\{\widehat{S}_{ \text{ LM },j}^{ (b) }(t), b=1,\ldots ,B\}\). This procedure can be used to obtain \(\widehat{\Delta }_{ \text{ LM }}^{ (b) }(t) = \widehat{S}_{ \text{ LM },1}^{ (b) }(t) - \widehat{S}_{ \text{ LM },0}^{(b) }(t)\) for \(b=1,\ldots ,B\). Then one can estimate \(\hat{\sigma }(\widehat{\Delta }_{ \text{ LM }} (t))\) as the empirical variance of \(\{ \widehat{\Delta }_{ \text{ LM }}^{ (b) }(t), b=1,\ldots ,B\} \). In the numerical examples, we use this approach to obtain variance estimates for the standard KM estimator, the IPTW KM estimator, and the RCT version of the landmark estimator as well.

To construct \(100(1-\alpha )\%\) confidence intervals, one can either use the empirical percentiles of the perturbed samples (i.e., \(100\alpha /2^{th}\) and \(100(1-\alpha /2)^{th}\) percentiles) or a normal approximation (i.e. \(\widehat{S}_{ \text{ LM },j}(t) \pm c \widehat{\sigma }_{ \text{ LM },j}(t)\) where \(\widehat{\sigma }_{ \text{ LM },j}(t)\) is the empirical variance of \(\{\widehat{S}_{ \text{ LM },j}^{ (b) }(t), b=1,\ldots ,B\}\) and c is the \(100(1-\alpha /2)^{th}\) percentile of the standard normal distribution). The validity of the perturbation-resampling procedure can be shown using similar arguments as in Cai et al. (2010) and Zhao et al. (2010) since the distribution of \(\sqrt{n}\{\widehat{S}_{ \text{ LM },j}(t) - S_j(t) \}\) can be approximated by the distribution of \(\sqrt{n}\{\widehat{S}_{ \text{ LM },j}^{ (b)}(t) - \widehat{S}_{ \text{ LM },j}(t) \}\) conditional on the observed data.

5 Simulation study

We conducted simulation studies to examine the finite sample properties of the proposed estimation procedures. For illustration, \(t_0\) =1 year and t = 2 years i.e. we are interested in the probability of survival past 2 years. In all simulations, \(W_j(\mathbf{Z}_i)\) is estimated using logistic regression, n=2000 for each treatment group and results summarize 1000 replications. The single baseline covariate Z was generated from a N(1, 2) distribution in the treatment group and from a N(0.5, 2) distribution in the control group. Censoring, C, was generated from a mixed distribution where \(C = BC_1 + (1-B)C_2\), \(B \sim Bernoulli(0.5)\), \(C_1 \sim Exp(0.5)\), and \(C_2 \sim Exp(0.9)\). In all settings, Assumption A.1 (censoring is independent of potential outcomes and Z) and Assumption A.2 (treatment group is independent of potential outcomes given Z) hold.

In simulation setting (i), there is no treatment effect, event times for the single intermediate event are generated as \(T_{\scriptscriptstyle {\mathbb {S}}}= \exp \{-Y + \epsilon _S\}\) where \(Y\sim N(0.7,4)\) and \(\epsilon _S \sim N(0, 0.49)\) in both groups, and survival times are generated as \(T_{\scriptscriptstyle {\mathbb {L}}}={ T_{\scriptscriptstyle {\mathbb {S}}}} + \exp \{ (-2 Z + \epsilon _L )/8 \}\) where \(\epsilon _L \sim N(1,2.25)\) in both groups. That is, there is selection bias through Z. This two-part distribution was selected to reflect a situation where the model describing the relationship between \(T_{\scriptscriptstyle {\mathbb {L}}}\), \(T_{\scriptscriptstyle {\mathbb {S}}}\) and Z would be difficult to correctly specify. Note that in these simulations \(T_{\scriptscriptstyle {\mathbb {S}}}\) occurs before \(T_{\scriptscriptstyle {\mathbb {L}}}\) but our method does not require this to be true. In this setting, \(P(T_{{\scriptscriptstyle {\mathbb {L}}}1i}> t) = P(T_{{\scriptscriptstyle {\mathbb {L}}}0i}> t) = 0.436\), about 61 % of individuals in the treatment group are censored, 63 % of individuals in the control group are censored, 39 % of individuals in the treatment group survive past \(t_0\), 41 % of individuals in the control group survive past \(t_0\), of those that survive past \(t_0\), 52 and 54 % have the intermediate event before \(t_0\) in the treatment and control groups, respectively. In simulation setting (ii), there is a moderate treatment effect, event times for the single intermediate event and survival times for the control group are generated as in setting (i), event times for the single intermediate event in the treatment group are generated as \(T_{\scriptscriptstyle {\mathbb {S}}}= \exp \{-Y + \epsilon _S\}\) where \(Y\sim N(0.7,4)\) and \(\epsilon _S \sim N(0.1, 0.49)\), and survival times in the treatment group are generated as \(T_{\scriptscriptstyle {\mathbb {L}}}= { T_{\scriptscriptstyle {\mathbb {S}}}} + \exp \{ (-1.5 Z + \epsilon _L )/8 \}\) where \(\epsilon _L \sim N(2,2.25)\). That is, treatment prolongs survival. In this setting, \(P(T_{{\scriptscriptstyle {\mathbb {L}}}0i}> t) = 0.436\), \(P(T_{{\scriptscriptstyle {\mathbb {L}}}1i}> t) = 0.483\), about 64 % of individuals in the treatment group are censored, 63 % of individuals in the control group are censored, 43 % of individuals in the treatment group survive past \(t_0\), 41 % of individuals in the control group survive past \(t_0\), of those that survive past \(t_0\), 55 and 54 % have the intermediate event before \(t_0\) in the treatment and control groups, respectively.

Table 1 Resulting survival estimates, \( \widehat{S}_{ \text{ KM }, j}(t)\), \(\widehat{S}_{ \text{ IPTW }, j}(t)\), \( \widehat{S}^{ \text{ RCT }}_{ \text{ LM }, j}(t)\), and \(\widehat{S}_{ \text{ LM }, j}(t)\) for \(j =0\) and 1 and corresponding bias, empirical standard error (ESE), average standard error (ASE), mean squared error (MSE), relative efficiency (RE) for the unbiased estimates only with respect to the IPTW KM estimator, and coverage (of 95 % confidence intervals) in the null treatment effect setting (i) and moderate treatment effect setting (ii); note that the control estimates in the moderate treatment effect setting are the same as the control estimates in the null treatment effect setting
Full size table
Table 2 Resulting treatment effect estimates, \( \widehat{\Delta }_{ \text{ KM }}(t)\), \(\widehat{\Delta }_{ \text{ IPTW }}(t)\), \( \widehat{\Delta }^{ \text{ RCT }}_{ \text{ LM }}(t)\), and \(\widehat{\Delta }_{ \text{ LM }}(t)\) and corresponding bias, empirical standard error (ESE), average standard error (ASE), mean squared error(MSE), relative efficiency (RE) for the unbiased estimates only with respect to the IPTW KM estimator, and Type 1 error in the null treatment effect setting (i) and power in the moderate treatment effect setting (ii)
Full size table

In each setting, we estimate \(S_j(t)\) in each group using the Kaplan–Meier estimate, \(\widehat{S}_{ \text{ KM }, j}(t)\), the IPTW KM estimate, \(\widehat{S}_{ \text{ IPTW }, j}(t)\), the landmark estimator developed in an RCT setting, \( \widehat{S}^{ \text{ RCT }}_{ \text{ LM }, j}(t)\), and the landmark estimator proposed here, \(\widehat{S}_{ \text{ LM }, j}(t)\). We summarize our simulation results in terms of the average estimate, bias, empirical standard error (the standard deviation of the 1000 estimates), average standard error (the average of the 1000 standard error estimates), mean squared error (the average of the 1000 squared bias estimates), relative efficiency (relative to the IPTW KM estimate), and coverage of the truth for the 1000 95 % confidence intervals. Table 1 shows the performance of the resulting survival estimates for the control group (\(j=0\)), and for the treatment group (\(j=1\)) in setting (i) and (ii). Note that only the distribution of the treatment group differs in setting (i) and (ii) and therefore the distribution of the control group is the same in both settings. Results show that estimates obtained using the standard Kaplan–Meier and the landmark estimation procedure for the randomized setting are biased, as expected. Estimates obtained using either the IPTW Kaplan–Meier estimate or the proposed landmark estimation procedure have very small bias and the proposed landmark estimation procedure provides improved efficiency with respect to the MSE ranging from 16–23 %. For the proposed landmark estimation procedure, standard error estimates obtained using perturbation-resampling procedure are close to the empirical estimates and coverage levels are close to the nominal 0.95 level. Table 2 shows the performance of the treatment effect estimates, \( \widehat{\Delta }_{ \text{ KM }}(t)\), \(\widehat{\Delta }_{ \text{ IPTW }}(t)\), \( \widehat{\Delta }^{ \text{ RCT }}_{ \text{ LM }}(t)\), and \(\widehat{\Delta }_{ \text{ LM }}(t)\) in both settings. Unweighted estimates, \( \widehat{\Delta }_{ \text{ KM }}(t)\) and \( \widehat{\Delta }_{ \text{ LM }}(t)\) have large bias in both settings, Type 1 error rates much larger than 0.05 in the null setting, and poor power in the moderate treatment effect setting. Both IPT weighted estimates have very small bias and Type 1 error rates close to 0.05 in the null setting. In terms of treatment effect estimation, the proposed landmark estimation procedure provides increased efficiency (24–28 %) compared to the IPTW KM estimate and improved power in setting (ii) (0.439 vs. 0.525). We also obtained estimates of survival and treatment effect using the two-stage approach incorporating baseline Z information only and observed efficiency gains in terms of MSE ranging from 5 to 7 % demonstrating that the efficiency gains of 24–28 % observed using the proposed approach can be attributed to incorporating both baseline and intermediate event information.

6 Example

We illustrate the proposed procedures using a dataset from the acquired immunodeficiency syndrome (AIDS) Clinical Trial Group (ACTG) Protocol 175 (Hammer et al. 1996). This dataset consists of 2464 patients with human immunodeficiency virus (HIV) randomized to 4 different treatments: zidovudine only, zidovudine + didanosine, zidovudine + zalcitabine, and didanosine only. In the original study the goal was to compare the relative effectiveness of these four treatment conditions on time until progression to AIDS (measured by a 50 % decline in CD4 cell counts) or death with death alone being a secondary end point. In this paper, we aim to examine the effect of previous antiretroviral treatment on time until death using patients from ACTG 175. Prior use of antiretrovirals (ART) was measured at baseline in the study for all study participants and it has been shown that previous antiretroviral therapy is highly predictive of survival. Results on the direction can vary. While ART itself is generally associated with improved survival rates, individuals receiving or who have received ART tend to be sicker which means that selection bias can result in that group showing worse survival (Hammer et al. 1997; Patel et al. 2008; Bhatta et al. 2013; Wood et al. 2003; Mocroft et al. 1999). Thus, it is important for any analysis involving prior antiretroviral to appropriately take into account the fact that patients who are antiretroviral naïve and patients with prior antiretroviral may differ from one another on a number of important baseline characteristics. We aim here to understand how such characteristics might bias the estimated relationship between prior antiretrovirals and survival in patients with HIV. Specifically, our analysis compares survival among the 1065 individuals who were antiretroviral naïve (Group 0) versus the 1399 individuals with prior antiretroviral therapy (Group 1).

Our long term event of interest, \(T_{\scriptscriptstyle {\mathbb {L}}}\), is the time from treatment randomization to death and intermediate event information consists of two intermediate events, \(\mathbf {T_{{\scriptscriptstyle {\mathbb {S}}}}}= (T_{{\scriptscriptstyle {\mathbb {S}}}1}, T_{{\scriptscriptstyle {\mathbb {S}}}2})^{\mathsf{\scriptscriptstyle {T}}}\) where \(T_{{\scriptscriptstyle {\mathbb {S}}}1}= \) time from randomization to an AIDS-defining event e.g. pneumocystis pneumonia and \(T_{{\scriptscriptstyle {\mathbb {S}}}2}= \) time from randomization to a 50 % decline in CD4. If a patient experienced multiple intermediate events of one kind, for example multiple AIDS-defining events, the earliest occurrence of the event was used. For illustration, \(t_0 = \) 1 year and \(t = \) 2.5 years. Among individuals with prior antiretroviral therapy experience, 15.7 % were censored before 2.5 years while 31.8 % of antiretroviral therapy naïve individuals were censored before 2.5 years. Seventy individuals (5.0 %) with prior antiretroviral therapy experience and 25 (2.3 %) antiretroviral therapy naïve individuals experienced a decrease in CD4 count of at least 50 % within the first year of the study and survived past the first year, respectively. Twenty-seven (1.9 %) individuals with prior antiretroviral therapy experience and 9 (0.8 %) antiretroviral therapy nave individuals experienced an AIDS defining event within the first year of the study and survived past the first year, respectively.

Table 3 Balance tables when using (a) no weights and (b) IPTW obtained using logistic regression across all covariates for the group with more than 52 weeks of antiretroviral therapy experience (Group 1) and the group with no antiretroviral therapy experience (naïve) (Group 0) where SD denotes standard deviation and ASMD denotes the absolute standardized mean difference
Full size table

We estimate the average treatment effect using IPTW estimated using a logistic regression model that included all available baseline covariates. Namely, we aim to balance patients in our two exposure groups on the available observed covariates: the mean of two baseline CD4 counts, Karnofsky score, age at randomization, weight, symptomatic status, and treatment group to which they were originally randomized. Assessing balance is an important step given our requirement that our weights are consistently estimated. While it can be difficult to ensure that this assumption holds in practice, achieving balance in the two groups after weighting provides a good indication that bias in the treatment effect estimate due to observed covariates will be minimized (Stuart et al. 2013; Harder et al. 2010; Marcus et al. 2008). Table 3 shows balance for the groups before and after IPT weighting where we evaluate balance between the two prior therapy groups on the observed baseline covariates by examining a balance metric that summarizes the differences between the two univariate distributions of each baseline covariate, the absolute standardized mean difference (ASMD). For each covariate, the ASMD is the absolute value of the Group 1 mean minus the Group 0 mean divided by the pooled sample (Group 0 and 1) standard deviation. Sufficient balance is achieved when ASMD \(<\) 0.10 for all baseline covariates (Austin 2007; Austin and Stuart 2015; Austin 2009; Normand et al. 2001; Hankey and Myers 1971). The unweighted portion of the table shows that there were three notable differences between two prior therapy groups. Specifically, individuals in the antiretroviral therapy experienced group are more likely to have a lower average CD4 count at baseline (ASMD = 0.316), a lower mean weight (ASMD = 0.154) and a higher mean age at randomization (ASMD = 0.181). These characteristics associated with antiretroviral therapy experience are also known to be highly associated with survival among individuals with HIV. For example, patients who are older and skinnier are likely to be less healthy than other patients and at a higher risk of death. After IPT weighting, the two prior therapy groups appear balanced on all covariates. After weighting, there are no meaningful differences between the two prior therapy groups (all ASMD’s below 0.005). Given this, the IPTW obtained using logistic regression are used to estimate survival and the effect of prior antiretroviral therapy in both the IPTW KM estimates and the IPTW landmark estimation procedure.

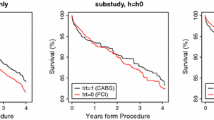
Figure 1 displays the unweighted KM estimate of survival in each group. As shown, without adjustment, individuals in the prior antiretroviral group appear to have worse survival than those in the naïve group. Table 4 shows the estimated 2.5-year survival for each prior therapy group and the estimated treatment effects comparing the two groups using four different methods: unweighted KM, IPTW KM, RCT landmark estimation, and IPTW landmark estimation. As shown, the unweighted KM estimates show 2.5-year survival in the naïve therapy and prior therapy groups to be 0.953 and 0.937, respectively (p = 0.1034). The RCT landmark estimation supports similar survival estimates for the two groups. After weighting by the IPTW in either the KM or landmark estimation approach, we find the survival estimates for the two groups to be more similar, 0.948 versus 0.945, with IPTW KM and 0.950 and 0.947 with IPTW landmark estimation. This shift in survival estimates shows a clear connection to the imbalances in the baseline covariates between the two groups. Without IPTW adjustment, the group of individuals with prior ART appeared to have worse survival because they also tended to have higher CD4 counts, lower weight, and higher mean age. After proper adjustment for the imbalances, no significant differences are found between the two groups (p-values for both IPTW methods \(>\)0.50). Nonetheless, the IPT weighted landmark estimation procedure is roughly 16 % more efficient than that from the IPTW KM estimate, showing one example of the types of increases in precision that might be gained by using landmark estimation in observational studies.

Fig. 1
figure 1

Kaplan–Meier estimate of survival for antiretroviral naïve group (black line) and antiretroviral experienced group (grey line)

Full size image
Table 4 Resulting estimates of (a) S(t) and (b) \(\Delta (t)\) for t = 2.5 years in two exposure groups from ACTG Protocol 175 using the Kaplan–Meier estimator, \(\widehat{S}_{ \text{ KM }, j}(t)\), \(\widehat{\Delta }_{ \text{ KM }}(t)\); the IPTW KM estimator, \(\widehat{S}_{ \text{ IPTW }, j}(t)\), \(\widehat{\Delta }_{ \text{ IPTW }}(t)\); the landmark estimator from an RCT setting, \( \widehat{S}^{ \text{ RCT }}_{ \text{ LM }, j}(t) \), \( \widehat{\Delta }^{ \text{ RCT }}_{ \text{ LM }}(t)\); and the proposed landmark estimator, \( \widehat{S}_{ \text{ LM }, j}(t) \), \( \widehat{\Delta }_{ \text{ LM }}(t)\), with corresponding standard error from the perturbation-resampling method (SE), and relative efficiency (RE) for the unbiased estimates only with respect to the IPTW KM estimator, and corresponding p-values in (b), where \(j=0\) indicates antiretroviral naïve and \(j=1\) indicates antiretroviral experienced
Full size table

To shed light on whether this observed efficiency gain is due to the incorporation of both intermediate event information and baseline covariate information, we compared our estimates to those obtained using the two-stage procedure with only baseline covariates. The estimate of survival in the antiretroviral naïve group was 0.949 (SE = 0.008), the estimate of survival in the antiretroviral experienced group was 0.946 (SE = 0.006), and the estimate of the treatment effect in terms of the difference in survival was \(-\)0.0027 (SE = 0.01). The gains in efficiency using only baseline information compared to the IPTW KM estimate were thus about 3 % for the survival estimates and 6 % for the treatment effect estimate. Comparing these efficiency gains to those obtained using intermediate event information and baseline covariate information (5–10 % for survival, 16 % for treatment effect) demonstrates that in this particular application, the use of intermediate event information leads to improved efficiency over just using baseline measures.

Among the 1399 individuals with prior antiretroviral therapy in the trial, 476 individuals had 1–52 weeks of prior antiretroviral therapy and 923 individuals had over 52 weeks of prior antiretroviral therapy. Because the effect of antiretroviral therapy on survival may be quite different for those with extended prior therapy, we provide an additional analysis in the Supplementary Material comparing individuals who were antiretroviral naïve to those who had over 52 weeks of prior antiretroviral therapy. We discuss this further in the Discussion.

7 Discussion

In this paper we have developed the landmark estimation procedure of Parast et al. (2014) for use in an observational setting. It is particularly important to account for the possibility of selection bias in an observational setting when treatment is not randomized since failure to do so may lead to biased estimates. Our simulation study shows that the use of the landmark estimation procedure from an RCT setting in the presence of selection bias does lead to biased estimates of survival and treatment effects. Furthermore, our proposed extension leads to unbiased estimates and improved efficiency compared to the unbiased IPTW KM estimator.

In addition to providing improved efficiency, our approach is robust to model misspecification of (4) and (7). If one were to assume that the outcome models (4) and (7) were correctly specified, one could simply use these models to obtain the desired survival probabilities and average over the observed covariate patterns. If these models are indeed correct, this approach would likely be more efficient than our proposed approach. However, if these models are not correct, this approach may lead to biased estimates. While such robustness is desirable, it is important to note that our proposed approach does still rely on the consistency of our IPTW. The literature is now rich with methods available to estimate IPTW (McCaffrey et al. 2004; van der Laan 2014; Breiman et al. 1984; Hill 2011; Imai and Ratkovic 2014; Liaw and Wiener 2002). In all applications of IPTW, concerns about the treatment assignment model being misspecified arise. In practice, parametric methods, such as logistic regression, tend to be used to model the treatment assignment indicator and estimate associated probabilities. However, generalized boosted models (GBM) and other machine learning techniques like the super learner have been proposed as an alternative for IPTW estimation as a way to minimize bias from incorrect assumptions about the form of the model used (McCaffrey et al. 2004; van der Laan 2014; Imbens 2000; Robins et al. 2000). These methods eliminate reliance on a simple parametric logistic regression model and do not require the researcher to determine which covariates and interactions should be included in the model. It has been shown that the resulting weights from these approaches yield more precise treatment effect estimates and lower mean squared error than traditional logistic regres- sion methods and other alternative machine learning techniques (Harder et al. 2010; Lee et al. 2010). As a sensitivity analysis, we examined weights and resulting balance from GBM applied to the AIDS Clinical Trial dataset from Sect. 6 and our results were similar. In our approach, there is a trade-off between using parametric models like the logistic regression model and machine learner methods like GBM when constructing the IPTW. When utilizing logistic regression, the perturbation-resampling procedure described in Sect. 4 is straightforward and easily applied as it only involves fitting a weighted logistic model for each iteration while with GBM and other machine learners, perturbation-resampling becomes computationally intensive and in some cases infeasible if the machine learner method cannot incorporate the weights \({\mathbf {V}}_i^{(b)}\). Future work is still needed to develop best practices for perturbation-resampling with machine learning procedures. In light of these trade-offs, we suggest that IPTW estimated by logistic regression models be utilized as long as balance between treatment and comparison groups has been obtain (e.g., a sign that bias from observed covariates in the treatment effect estimate should be limited) to allow for efficient use of the perturbation resampling approach. In contrast, if poor balance is obtained using parametric models we suggest the use of more state of the art methods like GBM to estimate the IPTW at the expense of foregoing perturbation-resampling of the IPTW.

We illustrated our proposed method using an AIDS clinical trial dataset and examined the effect of prior antiretroviral therapy on survival. We performed two analyses, one using all individuals and dichotomizing into prior therapy naïve compared to prior therapy experienced, and a second analysis removing individuals with 1-52 weeks of prior antiretroviral therapy (presented in the Supplementary Material). However, it would be of interest to instead use the actual time of prior antiretrovival therapy experience rather than dichotomizing into two groups. The use of methodology that allows for treatment effect estimation with a continuous treatment, rather than dichotomous treatment groups, would be applicable in this example (Imai and Van Dyk 2004; Hirano and Imbens 2004; Zhu et al. 2015). Furthermore, future development of a landmark estimation procedure that can accommodate continuous treatment would be warranted.

A limitation of our proposed method is the required strong assumption that there are no unmeasured confounders in the model for the IPTW (Assumption A.2). In practice, one could consider sensitivity analyses to examine how sensitive the observed findings might be to violations of this assumption (Griffin et al. 2013; Rosenbaum and Rubin 1983a; Higashi et al. 2005).

A second limitation of our proposed method is the assumption that \(t_0\) is pre-selected and fixed. There are several issues to consider when selecting \(t_0\). First, as was shown in Parast et al. (2014), the gain in efficiency that is observed when using a landmark estimation approach that incorporates intermediate event information is due to both the correlation between \(T_{\scriptscriptstyle {\mathbb {L}}}\) and \(\{T_{\scriptscriptstyle {\mathbb {S}}}, Z\}\) and censoring. If there was weak correlation or very little censoring between \(t_0\) and t, we would not expect to gain much efficiency using this approach. Second, if \(t_0\) is chosen to be too close to baseline (or time of treatment initiation), we would not expect to observe many intermediate events between baseline and \(t_0\) and thus incorporating intermediate event information is unlikely to lead to large gains in efficiency. On the other hand, if \(t_0\) is chosen to be too close to t, then the subgroup with \(X_{{\scriptscriptstyle {\mathbb {L}}}}>t_0\) may be very small and thus we may also expect only small gains in efficiency and/or potentially small bias due to smoothing over a small sample. In the Supplementary Material we present simulation results across a range of \(t_0\) (fixing \(t=2\)) and results from the example across a range of \(t_0\) (fixing \(t=2.5\) years). While the results for the example show that our findings are quite robust to the choice of \(t_0\), the results for the simulation study do demonstrate variability in relative efficiency with respect to the choice of \(t_0\). For example, when \(t_0=0.5\) in the moderate treatment effect setting, the relative efficiency with respect to the IPTW KM estimator is almost 27 % but when \(t_0=1.5\) in this setting, the relative efficiency is less than 6 %. Future work on the selection of \(t_0\) either by examining efficiency across a range to identify the optimal \(t_0\) (accounting for the selection procedure when making inference) or by considering a combination of multiple landmark times would be very useful in practice.

An R package implementing the methods described here, called landest, is available on CRAN.