Introduction

The proportion of energy consumption and greenhouse gas (GHG) emissions generated by domestic and industrial refrigeration and air-conditioning applications continues to soar worldwide. This energy consumption is likely to increase rapidly due to global warming. Current environmental requirements and green standards limit conventional technologies, particularly thermodynamic techniques based on the compression–expansion cycle of gases (such as CFCs and HCFCs) [1,2,3]. Research into future refrigeration technologies is moving toward other principles, such as magnetocaloric refrigeration, whose advantages include zero GHG emissions, silent operation, and high efficiency [4]. Another fundamental benefit is that magnetic refrigeration can reach very low temperatures if the operating parameters are well chosen. In particular, this type of refrigeration can be used to liquefy hydrogen, which has a condensation temperature of around 22 K at atmospheric pressure, or any other cryogenic uses that are impossible with conventional refrigeration systems.

All magnetic refrigeration technologies use properties and physical phenomena specific to materials resulting from the application of a magnetic field. Applying a magnetic field to a material causes the spins to orient themselves in a specific direction resulting in a reduction in disorder and, thus, in magnetic entropy (∆Sm). Also, reducing the magnetic field causes the opposite phenomenon, i.e., an increase in magnetic entropy. In an adiabatic process, the change in total entropy (∆S), the sum of the change in magnetic entropy, and the change in lattice entropy (∆Sr) is zero (∆S = ∆Sm + ∆Sr = 0, the electron entropy is neglected). Therefore, any decrease in ∆Sm is offset by an increase in ∆Sr, and vice versa. The increase in a material's ∆Sr is due to the increased agitation of its molecules, which in turn implies an increase in the material's temperature. The decrease in ∆Sr is due to the decrease in the agitation of the molecules, which in turn leads to a decrease in the material's temperature. The magnetocaloric effect can, therefore, be summed up by the fact that the application of a magnetic field aligns the magnetic moments, creating a form of order in a magnetocaloric material. Under adiabatic conditions and for paramagnetic or ferromagnetic materials, this transition from a disordered magnetic state to an ordered one is accompanied by an increase in the intensity of atomic vibrations, raising the temperature in the material. Decreasing the magnetic field causes the opposite phenomenon, i.e., a decrease in temperature. [5,6,7,8].

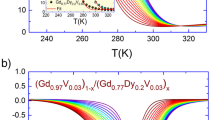
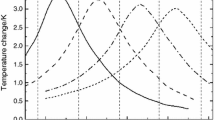
The magnetocaloric effect is only noticeable at temperatures very close to the material's Curie temperature (Tc) (the critical transition temperature between the ferromagnetic and paramagnetic phases). Figure 1b shows that the Tc changes if the active material changes [9]. Figure 1a shows that the variation of magnetic entropy increases considerably as a function of the applied magnetic field; this variation is maximal at the Tc but lower on either side of the Tc temperature [10].

Fig. 1
figure 1

a Magnetic entropy changes in the Gd0.4Tb0.6Co2 as a function of temperature and magnetic field [10] b Temperature dependence of magnetic entropy for (Tb1−xDyx) FeSi (x = 0–1) compounds and the composite material under a magnetic field of 1T [9].

Full size image

The response of a magnetocaloric material to a magnetic field (magnetization and demagnetization) is similar to the reaction of gas to compression or expansion replaced by magnetization (heating) and demagnetization (cooling), respectively. The direct exploitation of the magnetocaloric effect around the material's transition temperature is limited because existing magnetocaloric materials are unable to achieve high temperature differentials. This technical barrier can be overcome by applying active magnetic regenerative cooling [11]. Figure 2 gives a schematic presentation of an active magnetic regenerative refrigeration system. The four stages of this cycle are as follows:

Fig. 2
figure 2

Schematic representation of an active magnetic regenerative refrigeration system

Full size image

Step 1 Material magnetization. The entire system is at an initial temperature. The temperature of each point of the regenerator material increases by ∆T.

Stage 2 Fluid flows from cold source to hot source. The heat of magnetization is dissipated by the fluid flowing from the cold source to the hot one. A temperature gradient is created along the bed.

Stage 3 Material demagnetization. The temperature at each point of the regenerator drops by ∆T as a result of demagnetization.

Stage 4 Fluid flows from the hot source to the cold source. The fluid flowing from the hot source to the cold one transfers its heat to the regenerator. The gradient is amplified.

Based on a previous study [12] and the resolution of the continuity, momentum, and energy conservation equations [13,14,15,16,17,18], we determined the temperature profile along the active material. Figure 3 shows the profile found by numerical simulation, where the material is gadolinium, the heat transfer fluid is water, the pressure is atmospheric, and the temperature difference between the hot and cold sides is 20. The temperature profile is not constant along the entire material’s length, and after a transient, the material temperature profile is almost linear between the cold and hot sides. If the temperature gap between the hot and cold sides is large, a multi-layer regenerator is required since the magnetocaloric effect only manifests at the Tc of the material used.

Fig. 3
figure 3

Temperature variation along the length of the active material between cold and hot sides.

Full size image

Improvements in heat transfer between the regenerator (active material) and the heat transfer fluid are possible using nanofluids [19,20,21,22,23,24,25,26]. To master this technology and increase its efficiency, we need to control the parameters on which the value of the regenerator's magnetocaloric effect depends, including the material’s Tc, the applied magnetic field, and the material's mass (since entropy is an extensive quantity).

These quantities are generally determined experimentally by characterizing the materials, and a database can be built from them, but the exploitation of this database is difficult because it is random. However, we can find some theoretical models to predict the thermodynamic properties of the material [27]; However, these models are rare and still in differential form. A model of these quantities is therefore necessary for their subsequent use. Extensive research has been carried out worldwide to develop promising magnetocaloric refrigeration technologies, which have enabled us to understand the mechanisms of the magnetocaloric effect exhibited by many materials and to manufacture new alloys likely to be used massively for refrigeration and air conditioning in the years to come. A summary of recent advances in materials development and the development of magnetocaloric cooling and heating prototypes shows that there are no methods for sizing a magnetic refrigeration system.

Our work is part of an effort to highlight the importance of an optimized design of the magnetocaloric regenerators at the heart of these machines. In this work, theoretical approaches were developed, validated, and exploited to find original models and methods for choosing the appropriate magnetic material to use according to well-defined specifications. A method for sizing a multilayer magnetic regenerator will then be developed.

Theoretical modeling

Before presenting the theoretical modeling of magnetic entropy, we introduce the thermodynamic and statistical approaches.

Thermodynamic approach

The differential of the free energy F [28, 30] is:

$$\text{d}F\left( {V,B,T} \right) = - P{\text{d}}V - M{\text{d}}B - S{\text{d}}T$$
(1)

The material is solid, so there is no change in volume, hence:

$$\text{d}F\left( {B,T} \right) = - M\text{d}B - S\text{d}T$$
(2)

So,

$$M = - \left( {\frac{\partial F}{{\partial B}}} \right)_{{\text{T}}}$$
(3)

F(B, T) is a state function; therefore, its differential is an exact total differential. Thus, we can write:

$$\Delta S_{{\text{m}}} \left( {T,B} \right) = \mathop \smallint \limits_{0}^{{\text{B}}} \left( {\frac{\partial M}{{\partial T}}} \right)_{{\text{B}}} \text{d}B$$
(4)

Statistical approach

The free energy of the system, made up of N magnetic atoms, has the following form [31,32,33,34,35]

$$F = - Nk_{{\text{B}}} TLnZ$$
(5)

N is the Avogadro number, kB is Boltzmann's constant, and Z is the partition function.

The statistical sum (partition function) of a system can be determined as follows:

$$Z = \frac{{{\text{sinh}}\left( {2J + 1} \right)\frac{x}{2}}}{{{\text{sinh}}\left( \frac{x}{2} \right)}}$$
(6)

with

$$x = \frac{{J\mu_{{\text{B}}} gB}}{{k_{{\text{B}}} T}}$$
(7)

where g is the Lander factor, and J is the total angular momentum.

The free energy of the system is therefore as follows:

$$F = - Nk_{{\text{B}}} T{\text{Ln}}\left( {\frac{{{\text{sinh}}\left( {2J + 1} \right)\frac{x}{2}}}{{{\text{sinh}}\left( \frac{x}{2} \right)}}} \right)$$
(8)

We can write:

$$M = NJg\mu_{{\text{B}}} B_{{\text{J}}} \left( x \right)$$
(9)

where BJ(x) is the Brillouin function given by the following equation:

$$B_{{\text{J}}} \left( x \right) = \frac{ 2J + 1}{{2J}}\text{coth}\left( {\frac{ 2J + 1}{{2J}}x} \right) - \frac{1}{2J} \text{coth} \frac{x}{2J}$$
(10)

Theoretical modeling of magnetic entropy

The Curie temperature, or critical temperature (Tc), is the temperature at which magnetic materials undergo a sudden change in their magnetic properties. It is considered the critical point at which a material’s intrinsic magnetic moments change direction. An abrupt change in the magnetic properties of materials occurs when the magnetic phase changes.

For each interval of variation of x, we can approximate the Brillion function BJ(x) and then deduce the expression of the magnetic entropy.

  • For x << 1 (T >> Tc).

For this temperature range, we can write that:

$$B_{{\text{J}}} \left( x \right) = \frac{{x\left( {J + 1} \right)}}{3 J}$$
(11)

So, from Eqs. 4 and 12, we can write that:

$$\Delta S_{{\text{m}}} = \frac{{ - N\left( { g \mu_{{\text{B }}} } \right)^{2} \left( {J + 1} \right) J B^{2} }}{{6 KT^{2} }}$$
(12)

  • For x >> 1 (T << Tc).

The Brillouin function BJ(x) is:

$$B_{{\text{J}}} \left( x \right) \cong 1 - \frac{1}{J} e^{{ - \frac{\text x}{\text J}}}$$
(13)

And after all the calculations, we find:

$$\Delta S_{{\text{m}}} = \left( {\frac{{N g \mu_{{\text{B}}} B }}{ T } + k_{{\text{B}}} N} \right)\left( {e^{{\frac{{ - \text{g} \upmu_{{\text{B}}} \text{B}}}{{{\text{k}}_{{\text{B}}} \text T}}}} - 1} \right)$$
(14)

  • For T \(\cong\) Tc

Oesterreicher and Parker [29, 35] give the following equation for ∆Sm for a ferromagnetic material whose temperature is close to its Tc.

$$\Delta S_{{\text{m}}} = - 1.07Nk_{{\text{B}}} \left( {\frac{{g\mu_{{\text{B}}} JB}}{{k_{{\text{B}}} T_{{\text{c}}} }}} \right)^{2/3}$$
(15)

  • For T > Tc

Curie–Weiss law [7] gives the following expression:

$$\frac{1}{{\chi_{{\text{m}}} }} = \frac{{T - T_{{\text{c}}} }}{C}$$
(16)

with \(\chi_{{\text{m}}}\) is the magnetic susceptibility, and C is the Curie constant:

$$C = \frac{{Ng^{2} \mu_{{\text{B}}}^{2} \mu_{0} J\left( {J + 1} \right)}}{{3k_{{\text{B}}} }}$$
(17)

Indeed,

$$M = \chi_{{\text{m}}} \frac{B}{{\mu_{0} }}$$
(18)

So,

$$M = \frac{{Ng^{2} \mu_{{\text{B}}}^{2} J\left( {J + 1} \right)}}{{3k_{{\text{B}}} \left( {T - T_{{\text{c}}} } \right)}}B$$
(19)

The variation of magnetization with temperature at constant B is:

$$\frac{\text{d}M}{{\text{d}T}} = - \frac{{Ng^{2} \mu_{{\text{B}}}^{2} J\left( {J + 1} \right)}}{{3k_{{\text{B}}} \left( {T - T_{{\text{c}}} } \right)^{2} }}B$$
(20)

Therefore,

$$\Delta S_{{\text{m}}} = - \mathop \smallint \limits_{0}^{B} \frac{{Ng^{2} \mu_{{\text{B}}}^{2} J\left( {J + 1} \right)}}{{3k_{{\text{B}}} \left( {T - T_{{\text{c}}} } \right)^{2} }}B\text{d}B$$
(21)

After integration, we find:

$$\Delta S_{{\text{m}}} = - \frac{{Ng^{2} \mu_{{\text{B}}}^{2} J\left( {J + 1} \right)B^{2} }}{{6k_{{\text{B}}} \left( {T - T_{{\text{c}}} } \right)^{2} }}$$
(22)

Theoretical modeling of the magnetocaloric effect

The total differential of entropy is also exact since it is a state function, so:

$$\frac{{C_{{\text{P}}} }}{T} = \left( {\frac{\partial S}{{\partial T}}} \right)_{{\text{B}}}$$
(23)

For an adiabatic transformation, we can write:

$$\text{d}T = - \frac{T}{{C_{{\text{p}}} }}\left( {\frac{\partial S}{{\partial B}}} \right)_{{\text{T}}} \text{d}B$$
(24)

Under such conditions, the magnetocaloric effect for an adiabatic transformation (\(\Delta T_{{{\text{ad}}}} \left( {T,B} \right)\)) can be calculated using the formula below:

$$\Delta T_{{{\text{ad}}}} \left( {T,B} \right) = - \frac{{T\Delta S_{{\text{m}}} \left( {T,B} \right)}}{{C_{{\text{p}}} }}$$
(25)

Consequently, it is sufficient to determine the magnetic entropy to deduce \(\Delta T_{{{\text{ad}}}} \left( {T,B} \right)\).

Theoretical modeling of the Curie temperature

The material to be used is active at its Tc. For example, when designing a magnetic refrigeration system, we need to choose a material with a Tc close to its operating temperature. Considering a Gd alloy Rα(1−α), where α is the concentration of Gd, we can write the following relationships [37,38,39,40,41]:

$$m_{{{\text{Gd}}_{\upalpha } {\text{R}}_{{\left( {1 - \upalpha } \right)}} }} = \alpha m_{{{\text{Gd}}}} + \left( {1 - \alpha } \right)m_{{\text{R}}}$$
(26)
$$\mu_{{{\text{Gd}}_{\upalpha } {\text{R}}_{{\left( {1 - \upalpha } \right)}} }}^{2} = \alpha \mu_{{{\text{Gd}}}}^{2} + \left( {1 - \alpha } \right)\mu_{{\text{R}}}^{2}$$
(27)

m is the molecular mass.

The effective magnetic moment µ can be calculated by:

$$\mu_{{}} = g\sqrt {J\left( {J + 1} \right)}$$
(28)

Furthermore, the Tc of alloys obeys the empirical law established by P. Gilles Gennes [34] evaluated as:

$$G_{{{\text{Gd}}_{\upalpha } {\text{R}}_{{\left( {1 - \upalpha } \right)}} }} = \alpha G_{{{\text{Gd}}}} + \left( {1 - \alpha } \right)G_{{\text{R}}}$$
(29)
$$G = \left( {g - 1} \right)^{2} J\left( {J + 1} \right)$$
(30)

where G is the de Gennes factor

The Landé g-factor \({\text{g}}_{{{\text{Gd}}_{\upalpha } {\text{R}}_{{\left( {1 - \upalpha } \right)}} }}\) and the total angular momentum \({\text{J}}_{{{\text{Gd}}_{\upalpha } {\text{R}}_{{\left( {1 - \upalpha } \right)}} }}\) are given by:

$$g_{{{\text{Gd}}_{\upalpha } {\text{R}}_{{\left( {1 - \upalpha } \right)}} }} = \frac{{\mu_{{{\text{Gd}}_{\upalpha } {\text{R}}_{{\left( {1 - \upalpha } \right)}} }} }}{{\mu_{{{\text{Gd}}_{\upalpha } {\text{R}}_{{\left( {1 - \upalpha } \right)}} }} - \sqrt {G_{{{\text{Gd}}_{\upalpha } {\text{R}}_{{\left( {1 - \upalpha } \right)}} }} } }}$$
(31)
$$J_{{{\text{G}}_{{{\text{Gd}}_{\upalpha } {\text{R}}_{{\left( {1 - \upalpha } \right)}} }} }} = \frac{1}{2}\left( {\sqrt {1 + \left( {\frac{{2\mu_{{{\text{Gd}}_{\upalpha } {\text{R}}_{{\left( {1 - \upalpha } \right)}} }} }}{{g_{{{\text{Gd}}_{\upalpha } {\text{R}}_{{\left( {1 - \upalpha } \right)}} }} }}} \right)^{2} } - 1} \right)$$
(32)

Knowing that the Tc is calculated by the following relationship [34]:

$$Tc = 46\left( {G_{{{\text{Gd}}_{\upalpha } {\text{R}}_{{\left( {1 - \upalpha } \right)}} }} } \right)^{\frac{2}{3}}$$
(33)

Validation and discussion

Magnetic entropy

To validate the models, we compared the values found by these models with experimental values from the literature. Figure 4 compares theoretical and experimental values of magnetic entropy as a function of temperature for gadolinium. Experimental values are taken from [35,36,37,38,39]. The figure shows that the variations between experimental and theoretical values are in good agreement only in the paramagnetic phase. Coincidence is not good in the ferromagnetic state, and the difference increases with a growing magnetic field. At Tc, the coincidence between theoretical and experimental values is high. This finding can be explained by the fact that a paramagnetic material has no spontaneous magnetization; However, under the effect of an external magnetic field, it acquires a magnetization in the same direction as the applied magnetic field. For temperatures T << Tc, the theoretical values do not coincide with the experimental ones. The non-coincidence can be explained by the fact that temperatures between 200 and 280 K are not much lower than Tc, and the model is no longer applicable in this temperature range. For T ≥ Tc, the relative error between model-calculated and experimental values is 15% for B = 1T, 12% for B = 2T, 10% for B = 3T, and 9% for B = 4T.

Fig. 4
figure 4

Comparison of theoretical and experimental values of magnetic entropy as a function of temperature (gadolinium)

Full size image

Figure 5 compares theoretical and experimental values of magnetic entropy [35] as a function of temperature for GdAl2.

Fig. 5
figure 5

Comparison of theoretical and experimental values of magnetic entropy as a function of temperature for GdAl2

Full size image

The same applies to GdAl2 and Gd at temperatures above the Tc; Thus, the model is valid. But for T = Tc, there is a difference between the theoretical model and the experimental values, in contrast to the results found with Gd, Fig. 4. This difference increases with the applied magnetic field. We can therefore say that the Oesterreicher equation is valid if the temperature Tc of the material is close to room temperature and the magnetic field is not very high. For T < Tc, there is no coincidence. In the molecular field model, material magnetization can be described using the Brillouin function, which is no longer applicable for ferromagnetic states. In the remainder of this work, we focus on temperatures above Tc. We applied the model for the alloys Gd0.7Tb0.3 and Gd0.87Dy0.13. The results of the calculations are shown in Figs. 6 and 7. The curves are limited to the models with T ≥ Tc. We note that the theoretical models fit the experimental ones [40, 41]. Thus, we found that the models are equally applicable for Gd0.7Tb0.3 and Gd0.87 Dy0.13.

Fig. 6
figure 6

Comparison of theoretical and experimental values of magnetic entropy as a function of temperature for Gd0.7Tb0.3

Full size image
Fig. 7
figure 7

Comparison of theoretical and experimental values of magnetic entropy as a function of temperature for Gd0.87 Dy0.13

Full size image

Five magnetic entropy expressions are determined: for T << Tc, T < Tc, T ≅ Tc, T > Tc, and T >> Tc. Comparison with experimental values has shown that three models are valid for T << Tc, T > Tc, and T >> Tc. For temperatures such as T < Tc, we verified that the semi-empirical method was the most suitable [42,43,44]. Moreover, for temperatures such as T ≅ Tc, theoretical modeling is the most suitable [28, 35]. Table 1 lists the established magnetic entropy models.

Table 1 Magnetic entropy variation expressions
Full size table

Magnetocaloric effect

According to Eq. 25, we can deduce the expression for the magnetocaloric effect (∆Tad). The comparison between theoretical and experimental values of the magnetocaloric effect [39] as a function of temperature for T ≥ Tc for gadolinium is depicted in Fig. 8. Note the agreement of the model with the experimental values for this temperature range.

Fig. 8
figure 8

Comparison between theoretical and experimental values of the magnetocaloric effect as a function of temperature for T ≥ Tc for gadolinium

Full size image

Table 2 lists the established magnetocaloric effect models for each temperature range.

Table 2 Expressions of magnetocaloric effect
Full size table

Having shown that the theoretical model is valid for temperatures equal to or higher than the material’s Tc, we can apply it to determine a material's Tc and magnetocaloric effect.

Exploitation of validated models

Curie temperature modeling

By exploiting the theoretical model, the Tc can be determined as a function of the concentration α of gadolinium (Figs. 9 and 10).

Fig. 9
figure 9

Variation of Tc as a function of the gadolinium concentration in the alloys GdαTb(1−α)

Full size image
Fig. 10
figure 10

Variation of Tc as a function of gadolinium concentration in alloys GdαDy(1−α)

Full size image

Smoothing the curve gives us a model of Tc as a function of the α concentration of gadolinium as follows:

  • For GdαTb(1−α) (B = 1T):

    $$Tc\left( \alpha \right) = 68.40\alpha + 221.29 \left( {R^{2} = 0.99} \right)$$
    (34)

  • For GdαDy(1−α) (B = 1T):

    $$Tc\left( \alpha \right) = 121.21\alpha + 170.06 \left( {R^{2} = 0.99} \right)$$
    (35)

Modeling of the maximum magnetocaloric effect

When sizing a regenerator of a magnetic refrigeration system, a material is chosen such that its magnetocaloric effect is maximal. Therefore, using the previous theoretical model, we can determine gadolinium concentration α in GdαR(1−α) alloy to have a desired magnetocaloric effect. The magnetocaloric effect at the material’s Tc \(\left( {\Delta T_{{{\text{ad}}}} } \right)_{\max }\) as a function of gadolinium concentration α in GdαTb(1−α) alloy and \(\left( {\Delta T_{{{\text{ad}}}} } \right)_{\max }\) as a function of gadolinium α concentration in Gdα Dy(1−α) alloys are shown in Figs. 11 and 12, respectively. Smoothing the curve gives us two models of \(\left( {\Delta T_{{{\text{ad}}}} } \right)_{\max }\) as a function of the concentration α of gadolinium as follows:

  • For Gdα Tb(1−α) (B = 1T):

    $$\left( {\Delta T_{{{\text{ad}}}} } \right)_{\max } = 96.85\alpha^{5} - 248.40\alpha^{4} + 214.81\alpha^{3} - 68.15\alpha^{2} + 5.58\alpha + 3.42 (R^{2} = 0.92)$$
    (36)

  • For Gdα Dy(1−α) (B = 1T):

    $$\left( {\Delta T_{{{\text{ad}}}} } \right)_{\max } = 1.42\alpha^{2} - 1.99\alpha + 4.65\quad \left( {R^{2} = 0.97} \right)$$
    (37)
Fig. 11
figure 11

Variation of \(\left( {\Delta T_{{{\text{ad}}}} } \right)_{\max }\) as a function of gadolinium concentration in GdαTb(1−α) alloy (B = 1T)

Full size image
Fig. 12
figure 12

Variation of \(\left( {\Delta T_{{{\text{ad}}}} } \right)_{\max }\) as a function of gadolinium concentration in GdαDy(1−α) alloy (B = 1T)

Full size image

Using models to select an active material

Magnetic refrigeration is based on the magnetocaloric effect, an intrinsic property of magnetic materials, which results in the heating or cooling of the material when it is adiabatically magnetized or demagnetized. This phenomenon is maximal when the temperature of the material is equal to its Tc. Consequently, for the cooling system to be effective, the material must be chosen so that its Tc is close to the operating temperature (so that the magnetocaloric effect is at its maximum and the amount of heat transferred is significant). The flow chart in Fig. 13 gives a method for the correct selection of the regenerator’s magnetic material to be used in the refrigeration system. This method is not applicable to Gdα R(1−α) but is general for all materials at temperatures close to their Tc. This method enables the selection of the material to be used for the regenerator in a magnetic refrigeration system.

Fig. 13
figure 13

Method for selecting magnetic materials

Full size image

Sizing a multilayer magnetic regenerator

The principle of magnetic refrigeration is based on the magnetocaloric effect. The material is only active if its temperature is equal to the Curie transition temperature (Fig. 1). According to previous numerical studies, the regenerator temperature is not equal to the material temperature Tc, but the profile is linear (Fig. 3). Accordingly, only one layer of the magnetic regenerator is active, and the rest of the regenerator, where temperatures are different at Tc, is not active. Therefore, to improve the efficiency of the magnetic refrigerator, we use a multi-layer regenerator (several layers of different materials) and each layer i is at the Tci of the material of which it is composed.

The flowchart in Fig. 14 details the various steps involved in sizing a multi-layer regenerator used to cool any fluid.

Fig. 14
figure 14

Method for sizing a multilayer magnetic regenerator

Full size image

Conclusions

In this work, we proposed a theoretical model of magnetic entropy for each temperature range, as well as for the magnetocaloric effect. Comparisons with the experimental values were carried out to investigate the validity of these models. The conclusion drawn is that these theoretical approaches are valid for paramagnetic states. Oesterreicher's expression for the magnetic entropy near Tc is valid when Tc is close to room temperature and a relatively low magnetic field. The most useful and validated models for an engineer to dimension a magnetic refrigeration system are the expressions for the magnetocaloric effect of a material:

  • For T = Tc: \(\Delta T_{{{\text{ad}}}} = \frac{T}{{C_{{\text{B}}} }}1.07Nk_{{\text{B}}} \left( {\frac{{g\mu_{{\text{B}}} JB}}{{k_{{\text{B}}} T_{{\text{c}}} }}} \right)^{2/3}\)

  • For T > Tc: \(\Delta T_{{{\text{ad}}}} = \frac{T}{{C_{{\text{B}}} }}\frac{{Ng^{2} \mu_{{\text{B}}}^{2} J\left( {J + 1} \right) B^{2} }}{{6k_{{\text{B}}} \left( {T - T_{{\text{c}}} } \right)^{2} }}\)

The Tc as a function of gadolinium concentration α in a GdαR(1−α) is given by:

  • For GdαTb(1−α) (B = 1T): \(T_{{\text{c}}} \left( \alpha \right) = 68.40\alpha + 221.29\)

  • For Gdα Dy(1−α) (B = 1T):\(T_{{\text{c}}} \left( \alpha \right) = 121.21\alpha + 170.06\)

These models facilitate the sizing of regenerators for magnetic refrigeration systems. The flowchart of a calculation code based on a new method for choosing the appropriate regenerator material for a magnetic refrigeration system is presented. Another flowchart of an original method and its steps for sizing a multilayer magnetic regenerator is detailed.

In future work, we will choose the heat transfer fluid suitable for a well-defined application.